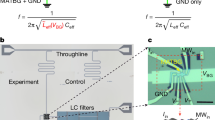
Abstract
Magic-Angle Twisted Bilayer Graphene (MATBG) shows a wide range of correlated phases which are electrostatically tunable. Despite a growing knowledge of the material, there is yet no consensus on the microscopic mechanisms driving its superconducting phase. A major obstacle to progress in this direction is that key thermodynamic properties, such as specific heat, electron-phonon coupling and superfluid stiffness, are challenging to measure due to the 2D nature of the material and its relatively low energy scales. Here, we use a gate-defined, radio frequency-biased, Josephson junction to probe the electronic dynamics of MATBG. We demonstrate evidence for two processes determining the low-frequency dynamics across the phase diagram: thermalization of electronic quasiparticles through phonon scattering and inductive response of the superconducting condensate. A phenomenological approach allows us to relate the experimentally observed dynamics to several thermodynamic properties of MATBG, including electron-phonon coupling and superfluid stiffness. Our findings support anisotropic or nodal superconductivity in MATBG and demonstrate a broadly applicable method for studying properties of 2D materials with out-of-equilibrium nanodevice dynamics.
Similar content being viewed by others
Introduction
Magic-angle twisted bilayer graphene (MATBG) is one of the most prominent examples of a two-dimensional strongly correlated material. It consists of two layers of graphene twisted with respect to each other by an angle of 1.1 degrees. In reciprocal space, this results in the hybridization of the Dirac cones of the different layers, leading to the so-called flat bands. When the Fermi energy of the material is tuned, through field-effect, to such bands, electron-electron correlations determine the electronic state of the material. This results in a phase diagram1,2 that has drawn considerable attention due to the presence of insulating, topological and superconducting phases3. The combination of superconductivity and field-effect tunability make it a promising platform for versatile superconducting electronics.
Despite these remarkable discoveries, several questions remain open about the nature of the superconducting state and even less is understood about what is the driving mechanism behind it. The most central and pressing issues include whether the superconducting mechanism of MATBG is electronic or phonon-driven4,5,6,7 and whether its superconducting gap is nodal or not8,9. Furthermore, the electron-phonon coupling has been suggested as the origin of the observed (putatively) universal linear-in-T resistance4,10. Characterizing the electron-phonon coupling and the anisotropy of the superconducting gap is the first step towards answering these questions. However, the 2D nature of MATBG, the small moiré Brillouin zone, and the relatively low energy scales make the use of many standard techniques for investigating bulk materials, such as calorimetry, angle-resolved photoemission spectroscopy (ARPES) or neutron scattering, challenging or impossible. Similar concerns are relevant for all 2D superconductors, where in many cases the mechanism and character of superconductivity also remain undetermined11,12,13,14.
Superconducting mesoscopic devices have proven to be a useful characterization tool of the material they are built of15,16,17. In particular, Josephson junctions (JJs) have been used as a probe of electronic thermalization rates17, and the superfluid density, through characterizing the kinetic inductance in thin-film devices16. In the case of MATBG, superconducting devices have already proven instrumental for probing the charge of the Cooper pairs18,19, the long-range coherence of the superconducting condensate19 and its orbital magnetic properties20.
Here, we use a gate-defined Josephson junction (JJ) in MATBG18,20,21 to extract electron-phonon coupling, thermodynamic, and superfluid properties of MATBG across its phase diagram. Biasing the junction with a combination of DC and AC currents we probe the dynamics of both the electronic quasiparticles and the superfluid of MATBG. We show that the measured timescales governing the junction’s transition between resistive and superconducting states are directly related to the microscopic properties of the material, such as electronic cooling power due to phonons, specific heat, and superfluid density. The gate-tunability of the device allows us to probe these quantities across the density-tuned phase diagram of MATBG, for chemical potential both within and outside the flat bands. These measurements allow to constrain the electron-phonon coupling of MATBG, and the current bias dependence of the superfluid density is incompatible with isotropic pairing.
Our experimental setup and theoretical models can be applied to other two-dimensional materials, establishing a tool for the study of two-dimensional superconductors at cryogenic temperatures. They advance the state of the art for MATBG, directly probing the superfluid density, rather than spectroscopic8 properties of the superconducting state. They also allow for the characterization of the thermal relaxation across the whole phase diagram of MATBG and at cryogenic temperatures. Previous studies either accessed only parts of the phase diagram 22 or were limited to higher temperatures23, where correlation effects are suppressed1,2.
Results
Overview
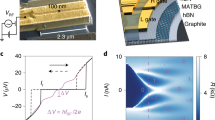
Our device is a JJ electrostatically defined in MATBG, with a twist angle of 1.06∘ ± 0.04∘, also studied in reference18 (Fig. 1a). The global carrier density n, tuned by the back gate, is set to n = −1.73 × 10−12 cm−2, at which the bulk has its highest critical current, 250 nA (See SI). Two layers of top gates, separated by a layer of Al2O3, tune the local density in the central region, allowing us to fine-tune the details of the junction.
a Schematics of the device. The device is depicted by a cross section schematics. The vertical red dashed lines represent the central (C) region highlighted in (b). b Top-view simplified schematics with the gold contacts on the side, connected by a stripe of magic-angle twisted bilayer graphene (MATBG). The central region, of length 100 nm, is highlighted. The leads are superconducting (SC). c I/V characteristic of the junction at a density of −2.8 × 1012 cm−2. In blue, solid line, a trace for increasing DC bias is shown. The dashed line represents the trace for decreasing bias. The green line is an extrapolation of the resistive part of the characteristic at 0 voltage. The green arrow highlights what is defined as excess current. d Switching (blue), retrapping (blue, dashed) and excess (green) currents as a function of density in the central region. The colors on the x-axis correspond to the filling of the band structure schematics shown in the inset. The upper part indicates whether the I/V characteristic shows a junction-like or bulk superconductor-like behavior. The black star, circle and square indicate, respectively, the densities at which is taken the data shown in (e, c, f). e I/V traces of the junction for AC bias of increasing frequency and fixed amplitude (red arrow) as a function of DC bias (horizontal axis). Solid lines show positive bias directions while dashed ones show negative directions. Curves are offset vertically for readability. f I/V traces at bias AC amplitude 1.4 nA and frequencies of 0.1 MHz and 20 MHz when the sample is tuned to all-bulk configuration see panel (d).
For each value of electron density in the central region (Fig. 1b) we analyze the current-voltage (I/V) characteristic. For densities in the central region close to nj = −2 we observe a gradual onset of resistance above a critical current value, consistent with bulk superconductivity (see also discussion of Fig. 1f below). For all other densities, we universally observe a hysteretic I/V trace with two characteristic voltage jumps ΔV, as shown in Fig. 1c. The two jumps correspond to switching from the superconducting to the resistive state (increasing current bias, blue line) and retrapping back (decreasing current bias, blue dashed). Together with Shapiro step measurements18 this indicates the formation of a weak superconducting link between the left and right parts of the device, where the weak link region can switch between resistive and superconducting states. From the band structure of MATBG2 (see inset of Fig. 1(d), for a schematic), the weak link region is expected to be metallic except for a narrow range of voltages placing the chemical potential into the gap between the flat and dispersive bands. Such assessment is consistent with the observation of a positive excess current, Iex,24,25 in the resistive state of a large portion of the phase diagram (green curve in Fig. 1d). In analogy to conventional superconductors17, the dynamic response of such metallic weak links should give access to the dynamics of the electronic quasiparticles and the superconducting condensate in MATBG. We probe the dynamics of our weak links by adding a small AC current component to the DC current flowing through the junction. Sweeping the frequency across three orders of magnitude (0.1–100 MHz), we focus on the changes in the I/V characteristics, as shown in Fig. 1e. At low frequencies, the AC drive brings the two hysteresis branches closer together, which can be understood as follows. The abrupt character of switching and retrapping with DC bias suggests that the junction will undergo a change whenever the total current IDC + IRF(t) reaches the critical value for switching (Isw) or retrapping (\({I}_{{{\rm{re}}}}\)). Consequently, one expects the switching to occur prematurely at Isw − IRF, and the retrapping to occur at a higher DC bias, \({I}_{{{\rm{re}}}}+{I}_{RF}\), reducing the size of the hysteresis loop.
For increasing frequency, the effect of AC bias gradually disappears (Fig. 1e), with a different rate for switching and retrapping. This indicates that both processes, in fact, do not occur instantaneously and are characterized each by a certain rate, which we denote as Γre and Γsw. We note that under switching (retrapping) rate we mean the characteristic scale for the switching (retrapping) current dependence on AC bias frequency, with a precise definition of that scale given below. At highest frequencies, the AC drive effect is absent, indicating that neither switching nor retrapping processes are fast enough to occur over one AC drive period. The switching and retrapping rates that can be extracted from Fig. 1e reflect the properties of superconducting MATBG. We now turn to their physical interpretation.
Modeling the weak link
We can first rule out switching and retrapping driven only by the dynamics of the superconducting phase difference across the junction, exemplified by, e.g., the Resistively and Capacitively Shunted Junction (RCSJ) model24. In that case, the characteristic frequency is fixed by the Josephson relation to 2eΔV/ℏ. For our weak links it is of the order of 10 GHz, several orders of magnitude larger than the frequencies used in our experiments. The RCSJ model also predicts the switching rate to be smaller than the retrapping one, inconsistent with experimental observations (see additional discussion in Supplementary Information). We therefore conclude that our experimental observations require a mechanism beyond the RCSJ model to explain the switching and retrapping charateristics.
Such an alternative mechanism, for both the retrapping and the hysteresis in metallic weak links is the heating of the electrons in the junction, followed by their thermalization17,26. In this case the retrapping branch at I < Isw is characterized by a higher temperature than the switching one due to the Joule heating in the resistive state (Fig. 2a, b). This overheating reduces the weak link critical current for the retrapping branch, leading to a hysteresis. Most importantly, retrapping back into the superconducting state requires the electronic temperature to equilibrate to base temperature, a process, depicted in Fig. 2c, that has been directly demonstrated in superconductor-normal metal-superconductor junctions17.
a Equivalent scheme of the MATBG junction for densities inside the lower flat band: the weak-link region modelled as a resistively shunted junction is coupled in series with the kinetic inductance of the leads. The superconducting regions (blue and red) are further shunted by normal regions (purple). b Illustration of switching and retrapping mechanism and hysteresis origin in MATBG junctions. \({I}_{{{\rm{re}}}}\) and Isw represent, respectively, the retrapping and switching currents. The retrapping branch of IV characteristic (red) is characterized by an increased electronic temperature Tr due to Joule heating, suppressing the critical current. Retrapping into the superconducting state requires cooling the electrons (c) to base temperature characterized by a rate dependent on electronic cooling power Gth. Switching rate (blue), on the other hand, is only limited by the shunting kinetic inductance of the bulk MATBG (a, d). c Electronic thermal relaxation in MATBG occurs via coupling to acoustic phonons. Two electronic quasiparticles in the junction release their thermal energy to the phonon bath and become cold enough to mediate Josephson coupling. This coupling is represented by an orange dashed line. Γre represents the thermalization rate. d Due to their inertia, Cooper pairs in a thin superconductor (blue region) prevent the transmission of RF signals at high frequencies. Instead, the AC current at frequencies above \({\omega }_{L}=\frac{{R}_{bulk}}{{L}_{{{\rm{leads}}}}}\) is rerouted through non-superconducting regions of the sample (purple region) and does not affect the junction. Z represents the impedance seen by the signal, Rbulk the resistance of the bulk and Lleads the inductance of the leads.
While there are several mechanisms for energy dissipation in graphene, at low temperatures the dominant one is the coupling between electrons and acoustic phonons. In particular, thermalization can occur via diffusion of hot electrons into the leads, emission of blackbody photons or interaction of electrons with acoustic phonons (as the optical ones are frozen out)27. The first mechanism is suppressed by the presence of a superconducting gap28 in the leads in our case, while the second one has been estimated to be negligible in MATBG29,30. This suggests that the dominant heat loss mechanism is via coupling to phonons, in agreement with conventional SNS junctions17,26.
The above mechanism on its own, however, still implies that switching occurs with the Josephson rate 2eΔV/ℏ, which is inconsistent with our observations, as detailed above. To understand the switching dynamics in our devices we now turn to the case without a central gate voltage, i.e., where the sample is homogeneously superconducting at the optimal density. We observe a frequency-dependent IV characteristic (Fig. 1f), despite the absence of a weak link. Note that there is no hysteresis, ruling out overheating as its origin.
In addition to these observations, it has been shown that a supercurrent can flow in MATBG in narrow superconducting paths separated by normal regions31. The normal region thus forms a resistive shunt Rbulk coupled in parallel to the superconducting regions (purple shaded path in Fig. 2a). At a non-zero frequency ω, the superfluid impedance is purely inductive due to the inertia of the Cooper pairs (blue shaded mechanism in Fig. 2d) and given by Zsc = jωLkin, with the kinetic inductance \({L}_{{{\rm{kin}}}}\propto \frac{{m}^{*}}{{n}_{{{\rm{s}}}}{e}^{2}}\), where m* is the effective mass, e the electron charge, and ns is the superfluid density. At frequencies larger than \(\frac{{R}_{{{\rm{bulk}}}}}{{L}_{{{\rm{kin}}}}}\), the impedance of the superconducting branch becomes higher than the resistance of the normal bulk and the AC current flows through the non-superconducting regions (purple shaded mechanism in Fig. 2d). Intriguingly, Lkin in MATBG is expected to be large19 due to two unique properties: extremely low electron densities, and high effective mass1. This explains our observation of a rather low characteristic switching rate in Fig. 1f. The same mechanism applies for MATBG weak links - the kinetic inductance of bulk MATBG is then coupled in series to the junction (Fig. 2a).
Using the ideas outlined above, we construct a model to describe the non-equilibrium dynamics of the Josephson junction. Importantly, this model allows us to relate the observed switching and retrapping rates, Γsw and Γre, to the microscopic and thermodynamic properties of MATBG. The dynamics of the current-biased junction are described by:
We highlight that this description has not been previously used to analyze either the MATBG18,19,21 or conventional17 Josephson junctions; in what follows below we show that it allows to describe the Josephson junction data in a self-contained way without invoking results of other measurements29,30,31.
Equation (1) describes a Josephson junction with a phase difference φ, a temperature-dependent critical current IJ(T), and a fixed excess current value Iex shunted by resistance RJ (Fig. 2(a), dashed box). For results in the main text we assume RJ ≪ Rbulk, the general case is discussed in Supplementary Information. We note that the form of IJ(T) has not been determined experimentally; we assume that it is a decreasing function of temperature with a single characteristic scale TJ that can be estimated to be of the order 0.1 K based on the disappearance of interference in superconducting quantum interference devices (SQUIDs)19. In the main text, we focus on an empirical model \({I}_{{{\rm{J}}}}={I}_{{{\rm{J}}}}(0)\sqrt{1-T/{T}_{{{\rm{J}}}}}\cdot \theta (1-T/{T}_{{{\rm{J}}}})\) that correctly captures the high-frequency asymptotic behavior of the retrapping current; we provide a discussion of different models and their general properties in the Supplementary Information.
Equation (2) describes the evolution of the electronic temperature T with respect to the base temperature. The left-hand side represents the total power dissipated in the link, Cel being the electronic heat capacity. On the right-hand side, the first term corresponds to Joule heating, while the second one is the electronic heat loss (Gth) attributed, as discussed above, to electron-phonon interactions. The processes relevant for the description of the Josephson effect occur at T ≈ TJ (see Supplementary Information), such that the value of the thermal conductivity Gth can be approximated by its value at T = TJ. The final equation describes the shunting of the junction by the resistive quasiparticles of bulk MATBG (Fig. 2 (a,d)). The current Isc(t) is the full external current driven through the weak link.
Remarkably, we find that the model defined by Eq. (1)-(3) captures all of the behaviors observed in the experiment. As an example, we consider a highly nonlinear regime where the RF amplitude is larger than the hysteresis \({I}_{{{\rm{sw}}}}-{I}_{{{\rm{re}}}}\). For a range of DC bias values the junction spends part of the AC period in the resistive regime and part of it being superconducting, resulting in a double step in voltage, as shown in Fig. 3a. Such voltage values are the average between the resistive and superconducting voltages weighted by the percentage of the time spent by the junction in each regime. Fig. 3d shows a simulated trace in the same regime, demonstrating remarkable agreement between the model and the experiment. As we increase the frequency of the current bias across the junction we recover the regular hysteresis (Fig. 3a, b, black line). The model captures the evolution of the I/V traces as the bias frequency increases, as is shown in Fig. 3e. Even finer details of the experimental data, discussed in the Supplementary Information are captured by the model. These comparisons confirm that our model accurately describes the dynamics of our junction.
a I/V traces of the junction at bias frequencies of 0.1 MHz (red) and 100 MHz (black) in the regime where the effective AC amplitude is higher than the hysteresis. \(\Delta {I}_{{{\rm{re}}}}\) and ΔIsw highlight the change in retrapping and switching currents, respectively, between the two bias frequencies. b I/V traces of the junction at bias frequencies of 8 MHz (red) and 100 MHz (black) in the regime where the effective AC amplitude is higher than the hysteresis. The mismatch in retrapping current between the red and black curves is probably due to a charge jump (note it is of the order of a few pA). c Switching and retrapping currents as a function of AC bias frequency. d–f Numerical simulations of our device in the same regime as the data shown in (a–c). The grey dashed line in (c) is a fit to the functional forms provided in equations (1)–(3).
To extract the retrapping and switching rates, Γre and Γsw, for a given density from the experimental data, we fit the evolution of the retrapping and switching currents as a function of bias frequency. An analysis of the data, discussed in the Supplementary Information, demonstrates that both currents asymptotically approach a constant high-frequency value as 1/ω. To fit the results at all frequencies, we use the following functions: \({I}_{{{\rm{sw}}}}(\omega )={I}_{{{\rm{sw}}},\infty }-{I}_{RF}{\Gamma}_{sw}/\sqrt{{\Gamma}_{sw}^{2}+{\omega }^{2}}\) and \({I}_{{{\rm{re}}}}(\omega )={I}_{{{\rm{re}}},\infty }+{I}_{RF}{\Gamma} _{re}/\sqrt{{\Gamma}_{re}^{2}+{\omega }^{2}}\). That allows to characterize the corresponding rates (see Fig. 3(c), gray lines). The model described in Eqs. (1),(2),(3), reproduces correctly the asymptotic behavior of the switching current, while for the retrapping current the result depends on the particular form of IJ(T) (see Supplementary Information). For a fixed density in the junction, we extract the switching and retrapping currents for all frequencies and fit the results. In the example shown in Fig. 3(c), for a density of − 4.5 × 1012cm−2, we extract Γre = 0.52 MHz and Γsw = 2.75 MHz. Therefore, the weak-link dynamics of our junction gives us access to the quasiparticle thermalization rate and kinetic inductance of MATBG (Fig. 2c, d).
Physical interpretation of the frequency dependence
We now provide a physical interpretation of the rates, Γsw and Γre that allows us to connect them to the properties of MATBG. We begin with the switching rate Γsw. From Eq. (3) we identify the switching rate as Γsw = Rbulk/Lkin ∝ ns (see additional discussion in Supplementary Information). Assuming that the resistance of normal regions Rbulk does not strongly depend on T or bias strength, Γsw−1 ∝ Lkin, which allows to probe the superfluid stiffness of MATBG.
Before discussing the thermalization rate of the weak link, we note that for ω ≫ Γsw the AC part of the current does not reach the junction at all: Isc ≈ IDC. Thus, for Γre > Γsw, the kinetic inductance would set the rate for both switching and retrapping. However, as shown in Fig. 4, we have Γre strictly smaller than Γsw for all densities (note the different y-axis in Fig. 4a, c), confirming that we can interpret the former as a thermalization rate.
a Retrapping rate as a function of junction density. The region between vertical dashed lines represents the range of densities in which we have a bulk superconductor (SC). b Relative hysteresis as a function of junction density. We observe a peak at the charge neutrality point and another one at the band insulator between lower dispersive and flat bands. c Switching rate as a function of junction density. The red shaded areas highlight the regions in density where a transition between bands takes place. They correspond to the Charge Neutrality Point (CNP) and Band Insulator (BI).
Retrapping rate and thermalization
The equation governing thermalization in the device in Eq. (2) contains two implicit frequency scales: \(\gamma \equiv \frac{{G}_{{{\rm{th}}}}}{{C}_{{{\rm{el}}}}}\) and \(k\equiv \frac{{I}_{{{\rm{J}}}}^{2}{R}_{J}}{{C}_{{{\rm{el}}}}{T}_{{{\rm{J}}}}}\). Importantly, the hysteresis size for DC driving depends on their ratio γ/k (which is proportional to Gth, but independent of Cel), while the retrapping rate Γre depends on both, allowing in principle, to determine both scales.
These observations allow for a qualitative discussion of the results (Fig. 4(a,b)) across the MATBG phase diagram. The noticeable peaks in ΔI/Is, Fig. 4(b), occur near the band insulator (BI) and charge neutrality points (CNP) and indicate a suppressed thermal conductance Gth. This can be attributed to a lower density of states near these points compared to other concentrations, expected from previous experiments32,33 and theoretical analysis34. In contrast, Γre (Fig. 4(a)), which also depends on Cel (Fig. 4(a)) shows weaker features at these concentrations, indicating a simultaneous reduction of Gth and Cel, again consistent with a suppressed density of states. Remarkably, the minimum of Γre occurs for densities within the dispersive band. A potential explanation for this behavior is an increased resistance RJ due to the mismatch between flat-band electrons outside the junction and dispersive ones within it. Deeper into the dispersive band, this effect can be offset by an increased Gth.
The quantitative nature of Γre depends on the particular form of IJ(T); for the square-root model introduced above and γ/k < 1/2 we obtain an analytical result for the retrapping rate: \(\Gamma_{\mathrm{re}}=\frac{k\sin \frac{2\pi \gamma }{k}}{2\pi }\). Furthermore, the ratio between DC retrapping current and switching is \({I}_{{{\rm{re}}}}/{I}_{{{\rm{sw}}}}=\sqrt{\frac{\gamma }{k}}\) (see Supplementary Information). We stress that the observed Ir and Is are rather close to one another, which results in γ and k being effectively of the same order of magnitude. For larger values of γ the model predicts an 1/ω2 dependence of the retrapping current under AC bias; therefore the model should not be applicable for \({I}_{{{\rm{re}}}}/{I}_{{{\rm{sw}}}} \, > \, 1/\sqrt{2}\). However, in the absence of direct measurements of IJ(T), we will use this model to estimate Cel and Gth.
We observe, across the whole density range, three sets of values of Γre: 0.5 MHz, 1 MHz and 1.5 MHz, corresponding to the chemical potential of the link tuned to the dispersive band, lower flat band and upper flat band, respectively. The change in the hysteresis width, Fig. 4(b) is relatively smaller. Using the analytical formula given above, we can estimate for ΔI/Isw ≈ 0.5 that γ ≈ 0.8−2.3 MHz. Reference22, where laser-mediated heating of a MATBG sample allows for the extraction of the same quantity, reports a value of γ ≈ 2 MHz. The fact that such different methods for extracting the thermalization rate agree on the obtained value strengthens both of them as reliable characterization tools.
This result already provides an important insight into the low-temperature behavior of electron-phonon coupling in MATBG when contrasted with those at higher temperatures. In particular, the cooling rate has been found to be of the order of hundreds of GHz above 5 K with a very weak temperature dependence23, attributed to effective moiré umklapp scattering35 (that is related to folding of the acoustic phonons by the moiré lattice) explaining the linear-in-temperature resistivity4,10,35. The strong difference with our result at T ~ TJ ≈ 100 mK suggests a suppression of the cooling rate much stronger than linear-in-temperature. This result is consistent with electron-phonon scattering at 100 mK being in the Bloch-Gruneisen regime where umklapp scattering is suppressed35 and resistivity from electron-phonon scattering should follow a stronger power-law dependence on temperature36. This excludes electron-phonon scattering as the origin of linear-in-temperature resistance at low temperatures37.
In the case of superconductivity, the most relevant quantity when discussing electron-phonon coupling is the dimensionless coupling constant, which we note here λ. The temperature relaxation rate at low temperatures is related to the strength of the coupling to acoustic phonons38,39,40. While this coupling does not take the contribution of optical phonons into account, it is expected to be of the same order of magnitude as the full coupling constant38. To obtain an estimate we use a Dirac electron model4,39,40, motivated by the theoretical34 and experimental evidence32,33 for their presence in MATBG bands, in particular in the vicinity of CNP (consistent with the peak in ΔI/Is discussed above). One finds that \(\gamma=\frac{{G}_{{{\rm{th}}}}}{{C}_{{{\rm{el}}}}}=\lambda \frac{16{\pi }^{2}}{5}\frac{{({k}_{B}{T}_{el})}^{2}}{{\hslash }^{2}s{k}_{F}}\), where s is the acoustic phonon velocity. Using Tel ~ TJ ~ 0.1 K from the extinction temperature of SQUID oscillations19, s ≈ 20 km/sec (the value for single-layer graphene41 is expected to be close to that in MATBG42), \({k}_{F}=\sqrt{\pi n}\) for n ~ 1 × 10−12 cm−2 and γ ~ 1 MHz we obtain λ ~ 10−3. Several comments are in order regarding this estimate of λ. We begin by stressing this estimate may not be directly comparable to other transport measurements (e.g., resistivity) as our estimates of λ stem from the electron-phonon cooling rate. While the relation between the way electron-phonon coupling enters the cooling rate, the resistivity, and the superconducting pairing is established in the Dirac model4,39,40, it is yet to be determined (and may be different) in the MATBG bands. Moreover, the potential inhomogeneity of the twist angle across the sample may reduce the average thermal relaxation rate, since regions that are away from the magic angle are expected to have lower density of states and thus slower thermal relaxation. Additionally, the above estimate is assuming the system is in the Bloch-Gruneisen regime T ≪ cskF; it has been however demonstrated35,43 that the crossover to this regime may be quite different in MATBG than in single-layer graphene and, in particular, it occurs at much lower temperatures. In fact, the strong reduction of the thermal relaxation rate in our experiments with respect to the values at 5 K23 may present a first demonstration of this crossover occurring in MATBG. We note that this estimate assumes coupling to lowest-energy acoustic phonons only, and does not address optical or any other phonons that are frozen out at the experimental temperatures. Finally, the Dirac model should be applicable only around certain fillings; in our case, a signature of Dirac physics is observed near the CNP in enhanced ΔI/Is indicating less efficient heat relaxation due to lower density of states near a Dirac point.
We can further estimate Gth and Cel taking IJ − Iexc ~ 5 nA, ΔV ~ 20 μV from Fig. 3. The result is Gth ~ 250 fW/K and Cel ~ 5 × 1019 J/K. From the junction area and n ~ 1 × 1012 cm−2 one expects above 103 electrons, with the usual Sommerfeld expression \({C}_{{{\rm{el}}}}=\frac{{\pi }^{2}}{2}kN\frac{{k}_{B}T}{{E}_{F}} \sim 1{0}^{-19}\frac{{k}_{B}T}{{E}_{F}}\) J/K. In usual metals, \(\frac{{k}_{B}T}{{E}_{F}}\ll 1\), while in our case this implies \(\frac{{k}_{B}T}{{E}_{F}} \sim 1\), that may be related to large residual entropy of interacting states of MATBG44,45. Both Gth and Cel are much higher than those expected in monolayer graphene40, consistent with strongly suppressed bandwidth and electron velocities of MATBG \(G\propto {v}_{F}^{-2},C\propto {v}_{F}\). However, the \(\gamma=\frac{{G}_{{{\rm{th}}}}}{{C}_{{{\rm{el}}}}}\) we find in MATBG at T ≈ TJ are of the same order as those predicted for monolayer graphene40.
Switching rate and superfluid stiffness
We now discuss the switching rate Γsw (Fig. 4c), related to the superfluid stiffness in the bulk of our MATBG device. Importantly, the AC measurements are still performed at a finite DC bias, thus, our measurements reveal the superfluid density at a finite current bias, ns(IDC) ≈ ns(Isw). Since ns(Isw) is a decreasing function of current, the steep increase in Γsw at the edges of the lower flat band is explained by the decreasing critical current of the junction (Fig. 1 (d)). On the contrary, the decrease of Γsw for densities in the top flat and dispersive bands, is unexpected - at such low critical currents ns(Isw) ≈ ns(0) should be density-independent and large. We suggest that this observation can be explained by the kinetic inductance of proximity-induced superconductivity in the junction region. Being very weak, the proximity-induced superfluid has an extremely large kinetic inductance that is in parallel to the smaller one from the bulk TBG, effectively shunting it. Furthermore, since Γsw ∝ Rbulk, changes in the resistance with concentration can also affect its magnitude. In particular, this provides a plausible explanation of the peak of Γsw near CNP, where the normal-state resistance peaks.
Let us now return to the densities within the lower flat band, where Γsw is related to the superfluid density of bulk MATBG. The dependence of Γsw ∝ ns as a function of IDC, shown in Fig. 5, gives important information about the nature of the superconducting gap in MATBG. Current biasing a superconductor produces a Doppler shift46,47 of the quasiparticle bands in a superconductor, see inset of Fig. 5 (ΔE = vs × ℏk, where vs is the superfluid velocity and k the quasiparticle momentum). For an isotropic superconductor, depicted in the inset of Fig. 5, this does not affect the quasiparticle occupations until a critical value of bias current is reached. As a result, ns(I) dependence is highly nonlinear with an abrupt drop close to the critical current48. For a highly anisotropic or nodal superconductor, across its nodal axis in real space, the quasiparticle band structure presents cones instead of a gap in density (Fig. 5, inset). A small shift originating from a finite bias current, leads to a finite generation of quasiparticle pairs, thus reducing the superfluid density before breaking down the superconducting condensate. As Fig. 5 shows, the relation between superfluid density and bias current is linear in the case of MATBG in the range Idc ∈ [0.6Ic, 0.95Ic]. This result is inconsistent with the behavior expected of an isotropic superconducting gap, ruling in favor of a highly anisotropic or nodal pairing state in MATBG.
Inset, bottom left: Schematics of Bogoliubov-de Gennes quasiparticle band structure of a superconductor with isotropic gap. The solid straight line represents the Fermi energy at zero current bias. The dashed line represents the Fermi energy at a non-zero current bias. Inset, top right: Schematics of quasiparticle band structure of a superconductor with anisotropic gap. The red and blue areas represent respectively the hole and electron pockets that form at the band edges under a finite current bias.
Discussion
In conclusion, we have developed a method for characterizing electron dynamics in twisted bilayer graphene by combining electrostatic and radiofrequency current bias of an electrically-defined Josephson junction. This has resulted in a study of out-of-equilibrium dynamical properties of electrons at cryogenic temperatures in MATBG. Our results demonstrate the presence of two distinct characteristic timescales guiding the dynamics of electrons, attributed to the thermalization of electrons and the kinetic inductance of the superconducting condensate, respectively. A phenomenological model, capturing these processes, is found to describe the data well and allows to relate the measurement outcomes to the physical properties of the electrons in the material for a wide range of densities. In particular, we discuss the estimates for electron-phonon coupling (that may have bearing on theories of superconductivity4,5,6,7 or strange metal36,37), specific heat and superfluid density. The current bias dependence of the deduced superfluid stiffness points towards the superconducting gap of the material being anisotropic. The technique we developed in this work can be applied to a wide range of gate-tunable superconducting 2D materials, introducing a general way to access important thermodynamic quantities, such as specific heat and superfluid stiffness. In addition to being a valuable addition to experimental probes of 2D materials, we demonstrated a controllable driving of a correlated electronic system, opening the path to the realization of out of equilibrium states of electrons.
While writing this manuscript the authors became aware of two works where, by different experimental means, some of the quantities studied in this work are also probed49,50.
Methods
Fabrication details and measurement setup
To fabricate the device, we begin by assembling a so called ‘stack’ of two dimensional materials. Such flakes are exfoliated mechanically using a micro manipulator, polydimethylsiloxane/polycarbonate stamps, a moving stage and an optical microscope. The stack consists of a bottom layer of few-layer graphite, which is used as a global back-gate, 24 nm-thick hexagonal boron nitride (hBN), the magic angle graphene, and hBN again, this time with a thickness of 27 nm. The twisting and stacking are performed following the standard procedures of the field, with a cutting step of the graphene flake51. The graphene-cutting step is performed with a tungsten needle with a tip diameter of 2.5 μm. Once the stack is in place we move on to the lithography phase of the fabrication process. Gold contacts are defined by a combination of electron-beam lithography, reactive ion etching and electron-beam evaporation. We use chromium as adhesion layer for the gold (10/70 nm). Top gates are defined by electron-beam lithography and evaporation. The graphene is finally etched to define the mesa. A layer of aluminium oxide is deposited through atomic layer deposition. Finally, we define another layer of local gold gates with a chromium adhesion layer (10/110 nm). As a last remark, the device used for this work is the same one as the one presented in reference18.
In this work, there are however two modifications with respect to the setup of the aforementioned reference. The first one is that the AC bias is not sent to the central gate but to one of the leads, using a bias T to be able to send both AC and DC signals to the same contact. The other difference is that, because for the AC measurements we present in this study we need a higher degree of precision than for the ones presented in reference18, we must ensure that the AC amplitude reaching the device is neither frequency-dependent nor sample-resistance-dependent. The details of such procedure are given in the following section.
Radiofrequency biasing
When applying a radiofrequency bias to our junction two different aspects must be taken into account. The first one is the evolution of the amplitude as a function of its frequency. Indeed, having a frequency-dependent amplitude reaching our junction would make it impossible to disentangle such effects from the physical mechanisms taking place at the junction level. We performed simulations of our circuit using the software LTspice and obtain an evolution in amplitude of our radiofrequency bias reaching the junction of less than 5%, for frequencies ranging from 100 kHz to 100 MHz. We thus conclude that, in comparison to the experimental results, these effects can be neglected.
Because the junction changes its state during the acquisition of an I/V trace, we must also ensure that the change in resistance triggered by the RF biasing does not significantly affect the AC current flowing through the device. In order to achieve that, we place a 100 kΩ resistor in series between the RF feed line and the device. Like for the previous effect, this leads to a variation in AC amplitude reaching the device of the order of a few percents across the whole resistivity range of the device. We thus can also neglect this effect taking into account the precision of the claims made in our analysis. Supplementary Fig. 1 shows a schematics of the electronics set-up. We neglect in this schematics the capacitances from the MATBG to the gold or graphite gate electrodes because they are smaller than 30 fF18. They thus present, at the frequencies at which we bias our sample (up to 100 MHz), an impedance orders of magnitude higher than any other impedance in the set-up.
Data availability
The data that support the findings of this study, together with the code for plotting the figures, is available online through the ETH Research Collection at https://doi.org/10.3929/ethz-b-000722186.
References
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653–657 (2019).
Wu, F., Hwang, E. & Das Sarma, S. Phonon-induced giant linear-in-t resistivity in magic angle twisted bilayer graphene: Ordinary strangeness and exotic superconductivity. Phys. Rev. B 99, 165112 (2019).
Lian, B., Wang, Z. & Bernevig, B. A. Twisted bilayer graphene: A phonon-driven superconductor. Phys. Rev. Lett. 122, 257002 (2019).
Wu, F., MacDonald, A. H. & Martin, I. Theory of phonon-mediated superconductivity in twisted bilayer graphene. Phys. Rev. Lett. 121, 257001 (2018).
Kennes, D. M., Lischner, J. & Karrasch, C. Strong correlations and d + id superconductivity in twisted bilayer graphene. Phys. Rev. B 98, 241407 (2018).
Oh, M. et al. Evidence for unconventional superconductivity in twisted bilayer graphene. Nature 600, 240–245 (2021).
Kim, H. et al. Evidence for unconventional superconductivity in twisted trilayer graphene. Nature 606, 494–500 (2022).
Polshyn, H. et al. Large linear-in-temperature resistivity in twisted bilayer graphene. Nat. Phys. 15, 1011–1016 (2019).
Zhou, H. et al. Isospin magnetism and spin-polarized superconductivity in bernal bilayer graphene. Science 375, 774–778 (2022).
Jindal, A. et al. Coupled ferroelectricity and superconductivity in bilayer td − mote2. Nature 613, 48–52 (2023).
Xia, Y. et al. Superconductivity in twisted bilayer wse2. Nature 637, 1–6 (2024).
Han, T. et al. Signatures of chiral superconductivity in rhombohedral graphene. Preprint at https://arxiv.org/abs/2408.15233 (2024).
Wollman, D. A., Van Harlingen, D. J., Lee, W. C., Ginsberg, D. M. & Leggett, A. J. Experimental determination of the superconducting pairing state in ybco from the phase coherence of ybco-pb dc squids. Phys. Rev. Lett. 71, 2134–2137 (1993).
López-Núñez, D. et al. Magnetic penetration depth of aluminum thin films. Preprint at https://arxiv.org/abs/2311.14119 (2023).
Chiodi, F., Aprili, M. & Reulet, B. Evidence for two time scales in long sns junctions. Phys. Rev. Lett. 103, 177002 (2009).
de Vries, F. K. et al. Gate-defined Josephson junctions in magic-angle twisted bilayer graphene. Nat. Nanotechnol. 16, 760–763 (2021).
Portolés, E. et al. A tunable monolithic squid in twisted bilayer graphene. Nat. Nanotechnol. 17, 1159–1164 (2022).
Díez-Mérida, J. et al. Symmetry-broken josephson junctions and superconducting diodes in magic-angle twisted bilayer graphene. Nat. Commun. 14, 2396 (2023).
Rodan-Legrain, D. et al. Highly tunable junctions and non-local josephson effect in magic-angle graphene tunnelling devices. Nat. Nanotechnol. 16, 769–775 (2021).
Di Battista, G. et al. Revealing the thermal properties of superconducting magic-angle twisted bilayer graphene. Nano Lett. 22, 6465–6470 (2022).
Mehew, J. D. et al. Ultrafast umklapp-assisted electron-phonon cooling in magic-angle twisted bilayer graphene. Sci. Adv. 10, eadj1361 (2024).
Tinkham, M.Introduction to superconductivity (Dover, 2004).
Blonder, G. E., Tinkham, M. & Klapwijk, T. M. Transition from metallic to tunneling regimes in superconducting microconstrictions: Excess current, charge imbalance, and supercurrent conversion. Phys. Rev. B 25, 4515–4532 (1982).
Courtois, H., Meschke, M., Peltonen, J. T. & Pekola, J. P. Origin of hysteresis in a proximity josephson junction. Phys. Rev. Lett. 101, 067002 (2008).
Fong, K. C. & Schwab, K. C. Ultrasensitive and wide-bandwidth thermal measurements of graphene at low temperatures. Phys. Rev. X 2, 031006 (2012).
Angers, L. et al. Proximity dc squids in the long-junction limit. Phys. Rev. B 77, 165408 (2008).
Fong, K. C. et al. Measurement of the electronic thermal conductance channels and heat capacity of graphene at low temperature. Phys. Rev. X 3, 041008 (2013).
Seifert, P. et al. Magic-angle bilayer graphene nanocalorimeters: Toward broadband, energy-resolving single photon detection. Nano Lett. 20, 3459–3464 (2020).
Uri, A. et al. Mapping the twist-angle disorder and landau levels in magic-angle graphene. Nature 581, 47–52 (2020).
Zondiner, U. et al. Cascade of phase transitions and dirac revivals in magic-angle graphene. Nature 582, 203–208 (2020).
Tian, H. et al. Evidence for dirac flat band superconductivity enabled by quantum geometry. Nature 614, 440–444 (2023).
Carr, S., Fang, S., Zhu, Z. & Kaxiras, E. Exact continuum model for low-energy electronic states of twisted bilayer graphene. Phys. Rev. Res. 1, 013001 (2019).
Ishizuka, H., Fahimniya, A., Guinea, F. & Levitov, L. Purcell-like enhancement of electron–phonon interactions in long-period superlattices: Linear-temperature resistivity and cooling power. Nano Lett. 21, 7465–7471 (2021).
Das Sarma, S. & Wu, F. Strange metallicity of moiré twisted bilayer graphene. Phys. Rev. Res. 4, 033061 (2022).
Jaoui, A. et al. Quantum critical behaviour in magic-angle twisted bilayer graphene. Nat. Phys. 18, 633–638 (2022).
Allen, P. B. Theory of thermal relaxation of electrons in metals. Phys. Rev. Lett. 59, 1460–1463 (1987).
Viljas, J. K. & Heikkilä, T. T. Electron-phonon heat transfer in monolayer and bilayer graphene. Phys. Rev. B 81, 245404 (2010).
Walsh, E. D. et al. Graphene-based josephson-junction single-photon detector. Phys. Rev. Appl. 8, 024022 (2017).
Cong, X. et al. Probing the acoustic phonon dispersion and sound velocity of graphene by raman spectroscopy. Carbon 149, 19–24 (2019).
Koshino, M. & Son, Y.-W. Moiré phonons in twisted bilayer graphene. Phys. Rev. B 100, 075416 (2019).
Davis, S. M., Wu, F. & Das Sarma, S. Acoustic phonon contribution to the resistivity of twisted bilayer graphene. Phys. Rev. B 107, 235155 (2023).
Rozen, A. et al. Entropic evidence for a pomeranchuk effect in magic-angle graphene. Nature 592, 214–219 (2021).
The proximity effect through a junction is related to its excess current. We discuss such relation in our device in Supplementary Material.
Yip, S. K. & Sauls, J. A. Nonlinear meissner effect in cuo superconductors. Phys. Rev. Lett. 69, 2264–2267 (1992).
Volovik, G. E. Superconductivity with lines of gap nodes: density of states in the vortex. JETP Lett. 58, 457 (1993).
Clem, J. R. & Kogan, V. G. Kinetic impedance and depairing in thin and narrow superconducting films. Phys. Rev. B 86, 174521 (2012).
Tanaka, M. et al. Superfluid stiffness of magic-angle twisted bilayer graphene. Nature 638, 99–105 (2025).
Banerjee, A. et al. Superfluid stiffness of twisted trilayer graphene superconductors. Nature 638, 93–98 (2025).
Kim, K. et al. van der waals heterostructures with high accuracy rotational alignment. Nano Lett. 16, 1989–1995 (2016).
Acknowledgements
We thank Peter Märki, Wister Huang and the staff of the ETH cleanroom facility FIRST for technical support. We thank Landry Bretheau for helpful and detailed discussions on radiofrequency biasing of superconducting devices, Sankar das Sarma for discussions on electron-phonon coupling estimates and members of the quantum e-leaps consortium for comments on our data. We acknowledge financial support by the European Graphene Flagship Core3 Project, H2020 European Research Council (ERC) Synergy Grant under Grant Agreement 951541, the European Union’s Horizon 2020 research and innovation program under grant agreement number 862660/QUANTUM E LEAPS, the European Innovation Council under grant agreement number 101046231/FantastiCOF, NCCR QSIT (Swiss National Science Foundation, grant number 51NF40-185902). K.W. and T.T. acknowledge support from the JSPS KAKENHI (Grant Numbers 21H05233 and 23H02052), the CREST (JPMJCR24A5), JST and World Premier International Research Center Initiative (WPI), MEXT, Japan. E.P. acknowledges support of a fellowship from “la Caixa” Foundation (ID 100010434) under fellowship code LCF/BQ/EU19/11710062. J.H.P. acknowledges NSF Career Grant No. DMR-1941569. P.A.V. acknowledges support by a Quantum-CT Quantum Regional Partnership Investments (QRPI) Award. This work was initiated and partly performed at the Aspen Center for Physics, which is supported by National Science Foundation grant PHY-2210452.
Author information
Authors and Affiliations
Contributions
P.R. and E.P. fabricated the device. F.K.d.V., E.P., and P.R. characterized the device. T.T. and K.W. supplied the hBN crystals. E.P. and M.P. performed the measurements for this experiment. E.P., P.A.V., M.P., M.T., and Y.K. analyzed the data with input from A.M-T, A.O.D., and G.Z.; P.A.V. developed the theoretical model and performed the numerical and analytical calculations. K.E., T.I., and E.P. conceived and designed the experiment. J.H.P., T.I., and K.E. supervised the project. E.P. and P.A.V. wrote the manuscript with comments from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Jianpeng Liu, and the other, anonymous, reviewer for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Portolés, E., Perego, M., Volkov, P.A. et al. Quasiparticle and superfluid dynamics in Magic-Angle Graphene. Nat Commun 16, 4273 (2025). https://doi.org/10.1038/s41467-025-58325-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-58325-0