Zero-field Hall effect emerging from a non-Fermi liquid in a collinear antiferromagnet V_1/3NbS₂

Abstract

Magnetically intercalated transition metal dichalcogenides (TMDs) provide a versatile three-dimensional (3D) material platform to explore quantum phenomena and functionalities that emerge from an intricate interplay among magnetism, band structure, and electronic correlations. Here, we report the observation of a nearly magnetization-free anomalous Hall effect (AHE) accompanied by non-Fermi liquid (NFL) behavior and collinear antiferromagnetism (AFM) in V_1/3NbS₂. Our single-crystal neutron diffraction measurements identify a commensurate, collinear AFM order formed by intercalated V moments. In the magnetically ordered state, the spontaneous AHE is tenfold greater than expected from empirical scaling with magnetization, and this strongly enhanced AHE arises in the NFL regime that violates the quasiparticle picture. V_1/3NbS₂ challenges the existing single-particle framework for understanding AHEs based on one-body Berry curvature and highlights the potential of magnetically intercalated TMDs to unveil new electronic functionalities where many-body correlations play a critical role.

Introduction

The interplay between many-body correlations and topology gives rise to new material properties and functionalities, triggering massive interest extending from condensed matter physics to a broad, multidisciplinary spectrum. One versatile material family for this theme is transition-metal dichalcogenides (TMDs)^1,2,3. These materials often exhibit strongly correlated states, and their two-dimensional (2D) heterostructures open up new pathways for correlated quantum phenomena, ranging from Mott and heavy-fermion physics to quantum criticality and non-Fermi liquid (NFL) behavior^{2,3,4,5,6,7,8,9}. Another groundbreaking discovery based on TMDs is the zero-magnetic field fractional quantum Hall effect (FQHE) engendered by topological flat bands and enhanced electron correlation in moiré heterostructures, a discovery that could produce the next great leap in quantum computing and topological quantum devices^10,11,12,13.

Stepping from the 2D heterostructures to three-dimensional (3D) materials, the intercalation of transition-metal elements between van der Waals layers of bulk TMD compounds introduces magnetism and electron correlations. This offers an alternative means to tune the carrier density and engineer the band topology in TMD systems, similar to the effects of electrostatic gating applied in moiré heterostructures^14,15. The magnetically intercalated TMD family has diverse magnetic structures and electronic properties^{15,16,17,18,19,20,21,22,23,24,25}. While the interplay between magnetic ordering and topological band structure is widely investigated, less is known about the possibility of realizing novel electronic properties driven essentially by strongly correlated electrons. Berry curvature—the intrinsic mechanism of AHE—is currently understood within effective single-particle theories of non-interacting electronic bands without considering electron correlations or many-body entanglement^26,27. Thus, a realization of AHE emerging in an NFL state that defies Landau’s paradigm and does not have well-defined quasiparticles may incentivize the establishment of a new framework to explain Berry-curvature-driven phenomena in strongly correlated quantum phases.

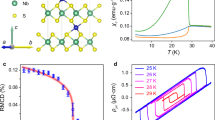
Our focus here is V_1/3NbS₂, which comprises magnetic V ions intercalated between parent NbS₂ layers (Fig. 1a). The shifted stacking between the two neighboring V planes breaks inversion and mirror symmetries, resulting in a non-centrosymmetric chiral structure (space group: P6₃22) (Supplementary Tables 1, 2). The combination of structural chirality and magnetism is known as a feasible pathway toward novel electrical transport phenomena. Band filling by 3d electrons of the intercalated V is predicted to modify the electronic band structure of the parent NbS₂ dramatically, with the potential of realizing topological semimetal states¹⁴. Moreover, the band structure obtained by density functional theory plus dynamical mean-field theory (DFT + DMFT) features nearly flat bands with a substantial density of states (DOS) near the Fermi level, attributed to Kondo hybridization between V-3d and Nb-4d orbitals (Fig. 1c–e). Thus, V_1/3NbS₂ offers unique opportunities to engineer exotic quantum phases through the mixing of spontaneous symmetry breaking, electron correlation, and non-trivial band topology.

Fig. 1: Crystal and collinear antiferromagnetic structure of V_1/3NbS₂.

a Schematics of the crystal structure depicting V, Nb, and S atoms with red, blue, and yellow balls, respectively. The V atoms lie in between the host NbS₂ layers. A unit cell (solid lines) contains two V layers. The magnetic moments of V (red arrows) form the collinear antiferromagnetic (AFM) order; they are ferromagnetically ordered within the layer and antiferromagnetically stacked along the [0001] direction. b Six domain configurations of the Γ₆ collinear AFM state, α⁺, β⁺, γ⁺,α⁻, β⁻, γ⁻. The balls represent V atoms, and the arrows represent the staggered magnetic moments. The circular plot shows the orientation of the staggered moment for each domain configuration. The sign of the induced AHE is marked by  + or  − . The dashed lines mark the staggered moment directions that forbid the AHE. The x, y, and z directions, respectively, refer to the real-space crystal directions $[2\bar{1}\bar{1}0]$, $[01\bar{1}0]$, and [0001]. c The DFT + DMFT band structure: the spectral function for the antiferromagnetic state. The nearly flat band mentioned in the main text is marked by the gray box. d The density of states (DOS) per unit cell. The solid blue line represents the total DOS. The solid red line and the dashed black line represent the contributions from the V t_2g orbital and other orbitals, respectively. e The up-spin and down-spin DOS at a V site.

Among the candidate AFM structures for V_1/3NbS₂, the collinear AFM is particularly intriguing^20,21. Large zero-field AHE has been established in noncollinear and noncoplanar AFMs, presenting compelling new opportunities for ultrafast non-volatile information storage^{17,18,19,28,29,30,31,32,33}. Widening the landscape of such functional AFM orders may yield broad scientific and technological impacts. Collinear AFM structures exhibiting sizable spontaneous time-reversal-symmetry-breaking responses (i.e., zero-field AHE), termed altermagnets^34,35, have recently attracted immense interest, yet their physical realization remains elusive. Recent studies on candidate altermagnets, such as MnTe and Mn₅Si₃, have identified zero-field AHE^36,37. However, these observations have been limited to thin films, which hampers experimental determination of the microscopic magnetic structure and crystal structure. In this work, we combine high-quality single-crystal synthesis with neutron and X-ray diffraction, transmission electron microscopy, and electrical transport measurements to demonstrate that the collinear AFM state of V_1/3NbS₂ displays enhanced zero-field AHE. This constitutes the first experimental evidence for the anomalous Hall effect in a collinear antiferromagnet.

Results

Magnetic structure of V_1/3NbS₂

We shall first determine the magnetic structure of our V_1/3NbS₂ crystals through single-crystal magnetization and neutron diffraction measurements. We use a right-handed coordinate system with axes x, y, and z to respectively represent the $[2\bar{1}\bar{1}0]$, $[01\bar{1}0]$, and [0001] real-space directions of the hexagonal V_1/3NbS₂ indicated through Miller-Bravais indices. Following Ashcroft and Mermin, we use square brackets for real space and rounded brackets for reciprocal space. The set of three symmetry-related x and y directions are labeled as 〈x〉 and 〈y〉, respectively. The magnetization M measured in a small field rises abruptly upon cooling below 50 K (Fig. 2a and Supplementary Fig. 6), marking a transition to AFM order with a Néel temperature T_N  =  50(1) K. Further cooling reveals anisotropic magnetic properties with small ferromagnetic (FM) components arising both in the xy plane and along the z-axis: While the out-of-plane M forms a plateau between about 10 K and 40 K and develops a weak upturn below about 10 K, the in-plane M decreases with T after reaching a 30 K maximum (Fig. 2a). Magnetization isotherms M(B) measured at 2 K show a spontaneous moment of about 0.01μ_B/V with finite coercivity for B∥z (Fig. 2b) and about 0.04μ_B/V without coercivity for B⊥z (Supplementary Fig. 2a). These weak ferromagnetic moments are less than 1% of the V³⁺ moment size (Methods) and may correspond to sample-averaged spin canting of less than 1^∘ relative to a predominantly collinear AFM order. The M-T curves differ from those reported in a previous single-crystal neutron diffraction study²¹. There are also considerable differences between previously published magnetization data^20,21,38 indicating differences in V composition and disorder. To facilitate interpretation here we report magnetic, electrical transport, specific heat, and neutron diffraction measurements on the same crystal. This crystal has near-perfect stoichiometry and exhibits the ideal ABAB stacking of V without the ABC-type stacking fault, as discussed in the “Methods” section, Supplementary Note 8, and Supplementary Fig. 12.

Fig. 2: Magnetic properties of V_1/3NbS₂.

a Temperature dependence of the magnetization M of V_1/3NbS₂ measured for B =  0.1 T applied along the x ($[2\bar{1}\bar{1}0]$), y ($[01\bar{1}0]$) and z ([0001]) directions, respectively. Data obtained under zero-field-cooling (ZFC) and field-cooling (FC) protocols are shown using solid and open symbols, respectively. The arrow marks the transition into the AFM state at the Néel temperature T_N  = 50(1) K. Inset: the inverse susceptibility (1/χ) vs. temperature T for B∥y and z, The linear fit (solid line) to the high-T data above 300 K yields a Curie-Weiss temperature θ_W = −70(4) K (Methods). b Isothermal magnetization M loop measured at select temperatures by sweeping the magnetic field between B  =  ±7 T aligned along the z-direction. Inset: zoomed plot showing the hysteresis loop in M that develops at low T. c Magnetic Bragg peak at Q  =  (0001). The change in line shape reflects hysteretic changes in the magnetic domain size ξ along y under up- and down-sweeps of B∥x measured at 2 K. Relative to the zero field and 8 T state, ξ is strongly reduced upon raising the field from zero to 4 T. d Peak intensity of the (0001) magnetic Bragg peak as a function of temperature. The solid line in the main panel is a fit to the power-law form $I \sim {({T}_{{{{\rm{N}}}}}-T)}^{2\beta }+{I}_{0}$, where β is the critical exponent, and I₀ is the background intensity above T_N. This fit yields β =  0.363(2), T_N  =  50.1(1) K, and I₀  = 247(5) counts per 1500 monitor counts. Inset: a log-log plot of the magnetic peak intensity vs. the reduced temperature (T_N  − T)/T_N. The solid line shows power-law behavior near the critical temperature. Error bars in all neutron scattering figures represent one standard deviation.

Our single-crystal neutron diffraction measurements identify an exclusively magnetic Bragg peak that appears at Q  =  (0001) upon cooling below T_N  =  50.1(1) K (Fig. 2c, d). The temperature dependence of the peak intensity follows an order-parameter-like form (Fig. 2d). Temperature-dependent Bragg scattering is also detected at Q  =  (0003) but with weaker intensity (Supplementary Fig. 3), consistent with the V³⁺ magnetic form factor. The $(11\bar{2}\ell )$ (0  <  ℓ  <  1) scan at T  =  2 K shows no extra magnetic Bragg scattering at low T (Supplementary Fig. 2c). Based on the polarization factor for unpolarized neutron diffraction, this sets an upper limit of 0.1μ_B/V on the ordered z-axis moment in our sample. Thus, we can rule out the possibility of the Q = (000$\frac{1}{3}$) noncoplanar spin configuration reported in ref. ²¹. The structure factor for a series of magnetic Bragg peaks in the $(h0\bar{h}\ell )$ and $(hh\overline{2h}\ell )$ reciprocal lattice planes is best accounted for by the Γ₆ irreducible representation (IR), that describes an antiferromagnetic stacking of ferromagnetic vanadium layers (Supplementary Fig. 10a–c). Refinement against the Γ₆ structure yields a V moment of 1.7(1) μ_B/V, which is comparable with the moment size of 1.5(1) μ_B/V reported in ref. ²⁰ and is consistent with the expected moment size gS  =  2μ_B with effective spin S  =  1 and g  =  2. The local easy axis of the collinear AFM structure is identified as $\langle 2\bar{1}\bar{1}0\rangle$ through the field dependence of the ${{{\bf{Q}}}}=(10\bar{1}0)$ magnetic Bragg peak intensity under a magnetic field applied along the perpendicular $[\bar{1}2\bar{1}0]$ (〈x〉) direction (Supplementary Note 2 and Supplementary Fig. 2b).

To detect a potential change in the antiferromagnetic structure associated with the weak upturn in out-of-plane M for T <  10 K (Fig. 2a), we first note that there is no anomaly in the temperature-dependent intensity of the (0001) magnetic Bragg peak (Fig. 2d). This shows the domain averaged in plane staggered magnetization does not change at 10 K. For sensitivity to the in-plane AFM domain distribution, we turn to the $(10\bar{1}0)$ Bragg peak. Supplementary Fig. 5g, h shows there is no change in the field dependence of the $(10\bar{1}0)$ intensity around T  =  10 K. This precludes a substantial change in the magnetic structure or its easy axis at 10 K. Thus, our neutron diffraction experiments show that the Γ₆ collinear AFM structure with a staggered moment lying along 〈x〉 is retained as the sample-averaged magnetic structure down to at least 2 K. Moreover, the temperature dependence of the specific heat, C(T), exhibits no noticeable anomaly around 10 K (Methods, Supplementary Note 3, and Supplementary Fig. 8a). These findings exclude the possibility of a magnetic phase transition into a noncoplanar AFM order below 10 K. Because an out-of-plane uncompensated FM moment does not break symmetry elements of the Γ₆ collinear AFM configuration (Supplementary Note 5), it must emerge concurrently with the collinear AFM order in a single phase transition, albeit potentially with a very small magnitude as indeed observed (Supplementary Note 6). However, the in-plane FM component associated with the enhanced in-plane M for T  <  50 K is incompatible with the symmetry properties of the prevailing AFM order and is likely associated with stacking faults, as detailed in the discussion section below.

Anomalous Hall effect in the collinear AFM state

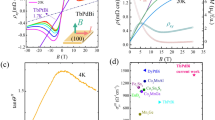
Though the collinear AFM state of V_1/3NbS₂ state has a vanishingly small M, it hosts a sizable spontaneous (zero-field) Hall effect. Figure 3a shows the Hall resistivity ρ_xy measured for B∥z. The spontaneous component of ρ_xy(B  =  0) appears below 10 K and grows upon cooling, reaching  ≈ 0.1 μΩcm with a clear field coercivity of  ≈200 Oe at 2 K. For T  >  10 K, the spontaneous Hall effect vanishes, and ρ_xy shows nearly linear field dependence without hysteresis. Correspondingly, a spontaneous Hall conductivity σ_xy(B  =  0) ≈  ρ_xy/(ρ_xxρ_yy) only appears below 10 K, where it rises to approximately 3Ω⁻¹cm⁻¹ at 2 K (Fig. 3b).

Fig. 3: Anomalous Hall effect (AHE) observed in V_1/3NbS₂.

a Field dependence of the Hall resistivity, ρ_xy, obtained at various temperatures under a magnetic field B∥z for the V_1/3NbS₂ single-crystal exhibiting the ideal ABAB stacking. b Temperature dependence of the zero-field Hall conductivities, σ_xy(B  =  0) (red circles; left-axis) and σ_yz(B  =  0) (blue circles; right-axis), obtained under B∥z and B∥x, respectively. The current I is applied along the y-direction. Inset: The Hall resistivity ρ_zy obtained at T  = 32 K with B∥x and I∥y. Error bars represent uncertainties in measured data. c The scaling relation between the net magnetization M and the spontaneous Hall conductivity σ_H(B  =  0). The Hall conductivity σ_xy(B = 0) of V_1/3NbS₂ (solid red circles) deviates greatly from the linear scaling for conventional ferromagnets (blue-shaded region), constituting the unconventional regime (red-shaded regime) associated with known Weyl magnets. In contrast, σ_yz(B  =  0) for V_1/3NbS₂ (half-filled red circles) is linearly related to the in-plane M as in ordinary ferromagnetic materials^28,29.

In ordinary ferromagnets, the spontaneous anomalous Hall conductivity σ_H is proportional to M, and the ratio S_H  =  σ_H/M is of order (0.01–0.1) V⁻¹, constituting the conventional regime (blue shaded region in Fig. 3c)^26,29. In contrast, the observed Hall conductivity σ_xy in V_1/3NbS₂, when compared to its tiny net ferromagnetic moment of  ~0.01μ_B/V leads to S_H  ~  1 V⁻¹ for T ≤ 10 K (solid red circles in Fig. 3c), which is well beyond the linear relation for conventional ferromagnets. Instead, the AHE in V_1/3NbS₂ falls in the same regime as topological magnetic materials such as the Weyl magnets Mn₃X (X  = Sn, Ge)^28,29, Co₃Sn₂S₂³⁹, and Co₂MnGa⁴⁰ (red shaded region in Fig. 3c). Note that the net magnetization, μ₀M <  10⁻³ T, in V_1/3NbS₂ is about one-tenth of the value found in the antiferromagnetic Weyl semimetals Mn₃X (X  = Sn, Ge), and just 1% of that in the ferromagnetic Weyl magnet Co₃Sn₂S₂. The deviation from the conventional scaling relation indicates that an order parameter other than the net magnetization (i.e., cluster multipoles as discussed below) characterizes the symmetry-breaking mechanism in the AFM state, and there exists a significant contribution to the Berry curvature that is independent of the net magnetization³². Moreover, with such deviation recognized as a universal signature in topological magnets³², we anticipate that the out-of-plane spontaneous AHE in V_1/3NbS₂ might arise from topologically non-trivial band features, though further confirmation through spectroscopic probes is required for a firm conclusion^41,42,43.

The in-plane spontaneous AHE, ρ_zy(B =  0), differs qualitatively from the out-of-plane AHE ρ_xy(B  =  0) in two aspects: (1) ρ_zy(B  =  0) peaks near 30 K and then decreases toward zero around 10 K (Fig. 3b); (2) the corresponding zero-field Hall conductivity σ_yz  ≈  −ρ_yz/(ρ_yyρ_zz) is an order of magnitude smaller than σ_xy(B  =  0) and lies within the regime for ordinary ferromagnets in the scaling plot for the anomalous Hall conductivity ∣σ_H∣ vs. M (Fig. 3b, c). Thus, the AHE ρ_zy(B  =  0) can be understood as driven by the in-plane FM component within the conventional scheme.

Non-Fermi liquid behavior accompanying the enhanced anomalous Hall effect

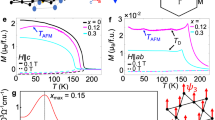
Another striking observation in V_1/3NbS₂ is the emergence of pronounced NFL resistivity within the same temperature regime (T  ≲  10 K) as the disproportionately large spontaneous AHE. The zero-field longitudinal resistivity ρ (Fig. 4a) is T-linear in the paramagnetic phase between 350 K and T_N. It then drops sharply for temperatures below T_N, which we ascribe to a reduction in magnetic scattering. On further cooling, ρ(T) once again exhibits linear T-dependence for T  ≲  10 K (Fig. 4a, c) before settling into a T^1.6(1) behavior below about 1 K for B  ≲ 1 T (Fig. 4d, e and Supplementary Fig. 7c).

Fig. 4: Strange-metal transport in V_1/3NbS₂ exhibiting ABAB stacking.

a The zero-field resistivity ρ(T). The downward arrow denotes the Néel temperature T_N  = 50(1) K. The two solid lines represent linear fits in two T regimes: T_N  ≲  T  ≲  350 K and T  ≲  10 K, where T^* (upward arrow) marks the upper limit of the low-T linear behavior. Inset: the temperature derivative, dρ/dT. The dashed line and the downward arrow denote T_N and T^*, respectively. b Temperature vs. field (T  − B) phase diagram showing the non-Fermi liquid (NFL) regimes with ρ(T)  ~  T (orange) and ρ(T)  ~  T^1.6 (red), and the field-induced Fermi liquid (FL) state (blue). The vertical line indicates the temperature range of finite zero-field Hall conductivity σ_xy  > 0. c Evolution of the T  − linear resistivity under B∥z. The curves measured under fields are shifted vertically for clarity. The solid lines show the linear fit $\rho (T)={\rho }_{0}+{A}^{{\prime} }T$ to the low-T behavior, for which the upper limit T^* is marked by downward arrows. Inset: Representative temperature dependence of $\rho /({\rho }_{0}+{A}^{{\prime} }T)$, with $\rho /({\rho }_{0}+{A}^{{\prime} }T)\approx 1$ corresponds to T-linear behavior; the upward arrows mark T^* for each B. d ρ(T) down to 0.1 K under B∥z. The black arrows mark the onset of the NFL state ρ(T)  ~  T^1.6 (solid lines). Above 1 T, ρ(T) recovers the FL T² dependence (dashed lines), with the red arrows denoting its upper limit. e Representative R-squared R² of power-law fitting to ρ(T)  =  ρ₀  +  ATⁿ versus n. The maximum value of R² (dotted lines) indicates optimal fitting. f Power-law exponent n (left-axis) and the inverse of the FL coefficient A (right-axis) versus B. The blue dashed lines are guides for the eye. The linear fit 1/A  ~  ∣B  − B_c∣ (red dashed line) provides a critical field B_c  =  1.2(2) T. Error bars in b, f represent uncertainties in the measured data.

The zero-field electronic specific heat coefficient exhibits a logarithmic increase C_el(T)/T  ~ log(T^*/T) below 1.3 K, which overlaps with the onset of ρ(T) ∝  T^1.6(1) (Methods, Supplementary Note 3, and Supplementary Fig. 8b). As shown in the temperature-field (T - B) phase diagram (Fig. 4b), the NFL regime characterized by T-linear resistivity extends from approximately 10 K to 2 K within the AFM phase. For B  ≲  1 T, ρ(T) does not enter a Fermi liquid (FL) regime with ρ(T)  ~  T² even in the T  →  0 limit.

The T-linear resistivity above 2 K persists for B∥z up to 8 T (Fig. 4b, c), with its onset temperature shifting to higher values with increasing B. In contrast, the T^1.6(1) NFL phase below  ~1 K is replaced by a FL with T² resistivity for B  ≳  2 T (Fig. 4d–f and Supplementary Fig. 7b). In the field-induced FL phase, the coefficient A characterizing the T² resistivity ρ =  AT² increases by a factor of five with decreasing B and appears to diverge near  ~1.5 T, as indicated by the linear field dependence of 1/A  ~  ∣B  −  B_c∣, with B_c  =  1.2(2) T (Fig. 4f and Supplementary Fig. 7b). Since A measures the quasi-particle effective mass m^*, the divergence of A near B_c marks a quasi-particle breakdown.

The NFL behavior in V_1/3NbS₂ recalls observations in correlated quantum materials, ranging from high-temperature superconductors, heavy fermions, to twisted bilayer systems^{2,9,44,45,46,47,48,49}. A generic feature of these materials is the T-linear resistivity governed by a universal transport scattering rate 1/τ that obeys the Planckian limit: ℏ/τ  =  αk_BT, where ℏ and k_B are the Planck and Boltzmann constants, respectively^{45,46,47,48,50}. Following the procedure used in refs. ^46,47,48, we obtained α  = 0.7  ±  0.2 for V_1/3NbS₂, which is of order unity as expected for Planckian behavior (Supplementary Note 4). The Debye temperature of V_1/3NbS₂ is as high as  ~380 K²¹, and the phonon contribution to the specific heat is negligible below  ~10 K (Methods, Supplementary Note 3, and Supplementary Fig. 8a). Thus, the observed T-linear resistivity at low temperatures cannot be attributed to conventional electron-phonon scattering mechanisms. We can also rule out extrinsic factors, such as impurity phases and chemical inhomogeneity, as the cause of the observed NFL based on the single-crystal X-ray diffraction and chemical composition analysis (Methods and Supplementary Note 8). On the other hand, two unique aspects of the NFL behavior in V_1/3NbS₂ stand out: (i) Unlike typical quantum critical systems where the NFL behavior emerges at the margin of an ordered phase, the NFL regime in V_1/3NbS₂ occurs well within the AFM order without tuning (i.e., zero field and ambient pressure)^51,52; (ii) The low-temperature T-linear resistivity covers a broad B range with the monotonically increasing onset temperature up to 8 T (Fig. 4b). This seems to defy straightforward explanation based on proximity to a magnetic-field-tuned QCP, for which the NFL behavior is typically confined near a critical field^44,45.

Discussion

The symmetry properties of the underlying AFM spin texture provide an essential basis for understanding the emergence of magnetization-free spontaneous AHE. The collinear AFM state in V_1/3NbS₂ can be viewed as a ferroic order of cluster dotriacontapoles that belongs to the Γ₆ irreducible representation (IR) (Supplementary Note 6, and Supplementary Fig. 10)⁵³. The two possible spin configurations Γ₆(1) and Γ₆(2) shown in Supplementary Fig. 10(a) are symmetrically distinct: Γ₆(1) forces the spontaneous anomalous Hall conductivity σ_xy to be zero, whereas Γ₆(2) allows out-of-plane spin canting and finite σ_xy. With the staggered moment lying along the x-axis, the observed AFM order corresponds to the Γ₆(2) configuration at zero field, which breaks time-reversal symmetry (TRS) and can exhibit a finite spontaneous AHE even with vanishing net magnetization (Supplementary Note 6). Figure 1b illustrates the six equivalent domain patterns hosted by the Γ₆ collinear AFM state, α⁺, β⁺, γ⁺, α⁻, β⁻, γ⁻, where the  + and  − refer to the different signs of the AHE signal. The presence of magnetic domains is evident from the hysteric behavior observed in ρ_xy(B) (Fig. 3a) and in the field dependence of rocking scans through the (0001) magnetic Bragg peak (Supplementary Fig. 5e, f). An out-of-plane magnetic field B∥z can shift the balance between  + and  − domain populations (Supplementary Note 6). This effect may result in a finite spontaneous AHE, σ_xy(B  =  0), which aligns with the experimental observation for T  ≲ 10 K (Fig. 3a).

Aside from the unique characteristics of the collinear AFM order, our experimental findings, in combination with the DFT+DMFT calculation (Method, Supplementary Note 7), suggest that electronic correlation effects play a role in generating the novel electronic state at zero fields. The NFL behavior and signature of quasi-particle breakdown near zero fields are reminiscent of the strange metal state observed in various classes of strongly correlated materials. On the theoretical front, the DFT band structure features narrow V-3dt_2g bands hybridizing with Nb-4d bands near the Fermi level E_F (Supplementary Fig. 11). Taking into account the electronic interactions between V-3dt_2g orbitals within the DMFT, we obtain an itinerant AFM with the local magnetic moments of approximately 1.3μ_B at T_N  ≈  50 K, comparable to the experimental staggered moment of 1.7(1)μ_B observed at T  = 2 K. With increasing on-site interaction U, the DFT+DMFT calculations predict that the ground state of V_1/3NbS₂ can be tuned through a quantum phase transition (QPT) separating the itinerant AFM and a correlated metallic paramagnet (PM); the latter hosts heavy quasiparticles with a significant mass enhancement factor of 50– 100 due to Kondo hybridization between the V-3d and Nb-4d electrons. The low-T specific heat data above the  ~log(1/T) upturn yields a large value of the electronic specific heat coefficient γ  =  40.6(3) mJmole⁻¹K⁻², more than two orders of magnitude larger than the DFT value of 0.14 mJmole⁻¹K⁻². By assessing γ under detailed tuning of the interaction parameters, we find that the experimentally observed mass enhancement can be reproduced only when the AFM ground state lies near the AFM-PM QPT. Thus, the experiment-theory comparison suggests that the zero-field AHE appears in a setting where correlated effects and quantum fluctuations play prominent roles. An effective non-thermal tuning parameter for accessing this anticipated QPT remains to be identified, with disorder strength being a plausible candidate. Below, we elaborate further on the nature and role of disorder in V_1/3NbS₂.

Two of our experimental observations defy symmetry-based expectations for a single macroscopic domain of AFM order: (i) The small yet finite in-plane ferromagnetic moment observed in M_x(B)(B  =  0) and the resulting spontaneous Hall signal σ_yz(B  =  0) (Figs. 2a and 3b and Supplementary Fig. 2a) are incompatible with the symmetry of bulk Γ₆ AFM order (Supplementary Note 6, and Supplementary Fig. 10); (ii) The out-of-plane spontaneous Hall signal σ_xy(B  =  0) becomes finite at approximately 10 K (Fig. 3a) where there is no peak in the specific heat nor a thermal anomaly in the temperature dependence of the magnetic Bragg diffraction to indicate a thermodynamic phase transition (Supplementary Fig. 8a, Fig. 2c, d, Supplementary Fig. 5g, h). This suggests that structural disorder plays a role. Refinement of a structural model of the single-crystal X-ray diffraction data reveals  ~85% V occupancy on the 2d site and  ~15% V occupancy on the 2b site (Methods, Supplementary Note 5, and Supplementary Tables 1, 2). In an intercalated layered structure such as V_1/3NbS₂, occupational disorder typically takes the form of planar stacking faults; defect V layers interspersed within the prevailing ABAB stacking pattern. Planar defects can strongly impact Hall and magnetization measurements, which rely on macroscopic coherence. In analogy to the interfacial Dzyaloshinskii-Moriya interaction (DMI) in multilayer magnetic thin films⁵⁴, the localized DMI associated with a planar defect can introduce a local twist or phase slip in the otherwise collinear Γ₆ AFM order. A low density of planar stacking faults thus might induce the unexpected M_x(B)(B  =  0) and σ_yz(B  = 0) (Fig. 3b and Supplementary Fig. 2a) and suppress M_z and the out-of-plane spontaneous Hall signal σ_xy(B  =  0) (Fig. 2a and Fig. 3a, b). We thus hypothesize that the 10 K temperature scale is associated with a planar defect-induced crossover in domain wall dynamics of an otherwise collinear AFM.

We next discuss the possible physical origin of the low-T NFL behavior. Inside an AFM phase, spin fluctuations typically cannot give rise to divergence in self-energy required for quantum criticality. Another relatively underexplored mechanism for NFL behavior is related to chiral spin texture with non-trivial topologies, such as a skyrmion lattice underlying the pressure-induced NFL behavior in MnSi⁵⁵. The broad crossover around 1.3 K in ρ(T) of V_1/3NbS₂ and the subsequent power-law behavior ρ(T)  ∝  T^1.6(1) aligns well with the MnSi case⁵⁵. However, the spontaneous AHE occurring in the same T regime requires time-reversal symmetry breaking, a condition not fulfilled by magnetic skyrmion bubbles. Thus, the concurrent NFL and spontaneous AHE suggest the possibility that the aforementioned AFM domain walls represent a new type of topological nano-magnetic entity. The AFM domain structure and domain wall dynamics are expected to be sensitive to variations in the stacking order. Thus, if one can manipulate the type and strength of the V disorder, V_1/3NbS₂ may hold the potential to serve as a physical example demonstrating the controlled disorder-tuning of strange-metal behavior and Planckian transport, as recently proposed in ref. ⁵⁰.

In summary, we identify a substantial zero-field AHE in a collinear AFM state of V_1/3NbS₂ with vanishingly small magnetization. This observation suggests that 3d band filling by V intercalants could lead to topological band features, for which spectroscopic evidence is worth pursuing. Most remarkably, this spontaneous Hall signal co-occurs with pronounced NFL behavior that defies a conventional quasi-particle description. Strong correlation effects play a vital role in the emergence of zero-field AHE inside the NFL phase, the description of which goes beyond the widely-used free fermion Berry-curvature framework. These findings showcase a promising outlook for magnetically intercalated TMDs to realize exotic electronic states characterized by a rich interplay of many-body correlations, band topology, and magnetism. Structural disorders are known to substantially influence the intrinsic quantum phases and properties of intercalated TMDs. Anticipating improved understanding and control of disorder-related effects, the unusual electronic states found in the collinear AFM state of V_1/3NbS₂ could lead to electronic and spintronic functionalities that extend beyond current paradigms.

Methods

Single crystal growth

The V_1/3NbS₂ single crystals were synthesized by the chemical vapor transport method using iodine as the transport agent. We first obtained polycrystalline samples by heating stoichiometric amounts of high-purity vanadium (Rare metallic, 99.999%), niobium (Rare metallic 99.999%), and sulfur (Rare metallic 99.9995%) in an evacuated silica ampoule at 1000 ^∘C for 24 h. This heating process was done stepwise in a controlled manner before naturally cooling the material to room temperature. We then mixed 2 g of polycrystalline powder with 0.1 g of iodine in an evacuated silica tube (20 mm inner diameter, 15 cm length). Next, this ampule was loaded in a three-zone furnace in which the hot and cold zones were kept at 1000 ^∘C and 800 ^∘C, respectively, for 7 days. This resulted in several plate-like and well-faceted V_1/3NbS₂ crystals (maximum size  ~3 mm ×  ~2 mm) at the cold zone side of the ampoule.

Crystal characterization

We determined the chemical composition of the V_1/3NbS₂ crystals using electron probe micro-analyzer (EPMA) JXA-iSP100 (JEOL). The measurements provide an average atomic percentage ratio of V:Nb:S = 9.97: 29.80: 60.23, which corresponds to a composition of V_1.004Nb₃S_6.06.

The structure of the V_1/3NbS₂ samples was determined by single-crystal X-ray diffraction. The diffraction data were collected on a single crystal of 0.16  ×  0.15  ×  0.02 (mm)³ on a Bruker Kappa D8 Quest diffractometer equipped with an IμS microfocus source (Mo Kα, λ = 0.71073 Å), a HELIOS optics monochromator, and a Photon II CPAD detector. The Bruker SAINT program was used to integrate the diffraction data. Scaling and multi-scan absorption corrections were performed using SADABS. The crystal structure of V_1.00Nb₃S₆ was solved using intrinsic phasing methods in SHELXT⁵⁶ and anisotropically refined using SHELXL⁵⁷. All atomic parameters were refined anisotropically. The V content was restrained to 1.00 to match the total amount determined by EPMA. The data collection and refinement parameters are presented in Supplementary Table 1, and the atomic positions are presented in Supplementary Table 2.

We further investigated the local crystal structure of the V_1/3NbS₂ samples using transmission electron microscopy (TEM) with a JEOL JEM-2010F instrument operated at 200 kV at the Institute for Solid State Physics (ISSP), the University of Tokyo. The specimen was put on a holder that allowed a tilt angle of  ± 30^∘ for the TEM observation. Selected area electron diffraction patterns were obtained using an aperture of 10 μm diameter, being ca.125 nm in real space, and recorded using an imaging plate. Specimen for the TEM observation was initially prepared using a JEOL Ion-Slicer, but since it was altered during processing, a powder sample obtained by crushing the single crystal in an agate mortar was used instead. The powder was diffused into a solvent and dropped onto a microgrid together with the solvent to prepare an observation sample for TEM. The TEM results shown in Supplementary Fig. 1 confirm the non-centrosymmetric P6₃22 space group with (√3 × √3) V ordering at room temperature.

Magnetization measurements

The behavior of bulk magnetization reported across existing studies on V_1/3NbS₂ reveals notable sample dependence^20,21. To ensure consistency, we report the magnetic properties of the same crystal used for measuring electrical transport and specific heat, which is stoichiometric to within 1%, as mentioned above, and exhibits ABAB stacking (Supplementary Note 8). The magnetization data shown in Fig. 2a, b, and Supplementary Fig. 2a were obtained on oriented samples using a commercial SQUID magnetometer (MPMS, Quantum Design) under both zero-field cooled (ZFC) and field-cooled (FC) conditions. The ZFC data were obtained by cooling the sample from 300 K to 2 K at zero field. A magnetic field of 0.1 T was then applied, and measurements of the magnetization were conducted while warming the sample to 400 K. Maintaining the B  = 0.1 T magnetic field, the sample was then cooled to base temperature. The FC M(T) data were subsequently acquired while warming the sample to 400 K. To obtain the isothermal magnetization M(H) curves, we first cooled the sample in zero field from T  =  300 K to the target temperatures. We then measured M(H) while scanning the magnetic field between  ±7 T. The magnetic susceptibility measured at a magnetic field B  = 0.1 T exhibits nearly isotropic Curie-Weiss behavior at high temperatures, as shown in Fig. 2a, inset. The inverse susceptibility, 1/χ, is linear in the temperature range between 300 K and 400 K, yielding a Curie-Weiss temperature θ_W = −70(4) K and an effective moment per V atoms μ_eff  = 2.9(1) μ_B for both the in-plane and out-of-plane field directions. The negative sign of θ_W indicates antiferromagnetic correlations in the paramagnetic state, and the fitting parameter of μ_eff  = 2.9(1)μ_B is close to the value of $g\sqrt{S\cdot (S+1)}{\mu }_{{{{\rm{B}}}}}=2.83{\mu }_{{{{\rm{B}}}}}$ expected for a V³⁺ ion with a spin-only local moment where g =  2 and S  =  1. This result is consistent with previous reports^21,58.

Specific heat measurements

Zero-field specific heat measurements down to 2 K were carried out using a physical properties measurement system (PPMS, Quantum Design) through the relaxation method. The corresponding data are shown in Supplementary Fig. 8a. The low-T specific heat data shown in Supplementary Fig. 8b were acquired using the quasi-adiabatic method at the International Megagauss Science Laboratory of ISSP. Details of this technique are described in ref. ⁵⁹. Each data point in the measurement was obtained within a short timescale of  ~5 ms under a 0.1 ms heat pulse, as shown in the inset of Supplementary Fig. 8b.

Electric transport measurements

The longitudinal and Hall resistivities were measured in six-point geometry. Crystals were polished into bar shapes, with their long edge parallel to the in-plane x and y directions, respectively. Electrical contacts to the crystals were made by attaching 20 μm gold wires with silver epoxy. Measurements in the temperature range of 2 K–400 K were performed using the DC option of the PPMS system (Quantum Design). The resistivity data in the 0.1 K–4 K temperature range were obtained using a dilution refrigerator (Kelvinox 25, Oxford Instruments) and the AC method with an excitation current of 0.1 mA. The Hall contribution to the resistance and vice versa were extracted by subtracting and adding the resistance of positive and negative field scans, respectively.

Neutron diffraction measurements

A 20 mg plate-like single crystal with the z-axis perpendicular to the surface was used for neutron diffraction experiments. The experiment was performed on the triple-axis spectrometer BT-7 at the NIST Center for Neutron Research (NCNR)⁶⁰. The sample was mounted on an aluminum sample holder with the [$\bar{1}2\bar{1}$0] direction (〈x〉-axis) vertical and perpendicular to the horizontal scattering plane of the instrument for observing scattering signals in the $(h0\bar{h}\ell )$ plane. All measurements were performed with a fixed final neutron energy of 14.7 meV, filtered through 25 mm pyrolytic graphite (PG) before the saggital focusing PG (002) monochromator and an additional 25 mm thick PG filter between the sample and the PG (002) analyzer. To determine the magnetic structure we used open-50’-50’-120’ collimation and conducted rocking scans on the accessible magnetic and nuclear Bragg peaks. We inferred the fully Q-integrated intensity of Bragg peaks from rocking scans using Reslib. Specialized software was developed for the subsequent structural refinement to account for the resolution effect. A comparison between the calculated and observed structure factor is shown in Supplementary Fig. 5a–c. The magnetic Bragg peaks detected in the $(h0\bar{h}\ell )$ plane contain contributions from two out of three magnetic domains, which were taken into account in the analysis. The experimental moment size is within 15% of the spin-only value (see main text), confirming the assumption of a uniform distribution of domain size.

To investigate the field dependence of the magnetic structure, we conducted rocking scans at ${{{\bf{Q}}}}=(10\bar{1}0)$ and (0001) at the base temperature of 2 K with a magnetic field between 0 and 8 T applied along the vertical [$\bar{1}2\bar{1}$0] direction. To achieve sensitivity to the magnetic correlation length/domain size, we used tight collimation around the sample for these measurements: Open-10’-10’-120’. Rocking scans at ${{{\bf{Q}}}}=(10\bar{1}0)$ are sensitive to the correlation length along the c-axis, which was found to exceed 800 nm for all field values (Supplementary Fig. 5d). Rocking scans at Q  =  (0001) are sensitive to the in-plane correlation length along the $[10\bar{1}0]\,\langle y\rangle$-direction, which shows strong field dependence (Supplementary Fig. 5e). The contrast between the in-plane and out-of-plane correlation length indicates the formation of magnetic field tunable domains extending in the z-direction, which survive up to a field of 8 T applied along [$\bar{1}2\bar{1}$0] (〈x〉). This is evident from the hysteresis observed in the field dependence of the y-axis correlation length (Supplementary Fig. 5e). The observed asymmetry in the hysteresis can be attributed to the hysteresis occurring only within a specific range of the applied magnetic field. In the negative field sweep, the applied field strength was not high enough to fully polarize the magnetic domains. This results in partial polarization, creating a minor loop.

To look for changes in the antiferromagnetic structure upon cooling below 10 K where a small c-oriented magnetization and the anomalous Hall effect appears, we examined the temperature and field dependence of the Q = (10$\bar{1}$0) magnetic Bragg peak. These data were acquired using 14.7 meV neutrons on the EIGER triple-axis spectrometer at the Swiss spallation neutron source SINQ, Paul Scherrer Institute, Villigen, Switzerland. The magnetic diffraction intensity is proportional to the sum squared staggered magnetization along the perpendicular $[\bar{1}2\bar{1}0]$ and [0001] directions. With a field applied along the vertical $[\bar{1}2\bar{1}0]$ direction, there is thus sensitivity to the in-plane domain distribution. Though data marked with blue symbols have lower counting statistics, Supplementary Fig. 5g shows the field dependence of the overall domain fraction is indistinguishable above (blue symbols, 12 K) and below (red symbols, 1.5 K) 10 K. Supplementary Fig. 5h shows the temperature dependence of the Q = (10$\bar{1}$0) magnetic Bragg peak intensity in the presence of a 2 T magnetic field along $[\bar{1}2\bar{1}0]$, which disfavors domains with staggered magnetization along that direction. The temperature dependence is indistinguishable from that acquired in zero fields at the (0001) peak, where all domains contribute equally to the scattering. These data show the magnetic structure of V_1/3NbS₂ is virtually unchanged across 10 K. We propose that the appearance of a zero-field Hall response and remnant magnetization along the c-axis for T  <  10 K results from a subtle change in domain wall dynamics at this temperature.

The line shape and integrated intensity of a rocking scan is affected by all components of the resolution function, including the out-of-plane resolution. To account for these effects, we assume an infinite correlation length along the c-axis and adopt the following isotropic form for the in-plane correlation function:

$$\langle {S}_{i}{S}_{j}(r)\rangle \sim {e}^{-r/\xi },r\equiv \sqrt{{x}^{2}+{y}^{2}}$$

(1)

The corresponding Bragg peak profile can be obtained analytically by Fourier transformation and the result is isotropic in 2D in-plane q-space:

$$I({{{\bf{q}}}})={I}_{0001}\frac{2\pi \kappa }{{({q}_{x}^{2}+{q}_{y}^{2}+{\kappa }^{2})}^{3/2}}\delta ({q}_{z})\delta (\hslash \omega ),\kappa=1/\xi,$$

(2)

where I₀₀₀₁ is the integrated peak intensity at Q = (0001).

The experimental peak profile is obtained via convolution with the resolution function defined as:

$$R({{{\bf{q}}}},{{{{\bf{q}}}}}_{0})= {(2\pi )}^{-2}\det ({{{\bf{M}}}})\exp \{-\frac{1}{2}({{{\bf{q}}}}-{{{{\bf{q}}}}}_{0}){{{\bf{M}}}}({{{\bf{q}}}}-{{{{\bf{q}}}}}_{0})\}\\ {{{\bf{M}}}}= \left[\begin{array}{cccc}{M}_{11}&{M}_{12}&{M}_{13}&0\\ {M}_{21}&{M}_{22}&{M}_{23}&0\\ {M}_{31}&{M}_{32}&{M}_{33}&0\\ 0&0&0&{M}_{44}\end{array}\right]$$

(3)

Here q₀ = (q_0,z, q_0,y, ℏω₀, q_0,x) is the instrument-targeted energy and wave-vector transfer for each point in the rocking scan passing through Q = (0001).

Reflecting the mirror symmetry of the instrument about the horizontal plane, the structure of M allows us to complete the integration over x:

$$\tilde{I}({{{{\bf{q}}}}}_{0})= \int{R}_{0001}({{{\bf{q}}}}-{{{{\bf{q}}}}}_{0})I({{{\bf{q}}}})d{{{\bf{q}}}}=\int{R}_{\parallel }({{{{\bf{q}}}}}_{\parallel }-{{{{\bf{q}}}}}_{0,\parallel })\int{R}_{\perp }({q}_{x}-{q}_{0,x})I({{{\bf{q}}}})d{q}_{x}d{{{{\bf{q}}}}}_{\parallel }\\= \sqrt{\frac{{M}_{44}}{2\pi }}\int{R}_{\parallel }({q}_{y}-{q}_{0,y}){| }_{{q}_{z}-{q}_{0,z},\hslash \omega -\hslash {\omega }_{0}=0}\int\exp (-\frac{1}{2}{M}_{44}{q}_{x}^{2})I({q}_{x},{q}_{y})d{q}_{x}d{q}_{y}\\= \frac{\sqrt{\det ({{{\bf{M}}}})}}{4{\pi }^{2}}{I}_{0001}\int\exp [-\frac{1}{2}{M}_{22}{({q}_{y}-{q}_{0,y})}^{2}]\int\exp (-\frac{1}{2}{M}_{44}{q}_{x}^{2})\frac{2\pi \kappa }{{({\kappa }^{2}+{q}_{x}^{2}+{q}_{y}^{2})}^{3/2}}d{q}_{x}d{q}_{y}\\= \kappa \sqrt{\frac{\det ({{{\bf{M}}}})}{2\pi }}{I}_{0001}\int\frac{1}{{\kappa }^{2}+{q}_{y}^{2}}\exp [-\frac{1}{2}{M}_{22}{({q}_{y}-{q}_{0,y})}^{2}]U(1/2,0,\frac{{\kappa }^{2}+{q}_{y}^{2}}{2}{M}_{44})d{q}_{y}$$

(4)

Here q_∥ is the wave-vector within the scattering plane (yz plane). R₀₀₀₁ is the Gaussian resolution function at Q  = (0001). $U(a,b,z)=1/\Gamma (a)\int_{0}^{+\infty }{e}^{-zt}{t}^{a-1}{(1+t)}^{b-a-1}dt$ refers to the confluent hypergeometric function⁶¹. The delta function within the peak profile and condition of rocking scans q_0,x  =  0, q_0,z ≈ 0 was applied from the first line to the second line of Eq. (4).

The q_y integrated intensity is thus given by

$${I}_{ob,0001}= \kappa \sqrt{\frac{\det ({{{\bf{M}}}})}{2\pi }}{I}_{0001}\iint \frac{1}{{\kappa }^{2}+{q}_{y}^{2}}\exp [-\frac{1}{2}{M}_{22}{({q}_{y}-{q}_{0,y})}^{2}]U(1/2,0,\frac{{\kappa }^{2}+{q}_{y}^{2}}{2}{M}_{44})d{q}_{y}d{q}_{0,y}\\= \kappa \sqrt{\frac{\det ({{{\bf{M}}}})}{{M}_{22}}}{I}_{0001}\int\frac{1}{{\kappa }^{2}+{q}_{y}^{2}}U(1/2,0,\frac{{\kappa }^{2}+{q}_{y}^{2}}{2}{M}_{44})d{q}_{y},$$

(5)

This one dimensional integral can readily be evaluated through numerical integration. To duly account for the field dependent correlation length κ, I_ob,0001 was used to convert the measured (0001) rocking scan integrated intensity into a full integrated intensity measure of the total coherent staggered magnetization.

The DFT+DMFT calculation

The density functional theory (DFT) calculation was performed by the ab initio code OpenMX. The generalized gradient approximations (GGA) of Perdew-Burke-Ernzerhof (PBE) were adopted for the exchange-correlation potential. An 8 × 8 × 4 k-point grid was used for the calculation. We employed the valence orbital sets V6.0-s3p3d2, Nb7.0-s3p2d2, and S7.0-s3p3d2f1, and set a cutoff energy of 150 Ry for the numerical integrations. The Wannier functions of the t_2g vanadium orbitals and the ${d}_{{z}^{2}}$, ${d}_{{x}^{2}-{y}^{2}}$, and d_xy niobium orbitals were constructed from an outer energy window of [−5 eV: 5 eV].

The dynamical mean-field (DMFT) calculation was performed with the finite-temperature exact diagonalization solver, where the dynamical mean field was represented by six bath sites. We chose a reasonable value of the intra-orbital Coulomb interaction U  =  3 eV and Hund’s coupling J  =  0.5 eV for V-t_2g orbitals; the inter-orbital Coulomb interaction was determined by $U{\prime}=U-2J$. For the double-counting correction, we subtracted the self-energy in the high-frequency limit of the paramagnetic solution, which corresponds to a static mean-field value with inter-orbital components. The spectral function was obtained with 10 meV energy smearing.