Altermagnetism in the layered intercalated transition metal dichalcogenide CoNb₄Se₈

Abstract

Altermagnets (AMs) are a new class of magnetic materials that combine the beneficial spintronics properties of ferromagnets and antiferromagnets, garnering significant attention recently. Here, we have identified altermagnetism in a layered intercalated transition metal diselenide, CoNb₄Se₈, which crystallizes with an ordered sublattice of intercalated Co atoms between NbSe₂ layers. Single crystals are synthesized, and the structural characterizations are performed using single crystal diffraction and scanning tunneling microscopy. Magnetic measurements reveal easy-axis antiferromagnetism below 168 K. Density functional theory (DFT) calculations indicate that A-type antiferromagnetic ordering with easy-axis spin direction is the ground state, which is verified through single crystal neutron diffraction experiments. Electronic band structure calculations in this magnetic state display spin-split bands, confirming altermagnetism in this compound. The layered structure of CoNb₄Se₈ presents a promising platform for testing various predicted properties associated with altermagnetism.

Introduction

Reducing power consumption and developing materials for smaller and faster devices is one of the principal targets in the field of spintronics. Antiferromagnetic materials (AFMs) hold significant potential in this area because they offer greater stability and faster dynamics compared to ferromagnetic (FM) materials¹. However, unlike FMs, it is challenging to obtain an external response from AFMs, particularly from collinear AFMs, due to their zero net magnetization. Recent theoretical advancements have shown that, under specific crystallographic conditions, even collinear AFMs can exhibit non-zero anomalous Hall effect (AHE), magneto-optical Kerr effect, and spin-splitting of electron bands, similar to FMs^2,3,4,5. These materials have been termed “altermagnets” (AMs)^6,7,8.

In a collinear antiferromagnet, there exists at least one symmetry operation that maps one spin sublattice onto the other. Typically, this symmetry operation is a lattice translation or spatial inversion, which preserves the electron energy, resulting in Kramers (spin) degenerate electron bands, unlike in ferromagnets. However, in certain (so-called altermagnetic) cases this operation is neither translation nor inversion, but a mirror, glide, rotation, or similar operation. In these cases, the electron states at a general k-point are not spin-degenerate. At the same time, the sign of the spin splitting alternates in momentum space, giving rise to the name “AMs.” As exciting as the new realization is, the symmetry requirements are quite stringent, and hence, there are just a handful of materials identified as AMs. Some have been predicted theoretically^5,6,7,9, while very few, such as MnTe and CrSb, have been realized experimentally^{10,11,12,13,14}. AMs combine the beneficial properties of both ferromagnets and antiferromagnets. For example, in momentum space, they feature spin polarized bands similar to those of FMs, while in real space, they exhibit collinear AFM ordering, resulting in resonance frequencies in the terahertz range, compared to the gigahertz frequencies typical of FMs. To this end, one of the most anticipated applications of AMs is in terahertz tunnel junctions, which could significantly enhance the read/write speeds of electronic devices⁷. Additionally, new theoretical proposals suggest that proximity of AMs to topological and superconducting materials could give rise to several interesting phenomena^{15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30}. This emerging field not only requires the discovery of new materials but also the development of easily exfoliable materials to create devices that could instantiate these phenomena.

In this article, we report altermagnetism in a layered intercalated transition metal dichalcogenide (ITMD) compound CoNb₄Se₈. We grew single-crystal samples and verified the hexagonal crystal structure with an ordered interstitial Co sublattice using single crystal X-ray diffraction (SC-XRD). Our measurements of magnetic, transport, and thermal properties suggest that the material exhibits easy-axis anti-FM ordering. Our density functional theory (DFT) calculations predict this spin orientation and the A-type magnetic pattern, which we subsequently confirmed through single-crystal neutron diffraction experiments. The DFT calculations yield an anisotropy energy of 0.7 meV per Co atom and a magnetic moment of 1.3 μ_B, with the spin-flop field estimated to be on the order of 100 T. The calculated band structure reveals a clear spin splitting in the compensated collinear anti-FM state, consistent with the altermagnetic symmetry of this compound.

Results and discussion

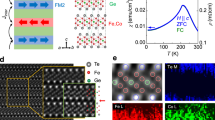
It is well known that intercalating a 3d transition metal element into the 2H-NbX₂ (X = S, Se) layers results in two distinct sets of ordered compounds^31,32. When a 3d transitional metal element occupies 1/4 of the octahedral holes, it forms an ordered centrosymmetric structure with a 2 × 2 superlattice based on the NbX₂ unit cell in the hexagonal space group P6₃/mmc. In contrast, when the intercalant atom occupies 1/3 of the holes, it creates an ordered $\sqrt{3}\times \sqrt{3}$ superstructure within the non-centrosymmetric hexagonal space group P6₃22. CoNb₄Se₈ falls into the former category, and its schematic is depicted in Fig. 1a. We synthesized single crystals of CoNb₄Se₈ using a chemical vapor transport method (see Methods for details) and determined the crystal structure through SC-XRD. The diffraction peaks obtained from a single crystal of CoNb₄Se₈ are shown in Fig. 1b, with an optical image of the crystals in the inset. The 2 × 2 superlattice unit cell, corresponding to the ordered structure in space group P6₃/mmc (associated with the 1/4th intercalation), is clearly visible in the diffraction peaks, highlighted by the yellow lines in Fig. 1b. The ordered structure contrasts with the original 1 × 1 disordered model³³. Further details on the structural refinement can be found in Tables S1–S4.

Fig. 1: Structure and structural characterization.

a Sketch of crystal structure of CoNb₄Se₈. b Measured (hk0) zone of CoNb₄Se₈. The reciprocal unit cell of the ordered structure is outlined in yellow, while the subcell corresponding to that of NbSe₂ base unit cell reported in ref. ³¹ is outlined in blue (also see Fig. S1). Inset shows an optical image of single crystals of CoNb₄Se₈. c STM topographic image of as-cleaved CoNb₄Se₈. Inset: a zoomed-in STM topographic image showing well-ordered Co triangular lattice.

The structural characterization was further examined using STM topography, as shown in Fig. 1c, where a triangular lattice of Co atoms is observed, with clearer visualization in the inset. The distributed defects are likely due to the cleaving process. The 2 × 2 superstructure of the Co layer, with a lattice constant of 6.8 Å, aligns with the measurements from SC-XRD and is confirmed by the Fourier transform presented in Fig. S2. In this structure, the bond center between two Co atoms along the c-axis lacks inversion symmetry due to the NbSe₂ prismatic layer, as illustrated in Fig. 1a. An A-type anti-FM ordering (FM Co planes coupled antiferromagnetically along c-axis, verified by our experiments and calculations presented below) in such a structure satisfies the criteria for altermagnetism^2,34,35. This was recently also pointed out for the isostructural and isomagnetic compound FeNb₄S₈³⁶. While chemical substitution is necessary to stabilize FeNb₄S₈ in single crystal form, potentially affecting its band structure, unsubstituted CoNb₄Se₈ naturally forms single crystals with a well-ordered Co sublattice, offering a pristine platform for studying the altermagnetic properties.

Physical properties of CoNb₄Se₈ were measured using single crystals, as shown in Fig. 2. DC magnetic susceptibility (χ = M/B), where M represents the magnetic moment and B is the external magnetic field, was measured with B set at 0.1 T, as depicted in Fig. 2a. When B is aligned parallel to the c-axis, the susceptibility χ_c exhibits a sharp decrease below 168 K. In contrast, with B in the ab-plane, there is a slight kink at 168 K in the susceptibility χ_ab followed by a gradual and modest increase at lower temperatures. This behavior is characteristic of anti-FM ordering with moments aligned parallel to the c-axis³⁷. However, what is less typical is that χ remains large and anisotropic even above the Néel temperature (T_N). We attribute this unusual behavior to the strong Stoner-enhanced Pauli susceptibility of the host material NbSe₂, as discussed in Supplementary section S2 and Fig. S3.

Fig. 2: Physical properties of CoNb₄Se₈.

a Magnetic susceptibility measured in a magnetic field of 0.1 T applied along c-axis (χ_c) and within the ab-plane (χ_ab). FC and ZFC represent the magnetic susceptibility measured with field-cooled and zero-field-cooled protocol, respectively. b Magnetization measured for the magnetic field applied along c-axis at two representative temperatures 2 K (red line) and 100 K (blue line). c Electrical resistivity as a function of temperature. Inset shows the magnetoresistance at 1.8 K. d Heat capacity as a function of temperature. Inset shows a magnified view of the lambda-type anomaly at T_N.

Furthermore, both χ_c and χ_ab exhibit a bifurcation between the field-cooled (FC), and zero-FC (ZFC) data below T_N, likely due to domain walls freezing during the ZFC measurement. Additionally, a cusp-like feature in χ along both directions is observed at 30 K as indicated by an arrow in Fig. 2a. This feature may indicate either a second phase transition or the presence of a small unknown impurity phase in the crystal, neither of which affects the conclusions presented here. The magnetization data M(B), presented in Fig. 2b, is consistent with the anti-FM ordering below 168 K. M(B) at 2 and 100 K is linear with respect to B, with a small hysteresis observed between  ±2 T at 2 K (only as the broadening of the line, the magnified version of which is presented in Fig. S4.), possibly linked to the 30-K susceptibility kink.

The magnetic transition at 168 K influences both the electrical resistivity and heat capacity, as depicted in Fig. 2c, d, respectively. Similar to its sulfide counterparts^{38,39,40,41,42,43}, CoNb₄Se₈ is also a metal with a relatively high residual resistivity, a very small residual resistivity ratio of 2.3, and a small magnetoresistance (MR) of  ≈1% at 1.8 K and 12 T [see inset of Fig. 2a].

After identifying the anti-FM nature of the magnetic ordering, we conducted single-crystal neutron diffraction experiments to investigate the microscopic characteristics of the magnetic ordering. Intensity of the magnetic Bragg peak at (1 0 1) as a function of temperature is shown in Fig. 3a, which indicates a magnetic transition near T_N = 168 K, consistent with the results from magnetic and transport measurements. Magnetic symmetry analysis using the Bilbao Crystallography Server⁴⁴ suggested two possible magnetic space groups (MSG): $P63/{{{{\rm{mm}}}}}^{{\prime} }{{{{\rm{c}}}}}^{{\prime} }$ and $P{6}_{{3}^{{\prime} }}/{{{{\rm{m}}}}}^{{\prime} }{{{{\rm{m}}}}}^{{\prime} }{{{\rm{c}}}}$. Among these, the MSG $P{6}_{{3}^{{\prime} }}/{{{{\rm{m}}}}}^{{\prime} }{{{{\rm{m}}}}}^{{\prime} }{{{\rm{c}}}}$, corresponding to A-type magnetic order, provided a better fit to the observed data, as illustrated in Fig. 3b. The lattice parameters obtained from neutron diffraction data are a = b = 6.904(14) Å and c = 12.321(11) Å at 5 K, and a = b = 6.908(11) Å and c = 12.329(10) Å at 200 K, which are in good agreement with those from X-ray diffraction (a = 6.9178(13) Å and c = 12.390(3) Å at 295 K). The refined ordered moment of Co is 1.374(98) μ_B, which aligns with the results from DFT calculations. The DFT calculations, including spin–orbit coupling (SOC), yield a spin moment of  ≈1.35 μ_B and an orbital moment of  ≈0.11 μ_B, totaling  ≈1.46 μ_B per Co. It’s worth noting that DFT calculations in good metals may slightly overestimate the ordered moment due to spin fluctuations. The itinerant nature of the magnetic moment on Co is further supported by the fact that other, less favorable magnetic patterns, such as two variants of the q = (1/2, 0, 0) order or the FM q = (0, 0, 0) order, yield significantly reduced moments in the range of 0.9–1.2 μ_B.

Fig. 3: Single crystal neutron diffraction and magnetic structure of CoNb₄Se₈.

a Magnetic ordering parameter measured at the magnetic Bragg peak at (1 0 1) showing the AFM transition temperature near T_N= 168 K. b The observed squared structure factors ${F}_{{{{\rm{Observed}}}}}^{2}$ versus calculated structure factors ${F}_{{{{\rm{Calculated}}}}}^{2}$. The solid blue line is a guide to the eyes. c Magnetic structure determined by single crystal neutron diffraction at 5.6 K. Arrows represent the ordered magnetic moments.

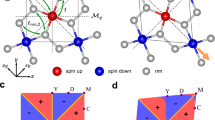
The A-type anti-FM structure identified through neutron diffraction was also found to be the most energetically favorable according to DFT calculations (refer to Fig. S5 for details). As pointed out above, in this specific crystal structure, the A-type magnetic configuration exhibits altermagnetism. This is because the symmetry operation associated with spin reversal is a mirror, not an inversion. The altermagnetic spin–split bands are clearly visible in the band structure calculations shown in Fig. 4. Despite the presence of numerous symmetry-degenerate planes in the Brillouin zone (horizontal planes at Γ and at A, and vertical planes passing through Γ-K and M-K lines), there is a significant induced spin splitting at intermediate k_z’s, which reveals the altermagnetism in CoNb₄Se₈.

Fig. 4: Calculated electronic band structure and Fermi surface of CoNb₄Se₈.

a Calculated band structure of CoNb₄Se₈ with the A-type AFM (altermagnetic) structure. ${\Gamma }^{{\prime} }$, ${{{{\rm{M}}}}}^{{\prime} }$ and ${{{{\rm{K}}}}}^{{\prime} }$ points correspond to midpoints between ΓA, ML, and KH, respectively. b Fermi surface of the same. Green (brown), cyan (magenta) and blue (red) colors correspond to the first (second) spin direction. Note the degeneracy planes, as described in the text. c The Fermi surface cut at k_z = π/2c, i.e., through the ${\Gamma }^{{\prime} }-{{{{\rm{M}}}}}^{{\prime} }-{{{{\rm{K}}}}}^{{\prime} }$ plane.

As shown in the Fermi surface plot in Fig. 4, this material belongs to the class of g-wave altermagnet⁷, with the aforementioned nodal planes parallel to z and passing through Γ–K and K–M lines, as well as a horizontal nodal plane at k_z= 0 and π/c. The Fermi surface consists of one hole pocket around Γ and three compensating electron pockets around M (neglecting a tiny hole pocket around Γ). As depicted in Fig. S6, at T ~ 80 K, these pockets exhibit the same mobility and perfectly compensate each other in the ordinary Hall conductivity.

One manifestation of AM is the potential to exhibit an AHE. However, this effect is contingent on alignment of the spins (Néel vector) relative to the crystal structure. In CoNb₄Se₈, analyses^34,35 have shown that the only high-symmetry direction of the Néel vector that supports AHE is [210], meaning the easy axis must lie in the ab-plane and be perpendicular to the Co–Co bond. Since the magnetic easy axis in CoNb₄Se₈ is out-of-plane, the altermagnetic state does not permit AHE in any orientation, which aligns with the Hall resistivity data shown in Fig. S6.

However, the more significant aspect of AM, which is spin polarized bands, combined with the layered crystal structure of CoNb₄Se₈, could lead to many fascinating possibilities. The well-ordered Co sublattice observed in structural characterizations makes this compound promising. Based on our previous experience with two other ITMDs CrNb₃S₆⁴⁵, and CoNb₃S₆⁴⁶, spin–split bands should be observable in photoemission experiments. Moreover, the ease of exfoliation into nanosheets makes it practical to interface the AM with other materials such as topological insulators and superconductors to test the proposed novel phenomena enabled by AM. The potential for epitaxial growth of the Se-based ITMDs⁴⁷ also makes this system attractive for the fabrication and testing of anticipated AM tunnel junctions. Another possibility is to create heterostructures with other A-type or some other antiferromagnets with FM planes, which could positively influence the Néel vectors and enhance the coupling of altermagnetic domains with an external field, as suggested in some studies⁴⁸.

Additionally, it’s important to note that Co intercalation leads to a noticeable lattice distortion in the NbSe₂ layer. As illustrated in Fig. S7a, Nb atoms farther away from Co are displaced, forming triangles with a side length of 3.295 Å, while the other two Nb-Nb bonds have lengths of 3.460 and 3.623 Å, respectively, with the longest bond about 0.33 Å longer than the shortest. Simultaneously, the Se plane undergoes a vertical warping, where, somewhat counterintuitively, Se atoms above the smaller Nb triangles are pulled down, even closer to Nb, and the others are pushed up [see Fig. S7b]. Similar results are consistently observed in DFT optimization of the crystal structure. These distortions can be described as a 3 × 3 charge density wave in both the Nb and Se planes. An intriguing, yet unexplored question is the potential phonon-magnon coupling—specifically, how these atomic displacements might affect the exchange interactions and, conversely, how magnetic order might affect the phonons.

In conclusion, we successfully synthesized single crystals of CoNb₄Se₈, where the Co atoms occupy the 1/4 octahedral holes between NbSe₂ layers, resulting in a structure belonging to the space group P6₃/mmc. The A-type anti-FM structure, characterized by easy-axis spin orientation as determined by neutron diffraction experiments, aligns well with the predictions from DFT calculations. These calculations also reveal spin-split bands characteristics indicative of altermagnetism. To establish altermagnetism, two criteria must be met: the crystal symmetry should ensure that bonds between any two anti-FM atoms lack a center of symmetry, and there should be anti-FM ordering with a zero propagation vector. CoNb₄Se₈ meets both criteria, and spin–split bands are clearly observed in the band structure calculations, confirming altermagnetism in this compound. Experimentally observing this should be straightforward, especially using spin-polarized ARPES experiments. The layered structure of CoNb₄Se₈ could open up new possibilities for testing various properties, particularly at interfaces with phenomena such as ferromagnetism, antiferromagnetism, band topology, and superconductivity. After the submission of this work for publication, experimental verification of altermagnetic spin-splitting by means of spin resolved ARPES and spin- and angle-resolved electron reflection spectroscopy has been reported⁴⁹.

Methods

Single crystals of CoNb₄Se₈ were grown by chemical vapor transport using iodine as the transport agent. First, a polycrystalline sample was prepared by heating stoichiometric amounts of cobalt powder (Alfa Aesar 99.998%), niobium powder (Alfa Aesar 99.8%), and selenium pieces (Alfa Aesar 99.9995%) in an evacuated silica ampule at 950 ^∘C for five days. Subsequently, 2 g of the powder was loaded together with 0.4 g of iodine in a fused silica tube of 14 mm inner diameter. The tube was evacuated and sealed under vacuum. The ampule of 10 cm length was loaded in a horizontal tube furnace in which the temperature of the hot zone was kept at 950 ^∘C and that of the cold zone was  ≈850 ^∘C for seven days. Several CoNb₄Se₈ crystals formed with a distinct, well-faceted flat plate-like morphology.

The crystals of CoNb₄Se₈ were examined by SC-XRD. The SC-XRD data were collected at room temperature using a Bruker D8 diffractometer equipped with APEX2 area detector and Mo Kα radiation (λ = 0.71073 Å). Data integration, cell refinement, and numerical absorption corrections were performed by the SAINT program and SADABS program in APEX3 software^50,51. The precession images were also synthesized in APEX3. The structure was solved by Olex2 using direct methods with the XS structure solution program and refined with full-matrix least-squares methods on F² by the XL refinement package^52,53.

The STM measurements were performed in a Unisoku 1500 microscope at a temperature of 4.2 K in ultrahigh vacuum with SPECS Nanonics electronics. The crystals were cryogenically cleaved at a temperature of 80 K before inserting into the STM head. Gwyddion was used to process STM images.

Compositional analysis was done using an energy-dispersive X-ray spectroscopy (EDS) at the Notre Dame Integrated Imaging Facility at room temperature. A Bruker EDS attached to a Magellan 400—field emission scanning electron microscope was used for the measurement.

DC magnetic susceptibility, and magnetization were measured using a quantum design magnetic property measurement system (MPMS XL 7-T). Resistivity, MR, Hall resistivity, and heat capacity measurements were performed in a 14-T quantum design dynacool physical property measurement system. Single crystals of CoNb₄Se₈ were trimmed to adequate dimensions for electrical transport measurements. Crystals were oriented with the [0 0 1] direction parallel to the applied field for the c-axis. Magnetic field and electric currents both in magnetic and magnetotransport measurements were applied to a random direction in the ab-plane. Resistivity and Hall measurements were performed using the 4-probe method. Pt wires of 25 μm were used for electrical contacts with contact resistances less than 30 Ohms. Contacts were affixed with Epotek H20E silver epoxy. An electric current of 2 mA was used for the electrical transport measurements. Contact misalignment in the MR measurement was corrected by symmetrizing the measured data in positive and negative magnetic fields. Magnetic and magnetotransport measurements were verified in more than one crystal grown in more than one growth batch for reproducibility.

Single crystal neutron diffraction was carried out on the HB-3A DEMAND⁵⁴ at the high flux isotope reactor at Oak Ridge National Laboratory. A wavelength of 1.533 Å from a bent Si-220 monochromator⁵⁵ was used for mapping the reciprocal space at selected temperatures and the data collection at 5.6 and 200 K. The Bilbao Crystallography Server⁴⁴ was used for the magnetic symmetry analysis and Fullprof software⁵⁶ for the nuclear and magnetic structure refinement.

For the DFT calculations a projector-augmented wave method as implemented in the Vienna ab initio simulation package⁵⁷. It was used both for structure optimization and for the search of the magnetic pattern. For the latter, a doubled supercell consistent with a hypothetical in-plane propagation vector (1/2,0,0), similar to that in CoNb₃S₆, was used. The results were fitted to the two nearest neighbors Heisenberg Hamiltonian, with excellent fit quality. The intraplanar exchange appears to be FM, J_∣∣ ≈ 5.8 meV, and interpalnar anti-FM, J_⊥ ≈ 25.6 meV, normalized to a unit magnetic moment. In all cases, a generalized gradient approximation for the exchange and correlation functional⁵⁸ was utilized. No LDA+U or other corrections beyond DFT were applied. Up to 11 × 11 × 6 k-point mesh (64 irreducible points) was used to structural optimization, and 48 × 48 × 25 for the Fermi surface and transport analyses. All calculations except those for magnetic anisotropy were performed without the SOC.

The optimized structure was then used with an augmented plane wave Wien2k code WIEN2K⁵⁹ for the Fermi surface analysis.

Schematic of both crystal and magnetic structures were constructed using the three-dimensional visualization system VESTA⁶⁰.