Introduction

Semiconductor white LEDs (WLEDs) have penetrated every aspect of people’s daily lives and are rapidly replacing traditional artificial light sources (e.g., incandescent lamps) due to their long lifespan and low energy consumption1,2,3,4. The main fabrication method of WLEDs is through coating phosphors on blue LEDs, which makes the resulting WLED spectrum lack specific bands, especially the cyan (commonly known as cyan gap) and red (ultra-low value of R9) bands5. Current WLEDs will, therefore, be limited in colour-critical high-level applications6. Besides, the inevitable high blue light component will lead to severe blue light pollution that can result in sleep disorders, retinal damage and a profound adverse effect on the habitat and reproduction of natural creatures7,8,9. Thus, exploring novel mechanisms of white light generation and balancing white light components to realise sunlight-like full-spectrum white light is of tremendous significance.

Single broadband or multi- and discrete emission directly excited by electricity would be a promising approach to generating sunlight-like full-spectrum white light. Materials with self-trapped exciton (STE) characteristics have shown great promise due to their broadband emission capability from single-layer emitters10,11,12,13,14,15,16. However, precisely tuning the spectral component of the single broadband emission is almost out of reach. For materials with multi- and discrete luminescence centres, regulating the flow and distribution of charges between different luminescence centres is still challenging17.

The quality of a white light source can be evaluated using five core indicators: Commission Internationale de l’Eclairage (CIE) coordinates, Colour Rendering Index (CRI), Correlated Colour Temperature (CCT), Delta u,v (Duv, distance from the Planckian locus) and Melanopic ratio. An ideal and healthy artificial white light source is supposed to meet the following requirements: (i) CIE coordinates close to standard white light (0.33, 0.33); (ii) a CRI close to 100, which evaluates the ability to restore the colours of the object it illuminates accurately; (iii) a CCT close to standard daylight of 5800 K18; (iv) low value of Duv close to 0, which is a metric that quantifies the distance between the chromaticity of a given light source and an ideal blackbody radiator curve (commercial standard is between −0.02 and 0.02); (v) Melanopic ratio (M/P ratio) close to standard sunlight of 1, which quantifies the effect of light on circadian rhythm.

Here, we report a large-area WLED with sunlight-like full-spectrum white electroluminescence (EL) originating from heterophase γ/δ-CsPb(I/Cl)3. According to the theoretical calculation results, we precisely regulate γ/δ-CsPb(I/Cl)3 heterophase emitter at the nanoscale for uniformising heterophase films, balancing flow and distribution of charges and modulating white emission—further enabling uniform and high-quality white emission. As-fabricated WLED device exhibits CIE coordinates of (0.33, 0.33), a CRI of 95 (R9 = 97), a CCT of 5829 K, a Duv of −3 × 10−4 and an M/P ratio of 1.004, with an emitting area of 100 mm2. The match indices of the five core indicators (CIE coordinates, CRI, CCT, Duv and M/P ratio) to standard sunlight reach 100%, 95% (97% for R9), 99.5%, 99.97%, 99.6%, respectively. Such sunlight-like white EL owes much to the mechanism of white light generation: In the heterophase γ/δ-CsPbI3 film, a fraction of the carriers recombine in γ-CsPbI3 and emit deep-red emission. In contrast, other carriers diffuse to the γ/δ-CsPbI3 heterophase interface and release broadband emission. The alloyed γ/δ-CsPb(I/Cl)3 ensures uniform heterophase distribution and balanced carrier transport and distribution, enabling tuneable full-spectrum white EL ranging from 400 to 780 nm. Benefiting from the low cost, simple structure, solution processing and area light source characteristics, such WLEDs present enormous potential in next-generation flat panel lighting and display applications.

Results

Design criteria and theoretical calculation

An ideal full-spectrum white light is supposed to cover the entire visible spectrum (Region I-III, 400–780 nm) continuously, showing no specific emission lack (Fig. 1a). Commercial WLED combines the blue emission from the blue LED chip and orange or red emission from the phosphor, suffering from cyan and deep-red gap. Thus, to design and achieve ideal full-spectrum white light, two core criteria need to be met: (i) such emitting material has multi- and discrete luminescence centres (covering Region I–III simultaneously). (ii) the flow and distribution of charges between different luminescence centres should be regulated to achieve a balanced white light spectrum.

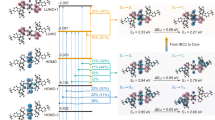
Fig. 1: The design of full-spectrum white light.
figure 1

a Schematic spectrum of sunlight, commercial WLED and ideal WLED. b Crystal structure and optical performance of the different CsPbI3 phases. c Material design for full-spectrum white light. d The total energy differences at 0 K (red) and the Helmholtz free energy differences at 300 K (turquoise) between the γ and δ phases in the form of ∆E(T) = Eγ(T) − Eδ(T), as a function of the Cl− concentration. e Schematic diagrams of the relative thermodynamic stability between the γ and δ phases for pure CsPbI3 and CsPb(I/Cl)3 systems, respectively.

Full size image

The CsPbI3 system has multiple polymorphs, including the optically active perovskite/black phases: α (cubic), β (tetragonal), and/or γ (orthorhombic), and non-perovskite/yellow phase (δ-phase), as shown in Fig. 1b. α/β-phase is a metastable phase, while γ/δ-phase is a metastable phase. Black phases typically exhibit similar optoelectronic properties (covering Region III in Fig. 1a), and the series of structural distortions mediate the phase transition between different black phases. The phase stability increases in the order α, β and γ19. The α-phase spontaneously undergoes a phase transition to β-phase, then to γ-phase, and finally to δ-phase at room temperature (Supplementary Fig. 1). δ-phase has STE characteristics originating from lattice twisting, which enables broadband emission (covering Region I and Region II in Fig. 1a) and large Stokes shift17. Thus, a heterophase film consisting of yellow and black phases could cover the entire visible spectrum (Region I–III) theoretically (Fig. 1c). Here, we fabricated heterophase films comprised of mixtures of phases achieved by spin-coating α-CsPbI3 quantum dot (QD) solutions (Supplementary Fig. 2 and Supplementary Fig. 3) and annealing the QD film (Supplementary Fig. 4)20. The resulting heterophase film could exhibit a combination of deep-red emission from the black phase and broadband emission from the yellow phase, which will be detailed further below.

Next, we introduced Cl− to form alloyed and thermodynamically stable heterophase γ/δ-CsPb(I/Cl)3 for balanced flow and distribution of charges between different luminescence centres. We investigated the relative stability between the γ- and δ-phase in the γ/δ-CsPb(I/Cl)3 system by first-principles and thermodynamic calculations (Fig. 1d, Supplementary Fig. 5 and Supplementary Fig. 6). The Helmholtz free energy difference approached zero at 33% Cl− component at room temperature, indicating that the γ-phases and δ-phases could coexist much more uniformly, as depicted in Fig. 1d and Supplementary Fig. 5b–e. It turns out that alloyed Cl− brought down the phase-transition temperature between the γ and δ phases (Supplementary Fig. 5b–e) and facilitated the stabilisation of the γ phase in thermodynamics (Fig. 1d). Mixed halide engineering [CsPb(Cl/Br)3 or CsPb(Br/I)3] is a common strategy to tune the emission. However, alloying Cl− in CsPbI3 could only regulate the tilting angles of the lattice instead of dramatically changing the optical properties of CsPbI3 dramatically (Supplementary Fig. 6)21. In brief, the theoretical analysis supports that up to 30% proportion of the Cl− component enables a more uniform heterophase distribution and feasible lattice twisting, providing the possibility for achieving balanced carrier distribution and tuneable full-spectrum white light (Fig. 1e), as observed experimentally later.

Nanoscale heterophase structure and composition

To understand the phase composition and structure of the heterophase films, we performed scanning electron diffraction (SED) measurements to identify the specific nature of octahedral tilting in a given perovskite sample. The annular dark field image of the SED scan revealed a varied and heterogeneous phase composition and structure, as illustrated in Fig. 2a. The diffraction signals from the regions of interest were summed to extract mean diffraction patterns. For the region of interest marked using a red box in Fig. 2a, the resulting mean diffraction pattern was presented in Supplementary Fig. 7. The observed diffraction rings corresponded well to the diffracting planes of the γ-phase, Pnma perovskite. However, we also observed short reflections at 0.10 Å−1, as indicated by the yellow arrows in Supplementary Fig. 7a. These very short vector lengths were inconsistent with any of the black phases of CsPbI3, where the shortest lengths expected are 0.16 Å−1 (observed as the vector length of the first diffraction ring). In contrast, a mean diffraction pattern extracted from the region of interest marked using a blue box in Supplementary Fig. 7b (comprising of smaller crystallites) showed no very short reflections. Instead, the shortest diffraction ring corresponds to a length of 0.16 Å−1, which is likely indicative of black-phase CsPbI3.

Fig. 2: Scanning electron diffraction microscopy reveals heterophase films are composed of mixtures of γ- and δ-phases.
figure 2

a Annular dark-field images reconstructed from SED data of heterophase film. Scale bar, 100 nm. b Annular dark field image of a region of interest from a marked in red and electron diffraction pattern corresponds to the relevant sequence numbers. Scale bar, 100 nm. c Annular dark field image of a region of interest from a marked in blue and electron diffraction pattern corresponds to the relevant sequence numbers. Scale bar, 100 nm. All scale bars in all experimental diffraction patterns shown are 0.6 Å−1. GIWAXS patterns of (d) pristine α-CsPbI3 film, (e) α-CsPb(I/Cl)3 film, (f) pristine γ/δ-CsPbI3 film and (g) γ/δ-CsPb(I/Cl)3 film.

Full size image

In order to investigate the nature of the short reflections further, we examined the two-dimensional electron diffraction signals from both regions of interest. In the region of interest highlighted in red in Fig. 2a, shown zoomed in in Fig. 2b, the diffraction intensity from most grains can be indexed to an orientation of γ-phase, Pnma perovskite. There was a significant grain-like feature on the right-hand side of the scan where diffraction taken from two smaller regions of interest (No.3 and No.4) can both be indexed to δ-phase CsPbI3. However, this starkly contrasted with the region of interest marked in blue, where no evidence of δ-phase grains was found. Instead, only γ-phase was observed, as shown in the electron diffraction patterns in Fig. 2c.

The co-existence of γ-phase (expected to emit at ~700 nm) and δ-phase (expected to emit 400–600 nm) CsPbI3 explained the broadband white emission observed in heterophase film. Generally, emission is expected from the lowest bandgap regions in a mixed-band-gap semiconductor (as is the case here). This would suggest that the emission should originate primarily from the lower bandgap γ-phase. However, the combined optoelectronic and nanoscale structural evidence indicated that the δ-phase can still emit a substantial fraction of broadband blue emission. The much larger sizes of the δ-phase grains (see Supplementary Fig. 8), compared to the γ-phase, suggested that any charges generated in the wider band gap δ-phase may not be able to diffuse far enough to emit in lower bandgap regions. The two distinct structural phases and their respective emissions combine to provide the desired broadband white light emission.

We used X-ray diffraction (XRD) and Synchrotron grazing incidence wide-angle X-ray scattering (GIWAXS) to resolve further the evolution of the structure of the materials in α-CsPbI3 QD films and heterophase films (Fig. 2d–g and Supplementary Fig. 9). As seen in XRD patterns presented in Supplementary Fig. 10, the main diffraction peaks of pristine α-CsPbI3 QD films were located at 14.1°, 20.0° and 28.6°, corresponding to the characteristic diffraction peaks of the α-CsPbI3 structure22. After alloying Cl−, the diffraction peaks slightly shifted towards larger angles, signifying structural contraction. After annealing, the Bragg peak (100) orientation of the perovskite film transferred from the face-on orientation to isotropic orientations (Fig. 2d–g). This confirmed that the annealing process could cause phase transitions and orientation modifications at the same time. XRD results of heterophase films presented the characteristic diffraction peaks of both γ-CsPbI3 (14.1°, 20.2° and 28.5°) and δ-CsPbI3 (13.5°, 23° and 27°)23,24,25. Thus, thermal annealing transformed the α-phase into the γ/δ-phase film.

Optical characteristics and carrier dynamics

There are many challenges to realise large-area WLED based on the heterophase film. On the one hand, defects and pinholes will increase dramatically after the emitting area is greatly expanded (>100 mm2) from more typical lab-based device active areas (<4 mm2), significantly increasing carrier shunting paths and non-radiative recombination centres within a given active area26. On the other hand, microscopic spatial inhomogeneities of the heterophase distribution could result in unbalanced carrier distribution and non-uniform heterophase emission27. Hence, it is essential to homogenise the large-area film and decrease spatial variations of carrier shunting paths to achieve a large-area WLED with uniform emission.

We calculated that the alloying Cl− substantially helped make the heterophase films more spatially uniform and regulate the white emission. First, alloying Cl− could help develop a high-quality and uniform large-area heterophase film. As presented in Supplementary Fig. 11, the atomic force microscopy (AFM) images of γ/δ-CsPbI3 films showed uniform, dense morphology and a smoother surface. The root-mean-square roughness values of the γ/δ-CsPbI3 and γ/δ-CsPb(I/Cl)3 film were 9.09 and 7.98 nm, respectively. We then investigated the nanoscale structural landscape and optical microhomogeneity of heterophase films. For macroscale morphology, the pristine heterophase film showed heterogeneous appearances and properties in different regions, while the target heterophase film had good uniformity (Supplementary Fig. 12). We employed hyperspectral wide-field microscopy to spatially map the heterophase film’s photoluminescence (PL) uniformity on a microscale (Fig. 3a–c). Before annealing, the pristine α-CsPbI3 and α-CsPb(I/Cl)3 films showed uniform deep-red emission (680–700 nm), while the alloyed α-CsPb(I/Cl)3 film presented a blue shift and a narrower peak spectral distribution (Fig. 3a and Supplementary Fig. 13). After annealing, the γ/δ-CsPbI3 and γ/δ-CsPb(I/Cl)3 heterophase film exhibited the co-existence of deep-red emission (680–700 nm) and broadband emission (400–600 nm), originating from the black and yellow phases, respectively (Fig. 3b, c). Furthermore, a deeper red band was detected in the heterophase film compared with α-CsPbI3 QD films, consistent with the phase transition from α-CsPbI3 to γ-CsPbI3. Moreover, for the pristine heterophase film, γ-phase and δ-phase tended to be concentrated in specific regions. By contrast, the γ/δ-CsPb(I/Cl)3 heterophase film presented much more uniform phase distributions (Fig. 3b, c). We spied hyperspectral wide-field microscopy to analyse the carriers’ lifetime and behaviour (Fig. 3d–f and Supplementary Fig. 14). PL lifetime was determined when the PL decayed to e−1 of its maximum intensity, and the average lifetime of all pixels was captured to plot carrier lifetime maps28. Carrier lifetime maps also indicated a more uniform phase distribution in γ/δ-CsPb(I/Cl)3 heterophase film. γ-phase and δ-phase had become closely intertwined, which greatly increased the area of the heterophase interface, further resulting in the balanced carrier distribution and the excellent electrical properties of the film we present below.

Fig. 3: Uniform and spectrally tuneable heterophase films.
figure 3

a–c Hyperspectral images of α-CsPbI3 and α-CsPb(I/Cl)3 QDs film (a), the γ/δ-CsPbI3 and γ/δ-CsPb(I/Cl)3 film ranging from 660 to 700 nm (b) and the γ/δ-CsPbI3 and γ/δ-CsPb(I/Cl)3 film ranging from 400 to 600 nm (c), the scalebar is 2 μm. Spatially resolved confocal fluorescence-lifetime imaging microscopy of the heterophase film (> 600 nm) (d) and the heterophase film (<600 nm) (e), the scalebar is 2 μm. f PL lifetime of the γ/δ-CsPbI3 and γ/δ-CsPb(I/Cl)3 film. The temperature-dependent PL spectroscopy of α-CsPbI3 and α-CsPb(I/Cl)3 QDs film (g), γ/δ-CsPbI3 film (h) and γ/δ-CsPb(I/Cl)3 film (i). Early-time transient absorption spectra measurements of perovskite thin films (0–2 ps average) with different annealing times under 400 nm pump (j) and 560 nm pump (k). l Schematic of PL phenomena of band-to-band luminescence from γ-CsPbI3 and STE luminescence from δ-CsPbI3.

Full size image

Second, alloying Cl− could finely regulate the emission of heterophase film, which enables a near-perfect white emission with a low blue light component. We investigated temperature-dependent PL spectroscopy to study the emission energetics of the heterophase films. The pristine and alloyed α-CsPbI3 QDs film always showed single deep-red emission when the temperature changed from 77 K to 300 K (Fig. 3g). For the heterophase film, broadband emission and deep-red emission were both detected under 77 K, originating from δ-CsPbI3 and γ-CsPbI3, respectively. As the temperature rose, dual-emission in δ-phase was observed (Fig. 3h, i), which are named Eδ1 (380 nm–480 nm) and Eδ2 (480 nm–660 nm), respectively.

We employed ultrafast transient absorption (TA) spectroscopy to gain further insights into the electronic and structural evolution in α-phase and heterophase films (Supplementary Fig. 15). Figure 3j, k presented the early time TA spectra (0 to 2 ps average) of the pristine and annealed α-phase QDs thin films under 400 nm (3.10 eV) pump with a fluence of 76.4 μJ cm−2, corresponding to an initial carrier density of N = 8.1 × 1018 cm−3. In the pristine sample, two distinct ground-state bleach (GSB) features were observed at 665 nm and 445 nm. Since these two bleaches can also be observed under a 560 nm pump, we attributed them to the transition at the optical bandgap and the intrinsic high-energy band of α-phase QDs, labelled as α1GSB and α2GSB. With increasing annealing time, the band-edge bleach (α1GSB) redshifted, and the intensity decreased, whereas two additional GSBs peaking at 495 nm and 425 nm were observed under the 400 nm pump. This is expected as the annealing leads to the formation of mixed γ- and δ-phases. Therefore, we attributed the additional positive features in the annealed samples to the GSBs of δ-phases, labelled as δ1GSB and δ2GSB. This is consistent with the absence of the δ1GSB and δ2GSB signals under the 560nm pump, as the low-photon-energy pump is not able to depopulate the ground states of the energy levels for either δ1GSB or δ2GSB bleach. Unlike band-to-band luminescence in α-phase or γ-phase, δ-phase revealed strong characteristics of STEs, with charges migrating to multiple excited states from the ground state (Fig. 3l). The excited states first transferred to the self-trapped state through ultrafast excited-state structural reorganisation, releasing lattice distortion and broadband emission (Eδ2). Then the carriers transferred to the exciton level (Eδ1) with energy compensation, and finally fell back to the ground state (Supplementary Fig. 16). Furthermore, temperature-dependent PL results also indicated that higher temperatures could promote the transfer of carriers between heterophases (Fig. 3h, i). Moreover, changing Cl− proportions (0–30%) could adjust the relative intensity between Eδ1 and Eδ2, as shown in Fig. 3h, i and Supplementary Fig. 17, meaning carrier distribution and the white light component could be finely regulated, which is consistent with theoretical calculation results.

It is important to note that the luminescence intensity of δ-phase was greatly enhanced in the heterophase film, even comparable to that of γ-phase (Fig. 3h, i). Given the poor transport characteristic of δ-phase, we assumed that γ-phase could act as a transmission channel of charges. In the heterophase film, a fraction of the photogenerated carriers recombined in γ-phase, leading to deep-red emission. Meanwhile, the other fraction of carriers diffuses to the heterophase interface and release broadband emission. Such a proposition was consistent with the phenomenon shown in Fig. 3, where the region of the heterophase interface (framed by the dotted line) showed a longer lifetime (Fig. 3d and Supplementary Fig. 14a), and the delayed life decay curve (<600 nm) in the first few nanoseconds (Fig. 3f and Supplementary Fig. 14b). Supplementary Fig. 18 presented the PL lifetime from selected representative zones in Fig. 3d. It could be found that the heterophase interface (Zone 2) had a longer lifetime compared to γ-phase (Zone 1) and δ-phase (Zone 3) zones. Besides, continuous cross-distribution of γ-phase and δ-phase greatly increased the interface area of heterophase, which is beneficial for carrier transfer and broadband emission.

Large-area full-spectrum white electroluminescence

The large-area heterophase γ/δ-CsPbI3 film was taken as a single emitting layer in WLED to release broadband emission from 400 to 780 nm. Figure 4 presents the structure and performance of large-area WLED. WLEDs were constructed with an architecture of ITO, poly(3,4-ethylene dioxythiophene) polystyrene sulfonate (PEDOT: PSS), poly(9,9-dioctylfluorene-co-N(4-butyl phenyl)diphenylamine) (TFB), γ/δ-CsPb(I/Cl)3, 1,3,5-tris(1-phenyl-1H-benzimidazol-2-yl)-benzene (TPBi), lithium fluoride (LiF) and Al, as illustrated in Fig. 4a. A diagram and typical photograph of as-fabricated WLED with an emitting area of 100 mm2 (the overlapped area of patterned ITO and Al electrode) were shown in Fig. 4b and Supplementary Fig. 19.

Fig. 4: Fabrication and performance of typical large-area white light-emitting diodes.
figure 4

a The structure of large-area WLED, where heterophase γ/δ-CsPb(I/Cl)3 film acts as an emitting layer. b A structure diagram of large-area WLED with the overlapped 1 cm × 1 cm emitting area of patterned ITO and Al electrode. EL performance of large-area WLED. J–V–L (c), EQE (d), and CE curves (e) of the control and champion devices. EL quality of large-area WLED. CIE coordinates (f), CRI (g), CCT (h), and Duv (i) of a typical device driven by different applied voltages.

Full size image

Figure 4c shows the current density–voltage (J–V) and luminance–voltage (L–V) characteristics of typical WLEDs. The target device presented a low turn-on voltage (Von, driving voltage corresponding to a luminance of 1 cd m−2) of 3.3 V, indicating excellent charge transport in the uniform large-area heterophase film. The maximum luminance approached 4536 cd m−2 under 6.6 V. The EQE as a function of current density and current efficiency (CE) as a function of luminance for devices were shown in Fig. 4d, e, respectively. The champion device showed an EQE of 2.54% and a CE of 3.46 cd A−1 with an emitting area of 100 mm2 (see Supplementary Fig. 20 for a typical device performance with an emitting area of 4 mm2), representing the first large-area WLED to date to the best of our knowledge (Supplementary Table 1 and Supplementary Table 2). For comparison, the control device showed a maximum luminance of 108 cd m−2, a peak EQE of 0.18% and a CE of 0.35 cd A−1. The specific half-lifetime (T50) was ~220 min (L0 = 164 cd m−2), showing decent operational stability (Supplementary Fig. 21) and spectrum stability (Supplementary Fig. 22). Up to now, the EQEs of reported perovskite WLED are usually less than 1% with limited operational stability, and there is much room for improving device performance to satisfy future commercial applications (Supplementary Table 1).

To explore the device invalidation mechanism and find strategies for performance boost at the root, we examined a typical device’s EL spectrum after its luminance decreased to 20% of the initial luminance (device invalidation stage) (Supplementary Fig. 23). Firstly, the emission from TFB layers (~425 nm) appeared and continuously strengthened, which was attributed to the degraded phase and damaged heterophase film inducing current leakage. Secondly, the intensity of deep-red emission from the γ-phase continuously weakened with the intensity of emission from the δ-phase enhancing, indicating the generated Joule heat during device operation promoted phase transition from γ-phase to δ-phase constantly (a similar phenomenon was also observed during the device operation stage). Thirdly, the evolution in the shape of white EL suggested how the changes or energy flows under the unbalanced heterophase system: charge injection into the γ-phase, γ to δ-phase (Eδ2), and δ-phase (Eδ2) to δ-phase (Eδ1), which is also consistent with temperature-dependent PL results. Thus, the EL evolution during the device invalidation stage suggested that balanced carriers’ distribution and recombination ensured the stability of device operation, carrier recombination region and white EL spectrum. In brief, beyond drawing reference from reported performance-improving strategies for monochromatic perovskite LEDs, we expect more reasonable designs of the heterophase structure, composition, and distribution could enhance the carrier recombination, coupled with more rational device structure designs, further improving the efficiency and stability of the devices29,30.

Next, we focused on evaluating the lighting quality of the typical WLED and compared it with standard sunlight. When a bias of 6.4 V was applied, the typical WLED achieved a broadband EL with the standard CIE coordinates of (0.33, 0.33), as shown in Fig. 4f. A histogram of CIE coordinates for 20 target devices showed an average CIE coordinate of (0.329, 0.331), indicating that the device performance is highly reproducible (Supplementary Fig. 24). Besides, a record-high CRI of 95 was realised, which could perfectly restore the colour of objects (Fig. 4g). Especially, in response to the lack of red light in commercial WLEDs, such full-spectrum white EL has an R9 of 97, which is much higher than commercial WLEDs (usually less than 20). The values of R1 to R15 under changing bias (from 5 V to 6.6 V) were listed in detail in Supplementary Table 3. The CRI of 95 together and a CCT of 5,829 K (Fig. 4h and Supplementary Fig. 25) could meet the demand for colour-critical high-level applications. The Duv was applied to assess the proximity of the white EL to the sunlight by measuring the distance from the white light point in a chromaticity coordinate system to the ideal black body curve. For lighting applications, the Duv must be within ±0.02 (better to be negative). Surprisingly, a low value of Duv of −3 × 10−4 was achieved in this work (Fig. 4i), two orders of magnitude better than the commercial standard. Moreover, such white EL was not merely close to standard sunlight but also steady under high changing bias or in continuous operation (Fig. 4f–i and Supplementary Fig. 26).

Carrier transport and recombination process

We summarised the proposed carrier transport and recombination mechanism for the WLED in Fig. 5a–f and Supplementary Fig. 27. α-phase and γ-phase exhibited excellent carrier transport characteristics, and carriers could easily migrate directionally and recombine in the emitting layer (Process 1). As to Process 2, because of the large bandgap and deep valence-band maximum of δ-phase, together with its poor transport characteristic, it is difficult for carriers to transport and inject into δ-phase, hence, no emission can be detected for δ-phase based device. However, for γ/δ-phase layers, broadband emission from the heterophase interface (Process 3) combined with deep-red emission form full-spectrum white EL. For the non-uniform film-based WLED, the concentrated phase distribution hindered the free transfer of carriers. Thus, Process 1 ultimately dominated the whole process, and carriers gave preference to injecting into the γ-CsPbI3, emitting primarily deep-red light (Fig. 5a, c). As presented in Fig. 5b, the control WLED showed heterogeneous multicolour emission. For uniform γ/δ-phase film-based WLED, Process 3 held sway, as illustrated in Fig. 5b. Therefore, the target device featured uniform and pure white emission (Fig. 5d). Furthermore, due to the excellent transport characteristics of γ-phase, the control WLED (Process 1 as the foremost element) showed higher current density and luminescence under low applied bias (Fig. 4c).

Fig. 5: The mechanism of carrier transport and recombination in the large-area white light-emitting diodes.
figure 5

a Demonstration of carrier transport and carrier recombination process in the control device, where Process 1 dominates the whole process. b Demonstration of carrier transport and carrier recombination process in the target large-area WLED, where Process 3 plays a crucial role. c The photograph of the control large-area WLED, showing heterogeneous multicolour EL. d The photograph of the target large-area WLED, showing uniform and pure white EL. e Normalised EL spectra of the control device as applied bias increasing from 3.6 V to 6.6 V. f Normalised EL spectra of the target WLED as applied bias increasing. g–i The normalised spectrum of three commercial WLEDs, where blue light acts as the excitation source. j The normalised EL spectrum of WLED with low blue-light component. k Comparison of match index of representative commercial WLEDs and this work.

Full size image

To further verify the proposed mechanism, we measured the normalised EL spectra of the WLEDs as a function of applied bias. For the control device, the red-emission component grew in line with the increasing bias (Fig. 5e), indicating that γ-phase dominates carriers’ transport and recombination. At the same time, it is hard to transfer further to spatially detached δ-CsPbI3. However, the reverse has taken place for the target device. With the increased applied bias, an increase in broadband emission corresponding to the δ-phase was observed (Fig. 5f), signalling that the electric field could facilitate more charges to inject into the δ-phase through heterophase interphase, which is consistent with the conclusions drawn from EL evolution during the device invalidation stage (Supplementary Fig. 23). The appearance of the TFB peak for the control device can be attributed to current leakage caused by the heterogeneous surface of the control heterophase film.

Finally, we fabricated three types of representative commercial WLEDs (respectively WLED-1, WLED-2 and WLED-3). The details of construction are listed in the Experimental Section. Benefiting from such a unique mechanism of white light generation, the EL spectrum of WLED is fundamentally different from that of the typical commercial WLEDs (Fig. 5g–j). The typical commercial WLED has high blue light intensity, which is the source of blue light pollution in modern society. The M/P Ratio quantifies how much a light source stimulates the human circadian system. We plotted human photopic (visual) and melanopic (circadian) response curves in Supplementary Fig. 28. Due to the fine regulation of carrier distribution, the calculated M/P ratio was 1.004 (@6.4 V), which is close to the standard sunlight (M/P ratio = 1) and demonstrated its bio-friendly properties. The values of the M/P ratio under different biases are listed in Supplementary Table 4.

We compared five core indicators of three commercial WLEDs, large-area WLED and standard sunlight, as presented in Table 1. We plotted the Match Index of these four WLEDs to sunlight (Fig. 5k). It can be found that the WLED presented here offered overwhelming advantages over the three commercial WLEDs, and all indicators were closest to the standard sunlight. For WLED, the calculated match indices of the five core indicators to standard sunlight reached 100%, 95% (97% for R9), 99.5%, 99.97% and 99.6%, respectively.

Table 1 The comparison between commercial WLEDs, this work and sunlight
Full size table

Discussion

In conclusion, we demonstrated a large-area WLED with near-perfect full-spectrum white EL, using heterophase γ/δ-CsPbI3 as the single emitting layer, achieved by annealing α-CsPbI3 QDs film. Alloyed γ/δ-CsPb(I/Cl)3 heterophase emitter could uniformise heterophase films, balance flow and distribution of charges and modulate white emission—further enabling uniform and high-quality white emission. The WLED presented CIE coordinates of (0.33, 0.33), CRI of 95 (R9 = 97), CCT of 5829 K, Duv of −3 × 10−4 and M/P ratio of 1.004. Furthermore, the match indices of such five core indicators to standard sunlight reached 100%, 95% (97% for R9), 99.5%, 99.97% and 99.6%, respectively. This work will offer a route to designing and fabricating sunlight-like full-spectrum large-area WLEDs, advancing next-generation bio-friendly and low-cost lighting technologies.

Methods

Materials

Lead (II) iodide (PbI2, 99.99% purity), lead (II) chloride (PbCl2, 99.999% purity), oleyl amine (OAm, 80–90% purity), oleic acid (OA, 80–90% purity), 1-octadecene (ODE, >80% purity), isopropanol, ethyl acetate (99% purity), and toluene were procured from Aladdin-reagent and used without further purification. Caesium stearate (CsSt, 98% purity) was purchased from J&K reagent and used without further purification. N-octane (>98% purity) was purchased from TCI-Reagent and used without further purification. PEDOT: PSS solution (Baytron P VPAl 4083), TFB and TPBi were purchased from Xi’an Yuri Solar Co., Ltd and used as received.

Synthesis of CsPbI3 QDs

For Cs-OA precursor preparation, 2.5 g CsSt, 40 mL ODE solution and 2 mL OA were mixed. Then, the mixture was heated up to 140 °C and kept at that temperature until it became transparent. For CsPbI3 crude QDs preparation, 0.25 g PbI2, 1.5 mL OAm, 2 mL OA and 10 mL ODE were loaded together into a flask. Then, the mixture was heated to 120 °C and kept at that temperature for 10 min, during which the mixture was degassed under N2 flow. Then, the heating temperature was raised to 180 °C, and the as-prepared Cs-OA precursor (1 mL) was rapidly injected into the mixture. The rapid crystallisation of QDs can be observed. After 15 s of reaction, the mixture was cooled in an ice bath to obtain the crude QD solution. The purification process of QDs is as follows: isopropanol is added to the crude QD solution with a 2:1 volume ratio. Then, the mixture was centrifuged at 8000 × g for 1 min. The supernatant solution was discarded, and the precipitate was dispersed in 2 mL toluene. Then, ethyl acetate was added to the mixture and centrifuged at 8000 × g for 1 min. The supernatant solution was discarded, and then the precipitate was dispersed in 2 mL hexane or n-octane. Then, the mixture was centrifuged at 4000 × g for 1 min to obtain the QD solution. For alloyed QDs, PbCl2 with a certain molar mass to PbI2 (10%–30%) was added together with PbI2. The rest of the steps are the same.

Fabrication of heterophase film

Perovskite α-phase QDs were spin-coated onto the glass substrates (for optical measurements) or glass/ITO/PEDOT: PSS/TFB substrates (for device fabrication) at 2000 rpm for 45 s and annealed at 120 °C for 20–40 min in air atmosphere. Air humidity should be maintained at 30%–50%, and the annealing time decreased with increased air humidity. The film’s colour changing from dark red to transparent indicated the successful transition to heterophase film.

Device fabrication

For Pe-WLED, the cleaned ITO-coated glass substrate was treated with plasma for 5–10 min. Then, the filtered PEDOT: PSS solution was spin-coated onto the substrates at 4000 rpm for 45 s. The PEDOT: PSS layer was baked at 140 °C for 15 min. The TFB/chlorobenzene solution (5 mg mL−1) was spin-coated onto the substrates at 3000 rpm for 60 s. The TFB layer was baked at 120 °C for 25 min. The emitting heterophase layer was fabricated following the details in the section on the fabrication of heterophase film above. The following functional layers were thermally evaporated under ~2 × 10−4 Pa, containing TPBi (40 nm), LiF (1 nm) and Al electrodes (100 nm). The overlapped area of the patterned ITO and Al electrode is the emitting area (1 × 1 cm). For commercial WLEDs, Silica gel IVS4742A and IVS4742B, phosphor Y959 from Hung Ta and phosphor ZYP640G3 from Beijing Yuji were adopted for WLED-1. The ratio of silica gel to phosphor is 4742A: 4742B: Y959: ZYP640G3 = 3.5:3.5: 1:1. Silica gel YD670A and YD670B, phosphor Y959, YP520 and ZYP640G3 were adopted for WLED-2. The silica gel to phosphor ratio is YD670A: YD670B: Y959: ZYP520: ZYP640G3 = 2.6:2.6:0.2:0.3: 0.029. Silica gel YD670A and YD670B, phosphor H102 and H104 were adopted for WLED-3. The ratio of silica gel to phosphor is YD670A: YD670B: H102: H104 = 11:11:0.2:1.8.

First-principles calculations

The first-principles calculations are performed by Vienna ab initio simulation package (VASP) code31,32, using the projected augmented wave (PAW) method33. The Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional in the generalised gradient approximation34 is implemented with Cs (5s25p66s1), Pb (5d106s26p2), I (5s25p5), and Cl (3s23p5) potentials. The kinetic cutoff energy is set to 800 eV. The total energy convergence threshold is less than 10−6 eV, and the atomic force convergence threshold is less than 0.001 eV Å−1 for atomic relaxation. The Brillouin zone is sampled using Monkhorst-Pack k-meshes with a spacing of 0.2 Å−1 for structure relaxation.

For the solid solution CsPb(I1-xClx)3 with x being 1/3 and 2/3, at least 20 anion-occupation configurations of both the γ and δ phases in the 20-atoms supercells are considered. The lowest-energy configurations among them are selected as the ground states, as shown in Supplementary Fig. 1a. The 160-atom supercells are used for the phonon calculations based on the density-functional-perturbation theory35,36.

Thermodynamic calculations

The thermodynamic stability of different phases is determined by their relative free energies in general. The ambient pressure and the volume dependence are ignored here in the harmonic approximation, and we calculate the Helmholtz free energy as follows37,

$$F\left(T\right)={F}_{{{{\rm{el}}}}}\left(T\right)+{F}_{{{{\rm{vib}}}}}\left(T\right)={E}_{T=0}+{F}_{{{{\rm{vib}}}}}\left(T\right)-T{S}_{{{{\rm{el}}}}}$$
(1)

where \({F}_{{{{\rm{el}}}}}\) and \({F}_{{{{\rm{vib}}}}}\) correspond to the electronic and vibrational contributions, respectively. The first term, \({E}_{T=0}\), on the right side of Eq. (1) is the total energy obtained from the density-functional calculations, and the last term \(T{S}_{{{{\rm{el}}}}}\) means the electronic entropy could be omitted for semiconductors and insulators.

Then, the vibrational free energy could be calculated from the phonon density of states via the PHONOPY software38,39,

$${F}_{{{{\rm{vib}}}}}\left(T\right)={\sum}_{{{q}}v}\frac{{{\hslash }}\omega \left({{{\rm{q}}}}v\right)}{2}+{k}_{{{{\rm{B}}}}}T {\sum}_{{{q}}v}{{{\rm{ln}}}}\left(1-{e}^{\frac{-{{\hslash }}\omega \left({{{\rm{q}}}}v\right)}{{k}_{{{{\rm{B}}}}}T}}\right)$$
(2)

Where \({{{\rm{q}}}}\) is the phonon wave vector, \(v\) is the index of the phonon modes, \(\omega\) is the phonon frequency, and \({k}_{{{{\rm{B}}}}}\) is the Boltzmann constant.

Effective Hamiltonian calculations

The antiferrodistortive (AFD) motions, including octahedral antiphase tilting \({\omega }_{{{{\rm{R}}}}}\) and in-phase tilting \({\omega }_{{{{\rm{M}}}}}\), are important approaches that could tune the electronic properties of the perovskites, such as band gap, polarisation, and magnetisation. It should be noted that the angles-fluctuation of the octahedral tilting exists in perovskite CsPbI3 at the finite temperature, as predicted from the effective Hamiltonian40. Therefore, we calculate the fluctuated antiphase and in-phase tilting angles of the γ-phase CsPbI3 at room temperature based on the effective Hamiltonian, and then investigate the effect of octahedral tilting angles on the band gap.

The fluctuation of the octahedral tilting is estimated here by using the effective Hamiltonian of CsPbI3 developed in ref. 40,

$${E}^{{{{\rm{tot}}}}}={E}^{{{{\rm{dipole}}}},{{{\rm{strain}}}}}\left(\left\{u\right\},\left\{v\right\},{\eta }_{H}\right)+{E}^{{{{\rm{AFD}}}}}\left(\left\{u\right\},\left\{v\right\},\left\{\omega \right\},{\eta }_{H}\right)$$
(3)

where \({E}^{{{{\rm{dipole}}}},{{{\rm{strain}}}}}\) is the energy of the local dipolar mode \(\{u\}\), inhomogeneous strain variable \(\{v\}\), homogeneous strain tensor \({\eta }_{H}\) and their mutual coupling, while \({E}^{{{{\rm{AFD}}}}}\) involves the octahedral tilting mode \(\{\omega \}\) and their interactions with strains and local mode. Note that such an effective Hamiltonian has correctly reproduced the phase transition sequence of perovskite CsPbI3. The simulation is performed on a 12 × 12 × 12 supercell of the five-atom perovskite unit cell (corresponding to 8640 atoms) at 300 K using the hybrid Monte Carlo (HMC) algorithm41, where perovskite CsPbI3 is in Pnma phase. In total, 40,000 HMC sweeps are performed. Among them, the first 10,000 sweeps are used to equilibrium the system and the distribution of tilting is collected during the following 30,000 sweeps. The following variables are collected during the simulation: (i) \({\omega }_{R}={\left(-1\right)}^{{n}_{x}\left(i\right)+{n}_{y}\left(i\right)+{n}_{z}\left(i\right)}{\omega }_{i}\) characterising the antiphase tilting, where \({\omega }_{i}\) is the tilting variable in unit cell \(i\) located at \({n}_{x}\left(i\right){{{\bf{a}}}}+\,{n}_{y}\left(i\right){{{\bf{b}}}}+\,{n}_{z}(i){{{\bf{c}}}}\), with \({{{\bf{a}}}},\,{{{\bf{b}}}},\,{{{\bf{c}}}}\) being the lattice vectors of the lattice vectors of the cubic perovskite unit cell; and (ii) \({\omega }_{M}={\left(-1\right)}^{{n}_{x}\left(i\right)+{n}_{y}\left(i\right)}\) characterising the in-phase tilting.

Characterisation and device measurements

For SED measurement, the SiN transmission electron microscope (TEM) substrate (4 × 4 mm) was stuck to a glass substrate (2 × 2 cm). Then, the α-CsPbI3 QD solution was dropped on the SiN TEM substrate, then spin-coated and annealed at 120 °C in the atmosphere. The QD solution’s PL spectra were collected by a Varian Cary Eclipse spectrometer. TEM measurement was conducted by a Tecnai G2 F30 S-TWIN at an acceleration voltage of 200 kV. XRD patterns were collected by using a Bruker D8 Advance X-ray diffractometer operating with Cu Kγ radiation (λ = 1.5406 Å). The AFM measurement was conducted by a Veeco D3100 AFM tool. For hyperspectral microscopy, PL mappings were captured using a wide-field hyperspectral microscope (IMA VISTM, Photon, etc.) with a low-noise silicon CCD camera, and the samples were illuminated by a continuous-wave 405 nm laser with an excitation density of 100 mW cm−2. The fluorescence-lifetime mapping was performed using a confocal microscope setup (MicroTime-200, PicoQuant, Germany) under a 405 nm pulsed diode (PDL 828 S “SEPIA II”, PicoQuant, pulse width ~100 ps) with an excitation fluence of 3.5 μJ cm−2 per pulse. For TA spectroscopy measurement, a Ti: sapphire amplifier system (the Spectra-Physics Solstice Ace) was employed. This system operates at a repetition rate of 1 kHz and generates laser pulses with a duration of around 100 fs. The output of this amplifier system was split into two distinct optical paths: one for the pump beam and the other for the probe beam. To generate the 400 nm pump pulses, we took the 800 nm fundamental beam output from the Solstice Ace and sent it through a second harmonic generating beta barium borate (BBO) crystal from Eksma Optics. We used a homemade noncollinear optical parametric amplifier (NOPA) when we needed pump pulses with a tunable wavelength. To ensure that the pump had a narrow bandwidth, a 560 nm bandpass filter was utilised. A chopper wheel rotating at a frequency of 500 Hz was used to block the pump beam intermittently. For the generation of the ultraviolet-visible broadband beam, which spans from 330 nm to 700 nm, we first sent the 800 nm fundamental beam through a mechanical delay stage (the Thorlabs DDS300-E/M). Afterwards, the beam was focused onto a 5 mm CaF2 crystal from Eksma Optics. This crystal was connected to a digital motion controller, the Mercury C863 DC Motor Controller. The pulses that passed through the CaF2 crystal were then collected using a monochrome line scan camera (the JAI SW-4000M-PMCL). This camera was paired with an Andor Shamrock SR-163 spectrograph. All the data collected by the camera was directly fed into a computer for further analysis. Grazing-incidence X-ray scattering was performed at the Diamond synchrotron SAXS/WAXS beamline. Sample-to-detector distance is 553.81 mm, and the X-ray energy is 15 keV. A Dectris Pilatus 2 M detector collected the 2D images. Data reduction containing typical geometrical and intensity corrections was processed by INSIGHT software. The Si attenuation is 3.50 mm−1, the horizontal polarisation is 0.98, and the air attenuation coefficient is 3.01 × 10−4 mm−1. The EL spectra, I–V, I–L curves and EQEs were measured by using a Keithley 2400 source, a fibre integration sphere, and a PMA-12 spectrometer for light output measurements (designed by Hamamatsu Photonics Co., Ltd).

Match index calculation

For a given light source with CIE coordinates of (XCIE, YCIE), CRI of XCRI, CCT of XCCT K, Duv of XDuv and M/P ratio of XM/P. Taking sunlight (CIE coordinates of (0.33, 0.33), CRI = 100, CCT = 5,800 K, Duv = 0, M/P ratio = 1) as standard, the match indices of the five core indicators will be:

$${{{\rm{Match}}}}\; {{{\rm{index}}}}\, \left({{{\rm{CIE}}}}\; {{{\rm{coordinates}}}}\right)=1-\sqrt{\frac{{({X}_{{{{{\rm{CIE}}}}}^{-}{0.33}})}^{2}}{0.3{3}^{2}}}+\frac{{({Y}_{{{{\rm{CI}}}}{{{{\rm{E}}}}}^{-}{0.33}})}^{2}}{0.3{3}^{2}} \\ \left(0.2\right. \le {X}_{{{{\rm{CIE}}}}}\le 0.5,\,0.2 \le {Y}_{{{{\rm{CIE}}}}}\le 0.5$$
(4)
$${{{\rm{Match\; index}}}}\, \left({{{\rm{CRI}}}}\right)={X}_{{{{\rm{CRI}}}}}$$
(5)
$${{{\rm{Match\; index}}}}\,({{{\rm{CCT}}}})=1-\frac{|{X}_{{{{\rm{CIE}}}}}-{{\mathrm{5800}}}|}{{{\mathrm{5 800}}}}({1 000}\le {X}_{{{{\rm{CCT}}}}}\le {{\mathrm{10,000}}})$$
(6)
$${{{\rm{Match\; index}}}}\,\left({{{\rm{D}}}}{{{\rm{uv}}}}\right)=1-{X}_{{{{\rm{Duv}}}}}$$
(7)
$${{{\rm{Match\; index}}}}\left(\frac{{{{\rm{M}}}}}{{{{\rm{P}}}}}{{{\rm{R}}}}{{{\rm{atio}}}}\right)={X}_{{{{\rm{M}}}}/{{{\rm{P}}}}}(0 \, < \,{X}_{{{{\rm{CCT}}}}}\le 1)\,{{{\rm{or}}}}\frac{1}{{X}_{{{{\rm{M}}}}/{{{\rm{P}}}}}}(1\le {X}_{{{{\rm{CCT}}}}})$$
(8)