Introduction

The electrical double layer (EDL), a key structure at solid-liquid interfaces characterized by two opposing layers of electric charges, plays a pivotal role in diverse interfacial phenomena1,2. Its implications extend to energy storage3, electrowetting4,5, and nanojunction gating6, serving as the foundation for the functionality of various devices such as supercapacitors and electric-double-layer field-effect transistors7,8. Despite the fundamental importance of the EDL, comprehensive understanding is hampered by the limited experimental methods available for probing its composition and electric potential distribution9. Even though the theoretical framework for EDL description was developed more than a century ago (Helmholtz, later Gouy-Chapman and Stern models) and remains the cornerstone of modern electrochemistry, only a limited number of experimental methods are available for measuring EDL composition and electric potential distribution10.

Conventional techniques like cyclic voltammetry (CV) and electrochemical impedance spectroscopy (EIS) are well-established for revealing the macroscopic properties of the EDL, providing valuable insights into the kinetics and thermodynamics of electron transfer and ion diffusion11,12,13. However, these techniques are limited by their inability to provide detailed information beyond the collective behavior of the whole electrode surface. Recent developments, such as Kelvin probe force microscopy (KPFM), enable nanoscale spatial mapping of surface potential within the EDL, while spectroscopic techniques like vibrational sum-frequency generation (VSFG) and second harmonic generation (SHG), examine molecular rearrangements at the charged interface14,15,16. Despite these advances, there remains a gap in achieving the needed temporal or spatial resolution for analyzing real electrochemical systems, like the edge effect of catalysts17, nanoscale kinetic studies18, and multi-functional electrolytes19,20. This limitation highlights the necessity for in-situ monitoring techniques capable of capturing the complex spatial and temporal dynamics at both the steady-state and transient-state electrolyte-electrode interface10,21.

Here, we report an in-situ optical method to visualize the zeta potential (ζ) potential distribution of two-dimensional (2D) materials. The ζ potential represents any relative motion between the Helmholtz and diffuse layers, a crucial aspect of the EDL critical for ion adsorption and electron transfer22,23. Our focus on 2D materials stems from their heterogeneous nature, which poses challenges in accurately measuring their ζ potential with most existing methods only providing an average surface potential of a dispersed material ensemble. Utilizing a label-free plasmonic-based imaging technique, based on the impedance perturbation, we achieve sensitive imaging of charge density variations indicative of ion slip in the diffuse layer. This method allows us to visualize the ζ potential distribution across 2D materials in aqueous solution. Unlike the existing techniques, this method enabled us to acquire the spatial information of heterogenous electrochemical properties within and among individual 2D materials.

Results

The principle of imaging ζ potential

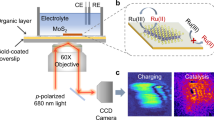
The principle and experimental setup to measure the ζ potential on 2D materials are illustrated in Fig. 1. This potential, occurring at the diffuse layer of the charging interface, arises from ions migration from the Helmholtz plane to the diffuse plane due to the interfacial electronegativity (Fig. 1a, b). The potential at the distance x from the interface is given by the Helmholtz equation:

$${{{\rm{d}}}}\varphi=\,\frac{x}{{\varepsilon }_{0}{\varepsilon }_{{{{\rm{r}}}}}}{{{\rm{d}}}}\sigma$$
(1)

where ε0 and εr are the permittivity of free space and the relative permittivity of electrolyte solution, respectively, and σ is the charge density of diffuse layer. In dilute solutions, the Debye screening length, κ−1, indicative of the thickness of diffuse layer is:

$${\kappa }^{-1}={\left(\frac{2{n}^{0}{z}^{2}{{{{\rm{e}}}}}^{2}}{{\varepsilon }_{0}{\varepsilon }_{{{{\rm{r}}}}}{{{{\rm{k}}}}}_{{{{\rm{B}}}}}T}\right)}^{-\frac{1}{2}}=\alpha {c}^{-\frac{1}{2}}$$
(2)

where c is the electrolyte concentration, n0 the ion number concentration, e the electron charge, kB the Boltzmann constant, T the temperature, and α a constant derived from these parameters. Hence at a given electrochemical situation, the diffuse layer potential depends on the charge density and ion concentration24,25. Therefore, the ζ potential, \(\zeta=f(\Delta \sigma,{c})\), can be determined by measuring the surface charge density of 2D materials.

Fig. 1: Illustrations of the ζ potential and the plasmonic imaging.
figure 1

Schematic of the surface structure (a) and potential distribution (b) of the MoS2-electrolyst interface. Molecular models were produced by VESTA47. c Schematic of the plasmonic-based electrochemical impedance technique for mapping ζ potential on 2D materials. d The image sequence capturing the plasmonic intensity change of MoS2 under a sinusoidal potential modulation and its frequency domain signal extraction. e The FFT amplitude image of MoS2 showing the distribution of surface charge density, which was later conversed to ζ potential. The optical transmission image (f) and AFM image (g) of the exfoliated MoS2 nanosheet on the gold-coated substrate shown in d–e. h Raman spectra of MoS2 marked in f. Source data are provided as a Source Data file.

Full size image

To quantify the surface charge density, we adopted an in-situ electrochemical plasmonic imaging technique, integrated with a fluidic system (Fig. 1c, detailed in Suppl. Notes 1, 2). The plasmonic imaging is highly responsive to changes in the local dielectric environment near the metal-dielectric interface. When the surface charge density on the MoS2 nanosheet varies due to ion adsorption, it induces changes in the local refractive index, which in turn affects the plasmonic intensity. Modulating the electrochemical potential alters the dielectric constant of the material by shifting electrons, which in turn affects the plasmonic intensity (\(\frac{\Delta I}{I}\))—a measure sensitive enough to detect subtle changes in surface charge density. The plasmonic intensity is directly correlated with surface charge density (Suppl. Note 2), given by \(\frac{\Delta I}{I}\) = α−1∆σ, where α is a constant parameter influenced by the layer-dependent capacitance of the 2D material26. The modulation of its plasmonic intensity by electrochemical potential was captured using a charged-coupled device (CCD) camera (Fig. 1c, d). By conducting a pixel-to-pixel fast Fourier transform (FFT) of the captured image sequence from the time domain into the frequency domain, we acquired the response amplitude of plasmonic intensity to electrical modulation across each pixel (Fig. 1d). This analysis allowed us to convert these amplitude data into a surface charge density distribution image as shown in Fig. 1e. For demonstration, we used a MoS2 nanosheet, which was exfoliated from a bulk single crystal and etched to certain thickness using a surface plasmon polariton etching method27. We characterized the nanosheet to verify the thickness using an optical micrography, atomic force microscopy (AFM), and Raman spectroscopy (Fig. 1f–h). This particular MoS2 nanosheet comprises both single and five layers.

Mapping the surface charge density

Prior to conducting the batch testing, we systematically evaluated the variations in imaging amplitude in response to different frequencies and modulation amplitudes on the surface of a monolayer MoS2 (Suppl. Notes 1, 3). A frequency of 5 Hz elicits the highest adjusted response amplitude. The modulation frequency was limited to 25 Hz due to the maximum sampling rate of our real-time imaging camera, which is 200 Hz. According to Shannon’s sampling theorem, the sampling rate is required to be at least eight times greater than the modulation frequency to preserve the amplitude accurately. For modulated voltage, a 100-mV modulation amplitude falls in the center of the linear response region, ensuring reliable measurements without nonlinear distortions. Based on these findings, we selected a 5 Hz frequency and a 100-mV modulation amplitude as optimal parameters for our following studies.

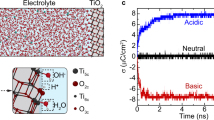
Considering that the ionization process within EDL affecting the ζ potential is controlled by the potential bias, we tested the surface charge density of MoS2 under different bias using a plasmonic imaging method (Suppl. Note 4, Suppl. Figs. 5-8). Figure 2a illustrates swift alteration in field intensity near the electrode, where the adsorption of ionic species on the electrode surface correlates with its polarity. Due to the intrinsic capacitance of MoS2, the charge density on the surface of the gold electrode, when biased, significantly reduces compared to that on monolayer MoS2, as shown in Fig. 2b. At a bias voltage of −0.3 V, the surface of the electrode is negatively charged, and the surface charge density of MoS2 is slightly higher. Moreover, surface plasmon polariton etching introduces heterogeneity in the surface morphology of MoS2, which is also reflected in its surface charge density distribution. Correspondingly, under +0.3 V bias, the surface charge density of MoS2 is still higher than that of gold background, and the electrode surface is positively charged. We observed a non-uniform surface charge density in monolayer MoS2, likely due to defects introduced by SPP etching. To further investigate the defect distribution, we employed photoluminescence spectroscopy, which revealed a higher defect concentration in regions with lower charge density and a lower defect concentration in areas with higher charge density (Suppl. Note 4.2).

Fig. 2: Bias effects on surface charge density of monolayer MoS2.
figure 2

a Schematic representation of the influence of bias on the ion adsorption at the MoS2-electrolyte interface. Molecular models were produced by VESTA47. b Surface charge density images of the monolayer MoS2 at the potential biases of −0.3 and +0.3 V. Scale bar: 5.0 μm. c Surface potential of the monolayer MoS2 measured via KPFM at the potential biases of −0.3 and +0.3 V. Scale bar: 4.0 μm. d Surface charge density of the monolayer MoS2 in 0.3 mM KCl solution at varying potential biases. Vpp = 100 mV. The box plot shows the median (center dot), interquartile range (box limits), whiskers extending to 1.5× interquartile range, outliers as circles beyond the whiskers, and 8597 independent pixels per box. Source data are provided as a Source Data file.

Full size image

Typically, the accumulated charge on the surface of 2D materials is calculated using the contact potential measured by KPFM. Therefore, we measured the contact potential of monolayer MoS2 (Fig. 2c, Suppl. Note 5). Interestingly, there exists a discrepancy between the bias effect depicted in the plasmonic imaging (Fig. 2b) and KPFM measurement (Fig. 2c) where the surface potential of MoS2 remains negative under both −0.3 V and +0.3 V bias. This difference is attributed to the distinct measurement principles. KPFM quantifies the potential difference, influenced by the work function disparity between MoS2 and gold electrodes28. In contrast, our in-situ probe-free optical imaging method evaluates the ζ potential at the electrolyte-electrode interface, directly reflecting the relationship between 2D material and aqueous solution. To avoid leak currents from the substrate, we also performed conductive atomic force microscopy (CAFM) measurements on MoS2 nanosheets, which showed similar results to that from KPFM (Suppl. Note 6).

As the bias voltage changes from negative to positive, cations adsorbed on the surface of MoS2 are progressively replaced by anions. Correspondingly, the surface charge density of MoS2 gradually decreases to close to zero charge as the bias voltage increases from -0.5 to 0 V (Fig. 2c). From 0 to +0.3 V, the surface charge density of MoS2 remains nearly unchanged, close to zero. The weak surface charge density measured for MoS2 within this voltage range is due to the potential impedance disturbance of 25 mV. It has been reported that under higher forward bias voltage, MoS2 underwent electrochemical oxidation, transforming into molybdic and sulfuric acids29, evidenced by an anomalous increase in charge density at +0.4 and +0.5 V (Fig. 2c). Bright-field image contrasts before and after applying positive bias voltage suggested that the MoS2 was gradually disappeared on the electrode surface by electrochemical oxidation at these voltages30,31,32. Therefore, the monolayer MoS2 nanosheet experiences three states from -0.5 to +0.5 V: charging, inertia (near the potential of zero charge), and oxidation. Given the low surface charge density of MoS2 under positive bias and its susceptibility to electrochemical oxidation, subsequent experiments were conducted at a -0.3 V bias to mitigate these effects.

To facilitate the ionization process near the surface, we examined the influence of electrolyte flow velocity on the surface charge density of monolayer MoS2 (Suppl. Notes 7, 8). Suppl. Fig. 13a shows the surface charge density of MoS2 as a function of pH in 0.3 M KCl solution without flow. A slight decrease in the surface charge density of MoS2 was detected with increasing alkalinity, which is also consistent with the decrease in the electron-donating ability of MoS2 in alkaline solution. Thus, in a static electrolyte solution, the EDL structure on the surface of MoS2 is relatively stable, making it challenging to change the ion distribution by potential perturbations. In real electrochemical reactions, to promote the diffusion of reactants and products, the electrolyte solution at the electrode surface is typically in motion. This flow disrupts the ion arrangement within the Helmholtz and diffuse layers, establishing a stable ion exchange state. We imaged the single MoS2 nanosheet in a flowing electrolyte with the same electrochemical conditions (Suppl. Fig. 13b). The surface charge density of MoS2 in the flowing electrolyte is significantly higher than that in the static solution (Suppl. Fig. 13c, d). Moreover, the increase in alkalinity resulted in a more pronounced decrease in the surface charge density of MoS2. Therefore, to simulate real electrode surface conditions more accurately, subsequent experiments were conducted in a flowing electrolyte solution.

Visualizing the distribution of ζ potential

We then quantified the ζ potential based on the quantitative link to the plasmonic intensity. This relationship is encapsulated in the equation \(\zeta={f}\left(c,\,\Delta \sigma \right)=g(c,\,\frac{\Delta I}{I})\), where ζ potential is expressed as:

$$\zeta=\frac{2{{{\rm{R}}}}T}{{{{\rm{F}}}}}{{{\rm{arsinh}}}}\left(\frac{\alpha }{\sqrt{8{\varepsilon }_{0}{\varepsilon }_{{{{\rm{r}}}}}{{{\rm{R}}}}{Tc}}}\times \frac{\Delta I}{I}\right)$$
(3)

Here R denotes the gas constant, F the Faraday constant and c the ion concentration. This formula also highlights the direct influence of ambient electrolyte concentration on the surface ζ potential, with the Debye screening length (κ−1) of the electrolyte solution defining the boundary of the diffuse layer where ζ potential is localized (Fig. 1b, Eq. (2)). As electrolyte concentration diminishes, the Debye screening length expands, impacting the ζ potential accordingly.

In low (0.3 mM) and high (3 mM) KCl solutions, the thickness of the diffuse layer on MoS2 adjusts in response to ion adsorption at the surface, as depicted in Fig. 3a, b. Especially, the surface charge density of the MoS2 nanosheet increases dramatically with increasing solution concentration (Suppl. Note 9, Suppl. Fig. 15). Using Eq. (3), we mapped the ζ potential distribution of the MoS2 nanosheet in both 0.3 and 3 mM KCl solutions, showing a decreasing trend with increasing alkalinity (Fig. 3c). Based on the mapping, a box plot of the ζ potential values was also drawn for detailed description (Fig. 3d). At lower ionic strengths, the ζ potential markedly surpasses that observed at higher ionic strengths, where the voltage drop predominantly occurs across the Helmholtz plane. Consequently, at high ionic strength, only a small number of cations adsorb and slip on the electrolyte-MoS2 diffuse layer, diminishing the exchange of anions and cations on the surface of MoS2 and forming a more stable EDL structure. In colloid science, a negative ζ potential in the tens of mV indicates enhanced colloidal stability, whiles a ζ potential near zero mV suggests a structural imbalance, leading to potential colloid dissociation or sedimentation33,34. However, this framework is not directly applicable to individual 2D materials without a colloidal structure. Therefore, the observed variability in ζ potential across the MoS2 nanosheet in solutions of differing ionic strengths reflects the different electrical characteristics of its changed EDL in these solutions.

Fig. 3: Mapping the distribution of ζ potential.
figure 3

a, b Schematic illustrations of ion distribution in the EDL on MoS2 at ionic strengths of 0.3 mM and 3 mM KCl, respectively. Molecular models were produced by VESTA47. c Spatial distribution of ζ potential on the MoS2 surface as a function of pH in flowing 0.3 mM and 3 mM KCl solutions. Scale bar: 3.0 μm. VDC = −0.3 V, Vpp = 200 mV. d A box plot depicts the numerical distribution of ζ potential values on the MoS2 surface (delineated by the dashed line in Fig. 3c) for two ionic strengths as a function of pH, revealing that spatial variation yields pronounced differences in ζ potential across the nanosheet within a single chemical environment. The box plot shows the median (center line), interquartile range (box limits), whiskers extending to 1.5× interquartile range, and 12249 independent pixels per box. e Schematics of the ζ potential in the Helmholtz and diffuse layers on the surface of MoS2 nanosheets with varying thicknesses. Cq, Ch and Cdl represent the capacitances of the MoS2, Helmholtz layer, and diffuse layer, respectively; and \({R}_{{{{{\rm{MoS}}}}}_{2}}\), Rh and Rs denote their resistances. f ζ potential increasing with pH in the triangular areas of the MoS2 nanosheet marked in Fig. 3c. Source data are provided as a Source Data file.

Full size image

Importantly, the ζ potential distribution on the single MoS2 nanosheet exhibits significant variability due to changes in thickness (Fig. 3c). The layers of MoS2 are bonded by van der Waals forces, leading to increased electrical resistance and decreased electronic transport with greater thickness35. Consequently, thicker MoS2 layers on the same electrode surface experience smaller surface potential drops, resulting in reduced ion adsorption at the solid-liquid interface (Fig. 3e). These processes, in turn, reduced the interfacial charge density, observed as a compression in the plasmonic response intensity from the detection laser36,37. Using Eq. (3), variations in thickness across different regions (the upright triangle, single layer; the inverted triangle, multilayer; also marked in Fig. 1g, h) result in marked contrasts in the ζ potential change (Fig. 3f). The observed variation in ζ potential across the MoS2 sheet reflects both the changes in physical and chemical properties with increasing layer number, and the inherent spatial inhomogeneity even within a uniform material composition. Conventional macroscopic measurement techniques often obscure these underlying interfacial properties of materials.

To elucidate the influence of electrolyte on the ζ potential of the MoS2 surface in acidic and alkaline media, we calculated the electrostatic potential energy (EPE) on the MoS2 surface using first-principles methods (Suppl. Note 10)38. As the pH increased, adsorption transitioned from hydronium to hydroxide ions at the solid-liquid interface, employing an explicit model to simulate the vacuum layer of the EDL between the MoS2-electrolyte interface (Fig. 4a). Variations in EPE on the MoS2 surface in different electrolytes were calculated (Suppl. Fig. 16). In both 0.3 and 3 mM KCl solutions, the EPE exhibited a progressive decrease from pH 4 to 9. EPE is defined as the energy required to transport a charge from infinity to a specified surface, whereas the ζ potential refers to the voltage drop across the diffusion layer, specifically the potential difference between the MoS2 interface and the bulk phase of the solution. The observed decrease in EPE is consistent with the experimentally observed increase in ζ potential (Fig. 3c). We normalized and differentiated the interfacial EPE for dilute and concentrated solutions (Fig. 4b). This analysis demonstrated that the MoS2-electrolyte interface was not uniformly influenced by ionic strength. From acidic to neutral conditions, the EPE at the solid-liquid interface was consistently higher for the dilute solution compared to the concentrated solution, with the gap narrowing; in alkaline solutions, this trend reversed. First-principles calculations did not match experimental findings regarding the electrolyte effect of ionic strength, largely because ionic strength is typically represented as an implicit model in theoretical calculations39,40. Given the vast amount of water molecules at the solid-liquid interface, the relative number of anions and cations from KCl electrolyte is negligible. In contrast, imaging ζ potential serves as a valuable complement for studying the influence of electrolytes.

Fig. 4: Proposed adsorption model and the electrostatic potential energy of layered MoS2.
figure 4

a Explicit model of hydronium atoms and hydroxide ions in acidic and alkaline media on the layered MoS2 surface in first-principles calculations. Molecular models were produced by VESTA47. b The mean normalized electrostatic potential energy and its electrostatic potential energy difference at the MoS2-electrolyte (0.3 mM KCl, orange bar; 3 mM KCl, purple bar) interface as the pH changes. Source data are provided as a Source Data file.

Full size image

To demonstrate the generality of our method, we extended our analysis to the ζ potential of graphene (Suppl. Note 11, Suppl. Fig. 17). Unlike the MoS2 nanosheets, graphene exhibited an inverse trend in ζ potential with increasing pH values, favoring anion accumulation on its surface, a finding we confirmed using other conventional ζ potential measurement methods (Suppl. Fig. 18). The inverse trends in ζ potential of the two materials highlight the significant influence of the solution environment on their respective electrostatic potentials. The pronounced differences in ζ potential behavior between MoS2 and graphene reflect variations in their surface electrostatic potential energy under hydraulic conditions, suggesting distinct application scenarios in membrane technologies41,42. Graphene possesses a rich surface electron cloud and exhibits stable electrical properties, which influence its interaction with ions in solution. As pH increases, the surface of graphene tends to attract more anions, leading to an increase in negative ζ potential. This behavior is consistent with graphene’s electron-rich surface facilitating anion accumulation. By contrast, MoS2 has different surface chemistry and electronic structure, which affect its ion adsorption behavior. With increasing pH, the surface of MoS2 becomes less negatively charged, resulting in a decrease in ζ potential. This trend is related to the reduction in protonation and changes in the adsorption of hydroxide ions at higher pH levels. These differences are not solely due to catalytic properties related to HER and OER but are fundamentally rooted in the distinct surface electronic structures and ion adsorption behaviors of the two materials. Additionally, the electrostatic potential energy at the catalytic interface, strongly influenced by the type and concentration of electrolytes, plays a crucial role in determining the ζ potential. This, in turn, shapes the microenvironment for catalytic reactions and affects the direction of the reaction38,43,44. These findings highlight the pivotal role of surface charge dynamics on the electrochemical activity of 2D materials.

The optical method offers a more precise approach for examining the heterogeneous interfacial properties across various electrolyte-material systems. In our optical setup, the lateral resolution is constrained by the optical diffraction limit (on the order of a few hundred nanometers), while the out-of-plane (z-axis) resolution is constrained by the evanescent field of the surface plasmon, typically around 100 nm45. As a result, morphological or structural defects smaller than these dimensions will appear as averaged signals rather than distinctly resolved features. However, larger defect clusters or areas of local anisotropy that surpass these resolution thresholds can be clearly visualized and quantified in terms of their ζ potential and charge density distributions. Nevertheless, compared to conventional commercial systems such as SurPass3, which measure only the averaged ζ potential over a macroscopic area of approximately 0.5 × 1 cm2, our method represents a substantial advance in spatial resolution for ζ potential measurements. This higher resolution allows us to delineate and quantify localized variations on 2D materials without the averaging effects that occur in macroscopic measurements. When applied to imaging 3D materials, whose morphologies often extend beyond the z-axis limits of plasmonic imaging, our optical method may encounter challenges in accurately capturing ζ potential distributions without modifications to accommodate deeper interfaces.

Discussion

In summary, our study presents an optical method for in-situ visualization of the ζ potential on 2D materials, facilitating a deeper understanding of EDL at solid-liquid interfaces. By leveraging the high sensitivity of plasmonic imaging to surface charge density, we establish a correlation between surface charge density and ζ potential. This enables us to map the heterogenous spatial distribution of ζ potential and elucidate the influence of the electrochemical environments within the EDL on the interface. Using MoS2 nanosheets as a model system, our findings elucidate how bias voltage, ionic strength, and pH influence the ζ potential, revealing the complex relationship between the intrinsic properties of the material and its electrochemical behavior. Furthermore, comparative analysis with graphene under identical conditions highlights the capability of this method to identify optimal catalytic materials for specific applications. Our work not only offers a foundational platform for advancing the understanding of EDL, but also provides support for developing advanced materials and devices in electrochemistry and beyond.

Methods

Electrochemical setup

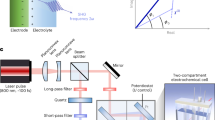
The electrochemical measurement system comprised a 1-mL polydimethylsiloxane cell, a three-electrode system, a multi-channel fluidics system, and an electrochemical potentiostat (CS Studio 5, CorrTest Instrument). The three-electrode configuration utilized a gold-coated coverslip (1 cm2, 48 nm gold) as the working electrode, an Ag/AgCl electrode (3 M KCl) as the reference electrode, and a platinum wire (≥99.99%, CHINA NEW METAL Co., Ltd) as the counter electrode. The potentiostat was connected to a waveform generator (DG1022Z, Rigol) to apply a sinusoidal perturbation voltage, ensuring precise potential control through the three-electrode system. The potentiostat controlled the bias voltage of the electrochemical cell, while the waveform generator regulated the waveform, frequency, and perturbation potential. Voltage and current data crucial for the time-series analysis were systematically acquired by a data acquisition card (DAQ, USB-6210, National Instruments).

The multi-channel fluidics system was configured to open a single channel at a time; prior to each test, the cell was flushed with the selected flowing phase for one minute to ensure complete switching of the electrolyte concentration or pH at the sample surface. The electrolyte flow velocity was measured and controlled by a glass rotor flow meter (DK800-6F, YUANKAI). Once stabilized, 800 µL of electrolyte was retained in the cell.

Optical imaging setup

The imaging platform was constructed using a commercial inverted microscope (Nikon Ti-E, Nikon Instruments Inc., Japan) to create surface plasmons. It incorporated an inverted a monochrome laser imaging module, a motorized stage for positioning an electrochemical cell, and a multi-channel fluidics system for switching electrolyte and controlling the flow pressure. Illumination of the electrochemical cell was performed using a 680 nm laser (PILOT4-AC, Superlum Corp., Ireland), directed from the bottom of the coverslip. The generated surface plasmonic resonance, encapsulating valuable information on the interaction between the laser light and the gold surface, was captured by the reflected and scattered light. The plasmonic information was acquired by a CCD camera (Pike F-032B, Allied Vision Technology, Germany).

Data collecting and processing

System analysis required synchronized voltage, current, and imaging data, acquired via the electrochemical workstation-DAQ and the CCD camera-DAQ, respectively. The procedure began by aligning the signal timelines from the DAQ with the voltage-modulation waveform generated by the electrochemical workstation, ensuring synchronization of the image sequences. Data processing was conducted in MATLAB. A Fourier transform was subsequently performed on the time-series image data to extract amplitude and phase, thus obtaining the impedance-related plasmon response signal. The surface charge density distribution was then calculated using a plasmon-charge density calibration factor and converted into potential data via the charge density-potential relationship. Finally, we cropped the potential distribution maps to extract the ζ potential values for each pixel on the 2D materials’ surface, and subsequently compiled these data for statistical analysis.

Sample preparation

Bulk MoS2 (≥99.995%) and graphene (≥99.99%) single crystals were purchased from Nanjing MKNANO Tech. Co., Ltd. The MoS2 and graphene multilayers were mechanically exfoliated from bulk single crystals and transferred onto gold-coated coverslips. The monolayer MoS2 nanosheets were converted from multilayer MoS2 nanosheets on the gold-coated coverslips by the surface plasmon-driven etching in deionized water.

KCl (≥99.5%), HCl (36.0–38.0%), and KOH (≥85.0%) were purchased from Sinopharm Chemical Reagent Co., Ltd. All reagents were directly used without further purification. The KCl solutions, ranging from 0.3 to 3 mM, were adjusted to pH 4-9 by adding 0.1 M HCl and 0.1 M KOH. The deionized water (a resistivity of 18.2 MΩ cm−1) used in the experiments was supplied from a deionized water system (Milli-Q, Millipore).

Sample characterizations

AFM (Dimension Icon, Bruker) was employed to characterize the surface morphology and thickness of 2D materials, with its KPFM and CAFM mode specifically utilized to measure the surface potential of MoS2. Raman spectroscopy (LabRAM HR Evolution, Horiba) was used to determine the number of layers in the 2D materials, while photoluminescence spectroscopy performed on the same instrument characterized the defect density of monolayer MoS2. Streaming current measurement (SurPass 3, Anton Paar GmbH) served as the conventional technique for validating ζ potential values obtained via our optical method.

Theoretical calculations

All theoretical calculations were conducted using the Vienna Ab initio Simulation Package, employing the Projector Augmented Wave method. This approach was utilized to simulate the electrostatic potential energy of monolayer MoS2 under various electrochemical environments.