Introduction

In astrophysics, relativistic collisionless shocks can happen in the expansion of intense plasmas into interstellar or intergalactic media1,2,3,4. Examples of such phenomena include the shocks observed in gamma-ray bursts, supernova explosions, and pulsar wind nebulae2,5,6. The formation of collisionless shocks could depend on a turbulent magnetic field induced by Weibel instability which can generate a magnetic field from unmagnetized plasmas7,8,9. When the plasmas are highly anisotropic, Weibel instability occurs, and the enhanced magnetic field could divert the trajectory of the charged particles, thereby converting the plasma into isotropic10,11. In this process requiring enormous energy, black holes, and supernova explosions function as the central engine for driving the collisionless shocks12. Consequently, various phenomena such as PeVatrons13 and their relevant energetic radiations from synchrotron radiation or inverse Compton scattering14,15 are observed. The high energy gamma ray from these PeVatrons also serves as an important tool for positioning these central engines such as those discovered by HESS and LHAASO telescopes16,17.

Recent exploration of astrophysics has seen a new trend in the laboratories. During recent decades, a succession of experiments has been conducted to investigate the Weibel instability-mediated collisionless shocks by utilizing large laser facilities of OMEGA18,19, and NIF7. With driving energy in the range of about kilojoule, the characteristic expanding plasma plumes have showcased velocities up to ~106 m/s and temperatures around 1 keV, demonstrating a platform for studying extraordinary phenomena in astrophysics. Meanwhile, in contrast to experimental approaches that aimed at stimulating intense filamentary magnetic fields by counter-streaming two laser-produced plasma plumes, a theoretical prototype design utilizing a laser piston-driven scheme to induce forward near-relativistic collisionless shocks has been proposed20,21. However, this kind of forward-propagating relativistic collisionless shock experiment does not seem realizable very shortly.

For collisionless shocks to form, the mean free path li of the ion7

$$l_{i}({{{\rm{cm}}}})=167.5{A}_{i}^{2}{\left({v}_{i}\left({10}^{6}{\rm{m/s}}\right)\right)}^{4}/{q}_{i}^{4}{n}_{i}\left({10}^{19}{\rm{c{m}}}^{-3}\right){ln}\lambda$$
(1)

should be greater than the length of the interacting region Lint, where vi is the ion velocity, ni is the density, Ai is the atomic number of the ion, qi is the charge state of the ion and lnλ is the coulomb logarithm. In Weibel instability, due to energy conservation, the amplification of the magnetic field is accompanied by the deceleration of the charged particles. As a result, ions that drives the instability will be scattered and trapped in the interaction region by the magnetic field, decelerating without collisions. This will result in the pile-up of the charged ions and the formation of a collisionless shock. For a typical interaction region of ~100 μm, a magnetic field >1000 T is needed. Nevertheless, since the growth rate of the Weibel instability is proportional to the anisotropic parameter and the shock formation time is τshock ~ (βdωp)−1 ~ (γF)−1, which is approximately an e-folding time of the ion Weibel instability, where βd is the normalized velocity of the accelerated ions, ωp is ion plasma frequency and γF is the growth rate of the Weibel instability. The formation length of the shock wave can be greatly reduced if a highly directional ion beam with low energy divergence is used for driving the instability. Unlike picosecond or nanosecond laser pulses for producing collisionless shocks, compressing the pulse duration to femtosecond provides unprecedented intensity for creating extreme plasma environments that are naturally collisionless. Particularly, the interaction scale of ~100 μm allows for a forward propagating collisionless shock by using merely a tabletop 10-mJ-level femtosecond laser beam.

Results

Our design draws on the idea of a laser engine. Specifically, energetic expanding plasmas are induced in the laser-plasma interaction which then leads to collisionless shocks, analogous to the black hole engine. As shown in Fig. 1a, a customized laser pulse is used. The highly controllable laser beams are analogous to those applied in inertial confinement fusion experiments whose temporal profiles could tune between a high-foot and low-foot pulse mode (Methods), allowing for precise density control of the preplasmas.

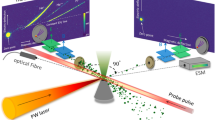
Fig. 1: A schematic of the laser-engine-driven collisionless shock.
figure 1

a The experimental setup: By illuminating a customized laser pulse (which can be tuned between the low-foot and high-foot modes by the two Pockels cells in the regeneration cavity) onto a solid target, sub-relativistic collisionless shocks are driven in the vicinity of the target. The magnetic field and the plasma density are monitored by the Faraday rotation method and the interferometry. OAP, off axis parabola. GL, Glan polarizer. CCD, Charge-Coupled Device. BS, Beam Splitter b A characteristic filamentary magnetic structure observed in front of the target and the formation of a collisionless shock c Five consecutive frames of the experimental result at preplasma density ~ 0.1nc are displayed, which shows the temporal evolution of the magnetic field after the action of the laser engine. A shock breakout is observed at a time delay of ~ 4 ps.

Full size image

The first-stage ignitor (leakage pulses from the regeneration cavity) is employed to generate an expanding plasma within a nanosecond time scale. This highly reproducible plasma with a background magnetic field of ~ 10 T is homogeneous. As shown in Fig. 1b, the electromagnetic energy of the main laser beam functions as a Laser engine, which drives the expanding energetic plasma out of the target as well as the subsequent collisionless shock22.

As demonstrated in Fig. 1c, the experiment reveals a Weibel instability-mediated collisionless shock with a velocity of ~ 0.03c at preplasma density ~ 0.1nc(To see the shock is collisionless, for ions with a velocity ~ 0.03c, the Al+8-Al+8 collision mean free path is \({\lambda }_{A{l}^{+8}-A{l}^{+8}}\) ~ 30 m), almost on par with the expanding plasmas at the boundary of an exploding supernova23,24. With a velocity of ~10000 km/s, we can study the shocks relevant to the youngest supernova remnant (SNRs) (~ 100year) in the laboratory, such as the SNR G1.9 + 0.3 which25 has a shock velocity of ~ 13000 km/s. The magnetic field peaks at ~ 2.7 ps and lasts for about 5 ps, and the formation time of the shock \({\tau }_{{shock}}\) ~ \({({\beta }_{d}{\omega }_{p})}^{-1} \sim \,{({\gamma }_{F})}^{-1}\) is estimated to be ~1 ps and can be clearly seen in the density profile measured in experiment. The topological structures of the magnetic field experienced an abrupt change after a time delay of ~ 4 ps, indicating the breakout of the shock wave.

We note in Fig. 1c that for time delays smaller than 2 ps, magnetic tube structures emerge through Weibel instability self-organization. Soon later, at time delays of ~ 2.7 ps, the magnetic filaments demonstrate a curved structure, which is regarded as a precursor for the nonlinear stage of the collisionless shock. The energy spectrum of the magnetic field is displayed in Fig. 2a, b. Filamentary peaks are apparent in the figures as indicated by the blue shaded area which is indicative of the Weibel instability. From time delays ~ 2.7 ps to ~ 4.0 ps, the scaling law of the magnetic energy spectrum evolves from \({k}_{s}^{-8/3}\) to \({k}_{s}^{-2}\), suggesting the magnetic energy cascade during the interaction.

Fig. 2: Time evolution of the magnetic fields.
figure 2

The magnetic energy spectrum Fs at time delays (a) blue: 1.3 ps and yellow: 2.7 ps, (b) dark blue: 4.0 ps and orange: 5.3 ps. The dashed lines shows a fit to the scaling law of the magnetic energy spectrum. The blue-shaded area in both figures represents the range of the most unstable scale; Particle-in-cell simulation of the time evolution of the magnetic field space distribution at (c) 2.7 ps and (d) 4.0 ps; The density of the preplasma are ~ 0.1\({n}_{c}\).

Full size image

For shock formation, the time required can be expressed26 as τshock = nτi + τe, where τe and τi are the saturation times of electron and ion Weibel instability respectively, and n accounts for the time needed for the current filaments to merge. However, for our specific experiment conditions, a revision of the equation is required20. Since the expanding plasma is ion-dominated, electron Weibel instability can be neglected, as is the time needed for the merging of the current filaments. Thus, as the initial filament distance is already near its maximum, only τi is taken into consideration for the shock formation. In fact, an e-folding time of the ion Weibel instability is needed for the shock to form, which is τshock ~ (γF)−1 ~ (βdωp)−1 ~ 1 ps and is consistent with our experimental observation (See Supplementary Fig. 1). In the later stage of nonlinear ion Weibel instability, the deceleration of ions and the pile-up of ions at the front of the expanding plasma contribute to the formation of the collisionless shock27. A \({k}_{s}^{-8/3}\) law of plasma spectrum at scales smaller than the ion gyroradius can be induced due to structure formations28 and turbulent motion of electrons, since electron gyroradius is ~ 1μm. Electrons can be heated during the interaction, leading to a change in the scaling law from \({k}_{s}^{-8/3}\) to \({k}_{s}^{-2}\), which implies that magnetic field is dominant in the collisionless shock29.

Under our experimental conditions, the steady shock velocity is ~ 0.03c and the maximum plasma expanding velocity observed in the experiment is ~ 0.07c before shock formation. The peak magnetic field estimated from the experiment is ~ 5000 T. After the formation of the shock wave, by assuming an effective degree of ionization Z = 8 for the aluminum target, the gyroradius of the accelerated Al+8 ions in the target can be calculated to be \({\widetilde{R}}_{g}={p}_{i}/{q}_{i}B\) ~ 35μm, which is comparable to the filament distance λF = 31 μm. Since the particles are all ionized, the influence of neutral particles, which could potentially have a cooling effect, can be neglected. Based on the magnetic bouncing mechanism, the maximum magnetic field is determined by Bsat ~ \({\gamma }_{F}^{2}{m}_{i}c/{q}_{i}v{k}_{{sat}}\). Where γF is the growth rate of the instability and qi is the charge of the ion, v is the shock velocity, ksat = 2π/λsat is the saturation wave vector, this gives a maximum magnetic field of ~ 4000 T. It indicates that the Weibel instability-induced magnetic field is already saturated which takes ~ 2-3 e-folding time of the instability. The magnetic field energy density reaches ~14% of equipartition with the plasma kinetic energy density (ek =(B2/8π)/(nimiv2/2) ~ 0.14, where ni is the density of the ions), which indicates that a magnetized collisionless shock is induced.

The plasma dynamics and the formation of the collisionless shocks are investigated using Particle-in-cell (PIC, EPOCH)30 (See in Supplementary Information 3). Our simulation results feature a laser-heated electron expanding time of about 100 fs, after when the ions are drawn out of the target by the sheath field. Since the sheath field is perpendicular to the surface of the target, ions can be accelerated to velocities as high as ~ 0.07c. This acceleration leads to the occurrence of Weibel instability within 1 ps, as well as the formation and amplification of a filamentary magnetic field. Turbulent magnetic islands are then created, as demonstrated in the temporal dynamics of the magnetic fields in Fig. 2c, d. A peak magnetic field as high as ~ 5000 T is approached in the simulation and is consistent with our experimental results (Fig. 3a).

Fig. 3: The shock breakout dynamics.
figure 3

a The time evolution of the maximum magnetic field in front of the target at different time delays. The solid lines show the experimental results, whereas the dashed lines display our simulation results. As indicated by the legend, the curves with different colors correspond to pre-plasma densities of 0.4nc, 0.2nc, and 0.1nc respectively. The error bar represents the standard deviation of multiple shots. b The leading-edge position of the expanding plasma; The red solid line presents the experimental results measured when the preplasma density is ~ 0.2nc. The blue line presents the front of the expanding plasma when the density of the preplasma is ~ 0.1nc. The yellow dashed line is a linear fit of the leading edge of the expanding plasma when the preplasma density is ~ 0.1nc; the equation for the fitted curve is kt3/5, where k = 27 is used; The yellow-shaded area delineates the shock wave impact region associated with the fitted curve; The error bar represents the standard deviation of multiple shots; (c) PIC simulation results of the time evolution of the density of the plasma along the line y = 0. The horizontal solid red line indicates the position of shock formation; The vertical dashed yellow line indicates the time of shock breakout; The dashed white curve shows the fitted curve with a function R(t) = 27t3/5. d The catastrophe model: density of the plasma at shock front.

Full size image

After the shock formation, the otherwise hardly accessible dynamics of the collisionless shock wave become detectable by pump-probe recording of its propagation processes. We have tracked the leading-edge position of the expanding plasma by monitoring the plasma density and the magnetic field (Fig. 1c). The leading-edge position can be fitted by a function of R(t)=27t3/5, t in ps and R in μm, which describes well the experimental results, as shown in Fig. 3b. We note that this function is slightly different from a 2/5 power law that is expected with a spherical shock. This discrepancy could arise from the finite size of the laser focus spot which leads to an ellipsoidal expanding wavefront rather than strictly spherical. By comparing Fig. 3a and b, we observe that an increase in magnetic field energy is accompanied by a decrease in shock velocity. Some portion of the ion energy is lost during shock formation due to the driving of the return current and the amplification of the magnetic field. This results in a magnetic field-dominated collisionless shock that resembles what happens in a supernova remnant25. The fitting function for the shock front is consistent with our PIC simulations and follows a curve R(t) ~ 27t3/5. Meanwhile, the density jump npk/nbg measured in the experiment is ~ 5 as shown in Supplementary Fig. 1, where npk and nbg is the peak plasma density and background plasma density measured in the experiment respectively. Since for a strong shock30 the density jump is determined by npk/nbg ~ (γg + 1)/(γg−1), this gives an adiabatic index γg ~ 1.5. The adiabatic index indicates the distribution of energy among different degrees of freedom, which implies that the magnetic field is crucial to the formation of the density jump, and the eventual collisionless shock mediated by Weibel instability.

The shock wave observed in experiment resembles that observed in the supernova remnant, such as SNRs G1.9 + 0.3 like SNRs. Though the total scale of the shock wave is ~70 μm, the radius—time relation for our experiment and SNRs G1.9 + 0.3 like SNRs are both approximately R(t) ~ t0.6 which can be seen as the selfsimilar solution of a central engine-driven spherical collisionless shock. The characteristic dimensionless parameters in our experiment, such as the Sonic Mach number(vsh/cs) and the Alfven Mach number(vsh/va) are 40 and 300 respectively. Meanwhile, for the dimensionless magnetic energy (magnetization), ek =(B2/8π)/(nimiv2/2) ~ 0.14, which is comparable with that observed in the SNRs G1.9 + 0.3 like SNRs. Thus our experimental results can be used for the probe of the dynamics related to the SNRs G1.9 + 0.3 like SNRs. A comparison between plasma parameters in our experiments and SNRs G1.9 + 0.3 type young supernova remnant is listed in Table 1.

Table. 1 Comparison between plasma parameters in our experiments and SNRs G1.9 + 0.3 type young supernova remnant
Full size table

In the cosmos, a shock breakout is initiated when the shock reaches the edge of a star31,32, such as that during a supernova explosion. Interestingly, our experiment observations have shown a resemblance to the collisionless shock breakout: the shock structure experienced a catastrophic breakdown at about 4.0 ps after the illumination of the pump pulse. Meanwhile, the magnetic field also vanishes in accompany with the shocks (Fig. 1c) and this may indicate a release of electromagnetic energy. The sudden disappearance of the magnetic field will cause the accumulated high-density shock front to explode. The Weibel-mediated collisionless shock breakout is reproduced in a laboratory. Since the trapped ions can expand almost isotropically inside the intense magnetic field, the duration of the shock breakout can be roughly estimated by the ions’ expanding velocities. Specifically, the steady shock velocity of ~0.03c in our experiment suggests that approximately 1 ps is required for the plasma to expand to a density of <0.01nc, where the plasma’s volume has increased by six-fold (plasma radius raised by ~10 μm) and the shock breakout has stopped.

The experimental results are supported by our PIC simulations. Figure 3c shows the density profile of the plasma density at different time delays. It shows that the Al+8 ions continue to expand after 4 ps at an almost constant velocity, which is consistent with our basic estimation of the shock breakout time and is a hallmark of the breakout of a shock wave. This ultrafast release of energetic ions from the target surface, as revealed by the shock breakout process, has important implications not only for astrophysics but also for multiple plasma and radiation phenomena. Specifically, the detachment of the ions in the acceleration process directly indicates the basic mechanisms behind the laser-driven ion acceleration, which has yearned for further explorations.

Given the complexity of the breakout process, a simple catastrophe model is developed to show the basic working principles33. By assuming a Gaussian curve of the shock front density,

$${n}_{p}=\frac{{n}_{0}}{\sqrt{2\pi }\sigma \left(t\right)}\exp \left(-{\left(x-27{t}^{\frac{3}{5}}\right)}^{2}/2{\sigma }^{2}(t)\right)$$
(2)

we assume that the width of the shock, σ(t), expands with a small velocity and is on the order of the ion skin depth before reaching the edge of the preplasma, and we take n0 to be a constant. The shock front expands with the fitted curve 27t3/5 before breakout and the expanding velocity of the width of the shock front σ(t) is set to ~0.03c while reaching the plasma edge. As shown in Fig. 3d the plasmas show an abrupt decrease in density which eventually leads to the disappearance of the shock. To compare with shock breakouts observed in astrophysics, we have listed several characteristic duration times of the shock breakouts34 in Table 2. Besides the catastrophic disappearance of the shock front observed in the experiment, an electromagnetic pulse with a duration of ~1 ps, which indicates the occurrence of the breakout, should be detectable in the experiment and this calls for further exploration.

Table. 2 Shock breakout and its time of duration34
Full size table

Given the complexity of the interaction between the intense laser pulse and the plasma, a proper preplasma density that depends on the laser’s contrast ratio is decisive for the shock formation. This is because high preplasma densities will prohibit the ion dynamics as electron Weibel instabilities will dominate the plasma expansion. In our experiment, this specific threshold for the collisionless shock formation is below 0.1nc, corresponding to high contrast (or the low-foot mode) of the laser conditions (see Methods). Otherwise, at high preplasma densities of ~ 0.4nc or ~ 0.2nc, filamentary magnetic tubes are formed at the boundary of the preplasma region, and no shock waves are visible.

To qualitatively characterize the underlying interaction processes, we now examine other two particular cases of preplasma densities of 0.4nc, and 0.2nc—each representative of the Weibel instability in the unsaturated and saturated regime. Figure 4 compares the spatiotemporal evolution of the magnetic fields at the target front in these two scenarios, respectively. At the preplasma density of ~ 0.4nc, it is clear a concentration of the filamentary structures appears in the middle of the plasma region with three recognizable magnetic filaments. The physical origin of these ion Weibel instability-related filaments is seeded by electron Weibel instabilities. Since ions cannot undergo adequate acceleration for preplasma densities of 0.4nc, the expanding hot electrons from the target surface account primarily for the filamentary structures, which are then amplified by the insufficient accelerated ion beams. To account for this process, a hot electron expanding model is developed in Supplementary Information 2 (A sketch map of the model is shown in Supplementary Fig. 2, and the calculated anisotropic parameter is shown in Supplementary Fig. 3.).

Fig. 4: Spatiotemporal evolution of the magnetic field under different preplasma densities.
figure 4

Spatiotemporal evolution of the magnetic field in front of the target when the preplasma density npre is (a) npre = 0.4nc; (b) npre = 0.2nc, τd is the time delay; The target surface is located at x = 0 which is indicated by an arrow in each picture.

Full size image

With declining preplasma density, the peak sheath field gradually migrates from the preplasma boundary to the target surface. The ions thus can gain greater energy, leading to a nearly saturated magnetic field induced by the ion Weibel instability at the preplasma density of ~0.2nc (Fig. 3b). The gyroradius of an Al+8 ion in the magnetic field can be estimated as \({\widetilde{R}}_{g} \sim 100\mu m\). The filament distance, dF, as determined by the experiment is ~15 μm, indicating that the Weibel instability is nearly at the saturation point.

In comparison with the higher preplasma density situation, a major difference between 0.2nc and 0.4nc is the trajectory of the Al+8 ions. For the preplasma density of ~ 0.2 nc, the deflection angle θ of Al+8 ions in the magnetic field can be calculated as,

$$\theta={{{\rm{asin}}}}({d}_{F}/{\widetilde{R}}_{g}) \sim {d}_{F}/{\widetilde{R}}_{g}=0.2{rad} \sim 10^\circ$$
(3)

which indicates that the Al+8 ions can propagate somewhat freely in the magnetic field. The expanding ions hence can be regarded as a Weibel instability-mediated rarefactive wave. Near the boundary of the preplasma, the magnetic field structures stop moving, as being frozen because the return currents cannot be supported outside of the preplasma region.

Figure 3a presents the temporal evolution of the peak magnetic field for three different preplasma densities. Notably, for preplasma density ~ 0.1nc, the magnetic field increases to its maximum value of B ~ 5000 T at around 2.7 ps. It suggests that the growth rate \({\gamma }_{F}\) of the magnetic field is approximately three times greater than in the case of a low-foot laser and is estimated to be ~ 1 × 1012 s−1, which is compatible with our estimation of the growth rate of the Weibel instability: γF ~ βdωp.

Discussion

We have obtained the unambiguous experimental evidence of sub-relativistic collisionless shock driven by a table-top femtosecond laser using a concept which we termed laser engine. In this concept, a carefully adjusted laser temporal profile is used to create a low-density isotropic preplasma and the ensuing ion acceleration by the second femtosecond main laser pulse. Afterward, a strong flow of highly directional ion beams develops, which in turn drives a rapidly growing Weibel magnetic field and leads to the formation of a collisionless shock wave. Much different from the amplification of the Weibel magnetic fields observed in ref. 18, a real Weibel instability mediated forward propagating collisionless shock with subrelativistic velocity is observed in the experiment. When the shock propagates out of the plasma region, collisionless shock breakout is observed in the experiment. Importantly, our experimental results identify the Weibel instability as an efficient mechanism for escalating the magnetic field and could provide an essential boost in the formation of relativistic collisionless shocks in the universe. Meanwhile, femtosecond laser beams can provide far larger energy densities and, concomitantly, significantly reduced time and space scales required for studying the laser-plasma interactions. As a general application, we anticipate the use of femtosecond laser systems for studying collisionless shock formation, propagation, and breakout, as an alternative to large laser facilities that are beyond the reach of common researchers. This simple scheme, conducted with only a mJ-level laser system, is flexible and can, in principle, be extended to much higher laser energies to escalate the collisionless shock velocity beyond our current observations. Looking ahead, since vshock\(\,\propto \,\)E for a spherical shock, relativistic collisionless shock mediated with a turbulent magnetic field as high as 105 – 106 T with picosecond-scale duration can be induced with currently available petawatt-level femtosecond laser facilities35. With this high magnetic field, the atomic properties and the behaviors of matter will be changed fundamentally. Extreme physics resembling that observed on the surface of neutron stars and similar compact objects can be explored36.

Methods

Laser parameters and experimental setup

A laser system with 30-fs pulse width and central wavelength of ~800 nm is used in the experiment. The laser beam is split into two parts with a beam splitter, the laser beam with about ~ 90% of the total energy is named the pump pulse. This beam with ~ 4-mJ energy was focused at 90° with an off-axis parabola mirror onto the surface of fused quartz that is coated with ~30 μm thick aluminum film. The peak intensity of the laser beam is ~ 1 × 1017 W cm–2. Another beam with ~10% of the total energy is frequency doubled to 400 nm to be used as a probe beam. The off-axis parabola and the targets were held in a vacuum chamber with ambient air pressure ~10−3 Pa. The relative time delay of the main beam and the probe beam is controlled by an electric stepper motor.

The control of preplasma density and methodology

The laser temporal contrast is defined as the ratio of the peak intensity of the main pulse to the prepulse intensity. The temporal contrast can be controlled by the relative time delays between different Pockels cells in the Chirped Pulse Amplification system (CPA system). The laser consists of a Ti:sa oscillator, a repetition amplifier, and a single-pass amplifier. The repetition rate of the oscillator is 80 MHz, i.e., the time interval between two neighboring oscillator pulses is 12.5 ns. The cavity length of the regeneration amplifier is 3 m, which corresponds to a round-trip time of 10 ns. A schematic drawing of a time series of laser pulses is shown in Fig. 5. As the extinction ratio of the Pockels cell is ~1000:1, when the selected oscillator pulses (PC I in Fig. 5) enter the regeneration cavity, leakage pulses are accompanying with the selected ones. When the cavity is dumped at a second Pockel cell, the leakage pulses are output with the selected pulses (PC II in Fig. 5) which affects the contrast in nanoseconds. And the contrast can be controlled by the switching time of the second Pockel cell.

Fig. 5: Schematic drawing of time series of laser pulses.
figure 5

The temporal separation between consecutive seed pulses is 12.5 ns. Within the regeneration cavity (Regen), the round-trip time is 10 ns. When the selected seed pulses are injected into the regeneration cavity (via Pockels cell I), they are accompanied by leakage pulses. The contrast of the amplified laser pulse can be controlled by the switching time of the second Pockels cell (Pockels cell II).

Full size image

The prepulse approaches the target ~2.8 ns before the main pulse, and a preplasma is induced. Due to the long-time delay between the main pulse and the prepulse, when the main pulse illuminates on the target the preplasma density distribution is almost homogeneous in front of the target. The density of the preplasma is determined by the intensity of the prepulse, thus the temporal contrast of the laser beam can be easily monitored by the density of the preplasma at the zero delay.

To diagnose the plasma density in front of the target, complex laser interferometry is used in the experiment37. The interference fringes are used to reconstruct the phase changes due to the presence of plasma in front of the target. This phase change can then be used for the extraction of the density distribution of the plasma.

The magnetic field is measured by the classical Faraday rotation method. To overcome the difficulties meeting in two-channel Faraday rotation experiments, we follow a method developed in ref. 37, in which only one CCD camera is needed, thus overcoming the difficulties of perfectly matching two images from different CCD channels. Glan-type polarizing prisms are used in the experiment to measure the rotation of the polarization plane of the probe beam transmitted through the plasma region. By comparing this rotation angle with the background polarization state of the probe beam the magnetic field can be extracted.

Ion acceleration and Weibel instability-mediated shocks

Precise control of the time delay between the main pulse and the prepulse, as well as adjustment of the prepulse intensity, can be used for the regulation of the preplasma density situated ahead of the target. This control facilitates achieving a preplasma density on the order of near critical density, such as ~0.1nc. In the target normal sheath acceleration mechanism (TNSA), ~ MeV level proton beams (vi ~ 1 × 107 m/s) can be easily induced with a millijoule level femtosecond laser system as it is demonstrated in ref. 22. When the accelerated ion beams penetrate into the preplasma in front of the target, the mean free path of the ion beam is ~30 m which ensures that the ion plasma interaction is collisionless and can be used for the study of the collisionless shocks.

While hot electrons are stimulated by the ultrashort laser beam expanding out of the target an electrostatic sheath field is formed at the boundary of the target which can accelerate the charged ions. However, if the density of the preplasma is very high, this acceleration field can be shielded by the preplasma, which can lead to low efficiency in the acceleration of ion beams. There must be some critical density ncrt, below which the ion beams can be efficiently accelerated. Based on a model developed in ref. 38, in TNSA the energy gained by an ion beam in a plasma with two electron temperatures Th and Tc can be written as Eion ~ Ze(nhTh + ncTc)/(nh + nc). The kinetic energy of the accelerated ions in our experiment is ~ MeV. The growth rate γF of the ion Weibel instability is γF ~ βiωi. Based on PIC simulations, the maximum ion velocity can reach ~ 0.07c which is consistent with the experiment. The growth rate of the Weibel instability decreases exponentially with increasing preplasma density because the sheath field also decreases exponentially with preplasma density. As shown in the article, just like in high harmonic generation, a “phase transition-like” behavior should be observed, and this transition has been observed in the experiment.