Introduction

In metallic materials, dispersing obstacles (such as hard particles and precipitates) to block moving dislocations is a commonly used approach for strengthening purposes1,2,3. This widely adopted “dispersion hardening” mechanism, however, often sacrifices ductility, because dislocation pile-ups at the obstacles lead to stress concentration, facilitating the nucleation of cracks4,5,6. We propose here to replace the conventional crystalline dispersions with amorphous nanoparticles. This is a likely solution to the problem, because an amorphous phase and its interface with the matrix have been reported to act as dislocation sources and sinks7,8, which would help alleviate the stress concentrations at the obstacles. As such, amorphous nanoparticles would be the dispersion of choice, in delaying damage nucleation to significantly improve ductility and other damage-sensitive in-service properties such as fatigue resistance.

The question is then how to realize a dense and uniform dispersion of amorphous nanoparticles inside the metals. To this end, we take advantage of additive manufacturing (AM)9,10,11. This non-equilibrium processing route and associated complex melt flow have been known to provide opportunities for tailoring the microstructure, including the grain morphology, subgrain dislocation structure and chemical segregation, leading to vastly improved mechanical properties over those from traditional processing9. For example, we recently showed that laser powder bed fusion (L-PBF) can achieve spontaneous and intragranular dispersion of microparticles in conventional composite systems12. Herein, we exploit L-PBF to create a new type of nanocomposite consisting of a metal matrix with uniformly and densely distributed reinforcing amorphous nanoparticles. An in situ nano-fragmentation process is exploited to spontaneously refine the crystalline reinforcing microparticles into amorphous nanoparticles during L-PBF (Fig. 1a). For the reinforcing phase, we set three criteria for the materials selection: (1) high strength and elastic modulus to ensure the desired strengthening; (2) a melting point within a control window (~ 3000 K) that is accessible to the L-PBF process, such that the dispersions can be turned amorphous via melting, which are then torn apart during turbulent fluid flow and rapidly quenched; and (3) no chemical decomposition or extensive reaction with the matrix pool during the melting of reinforcements13. We integrate Thermo-Calc software with the latest substance database to evaluate the thermally stable phases of different metal–ceramic particle systems. The above criteria led us to a system of simple boron carbide (B4C) reinforced copper as the first model. We demonstrate in the following that L-PBF produces a high density of amorphous nanoparticles that are embedded within pure copper grains.

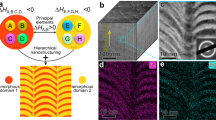
Fig. 1: Design principles and microstructures of nanocomposites by laser powder-bed-fusion (L-PBF).
figure 1

a Schematic illustrating the manipulation of reinforcing particle structures via additive manufacturing (AM). An in situ nano-fragmentation process is utilized to spontaneously refine crystalline reinforcing microparticles into amorphous nanoparticles during L-PBF. This process involves the melting, nano-fragmentation, and rapid solidification of the reinforcing particles. GB denotes grain boundary. b Three-dimensional reconstructed scanning electron microscopy (SEM) images of the as-built composite. A cross-sectional electron backscatter diffraction (EBSD) image is superimposed to show the equiaxed grain structure. Melt pool boundaries (MPBs) and build direction (BD) are illustrated by the yellow dashed line and white arrow, respectively. c Aberration-corrected high-resolution transmission electron microscopy (HRTEM) image of a representative nanoparticle, with ultranano black regions distributed within the amorphous nanoparticles. At least twenty nanoparticles were characterized for microstructural identificaiton. d Enlarged view of the selected region in (c). The inset shows a fast Fourier transform (FFT) image of a region in the nanoparticle that does not contain Cu nanocrystals, suggesting an amorphous nature. e high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) image of a tiny nanocrystal along the [110] FCC zone axis and energy-dispersive X-ray spectroscopy (EDS) images of Cu, B and C atoms. f Three-dimensional atomic probe tomography (APT) reconstructions of Cu, B and C atom distributions in a typical APT tip including a matrix Cu–nanoparticle interface. The Cu, B and C atoms are coloured blue, yellow and red, respectively. g, h Measured distributions of the three atomic species near the interface and inside the nanoparticle, respectively. The phase boundary (PB) is indicated by the white line, and a representative tiny Cu cluster/nanocrystal is highlighted by a red circle. i Near-edge X-ray absorption fine-structure (NEXAFS) spectrum at the B–K edges of the extracted nanoparticles from the as-built composite.

Full size image

Results

Microstructures and their formation mechanism

High-purity copper powders (average size of ~35 μm) were mixed with crystalline B4C microparticles (average size of ~4 μm, 12 vol.%). A porosity-free bulk composite (density: >99.8%) was then built using L-PBF (Methods). Notably, the B4C microparticles were melted and transformed into nanoparticles with an average size of ~47 nm (see Supplementary Fig. 1a for particle size distributions), which are densely and uniformly dispersed in the copper matrix (Fig. 1b). These nanoparticles are amorphous, as indicated by the X-ray diffraction (XRD) pattern and nuclear magnetic resonance (NMR) spectrum (Supplementary Fig. 1b, c)14. Electron backscatter diffraction (EBSD) imaging of the cross-sectional regions indicates that the copper grains are equiaxed, with ultrafine grains averaging to 0.39 ± 0.14 μm (Fig. 1b). High-resolution transmission electron microscopy (HRTEM) indicates the presence of nanocrystals (black regions, sizes of ~2.9 nm) inside the amorphous nanoparticles (Fig. 1c, d). Observing along the [110] face-centred cubic (FCC) zone axis via high-angle annular dark-field (HAADF) scanning transmission electron microscopy (STEM), we find that the lattice spacings of these nanocrystals correspond to copper (Fig. 1e), which was confirmed by energy-dispersive X-ray spectroscopy (EDS) spectrum. Therefore, these fragmentated nanoparticles are “quasi-amorphous”. We used atom probe tomography (APT) to study the nanoscale compositions of the amorphous nanoparticles and the atomic diffusion across the interface (Fig. 1f–h). The nanoparticle composition (B3.89C) is close to B4C, with 8 at% copper incorporated. Figure 1h indicates very limited diffusion of the B and C atoms into copper (~5 nm). This is because B–C has strong chemical affinity such that their robust atomic bonding did not allow the diffusion of individual elements even under molten conditions, as indicated by our ab initial molecular dynamics calculations of the formation enthalpy of B4C at various temperatures (Supplementary Fig. 2). On the other hand, copper atoms diffuse into the B4C nanoparticles, forming the nanoscale clusters seen under TEM. Near-edge X-ray absorption fine-structure (NEXAFS) spectroscopy of the extracted nanoparticles (Fig. 1i) shows broadened π* peak with a relatively low intensity, which can be attributed to the amorphous structure15,16. Thus, amorphous nanoparticles are generated by melting and fragmentation of the B4C microparticles upon laser scanning, followed by rapid quenching, which kinetically inhibits the thermodynamically favoured crystallization.

The in situ nano-fragmentation of ceramic particles was achieved by increasing the input energy density of the L-PBF. We find that microparticles are retained at low energy density (86.9 J/m3) but fragmented as the energy input increased, eventually into nanoscale particles at 180.6 J/m3 (Fig. 2a). Importantly, the fast Fourier transform (FFT) images demonstrate that most of the produced fine particles are amorphous upon rapid solidification. To reveal the particle melting and fragmentation dynamics, we conducted high-fidelity simulations to track the changes in B4C microparticles, which produced three-dimensional data at nanoscale and meso-nanosecond time resolutions (Methods). As shown in Fig. 2b–d, we observe the following microstructural changes during a single-track scan. Initially, a laser impinging on the composite powder bed increases the local temperature to a maximum value of 3800 K, directly melting the B4C microparticles. Then, the strong and complex fluid flow induced by the large thermal gradient of L-PBF (reaching 108 K/m, Supplementary Fig. 3) tears the ceramic droplets apart, gradually turning them into very fine droplets that are tens of nanometres in size (Fig. 2e). Notably, the above fragmentation process operates on the first track when the laser directly irradiates the microparticles. The subsequent laser tracks do not raise the melt pool temperature to reach the melting point of B4C. Eventually, the Marangoni convection-induced intermixing of solidified amorphous nanoparticles with copper melt prevents particle agglomeration12, which facilitates the observed high dispersion uniformity. The same melt-quench and fragmentation is expected to happen in other metal-ceramic particle systems to obtain similar composite structures. For example, we have achieved B4C amorphous nanoparticles in pure aluminium using the same in situ nanofragmentation strategy (Fig. 2f). We have also confirmed the generality in other ceramic–copper systems (e.g., CrB2-copper nanocomposites, Fig. 2g). In all cases, the ceramic particles are fragmented to the nanoscale without marked changes in their compositions.

Fig. 2: Nanofragmentation mechanism of microparticles.
figure 2

a Changes in the morphologies of reinforcing particles as a function of the input volumetric energy density, Ed. (Ed = P/vhd, where P is the laser power, v is the scan speed, h is the hatch distance, and d is the layer thickness). A representative HRTEM image of the interface and the corresponding FFT image of a region in the refined particle, displayed for samples processed with different Ed. The volume fraction of B4C is 12% in all samples. Images at different locations (at least five) show similar morphologies with the representative ones. Note that most of the refined particles (with an Ed value larger than 118.1 J/m3) have amorphous structures, thereby suggesting the melting–fragmentation–solidification process of B4C microparticles upon L-PBF. b–d High-fidelity multiphysics modelling of the change in the particle morphology during L-PBF. The coloured arrows represent the velocity vector in the melt, under which the initially microsized (~4 μm in diameter) particle is gradually fractured into nanoparticles. The particles are coloured based on their local temperatures. e Statistical calculation of the particle size distribution as a function of scanning time, as obtained from the simulation results. f SEM image of the as-built Al-B4C composites and HAADF-STEM image of interfacial structure of the selected region, showing the same in-situ nanofragmentation behaviour as in Cu, now forming ANPs with sizes ~200 nm. BD stands for build direction. Beam direction is along the [100] zone axis of aluminium. EDS mapping indicates that the composition of the nanoparticle is 78.7 ± 3.5 at% of B, 18.8 ± 3.6 at% of C and 2.5 ± 0.7% of Al, with little elemental diffusion or reaction at the interface. g The representative SEM image and HAADF-STEM image of as-built Cu-CrB2 composites. Micron-sized CrB2 with diameters of ~10 μm were used as the starting reinforcing particles, which have been spontaneously turned into amorphous nanoparticles with sizes of ~40 nm. Beam direction is along the [110] zone axis of copper. At least five different locations were independently observed for microstructures shown in (f and g) showing similar results.

Full size image

Tensile properties and the elimination of printing defects

We employed tensile tests to investigate the mechanical properties of the L-PBF nanocomposites. Figure 3a shows the representative tensile responses of the as-printed copper reinforced with three volume fractions (12%, 8% and 4%) of the amorphous nanoparticles (ANPs) (hereafter referred to as Cu–ANP). Copper grains show no obvious texture in the as-built samples, and their sizes decrease from 7.17 ± 4.48 μm to 0.39 ± 0.14 μm (Supplementary Fig. 4a) with increasing particle volume fraction inside. A tensile curve for conventional high-strength pure copper with a grain size (~ 400 nm, Methods) similar to that of Cu-12%-ANP is presented for comparison. Clearly, Cu–ANPs show much better tensile strengths and strain hardening beyond plastic yielding, leading to high ductility. Specifically, Cu-12%-ANP exhibits very high yield and tensile strengths of 729 ± 27 and 1036 ± 35 MPa, respectively, along with relatively large uniform and total elongations of 7.2% ± 0.4% and 9.7% ± 0.4%, respectively. This enhanced tensile ductility of Cu-ANPs is further evidenced by the improvement in true fracture strain, estimated from the reduction in area at fracture (Supplementary Fig. 5). Previous AM attempts have also achieved excellent mechanical properties in other types of advanced alloys, such as titanium-based alloys, high-strength steels and high-entropy alloys; on a normalized basis, the properties of our L-PBF nanocomposites are even better than those state-of-the-art AM materials (Fig. 3b, see Supplementary Note 1 for the symbol description and associated reference details). Our copper nanocomposites also demonstrate strength–ductility combinations that surpass previous types of copper-based alloys and are comparable to the well-known high-strength copper-beryllium alloy (noting that beryllium is toxic) (Fig. 3c; see Supplementary Note 2 for referential data). It is worth mentioning that ANP-reinforced pure copper is used here to demonstrate the basic principle of dispersion hardening with amorphous nanoparticles. Nanocomposites with unprecedented mechanical properties are highly anticipated when this strategy is applied to typical high-strength copper alloys. To see the advantage of ANPs, we also annealed the as-built samples at 1173 K for 6 h, after which the amorphous B4C became crystallized nanoparticles (CNPs) (referred to as Cu–CNPs) (Supplementary Fig. 4b). Because of the strong pinning of grain growth by the nanoparticles, the grain size of the annealed nanocomposite remained almost unchanged (Supplementary Fig. 4c). Cu-12%-CNP shows a tensile elongation of only ~3%, followed by sudden failure. The superiority of ANP in tuning mechanical properties is primarily manifested in its ability to enhance strain hardening, as shown by the Kocks-Mecking hardening rate plot and the increased strain hardening exponent based on the Hollomon equation (Supplementary Fig. 6a–c). As a result, Cu–ANP exhibits twice the total elongation of Cu–CNP with the same nanoparticle content.

Fig. 3: Mechanical and functional properties of the laser powder-bed-fusion copper nanocomposites.
figure 3

a Tensile stress–strain curves of the as-printed Cu-B4C nanocomposites with different volume fractions of B4C (12%, 8% and 4%). The as-built nanocomposites with amorphous nanoparticles are referred to as Cu–ANP. The ultimate tensile strength at which unstable deformation (i.e., necking) occurs is marked on each curve. The inset shows a schematic of a dog-bone-shaped tension specimen. A tensile curve (green) for conventional high-strength cold-rolled pure copper with a similar grain size to that of Cu-12%-ANP (i.e., ~400 nm) is presented. b Mechanical property comparison of our as-built copper nanocomposites with that of previous copper alloys. The referential literature data are provided in Supplementary Note 1. c Tensile strength versus uniform elongation of AM copper nanocomposites compared with those of representative high-performance AM metal alloys in the literature, including aluminium (Al)-based alloys, high-strength steels, titanium (Ti)-based alloys, high-entropy alloys (HEAs) and Cu-based alloys. For fair comparisons of different metallic materials, the tensile strength is normalized by the Young’s modulus. The symbol descriptions and associated references can be found in Supplementary Note 2. d Fatigue life (the number of cycles to failure) against the fatigue strength-to-tensile strength ratio of the Cu-4%-ANP and Cu−12%-ANP nanocomposites, along with references for the reported state-of-the-art copper materials, including nanograined, gradient and nanotwinned microstructures. The fatigue properties of the well-annealed coarse-grained copper are shown. Each comparison sample has a stress ratio R of 0.1. The symbol description and associated references can be found in Supplementary Note 4. e Strength (hardness) retention of our L-PBF Cu–ANP after annealing at different temperatures for 1 h compared with that of conventional copper-based alloys (see Supplementary Note 5 for more reference information).

Full size image

We now discuss the several noteworthy attributes of our AM Cu-ANP composite. First of all, the complete elimination of printing defects (such as microvoids) due to inadequate fusion, is difficult for L-PBF copper-based materials because of their low laser absorptivity in the infrared laser range13,17,18. We measured the laser absorptivity of our initial Cu-B4C powder mixtures with different microparticle fractions, revealing a surprisingly high laser absorptivity of more than 70% for composite powders (8 and 12 vol.%) at a wavelength of 1064 nm (Supplementary Fig. 7a). This represents a nearly fourfold improvement in absorptivity compared to pure copper. The mechanisms of microparticles in mediating the laser-powder interaction can be revealed by using computational full laser ray tracing (Methods). The majority of laser rays, which penetrate the powder via multiple reflections, are found to be eventually absorbed by the microparticles as a result of their significantly higher absorptivity compared to copper powders (Supplementary Fig. 7b–d). This prevents powder spattering and localized laser heating in the composite powder bed, promoting a uniform energy absorption process19. Moreover, previous reports indicate that the particle-induced increase in melt viscosity can stabilize vapor depression fluctuations and control liquid droplet coalescence20,21, enabling a dramatic reduction of defects. Due to these effects, the relative density of all our as-built samples is as high as >99.8%. Such an improvement of microstructural consistency and the elimination of printing porosities would help the nanocomposites to fully display their intrinsic mechanical properties.

Strengthening and stress delocalization behaviour

The high yield strength of our as-built copper nanocomposites can be explained by the Orowan strengthening mechanism due to densely distributed nanoparticles, aided also by the high densities of dislocations and grain refinement introduced during L-PBF, as revealed by our strengthening mechanism analyses in Methods subsection ‘Estimating the yield strength of the as-built nanocomposites’. Traditionally, dislocations bypassing obstacles could accumulate in the form of Orowan loops22. The microstructural heterogeneity adds long-range back stresses on the ensuing dislocations to promote hardening. However, the dislocations stored would normally cause interface stress concentrations and crack nucleation, leading to reduced ductility. Our Cu–ANP does not face this traditional dilemma, such that the ductility is much improved. This is evidenced by the findings via fracture surface analyses. Notably, Cu-12%–ANP shows no evidence of nanoparticles in the dimples, in contrast to the corresponding Cu-12%-CNPs, which contain many nanoparticles at the bottoms of their dimples (Supplementary Fig. 8a, b). This observation indicates that the CNPs led to stress concentrations at interphase interfaces and tend to nucleate cracks/decohesion upon deformation, similar to the failure behaviours of precipitate-strengthened alloys22. In stark contrast, amorphous nanoparticles do not suffer from this drawback. The absence of premature failure in Cu-ANP nanocomposites is consistent with the presence of necking, as predicted by the Considère criterion (see Supplementary Fig. 6d); however, the Cu-12%-CNP nanocomposite fractures before necking occurs, indicating significant stress concentration. As shown in Fig. 4a, a group of grains after 3% strain is examined using high-resolution EBSD, which enables a quantitative cross-correlation-based analysis of strain and stress (Methods). As observed, the residual elastic strain field relative to the reference region (i.e., the lowest kernel average misorientation value within a grain) in the Cu–ANP sample exhibits much lower magnitudes and more uniform distributions across all selected grains, compared with its crystallized counterpart. For a further precise evaluation of the deformation compatibility in Cu–ANP, we conducted precession electron diffraction (PED)-based automated crystal orientation mapping (ACOM) via TEM for the 3%-deformed sample, with a mapping spatial resolution of 1 nm (Fig. 4b). Specifically, the two-beam bright-field TEM images show random distributions of dislocations inside the copper grains, and no discernible dislocation pile-ups are observed at the matrix-nanoparticle interface. The overall dislocation density, as estimated from the TEM images of the deformed Cu–ANP, is higher (~1.1 × 1015 m−2) than that in the as-printed state (~2.3 × 1014 m−2), suggesting dislocation multiplication and therefore strain hardening. Note that the point-to-point misorientation profile reveals a very low local misorientation across the interface (less than 0.5°, Fig. 4b), indicating a more uniform spread of the stored dislocations. It appears that the geometrically necessary dislocations that would otherwise pile-up near the interfaces have been accommodated via shear transformations at the surface of the ANPs (to be discussed below). On the contrary, in the CNP case dislocations piled up as expected, to accumulate at the Cu-CNP interface, as evidenced by both the post-deformation TEM and electron channelling contrast imaging analyses (Supplementary Fig. 9). This ANP-induced stress delocalization at the interface is the primary mechanism driving stable deformation without pre-mature failure in the L-PBF nanocomposites.

Fig. 4: Deformation mechanism in laser powder-bed-fusion copper nanocomposites.
figure 4

a Strain mapping analysis of grains in Cu-12%-ANP and Cu-12%-CNP nanocomposites after tensile strain of 3%, as obtained from high-resolution EBSD (HR-EBSD) images. CNP refers to a crystallized nanoparticle. The zero-stress reference point is chosen as the position with the lowest kernel average misorientation (KAM). b Representative two-beam bright-field TEM image of the deformed Cu-12%-ANP nanocomposites (3% strain). The right column shows the inverse pole figure (IPF; top panel) map of the selected region, with the associated image quality map superimposed. The data are acquired using precession electron diffraction (PED)-based automated crystal orientation mapping (ACOM) in a TEM with a step size of 1 nm. Three experiments were repeated independently and get the similar results. Plots of the variation in the misorientation angle, measured with respect to the origin and from point to point, across the representative ANP after deformation, indicated by the solid black line in the IPF map. c Changes in the lattice strains in Cu-8%-ANP and Cu-8%-CNP nanocomposites against macroscopic true stress for representative FCC (including {111}, {200}, {220}, {311} and {222}) crystallographic plane families along the loading direction. The experimental and crystal plasticity finite element (CPFE) modelling results are represented by symbols and solid lines, respectively. The macroscopic yield strengths of the different samples are marked with dashed lines. d CPFE simulation results of the macroscopic stress–strain responses with the corresponding stress partitioning in the copper matrix and nanoparticles. e Snapshots of the forward-moving dislocation interacting with the primary ANP, as observed in molecular dynamics (MD) simulations. The corresponding maps showing the atomic von Mises strain in copper are displayed in the right panels. f Corresponding von Mises shear strain maps in the ANP and CNP after dislocation bypassing. The whole deformation process of nanoparticles in different samples can be seen in Supplementary Movies S2 (for ANP) and S3 (for CNP). g Changes in the relative potential energies of atoms in the ANP (energy change relative to its original state) as functions of applied shear strain.

Full size image

In situ synchrotron XRD and atomic scale modelling

We also employed in situ synchrotron XRD experiments with crystal plasticity finite element (CPFE) modelling (Methods)9. This approach allows us to dissect the mechanical behaviour of each sample component despite the amorphous nature of the nanoparticles. Figure 4c shows the lattice strain εhkl along the loading direction against the applied true stress (σ) for several representative {hkl} reflections of copper in different nanocomposites (hollow symbols, 8 vol.% of nanoparticles). Initially, all reflections exhibit elastic deformation, with slopes differing due to the elastic anisotropy of diffraction planes. Upon straining, the lattice strain of the {220} reflection in both samples first shows a nonlinear trend, turning upwards, and the lattice strain of the {200} reflection deviates from a linear trend in a downward direction due to the occurrence of load transfer from the soft {220} to hard {200} reflections, revealing the early onset of microplastic yielding. As deformation proceeds, progressive yielding occurs sequentially from the {111}, {311} to {200} reflections. Notably, compared with those of Cu–CNPs, the crystallographic families of Cu–ANPs are more resistant to softening due to the greater uniform elongation values of the composites. We calibrate our CPFE model in terms of simulated lattice strain responses based on in situ diffraction data (solid lines in Fig. 4c). The stress‒strain curves derived from the CPFE model closely match the experimental data (Supplementary Fig. 10a). Then, we inversely determine the constitutive relationships between copper and nanoparticles as a function of applied strain during deformation, the results of which are displayed in Fig. 4d. Copper in Cu–ANP has a lower initial yield strength due to the lower initial dislocation density (Supplementary Fig. 10b; a higher dislocation density in Cu–CNP may be attributed to thermal misfit upon sample cooling after heat treatment23); however, its dislocation accumulation and strain hardening rates are slightly greater. Importantly, the ANPs demonstrate remarkably improved strain hardening, contributing to most (61%) of the strain hardening magnitude of Cu–ANP (the true strain ranges from 1% to 7%). This significantly improved hardening is primarily attributed to the self-hardening (and stiffening) of the ANPs as well as the associated hardening of the interface-affected zone24. Here, the ANPs have been rapidly melt-quenched at cooling rates around 108 K/s, such that many dangling bonds and much excess volume would be available for bond switching to accomplish shear transformations25. This latter process accommodates the dislocations running into the nanoparticles, and relieves the strain incompatibility across the metal-nanoparticle interface. Hence, ANPs can play a dual role in the tensile properties of the L-PBF nanocomposites. They themselves dynamically work harden while simultaneously eliminating excessive dislocation loops and stress concentrations at the interfaces. In addition, the dislocation segments that interact locally with ANP at the interface undergo a thermally activated process with small activation volumes. This behaviour is reflected in multiple stress relaxation tests, which revealed a physical activation volume (V*) of ~20 b3 for the representative Cu-8%-ANP nanocomposite (Supplementary Fig. 11). This value is comparable to, or even smaller than, those reported in nanograined metals (on the order of tens of b3), highlighting the unique dislocation manipulation behaviour induced by ANPs.

Atomic scale information lends support to the above mechanisms in our Cu–ANPs. Recent studies have shown that the nanosized amorphous phases in crystal–glass composites can act as high–capacity sinks for dislocations26,27,28, enabling the absorption of excess energy transported by the dislocations. In our molecular dynamics (MD) simulations, we do not observe any dislocation loops storing at the ANPs after the dislocation bypassing (Fig. 4e), suggesting their absorption by the ANPs along with straining. This is a key difference from the stress concentration at the usual crystalline dislocation obstacles. Moreover, the elastic strain field induced by incoming dislocations and the residual interfacial stress after the previous dislocation bypass is also relieved by the emission of dislocations on a different slip plane from the ANP interface (Supplementary Movie S1). As a result, the local nonhomogeneous deformation at the interfaces and the loops after dislocation bypassing can be effectively accommodated in the Cu–ANP nanocomposites, leaving minimal stress concentrations at the interfaces (Fig. 4e, right panel). The accommodating ability of the rapidly quenched amorphous nanoparticles is noteworthy: the pre-existing excess volume within the particles would enhance the atomic shuffling events (collective atomic rearrangements are known as shear transformations via bond switching) to accommodate the incoming dislocations and local strain7,27. In other words, the local structural configurations inside the ANPs evolve during straining, and the associated bond breaking and reforming (with other neighbours) help to relieve stress concentrations at metal–ANP interfaces. This is consistent with the dynamic evolution of local strains in the ANP (Supplementary Movie S2) and the nonuniform distribution of the von Mises equivalent strain at the moment of dislocation bypassing (Fig. 4f). The high cooling rate of up to 108 K/s during L-PBF endows the formed ANPs a highly rejuvenated state with a high potential energy. Such a rejuvenated state contains many fertile sites for bond-switching shear transformations under loading, and also for subsequent structural relaxation to relatively low energy states. The easier-to-activate fertile sites get gradually consumed with increasing straining, making the ANP more and more load bearing29. This is supported by the observed continuous decreases in configurational potential energy with applied strain in our MD simulations (Fig. 4g), as well as the reduced strain hardening rate in a partially relaxed sample via annealing (Supplementary Fig. 8c, d). Previously, amorphous phases have been incorporated in metallic systems, such as in copper and intermetallic-based alloys7,30,31. However, those studies are limited to thin-film samples, which contain amorphous phases in the form of two-dimensional laminates or three-dimensional continuous networks, rather than nano-dispersions in bulk alloys. We further note that the copper nanocrystals in ANPs could play an insignificant role in the deformation mechanisms (see additional discussion in Supplementary Note 3 for more details).

Exceptional fatigue resistance and other properties

Our reduced propensity for damage initiation/accumulation at interfaces may also render exceptional fatigue resistance. This is found to be true, as demonstrated in Supplementary Fig. 12a. Both the ascending and descending branches of the hysteresis loops of Cu–ANP (4% B4C as a representative) overlap completely throughout the cyclic loading process, even after 107 cycles at a maximum stress of 70% of its tensile strength. This stable cyclic deformation is distinct from the strain localization and cyclic hardening characteristics of alloys or conventional metal composites32,33. The fatigue strength limit is greater than 70% of the tensile strength, surpassing that of state-of-the-art copper materials, including nanograined, gradient and nanotwinned copper (Fig. 3d), see Supplementary Note 4. Other properties of interest, which have also been much improved, include the electrical conductivity and thermal stability. Precipitates in alloys at high number densities (1020–1024/m3)34 usually scatter electrons and reduce electrical conductivity. Also, these precipitates suffer from diffusion-controlled coarsening (i.e., Ostwald ripening) and are microstructurally unstable at high temperatures35. As indicated in Fig. 3e, the L-PBF copper nanocomposites retain 90% of the initial strength to temperatures as high as 1173 K (or 0.87Tm, where Tm is the melting point of copper), which is better than the immiscible copper–niobium alloy (one of the most thermally stable copper alloys). The combination of high strength and high conductivity (Supplementary Fig. 12b) rivals Cu-Ag alloys, which are believed to have the best combination of strength and conductivity among all copper alloys but usually have low thermal stability. This synergy of excellent mechanical and functional properties in one material has prospective applications. For example, as-built strong yet ductile copper nanocomposites with high fatigue and thermal resistance properties are highly sought after for combustion chambers in rocket engines36,37,38.

Discussion

Our study demonstrates an in situ nano-fragmentation and rapid-quenching mechanism for dispersions during L-PBF, by which densely populated amorphous nanoparticles can be deployed inside the metal matrix grains. These amorphous ceramic nanoparticles impose significant resistance to dislocation propagation, and at the same time absorb excess dislocations to avoid stress concentration. This, together with its self-hardening capability and thermal stability, renders the AM copper-based nanocomposites an unprecedented combination of mechanical and functional properties. This dispersion strategy is applicable to a variety of particle-metal systems, and particularly useful (or even indispensable) for those reflective metals (demonstrated above for Cu and Al) that are not amenable to L-PBF additive manufacturing. The idea of utilizing amorphous nanoparticles should also stimulate new designs when processing metals via other routes, such as powder metallurgy and chemical vapour deposition, where multiple options exist to tune the distributions and metastable states of the nanoparticles. We believe this innovative composite design strategy can greatly expand the field of the microstructure engineering of metallic materials, towards unparalleled combination of properties for cutting-edge applications.

Methods

Materials fabrication

Gas-atomized copper powders with an average diameter of ~30 μm were mixed with highly crystallized B4C particles with sizes ranging from 2 to 4 μm (Aladdin Ltd., Shanghai, China). The powder mixing was facilitated by using a high-shear dispersion facility (Nobilta, Hosokawa Micron Ltd., Japan) for 20 min at a rotation speed of 1600 rpm under the protection of argon. Composites were then built using a selective laser melting machine (S210, BLT, China) under high-purity argon to minimize oxidation (oxygen content: <50 ppm). This system was equipped with a single-mode fibre laser (500 W, 1064 nm wavelength) with a spot size of 60 μm. A cooling substrate system was designed in the printing machine to ensure a constant substrate temperature of −20 °C during L-PBF to ensure a high cooling rate upon sample building, and a continuous scanning strategy involving a 67° rotation before scanning another layer was adopted to randomize the crystal orientations and alleviate residual stresses in the built samples. The processing windows for high-density (>99.5%) metal nanocomposite samples were probed, and the key printing parameters are provided in Supplementary Table 1. Conventional high-strength copper was produced via cold rolling high-purity copper (70% thickness reduction), in which samples with grain sizes of ~400 nm were obtained. These samples were used for the comparison of mechanical properties in Fig. 3a.

We extracted nanoparticles from the composite made via L-PBF to enable a direct characterization of the nanoparticle structures. The as-built copper nanocomposites were etched in FeCl3 solution acidized with hydrochloric acid, which allowed for the removal of the copper matrix. The residual nanoparticles were washed with deionized water three times, collected and dried at 60 °C for 24 h in a vacuum oven. For comparison, we annealed the as-built copper nanocomposites at 1173 K for 6 h to crystallize the B4C nanoparticles. To minimize oxidation, the annealing process was conducted in a glove box with oxygen and water contents of less than 0.5 ppm.

Microstructural characterizations

XRD and NMR

The structures of the nanoparticles in the as-built copper nanocomposite were identified using XRD with a Cu target and an X-ray wavelength of 1.54059 Å on a D/Max-2500 instrument from Rigaku. Moreover, the chemical environments of the B atoms in the extracted nanoparticles were studied using 11B NMR, in which the spectra were recorded at 14.1 T on a 600 MHz Bruker Avance Neo spectrometer. The spectrometer operated at νL = 160.5 MHz with a 4-mm Bruker probe and a spinning frequency of 14 kHz for the rotor. We acquired the spectra by using a spin−echo θ − τ − 2θ pulse sequence (with θ = 90°). The spectra of the raw B4C microparticles were obtained and compared under the same conditions.

NEXAFS

The atomic bonding structures of the extracted B4C nanoparticles were probed using NEXAFS spectroscopy at the BL10B beamline of the National Synchrotron Radiation Laboratory, China. The B 1 s NEXAFS spectra were recorded at room temperature under ultrahigh vacuum conditions of less than 10−8 Pa. The data were collected in total electron yield mode, with a rectangular beam size of 0.2 × 0.1 mm2.

EBSD

A high-resolution EBSD system (Symmetry S2, Oxford) equipped with SEM (Scios, Thermal Fisher) was employed, with an angular resolution below 0.05°. AZtecCrystal and CorssCourt4 data processing software were used for EBSD data analysis. An accelerating voltage of 30 kV was used for EBSD data collection. Grain boundaries (GBs) with misorientation angles of 2°–10° and >10° were considered low- and high-angle GBs, respectively. EBSD samples were prepared using standard metallographic techniques, where the sample surface was finally polished with an ion-milling system (Model 1060, Fischione) to achieve a high validated hit rate (>90%). For the quantitative strain/stress analyses of the deformed copper nanocomposite (with an applied strain of ~3%), cross-correlation-based EBSD was conducted to measure the elastic strain fluctuation and local misorientation characteristics. The parameters of a long exposure time (1.5 s), zero gain and 1 × 1 binning were applied to collect high-quality Kikuchi patterns.

TEM

HRTEM was conducted at an operating voltage of 300 keV on a Thermo Fisher Spectra 300 transmission electron microscope equipped with an imaging aberration corrector. HAADF–STEM images with maximum point-to-point spatial resolutions of 0.05 nm were obtained with convergence angles of 26 mrad and collection semiangles ranging from 50 to 180 mrad. The elements were identified and their distributions were analysed in the nanoparticles using EDS (Bruker Super-X). TEM samples were prepared via the standard lift-out method using a focused ion beam (FIB) system. Further nanomilling (Nanomill 1040, Fischione) at 800 V was employed to remove the surface amorphous layer produced during FIB milling. PED-based ACOM was conducted via TEM at a step size of 1 nm.

APT

Atom probe tomography analyses were carried out in a CAMECA LEAP 4000× SI instrument under ultrahigh vacuum conditions of ~2.5 × 10−11 Torr. The specimen temperature was 40 K, and the target evaporation rate was 0.5% per pulse under ultraviolet (UV) laser pulsing conditions with an energy of 40 pJ. APT specimens were prepared in a FIB system, where a very low accelerating voltage (5 kV) and beam current (5 pA) were employed in the final milling step to minimize Ga+ implantation. The CAMECA integrated visualization and analysis software IVAS 3.6.12 was used for data processing and three-dimensional atomic reconstruction.

Mechanical testing

Tensile and fatigue tests

Dog-bone specimens, each with a 10-mm gauge length, 2-mm width, and 1-mm thickness, were cut from AM-built copper nanocomposites and from conventional high-strength copper by electrodischarge machining (EDM). The tensile direction was perpendicular to the build direction for the printed samples, and was aligned with the rolling direction for grain-refined pure copper. The surfaces and sides of the tensile samples were polished with 360–4000-grit European metallographic silicon carbide papers, followed by polishing in 3-μm and 1-μm diamond suspensions. The final thicknesses of the tensile specimens were ~0.9 mm. Quasistatic uniaxial tensile tests were conducted in a universal testing machine (Instron 3344) at a constant strain rate of 5 × 10−4 s−1. At least five tensile tests were carried out to obtain statistically meaningful values. Tensile elongation was measured using a static axial clip-on extensometer (Model 2630-101, Instron) with a 1-μm displacement resolution. The fatigue test specimens were machined according to the American Society for Testing and Materials E466-21 standard for a pull–pull fatigue test with R = 0.1. The specimens for fatigue testing were polished following the same procedures used for the tensile tests, and the fatigue tests were conducted with a high-frequency fatigue testing machine (Care M-6000, Tianjin, China) at a frequency of 15 Hz (sinusoidal wave).

Multiple stress relaxation tests

Multi-cycle relaxation was performed on Cu-8%-ANP nanocomposite at the specific engineering strain values of 1%, 2%, 3% and 4%, from which the evolution of physical activation volume as a function of applied strain can be deduced39. The specimens underwent tensile testing at a strain rate of 5 × 10−4 s−1 until the preset strain was reached, at which point the frame stopped, followed by a holding time of 90 seconds. The stresses decreased during the relaxation period due to the continued glide of mobile dislocations. At the end of each relaxation cycle, the specimen was reloaded to the stress level before stress relaxation at a constant rate (50 N/s). Four relaxation cycles were conducted for each preset strain, allowing for the determination of the evolution of physical activation volume and the mobile dislocation exhaustion rate. The details of the calculation process can be found in our previous work39.

In situ synchrotron X-ray diffraction experiment

In situ synchrotron X-ray diffraction (SXRD) tensile tests were conducted at beamline ID-3A, the Cornell High Energy Synchrotron Source, using an acceleration voltage of 52 keV. A dog-bone-shaped tensile specimen with nominal gauge dimensions of 2 mm (length) × 1.2 mm (width) × 1 mm (thickness) was loaded at a constant strain rate of 5 × 10−4 s−1. Specimens for synchrotron-diffraction tensile tests were prepared following the same procedures as those for the tensile tests mentioned above. With a slit size of 0.5 mm (length) × 2 mm (width), two-dimensional (2D) XRD patterns were collected in transmission mode at the gauge section of the tensile specimen with a Dexela flat panel detector positioned 600 mm behind the sample. Single-peak fitting was performed by using GSAS-II software. The lattice strain for the {hkl} reflection, εhkl, was calculated by εhkl  =  (dhkl–d0,hkl)/d0,hkl, where dhkl and d0,hkl denote the interplanar spacings of the {hkl} planes under loading and in the stress-free state, respectively.

Computational modelling

Mesoscale powder bed fusion simulation

An unresolved computational fluid dynamics (CFD) and discrete element method (DEM) coupling model was applied to elucidate the laser powder bed fusion process of mixed copper and B4C powders40. The copper powder layer was generated by modelling the powder spreading process (i.e., a rake being pushed over a powder bed)41. The B4C particles were randomly dispersed in the copper powder layer, where the volume fraction and powder diameter distribution were identical to those in the experimental setup. The mesoscale simulation applied a structural Eulerian mesh in the computational domain, and the finite volume method was employed to solve the governing fluid equations. A mesh size of 5 μm was adopted to balance the accuracy and efficiency. The size of the computational domain was 2 × 0.5 × 0.5 mm3. In the present work, the vapour flow and the resultant powder spattering were not included for simplification. The thermophysical properties (and the temperature-dependent thermophysical parameters) of copper and B4C are listed in Supplementary Tables 2–4. Additional details of our modelling framework can be found in the Supplementary Materials.

Multiphysics modelling of droplet dispersion

A microscale model was developed to reveal the details of the fragmentation of B4C from micro-sized to nano-sized droplets in the melt pool. A two-fluid CFD model with a sharp interface identification technique was applied to reveal the dispersion of microscale B4C in the copper matrix. In this model, copper and B4C were treated as fluid 1 and fluid 2, respectively. The governing equations of the two-fluid model were similar to those of the mesoscale CFD model, except that F in the VoF equation represented the volume fraction of fluid 1. In the present work, the van der Waals forces between different B4C particles were not incorporated into the simulation since the van der Waals force was not significant compared with the hydraulic force exerted on the particle, even when the particle diameter was less than 10 nm12,42.

In the present work, we chose a representative elementary volume (REV; with a size of 5.0 × 5.0 × 5.0 μm3) from the mesoscale simulation domain as the simulation domain of the microscale model. The temperature and velocity histories of the REV from the mesoscale simulation were then extracted and set as the flow pattern (e.g., temperature and average velocity of fluid) of the microscale simulation. The mesh size was set to 0.025 μm to balance the accuracy and efficiency of the microscale simulation. During the dispersion process, if the B4C fluid was dispersed into a submesh isolated droplet (i.e., the volume of the B4C droplet was smaller than the mesh cell volume), the submesh isolated droplet was replaced with a DEM particle, where the mass, momentum and energy of the DEM particle were identical to those of B4C. After the solidification of copper, we calculated the number and volume of isolated B4C droplets in the domain. For the counting of submesh isolated droplets, if the distance between the centres of two particles \({d}_{12}\) was smaller than the summation of their radii \(({r}_{1}+{r}_{2})\), the two particles were treated as one droplet with a volume equal to the summation of these two isolated droplets.

Laser absorptivity modelling

We developed a ray-tracing simulation to assess laser absorption in mixed powder beds, including two different powders: copper (40 μm in diameter) and B4C (5 μm in diameter). For copper particles, we utilized geometric optics to model reflection, enabling us to trace ray propagation and calculate energy absorption based on incidence angles and reflection properties of copper. In contrast, scattering of laser beam was considered in the simulation of B4C particles due to their small size. This method allowed us to capture the intricate interactions between the laser and the mixed powder beds, and to identify the absorbed laser energy for copper and B4C microparticles, respectively.

MD simulation

Molecular dynamics simulations were performed using large-scale atomic/molecular massively parallel simulator43 software to examine the interactions between dislocations and B4C nanoparticles during deformation. The Cu–Cu interaction was described by the embedded atom method potential44. The Stillinger–Weber (SW) potential was adopted for B–B, C–C and B–C interactions45. The Lennard‒Jones potential was used for Cu–B46,47 and Cu–C interactions48. The radii of the ANPs and CNPs were set to 3 nm, and the particles were embedded in a copper matrix with preexisting edge dislocations of \(\,{{{\boldsymbol{b}}}}={{{{\rm{a}}}}}_{0}/2\,[10\bar{1}]\) on the {111} plane. Crystalline B4C with a C–B–C chain was chosen for the structures of the CNPs. ANP was generated by packing B11C clusters and C–B–C chains and relaxed using the SW potential45. The simulation cell was oriented with the X, Y and Z directions aligning along the \([10\bar{1}]\), \([1\bar{2}1]\), and [111] directions of the copper matrix. The simulation cells were 38.2, 22.1 and 25.0 nm in length along the X, Y and Z directions, respectively, with ~1.7 million atoms. The time step in the simulation was 2 fs. After the B4C nanoparticles were embedded in the copper matrix, the simulation cell was optimized using the conjugate gradient method and subsequently held at 10 K for 30,000 steps. Then, the upper and lower regions with thicknesses of 5 atomic layers were selected and moved along the positive and negative X directions, respectively, at a fixed velocity. The rate of applied shear strain was 107 s−1. The open visualization tool package49 was adopted to produce the von Mises equivalent atomic strain map and visualize the atomic structures, as shown in Fig. 4e, f.

Moreover, the structures of the ANP generated by different methods were analysed via MD simulations. Following previous work45, B11C units and C–B–C chains were randomly packed using packmol50, and the structures were annealed at 300 K and optimized by minimizing the potential energy (PE). The amorphous B4C structure was cut into spheres and embedded into a Cu matrix to obtain the Cu–ANP atomic model. Alternatively, crystalline B4C particles with radii of 3 nm were embedded into a Cu matrix. Then, the temperatures of the B4C particles were all increased to 3500 K for 0.5 ns, while the temperature of the matrix was maintained at 300 K. Different temperatures were used for the particles and the matrix to avoid melting the Cu matrix (hence, the formation of solidification defects upon cooling). Afterwards, the simulation cell was optimized to obtain the ANP/Cu atomic model. The alternative modelling process showed similar atomic deformation mechanisms. Specifically, the potential energies of the ANPs generated by packmol or by the melting of B4C CNPs both decreased as shearing strain was applied. Different melting times (0.3 ns vs. 0.5 ns) led to the presence of distinct amorphous particles, but for both cases, the potential energies of the B4C particles decreased during shearing loading. Therefore, the ability to accommodate the shearing strain originated from the ANPs, irrespective of the method used to construct the ANP/Cu atomic model. To analyse the changes in the ANPs during deformation, every 10,000 atomic structures during shearing were optimized to produce a stress-free state, and the PEs of the stress-free ANPs were subsequently calculated. The stress-free state was obtained by minimizing the PE of the whole cell; the largest components of forces on any atoms were lower than 10−15 eV/Å. The PEs of the stress-free ANPs generated by the random packing of B11C units and C–B–C chains are shown as a function of the applied shear strain in Fig. 4g.

CPFE simulations

A dual-phase crystal plasticity model was developed to understand the lattice strain changes in in situ synchrotron–diffraction experiments. We used the rate-dependent finite strain crystal plasticity constitutive model for the copper matrices and the rate-independent finite strain J2 plasticity model for the CNPs/ANPs. We simulated the uniaxial tension of copper nanocomposites containing 12 vol.% B4C nanoparticles at a strain rate of 10−4 s−1.

For the copper matrix, the deformation gradient in each grain F was decomposed into \({{{\boldsymbol{F}}}}={{{{\boldsymbol{F}}}}}^{e}{{{{\boldsymbol{F}}}}}^{p}\), where \({{{{\boldsymbol{F}}}}}^{e}\) is the elastic deformation gradient and \({{{{\boldsymbol{F}}}}}^{p}\) is the plastic deformation gradient. Then, the elastic Green strain tensor was calculated as \({{{{\boldsymbol{E}}}}}^{e}=1/2\left({{{{\boldsymbol{F}}}}}^{{e}^{T}}{{{{\boldsymbol{F}}}}}^{E}-{{{\boldsymbol{I}}}}\right)\), and the second Piola–Kirchhoff stress T* in the intermediate configuration was determined as \({{{{\boldsymbol{T}}}}}^{*}={{{\boldsymbol{C}}}}:{{{{\boldsymbol{E}}}}}^{e}\), where I is the second-order identity tensor and C is the fourth-order elastic tensor of a single crystal Cu. The change in the plastic deformation gradient was determined by the plastic velocity gradient:

$${\dot{{{{\boldsymbol{F}}}}}}^{p}={{{{\boldsymbol{L}}}}}^{p}{{{{\boldsymbol{F}}}}}^{p}\,{{{\rm{and}}}}\,{{{{\boldsymbol{L}}}}}^{p}={\sum }_{i=1}^{12}{\dot{\gamma }}_{i}^{p}{{{{\boldsymbol{m}}}}}_{i}\otimes {{{{\boldsymbol{n}}}}}_{i}$$
(1)

where \({\dot{\gamma }}_{i}^{p}\) is the plastic shearing rate on the i-th slip system and \({{{{\boldsymbol{m}}}}}_{i}\) and \({{{{\boldsymbol{n}}}}}_{i}\) are the associated slip direction and slip plane normal, respectively. Twelve {111} <110> slip systems were considered for the FCC copper phase. The plastic shearing rate \({\dot{\gamma }}_{i}^{p}\) was determined to follow a power law relationship:

$${\dot{\gamma }}_{i}^{p}={\dot{\gamma }}_{0}^{p}{\left|{\tau }_{i}/{s}_{i}\right|}^{1/m}\,{sgn}\left({\tau }_{i}\right)$$
(2)

where \({\dot{\gamma }}_{0}^{p}\) is the reference shear rate, \({\tau }_{i}={{{{\boldsymbol{m}}}}}_{i}\cdot {{{\boldsymbol{T}}}}\cdot {{{{\boldsymbol{n}}}}}_{i}\) is the resolved shear stress, \(m\) is the rate sensitivity and \({s}_{i}\) is the slip resistance of the i-th slip system. The slip resistance of each slip system began with an identical initial value \({s}_{0}\) and hardened according to \({\dot{s}}_{i}={\sum }_{j}{h}_{{ij}}|{\dot{\gamma }}_{j}^{p}|\). The hardening matrix was expressed as follows:

$${h}_{{ij}}={q}_{{ij}}{h}_{0}{\left(1-{s}_{j}/{s}_{{sat}}\right)}^{a}$$
(3)

where the latent hardening matrix \({q}_{{ij}}\) is equal to 1.0 and the off-diagonal elements are equal to 1.4.

For the B4C nanoparticles, the isotropic hardening plasticity model was adopted. The constitutive equation was formulated in a corotational framework based on the Jaumann stress rate. The Jaumann rate of stress was determined by the following equation:

$${\dot{{{{\boldsymbol{\sigma }}}}}}^{J}={{{\boldsymbol{C}}}}:{\dot{{{{\boldsymbol{\varepsilon }}}}}}^{e}$$
(4)

where \({{{\boldsymbol{C}}}}\) is the elastic tensor of the boron carbide nanoparticles calculated from the Young’s modulus ENP and Poisson’s ratio vNP. The rate-independent yield function was as follows:

$$\sqrt{\frac{3}{2}{S}_{{ij}}{S}_{{ij}}}-{\sigma }_{y}\left({\bar{\varepsilon }}^{{pl}}\right)=0$$
(5)

where \({S}_{{ij}}={\sigma }_{{ij}}-\frac{1}{3}{\delta }_{{ij}}{\sigma }_{{kk}}\) is the deviatoric stress and \({\bar{\varepsilon }}^{{pl}}={\int }_{0}^{t}{\dot{\bar{\varepsilon }}}^{{pl}}{dt}\) is the equivalent plastic strain with \({\dot{\bar{\varepsilon }}}^{{pl}}=\sqrt{\frac{2}{3}{\dot{\varepsilon }}_{{ij}}^{{pl}}{\dot{\varepsilon }}_{{ij}}^{{pl}}}\). The plastic flow law determined the plastic strain rate, \({\dot{\varepsilon }}_{{ij}}^{{pl}}=\frac{3}{2}\frac{{S}_{{ij}}}{{\sigma }_{y}}{\dot{\bar{\varepsilon }}}^{{pl}}\). The yield strength was assumed to be linear isotropic hardening, \({\sigma }_{y}={\sigma }_{y}^{0}+{h}_{{{\rm{NP}}}}{\dot{\bar{\varepsilon }}}^{{pl}}\). The radial return scheme was applied to determine the plastic strain increment. The dual-phase crystal plasticity model was solved using the vectorized user material (VUMAT) subroutine in Abaqus/Explicit. The parameters used in the above constitutive model are listed in Supplementary Table 5.

Electrical conductivity and thermal stability measurements

The electrical conductivities of the AM-based copper nanocomposites were measured by an eddy current conductivity meter at room temperature, and the values are expressed in terms of the International Annealed Copper Standard. High-purity annealed copper was used for calibration purposes. All samples used for electrical conductivity measurements were polished to a metallurgical grit of 4000 with SiC paper. The as-built copper nanocomposites were annealed at different temperatures (from 673 K to 1173 K) for 1 h to evaluate their thermal stabilities. Annealing was performed in an argon environment, and the Vickers hardness was measured under a load of 294.2 N for 10 s. The annealing temperature–strength (hardness) retention curve, as shown in Fig. 3e, was plotted because the strength of a material was proportional to its hardness51.

Estimating the yield strength of the as-built nanocomposites

We estimated the yield strength of the Cu-12%-ANP nanocomposite by considering the contributions from grain refinement, dislocations and nanoparticle-induced strengthening. The contribution of the Orowan strengthening (ΔσOrowan) mechanism induced by well-dispersed particles was calculated by the following equation52:

$$\Delta {\sigma }_{{{{\rm{Orowan}}}}}=\frac{\varphi {Gb}}{{d}_{p}}{\left(\frac{6f}{\pi }\right)}^{1/3}$$
(6)

where G, b, f and dp are the shear modulus of the matrix, the magnitude of the Burgers vector, the volume fraction and the average size of the nanoparticles, respectively. φ is a constant equal to 252. Considering that in this study Gm  =  47.7 GPa, b  =  0.256 nm, Vp  =  0.12 and dp  =  82.6 nm, the calculated ΔσOrowan was 318 MPa. We estimated the dislocation density (ρ) in our as-built Cu-12%-ANP to be (2.3  ±  0.3) × 1014 m−2 according to the modified Williamson–Hall method53,54. Their contribution to yield stress (ΔσDis) was estimated from the classical Taylor relationship:

$$\Delta {\sigma }_{{{{\rm{Dis}}}}}=\alpha MGb{\rho }^{0.5}$$
(7)

where α is a geometrical factor (~0.23) and M is the Taylor factor (~3.06 for FCC metals containing weak textures3). Therefore, the strengthening contribution from dislocations was 115.8 MPa in Cu-12%-ANP. The yield strength from the Hall–Petch effect (ΔσHP) was estimated by the following equations as a result of the grain refinement55:

$$\Delta {\sigma }_{{{{\rm{HP}}}}}={\sigma }_{0}+k{D}^{-1/2}$$
(8)

where D is the grain size (~390 nm), k is a constant (0.14 MPa·m1/2), and σ0 is the lattice friction stress and is ~25 MPa55). ΔσHP is then calculated to be 249.2 MPa. Therefore, the high yield strength of our as-built Cu-12%-ANP (~730 MPa) is mainly contributed by the Orowan strengthening of densely distributed nanoparticles and further enhanced by the high densities of dislocations and grain refinement after performing L-PBF.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.