Introduction

Solid-state systems, presently considered for quantum computation, are built from localised two-level systems. Prime examples are superconducting qubits or semiconducting quantum dots1,2. Being localised, they require a fixed amount of hardware per qubit. Conversely, flying qubits are the only existing quantum technology platform that uses propagating particles. They represent an interesting quantum architecture, as they naturally enable the implementation of quantum interconnects. Currently, flying qubits are associated with photons due to their highly coherent nature, on-demand generation, and inherent scalability3. Photons, however, travel so fast that in-flight dynamical manipulation is impossible, and their trajectories need to be set in advance. Moreover, they do not interact directly with each other, making photon entanglement challenging, and the ‘all-linear’ quantum optics approach4 requires post-selection methods. As a result of the very weak photon interaction, a large number of Mach-Zehnder interferometers must be implemented to construct a single two-qubit gate5. This inevitably leads to a tremendous increase in hardware overhead.

Despite their much shorter coherence time compared to photons, quantum nanoelectronic circuits have seen enormous progress over the last 10 years. This advancement was driven by the development of on-demand single-electron sources capable of generating single-electron wavepackets with high fidelity6,7,8,9. Moreover, Coulomb interactions between two individual co-10 and counter-propagating electrons11,12 have been successfully demonstrated. Such progress marks a significant milestone, paving the way for entanglement of multiple flying electron qubits in the future13,14,15.

The most convenient method to generate a single-electron excitation is by applying a short voltage pulse to the Ohmic contact of a two-dimensional electron gas (2DEG). This creates a single electron-excitation in the form of a plasmonic pulse16. Recent experiments have demonstrated the coherent manipulation of single-electron plasmonic pulses in the form of Levitons17,18 within a Mach-Zehnder interferometer (MZI) implemented in graphene19, highlighting their potential for quantum information processing. In addition, their relevance for quantum sensing applications has been demonstrated20,21.

The next milestone towards developing a competitive quantum architecture for flying electron qubits is to reach a regime where the wavepacket’s width is significantly shorter than the quantum device. Such achievement would allow multiple flying qubits to be accommodated within a single quantum processing unit and would enable the implementation of a large number of gate operations during their flight22. Moreover, as the wavepacket width decreases, it inevitably becomes comparable to or shorter than the characteristic timescales of the interferometer. This marks the transition into the non-adiabatic regime where dynamical effects are expected to play an important role23.

In this work, we demonstrate quantum coherence of ultrashort electron wavepackets in the non-adiabatic regime in an electronic Mach-Zehnder interferometer. After describing the working principle of the device in the DC regime, we present a detailed characterisation of its nonlinear behavior. This nonlinearity is harnessed to investigate the frequency response of the Mach-Zehnder interferometer via quantum rectification24. Through these measurements, we demonstrate the onset of the non-adiabatic regime for frequencies starting around 1 GHz. Finally, we utilize these findings to establish the presence of non-adiabatic coherent current oscillations driven by ultrashort plasmonic pulses of duration as short as 30 ps.

Results

Electronic Mach-Zehnder interferometer device

The cornerstone of a flying qubit platform is the Mach-Zehnder interferometer (MZI). Here, individual particles are injected on demand, put in a superposition of states at the initial beam splitter, guided through the interferometer, and ultimately, the quantum superposition can be discerned at the two output detectors. Throughout the particle’s trajectory, quantum manipulations can be implemented by electrical gate operations.

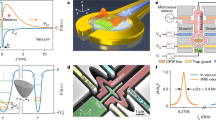
In our system, the qubit states are represented by the presence of an electron in the upper \(\left\vert 0\right\rangle \) or lower \(\left\vert 1\right\rangle \) arm of the electronic Mach-Zehnder interferometer of a total length of 14 μm, as shown in Fig. 1a. To create a superposition between the two states, tunnel-coupled wires (TCW) of a length of 2 μm is employed that acts as an electronic beam splitter. In this device, the electronic waveguides are brought into close proximity, enabling quantum tunneling of the injected wavepackets between them. The tunneling is controlled via the voltage applied to the the two tunnel-coupled wires VTCW, providing full electrical control of the beam splitter. The wavepackets are then allowed to propagate through an Aharonov-Bohm ring, where a phase difference between the upper and the lower arm can be induced by varying the magnetic flux ϕ enclosed by the two paths. Alternatively, the phase can be electrically controlled by applying a voltage Vsg to the side gates25. A second beam splitter is placed at the end of the ring to enable interference between the two wavepackets, thereby effectively implementing an electronic Mach-Zehnder interferometer25,26.

Fig. 1: Electronic Mach-Zehnder interferometer.
figure 1

a Scanning electron micrograph of the electronic Mach-Zehnder interferometer (MZI) device. The electrostatic gates highlighted in color define the electron trajectories indicated by the dotted lines. Electrons are injected into the interferometer through the left Ohmic contact (crossed white square). The output current I0 (I1), corresponding to the transmitted current in the upper (lower) electron waveguide, is measured using a lock-in amplifier. b Coherent anti-phase oscillations of the transmitted currents I0 and I1 when applying a DC bias where a smooth background has been subtracted. c. Coherent oscillations of I0 - I1 (total oscillating component of the transmitted current) as a function of the magnetic field and the side gate voltage Vsg.

Full size image

To investigate the coherent properties of our device, we adopt the following approach. Electrons are injected into the electronic MZI by applying a constant bias voltage Vdc to the injection Ohmic contact, as indicated by the left white square in Fig. 1a. The transmitted output currents I0 and I1 are then measured as a function of the applied magnetic field B. When the device is properly tuned into a two-path interferometer26, anti-phase oscillations in the currents are observed at the two outputs, as shown in Fig. 1b. Here we plot the oscillating component I where a smooth background current (≈1 nA) has been subtracted. We measure a magnetic field periodicity of the current oscillations of ΔB = 0.5 mT, corresponding to a surface area of S = 8.2 μm2, which is consistent with the device geometry. Varying the voltage Vsg of the side gate highlighted in green in Fig. 1a, a controlled phase shift between the propagating electrons through the lower arm with respect to the upper one can be achieved. In our case a voltage variation of ΔVsg ≈ 20 mV is sufficient to induce a phase shift of 2π (see Fig. 1c). Demonstrating interference with ultrashort voltage pulses requires a careful understanding of the device’s frequency response. When the MZI is driven by a purely sinusoidal signal, the net average current is theoretically expected to be zero. However, as shown in Fig. 3a and c, this is not the case. Instead, we observe current rectification, attributed to a nonlinearity in the device. In the following section, we provide a detailed characterisation of this nonlinearity, which is subsequently utilized to investigate the frequency response of the MZI.

Nonlinearity of the device revealed in DC measurements

We begin by investigating the source of the nonlinearity responsible for the rectification, and thoroughly characterising the device’s DC response. Nonlinear effects in mesoscopic transport systems have been studied in the past, with particular focus on quantum point contacts27 and Aharonov-Bohm (AB) rings28,29. In prior research, coherent oscillations in the nonlinear conductance of two-terminal AB rings have been observed, with different proposed origins: in28, the nonlinearity arose from spatial inversion asymmetry while its magnetic field asymmetry was attributed to electron-electron interactions, whereas in29, the nonlinearity was suggested to originate from bias-dependent transmission, though its precise microscopic origin remained unclear.

In our system, the nonlinearity originates from the tunnel-coupled wires at the entrance and exit of the electronic Mach-Zehnder interferometer. This is evidenced by experimental measurements of its nonlinear I-V curve and further corroborated by numerical simulations. To illustrate the device’s nonlinearity, we decompose the output current into its symmetric, \({I}^{S}(V,B)=\left(I(V,B)+I(-V,B)\right)\)/2, and antisymmetric, \({I}^{AS}(V,B)=\left(I(V,B)-I(-V,B)\right)\)/2, components. The symmetric current is indeed non-zero, as shown in the vertical line cut of the right panel in Fig. 2a, with nonlinearities appearing for bias voltages as low as 25 μV. In contrast, the antisymmetric current is dominated by a linear response, as seen in the vertical line cut of the right panel in Fig. 2b. To further emphasize the contribution of the nonlinearity towards the coherent oscillations, we analyze the magnetic field dependence. For the symmetric current, AB oscillations with minimal background current are observed (horizontal line cut of the bottom panel in Fig. 2a). On the contrary, the antisymmetric current shows AB oscillations superimposed on a significant background current (horizontal line cut of the bottom panel in Fig. 2b). These oscillations are the characteristic AB oscillations measured in a linear system. To further confirm that the nonlinearity primarily originates from the tunnel-coupled wires, we conducted a separate investigation focusing exclusively on this component of our MZI. We observed a similar nonlinearity to that seen in the entire MZI, reinforcing our hypothesis (for details see Supplementary Information, Section 1.6).

Fig. 2: Nonlinearity of the electronic Mach-Zehnder interferometer.
figure 2

The DC I-V curve is decomposed into its symmetric (IS) and antisymmetric (IAS) components with respect to the bias voltage Vdc. a Density plot of the symmetric component of the current as a function of the DC bias voltage Vdc and magnetic field B. The vertical line cut, shows the nonlinear I-V characteristic at a magnetic field of B = 10 mT. The horizontal line cut shows AB oscillations at a bias voltage of Vdc = 25 μV. b Same as (a), but for the antisymmetric component of the current. The I-V characteristic exhibits primarily a linear behaviour. The applied bias voltage is corrected to account for the effective reduction of the bias due to the electronic circuit (Supplementary Information, Section 1.1). c, d Quantum transport simulations of both the symmetric and antisymmetric components of the current, analogous to (a, b).

Full size image

Our experimental findings are supported by state-of-the-art quantum transport simulations (Fig. 2c, d). These simulations combine detailed electrostatic potential simulations30 with transport calculations using the Kwant software31,32. The electrostatic calculations account for the precise geometric configurations of the surface gates and the properties of the GaAs/AlGaAs heterostructure (see Supplementary Information, Section 2.1 for details). While the simulations reproduce the main features of our measurements in a semi-quantitative manner, some discrepancies persist. These differences likely arise from the simulations not accounting for disorder in the electrostatic potential caused by dopants or for decoherence phenomena. Nonetheless, our simulations indicate that the observed nonlinearity–and the resulting rectification in our system–originates from the energy-dependent transmission of the tunnel-coupled wires (see Supplementary Information, Fig. S8 for details).

Frequency response of the MZI

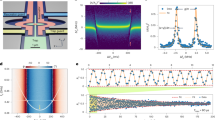
Having characterised our electronic MZI in the DC regime we now investigate the response of our device under sinusoidal drive at variable frequencies. At low frequencies, the sinusoidal signal is slow enough and the system adjusts instantaneously to the external drive—known as the adiabatic regime. In Fig. 3b, d, we show the amplitude of the coherent current oscillations, IAB, defined as the maximum amplitude of I0 − I1, extracted from the fast Fourier transform, as a function of frequency and drive amplitude Vac. We observe that for frequencies below 100 MHz, the coherent oscillations are independent of frequency and show the same evolution as a function of drive amplitude. To show that the frequency response at low frequencies (≤100 MHz) can be described in the adiabatic limit, we reconstruct the oscillating component IAB, generated by a sinusoidal signal directly from the raw DC data, using the following formula

$${I}_{\sin }(V,B)=\frac{1}{T}\int\,{I}_{{\rm{dc}}}\left(V(t),B\right)\,dt$$
(1)

where \({I}_{\sin }\) is the DC rectified current induced by a sinusoidal drive \(V(t)={V}_{{\rm{ac}}}\sin (\omega t)\). The evolution of the amplitude of the coherent oscillations IAB passes through a maximum and saturates at high bias. The overall shape of the evolution is well captured by the DC reconstruction (gray continuous line in Fig. 3b), as well as by the Floquet simulations (see Supplementary Information, Section 2.4). In these simulations, the exact position of the maximum with respect to the bias voltage depends on the microscopic parameters of the device. We observe that all experimental data at low frequency (≤100 MHz) follow the adiabatic limit.

Fig. 3: Frequency response of the MZI under sinusoidal drive.
figure 3

a, c AB oscillations of the current difference I0 − I1 for frequencies ranging from 100 kHz to 6 GHz. Experimental data are vertically offset for clarity. b Amplitude of the AB oscillations IAB versus sinusoidal drive amplitude Vac for frequencies from 100 kHz to 100 MHz. The thick gray line indicates the adiabatic limit calculated from the DC raw data using Eq. 1. d Same as (b) for frequencies ranging from 250 MHz to 6 GHz. The adiabatic limit (thick gray line) is shown for comparison. e Evolution of the relative amplitude change ΔIAB with frequency calculated using Eq. (2). The dashed line serves as a guide to the eye. Below 1 GHz, ΔIAB remains small, indicating adiabatic behavior. Above 1 GHz, ΔIAB deviates from the adiabatic limit, marking the transition to the non-adiabatic regime.

Full size image

We now investigate the frequency response of our electronic MZI under sinusoidal drive at frequencies above 100 MHz as shown in Fig. 3d. Contrary to the case at low frequency, as we increase the frequency, a distinct deviation from the adiabatic regime is observed, manifesting itself at frequencies around 1 GHz. This is further supported by our Floquet simulations, which show a similar evolution towards the non-adiabatic regime at similar frequencies as the ones observed in the experiment (see Supplementary Information Section 2.4). These simulations are based on Floquet scattering theory33, which describes electron transport under periodic voltage drives. Under a time-dependent voltage V(t), electrons acquire a time-dependent phase \(\phi (t)=\frac{e}{\hslash }\int\,V(t)dt\). The Fourier components of the phase factor e−iϕ(t) yield the photo-assisted probabilities Pn, where n > 0 (n < 0) corresponds to the absorption (emission) of n photons. These probabilities determine the AC transport properties and are used to calculate the rectified current in the system. Our Floquet simulations capture key features of both adiabatic and non-adiabatic regimes, including the emergence of a maximum as a function of voltage bias and deviations from adiabaticity at experimentally relevant frequencies. However, the peak position of coherent oscillations shifts oppositely to experimental observations (see Supplementary Information, Section 2.4), with additional discrepancies at high bias. These differences stem from the limitations of the Floquet scattering approach, which, while capturing essential physics, omits certain effects. In our model, electron-electron interactions are included at the mean-field level in a static way, enabling direct comparison with experiments without fitting parameters. However, this approach excludes some complex mechanisms. A more advanced treatment–time-dependent Hartree-Fock–has shown that interactions primarily renormalize plasmon velocity while maintaining coherence16,34. Fully accounting for decoherence would require accounting for the dynamical creation of electron-hole pairs which would require to treat higher-order Feynman diagrams, a challenge at the forefront of current research. We expect electron-electron interactions to be the dominant decoherence mechanism35, as observed in DC interferometry36.

To further highlight the frequency-dependent evolution of the oscillation amplitude, we define ΔIAB(f) as the absolute difference between the maximum oscillation amplitude measured at a given drive frequency f and the maximum oscillation amplitude in the adiabatic limit:

$$\Delta {I}_{{\rm{AB}}}(f)=\left\vert \max \left[{I}_{{\rm{AB}}}(f\to 0,{V}_{{\rm{ac}}})\right]-\max \left[{I}_{{\rm{AB}}}(f,{V}_{{\rm{ac}}})\right]\right\vert $$
(2)

This quantity is plotted in Fig. 3e. At low frequencies, the quantum oscillations follow the adiabatic limit up to roughly 1 GHz. Beyond this frequency, the system presents deviations from the adiabatic limit and gradually evolves towards the non-adiabatic regime.

Notably, accessing the non-adiabatic regime has remained elusive until now, as it was expected to occur at frequencies well above 1 GHz24. We demonstrate, that in our device, this regime is reached at surprisingly low frequencies due to the specific properties of the TCW’s conduction modes. Using realistic electrostatic potential simulations, as pioneered in30 (Supplementary Information, Section 2.4), we show that the modes near the Fermi energy exhibit strong energy dependence, leading to nonlinear transport and, consequently, a rectified current. Owing to their low kinetic energy, these modes dominate the frequency response of our device, causing deviations from the adiabatic regime even at frequencies around 1 GHz.

Electronic interference with on-demand single-electron wavepackets

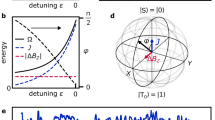
We now demonstrate quantum interference beyond the adiabatic regime with ultrashort wavepackets having a temporal width as short as 30 ps and containing as few as one electron. It is important to emphasize that, in our case, the generated wavepackets are plasmonic pulses influenced by electron interactions16. To begin, we characterise these ultrashort plasmonic wavepackets on-chip using a pump-probe technique37,38. We apply a voltage pulse with a duration of 25 ps39 to the injection Ohmic contact via the AC port of a high-bandwidth bias tee. By applying a second short voltage pulse to the quantum point contact, highlighted in white in Fig. 1a, with a precisely controlled time delay, we can measure the time-resolved trace of the plasmonic wavepacket directly on chip. Time traces for various pulse amplitudes, shown in Fig. 4a, reveal plasmonic pulses with a temporal duration of 30 ps. For such short pulses, we observe quantum oscillations in the output currents of our Mach-Zehnder interferometer device, which are perfectly anti-phased (see Fig. 4b). These interference patterns exhibit minimal background current and remain highly robust under applied bias voltages of up to several hundred microvolts.

Fig. 4: Quantum interference with on-demand single-electron plasmonic pulses.
figure 4

a Time-resolved measurements of a plasmonic pulse of width τp = 30 ps. The envelope is measured in a pump-and-probe experiment by varying the pulse amplitude. b Bottom panel shows raw data of Aharonov-Bohm oscillations for the shortest pulse for an amplitude of 100 μV. Top panel shows the total oscillating current I0-I1, where a smooth background has been subtracted. c Average number of transmitted charges nAB that contribute to the quantum coherence as a function of injected charges ninj, with pulses of temporal widths τp varying from 40 ps to 5 ns. nAB = n0 − n1 corresponds to the total number of transmitted charges from the upper and lower electron waveguide that contribute to the quantum coherence. The dashed lines are guides to the eye.

Full size image

To demonstrate that quantum interference can be observed with the on-demand injection of a single electron—a key requirement for realizing a flying electron qubit – we analyse our results in terms of the number of injected and transmitted electrons. We convert the amplitude of the coherent oscillations IAB, as defined above, into the average number of interfering charges nAB using the relation I = enf, where e is the electron charge, n is the average number of charges, and f = 100 MHz is the pulse repetition frequency. Similarly, we convert the pulse amplitude Vp into an effective number of injected electrons per pulse ninj (see Supplementary Information, Section 1.5). These results are presented in Fig. 4c for pulses of various temporal widths. We observe that, with ultrashort voltage pulses, it is straightforward to reach a regime where a single electron traverses the interferometer. Remarkably, the contrast of the oscillating signal is significantly enhanced for shorter voltage pulses. This enhancement is primarily attributed to the high-energy components of short plasmonic pulses, which probes a higher energy range of the I − V characteristic and is thus more sensitive to the nonlinearity. A detailed understanding of the enhanced contrast of the coherent oscillations compared to the DC regime is currently lacking. Achieving this would require a microscopic theory that incorporates electron-electron interactions40, which is computationally too costly at present.

Finally, let us comment on the relationship between the size of the plasmon pulse and the dimensions of the interferometer. As demonstrated above, the nonlinearity primarily stems from modes near the Fermi energy in the tunnel-coupled wires, which determine the effective propagation speed of the plasmon pulse. These modes exhibit the slowest Fermi velocity, vTCW ≈ 3 × 104 ms−1 while the plasmon propagates at a speed of  ≈ 106 ms−1 in the interferometer arms. Assuming these velocities for the two different sections of the MZI, the resulting total propagation time is calculated to be 144 ps. This timescale corresponds to half the period of a sine wave with a frequency of 3.5 GHz, matching well the frequency range where deviations from the adiabatic regime are observed. These insights suggest that the plasmon wavepacket is significantly smaller than the quantum device, supporting the consistency of our observations. In conclusion, we have demonstrated electronic quantum interference in a 14-micron-long Mach-Zehnder interferometer using plasmonic pulses containing a single charge. By employing GHz sinusoidal excitation and voltage pulses with durations of several tens of picoseconds, we identified a ‘non-adiabatic’ regime. This achievement represents a significant milestone towards realizing flying electron qubits, where the pulse width must be shorter than the dimensions of the quantum device.

Beyond providing the proof-of-principle demonstration of coherent control for ultrashort electron qubits in semiconducting systems, we expect that our detailed high frequency investigation will stimulate further theoretical and experimental research into the electron dynamics of these systems. To complete the implementation of a fully-fledged flying electron qubit, the integration of single-shot detection is essential. A recent advancement has been achieved in this direction41. The next crucial milestone is to increase the number of flying qubits that can be accommodated within a single processing unit, enabling the implementation of multiple gate operations during their flight. This can be achieved by further reducing the temporal width of the plasmonic pulses42, potentially reaching durations in the terahertz regime43.

Furthermore, our demonstration of coherence in the non-adiabatic regime opens new possibilities for electron quantum optics experiments. This achievement paves the way for exploring dynamical interference control23,44 and provides new avenues for investigating single-electron coherence45 and multi-particle interference phenomena in electronic MZIs46,47,48. The coherent manipulation of ultrashort wavepackets in an electronic MZI also represents a crucial step towards coupling multiple interferometers to study entanglement and test Bell inequalities49,50. Moreover, these short wavepackets offer a pathway to high-fidelity quantum teleportation of single-electron states51, marking a significant advance toward quantum information processing with flying electrons.

Methods

Sample fabrication

The sample is patterned on a GaAs/AlGaAs heterostructure, forming a two-dimensional electron gas (2DEG) located 145 nm below the surface, with carrier density ne = 1.9 × 1011 cm−2 and mobility μe = 1.8 × 106 cm2/(V ⋅ s). The electronic Mach-Zehnder interferometer (MZI) geometry is defined by Ti/Au surface gates patterned using electron beam lithography. Electrical connections to the 2DEG are established through Ohmic contacts formed by the successive deposition of Ni(5 nm)/Ge(140 nm)/Au(280 nm)/Ni(100 nm)/Au(15 nm), followed by annealing under a continuous flow of forming gas (5% H2 in Ar) at 370 °C for 2 min and 430 °C for 1 min. The injection Ohmic contact area measures 10 × 10 μm2.

High frequency signal injection

The high frequency signal (sinusoidal or pulses) was injected into the MZI through coaxial line with a bandwidth of 40 GHz. It was modulated at 170 Hz and injected into a high bandwidth (40 GHz) bias-tee to control independently the AC and DC components of the signal. The ultrashort voltage pulses used in this experiment were generated using a homemade voltage pulse generator based on frequency comb synthesis39, in conjunction with an arbitrary waveform generator with a sampling rate of 24 GS/s. The time-resolved measurement of the 30 ps pulse confirms the precise injection of ultrashort voltage pulses into the MZI without significant distortion.

Electrostatic and quantum transport simulations

Semi-quantitative quantum transport simulations are performed in two steps. First, the electrostatic potential in the silicon doped heterostructure is calculated by solving the Poisson equation with the commercial solver nextnano52. We follow the approach adopted in30. To implement the device geometry, we position metallic gold gates on the surface of GaAs crystal, taking into account the Schottky barrier. Surface charges are added to take into account Fermi-level-pinning. The dopant and the surface charge densities are calibrated in such a way that they reproduce an experimental pinch-off measurement between two metallic surface gates. In a second step, a 2D slice of the electrostatic potential at the 2DEG height is extracted and used to compute the DC current. The Landauer-Büttiker formalism53 is employed, and the calculations are performed using the open-source software Kwant31. The lattice constant is set to a = 5 nm, and the magnetic field is incorporated using the standard Peierl’s substitution. Additionally, the current under periodic drive is calculated from the DC current using Floquet scattering theory, as described in ref. 24.