Beating the Ramsey limit on sensing with deterministic qubit control

Abstract

Qubit frequency shifts, which often contain information about a target environment variable, are detected with Ramsey interference measurements. Unfortunately, the sensitivity of this protocol is limited by decoherence. We introduce a new protocol to enhance the sensitivity of a qubit frequency measurement in the presence of decoherence by applying a continuous drive to stabilize one component of the Bloch vector. We demonstrate our protocol on a superconducting qubit, enhancing sensitivity per measurement shot by 1.65 × and sensitivity per qubit evolution time by 1.09 × compared to Ramsey. We also explore the protocol theoretically, finding unconditional enhancements compared to Ramsey interferometry and maximum enhancements of 1.96 × and 1.18 × , respectively. Additionally, our protocol is robust to parameter miscalibrations. It requires no feedback and no extra control or measurement resources, and can be immediately applied in a wide variety of quantum computing and quantum sensor technologies.

Introduction

Ramsey interferometry¹ has been long established as the most sensitive measure of a qubit’s frequency². In a Ramsey measurement, a qubit is prepared in a superposition of energy states, allowed to evolve freely and acquire phase, and then measured along some axis. The phase acquired (and thus the measured state probability) depends on the qubit frequency. This protocol has been used for quantum sensing of magnetic field and other continuous variables^3,4,5, for foundational physics^6,7, for biomedical applications⁸, for detection of non-equilibrium quasiparticle densities^9,10,11, and for rapid recalibration of a qubit’s frequency¹², among many other applications. Decoherence at a rate γ₂ = 1/T₂ limits the signal-to-noise ratio (SNR) of quantum sensors. To date, most work has focused on SNR scaling beyond the standard quantum limit of $\sqrt{N}$ (where N is the number of independent qubits and/or measurements)^{13,14,15,16,17}, using dynamical decoupling to enhance frequency discrimination and reduce or characterize non-Markovian decoherence^18,19,20, using measurement-based feedback to rapidly lock in on large signals²¹, time-varying signals²², or an unknown signal axis²³, and compensating for measurement errors²⁴. Likewise, researchers have developed sensors which are less prone to decoherence^25,26,27 and couple more strongly to wanted signals^28,29,30. However, no results have shown improvement over traditional Ramsey interferometry for increasing the SNR from a single qubit measuring a small, static (zero frequency) signal.

Here, we demonstrate a protocol for enhanced quantum sensing of static fields. The protocol is based on a recent theory of quantum property preservation³¹ generalizing the coherence preservation results of ref. ³², showing how certain scalar functions of a quantum state can be stabilized using purely Hamiltonian control. We use deterministic Hamiltonian control of a single qubit to stabilize one Bloch vector component (v_x), enabling increased phase accumulation in the orthogonal component v_y and thus enhanced sensitivity. Our protocol gives a significant signal enhancement over standard Ramsey interferometry, up to a factor of 1.96 per measurement shot or 1.18 per qubit evolution time. We derive analytical expressions for the signal enhancement in the small-signal regime, and show simulations of the protocol’s robustness to miscalibrations. The protocol is robust to variation in environmental parameters, requires no feedback (i.e., is unconditional and deterministic), and can be applied in a wide variety of experimental systems. Our results demonstrate a general technique for enhanced quantum sensing.

Consider a sensor that maps some environmental variable B to a qubit’s frequency, and thus to the detuning Δ between qubit frequency and drive. We assume the transduction function Δ = f(B) is a fixed and known property of the sensor. The challenge is then to design a protocol that measures Δ as precisely as possible.

The qubit’s state is given by the Bloch vector $\overrightarrow{{{{\bf{v}}}}}=({v}_{x},{v}_{y},{v}_{z})=(\langle {\sigma}_{x} \rangle,\langle {\sigma}_{y} \rangle,\langle {\sigma}_{z} \rangle)$. We choose coordinates such that the initial state lies in the xz plane, $\overrightarrow{{{{\bf{v}}}}}(0)=({v}_{x}(0),0,{v}_{z}(0))$. Detuning causes rotation about the z-axis, leading v_y to grow proportionally to v_x at a rate Δ. For small rotation angle, v_y(t) is linearly proportional to Δ—this is the relevant limit for a weak signal with Δ ≪ γ₂ = 1/T₂. We can thus write v_y = aΔ, where a depends on the protocol used and on γ₂. The uncertainty in a measurement of Δ is thus

$$\delta \Delta=\frac{\delta {v}_{y}}{a}\approx \frac{1}{a\sqrt{N}}=\frac{\Delta}{\sqrt{N}{v}_{y}}$$

(1)

where N is the number of iterations of the measurement and the approximation is valid in the limit of small v_y (see Supplementary Material for derivation). This means that to minimize δΔ, one should maximize $a\sqrt{N}$, which is equivalent to maximizing $\sqrt{N}{v}_{y}$ for a given detuning Δ.

We assume that state preparation and measurement errors affect all protocols equally and, therefore, ignore them for this analysis. We further assume that γ₂ is a property of the sensor and is not affected by the protocol.

The task is thus to choose a protocol that will maximize $\sqrt{N}{v}_{y}=\sqrt{\frac{T}{t+{t}_{i}}}{v}_{y}(t)$ for a given detuning Δ and decoherence rate γ₂. Here T is the total experiment time, t is the time the qubit spends accumulating phase in an iteration, and t_i is the “inactive” time spent preparing, reading out, and resetting the qubit in an iteration. When t_i ≫ t ~ T₂, N is essentially fixed and the goal is to maximize v_y(t); when t ~ T₂ ≫ t_i, the goal is to maximize ${v}_{y}(t)/\sqrt{t}$.

Consider a qubit subject to relaxation at rate γ₁ = 1/T₁, dephasing at rate γ_ϕ, detuning Δ, and a coherent drive H_drive(t) = h_y(t)σ_y. In a Ramsey sequence the qubit is prepared in the state $\overrightarrow{v}(0)=(1,0,0)$ and allowed to freely evolve (h_y = 0). When Δ ≪ γ₂ = γ_ϕ + γ₁/2, this leads to a maximum y-component

$${v}_{y}^{R,\max}\approx \frac{1}{e}\frac{\Delta}{{\gamma}_{2}}$$

(2)

at time t ≈ T₂, and a maximum y-component per root evolution time

$$\frac{{v}_{y}^{R}({t}_{\max})}{\sqrt{{t}_{\max}}}=\frac{1}{\sqrt{2e}}\frac{\Delta}{\sqrt{{\gamma}_{2}}}\approx 0.429\frac{\Delta}{\sqrt{{\gamma}_{2}}}$$

(3)

at t ≈ T₂/2 (see Supplementary Material for derivations). These cases have $a={(e{\gamma}_{2})}^{-1}$ with $a\sqrt{N} \sim a$ and $a={(2\sqrt{e}{\gamma}_{2})}^{-1}$ with $a\sqrt{N} \sim a/\sqrt{t}={(2e{\gamma}_{2})}^{-1/2}$, respectively. As we can see, the value of a depends on the protocol used, including the measurement time chosen. We define the signal improvement ratio R_v (i.e., the SNR improvement per measurement shot) as the ratio of maximum v_y from the given protocol to that from the Ramsey experiment, the latter being given by (2). Likewise, we define the signal per root evolution time improvement ratio R_s (i.e., the SNR improvement for fixed total evolution time) as the ratio of maximum ${v}_{y}/\sqrt{t}$ from the given protocol to that from the Ramsey experiment, the latter being given by (3). Note that the uncertainty in a measurement of detuning δΔ is inversely proportional to $\sqrt{N}{v}_{y}$ as given in (1). This means that our protocol reduces δΔ by a factor of R_v when N is fixed and by a factor of R_s when N ~ 1/t.

Our protocol uses Hamiltonian control to preserve state coherence³² and enhance sensitivity. The general theory is derived in³¹. Here we report the central results, with full details given in the Supplementary Material. Again, we have initial state $\overrightarrow{{{{\bf{v}}}}}(0)=({v}_{x}(0),0,{v}_{z}(0))$. For small, unknown Δ ≪ γ₂, we can stabilize v_x(t) ≈ v_x(0) for 0 ≤ t ≤ t_b so long as v_z(t) ≠ 0 by setting

$${h}_{y}(t)=\frac{{\gamma}_{2}{v}_{x}(0)}{2{v}_{z}(t)}$$

(4)

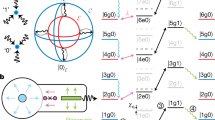
where the stabilization is exact to 2nd order in Δ/γ₂. In general, coherence will be transferred from v_z to v_x until v_z → 0. At this breakdown time t_b, the protocol fails and coherence must decay. However, stability can be achieved indefinitely if ${v}_{x}(0)\le \frac{1}{2}\sqrt{\frac{{\gamma}_{1}}{{\gamma}_{2}}}$, since at low temperature relaxation deterministically causes growth of v_z towards its thermal value v_z = 1—that is, relaxation takes the qubit to the ground state, and so the ground state population in an ensemble grows as a function of time. The drive can then rotate v_z towards v_x, transferring this ground state population to the desired v_x, preserving coherence. See Fig. 1 for an illustration of a Bloch trajectory with coherence stabilization. Temperature effects are discussed later in the text and in the Supplementary Material.

Fig. 1: Illustration of the coherence stabilization protocol.

a Simulated trajectories of the Bloch vector in the xz plane for a qubit state which is either allowed to freely evolve (star markers; steady decay of v_x) or stabilized with our protocol (triangle markers; stabilized v_x up to a breakdown time, followed by steady decay), with T₁ = T₂ = 1 and v_x(0) = 0.68. The black curve is the ∣v∣ = 1 limit for a pure state. b, c 3D Bloch sphere plot of the same trajectories for stabilization (b) and free evolution (c). d Pulse sequence schematic of our stabilization protocol. We prepare a state in the xz plane at an angle θ from the z-axis, then stabilize the Bloch component ${v}_{x}=\sin \theta$ up to a breakdown time. After the breakdown we turn off the control and the state is allowed to freely decay. After a variable evolution time we perform quantum state tomography.

When v_x is thus coherence-stabilized at ${v}_{x}^{c}\approx {v}_{x}(0)$ and the unknown detuning Δ ≠ 0, v_y grows to an asymptotic maximum ${v}_{y}^{c}\to \frac{{v}_{x}(0)}{{\gamma}_{2}}\Delta$, leading to a signal improvement ratio (SNR per measurement shot improvement ratio) relative to Ramsey of R_v = ev_x(0). The maximum stable ${v}_{x}(0)=\frac{1}{2}\sqrt{\frac{{\gamma}_{1}}{{\gamma}_{2}}}$ thus gives ${R}_{v}=\frac{e}{2}\sqrt{\frac{{\gamma}_{1}}{{\gamma}_{2}}}$. In the limit where relaxation dominates decoherence (γ₁ = 2γ₂), ${R}_{v}=\frac{e}{\sqrt{2}}\approx 1.922$.

We achieve a larger advantage, especially when γ₁ < 2γ₂, by using a state with a larger v_x(0) and thus a finite breakdown time t_b. We stabilize v_x(t) until breakdown and then set h_y = 0. In the small detuning limit, this gives improvement ratio

$${R}_{v}={e}^{1-{e}^{-{\gamma}_{2}{t}_{b}}}{v}_{x}(0).$$

(5)

While there is a closed-form expression for t_b in terms of v_x(0)³¹, it does not allow an analytical solution for the maximum of (5) over all values of v_x(0). Instead we optimize numerically, as discussed below, reaching a maximum of R_v = 1.96 when γ₁ = 2γ₂. Even in the limit of no relaxation where γ₁ → 0, we find R_v = 1.09. Thus, our protocol can achieve an unconditional v_y signal boost compared to Ramsey interferometry.

When the inactive time t_i is negligible and (3) applies, we instead maximize the signal per root evolution time ${v}_{y}^{c}/\sqrt{t}$ over all times and initial states. In this case, using a permanently-stabilized state gives a maximum achievable advantage (when γ₁ = 2γ₂) of only R_s = 1.052, and can be disadvantageous when dephasing is non-negligible. However, using an initial state with a finite breakdown time leads to a larger and unconditional SNR enhancement. Once again we can find an analytic expression for the maximum SNR and improvement ratio in terms of the initial state v_x(0) and breakdown time t_b, but must numerically optimize over v_x(0), as discussed in the Supplementary Material. We find R_s ≥ 1 for all values of γ₁/γ₂, reaching a maximum R_s = 1.184 when γ₁ = 2γ₂.

We can compare this protocol to others that use control to reduce the effects of decoherence such as spin locking and dynamical decoupling (DD). In spin locking, a strong constant drive along the axis of the Bloch vector causes any noisy Hamiltonian terms along orthogonal axes to average out, provided these terms are constant over the period required for the drive to rotate the vector a full revolution. Likewise, dynamical decoupling uses fast pulsed rotations to average out quasi-static noise. In both cases the protocols suppress decoherence due to slowly-varying noise and would cause complete insensitivity to detection of a static detuning, while sensitivity to an oscillatory detuning at particular frequencies is enhanced; this enhancement has been used in the past for optimizing sensing^18,19,20. In contrast, our coherence stabilization protocol works for broadband Markovian decoherence and maintains sensitivity to static Hamiltonian terms.

Results

We demonstrate our protocol using a superconducting qubit; device parameters and experimental details are given in the Methods. We first show coherence stabilization with Δ = 0. The experimental pulse sequence is shown in Fig. 1. We prepare a state in the xz plane with $\overrightarrow{{{{\bf{v}}}}}(0)=(\sin \theta,0,\cos \theta)$. We then continuously drive the qubit to rotate the Bloch vector about the y-axis towards the x-axis. If the control exceeds the maximum output amplitude of our control electronics (near breakdown), we set it to 0 for the remainder of the evolution. We cut off the control after breakdown to prevent rotations from v_x to v_z that would decrease v_x faster and reduce the growth of our v_y signal.

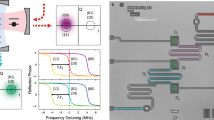
Quantum state tomography data showing coherence stabilization for two different initial states is presented in Fig. 2a, b, along with theoretical predictions (not fits) generated by solving the Bloch dynamics for our system parameters. Depending on the initial state and the ratio γ₁/γ₂, the stabilization may exhibit a breakdown (panel (a)) or long-time stability (panel (b)). When the qubit is detuned from the drive frequency by some small detuning Δ ≪ γ₂, v_y(t) grows to some maximum. We set Δ/2π = 396 Hz and 324 Hz for the same states as Fig. 2a, b, respectively, and measure v_y (Fig. 2c, d). We compare to v_y from Ramsey sequences (v_x(0) = 1) for the same detunings. For both states there is an enhanced v_y signal compared to Ramsey, validating the essential aspect of our protocol. Note that these data were taken on different days and T₂ drifted from 73 μs (c) to 89 μs (d), which accounts for the larger signal in (d) despite a smaller Δ.

Fig. 2: Experimental demonstration of coherence stabilization.

a, b Bloch vector evolution, as measured through quantum state tomography, for a state with a v_x(0) = 0.652 and breakdown at 148 μs and b v_x(0) = 0.599 with no breakdown (i.e, a stable state). c, d Evolution of v_y for the same initial states as in (a, b), with added small detuning Δ/2π = 396 Hz (c) and 324 Hz (d). Crucially, the stabilized states exhibit significantly larger signal than the Ramsey value.

To quantify the enhancement of signal R_v, we sweep the detuning Δ and measure the coherence-stabilized ${v}_{y}^{c}({t}_{\max},\Delta,\theta)$ for each initial state polar angle θ. Here, ${t}_{\max}$ is the predicted time of maximum ${v}_{y}^{c}$ (see Supplementary Material); for solutions with no breakdown we use ${t}_{\max}=350\,\mu {{{\rm{s}}}}\approx 5{T}_{2}$. We also measure the Ramsey evolution ${v}_{y}^{R}({T}_{2},\Delta)$ at t = T₂ when theory predicts ${v}_{y}^{R}$ will be maximized. We then fit the slopes of ${v}_{y}^{c}$ and ${v}_{y}^{R}$ vs Δ and take their ratio to compute R_v. Results are plotted in Fig. 3(a.i), along with the theoretically-predicted R_v for the measured T₁/T₂ ratio. During this experiment we measured T₁/T₂ = 0.749 ± 0.112 and T₂ = 83.4 ± 9.9 μs. Using our protocol with initial state θ = 0.198π and N shots, we are able to detect the qubit frequency with a minimum 1 − σ uncertainty of $\sqrt{N}\delta {f}_{c}=3.4\pm 0.8\,{{{\rm{kHz}}}}\sqrt{{{{\rm{shots}}}}}$, compared to $\sqrt{N}\delta {f}_{{{{\rm{R}}}}}=5.5\pm 0.7\,{{{\rm{kHz}}}}\sqrt{{{{\rm{shots}}}}}$ for Ramsey (variances are over repetitions of the experiment; see Supplementary Material for an explanation of the sensitivity calculation and units). Thus, our protocol reduces qubit frequency detection uncertainty by a factor of R_v = 1.62 ± 0.13 when t ≪ t_i. Theory predicts ${v}_{y}^{c}$ will be maximized when θ = 0.213π [v_x(0) = 0.671], with predicted R_v = 1.649. We find good agreement with the data with no free parameters, indicating that our protocol behaves as predicted.

Fig. 3: Experimentally measured signal improvement ratio R_v (a.i) and R_s (b.i) as a function of initial state, measured at the times that theory predicts maximum signal for stabilized and Ramsey data.

Error bars are calculated from the variance of the ratio across many measurements. The dashed line is a theoretical prediction, not a fit, showing good agreement. Bottom row: Numerically simulated improvement ratio R_v (a.ii) and R_s (b.ii) as a function of initial state and T₁/T₂ ratio, for small detuning. Also shown are numerically simulated (markers) and analytically derived (dashed line) improvement ratio R_v (a.iii) and R_s (b.iii) at optimal initial state as a function of T₁/T₂.

To test the protocol under different environmental parameters, we numerically simulate the evolution as a function of initial state and T₁/T₂ ratio, all at small detuning Δ = 0.01/T₂. Results are plotted in Fig. 3a.ii. We maximize over initial state at each T₁/T₂ and plot these maxima in Fig. 3a.iii. We find that R_v reaches a maximum value of 1.96 in the limit where relaxation dominates dephasing (T₂ = 2T₁), and has a minimum of 1.09 in the limit where dephasing dominates relaxation (T₁ ≫ T₂), as predicted by analytical theory (shown as a dashed line).

To quantify the enhancement of SNR per qubit evolution time R_s, we use a similar procedure as above, except that we measure the stabilized v_y and Ramsey v_y at the times theory predicts will maximize ${v}_{y}/\sqrt{t}$ (see Supplementary Material). Experimental, theoretical, and numerical results are plotted in Fig. 3b. During these measurements, T₁/T₂ = 0.764 ± 0.156 and T₂ = 69.5 ± 10.6 μs. Using our protocol with initial state θ = 0.315π and total experiment time T, we find a minimum frequency detection uncertainty of $\sqrt{T}\delta {f}_{c}=63\pm 4\,{{{\rm{Hz}}}}/\sqrt{{{{\rm{Hz}}}}}$, compared to $\sqrt{T}\delta {f}_{{{{\rm{R}}}}}=70\pm 1\,{{{\rm{Hz}}}}/\sqrt{{{{\rm{Hz}}}}}$ with Ramsey. Again, our protocol reduces uncertainty by a factor of R_s = 1.11 ± 0.03 when t_i ≪ t (see Methods). Our experimental results once more agree well with the theory, which predicts a maximum R_s = 1.094 at θ = 0.283π [v_x(0) = 0.776] for this T₁/T₂ ratio. Theory and simulation show the improvement ratio R_s ranges from 1.184 when T₂ = 2T₁ to 1 when T₁ ≫ T₂.

A quantum sensor may have comparable inactive time t_i and evolution time t, between the limits we study. For a fixed t_i, the problem is to optimize ${v}_{y}(t)/\sqrt{t+{t}_{i}}$. Again, the Ramsey protocol can be optimized analytically, while our coherence stabilization protocol can be optimized numerically by the same procedure used above. The SNR improvement ratio will land somewhere between our two limiting cases, but will always be ≥1. For instance, when T₂ = 2T₁ and t_i = 0.1T₂, the SNR improvement is by a factor of 1.23, by a factor of 1.43 when t_i = T₂, and by a factor of 1.76 when t_i = 10T₂.

Protocol robustness

Optimal sensing depends on accurate knowledge of T₁ and T₂. To quantify the robustness of our protocol to miscalibrations, we simulate the Bloch evolution using the initial state, control field, and measurement time that would be optimal for a nominal T₁ = T₂ = 1 while varying the actual values of T₁ and T₂ that control the dynamics. Thus, we simulate a situation in which T₁ and T₂ have changed unbeknownst to the experimenter. We simulate Ramsey experiments with the same miscalibration: measurements are performed at times determined by the nominal T₂, not the actual simulated one. We plot the SNR improvement ratios as a function of percentage change in γ₁ = 1/T₁ and γ₂ = 1/T₂ in Fig. 4. We see little change in the improvement ratios when T₁ and T₂ are miscalibrated by the same factor, as shown by the near-constant values along lines of constant T₁/T₂ ratio running diagonally from bottom left to top right. We see some dependence of the improvement ratios on changes in the T₁/T₂ ratio, as shown by the steepest gradient running approximately diagonally from top left to bottom right. The majority of this dependence is not due to miscalibration, but rather is due to the fact that R_v and R_s depend on T₁/T₂ even when perfectly calibrated. This can be seen in the plots as the large regions where SNR is improved even more than at the perfectly calibrated T₁ and T₂ (red color), due to the fact that T₁/T₂ has decreased. There is some additional SNR suppression due to using a suboptimal initial state and measurement time, which is evident in the top left corner of Fig. 4(b)—R_s dips slightly below 1, indicating worse performance than Ramsey, while an optimal protocol would always have R_s ≥ 1. Still, this requires quite a large deviation, with actual T₂/T₁ ~ 2/3 of its nominal value, and so the protocol is relatively robust to fluctuations in T₁ and T₂. Furthermore, we see from the experimental measurements in Fig. 3 that improvement on par with the theoretical maximum value for that T₁/T₂ ratio can be achieved, even in a real system with fluctuating coherence times.

Fig. 4: Simulated sensitivity of the improvement ratios.

a R_v and b R_s to miscalibrations of decoherence rates 1/T₁ and 1/T₂, for nominal T₁/T₂ = 1. Miscalibration of 1/T is defined as (T_nominal/T_actual − 1). White color is defined as the value at the perfectly-calibrated center point.

All results and theory thus far are derived or acquired in the low temperature limit where the qubit deterministically relaxes to the ground state (v_z grows to 1). Higher temperature reduces the improvement our protocol can provide since there is no longer as fast of a growth in v_z that can be transfered back to v_x for stabilization. However, this only applies if the qubit begins in a state that is more pure than the thermal equilibrium state. In the case where the qubit is initialized in a partially-mixed thermal state, both Ramsey and stabilization protocols are affected equally, the breakdown time becomes independent of temperature, and the improvement factors R_v and R_s recover their low-temperature values. The effect of high temperature is also mitigated when relaxation is negligible. Even when state preparation is perfect, our protocol provides an signal boost R_v by a factor of at least 1.05 so long as T₁ > 10T₂ or the thermal state has ${v}_{z}^{{{{\rm{thermal}}}}} > 0.5$. In all cases our stabilization protocol is guaranteed to be non-inferior to Ramsey, as it reduces to a Ramsey protocol in the limit where v_x(0) → 1.

Discussion

In conclusion, we have demonstrated a protocol for enhancing qubit sensitivity to weak environmental fields by stabilizing partial qubit coherence. Our protocol requires only deterministic Hamiltonian control and is therefore applicable to a wide variety of qubit technologies. In the limit where decoherence is dominated by relaxation, we show a theoretical maximum of a 1.96× improvement over standard Ramsey interferometry in SNR per measurement shot, and a 1.184× improvement in SNR per root qubit evolution time. In our experimental apparatus with dephasing comparable to relaxation and with fluctuating system parameters, we achieve improvements of 1.6× and 1.1× , respectively. Our results show a resource-efficient, broadly-applicable technique for unconditionally enhancing the SNR from qubit-based sensors and speeding calibration of qubit parameters.

A natural application of our technique is to sensing magnetic fields or, equivalently, measuring the field-to-frequency transduction function of a spin species. These measurements are typically done in ambient conditions far from the low-temperature limit which would seem to reduce the benefit that our protocol could give. However, often the system is initialized in a thermal state and so the low-temperature enhancement of signal versus Ramsey would apply.

While our technique provides a significant SNR boost over Ramsey interferometry, it is not fully optimal. For instance, if γ₁ > 0 and the optimal measurement time is after breakdown, there will be some nonzero v_z that could be used to boost signal. Thus, for each set of environmental conditions, there is likely a Bloch trajectory (i.e., an initial state and control Hamiltonian) that provides an even larger signal than our protocol of stabilizing coherence. This is a problem of optimal control, and as such can be tackled with control theory techniques^33,34. It is a relatively unconstrained problem, as the initial state, final state, and final time are all variable. Given this lack of constraint, numerical solution methods will likely be required. Such optimal control has already been pursued in quantum sensing of time-varying signals^20,35 and large signals³⁶, and inspiration can be drawn from these results. In addition, it should be possible to stabilize properties of multi-qubit states³¹, including various entanglement measures³⁷. Future work could therefore explore the possibility of extending our sensitivity enhancement to entangled states. We note that, like Ramsey, our protocol cannot achieve the Heisenberg limit of SNR scaling linearly with total experiment time T. Instead it maintains the standard quantum limit scaling of SNR with $\sqrt{T}$. Combining our stabilization protocol with entanglement-based sensing, continuous weak-measurement feedback, and other sophisticated techniques could allow for further sensitivity gains³⁸.

Methods

Our device is a standard grounded superconducting transmon qubit coupled to a quarter-wave transmission line cavity. Device parameters are given in Table 1, and the design is available on the SQuADDS database³⁹. The qubit and cavity are far off resonance. In this dispersive regime there is approximately 0 energy exchange between qubit and cavity, but the cavity frequency shifts by χ/2π = 150 kHz when the qubit changes state. We measure the qubit by driving the cavity with an on-resonant pulse generated by mixing a carrier at the cavity frequency with a Gaussian envelope. The pulse transmits through the device, interacting with the cavity as it passes, then passes through an amplification chain up to room temperature, where we mix it back down to DC with an IQ mixer, giving a two-channel DC voltage signal that we then digitize. A diagram of the experimental setup is given in Fig. 5. We project the measured two-channel voltage onto an axis which gives maximum discrimination between the signals for qubit ground and excited states. We drive rotations of the qubit state by driving it with an on-resonance microwave pulse. The amplitude and duration of the pulse determine the total rotation angle, while the phase determines the rotation axis in the xy plane.

Table 1 Qubit Device Parameters

Fig. 5: Diagram of our cryogenic measurement setup.

All qubit control envelopes are generated by the Zurich Instruments HDAWG, then upconverted and combined with measurement pulses from the ZI UHFQA before being fed into a heavily attenuated line. Readout signals are amplified and then downconverted and fed back into the UHFQA for analysis.

We begin by measuring the qubit’s T₁ (using a population decay measurement) and its T₂ and frequency (using a standard Ramsey measurement). If the qubit frequency has drifted, we reset the drive frequency to be resonant, then detune it by Δ. We then calculate the control waveform to stabilize v_x for our chosen initial state; in the case where we are stabilizing a state with a breakdown time and we want to extend the evolution past breakdown, we set the control to 0 after breakdown. We then calibrate the strength of our drives with a Rabi measurement, where we drive the qubit with a pulse of constant duration and variable amplitude. This pulse has a cosine envelope and is 2.35 μs in duration. We measure oscillations of the qubit population and thus extract the driven Rabi frequency at a given control output voltage. We use this to convert our calculated control waveform into output voltage units for our control electronics. Note that long qubit manipulation pulses are used because our control line is heavily attenuated in order to give fine resolution of the continuous control waveform.

We note that we initialize the qubit in a thermal state. Therefore the temperature factors into the state preparation fidelity and the low-temperature limit applies.

We use the same pulse envelope and duration for all qubit control pulses (except the continuous coherence-stabilizing drive)—we change the pulse rotation angle by changing the amplitude of the pulse, and change the rotation axis by changing the phase of the pulse. We therefore prepare a state with ${v}_{x}(0)=\sin \theta$ by driving a pulse with amplitude $\frac{\theta}{\pi}{A}_{\pi}$, where A_π is the amplitude of a π rotation pulse calibrated via the Rabi measurement. We next drive the continuous control waveform to stabilize the state for a time t. We then stop the control and perform quantum state tomography, measuring the qubit state along one axis. To measure v_x, we apply a -π/2 rotation pulse about the y-axis, then drive a readout pulse on the cavity. To measure v_y we use a π/2 rotation about the x-axis, then a readout pulse; to measure v_z we use a 2π rotation about the y-axis, then readout. After a measurement we either do nothing or drive a π rotation of the qubit, conditional on the measurement outcome, to reset it to the ground state. We wait an additional 60 μs to damp any residual excited state population. We repeat each time point three times to measure all three Bloch vector components, then sweep t. Before measuring the first time point, we perform a measurement to calibrate the voltage corresponding to the ground state v_z = 1; after the last time point, we perform a π rotation on the qubit and then measure to calibrate the voltage corresponding to the excited state v_z = −1. We then repeat this entire process many times and directly average the measured voltages. We use these voltages as the reference values for v_i = ±1 (i = {x, y, z}).

When comparing the signal from coherence stabilization vs Ramsey, we interleave the measurements to avoid errors due to drifts in qubit parameters. We use threshold assignment of the readout voltage to the ground or excited state in order to reduce noise in these small signals. To speed data collection, we only measure v_y and ignore the other Bloch components and only measure at the optimal times for maximizing v_y and ${v}_{y}/\sqrt{t}$ (T₂ and T₂/2, respectively, for Ramsey, and the times derived in the Supplementary Material for coherence-stabilized measurements). We interleave coherence-stabilized and Ramsey measurements for a given detuning and coherence-stabilized initial state, repeating many times to build up accurate estimates of v_y. We then move on to the next detuning while keeping θ constant. We repeat these detuning sweeps many times to build up statistics, re-measuring T₁ and T₂ before each sweep. We then move on to the next initial state θ.

We take this set of coherence-stabilized and Ramsey data from the many detuning sweep iterations for each θ and break it into chunks of  ~10 iterations, interspersed throughout the dataset. For instance, one chunk might contain our 1st, 11th, 21st, ...,91st iteration. We rescale the detuning axis of this data by the T₂ measured in that iteration, and likewise divide the measurement times by T₂ to render them dimensionless. We then take all the v_y data in a given chunk and fit it simultaneously to a linear dependence on ΔT₂, extracting a slope for coherence stabilized and Ramsey measurements. In the case where we are calculating R_s, we then divide each slope by √t/T₂, where t is the time at which the measurement was taken in each iteration. Note that t will vary linearly with T₂, so even as T₂ fluctuates through iterations, this ratio remains constant (so long as T₁/T₂ remains roughly constant). We take the ratio of the coherence-stabilized slope to the Ramsey slope, then average over all N ~10 chunks to give an estimate of R_v or R_s. We compute the variance of these ratios and divide them by N as an estimate of the error.