Introduction

The spectacularly colourful solutions of alkali metals in liquid ammonia have attracted the attention of researchers since the 19th century (for comprehensive reviews see refs. 1,2). At low alkali metal concentrations, the resulting deep blue solutions contain localised solvated electrons and dielectrons1,3,4,5, which found practical application as reducing agents for the hydrogenation of aromatic hydrocarbons within the Birch reduction process6. At higher (molar) concentrations, as the excess electrons become delocalised, the solution turns into a liquid metal with a characteristic golden metallic sheen and conductivity comparable to that of copper1,4,5.

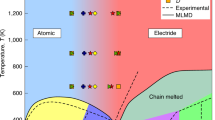
Models of the nonmetal-to-metal transition in liquid systems go back to the work of Landau and Zeldovich in the 1940s7 and have been experimentally tested on supercritical mercury or alkali metals numerous times8. The emerging picture has been that of a sharp transition occurring around the critical point, where metal clusters of sufficient size are formed in the dense supercritical vapour. However, the behaviour of alkali metals dissolved in liquid ammonia is qualitatively different. In these systems, the nonmetal-to-metal transition happens gradually, merely with an increase in the concentration of electrons dissolved in a dense liquid.

Thus, we refer to this phenomenon as the electrolyte-to-metal transition (EMT). In contrast to supercritical mercury8, alkali metals dissolved in liquid ammonia do not exhibit a sharp transition, but a gradual one in the concentration range of about 1–10 MPM (mole per cent metal; in liquid ammonia, 1 MPM equals roughly 0.4 mol/L)2,5. Three historical models have been suggested for the EMT in alkali metal-liquid ammonia systems:2 (i) a percolation model based on experimental findings of microscopic inhomogeneities9, (ii) an extension of the Landau and Zeldovich model introducing a critical electron density for metallisation10,11, and (iii) a model linking the transition to a polarisation catastrophe12. Despite these efforts, the molecular mechanism underlying the EMT remains inconclusive.

A phenomenon that has been closely connected to the EMT mechanism concerns inhomogeneities or fluctuations of concentration occurring in the alkali metal–ammonia solutions in the intermediate range of 1–8 MPM13,14. Experimental evidence for microscopic structural inhomogeneities was first provided by X-ray diffraction studies15. Subsequently, large concentration fluctuations in lithium and sodium ammonia solutions were deduced from investigations of the dependence of the chemical potential on the alkali metal concentration16. Finally, the nanometre-sized correlation lengths of the fluctuations were derived from small-angle neutron scattering studies17. Based on these experimental studies, a model was proposed suggesting the coexistence of dilute and concentrated voids in the intermediate concentration regime, which accounted for the spatial dimensions of the inhomogeneities18. However, no temporal information about these fluctuations has been provided so far, neither experimentally nor from modelling,2,19 making it hardly possible to deduce their molecular origins.

In such a situation, molecular dynamics (MD) simulations can serve as a very useful tool with an arbitrary spatial and temporal resolution, provided the underlying interactions are described with sufficient rigour and accuracy. For the present systems containing solvated electrons, a quantum description of the electronic structure is imperative. The first application of molecular dynamics to the EMT in alkali metal-liquid ammonia systems, accomplished 30 years ago, had to resort—due to limited methodology and computational resources available at the time—to semi-empirical methods for the description of the interactions of the excess electrons among themselves and with the rest of the system20. This severe approximation strongly limited both the range of accessible electronic structure scenarios and the fidelity of the predictions.

In this study, we overcome the above limitations by employing ab initio molecular dynamics (AIMD) with an explicit quantum mechanical description of all the excess and valence electrons in the system based on the density functional theory (DFT) benchmarked against the one-body Green’s function (GW) approximation. The use of revPBE38-D3, a state-of-the-art hybrid density functional, for MD ensures that our trajectories are faithful, providing accurate electronic structure information in quantitative agreement with test GW calculations involving a post-DFT description of Coulombic screening. The accuracy of our chosen density functional is also reflected in the close agreement between our DFT and GW results (see Supplementary Note 2, Supplementary Figs. 1–6). This simulation methodology is thus sufficiently robust to describe the dynamics and electronic structure of highly concentrated metallic solutions.

The present simulations, validated against existing experimental data, allow us not only to follow the ongoing molecular dynamics of all the species present in the solution but also to track the changes in the electronic structure of the investigated systems on a femtosecond scale. In this way, we are able to fill the existing knowledge gap concerning the temporal molecular-scale behaviour of solutions of alkali metals in liquid ammonia. As a key result for the understanding of the dynamics of the EMT, we observe and quantify the ultrafast transitions between metallic and non-metallic states on a sub-picosecond timescale.

Results and Discussion

Density of states and spherical band structure

We designed the simulation framework in a way that allowed us to capture the two principal—and at the same time opposing—aspects of EMT. On the one hand, we aimed for the size of the unit cell to be large enough to cover the concentration regime (about 1–10 MPM) where EMT takes place. On the other hand, since the average radius of the metallic and non-metallic domains pertinent to EMT has been estimated to be 15–25 Å9, the simulated unit cell should also be roughly commensurate with this size, i.e., small enough not to average out these structural inhomogeneities. Such a unit cell size would represent a sweet spot allowing for the capture of the flipping between electrolyte and metallic states and, at the same time, not making the computational costs prohibitive. Hence, we deliberately chose the size of the unit cell of about 15 Å, containing at the experimental density 64 ammonia molecules with a varying number of solvated dielectrons and Li+ cations to mimic concentrations of 3.0–13.5 MPM (for details see Supplementary Note 1).

Our AIMD simulations used the dispersion-corrected revPBE38 density functional21,22,23,24 (for details, see Supplementary Note 1). This functional incorporates a relatively high proportion (37.5%) of exact exchange, which has been found to be essential for describing systems susceptible to metal-insulator transitions25 and for a more reliable description of solvated electrons26,27,28,29,30. Panels a–d of Fig. 1 show representative snapshots taken from AIMD simulations at 3.0, 6.0, 11.1, and 13.5 MPM, covering the EMT concentration range. A 1 ps segment of each trajectory (100 snapshots taken at 10-fs intervals) was used to calculate the averaged densities of states (DoS) with the revPBE38-D3 functional (for details see Supplementary Note 1) as presented in panels f, h, j, and l of Fig. 1. We see a progressive narrowing and filling of the gap between the highest occupied and lowest unoccupied orbitals as the concentration of the alkali metal increases with rising density at the Fermi level as a signature of the gradual EMT.

Fig. 1: Representative AIMD snapshots and electronic properties of alkali metal-ammonia solutions.
figure 1

a–d AIMD simulation snapshots of alkali metal-ammonia solutions at concentrations of 3.0, 6.0, 11.1, and 13.5 MPM, illustrating the spatial distribution of solvated electrons within the solvent. e, g, i, k Corresponding spherical band structures (SBS) at the same concentrations. The SBS data are normalised such that the maximum displayed value is 1, with values exceeding 1 set to 1 to enhance contrast, consistently across all panels. f, h, j, l Associated density of states (DoS) for each concentration. For clarity, only the valence and conduction bands near the Fermi level (black dashed line), EF, are displayed.

Full size image

Next, we quantify the relationship between the energy of electrons and their momentum, which is typically represented by the band structure of a material. However, in (disordered) liquid metals, the first Brillouin zone cannot be rigorously defined,31,32,33,34 in contrast to periodic structures of crystalline solids. Nevertheless, a radial band structure has previously been measured, e.g., in a lead monolayer melted on a silicon surface35. Analogously, we introduce here the concept of a radial band structure in 3D. Denoted here as a spherical band structure (SBS), it represents the energy-momentum relationship in a spherically symmetrical space, where the electron energy is plotted versus the magnitude of the wave vector k.

The SBSs presented in panels e, g, i, and k of Fig. 1 were obtained from the same 1 ps segment used for the DoS calculations for each concentration (for further details, see Supplementary Note 1.7). Compared to the DoS alone, they provide a more detailed picture of the structure of the band gap and its gradual narrowing and filling with increasing alkali metal concentration. SBS also lends further insight into the EMT, providing information about the electron energy and momentum dispersion relations. This distinction is crucial to determine whether EMT occurs directly between a non-metallic and a metallic state or if an intermediate semimetallic band structure is formed36,37. In the following, we first perform a detailed temporal analysis of the AIMD data. Finally, we compare the calculated DoS with our reanalysed experimental data.

Rapid flipping dynamics

While Fig. 1 depicts SBSs and DoSs averaged over 100 geometries, analysing the results for individual snapshots allows us to distinguish between electrolyte and metallic configurations along the AIMD trajectory.

To probe this dynamics and the time evolution of transport properties, we analysed 500 configurations sampled from AIMD trajectories in 2-fs intervals at 3.0 and 6.0 MPM (intermediate regime), comparing them to 11.1 and 13.5 MPM (metallic regime), using the same 1 ps segment as before. For all concentrations, Fig. 2 shows the corresponding time evolutions of the simulated DoS and electron mobility.

Fig. 2: Time-resolved fluctuations between metallic and electrolyte states across varying concentrations, shown through the time evolution of density of states (DoS) and electron mobility.
figure 2

a–d Temporal evolution of the density of states (DoS) at 3.0, 6.0, 11.1, and 13.5 MPM, sampled every 2 fs along the corresponding trajectories. Blue indicates electrolyte states, and orange indicates metallic states, with colour intensity representing the DoS near the Fermi level (EF, black dashed line). The DoS data are normalised such that the maximum displayed value is 1, with values exceeding 1 set to 1 to enhance contrast, consistently across all panels. e–h Corresponding time evolution of the electron mobility, capturing fluctuations between metallic and electrolyte states.

Full size image

This analysis reveals that metallic states appear in about 30% of all snapshots already at 3.0 MPM, with an even larger fraction of metallic frames appearing at 6.0 MPM (see Supplementary Note 3, Supplementary Fig. 10, and Supplementary Table 1. for a further quantitative analysis of the observed bimodal distribution, distinctly categorising the snapshots as metallic or non-metallic). At 11.1 MPM and above, practically all the configurations are metallic, evidencing a completed transition to the metallic state, in agreement with previous experimental results5.

Let us now focus on the intermediate concentration regime, where the system flips fast between electrolyte and metallic states. From the EMT perspective, this regime is not only interesting for simulations but also from the point of view of experimental observables such as electrical conductivity or the related electron mobility, which are found to be highly dependent on concentration2,38.

Our main finding for the intermediate regime is that the average time interval between flips from an electrolyte to a metal and vice versa is only a few tens of femtoseconds (e.g., 29 fs at 3.0 MPM). Moreover, the flipping seems to be happening in a quasi-random fashion, i.e., without a characteristic frequency, exhibiting a relatively broad distribution of time intervals the system spends in either of the two states. In contrast, at 11.1 MPM, virtually all configurations manifest metallic behaviour, with zero transitions back to the electrolyte states at 13.5 MPM.

Next, we attempted to identify potential structural differences that may relate to the observed bimodal distribution of metallic and electrolyte states in the intermediate regime, namely at 3.0 MPM. To this end, we re-examined the same configurations as before at this concentration to determine which snapshot corresponds to an electrolyte or a metal. Panels a and b of Fig. 3 demonstrate that the excess electron densities for adjacent electrolyte and metallic configurations overlap to a large extent. Nevertheless, for separately averaged electrolyte vs metallic configurations, we see significant alterations in the excess electron gyration radii and radial profiles, with the excess electron being more spatially extended for the metal than the electrolyte, as expected (panels c and d of Fig. 3).

Fig. 3: Analysis of solvated dielectron density and volumetric properties in 3.0 MPM alkali metal–ammonia solution.
figure 3

a, b Electron density distributions of the dielectron in the electrolyte (blue) and metallic (orange) states, obtained from AIMD snapshots taken 2 fs apart. c Radii of gyration. d Spherically integrated electron density profiles.

Full size image

To zoom into the temporal dynamics of EMT in detail, we analyse the SBSs of two consecutive snapshots separated by 2 fs on either side of the transition (Fig. 4). At concentrations at which EMT transitions occur, we see large changes in the bands close to the Fermi level occurring during the flipping despite the fact that the atomic positions and electron densities right before and after the flip remain very close to each other. This indicates that the flips are induced by very small changes in molecular geometries, leading, nevertheless, to significant temporal variations in the band gap, which appears to be just enough to switch between metallic and electrolyte behaviour. In other words, the width and degree of filling of the band gap in the present system turn out to be highly sensitive to small changes in molecular geometry and the associated electron density.

Fig. 4: Spherical band structure before and after electrolyte-to-metallic state flipping.
figure 4

a, c, e, g Spherical band structures (SBS) of electrolyte frames at 3.0, 6.0, 11.1, and 13.5 MPM. b, d, f, h Corresponding SBS of metallic frames at the same concentrations, taken from consecutive AIMD snapshots immediately after the flipping event. The SBS data are normalised such that the maximum displayed value is 1, with values exceeding 1 set to 1 to enhance contrast, consistently across all panels. For clarity, only the valence and conduction bands near the Fermi level (black dashed line), EF, are displayed.

Full size image

Experimental validation

In this section, we directly compare the results of our calculations with available experimental data. While pump-probe measurements have been performed on liquid ammonia solutions39, no experiment has yet achieved the temporal and spatial resolution necessary to directly capture the femtosecond dynamics observed in our AIMD simulations. Nevertheless, our recent experimental study5, which combined liquid microjet techniques with synchrotron soft X-ray photoelectron (PE) spectroscopy, provides a direct comparison for the DoS of excess electrons in liquid ammonia over a broad concentration range of 0.08–9.7 MPM. Typical liquid jet experiments integrate the signal over at least 100 ms, making ultrafast time-resolved measurements impossible.

Figure 5 compares the calculated DoS (refined using the Boltztrap2 code40,41; see Supplementary Note 1.6) for 11.1 MPM and 3.0 MPM lithium–ammonia solutions with experimental spectra at the comparable concentrations of 9.7 and 3.4 MPM. First, we focus on the DoS in the metallic regime. Fig. 5a shows the computed spectral intensity distribution of the DoS at 11.1 MPM alongside the corresponding measured distribution at 9.7 MPM. The calculated and experimental spectral shapes and widths align well, reinforcing the reliability of the simulations while confirming that, at these concentrations, the DoS fully exhibits the characteristics of a metallic conduction band. The small offset of approximately 0.2 eV between the calculated and measured binding energies can be attributed, at least partially, to the experimental calibration procedure, in which the Fermi level is determined by fitting the slope of the measured signal intensity. Additionally, the simulated DoS reveals a subtle pre-edge feature near the Fermi level, contributing approximately 5% to the total spectral intensity. We note that the experimental sensitivity is insufficient to resolve such small signals as the average noise level is approximately 10% (further details are provided in Supplementary Note 4.1, Supplementary Figs. 16–18).

Fig. 5: Comparative analysis of the calculated DoS using the revPBE38-D3 functional with experimental PE spectroscopy data for an alkali metal–ammonia solution at two concentrations.
figure 5

a Total DoS at an elevated concentration of 11.1 MPM (\({I}_{{{{\rm{tot}}}}}^{{{{\rm{calc}}}}}\), green) with experimental results at 9.7 MPM (\({I}_{{{{\rm{tot}}}}}^{\exp }\), grey). b Total time-averaged DoS (\({I}_{{{{\rm{tot}}}}}^{{{{\rm{calc}}}}}\), green) at 3.0 MPM with the time-averaged PE signal (\({I}_{{{{\rm{tot}}}}}^{\exp }\), grey) at 3.4 MPM. c Calculated electrolyte contribution at 3.0 MPM (\({I}_{{{{\rm{E}}}}}^{{{{\rm{calc}}}}}\), blue) with the experimental PE spectra of the (di)electron only (\({I}_{{{{\rm{tot-CB,M}}}}}^{\exp }\), grey) at 3.4 MPM. d Comparison of the calculated metallic contribution at 3.0 MPM (\({I}_{{{{\rm{M}}}}}^{{{{\rm{calc}}}}}\), orange) with the experimental PE spectra of the isolated conduction band (\({I}_{{{{\rm{CB,M}}}}}^{\exp }\), grey) at 3.4 MPM. The shaded grey regions in all panels represent confidence intervals, estimated from the relative root mean square deviation (RMSD) between the fits and the scattered experimental data (details in Supplementary Note 4.1). The experimental data, obtained from ref. 5, were fitted using a free-electron gas model combined with a Gaussian function to account for solvated (di)electron peaks, as detailed in Supplementary Note 4.

Full size image

Let us now focus on the intermediate concentration of  ≈3 MPM. A direct comparison between theory and experiment is shown in Fig. 5b, where the time-averaged PE signal (grey) is plotted alongside the calculated DoS (green), averaged over the full 1 ps trajectory. While the binding energy ranges of the calculated and experimental spectra align reasonably well (with the Fermi edge in the experimental data exhibiting only a slight offset of approximately 0.1 eV relative to the calculated one, similarly to the situation observed for 11.1 MPM), their spectral intensity distributions differ significantly.

To further investigate this discrepancy, we decompose the time-averaged PE signal and the calculated DoS into their respective electrolyte and metallic components. This is done in two distinct ways for the experiment and calculation, respectively, as detailed below and shown in Fig. 5c, d.

In our previous experiments5, as well as in the present Supplementary Note 4, we applied a fitting procedure to the PE spectra accounting for the two phenomena present simultaneously, i.e., the solvated (di)electron peak representing the electrolyte and the conduction band and the plasmon spectral features pertinent to the metal. The (di)electron peak was modelled using a single Gaussian function, while the free-electron gas model was sufficient to describe the conduction band and plasmon features. This analysis enabled us to quantify the relative contributions of electrolyte and metallic states to the PE signal, providing a clear picture of a gradual electrolyte-to-metal transition (EMT) upon increasing alkali metal concentration5.

To decompose the computed total DoS into electrolyte-like and metallic components, we label each frame based on electron mobility (as shown in Fig. 2) and average the DoS over the two groups of frames separately, obtaining the two components. In Fig. 5c, the measured PE signal attributed to the solvated (di)electron peak is compared with the electrolyte-like component of the calculated DoS. The peak positions align well, taking into account the fact that the simulations do not account for certain broadening effects observed in the experiment, such as finite instrumental resolution. Next, in Fig. 5d, we compare the calculated DoS for metallic snapshots with the experimental PE signal corresponding to the metallic DoS derived from the fitting model. While both approaches provide a similar picture around the Fermi level (after arbitrarily scaling the experimental signal), the computed DoS also shows significant intensity at binding energies associated with (non-metallic) solvated (di)electrons. This discrepancy in the spectral width arises primarily from the fitting procedure used to decompose the experimental PE signal, which assumes a binary electronic structure, dividing the spectrum exclusively into contributions from localised solvated (di)electrons and delocalised conduction band electrons. Without additional information, this binary approach has been the only feasible way to interpret the experimental spectrum. However, the calculated DoS suggests a more nuanced picture. Namely, in the metallic snapshots, the excess electrons in the EMT concentration regime appear to have a mixed character—they retain to a significant degree properties of localised solvated (di)electrons while also exhibiting partial delocalisation, as evidenced by the finite DoS at the Fermi level.

The exact reasons for the deviation between the spectral intensity distributions of the time-averaged calculated DoS and the PE signal in Fig. 5b remain elusive. Differences in photoionisation cross sections or substantial variations in the angular distribution anisotropies of the emitted photoelectrons may contribute to this discrepancy. It may also be possible that the experimental setup probes solvated (di)electrons with higher sensitivity than delocalised conduction band electrons.

Conclusion

In conclusion, we have characterised and quantified the ultrafast flipping dynamics between metallic and electrolyte states in concentrated solutions of lithium in liquid ammonia. This allows us to provide, among others, the key missing characteristics of these systems, namely, the mean time interval between these flips, which turns out to be of the order of a few tens of femtoseconds. We show that the band gap is highly sensitive to minor changes in molecular geometry, which then drive switching between a liquid metal and an electrolyte. This can be understood from the fact that, as demonstrated by the present calculations, the densities of states of metallic configurations still, to a large extent, possess features pertinent to electrolyte configurations, with only a weak filling of the band gap.

To summarise, ab initio molecular dynamics simulations proved to be a powerful tool for following the flipping between a liquid metal and electrolyte with atomistic resolution at a femtosecond timescale. The validity of the computations has been supported by agreement between simulated and experimental photoelectron spectra of these systems. Direct measurements of the flipping phenomenon may prove difficult due to the ultrafast (femtosecond) timescale involved and the very small (nanometre) size of the metallic and electrolyte domains. Nevertheless, a feasible strategy to probe the flipping time indirectly may be a pump-probe experiment where one would follow the relaxation of the photoexcited (and thus electronically more delocalised) system back to equilibrium. In order to attain the temporal as well as the spatial resolution, ultrafast (attosecond) X-ray diffraction42—a technology that is now becoming within reach—is likely to be a game changer.

Methods

Initial force-field pre-equilibration

To generate structurally realistic ensemble samples for initialising ab initio molecular dynamics (AIMD), we first performed empirical force-field molecular dynamics (FFMD) simulations. We used the liquid-adapted force field for both ammonia and ions43 and conducted simulations with GROMACS44 following identical procedures across all systems:

  • Assembling the respective systems.

  • Running 5.0 ns canonical (NVT) ensemble simulations at 235 K to equilibrate each concentration. Four snapshots were then selected from each trajectory.

  • Conducting four additional 5.0 ns FFMD simulations for each snapshot under identical NVT conditions.

AIMD methodology

Further equilibration and production runs were performed using AIMD with VASP45,46,47,48 (version 6.3.2). We applied the revPBE38 hybrid functional21,22,23,24 with D3 dispersion corrections49, selectively disabling dispersion for Li+ cations50. Projector augmented-wave (PAW) pseudopotentials51,52 and a 400 eV kinetic energy cutoff were used.

Simulations were propagated with a 0.5 fs time step. Equilibration was conducted in the canonical ensemble at 235 K using a Langevin thermostat53 with a 50 fs time constant, followed by production runs in the microcanonical (NVE) ensemble. For each system, four independent trajectories were generated, consisting of 2 ps of equilibration followed by 3–5 ps of production per trajectory. The total production run durations for the 3.0, 6.0, 11.1, and 13.5 MPM systems were 19.70, 12.57, 13.53, and 13.97 ps, respectively.

Electronic structure calculations

We first performed DFT calculations using the revPBE functional to approximate the exchange-correlation energy. These calculations employed PAW potentials and a plane-wave basis set with a kinetic energy cutoff of 400 eV. The Brillouin zone was sampled using a 2 × 2 × 2 Monkhorst-Pack k-point mesh54, and Gaussian-type Fermi level smearing with a width of 0.075 eV was applied.

To refine the electronic structure, we conducted a follow-up DFT calculation using the hybrid revPBE38-D3 functional, which incorporates 37.5% exact exchange while maintaining the same computational settings as the initial GGA-based calculations. The revPBE38-D3 wave functions served as the basis for the density of states (DoS) analysis and transport property calculations.

For some selected calculations, we performed GW corrections on top of the revPBE38-D3 wave functions to achieve more accurate quasiparticle energies. Specifically, we applied the G0W0 (single-shot) method to obtain first-order corrections to the Kohn-Sham eigenvalues. These calculations were performed using a 2 × 2 × 2 k-point mesh with 2240 empty bands, corresponding to roughly four times the number of electrons in the simulation cell. Quasiparticle energies were evaluated for the 320 lowest bands, and the response function was computed with a 100 eV energy cutoff. The number of imaginary frequency and imaginary time grid points was set to 100, and a Gaussian-type Fermi level smearing with a width of 0.075 eV was applied.

To ensure statistical robustness and capture fluctuations in the electronic structure, we carried out a large number of calculations. For the analysis of DoS fluctuations in the 3.0, 6.0, 11.1, and 13.5 MPM systems, we sampled 500 different configurations per concentration, taken at 2-fs intervals. These samples were analysed using revPBE38-D3 on a 2 × 2 × 2 k-point mesh, covering a total of 1000 fs of trajectory per system. For each of the 500 sampled snapshots per concentration, transport properties were calculated.

In total, we performed 25 G0W0 calculations for benchmarking purposes. The majority of our analysis was conducted using revPBE38-D3, as it provided a well-balanced description of screening effects and charge localisation while maintaining consistency with the underlying AIMD trajectories. Additionally, revPBE38-D3 allowed us to sample a significantly larger number of configurations, enabling more comprehensive statistical analysis compared to the computationally demanding G0W0 method.

Transport properties

Thermoelectric properties were computed from either revPBE38-D3 DFT or G0W0 band energies using BoltzTraP240,41 within the rigid band approximation.

Excess electron density

Given that dielectrons (present at the studied concentrations) are spin-paired2,5, the spin density cannot be used to identify the excess charge distribution. Instead, we characterised the excess electron density using the squares of maximally localised Wannier functions obtained from revPBE38-D3 Γ-point calculations. These calculations were performed using WANNIER9055 (version 3.1.0) interfaced with VASP.

To investigate potential structural differences between metallic and electrolyte states, we extracted excess electron densities from 500 revPBE38-D3 Γ-point calculations for the 3.0 MPM system. These were sampled at 2-femtosecond intervals along the corresponding AIMD trajectory.

Interpolation of band eigenvalues

We used smooth Fourier interpolation (BoltzTraP240,41) to enhance the resolution of the DoS beyond the initial 2 × 2 × 2 k-point mesh.

Generation of the spherical band structures

The band structure of a material describes the relationship between the energy of electrons and their momentum. In crystalline solids, this relationship is typically represented by plotting energy bands E(k) along high-symmetry lines in the first Brillouin zone, a unit cell in momentum space. However, in disordered or liquid metals, the first Brillouin zone cannot be rigorously defined31,32,33,34. Instead, a spherical band structure (SBS) representation is used, where the electron energy is plotted as a function of the magnitude of the wave vector ∣k∣ in a spherically symmetric space. Such a representation provides not only insight into electron energy dispersion but also information about the extent of their (de)localisation in real space, as flat bands correspond to localised states.

To analyse electronic energy dispersion in disordered or liquid systems, we developed a specialised tool for generating SBSs. First, we computed orbital energies as a function of the wave-vector magnitude using either the revPBE38-D3 functional or the G0W0 method56,57. Our tool then employs a Fourier expansion of band energies, as implemented in Boltztrap240, to interpolate band structures across energy levels and k-points in 3D reciprocal space. Specifically, we generate SBSs by constructing band structures in spherical coordinates on a fine Γ-point centred k-point grid. We then interpolate the band structure from the original k-points to this spherical grid. By averaging over the angular variables and keeping only the radial one, we obtain a 2D representation of the electronic band dispersion as a function of the radial wavevector magnitude.

Experimental photoelectron spectra and fitting procedures

The acquisition of the measured photoelectron (PE) spectra shown in Fig. 5 was described in detail in the main text and the Supplementary Information of ref. 5. In Supplementary Note 4, we provide a detailed description of the fitting procedures applied to the PE spectra of lithium in liquid ammonia at four concentrations: 0.35, 0.97, 3.4, and 9.7 MPM. To account for the metallic spectral features, including the conduction band, Fermi edge, and plasmon peak, we employ a free-electron gas model. The spectral intensity of the solvated di-electron peak is modelled using a Gaussian function. This approach allows us to extend the data analysis in two key ways:

  • By decomposing the experimental data sets, enabling a more detailed comparison with the newly computed DoS.

  • By estimating confidence intervals5 through the calculation of relative root mean square deviations (RSMD) between the fits and the scattered experimental data.