Introduction

Topological states of materials have been one of the most remarkable research branches in condensed matter physics in the last decades, including the family of quantum Hall effect, topological insulators, semimetals, and superconductors1,2,3,4. According to unbroken or broken time-reversal symmetry, they can further be categorized into non-magnetic and magnetic topological phases (MTPs). Although classification and observation of non-MTPs are relatively mature5, studies of their magnetic counterparts so far are scarce6. Both theoretical prediction and experimental realization are more difficult for MTPs, partly because the long-range magnetism arising from electronic spin and orbit would further interact with the global topology depending on the symmetry or spin-orbit coupling. However, magnetic materials exhibit a more comprehensive range of topological phases since complete Shubnikov space groups consist of 1651 types, of which only 230 are non-magnetic as the type-II subgroups. In addition, magnetism offers tremendous potential possibilities for promoting information storage and quantum computation by manipulating topological states.

Actually, the very first MTP is the integer quantum Hall effect discovered in two-dimensional (2D) systems under strong external magnetic fields in 19801. The recent discovery of integer quantum anomalous Hall (QAH) material originating from its internal magnetism, inspired by the Haldane model, has significantly advanced the study of MTPs7,8. Experimental observations have also been made of its three-dimensional (3D) and fractional versions9,10. To date, although the classification of MTPs has become clear in theory6, their fabrication and measurement in electronic experiments remain challenging due to the interplay between the complex magnetic structure and topology. In particular, axion insulators (AXIs) represent a unique class of 3D MTPs with nontrivial \({{\mathbb{Z}}}_{4}\) phase protected by inversion symmetry11,12,13,14, manifesting amazing topological magneto-electric phenomena due to axion electrodynamics, e.g., quantized Faraday and Kerr rotation and half-integer surface Hall response3,15. However, its vital topological hallmark, i.e., higher-order 1D gapless hinge state with chiral spectral flow16,17, has yet to be observed in experiments.

In parallel, the classical-wave systems provide versatile platforms for studying the quantum Hall phenomena as well as topological physics, first introduced in 2008 and soon after realized based on magneto-optical materials18,19, giving rise to topological photonics20, topological mechanics21, and topological acoustics22. Most 2D and 3D non-magnetic topological and higher-order topological phases have successfully found their classical-wave analogs23,24,25,26,27,28,29,30, emerging application potentials in information communications and energy storage, such as robust topological lasers31, vortex cavities32, and light trapping33. Moreover, recent progress in the study of axion electrodynamic response34,35,36, anti-chiral states37, and 3D Chern vectors38 has employed various arrays of artificial magneto-optical components, further uncovering the flexibility of the photonic and electrical circuit platforms in exploring MTPs39,40, inspiring the construction of desirable photonic AXIs with more complex yet customizable magnetic structures.

Here, we realize the first photonic AXI using a bilayer square magnetic lattice. In neighboring layers, magneto-optical ferrites are arranged with opposite internal magnets to create antiferromagnetic-like structures, and two interlayer couplings are modulated to maintain inversion symmetry. We observe the gapless 1D chiral hinge states within the 3D bulk and 2D surface bandgaps, forming non-coplanar, non-reciprocal, and robust chiral hinge transport. This work underscores the interplay between the antiferromagnetic order and global topology, offering an unprecedented way to control electromagnetic waves.

Results

3D AXIs stacked from 2D

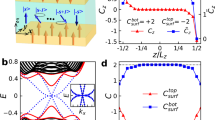
We start from the 2D single-layer QAH material hosting metallic 1D chiral edge states, depicted in Fig. 1a. Here, chirality refers to the in-plane energy flow direction respective to the out-of-plane magnetization. When reversing the magnetic fields associated with opposite topological invariant (Chern number), the chirality keeps, but the cyclic direction flips. For simplicity without losing generality, considering ferromagnetic arrays of identical polarity to form a 3D structure with weak interlayer coupling, the 1D chiral edge states extend along the stacking direction to become 2D gapless lateral surface states (Fig. 1b), behaving like the 3D quantum Hall effect. Instead of the scalar one, the Chern vector is introduced to characterize the topology, in which novel Hopf link of surface states could arise at the domain wall between perpendicular vectors38. Also, enlarging the interlayer coupling could turn it into the magnetic Weyl semimetal phase.

Fig. 1: From 2D to 3D magnetic structures.
figure 1

a 2D QAH effect with insulating bulk but conducting edge, characterized by Chern number (C). Reversing magnetization (M) flips the cyclic direction of edge energy flow. b 3D Chern vector from ferromagnetic stacking, characterized by Chern vector (C). Original 1D edge state expands to a 2D surface. c 3D AXI from antiferromagnetic stacking, characterized by \({{\mathbb{Z}}}_{4}\) topological invariant. The bulk and surface band structures open up a complete bandgap, wherein non-coplanar chiral hinge states exist. The gapless hinge state appears at the hinge formed by two surfaces with opposite signs of surface Dirac mass terms (m).

Full size image

Pictures are significantly different when antiferromagnetic arrays are adopted, as shown in Fig. 1c. Firstly, the lateral surface states will naturally open a bandgap due to the destruction of opposite cyclic energy flows between neighboring layers. Secondly, supposing an odd-layer scenario, intuitively, there always exists one net chiral cycle born of the single-layer QAH case, evenly distributed to the x/y-directional hinges of top and bottom facets. Thirdly, if the model further possesses inversion symmetry, the entirely closed rectangular loop is divided into two symmetric yet open halves. Finally, to ensure the eventual closure of the loop, two z-directional hinge states should be present, linking the separate halves. Consequently, the AXI appears, exhibiting non-coplanar chiral hinge states. From the view of topological hierarchy, AXIs may also relate to higher-order phases of 3D topological insulators, wherein the bandgap of Dirac surface states is opened by adding magnetic fields to break the time-reversal symmetry. These gapped surface states will then acquire finite Dirac masses, with the signs depending on the Berry curvature of the lower-energy surface band. Due to inversion symmetry, the mass terms for opposite surfaces have opposite signs. Those hinges formed by two surfaces with opposite signs of mass terms will give rise to gapless hinge states, as shown in Fig. 1c. The energy flow is clockwise around the positive surface Dirac mass region41.

3D photonic configuration of AXI

Our photonic design of the AXI is based on antiferromagnetic-like stacking of neighboring layers, as shown in Fig. 2a. Each layer consists of the simplest square lattice, effectively containing one magneto-optical yttrium iron garnet (YIG) rod at the center of the x-axis (y-axis) boundary inserted in dielectric foams, denoted as the A (B) layer. The interlayer is the metallic copper plate with 225° (45°) tilted T-shirt-like hollow holes around unit centers and circular holes at unit corners, which is elaborately designed to enlarge the directional interlayer coupling to obtain a relatively large bandgap. Magnets embedded in copper plates are placed on either end of YIG rods to provide magnetic biases, mimicking the internal magnetism of QAH material. Thus, by reversely placing the polarity of the inner magnets, one can conveniently tune the opposite magnetizations for YIG ferrites in A and B layers. The tetragonal lattice has lattice constant 15.5 mm in the x–y plane and periodicity of 10 mm along the z axis. Such an antiferromagnetic-like photonic structure possesses inversion symmetry \(\left\{-1|0\right\}\) (inversion center is located at the unit centre of A layer) and glide symmetry \(\left\{{M}_{\bar{1}10}|00(z/2)\right\}\), belonging to type-I magnetic space group P2/c (No.13.65).

Fig. 2: photonic design of 3D AXI.
figure 2

a 3D photonic configuration of antiferromagnetic-like structure. Ferrites in the A and B layers are in the presence of opposite magnetic bias. The AB and BA interlayers are inversion-symmetric. The periodicity in the x–y plane a = 15.5 mm, and height of each layer h = 5 mm. The structure parameters are h1 = 4 mm, h2 = 1 mm, r = 2.5 mm, r1 = 4 mm, r2 = 1 mm. b, Bulk band structure of the photonic AXI. The highlight regions denote the complete bandgap with nontrivial symmetry indicator. c Bulk Brillouin zone and simulated Bloch field distributions (z-component electric field) of two lower bands at eight high-symmetric points. The plus/minus markers indicate even/odd parity. d Measured forward and backward (S21 and S12) bulk transmission spectra along three principal axes.

Full size image

Band structures of the 3D photonic AXI host a complete bulk bandgap from 11 to 11.7 GHz, as shown in Fig. 2b. In calculations, the equal but opposite magnetic bias is set to be \(\pm\)1920 Oersted (Oe) for YIG rods in B and A layers, respectively. The copper plates are treated as perfect electrical conductors. Detailed parameters refer to Methods and Supplementary Fig. 1.

To analyze the topology, we mark the parity of the two lower-energy bands below the bandgap at high-symmetric points in the Brillouin zone (Fig. 2c). Bloch field distributions of electromagnetic waves in Fig. 2c indicate their even or odd symmetric fashion. These parity distributions reveal that such an inversion-symmetric 3D photonic insulator can be characterized by a \({{\mathbb{Z}}}_{4}\) topological invariant, which is defined by the even/odd parity (\({n}_{k}^{+}\)/\({n}_{k}^{-}\)) of occupied states at eight inversion-invariant momenta42,43.

$${{\mathbb{Z}}}_{4}={\sum }_{k=1}^{8}\frac{{n}_{k}^{+}-{n}_{k}^{-}}{2}\, {\mathrm{mod}}\,4$$
(1)

For the centrosymmetric insulators of class A, the complete symmetry indicators read as (\({{\mathbb{Z}}}_{2}\))3×\({{\mathbb{Z}}}_{4}\), where (\({{\mathbb{Z}}}_{2}\))3 component is related to the topology of three distinct surfaces and can be chosen as the weak indices of 3D topological insulators44. Therefore, the nontrivial indicator is (0, 0, 0; 2), classifying our case into AXI phase. Experimentally measured bulk transmission spectra along three principal axes further confirm the existence of the bandgap (Fig. 2d). Slight weak transmission may result from the flat z-directional bands via stacking configuration, which could be improved by enlarging interlayer couplings. Forward and backward bulk propagations are nearly reciprocal due to zero net magnetic field.

1D chiral hinge states

To map out 1D chiral hinge states of the photonic AXI, we label all twelve hinges of an odd-layer (e.g., 15-layer) tetragonal-lattice sample from 1 to 12. As shown in Fig. 3a, hinges 1-6 are chiral ones (C1-C6), while hinges 7-12 are trivial ones (T7-T12) in this odd-layer scenario. Such odd-layer configuration perfectly maintains the inversion symmetry, even in the presence of surface and hinge configurations, such as triple-layer ABA stacking. Eventually, six 1D hinges C1-C6 form a closed chiral loop. Each surface exhibits a half-turn of a closed chiral loop. The opposing surfaces combine to create a full turn, representing the nontrivial axion angle \(\theta=\pi\)45.

Fig. 3: Chiral hinge states of odd-layer photonic AXI.
figure 3

a Schematic of chiral hinge transport and its projections on different planes. Both the bottom and top layers are A-layer. Blue (green) arrow lines indicate energy flow along the positive (negative) directions of axes. All twelve hinges are labeled, i.e., C1-C6 chiral hinges and T7-T12 trivial hinges in this case. b Calculated projected band structures. Blue and green dots represent the corresponding chiral hinges. Black dots denote the projected bulk and surface states (shadow regions). c Measured dispersions of hinge states. Color scale represents the intensity. White dashed lines enclose the frequency window of the complete bulk and surface bandgap. For comparison, under the same color bar, the trivial hinge states (lower panels) are enlarged twice or thirty times (white numbers), corresponding to their chiral counterparts.

Full size image

The numerically calculated hinge states are shown in Fig. 3b. The blue and green dots in each panel belong to diagonal hinges of two separate surfaces, different from coplanar edge states in either 2D quantum anomalous or quantum spin Hall materials. Such a pair of hinge states relates to each other under inversion symmetry, with the energy flowing along or facing the principal axis. For example, the negative slope of hinge dispersion of C4 suggests the wave propagating along the negative x direction, and vice versa for its counterpart hinge C1. The trivial hinges are gapped.

The shared complete bandgap frequency window for chiral hinge states is 11–11.4 GHz, with ~3.6% relative bandwidth. The experimentally measured hinge dispersions, as color scale shown in Fig. 3c, are in good agreement with the theoretical results (blue and green dots). Hinges C1-C6 behave in gapless yet one-way chiral manners, shaping in a non-coplanar closed chiral loop. Meanwhile, no observable states for hinges T7-T12 are found in the bandgap region. The corresponding transmission spectra are measured for twelve hinges as well to demonstrate their non-reciprocal characters (See Supplementary Fig. 2).

To get a momentum resolution of less than 0.1\(\pi\), we experimentally probe 21 periods along each direction in three divided samples to save materials (See “Methods” and Supplementary Fig. 3). It also should be noticed that the lateral surfaces are slightly modified here to increase the complete bandgap, benefiting the measurements of chiral hinge states (See Supplementary Figs. 4–5). The bandgap width for the z-axis chiral hinge states (C3 and C6) shrinks slightly due to the influence of trivial hinge states (right panel of Fig. 3b), which could be removed after further boundary decoration (See Supplementary Fig. 6). We also numerically calculate the surface Dirac masses and related surface Chern numbers for our photonic AXI (See Supplementary Fig. 7), agreeing with those in Fig. 1c.

Non-coplanar chiral hinge transport

Figure 4a shows the simulated hinge transport along the C6-C1-C2 route at the frequency of 11.2 GHz, excited at the V6 vertex, where the frontal (100) and bottom (001) planes are set to be absorptive surfaces to suppress the other three chiral hinge states. Although such a compact photonic AXI only contains 5 periods in x-y plane and 11 layers along z-axis (the same as Fig. 2a), we can unambiguously observe the non-coplanar hinge transport. The electromagnetic fields are mainly localized around the hinge.

Fig. 4: Non-coplanar and non-reciprocal hinge transport.
figure 4

a Simulated chiral hinge transport along \({{\rm{C}}}6\)-C1-C2 route at the frequency of 11.2 GHz, using the V6 vertex excitation. All eight vertices are labeled from V1 to V8. The frontal (100) and bottom (001) facets are absorptive, while the copper plates cover the others. b Measured transmission spectra at V1–V3 and V8 vertices. Highlight regions denote the complete bandgap. c The case of C3-C4-C5 chiral route, using the V3 vertex excitation. The back (100) and top (001) facets are absorptive. d Transmission spectra at V4–V7 vertices.

Full size image

We detect the forward and backward transmission spectra at four corners of the top (001) facet (Fig. 4b) in experiment (See Supplementary Fig. 8 for experimental sample). Since the chiral route crosses V1–V3 vertices, we can observe the high-efficient and non-reciprocal transport within the complete bandgap. But for the V8 vertex outside of the chiral route, both S21 and S12 parameters remain at low values. The case for hinge transport along the C3-C4-C5 route is displayed in Fig. 4c, d, showing the similar non-coplanar and non-reciprocal hinge transport.

In experiments, the frequency window for chiral hinge states is much broader than the complete bandgap. The non-reciprocal hinge transmission still works from 10.3 to 11.4 GHz (Fig. 4b, d), which has ~10% relative bandwidth, also coinciding with the dispersions measured in directional bandgaps shown in Fig. 3c. Besides the inevitably intrinsic loss, the gradually weakening S21 parameters (V1–V3 and V4–V6) are possibly attributed to the finite size. The electromagnetic waves could be scattered into the surface or bulk when meeting corners. We also verify that our non-coplanar chiral hinge transport is robust against various defects (See Supplementary Fig. 9). The experimental results for closed loop route of chiral hinge transport refer to Supplementary Fig. 10.

Tunability of chiral hinge states

The hinge states may exhibit varying performance in the even-layer scenario. In this case, the rigorous inversion symmetry for hinges is absent after considering boundaries, e.g., bilayer AB stacking. However, the rotation symmetry \(\left\{{2}_{\bar{1}10}|00(z/2)\right\}\) is restored. Since the even-layer (e.g., 14-layer) configuration can be regarded as the removal of just one top layer from the odd-layer (e.g., 15-layer) case, the lateral and bottom chiral hinge states (C3-C6) remain unchanged as those in Fig. 3, while the surface Dirac mass term of the top facet now becomes negative \(({m}_{001} \, < \, 0)\). Under the restriction of rotation symmetry, hinges 7 and 8 become chiral hinges (relative to C5 and C4), while hinges 1 and 2 return trivial ones (relative to T11 and T10) at the current case (Fig. 5a).

Fig. 5: Even-layer scenario.
figure 5

a Schematic of chiral transport in the 14-layer case. The top (bottom) layer is B-layer (A-layer). Hinges 7-8 are chiral (C7-C8), while hinges 1-2 are trivial (T1-T2). b Measured hinge dispersions (color scale). The bandgaps are delineated by white dashed lines.

Full size image

The corresponding hinge dispersions of the top facet for a 14-layer photonic sample are measured in experiments (Fig. 5b), and they agree well with the above analysis and calculated results. If we add an additional B layer up to the bottom, it recasts to the odd-layer photonic AXI case, but with the BAB configuration different from those in Fig. 3a, equivalent to flip magnetic fields. Then, the chiral loop changes to be C6-C8-C7-C3-C11-C10. In all the cases mentioned above, hinges C3 and C6, restricted by the mirror plane of the glide symmetry, are kept unchanged. Their wave flow directions can still be reversed when exchanging AB and BA interlayers. Moreover, we could also tune hinges T9 and T12 (C3 and C6) into chiral (trivial) by rotating the T-shirt-like hollow holes in Fig. 2a.

Discussion

It is worth mentioning that despite the use of the non-dispersive permeability of YIG and the identical internal magnetic field in calculations, the experimental measurements coincide pretty well with the numerical results. This also indicates the superior robustness of our photonic AXI. Such AXI protected by the \({{\mathbb{Z}}}_{4}\) topological invariant exhibits a unique non-coplanar closed chiral loop for hinge transport, which is different from the 3D higher-order Chern insulator protected by Wannier-based Chern numbers with coplanar chiral hinge transport on the lateral surfaces40. It should be noticed that the nonreciprocal z-directional hinge states under the same z-directional magnetization cannot occur from the traditional picture of orbital bounding in topologically trivial cases. The underlying physics can be explained by the xy-plane fictitious magnetic field induced by the nontrivial Berry curvature, resulting from the simultaneous breaking of time-reversal symmetry and mirror symmetry in our antiferromagnetic-like structure (See Supplementary Figs. 11 and 12). This phenomenon is similar to the in-plane magnetization-induced Hall effect observed in electronic systems46,47. Compact photonic AXIs without magnets can be expected if self-biased ferrites are utilized instead of YIG materials48,49. Although the demonstrated photonic AXI with only about a dozen layers would yield discrete states, which may not be a rigorous 3D structure, it could perfectly match some few-layer situations of 2D electronic materials14.

In conclusion, based on artificially antiferromagnetic-like arrays in a 3D photonic crystal, we realize the photonic AXI, directly observing the robust and non-coplanar chiral routing for its 1D hinges. Our results provide a deeper understanding of AXIs, highlighting the relationship among the 2D QAH, 3D quantum Hall, and higher-order magnetic topological insulators, underscoring the intricate interplay between symmetry, magnetism, and topology42. The observed non-coplanar chiral hinge transport may facilitate photonic communications, microwave isolators, and circulators. Such a versatile photonic platform is ready to be extended to construct various ferromagnetic-, ferrimagnetic-, (non-coplanar) antiferromagnetic-like, and even canted structures50,51, offering enormous potential to address a myriad of theoretically predicted but experimentally challenging MTPs.

Methods

Numerical simulation

All band structures and field distributions are numerically simulated by a commercial software, COMSOL (RF Module), based on the finite-element method. We use periodic boundary conditions along all axes to calculate the bulk band structures in Fig. 2b. Supercell configurations are used to calculate projected band structures and chiral hinge states in Figs. 3b and 5b. In order to keep the same as the experimental samples in Supplementary Fig. 3, 5a\({{\boldsymbol{\times }}}\)15 h, 5a\({{\boldsymbol{\times }}}\)15 h, and 5a\({{\boldsymbol{\times }}}\)5a supercells in the xz, yz, and xy planes are chosen to calculate ky-, kx-, and kz-hinge states in Fig. 3b, where the corresponding axis is periodic boundary condition while the other surfaces are perfect electrical conductors. For even-layer case in Fig. 5b, 14-layer sample along the z axis is set. To simulate chiral hinge transport in Figs. 4a, 5a\({{\boldsymbol{\times }}}\)5a\({{\boldsymbol{\times }}}\)11 h sample is chosen. The experimental samples are shown in Supplementary Fig. 8.

The relative permeability tensor of the YIG magneto-optical material takes the form

$${{{\boldsymbol{\mu }}}}^{\leftrightarrow}=\left[\begin{array}{ccc}\mu & i\kappa & 0\\ -i\kappa & \mu & 0\\ 0 & 0 & 1\end{array}\right],$$
(2)

where \(\mu=1+\frac{{{{\omega }}}_{{{m}}}({{{\omega }}}_{{{0}}}+{{i}}{{\alpha }}{{\omega }})}{{({{{\omega }}}_{{{0}}}+{{i}}{{\alpha }}{{\omega }})}^{{{2}}}-{{{\omega }}}^{{{2}}}}\), \(\kappa=\frac{{{{\omega }}}_{{{m}}}{{\omega }}}{{({{{\omega }}}_{{{0}}}+{{i}}{{\alpha }}{{\omega }})}^{{{2}}}-{{{\omega }}}^{{{2}}}}\), \({\omega }_{m}=\gamma 4\pi {M}_{s}\), \({\omega }_{0}=\gamma H\). The measured saturation magnetization is \(4\pi {M}_{s}=1820\) Gauss (see Supplementary Fig. 1b), and the magnetic bias is chosen to be \(H=\pm 1920\) Oe along the z direction for YIG ferrites in B and A layers. Gyromagnetic ratio is \(\gamma=1.76\times {10}^{11}\) C/kg. The small damping coefficient \(\alpha=0.004\) (relative to the resonance loss width of 15 Oe) was omitted. In numerical simulations, the operating frequency is set to be \(\omega /2\pi=11.2\) GHz (at the mid-gap frequency of chiral hinge states), corresponding to \(\mu=0.72\) and \(|\kappa |=0.59\). The relative permittivity of YIG is 15. The relative permittivity of the dielectric foam is 1.05. The T-shirt-like hollow holes of copper plates and through holes are air. In the design of the axion insulator, the T-shirt-like hollow holes in one (the other) half of the AB (BA) interlayer provide a relatively large Mz-symmetry-breaking effect, and they are tilted 225°/45° to enlarge the directional interlayer coupling between YIG rods of neighboring layers (along the [\(11\bar{1}\)] direction).

Although we use the non-dispersive permeability parameters and uniform magnetic bias in calculations, the numerical results match well with experimental measurements. The dispersive \(\mu\) and \(\kappa\) at different operating frequencies and internal magnetic fields, associated the width of bandgaps, are given in Supplementary Fig. 1.

Tight-binding models

To qualitatively analyze the gyromagnetic photonic system, we consider a stacked bilayer square lattice with four atoms per unit cell. In each layer, the atoms are connected with the C4-rotation-symmetric next nearest neighbor hopping \({{{t}}}_{{{1}}}\) and the nearest neighbor hopping \({{{t}}}_{{{2}}}{{{e}}}^{{\varphi }}\) (See Supplementary Fig. 13a for detail). The nonzero phase \({{\varphi }}\) breaks the time-reversal symmetry and can be considered as a result from periodic magnetic fields without net flux through our antiferromagnetic-like unit cell. In different layers, both vertical (\({t}_{3}\)) and crossed interlayer hopping (\({t}_{4}\) and \({t}_{5}\)) represent the tilted T-shirt-like AB (BA) interlayer couplings. Such interlayer hopping breaks both the C4 rotation and mirror symmetries but maintains the inversion symmetry.

The corresponding 4-band Hamiltonian can be written as

$$H({{\bf{k}}})={f}_{1}{\sigma }_{z}+{f}_{2}{\sigma }_{x}+{f}_{3}{\sigma }_{y}{\tau }_{z}+{f}_{4}{\tau }_{x}+{f}_{5}\frac{{\sigma }_{x}+i{\sigma }_{y}}{2}{\tau }_{x}+{f}_{6}\frac{{\sigma }_{x}-i{\sigma }_{y}}{2}{\tau }_{x},$$
(3)

where the Pauli matrix \({\sigma }_{{{x}},{{y}},{{z}}}\) and \({\tau }_{{{x}},{{y}},{{z}}}\) acts on sublattice and layer degree of freedom, respectively. The other coefficients are \({{f}}_{1}=-2{{t}}_{1}[\cos ({{k}}_{{{x}}})-\,\cos ({{k}}_{{{y}}})]\), \({{f}}_{2}=4{{t}}_{2}\,\cos ({{k}}_{{{x}}}/2)cos({{k}}_{{{y}}}/2)cos({\varphi })\), \({{f}}_{3}=4{{t}}_{2}\,\sin ({{k}}_{{{x}}}/2)sin({{k}}_{{{y}}}/2)sin({\varphi })\), \({{f}}_{4}=2{{t}}_{3}\,\cos ({{k}}_{{{z}}}/2)\), \({{f}}_{5}=2{{t}}_{5}\,\cos ({{k}}_{{{z}}}/2+{{k}}_{{{x}}}/2-{{k}}_{{{y}}}/2)\), and \({{f}}_{6}=2{{t}}_{4}\,\cos ({{k}}_{{{z}}}/2+{{k}}_{{{y}}}/2-{{k}}_{{{x}}}/2)\). The theoretical bulk band structure and the corresponding parity of Bloch states of the eight inversion-invariant momentum are shown in Supplementary Fig. 13b, showing the same topological nature characterized by \({{\mathbb{Z}}}_{{{4}}}\) = 2.

In addition to the nearest coupling, long-range interactions between non-neighboring unit cells are inevitable in electromagnetic systems30. We theoretically investigate the influence of long-range interactions on the axion insulator phase. Even under a relatively large long-range interaction, the \({{\mathbb{Z}}}_{{{4}}}\) topology associated with gapless hinge states remains intact (Supplementary Fig. 14).

Experimental measurement

The experimental samples are fabricated layer by layer. In each layer, both ends of YIG rods are attracted by opposite magnets embedded in hollow copper plates. The dielectric foam is used to fix the positions of YIG rods and support the whole 3D structure. The circular through holes (radius r2) in the sample allow us to insert the detector to measure the internal electric fields of the sample. In microwave experiments, we use a vector network analyzer (Keysight N5224B) to excite and record the electromagnetic waves. The bulk transmission spectra in Fig. 2d are measured with propagation distances 12a, 12a, and 8 h along the y, x, and z directions, respectively, where both source and probe antenna are inserted in the sample.

For the measurement of chiral hinge dispersions, to get a better resolution, e.g., 0.1\({{\pi }}\) in momentum space, we need to scan the electric fields and phases for more than 20 periods in geometry space. Taking into account the additional influence of the couple in and out efficiency, the total sample size may reach to 23a\({{\boldsymbol{\times }}}\)23a\({{\boldsymbol{\times }}}\)46 h, requiring more than 20,000 YIG rods and double the number of magnets. To save materials and facilitate measurements, we fabricate three divided samples in experiments, i.e., 5a\({{\boldsymbol{\times }}}\)23a\({{\boldsymbol{\times }}}\)15 h, 23a\({{\boldsymbol{\times }}}\)5a\({{\boldsymbol{\times }}}\)15 h, and 5a\({{\boldsymbol{\times }}}\)5a\({{\boldsymbol{\times }}}\)46 h, to get ky-, kx-, and kz-hinge dispersions in Fig. 3b, respectively, in which the field can still be well localized around the hinges. Further considering the inversion or rotation symmetry, ~1800 YIG rods are enough for a single independent experimental set-up. For even-layer case in Fig. 5b,  5a\({{\boldsymbol{\times }}}\)23a\({{\boldsymbol{\times }}}\)14 h and 23a\({{\boldsymbol{\times }}}\)5a\({{\boldsymbol{\times }}}\)14 h samples are chosen. We probe 21 periods along each direction in experiments. The corresponding photographs of samples are shown in Supplementary Fig. 3.

In the realistic system, both non-radiative and radiative losses are very small, and their influence on the hinge states is negligible (Supplementary Fig. 15). We also simulated that the continuous increase of loss could tune the chiral route (radiative loss) or give rise to the phase transition (non-radiative loss), as shown in Supplementary Figs. 16–18.