Introduction

Energy storage dielectric capacitors are core components of high/pulsed power electronic devices, widely applied in fields such as hybrid electric vehicles, smart grids, and microwave communications, owing to their high-power density, ultrafast charge/discharge rates, and excellent reliability1,2,3,4,5,6,7. The primary parameters for evaluating energy storage performance of dielectric capacitors are recoverable energy density Ue and efficiency η, which are derived from the polarization-electric field (P-E) hysteresis loop by: \({U}_{{{\rm{e}}}}={\int }_{{P}_{{{\rm{r}}}}}^{{P}_{{{\rm{m}}}}}E{{\rm{d}}}P\), η = [Ue/(Ue + Uloss)] × 100% (Supplementary Fig. 1). Here, Pm and Pr represent maximum polarization and remnant polarization, respectively; Uloss refers to the energy loss caused by leakage or hysteresis, corresponding to the area inside the P-E loop (Supplementary Fig. 1). Therefore, achieving a large Pm, a small Pr, and a high breakdown field strength Eb is critical for optimizing both Ue and η. To quantitatively assess the balance between Ue and η, a figure of merit, UF = Ue/(1 − η) with an unit of J cm−3, is often employed3,8, where a higher value indicates better performance.

On the other hand, emerging technologies in extreme environments, including aerospace systems, nuclear energy, accelerator science, and radiation therapy technologies (e.g., nuclear imaging, radiotherapy, etc.)9,10,11, demand dielectric capacitors that can withstand increasingly harsh operational conditions. A growing area of research addresses this challenge by studying the positive and negative effects of radiation on dielectric energy storage materials. Recent studies have shown that low-dose radiation (e.g., ion6, electron12, ultraviolet13, and γ-ray14) can improve Ue in dielectrics, by inducing favorable defect complex, reducing leakage currents, and modifying defect structures. However, this positive effect often diminishes when exposed to high-doses radiation, which may attribute to the high density defect accumulation, structural degradation, and increased leakage currents. Consequently, a critical challenge is to understand the mechanisms of radiation-induced degradation and to develop novel strategies for designing higher-radiation-tolerant dielectric capacitors. Until now, there has been limited report on this aspect. It is particularly worth mentioning that γ-ray irradiation is the most wide radiation source existing in extreme environments15. Furthermore, commercially available dielectric capacitors suffer from relatively low energy storage density16 and poor radiation tolerance (e.g., BOPP <10 Mrad)17,18, restricting their potential for miniaturization and integration into advanced nanoelectronics in extreme environments. To address these challenges, it is imperative to develop next-generation dielectric capacitors that offer not only enhanced energy storage performance but also superior radiation resistance.

Ferroelectric (FE) oxide materials, such as BaTiO3, BiFeO3, and PbZrxTi1-xO3, are one of attractive candidates for energy storage applications in radiation environments19,20, owing to their large Pm and high radiation resistance. In previous reports, nanoelectronic devices based on these FE oxides, including ferroelectric random access memory21,22 and piezoelectric sensors23,24, have demonstrated resistance to radiation doses up to 10 Mrad10,11,14,22,25. However, FE oxides typically exhibit large Pr and low Eb, limiting their energy storage performance. Various strategies have been explored to overcome these limitations, such as domain engineering2,3,26, artificial heterostructures7,27,28,29,30,31, and defect design6,32. Despite these progresses, current strategies still face challenges, particularly the sacrificed Pm at their Eb. More than this, it should be emphasized that research on FE oxide-based capacitors targeting radiation-hardened energy storage systems remains largely unexplored.

Recently, nanocomposite materials with dendritic structure, featuring branching patterns and extensive interface regions, have been reported to effectively tailor a wide range of functionalities including conductivity33, catalytic activity34,35, and mechanical stability36, benefiting from microscopic heterogeneities, interfacial bandgap/strain matching, specific crystallographic orientations, and extensive interface areas37,38. Thus, we propose that incorporating dendritic-like structure into FE-dielectric oxide nanocomposites may offer a promising approach to enhancing both dielectric energy performance and radiation resistance. In this configuration, the abundant tilted FE-dielectric interfaces can simultaneously reduce Pr and introduce relaxor properties by the formation of polar nano-regions (PNRs)39,40,41, maintain Pm by preserving polar region connectivity, and enhance Eb by increasing electrical breakdown tortuosity. More importantly, these interfaces are well-established “defect sinks” that can absorb and annihilate radiation-induced defects42,43, such as oxygen vacancies and interstitial atoms, thereby significantly improving radiation resistance42,43,44,45. Therefore, in this work, we design high-performance film capacitors starting from introducing a dendritic-like nano-polar (DNP) microstructure into self-assembled nanocomposite films composed of representative FE and dielectric/insulating materials, such as PbZr0.53Ti0.47O3 (PZT) and MgO. PZT as the FE is chosen for its versatile phase structure46, offering design flexibility for optimizing energy storage properties, while MgO as the insulator, with its wide bandgap (~ 7.8 eV)47, effectively enhances breakdown strength compared to other insulators like ZnO (~ 3.4 eV)48 and TiO2 (~ 3.5 eV)49. By using this strategy, we achieve an ultrahigh energy density (217.8 J cm−3), high efficiency (78%), remarkable radiation resistance (tolerating doses over 20 Mrad), excellent reliability (sustaining up to 1010 cycles), and impressive temperature stability (maintaining performance from −100 °C to 170 °C).

Results

Theoretical analyses of energy storage performance and self-healing mechanism

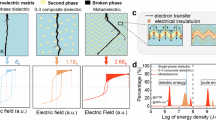
To evaluate the effectiveness of the DNP design in enhancing energy storage performance, we first conducted phase-field simulations to examine the dielectric breakdown and polarization switching processes for both plain PZT film and PZT-MgO (PM) film with DNP structures. The simulated PM film, consisting of a 50% PZT molar fraction, was generated by a simple dendritic crystal growth model50 (Supplementary Fig. 2a). From the breakdown dynamics (Fig. 1a and Supplementary Fig. 3), we observed that the tortuous breakdown paths in the PM film split and diffuse at the interfaces between PZT and MgO phases, resulting in notably more complex pathways compared to the plain PZT film. Furthermore, the breakdown process in the PM film progresses more slowly (Supplementary Fig. 3), contributing to the enhancing Eb observed in subsequent experiments. In addition, the superior Eb of the PM film is also attributed to the disparity in bandgap values between PZT (ranging from 3.4 eV to 3.5 eV)51,52 and MgO (7.8 eV)47, which creates energy level mismatches at the interfaces, forming deep energy traps that hinder charge transport. These traps, combined with the ultralow leakage current (discussed later), reduce thermal stress and further prevent electric breakdown. The corresponding P-E loops for plain PZT and PM films under their acceptable applied electric fields are shown in Fig. 1b. The plain PZT film exbibits a typical squared P-E loop, characterized by noticeable hysteresis loss and high Pr at a relatively low electric field. By contrast, the P-E loop for the PM film is significantly slimmer, while maintaining high Pm at a higher electric field. Consequently, high energy storage density (indicated by the shaded areas of Fig. 1b) and efficiency can be achieved simultaneously in the PM films.

Fig. 1: Design of self-assembled nanocomposite FEs with enhanced energy storage performance and radiation resistance.
figure 1

a, b Comparative display of breakdown paths and P-E loops for plain PZT and PM films, respectively. c Phase-field simulated local polarization distributions at various points in the P-E loop for the PM film, with arrows indicating the magnitude and directions of polarization at each site. The area shown is 18 nm × 18 nm. d Phase-field simulated energy density (top) and efficiency (down) of PM films as a function of PZT molar fractions at an electric field of 1 MV cm−1. e Schematic illustration of possible self-healing evolution modes for conventional single FE material (left panel) and dendritic-like FE/dielectric nanocomposites with a high density of phase boundaries (right panel).

Full size image

To understand the origin of large Ue in the PM films, we presented the evolution of local polarization configurations at different points in the P-E loop (Fig. 1c and Supplementary Fig. 2b). It should be noted that we incorporated charged point defects with certain concentration in the vicinity of the boundaries between the two phases, as such oxide nanocomposite film structures inevitably introduce numerous defects53,54,55,56 (see Methods for detail). Initially (Panel 1, no electric field), the domain patterns appear disordered due to the present of boundaries and defects. Because of depolarization fields and gradient energy, the polarizations near these boundaries tend to align parallel to them. Meanwhile, the electric fields generated by charged defects cause the polarizations to orient towards or away from the defect sites, resulting in a pinning effect. When subjected to a large electric field (Panel 2), the polarizations generally align along the field direction, though they are still influenced by the boundaries and defects, particularly these nearby. Comparing Panel 1 and Panel 2, we found that the overall domain patterns remain largely unchanged. As the electric field decreased (Panel 3 to 4), the pinned dipoles gradually return to their original states, thereby allowing the domain structures to revert to their initial configurations, which induces a small Pr and thus a large Ue. For comparison, we also simulated the same conditions for plain PZT film (Supplementary Fig. 4). In this case, the domain structure is permanently altered by the electric field, leading to a high Pr. In addition, we observed vortex-like domain structures in the PM film, as depicted by dashed rectangles in Fig. 1c. These domain patterns can be stabilized by the constraints imposed by defects and boundaries. Upon increasing and reducing the electric field, antiparallel domains disappear and then reappear, contributing to the antiferroelectric-like behavior observed in the P-E loop (Fig. 1b, right panel).

We further investigated the energy storage performance of the PM films across varying PZT fractions to identify the optimal composition (Fig. 1d). The plain PZT film, as anticipated, exhibits low Ue and η due to its squared P-E loop (Supplementary Fig. 4). Upon the incorporation of MgO, dendritic-like structures emerge (Supplementary Fig. 2), which introduce progressively more tortuous interfaces and enhanced pinning effects, leading to a significant reduction in Pr. Consequently, this enhances both Ue and η. However, when the PZT molar fraction drops below 50%, although Pr remains minimal, the excessive MgO content substantially diminishes Pm, resulting in a decline in Ue. Therefore, we found that high Ue values can be achieved with PZT molar fractions ranging from 45% to 60%, while η becomes sufficiently high for fractions above 50%. These simulation results suggest that the optimal PZT molar fraction for enhanced energy storage performance may be around 50%.

Regarding the radiation resistance, radiation-induced degradation of FE properties is typically attributed to atom-displacement events and ionization effects, both of which are caused by increased defect concentrations57,58. Thus, the ability of a material to resist radiation damage is closely linked to the effectiveness of its microstructure in mitigating radiation-induced defects43. Grain boundaries and interphase interfaces have long been recognized as effective sinks for various types of defects43. For clarity in subsequent discussions, we use phase boundaries (PBs) to denote the interfaces between PZT and MgO. In single FE materials with limited domain walls (Fig. 1e, left panel), interstitial atoms migrate rapidly to the material surface, leaving vacancies within the lattice. These point defects can self-order and aggregate, forming obstacles to dislocation motion and leading to material hardening as well as a decline in overall properties43. By contrast, the DNP-structured PM films (Fig. 1e, right panel) feature a high density of PBs and domain walls, thereby positioning lattice atoms in close proximity to these interfaces. PBs are considered as the representative internal interfaces, while domain walls within the PZT phase may also contribute to the self-healing. These PBs can capture radiation-induced interstitial defects and subsequently release them back into lattice vacancies. Consequently, most vacancies can be restored to a healed crystal state within the annihilation range of these PBs, significantly enhancing radiation resistance of the DNP-structured PM films.

Fabrication and energy storage performance of dendritic-like self-assembled FE-dielectric nanocomposite film

Guided by phase-field simulations, we fabricated plain PZT film and a series of PZTx-MgO1−x (PM, x = 0.65, 0.5, and 0.35 representing the PZT molar fraction) nanocomposite film with a thickness of ~100 nm on SrRuO3 (SRO)-buffered (001) SrTiO3 (STO) single-crystalline substrates by pulsed laser deposition. High-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) images and X-ray diffraction (XRD) analysis demonstrate the formation of a distinct separation between PZT (light parts) and MgO (dark parts) phases in PM films. And the desired dendritic-like nanocomposite structure was successfully achieved in PM film with x = 0.5 (Supplementary Fig. 5). Energy-dispersive X-ray spectroscopy mapping (Supplementary Fig. 6) further revealed a uniform distribution of chemical elements, with a well-matched elemental ratio of Pb:Zr:Ti:Mg ≈ 1:0.53:0.47:1 in the PM film with x = 0.5 (Supplementary Table 1). The PZT exhibits a slightly reduction in lattice parameter of c/a after the incorporation of MgO (Supplementary Table 2), which may contribute to its relaxor behavior and, consequently, enhance its energy storage performance. For ease of discussion, “P50M50” is used to denote PM film with x = 0.5.

The dielectric permittivity of plain PZT and P50M50 film was measured as a function of temperature at a frequency of 100 kHz (Supplementary Fig. 7). For plain PZT film, the maximal-permittivity temperature Tm (phase-transition Curie temperature for typical FE) is ~ 355 °C, consistent with previous report59. Upon MgO incorporation, we observed a substantial decrease in Tm and a more diffused phase-transition peak, indicating enhanced relaxor properties induced by PNRs in the P50M50 film. This was further quantified by an increase in the relaxor diffuseness factor γ (derived from modified Cuire-Weiss law, Supplementary Fig. 7c, d) from 1.05 (for plain PZT film, similar to an ideal FE) to 1.88 (for the P50M50 film, similar to an ideal relaxor FE), with notably suppressed dielectric loss tangent over a wide range of temperature (from 25 °C to 400 °C) (Supplementary Fig. 7b)4,5.

We then measured the P-E loops, a widely used method for evaluating the energy storage performance, of plain PZT film (1.0 MV cm−1, nearly approaching its breakdown field) and P50M50 film (4.0 MV cm−1) at a frequency of 1 kHz (Supplementary Fig. 8). The PZT film exhibits a typical square-shaped hysteresis with a large Pm of 67.1 μC cm−2 and a high Pr of 45.9 μC cm−2, consistent with previous report60, resulting in low Ue of 7.8 J cm−3 and η of 36.5% (Supplementary Fig. 8a). By contrast, the P50M50 film display relaxor-type slimmer P-E loops with a high Pm of 75.3 μC cm−2 and a remarkably low Pr of 6.5 μC cm−2, resulting in a substantial Pm–Pr of 68.8 μC cm−2. This large Pm–Pr value yields a high Ue of 99.0 J cm−3, while simultaneously preserving an η of 78.2%, thereby indicating excellent energy storage performance (Supplementary Fig. 8b). The higher Pm in P50M50 film compared to PZT film is due to its significantly higher tolerance to de applied electric field. We also observed an obvious antiferroelectric-like phenomenon in the P-E loops near zero electric field in P50M50 film (Supplementary Fig. 8b), which may be linked to Mg2+ diffusion between MgO and PZT phases61 and vortex-like domains, likely contributing to the improved energy storage performance, as discussed earlier in Fig. 1c. Overall, the P50M50 film, characterized by dendritic-like nanocomposite structure, demonstrates a significant enhancement in energy storage performance, which is attributed to its strong relaxor feature, high maximum polarization, and low remanent polarization. The relaxor behavior stems arises from the disordered rhombohedral and tetragonal nanodomains in PZT phase with size of 1 ~ 3 nm (Supplementary Fig. 9), which result from the disruption of long-range ferroelectric order in PZT phase by spatially distributed MgO phase and local lattice distortion caused by slight Mg²⁺ diffusion at MgO/PZT interfaces, leading to weakened domain intercoupling and reduced energy barriers for domain switching2,3. Furthermore, the smaller nanodomain size increases the number of domain walls, which, along with PBs, will benefit the film’s radiation resistance. In addition, the energy storage performance of the P50M50 film exhibits excellent frequency stability with variation less than 3% (Supplementary Fig. 10). Overall, the P50M50 film with an optimized 100 nm thickness was selected for radiation resistance investigation due to its combined large Ue, high η, and high tolerance for electric field (Supplementary Fig. 8).

Radiation resistance in dendrite-like self-assembled FE-dielectric nanocomposite film

To assess the radiation resistance of the P50M50 films, we exposed them to a 60Co gamma source radiation at doses of 0, 5, 10, 20, and 40 Mrad (equivalent Si dose) with a dose rate of ~0.801 Mrad(Si)/h. After exposure, XRD θ-2θ scans and X-ray reciprocal space maps show no observable shifts in the peak positions of PZT and MgO (Supplementary Figs. 11 and 12), indicating the robustness of crystal structure against radiation. We then measured P-E loops of the P50M50 films before and after radiation at an electric field of 4 MV cm−1 to characterize the polarization and energy storage performance (Fig. 2a). The variations in Pm, Pr, and Pm − Pr values as a function of radiation doses are summarized in Fig. 2b. Notably, from 0 Mrad to 20 Mrad, Pm changes slightly (less than 2%), while Pr decreased significantly by 31%, resulting in an increased Pm − Pr of 70.0 μC cm−2 for the 20 Mrad-irradiated P50M50 film. By contrast, when the dose is further increased to 40 Mrad, Pm decreases by 6%, Pr drops by 33.7%, and Pm − Pr decreases to 64.8 μC cm−2. We also observed a subtle rightward shift in the P-E loops from 5 Mrad to 40 Mrad (Fig. 2a), which is the primary factor contributing to the reduction of Pr. This shift and the degradation in polarization are likely attributed to the domain pinning effect induced by gamma-ray radiation.

Fig. 2: Ferroelectric and energy storage properties under different radiation doses.
figure 2

a P-E loops measured at 4.0 MV cm–1 and 1 kHz. b Variations of Pm, Pr, and Pm-Pr. c Comparison of energy density, efficiency, and UF derived from (a). d Leakage current densities as a function of the applied electric field.

Full size image

The energy storage performance of the radiated P50M50 films was further assessed from their P-E loops (Fig. 2c). The pristine P50M50 film (i.e., 0 Mrad) shows a Ue of 99.0 J cm−3, an η of 78%, and a high UF of 450. As the radiation dose increases to 10 Mrad, the P50M50 film exhibits a slightly improved energy storage performance, with Ue rising to 100.8 J cm−3, η remaining at 78%, and UF to 458. This increase in Ue is attributed to the increased Pm, a common phenomenon observed in FE oxides upon exposure to low-dose radiation11, likely due to the charging of internal interfaces induced by ionizing effect, thus neutralizing pre-existing internal bias within films. Particularly, thanks to the abundant PBs characteristics, the radiation threshold for this “low dose” effect has been significantly increased from 2 Mrad, as reported in previous literature11, to 20 Mrad in this work. At 20 Mrad, the P50M50 film still exhibits excellent energy storage performance, with Ue of 96.0 J cm−3, η of 77%, and UF of 417, comparable to the pristine P50M50 film (i.e., 0 Mrad). At 40 Mrad, however, the energy storage performance deteriorates significantly, with Ue dropping to 85.8 J cm−3, η to 69%, and UF to 276.7. This decline is attributed to the significant decrease in Pm from 76.2 μC cm−2 (20 Mrad) to 70.6 μC cm−2 (40 Mrad) (Fig. 2b) and the increase in leakage current from 5.3 × 10−6 A cm−2 (0 Mrad) to 1.2 × 10−5 A cm−2 (40 Mrad) (Fig. 2d). The increased leakage current at 40 Mrad is ascribed to the space-charge-limited conduction under high electric fields (Supplementary Fig. 13). In addition, the slight asymmetric leakage current at 40 Mrad may be attributed to the internal electric field caused by the accumulation of radiation-induced defects at electrode interfaces, which may affect charge transport differently under positive and negative bias. Therefore, as the radiation dose increases, Ue exhibits a trend of slight increase (≤ 10 Mrad) followed by a decrease (> 20 Mrad).

The mechanism of radiation effects on energy storage performance

Radiation-induced defects, including interstitial atoms and vacancies (most typically oxygen vacancies) from displacement effects and electron-hole pairs from ionizing effects, as well as their interactions, are the main factors contributing to the degradation of polarization switching in FE oxides62,63. As discussed earlier in Fig. 1e, PBs can act as sinks for these defects, healing vacancies to a healthy lattice and thereby enhancing the film’s radiation resistance. To better understand the mechanisms of high radiation tolerance (≤ 20 Mrad) and degradation (40 Mrad) in macroscopic energy storage performance in the P50M50 films, we conducted detailed microstructure characterizations using PFM and STEM measurements (Fig. 3 and Supplementary Fig. 14). As shown in Fig. 3a and Supplementary Fig. 14a, the pristine P50M50 film (i.e., 0 Mrad) exhibits a homogeneous surface with a uniform typical FE switching butterfly shape in amplitude-voltage loops and nearly 180° reversal in phase-voltage loops across the tested 3 × 3 matrix (Fig. 3b and Supplementary Fig. 15). Such homogeneous surface remains stable even at radiation doses up to 10 Mrad (Supplementary Fig. 14c), ensuring its robust stability in energy storage performance. This stability may be attributed to the strong self-healing ability of the P50M50 film with DNP structure, which can effectively repair most radiation-induced defects. At a radiation dose of 20 Mrad, while most defects are restored to a healthy state, minor residual defects begin to accumulate and self-order near the film surface (Supplementary Fig. 14d), slightly hindering domain wall motion. Nevertheless, this effect is not significant enough to impact large-scale domain wall motion or the macroscopic performance, as confirmed by the results at radiation doses ≤ 20 Mrad (Fig. 2).

Fig. 3: Microstructure analysis.
figure 3

AFM images with a range of 2 × 2 μm (a, c), local amplitude and phase hysteresis loops from (a, c) selected area (b, d), HAADF-STEM images (e, g), inverse Fast Fourier-filtered (FFT) images (f, h), and Mg intensity line profiles across PZT/MgO boundaries (i, j) for 0 Mrad and 40 Mrad irradiated P50M50 films, respectively.

Full size image

However, at 40 Mrad, numerous defect clusters appear on the film surface (highlighted by pink circles in Fig. 3c and Supplementary Fig. 14e). Compared to the non-clustered regions (represented by blue circles in Fig. 3c), these clustered regions (represented by pink circles, such as domain 2 in Fig. 3c) exhibit a decreased piezoelectric response by approximately 60% and non-180° reversal (Fig. 3d and Supplementary Fig. 16), which eventually leads to the obvious degradation in the macroscopic energy storage performance (Fig. 2). Defects and dislocations are inevitable during the fabrication of complex oxide films53,55,64, and the pre-existing dislocations were identified at PBs in the pristine P50M50 film (i.e., 0 Mrad, Fig. 3e, f). After irradiated by an ultrahigh dose (40 Mrad), a large population of mobile defects cannot be healed back to a healthy state, accumulating and self-ordering at PBs and film surface, ultimately resulting in additional misfit dislocations at PBs (Fig. 3g, h) and clusters on the film surface (Fig. 3c). In addition, ionization effects generate a large number of electron-hole pairs11, migrating to PBs and film surface, where they are trapped by dislocations beneath PBs. This trapping creates an internal bias, inducing domain pinning effect as observed in Fig. 3d, which explains the rightward shift of P-E loops and the attenuation of Pm in the 40 Mrad-irradiated P50M50 film (Fig. 2a). These findings suggest that the degradation in macroscopic energy storage performance at 40 Mrad may originate from the domain pinning effects induced by radiation. This align with previous studies on radiation-induced degradation of domain wall motion in FE oxide films22,65. Moreover, compared to the pristine P50M50 film (i.e., 0 Mrad, Fig. 3i), the P50M50 film exposed to 40 Mrad shows an increased diffusion of Mg2+ across PBs (Fig. 3j), which may further strengthen the domain pinning effect.

Radiation effects on comprehensively energy storage performance

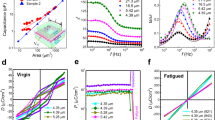
To comprehensively explore the radiation effects on the energy storage performance of the P50M50 films, we assessed their statistical breakdown strengths Eb using Weibull distribution fitting (Fig. 4a). The pristine P50M50 film (i.e., 0 Mrad) exhibits an ultrahigh Eb of 7.1 MV cm−1, surpassing those of most existing state-of-the-art dielectric oxide films3,4,5,6,7,27, such as 5.3 MV cm−1 in Sm-BiFeO3-BaTiO3 films3, 5.6 MV cm−1 in MoS2/BaTiO3/MoS2 heterostructures7, 5.9 MV cm−1 in ion-irradiated Pb(Mg1/3Nb2/3)O3-PbTiO3 films6, 6.35 MV cm−1 in (Bi3.25La0.75)(Ti3−3xZrxHfxSnx)O12 films4, and 7.0 MV cm−1 in Bi(Mg0.5Ti0.5)O3-SrTiO3 films27. After exposure to 20 Mrad, the P50M50 film still maintains an Eb of 6.8 MV cm−1, comparable to that of the pristine P50M50 film. At 40 Mrad, however, Eb decreases to 6.5 MV cm−1, accompanied by a diminished β value to 11.7, suggesting a reduction in the reliability of Eb data.

Fig. 4: Energy storage performance under radiation exposure.
figure 4

a Weibull distribution analysis of characteristic breakdown fields. b Energy density and efficiency at electric fields up to their Eb. c Comparison of energy density of the P50M50 films with the state-of-the-art dielectric films. d Charging-discharging reliability of energy storage performance at an electric field of 4 MV cm−1. e Temperature dependence of energy storage performances at an electric field of 4 MV cm−1 over a temperature range from −100 °C to 170 °C. f Discharge energy density as a function of time measured at different electric fields.

Full size image

We then evaluated Ue and η from the bipolar P-E loops at electric fields up to their respective Eb and at a frequency of 1 kHz (Fig. 4b and Supplementary Fig. 17). The pristine P50M50 film (i.e., 0 Mrad) achieves an exceptional Ue of 217.8 J cm−3, η of ~ 78%, and UF of 990, owing to the large Pm − Pr (90.7 μC cm−2) and ultrahigh Eb (7.1 MV cm−1). These values outperform the best lead-free and lead-based dielectric oxide films (Fig. 4c)2,3,4,5,6,14,27,29,66,67. After exposure to 20 Mrad, the P50M50 film still retains an excellent energy storage performance with Ue of 197.8 μC cm−2, η of 76.1%, and UF of 828, maintaining competitive (Fig. 4c). By contrast, at 40 Mrad, marked reductions in both Ue (156.9 μC cm−2), η (68.8%), and UF (503) are observed due to the reduced Pm − Pr and Eb, and the increased leakage current (Fig. 2).

For practical dielectric capacitor applications, we further evaluated the reliability and temperature stability of the P50M50 films by varying radiation doses (Fig. 4d, e and Supplementary Figs. 18 and 19). A triangle electric field of 4 MV cm−1 was applied during accelerated charge-discharge tests. We found that the P50M50 film exhibits robust reliability against fatigue with radiation doses up to 20 Mrad. For instance, compared to the pristine P50M50 film (i.e., 0 Mrad, ΔUe ≤ 8%, Δη ≤ 8%), the 20 Mrad-irradiated film sustains over 1010 cycles, with minimal degradation of Ue (ΔUe ≤ 8.9%) and η (Δη ≤ 3.6%) (Fig. 4d). By contrast, at 40 Mrad, a sharp decline is observed in both Ue (ΔUe ~ 34%) and η (Δη ~ 22%) after 3 × 105 cycles (Supplementary Fig. 20a), likely due to the high density of radiation-induced defects including oxygen vacancies, interstitial atoms, and their clusters9,20,22 (Fig. 3c, h, and j). In addition, we noticed that the antiferroelectric-like behavior gradually disappeared in the 40 Mrad irradiated P50M50 film (Supplementary Fig. 18e), which may be caused by cumulative irradiation damage during fatigue cycling. This damage disrupts the vortex-like domains, thereby destabilizing the antiferroelectric dipolar ordering.

In addition, the P50M50 films also demonstrate exceptional thermal stability, with slight variations from 0 Mrad (ΔUe ≤ 3.1%, Δη ≤ 2%) to 20 Mrad (ΔUe ≤ 4.5%, Δη ≤ 5%) across a broad temperature range from −100 °C to 170 °C (Fig. 4e). The remarkable thermal stability is attributed to the robust relaxor properties, i.e., the dielectric permittivity remains unaffected by temperature variations, even at radiation dose of 20 Mrad (Supplementary Fig. 21). This superior thermal stability enables the P50M50 film to function normally even under multiple harsh conditions such as high radiation and high temperature. However, at 40 Mrad, the P50M50 film shows a relatively lower Ue from −100 °C to 130 °C and undergoes breakdown at temperatures exceeding 130 °C (Supplementary Fig. 20b). We also measured the overdamped discharge at 4 MV cm−1 with a load resistor of 10 kΩ (Supplementary Fig. 22). An ultrahigh discharge energy density (Wd) and a fast discharge rate (τ0.9) are obtained at both 0 Mrad (Wd ~ 95.2 J cm−3, τ0.9 ~ 3.4 μs) and 20 Mrad (Wd ~ 93.6 J cm−3, τ0.9 ~ 3.4 μs) (Fig. 4f). These results, together with ultrahigh energy storage performance and radiation tolerance (over 20 Mrad), excellent temperature stability (−100 to 170 °C), and reliability (over 1010 cycles), highlight the promising charge-discharge performance of the P50M50 film in radiation environments, making it a potential candidate for pulsed-power applications, particularly under extreme conditions.

Discussion

In summary, we proposed a DNP structure in self-assembled FE-dielectric nanocomposite films, incorporating numerous phase boundaries and domain walls, to simultaneously enhance both energy storage performance and radiation resistance. The DNP structure-designed film capacitors achieve an ultrahigh energy density of 217.8 J cm−3 and an efficiency of 78%. More importantly, the phase boundaries and domain walls within the films effectively improve the radiation tolerance, temperature stability, and reliability, making them suitable for applications in spacecraft and satellite power systems, portable medical pulsed power systems, and harsh-environment industrial electronics. This work provides a strategy for developing high-performance and radiation-resistant energy storage capacitors. Future work should extend our DNP strategy to other lead-free ferroelectric-insulator composites, such as BiFeO3-based, BaTiO3-based, and HfO2-ZrO2 binary oxides68,69, to develop environmentally friendly energy storage devices.

Methods

Fabrication of the film

High-quality PbZr0.53Ti0.47O3 (PZT) and (PbZr0.53Ti0.47O3)0.5–MgO0.5 (P50M50) thin films were grown on (001) SrRuO3 (SRO) buffered SrTiO3 (STO) substrates by pulsed laser deposition with a KrF laser (λ = 248 nm) under 4 Hz and 1.23 J cm−2. Prior to the growth of PZT and P50M50 layer, the SRO buffer layer was deposited at a substrate temperature of 630 °C under an oxygen partial pressure of 0.15 mbar. The PZT and P50M50 films were fabricated by the growth temperature of 510 °C and the oxygen pressure of 0.15 mbar, and then annealed for 20 min under the same temperature and oxygen pressure before being cooled down to room temperature. Sputtered Pt top electrodes with an area of 1.962 × 10−5 cm2 were used for electrical measurement.

The P50M50 films were adhered to a Printed Circuit Board and then exposed to 60Co-gamma radiation with doses of 5, 10, 20, and 40 Mrad(Si) at a rate of 0.801 Mrad(Si)/h. The incident direction of γ-ray was set to 90° from the film surface using an open circuit state for devices during the radiation. High vacuum condition was used to store all films after γ-ray irradiation.

Structural characterizations

The crystal structures and surface morphologies of the films were analyzed by high-resolution four-circle XRD (Panalytical Empyrean, Kα radiation, λ = 1.5405 Å) and atomic force microscopy (AFM, Asylum Research MFP-3D), respectively.

Physical properties characterizations

Radiant Precision materials analyzer was used for ferroelectric hysteresis loops, current-voltage curves, and fatigue endurance measurements. The dielectric and piezoresponse force microscopy (PFM) measurements were conducted by an Impedance Analyzer (EA990A) and Asylum Research MFP-3D origin with an HVA 220 high-voltage amplifier, respectively.

Scanning transmission electron microscopy

Cross-sectional TEM specimens oriented along the [100]pc direction were prepared by an focused ion beam system (FEI Versa3D) with 30 kV Ga ions, followed by a low-voltage cleaning step. STEM studies were performed using a double aberration-corrected STEM (Thermo Fisher Scientific Spectra 300) equipped with a cold-field emission gun and Cs CETCOR/S-CORR double correctors operated at 300 kV. The HAADF-STEM images were obtained using an estimated probe current of 27 pA. The convergence and collection semi-angles were 25 and 49–200 mrad. The positions of the Pb and Ti (Zr) atomic columns were precisely determined using an iterative center-of-mass peak finding method. These coordinates were then used to calculate the cationic displacements of Ti⁴⁺ (Zr⁴⁺) relative to the centers of the nearest neighboring Pb²⁺ ions.

Phase-field simulation for dielectric breakdown

To simulate the dielectric breakdown process, we utilized a phase-field model that introduces a continuous variable η(r, t) to characterize the breakdown phase70. In this model, η = 1 indicates the broken regions, η = 0 indicates the non-broken regions, and 0 < η < 1 represents the interface between two phases. The total free energy, including the phase separation term fsepa, the gradient term fgrad, and the electrostatic term felec, can be written as

$$F={\int }_{V}({f}_{{{\rm{sepa}}}}+{f}_{{{\rm{grad}}}}+{f}_{{{\rm{elec}}}}){{\rm{d}}}V.$$
(1)

The phase separation energy density is described by a double-well function,

$${f}_{{{\rm{sepa}}}}=\alpha {\eta }^{2}{(1-\eta )}^{2},$$
(2)

where α is a positive coefficient.

The gradient energy density is defined by

$${f}_{{{\rm{grad}}}}=\frac{1}{2}\gamma |\nabla \eta {|}^{2},$$
(3)

where γ is the gradient energy coefficient.

The electrostatic energy density is expressed as

$${f}_{{{\rm{elec}}}}=-\frac{1}{2}{\varepsilon }_{0}{\varepsilon }_{r}{E}_{i}{E}_{i},$$
(4)

where ε0 is the vacuum dielectric constant, εr is the position-dependent relative dielectric constant, and Ei is the electric field which can be calculated by a spectral iterative perturbation method71. The Einstein notation is used.

To model the evolution of the dielectric breakdown process, a modified Allen-Cahn equation is used,

$$\frac{\partial \eta ({{\bf{r}}},t)}{\partial t}=-{L}_{0}H(|{f}_{{{\rm{elec}}}}|-|{f}_{{{\rm{crit}}}}|)\frac{{{\rm{\delta }}}F}{{{\rm{\delta }}}\eta ({{\bf{r}}},t)},$$
(5)

where L0 is the kinetic coefficient, \({f}_{{{\rm{crit}}}}=1/2{\varepsilon }_{0}{\varepsilon }_{r}{E}_{{{\rm{b}}}}^{2}\) is a position-dependent constant indicating the maximal energy endurance with Eb as the position-related breakdown strength, and \(H(|{f}_{{{\rm{elec}}}}|-|{f}_{{{\rm{crit}}}}|)\) is the Heaviside unit step function with \(H(|{f}_{{{\rm{elec}}}}|-|{f}_{{{\rm{crit}}}}| > 0)=1\) and \(H(|{f}_{{{\rm{elec}}}}|-|{f}_{{{\rm{crit}}}}| < 0)=0\).

In our simulations, α = 108 J m−3, γ = 10−10 J m−1, and L0 = 1/(t0α) with t0 as the characteristic time scale. The broken PM film is considered as a mixture of PZT, MgO, and broken regions. The position dependent εr = 101, 103, and 105 for MgO, PZT, and broken regions, respectively. The position dependent Eb = 10 MV cm−1 and 1.5 MV cm−1 for MgO and PZT regions, respectively. The whole system grid is 200∆x × 1∆x × 200∆x with ∆x = 0.4 nm.

Phase-field simulation for polarization evolution

To simulate the polarization evolution of plain PZT and PM films, we employed a phase-field model where the polarization vector Pi (i = 1, 2, 3) was chosen as the order parameter. The total free energy, including the Landau free energy term fLand, the gradient energy term fgrad, the elastic energy term felas, and the electrostatic energy term felec, is expressed as72

$$F={\int }_{V}({f}_{{{\rm{Land}}}}+{f}_{{{\rm{grad}}}}+{f}_{{{\rm{elas}}}}+{f}_{{{\rm{elec}}}}){{\rm{d}}}V.$$
(6)

The Landau free energy density is

$${f}_{{{\rm{Land}}}}= {\alpha }_{1}({P}_{1}^{2}+{P}_{2}^{2}+{P}_{3}^{2})+{\alpha }_{11}({P}_{1}^{4}+{P}_{2}^{4}+{P}_{3}^{4})\\ +{\alpha }_{12}({P}_{1}^{2}{P}_{2}^{2}+{P}_{2}^{2}{P}_{3}^{2}+{P}_{3}^{2}{P}_{1}^{2})+{\alpha }_{111}({P}_{1}^{6}+{P}_{2}^{6}+{P}_{3}^{6})\\ +{\alpha }_{12}[{P}_{1}^{2}({P}_{2}^{4}+{P}_{3}^{4})+{P}_{2}^{2}({P}_{3}^{4}+{P}_{1}^{4})+{P}_{3}^{2}({P}_{1}^{4}+{P}_{2}^{4})]\\ +{\alpha }_{123}{P}_{1}^{2}{P}_{2}^{2}{P}_{3}^{2},$$
(7)

where α1, α11, α12, α111, α112, and α123 are the Landau polynomial coefficients.

The gradient energy density is

$${f}_{{{\rm{grad}}}}= \frac{1}{2}{G}_{11}({P}_{1,1}^{2}+{P}_{2,2}^{2}+{P}_{3,3}^{2})+{G}_{12}({P}_{1,1}{P}_{2,2}+{P}_{2,2}{P}_{3,3}+{P}_{3,3}{P}_{1,1}) \\ +\frac{1}{2}{G}_{44}[{({P}_{1,2}+{P}_{2,1})}^{2}+{({P}_{2,3}+{P}_{3,2})}^{2}+{({P}_{3,1}+{P}_{1,3})}^{2}] \\ +\frac{1}{2}G{{{{{\mbox{'}}}}}}_{44}[{({P}_{1,2}-{P}_{2,1})}^{2}+{({P}_{2,3}-{P}_{3,2})}^{2}+{({P}_{3,1}-{P}_{1,3})}^{2}],$$
(8)

where G11, G12, G44, and G′44 are the gradient energy density coefficients, and Pi,j denotes ∂Pi / ∂xj with xj as the spatial coordinate.

The elastic energy density is

$${f}_{{{\rm{elas}}}}=\frac{1}{2}{c}_{ijkl}({\varepsilon }_{ij}-{\varepsilon }_{ij}^{0})({\varepsilon }_{kl}-{\varepsilon }_{kl}^{0}),$$
(9)

where cijkl is the elastic stiffness tensor, εij is the total strain, and ε0ij = QijklPkPl is the eigenstrain with Qijkl as the electrostrictive coefficients. The Einstein notation is used.

The electrostatic energy density is

$${f}_{{{\rm{elec}}}}=-{E}_{i}{P}_{i}-\frac{1}{2}{\varepsilon }_{0}{\kappa }_{{{\rm{b}}}}{E}_{i}{E}_{i},$$
(10)

where Ei = −∂φ/∂xi is the electric field with φ as the electrostatic potential, ε0 is the permittivity of vacuum, and κb is the background relative dielectric constant.

The temporal evolution of order parameters was simulated by the time-dependent Ginzburg-Landau equations using the semi-implicit Fourier spectral method73

$$\frac{\partial {P}_{i}}{\partial t}=-{L}_{P}\frac{{{\rm{\delta }}}F}{{{\rm{\delta }}}P},$$
(11)

where LP is the kinetic coefficient. For each time step, the elastic and electric driving forces were calculated by solving the mechanical equilibrium equations σij,j = 0 and the electrostatic equilibrium equation Di,i = 0, where σij = cijkl (εij–ε0ij) is the local stress and Di = ε0κbEi + Pi is the electric displacement.

The PM systems can be considered as a mixture of PZT regions, MgO regions, and boundary regions, distinguished by the coefficients. For PZT, according to previous literatures74,75, α1 = 1.583 × 105 × (T − 657) C−2m2N with T = 300 (in Kelvin) as the ambient temperature, α11 = 6.680 × 107 C−4m6N, α12 = 1.944 × 108 C−4m6N, α111 = 1.660 × 108 C−6m10N, α112 = 7.576 × 108 C−6m10N, α123 = −3.570 × 109 C−6m10N, c11 = 154 GPa, c12 = 84 GPa, c44 = 35 GPa, and κb = 40. For MgO, α1 = 5.650 × 109 C−2m2N, α11 = α12 = α111 = α112 = α123 = 0, c11 = 293 GPa, c12 = 92 GPa, c44 = 155 GPa, and κb = 10. For boundaries between PZT and MgO, the coefficients are the average of these of PZT and MgO. The spectral iterative perturbation method is used71. Meanwhile, for the gradient energy density coefficients, G11 = 0.6G110, G12 = 0, and G44 = G′44 = 0.3G110, where G110 = 5.658 × 10−11 C−2m4N. For the electrostrictive coefficients, Q11 = 0.09080 C−2m4, Q12 = −0.04158 C−2m4, Q44 = 0.07741 C−2m4.

The whole system grid is 500∆x × 1∆x × 400∆x with ∆x = 0.4 nm, including 100 layers for substrate and 260 layers for the PM film, as illustrated in Supplementary Fig. 2a. The film boundary conditions were solved by a superposition method76,77. The closed-circuit electric boundary conditions were adopted.

To simulate the pinning effect of defects, we randomly added point charges in the boundary regions. The charges obey a normal distribution of mean μ = ± 5.0 × 109 C/m3 (~2 e/u.c.) and standard deviation σ = 0.1μ.