Introduction

Optical setups have been established as leading simulation platforms for curved space: An analogy can be made between Fermat’s principle and geodesic motion in curved space as the refractive index has a similar role in light propagation as the metric tensor1,2. This analogy has been used extensively to emulate gravitational effects for light in tabletop optical experiments by employing transformation optics and metamaterials3,4,5,6,7 to simulate, for example, gravitational lensing8,9, curved-space settings10,11, and various well-known solution of Einstein’s equations of general relativity (GR)12,13. Although nonlinear metamaterials exist4, in simulation experiments the analogue metric was traditionally pre-designed, thus emulating merely the linear aspect of curved space.

In 2015 a nonlinear optical experiment14 emulated the nonlinear nature of gravity or self-gravitation. By utilizing a long-ranged nonlocal nonlinearity this experiment simulated the Newton–Schrödinger equation (NSE), a phenomenological model aimed to unify quantum mechanics and Newtonian gravity15,16,17,18. This set of equations, which can give insight into the long-standing puzzle posed by the unification of GR and quantum mechanics, had been studied merely in theory up to that point15,18,19,20,21,22,23,24,25,26. The first optical simulation of the NSE model14 was soon followed by simulations of various physical systems, such as boson-star dynamics, by utilizing a similar nonlinearity mechanism27,28.

An intriguing perspective is to simulate non-stationary and higher-order terms in the NSE, as it will enable the experimental study of the quantum nature of gravity, and the simulation of phenomena that remain inaccessible in the regime of Newtonian gravity. For example, frame-dragging, gravitational waves and compact binary inspirals29,30,31. Additionally, the numerical simulations of post Newtonian (PN) gravity is challenging due to time complexity and new phenomena may be more easily revealed in a simulation experiment. To obtain these PN corrections in an optical system, we must introduce additional nonlinear terms to our model, which are relevant only for sufficiently large beam intensity.

Here, We experimentally demonstrate self-gravity simulations in the post-Newtonian gravity regime. We do this by launching a high-intensity laser beams to interact within this nonlocal nonlinear material, which means that higher-order non-linearites become non-negligible in our material. Specifically, we identify a one-to-one mathematical mapping between the stationary post-Newton Schrödinger equation and the equations describing the evolution of light in a specific thermal nonlinear medium. We find that for very high-power beams and specific nonlinear terms the exact analogy occurs. Therefore, for an experiment designed with the right parameter the optical-beam evolution observed is analogous to a wavefunction obeying the nonlinear Schrödinger equation, with a post-Newtonian gravitational potential.

We find, both experimentally in the analogue optical system and numerically, solitons of this system that are distinct and distinguishable from the previously observed Newtonian solitons. In this never-explored territory of this nonlocal nonlinear system, we observe rich beam evolution, including beam splitting and evolution into doughnut-shaped beams that occur due to higher-order corrections to the refractive index.

Results

The simulation system utilizes the mathematical analogy between the Schrödinger equation in two transverse dimensions and time (i.e., 2D + 1) and the paraxial equation in optics. In our experiments the optical beam propagates within a nonlinear medium with long-range nonlinearity that is essential for simulations of gravity. This long-range nonlinearity stems from Coulomb-like interactions, which is traditionally referred to as an infinite-range nonlinearity in optics, in contrast to the local Kerr nonlinearity (see schematics in Fig. 1 and Eq. (4b))32,33,34,35. In order to obtain this we use a medium that has an optical thermal nonlinear effect36. As a laser beam is propagating through the nonlinear medium14 it is slightly absorbed in it, acting as a heat source, and for steady-state conditions the temperature change obeys Poisson’s equation. While previous work14 assumed a linear relation between the temperature change (ΔT) and the refractive-index deviation (Δn) from the linear refractive index n0, here we experiment with higher-power beams (beyond 2 W) and expect this assumption to break. In our system we observe a repulsive higher-order term which we model as:

$$\Delta n={\gamma }_{1}\Delta T+{\gamma }_{2}\Delta {T}^{2}$$
(1)

where γi define the relation between the change of refractive index and the change of temperature, and ΔT ≡ ΔT[ψ] is the change of temperature due to the intensity of ψ. In our experiment, ΔT reaches values of above 10 K, and γ2 < 0, which means that the higher-order correction of the refractive index is repulsive. The high-intensity beams discussed below are beams that fulfill the condition \(\frac{{\gamma }_{2}}{{\gamma }_{1}}\Delta T \sim 1\). That is, the next-order term affects the dynamics in a measurable way. To our knowledge this is the first work addressing a nonlocal effect of this type, where previously nonlocal repulsive perturbation was only studied theoretically, and for models that does not satisfy our gravity analogy37,38,39,40,41. We assume paraxial propagation (\(k| \frac{\partial \psi }{\partial z}| \gg | \frac{{\partial }^{2}\psi }{\partial {z}^{2}}|\)), where ψ is a slowly varying amplitude of the electromagnetic field (with wavenumber k), and steady-state conditions, \(\frac{\partial \Delta T}{\partial t}=0\). We write the coupled equations that describe the nonlinear dynamics in the material:

$$i\frac{\partial \psi }{\partial z}+\frac{1}{2k}{\nabla }_{\perp }^{2}\psi+\frac{k\Delta n}{{n}_{0}}\psi=0$$
(2a)
$${\nabla }^{2}\Delta T=-\frac{\alpha }{\kappa }| \psi {| }^{2}$$
(2b)

where κ is the thermal conductivity, and α is the linear absorption coefficient of the material. The dependency of Δn on ΔT is given by Eq. (1). For the case of Δn = γ1ΔT the refractive-index change obeys a Poisson’s equation (i.e γ1 = 14 ⋅ 10−6, γ2 = 0 as in ref. 14). However, in our experimental system the additional term in Eq. (1) is significant, leading to simulation experiments of a modified equation, rather than Poisson’s equation. This is exactly what enables us to go beyond Newtonian simulations, as Δn is the equivalent of the gravitational potential in our system, as we described in detail below. We now consider the analogy of post-Newtonian effects in our simulation system with γ2 < 0 in Eq. (1). In general, the post-Newtonian equations are derived by considering additional orders of a small energy scale \(\frac{G{M}^{2}}{r}\) in the metric tensor gμν (where G is the gravitational constant, and M, r being typical values of mass and displacement). Specifically for stationary and almost stationary solutions, the corrections appear only in the temporal term of the metric g0031:

$${g}_{00}^{PN}=-1-2\phi -2{\phi }^{2}-2\Psi$$
(3)

where ϕ is the Newtonian gravitational potential and Ψ is a PN correction that stems from the gravitational effects of velocity, pressure, internal energy, etc.31. The effect of Ψ has been shown to be negligible as long as the dynamics is near equilibrium and the energy does not drastically affect the dynamics42. We therefore set Ψ = 0. To capture the dynamics of wavefunctions under PN gravity, we add a PN gravitational potential to the Schrödinger equations, similar to ref. 15. Derivations of the equations is done either by applying canonical quantization to a classical PN hamiltonian42 or by taking the non-relativistic limit of the Klein–Gordon equation43. Analogously to the introduction of the NSE, we combine the Schrödinger equation with a Post-Newtonian potential term taken from the first order relativistic correction to Newtonian gravity31 to obtain the following set of equations, for which, a mass distribution is defined by the wavefunction:

$$i\hslash \frac{\partial \psi }{\partial t}+\frac{{\hslash }^{2}}{2m}{\nabla }_{\perp }^{2}\psi -mV\psi=0$$
(4a)
$${\nabla }_{\perp }^{2}\phi=4\pi Gm| \psi {| }^{2}$$
(4b)
$$V=\phi+{\gamma }_{PN}{\phi }^{2}$$
(4c)

where ϕ is the two-dimensional (2D) Newtonian gravitational potential that solves Eq. (4b) for a mass source that is linear to the wavefunction’s probability distribution (∣ψ∣2). V is the gravitational potential17,44 and γPN = 2 for GR.

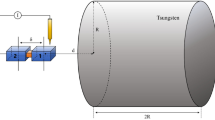
Fig. 1: Experiment setup for simulating post-Newtonian gravity.
figure 1

Schematics of experimental system for simulating post-Newtonian dynamics by probing the evolution of intense laser beams in a thermal nonlinear medium (SF11 lead glass). A laser is shaped to have a prescribed size by a telescope system and then focused inside the sample by a replaceable lens. Within the medium, light dynamics are strongly affected by the nonlocal nonlinearity where their nature is power-dependent. The experiments results in unique solitons and beam evolution due to second-order nonlinear effects. Inset: example raw data of beam profile in entrance and exit facets during post-Newton-type beam evolution.

Full size image

As ϕ is negative, the first and second term of V have opposite signs. That is, the second term γPNϕ2 is the PN correction that represents a second-order repulsive effect that is added to the attractive Newtonian term. Eqs. (4) capture the nonlinear dynamics of the wavefunction ψ under the Post-Newtonian approximation of small energy scale of GR. We are interested in finding Post-Newtonian solitons—optical self-consistent solutions of Eqs. (2) that are analogous to time-independent solitons of Eqs. (4). These solitons take the form ψsoliton = e−iΓzU(x, y). This means that they maintain their spatial waveform while only accumulating phase during their propagation along the z direction with propagation constant Γ. It is important to note that solitons, by their definition, are stationary. Likewise, the beams that we experiment with in practice are near equilibrium and justify the use of Eqs. (4). Quantitatively, the full width at half maximum (FWHM) of the beam σ varies slowly with respect to the Rayleigh length zR, \(| \frac{{z}_{R}}{\sigma }\frac{\partial \sigma }{\partial z}| \, \ll \, 1.\)

We solve the nonlinear set of Eqs. (1) and (2) self-consistently by employing an imaginary time method45, while applying the Distributed Loss Model approximation46. For an in-depth discussion on the numerical methods and the existence of solitons in our model, see Supplementary Materials sections 2 and 3. We extract the solitons’ full width at half maximum (FWHM) and display the solitons’ existence curve—the FWHM of the solitons for different powers for both Newtonian and post-Newtonian potentials (Fig. 2). We can clearly see that the post-Newtonian soliton is wider than the Newtonian solitons. This width difference occurs as the second-order correction of the refractive index has a opposite sign relative to the first, relaxing the attractive potential. In other words, for the same width the post-Newtonian soliton is expected to appear for a larger power (Fig. 2). We note that our self-consistence numerical solutions converge for γ2 ≈ 10−1γ1. As detailed above for PN gravity γPN = 2 (in Eq. (4c)) and an exact mathematical analogue requires γ2 = 2γ1. We also display the solitons’ calculated eigenvalues (Γ) for the different powers (see Fig. 2b). These eigenvalues are the propagation constants in the optical system and are analogous to the ground-state eigenvalues of Eq. (4a).

Fig. 2: Nonlocal nonlinear soliton solutions considering a second-order nonlinear term.
figure 2

Upper panel: Theoretical existence curve for soliton with nonlocal change of the refractive index. FWHM of the solitons vs. power, for Newtonian-type (γ2 = 0 in Eq. (1)) and Post-Newtonian type (γ2 = −3.43 ⋅ 10−6 in Eq. (1)) potentials. Inset shows the soliton spatial profile. Lower: Eigenvalues \(\left(\Gamma \right)\) of solitons vs optical power for Newtonian and post-Newtonian potentials. For the numerical solution we set the following physical parameters: λ = 532 nm, γ1 = 14 ⋅ 10−61/K, κ = 0.7W/(mK), α = 0.01 cm−1, L = 4 mm being the length of the rectangular boundary. For proof of convergence of the soliton solutions presented see Supplemantery Materials, section 2.

Full size image

We then conduct an experiment to observe the soliton and the beam dynamics under Eqs. (2). In the experiment a gaussian beam with wavelength of 532 nm is launched to incident a rectangular lead glass (SF11) with dimensions of 4 × 4 × 200 mm. The lead glass is covered with a 2-cm thick copper layer to maintain a constant temperature of the boundary conditions. We image the entrance and exit facets and compare the widths of the beam, probing its evolution. In order to find the stable soliton, we vary the power of the incident beam until the entrance and exit beams are identical in width. We display typical experimental results of the relative beam width at the exit facet and entrance facet in Fig. 3. As the power is increased the beam is undergoing a focusing effect until reaching approximately the soliton solution, for which the relative width is unity (after 1 Watt). We observe a stable soliton at relatively low powers, until the beam starts to refocus again (Fig. 3a). Then for powers above 2.5 W a different stable soliton appears for a finite power range, that we interpret as the post-Newtonian soliton, which we found numerically (see Fig. 2). We extract the existence curve of both solitons from measurements with varying initial beam conditions and display them in Fig. 4. This is done by manually searching for the minimum width during evolution where our estimated error is defined by the power range for which the soliton has an approximate constant width. For the same width the post-Newtonian soliton occur for higher power, which agrees with the post-Newtonian solitons trend we found theoretically (Fig. 2). This suggests that the second-order term of the refractive index (Eq. (1)) has an opposite sign relative to the first-order, relaxing the focusing effect to some extent and enabling the simulation of post-Newtonian dynamics.

Fig. 3: Experimental beam evolution.
figure 3

a, b Typical experimental data of beam width as a function of power, displaying the power depending evolution, for aimed soliton width of 150 μm (a) and 600 μm (b). The beam first focuses to the width of the Newtonian soliton, and maintains in constant width for some power range. As the power increases higher orders of the refractive index changes affect the evolution, and an additional stable state is found around 4 W (a). For both beams we see a final defocusing effect but with different curvatures: positive (b) and negative (a). c Experimental raw data of beam images for 150 μm entrance showing the defocusing for power higher than 4 W.

Full size image
Fig. 4: Measured existence curve.
figure 4

Existence curves extracted from experimental data. The graph shows two distinct existence curves that we interpret as the Newtonian (blue) and Post-Newtonian (red) solitons. We extract this data from typical experimental results, as displayed in Fig. 3. Error bars in soliton width are direct result of the imaging-resolution in the experiment, whereas error bars in power is caused by the manual extraction of the soliton power.

Full size image

For even higher powers (above 2.5 W), a defocusing effect of the beam occurs, supported by the second-order negative nonlinear term in Eq. (1), as shown in Fig. 3c. We further study the observed defocusing effect occurring for high powers by repeated experiments in powers beyond 4W. We witness an unexpected evolution of the beam into a doughnut-shaped beam and splitting of the initial beam into two separate lobes (see Fig. 5e, f). This effect occurs for high powers consistently and does not preserve the symmetry between x and y. For even higher power (>4.5 W) and slightly anistropic conditions the beam evolves into an anisotropic doughnut shape (see Fig. 5g). We numerically simulate the beam evolution by employing the split-step Fourier method, which propagates the waveform in the z direction (see example Fig. 5a). We find the evolution of the gaussian beam into a doughnut beam Fig. 5a, b. To understand the beam evolution we calculate the refractive index induced by the incident gaussian beam. At high-enough powers the gaussian beam induces a ’Mexican hat’ type potential as displayed in Fig. 5d. This happens due to the second-order defocusing term that for high powers creates a self-repulsive potential, that is most dominant in the peak intensity of the beam. This potential in turn repulses the beam outwards from the center, creating a doughnut-like beam (Fig. 5a). The initial gaussian beam evolves into states resembling the modes of the linear ‘Mexican hat’ potential, Fig. 5e, f, h47 (See page 91 in the reference. Figure 5,e,f,h resembles TEM01, TEM00, TEM11 respectively.). Moreover, to theoretically model the result of Fig. 5g, which does not resembles any of the modes of the linear ’Mexican-hat’ potential, we simulate a practical experimental incident beam that is slightly elliptical. This breaks the radially symmetric boundary conditions in Eqs. (2). We find the corresponding beam Fig. 5c that simulates the observed Fig. 5g. This effect of beam evolution under self-induced ’Mexican hat’ refractive index was never observed before as the experiments were limited to lower powers. Rich beam evolution and intriguing waveforms such as those displayed in Fig. 5e–h are supported by the induced nonlocal nonlinear potential, and are observed in this system for high-power laser beams (>4 W). Observing these waveforms and the fitting refractive index induced is an additional proof for a repulsive interaction and the existence of the additional negative term of the refractive index in Eq. (1). Furthermore, we have utilized high-power laser beams, and it is reasonable to assume we have reached γ2 ≈ γ1 in our experimental setting, as required for a quantitatively validity of the analogue. We note that despite previous numerical work on post-Newtonian Schrödinger eqs., the experimental analogue revealed new intriguing behaviour of the beam’s evolution42.

Fig. 5: Evolution of high power beams into exotic spatial shapes.
figure 5

a–c Simulations of evolution of a high-power Gaussian beam. The beam evolves into a doughnut-shaped beam (a, b), and an anisotropic doughnut-shaped beam for a slightly elliptical initial beam (c) The calculated refractive index showing the self-defocusing potential appearing around the peak intensity, resembling the 'mexican hat' potential (d). e–h Experimental data of an evolution of Gaussian initial beam into: two-lobe beam (e), doughnut-shaped beam (f), anisotropic doughnut beam (g), and even more complex shape for above 4.8 W (h).

Full size image

Discussion

In conclusion, this work opens the door to unexplored physical regimes with additional nonlinear terms. Our experiment offers a paradigm by which one can adjust the nonlocal nonlinear material and laser parameters in a way that mimic the post-Newtonian potential with a quantitative correspondence between the refractive index and the gravitational potential. Hence, this work sets the ground for future semi-classical simulations of a wave packet propagating with self interactions analogous to gravity15,18,19,20,21,22,23,24,25,26,29,30,31. It would be intriguing to experimentally simulate other GR effects which can be treated with PN formalism such as frame-dragging48 and boson-star formation. The beam evolution under the influence of a nonlinear refractive index with both self-focusing and self-defocusing terms offers unique beam evolution which supports unique waveforms, such as the doughnut-shape beam observed—calling for future research for varying initial beams. Furthermore, the existence of solitons in presence of a higher order defocusing term is not exclusive to our model, and we expect rich behavior from other systems with higher order defocusing terms. As other experimental systems have a nonlocal nonlinear nature, such as liquid crystal, Bose–Einstein condensates and saturable nonlinearity in atomic vapors49,50. For example, it would be intriguing to consider a different response function of physical interest, such as the Gaussian response function or working at a different dimensionality. It would be interesting to explore the existence and stability of other solitons (e.g., periodic, that are known to exist in the presence of the thermal nonlinearity) within this framework of second order nonlinearity.