The classical-to-quantum crossover in the strain-induced ferroelectric transition in SrTiO₃ membranes

Abstract

Mechanical strain presents an effective control over symmetry-breaking phase transitions. In quantum paraelectric SrTiO₃, strain can induce ferroelectric order via modification of the local Ti potential energy landscape. However, brittle bulk materials can only withstand limited strain range (~0.1%). Taking advantage of nanoscopically-thin freestanding membranes, we demonstrate an in-situ strain-induced reversible ferroelectric transition in freestanding SrTiO₃ membranes. We measure the ferroelectric order by detecting the local anisotropy of the Ti 3d orbital signature using X-ray linear dichroism at the Ti-K pre-edge, while the strain is determined by X-ray diffraction. With reduced thickness, the SrTiO₃ membranes remain elastic with >1% tensile strain cycles. A robust displacive ferroelectricity appears beyond a temperature-dependent critical strain. Interestingly, we discover a crossover from a classical ferroelectric transition to a quantum regime at low temperatures, which enhances strain-induced ferroelectricity. Our results offer new opportunities to strain engineer functional properties in low dimensional quantum materials and provide new insights into the role of ferroelectric fluctuations in quantum paraelectric SrTiO₃.

Introduction

Controlling the properties of emergent quantum phases is of fundamental importance for modern nanotechnology. Strain control provides a direct manipulation over the atomic spacing, resulting in effective tuning of quantum phases through the intertwined structural, electronic and magnetic degrees of freedom in quantum materials. While strain has been used to tune properties of a variety of bulk materials^{1,2,3,4,5,6,7}, its application to bulk crystals is limited due to their low tensile strain tolerance, typically around 0.1%⁸. The advent of low-dimensional quantum material membranes, such as van der Waals materials and oxide membranes, has enabled new opportunities for mechanical manipulation of quantum states of matter^4,9. Studies have demonstrated that these low dimensional materials, especially oxide freestanding nano-membranes, can sustain a degree of strain well beyond their bulk counterparts, allowing the exploration of coupling between lattice, charge, spin, and orbital degrees of freedom in unexplored strain regimes^{10,11,12,13,14}.

Since ferroelectricity arises from asymmetric ion displacement, strain provides an effective tuning parameter of the local potential energy and plays a central role in the control of ferroelectricity^10,15,16,17. In this study, we focus on SrTiO₃, known as a “quantum paraelectric”, whose ground state is believed to lie near a ferroelectric quantum critical point. Despite a dramatic increase in the dielectric constant when approaching zero Kelvin, strong quantum fluctuations destabilize the spontaneous development of long-range static ferroelectric order^18,19. Various non-thermal tuning parameters, such as oxygen isotope exchange²⁰, epitaxial strain^15,16, dopings, and dislocations^21,22, can overcome the fluctuations and stabilize the ferroelectric order in SrTiO₃. While widely acknowledged as a displacive transition^23,24,25, several studies have reported randomly oriented polar nanodomains preceding the ferroelectric order in SrTiO₃^{26,27,28,29,30,31}, illustrating a relaxor ferroelectric nature where the long-range order arises from the alignment of preformed ferroelectric nanodomains (Fig. 1a). The precise nature of the non-thermally induced ferroelectric transition remains elusive. To unravel the role of the thermal and quantum fluctuations as well as the displacive and relaxor characteristics, a comprehensive investigation of the SrTiO₃ ferroelectric phase diagram with consistent sample heterogeneity is essential. Previous studies on induced ferroelectricity, however, typically involve multiple samples^{10,15,16,20,21,22}, which unavoidably introduces sample variations and hinders a deeper understanding of the transition and limits the technology application via strain tuning.

Fig. 1: Straining SrTiO₃ membrane.

a Two scenarios of the strain-induced ferroelectric transition: displacive (left) and order-to-disorder (right). b Schematic of the uniaxial strain applied onto SrTiO₃ sample supported by polyimide films. The device is suspended over a hundred-µm gap defined by two cleaved silicon substrates. The schematic drawing is not to scale. c Image of the SrTiO₃ sample near the gap area. d–f Single crystal X-ray diffraction of three Bragg peaks [(002), (202), (022), in pseudocubic notation] during the tensile strain and release process at 40 K. g Refined lattice parameters of the strained SrTiO₃ with different applied forces along crystallographic a direction via piezo stacks. h The relationship between the lattice strain of two relevant lattice parameters, namely the length along the strain ${\varepsilon }_{a}=\Delta a/{a}_{0}$ and out-of-plane ${\varepsilon }_{c}=\Delta c/{c}_{0}$, for selected temperatures, where ${a}_{0}$ and ${c}_{0}$ are the lattice constants at zero strain.

In this study, we leverage the opportunity offered by freestanding membranes of SrTiO₃ by deploying in-situ strain capable of applying large uniaxial strain to low-dimensional membrane materials with multiple complementary X-ray measurements. This capability allows for the continuous and reversible manipulation of the lattice parameter of freestanding SrTiO₃ membranes, thus accessing the paraelectric-ferroelectric phase transition with temperature control. The strain response of the lattice constants at various cryogenic temperatures is monitored by X-ray diffraction (XRD) and the induced ferroelectric order parameter is tracked by linear dichroic X-ray absorption (XLD). By quantitatively correlating the Ti-K pre-edge XLD spectral feature with ferroelectric polarization moments across a wide strain and temperature range in a single SrTiO₃ nano-membrane, we present evidence of a temperature-dependent crossover from a high-temperature classical phase transition into a distinct low-temperature quantum paraelectric regime where quantum fluctuations contribute significantly.

Results

Reversible strain control

Figure 1b, c illustrates how reversible tuning of the lattice greater than 1% tensile strain in a 20-nm-thick SrTiO₃ membrane was achieved with the in-situ uniaxial strain setup. The strain is applied parallel to the pseudocubic a axis, with b in-plane orthogonal to the strain direction (along the edges of the silicon gap), and c out-of-plane direction of the SrTiO₃ membrane. The high-resolution X-ray diffraction of the SrTiO₃ membranes at 40 K and different strain values are shown in Fig. 1d–f. The (002), (202), and (022) Bragg peaks exhibit systematic shifts as the elastic strain is applied and released, indicating a reversible lattice constant tuning. Extensile strain generates an increasing a, decreasing c, while b remains unchanged due to the constraint of the silicon substrates (Fig. 1g). This allows us to determine the Poisson’s ratio by calculating the linear strain dependence ν = −ε_c/ε_a, where the strain is defined by ${\varepsilon }_{a}=\Delta a/{a}_{0}$, and ${a}_{0}$ is the lattice constant at zero strain. We found ν = 0.34 with little temperature dependence (Fig. 1h), which is notably larger than that of the bulk (ν = 0.22)³². The width of the in-plane (202), (022) Bragg peaks also increases upon strain, which indicates the decrease of in-plane lattice coherence. The peak width recovers when strain is released. While similar lattice responses were observed in SrTiO₃ membranes with varying thicknesses and temperatures, we found that the elastic strain limit increased fivefold upon decreasing membrane thickness from 50 nm to 10 nm (Supplemental Fig. 3).

Strain-induced ferroelectric order

Having established the elastic lattice response, we now demonstrate that the uniaxial strain can also induce a reversible paraelectric to ferroelectric transition in the SrTiO₃ membrane. X-ray absorption spectroscopy (XAS) provides a sensitive probe of local symmetry at a specific atomic site. The XAS near the Ti-K edge results from the dipole transition from Ti 1s to Ti 4p orbitals (around 4.982 keV in Fig. 2a), with mixtures of weaker transitions between Ti 1s and Ti 3d (e_g and t_2g) orbitals in the pre-edge region, where the latter is dipole-forbidden but quadrupole-allowed in the paraelectric states^33,34. Upon transition into the ferroelectric state that breaks inversion symmetry, the Ti 1s to Ti 3d e_g transition becomes dipole allowed when the X-ray polarization is parallel to the Ti atom displacement (E//a, throughout this manuscript)^33,34. Figure 2b shows the strain-induced ferroelectric transition by showing the change of the Ti-K XAS spectra at a series of strain values, taken at 20 K with grazing incident geometry E//a. We observe a gradual enhancement of the e_g XAS pre-edge peak centered at 4970.8 eV with increasing strain indicating a strain-induced change in the local environment of the Ti ions. The change in XAS is present when the X-ray polarization is along the tensile strain direction (E//a), as the induced ferroelectric polarization is parallel to the tensile strain (Fig. 2c). In contrast, the consistency of the E//c XAS spectra with tensile strain indicates no signature of ferroelectric polarization along c.

Fig. 2: Strain-induced ferroelectric state at 20 K.

a X-ray absorption spectra (XAS) of unstrained SrTiO₃ membrane across Ti K-edge. The inset shows the schematics of the strain geometry and the strain-induced Ti displacement. b, The strain evolution of the XAS in the pre-edge regime. The strained spectra correspond to the ferroelectric state. c Polarization-dependent XAS pre-edge feature along different crystallographic axis (E//a and E//c). The first two peaks in the unstrained spectra are quadrupole transitions of the Ti 1s electrons to the Ti 3d-derived t_2g and e_g orbitals. The non-trivial linear dichroic signal at e_g pre-edge peak (at 4970.8 eV, vertical dashed line) increases when SrTiO₃ is strained. d The evolution of the linear dichroic signal (purple dots) at e_g pre-edge peak (vertical dashed line in a-c) and the strain in a and c lattice parameter, denoted as ε_a and ε_c, respectively, upon applying uniaxial strain along a.

This observation is inconsistent with the order-disorder ferroelectric transition explanation, where microscopic preformed ferroelectric domains are randomly oriented along different directions in the unstrained disordered phase (Fig. 1a)²⁹. Uniaxial strain aligns Ti displacement along a and perpendicular to c (Fig. 1a). One might expect suppression of the e_g peak intensity in E//c channel upon tensile straining (${\varepsilon }_{a}$) if the transition is order–disorder in nature (Supplemental Information, Section C). The insensitivity of E//c spectra with respect to strain puts an upper bound on preformed polar nanodomains with maximum Ti displacement of δ_Ti < 0.7 pm, which is an order smaller than the thermal vibration at 50 K³⁵. Therefore, our results strongly support a displacive nature of the strain-induced ferroelectric transition in SrTiO₃.

As a measure of the ferroelectric order, XAS linear dichroism (XLD) is the difference between E//a and E//c, as shown in Fig. 2c. The strained XLD spectra shows elevated spectral weight at the e_g position. This intensity is proportional to the square of the ferroelectric order parameter: XLD $\propto$|P²|³⁴. Compared with previous XAS and DFT calculations³³, the maximum polarization is estimated to be around P = 14.0 µC/cm² with displacements for Ti and averaged O atoms are estimated to be around δ_Ti = 2.01 pm and δ_O = 7.30 pm (Supplemental Table 2).

The strain-dependent signal is monitored by the XLD e_g intensity as the strain force increases from zero. Figure 2d shows XLD intensity increasing monotonically, indicating a continuous growth of ferroelectric order under tensile strain. By monitoring the change of the a, c lattice constants during the strain loop, the calculated the a, c axis strain ε_a,c is overlaid in Fig. 2d. By relating the lattice response to XLD at the same strain state, a strain-dependent ferroelectric order parameter P(ε_a) is established. Figure 3a summarizes the strain response at different temperatures up to 100 K, with simultaneous XRD tracking the respective lattice response. At 20 K, a clear dichroic signature emerges at finite tensile strain, suggesting the appearance of ferroelectric order at a small tensile strain value. Whereas at higher temperatures, ferroelectric order appears only beyond a critical strain value ε₀(T) increasing with rising temperature. Importantly, at each temperature, the strain-induced ferroelectric order evolves smoothly across ε₀ without a discontinuous jump, signifying a second-order phase transition driven by strain³⁶.

Fig. 3: Temperature/strain-dependent ferroelectric order.

a Strain-dependent XAS linear dichroic (XLD) signal at different temperatures. The filled (open) circle marks the increasing (decreasing) strain sweep directions. The solid line is the fit to a power law behavior as in (b–e). Data are offset vertically for clarity. b–e Fits of power law dependence of ferroelectric order to the lattice strain at different temperatures.

Dramatic change in the critical exponent β upon cooling

Intriguingly, we find that the XLD signal vs. strain displays evolving curvatures at different temperatures. Near a critical phase boundary, physical quantities exhibit critical behavior following the order parameter $P(\varepsilon )\,\propto \,{[{\varepsilon }_{a}-{\varepsilon }_{0}\left(T\right)]}^{\beta }$, where $\beta$ is the order parameters critical exponent. The change in shape suggests a non-universal critical exponent $\beta$. Fitting the strain-dependent XLD to the power law behavior ${{{\rm{XLD}}}}$ $\propto \left|{P}^{2}\right|\propto {[{\varepsilon }_{a}-{\varepsilon }_{0}\left(T\right)]}^{2\beta }$ shows a temperature-dependent critical exponent 2$\beta (T)$, around 0.93 at 100 K, while increasing to around 1.5 at below 40 K (Fig. 3b–e).

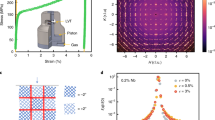
Figure 4 summarizes the temperature-strain phase diagram for the paraelectric-ferroelectric phase transition of a SrTiO₃ membrane. This phase boundary is consistent with previous studies that reported the strain-induced ferroelectricity in SrTiO₃ thin films and single crystals, where the phase boundary terminates at T = 0 quantum critical point (QCP) near zero strain^10,37. From the paraelectric-ferroelectric phase boundary, we determine the critical scaling behavior to be a power law, where T_c $\propto$ [ε_a – ${\varepsilon }_{0}\left(T=0\right)$]^1/Δ, with the extrapolated quantum critical strain being ${\varepsilon }_{0}\left(T=0\right)$ = 0.019% ± 0.016%, and 1/Δ = 0.606 ± 0.13 (Fig. 4a). We note that ${\varepsilon }_{0}\left(T=0\right)$ is shifted from zero strain, deviating from the ideal quantum ferroelectric. However, as achieving a strain-free state for membrane is challenging, and residual strain from the polyimide cannot be excluded, the extracted QCP position should be interpreted with significant caution. Figure 4b summarizes the order parameter critical exponent β across the paraelectric-ferroelectric phase boundary. At high temperatures, β ~ 0.5, which is consistent with the classical ferroelectric transition predicted in a mean-field theory, assuming a linear-quadratic strain-ferroelectric order coupling in the Landau free energy (Supplemental Information, Section E). Interestingly, with decreasing temperature, the critical exponent β substantially increases upon cooling below 100 K, suggesting a change in the nature of the phase transition.

Fig. 4: Paraelectric-ferroelectric phase boundary and phase diagram.

a Temperature–strain phase diagram of the paraelectric-ferroelectric phase. The dash-line is the fitted phase boundary to the power law. In the ferroelectric side of the phase diagram, the strength of the order parameter is color-coded. The grey data points are reproduced from ref. ¹⁰. b Temperature dependence of the order parameter critical exponent β. The error bars represent the standard deviation from the fit.

Discussion

SrTiO₃ has been argued to be a quantum paraelectric near a displacive ferroelectric QCP where the paraelectric-ferroelectric phase boundary terminates at zero Kelvin^10,37. Thus, as the temperature decreases, thermal fluctuations diminish, and quantum fluctuations should become dominant. Our observation of temperature-dependent β strongly supports the existence of the QCP. Furthermore, our results indicate that the influence of the quantum criticality sets in below ~ 100 K, consistent with the deviation from the classical Curie-Weiss behavior in paraelectric dielectric susceptibility¹⁸. The critical exponent β saturates at around ~50 K, also aligned with the temperature range where the dielectric constant exhibits a non-classical T² dependence^38,39. Apparently, to quantitatively understand the temperature variation of β in our data, a quantum correction is needed to account for the deviation from the classical critical behavior. In the dimensionality crossover theory, quantum criticality near a QCP increases the effective dimensionality to d + z, where d is the original dimensionality and z is the dynamical exponent^38,40. Such that the quantum critical behavior is analogous to a classical transition, but in a higher dimension. Our observation of an increasing β in the proximity of the quantum critical regime at low temperatures appears to be qualitatively consistent with the addition of an effective dimensionality. However, since strain-ferroelectric order coupling in SrTiO₃ is linear-quadratic, it cannot be simply described by the Ising model with a transverse conjugate field that is commonly used as a model system for QCP theories. Early theory based on ferroelectric systems suggested a logarithmic correction necessary for the quantum fluctuation effect under isotropic pressure^24,41. Whether a similar correction applies to our observed uniaxial strain-induced ferroelectric transition remains a compelling theoretical question.

Could the presence of spatial inhomogeneity at low temperatures account for the observed temperature dependence of β? Previous studies have suggested that frozen-in disorders at low temperatures, such as sample or strain inhomogeneity, could lead to a distribution of critical strain value ${{{{\rm{\varepsilon }}}}}_{0}$, smearing out the ferroelectric transition and increasing β⁴². We argue that this scenario is unlikely to explain our data. Inhomogeneity often leads to history-dependent ferroelectric responses, but our strain-dependent ferroelectric order parameter shows no hysteresis within experimental error (Fig. 3a). Moreover, we show the distribution of the lattice strain ${\varepsilon }_{a}$ across the gap region in the Supplementary Fig. 7. In the center of the gap, the strain is homogenous with a strain variation Δε_a smaller than 0.09%. Such small inhomogeneity is unlikely to induce a large shift in the order parameter critical exponent β.

To conclude, we have demonstrated reversible in-situ strain engineering of a single SrTiO₃ membrane device across the paraelectric-to-ferroelectric transition. Our results suggest that the strain-induced ferroelectric transition is displacive in nature with no preformed polar nanodomains. Combining X-ray techniques, we quantified the ferroelectric moment from the Ti-K pre-edge features and chart out the order parameter in an extended strain-temperature phase diagram. The temperature dependent strain-order parameter critical exponent β(T) indicates a classical-to-quantum crossover boundary.

In a broader context, the reversible strain-tuning appears to be a generic property of perovskite nanomembranes, as shown in Supplementary Fig. 4, in which the reversibility is demonstrated on two other strained perovskite oxide membranes, La_0.7Ca_0.3MnO₃ and LaNiO₃. Unlike previous works in bulk crystals, which often have high failure rates at higher strain values, laminating nano-membranes on a stretchable polymer platform offers additional support for strain engineering while maintaining structural integrity. This opens new avenues for controlling and probing exotic quantum states of matter through robust lattice control in a wide class of quantum materials. For example, we envision continuous and reversible control of the electronic structures^2,43 and complex magnetism⁴⁴ over an extended temperature–strain phase regimes, allowing precise access to critical phase boundaries of competing orders while remaining compatible to a broader range of measurement tools. These developments also promise novel microelectromechanical devices that can harness the properties of quantum materials, such as superconductivity, magnetism, resistive switching, and ferroelectricity, through nano-mechanical control. By providing flexible, lightweight, and highly durable quantum material platforms, this reversible strain-tuning approach has broad implications for soft quantum electronics, including wearable devices, implantable devices, and advanced sensors.

Methods

Thin film growth and membrane fabrication

The free-standing crystalline SrTiO₃ was synthesized by pulsed layer deposition with designed thickness with a 15.6 nm Sr₂CaAl₂O₆ sacrificial buffer layer on (001)-oriented single crystalline SrTiO₃ substrates. To improve the quality of resulting SrTiO₃ membranes and minimize fractures, the sacrificial buffer layer was chosen to closely match the SrTiO₃ lattice parameters. Before the growth, the (001)-oriented single crystalline SrTiO₃ substrate was pre-annealed at 900 °C and oxygen partial pressure of 5 × 10⁻⁶ Torr to achieve sharp step-and-terrace TiO₂-terminated surfaces. A 40-unit cell of Sr₂CaAl₂O₆ sacrificial buffer layer was first grown by pulsed layer deposition using a 248 nm KrF excimer laser with 2.1 J/cm⁻² laser fluence, 3.1 mm² laser spot size on the target, and substrate temperature of 710 °C. A subsequent SrTiO₃ with target thickness was grown with 0.89 J/cm⁻² laser fluence, 3.2 mm² laser spot size, and substrate temperature of 700 °C. The growth process was monitored via in-situ reflection high-energy electron diffraction (RHEED).

The thin, as-grown heterostructure was first coated with PMMA and placed in deionized water until the Sr₂CaAl₂O₆ sacrificial layer was fully dissolved. The released membrane was transferred onto a polyimide film. Prior to the transfer, the polyimide film was treated with oxygen plasma to obtain an activated surface. The samples were annealed at 110 °C for 10 min to enhance SrTiO₃-polyimide bonding. Finally, the PMMA was removed by acetone.

To be able to apply large strain to SrTiO₃ membrane, two pieces of cleaved silicon substrates were mounted onto a titanium flexure plate (Razorbill Instruments), with a well-defined hundred-µm parallel gap in between. The polyimide-supported SrTiO₃ was mounted across the gap using Angstrom Bond epoxy. The whole sample assembly is then mounted to an FC150 strain cell from Razorbill Instruments. The SrTiO₃ (100) pseudocubic crystallographic axis was chosen to align with the uniaxial strain direction. We use pseudocubic notation throughout the study. We note that the slight inequivalence in lattice constants a, b, and c at zero piezo force quantifies the level of residual strain (<0.05%) in the sample, which may arise from the sample preparation process. The schematic drawing and photo of the device are shown in Fig. 1b, c and Supplementary Fig. 6. The small gap defined by two cleaved silicon substrates can provide a maximum of more than 20% uniform tensile strain for the material suspended above the gap, given the sample does not fail.

X-ray measurements

X-ray diffraction (XRD) and absorption measurements were performed at the 6-ID-B and 4-ID-D endstation of the Advanced Photon Source, Argonne National Laboratory. Part of the measurements were conducted at XMaS beamline. The FC100 strain cell was mounted into an Advanced Research Systems Displex closed-cycle cryostat with a base temperature T ≈ 20 K. The X-ray beam spot was kept smaller than the gap size in any geometry to ensure only strained sample region is probed. XRD of (002), (202), (022) Bragg peaks were performed at photon energy of 11.212 keV with Gaussian fits to determine the pseudocubic lattice constants.

XAS spectra across the Ti-K edge resonance (4.97 keV) were recorded in partial fluorescence yield mode in a quasi-backscattering geometry with a Hitachi Vortex detector. At each incident energy, the polarization was rapidly switched between linear horizontal/vertical polarization states (LH/LV) using diamond phase plates in the sequence of LV/LH/LH/LV in order to determine the linear dichroism spectrum with a high signal-to-noise ratio. The X-ray was incident at 1° grazing angle along the gap, where LH/LV polarization corresponds to polarization vector along a/c pseudocubic axis of SrTiO₃, respectively. All XAS/XLD spectra were normalized to the Ti-K main edge jump up to 5.02 keV with the tabulated value⁴⁵. Back-to-back to XAS measurements, strain dependent c lattice constant was tracked from (002) Bragg peak XRD at photon energy of 5.5 keV. The compressive strain along c axis was converted to a axis tensile strain using the Poisson’s ratio ε_a = −ε_c/ν.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.