Abstract
The integration of large language models (LLMs) into drug design is gaining momentum; however, existing approaches often struggle to effectively incorporate three-dimensional molecular structures. Here, we present Token-Mol, a token-only 3D drug design model that encodes both 2D and 3D structural information, along with molecular properties, into discrete tokens. Built on a transformer decoder and trained with causal masking, Token-Mol introduces a Gaussian cross-entropy loss function tailored for regression tasks, enabling superior performance across multiple downstream applications. The model surpasses existing methods, improving molecular conformation generation by over 10% and 20% across two datasets, while outperforming token-only models by 30% in property prediction. In pocket-based molecular generation, it enhances drug-likeness and synthetic accessibility by approximately 11% and 14%, respectively. Notably, Token-Mol operates 35 times faster than expert diffusion models. In real-world validation, it improves success rates and, when combined with reinforcement learning, further optimizes affinity and drug-likeness, advancing AI-driven drug discovery.
Similar content being viewed by others
Introduction
Drug discovery traverses a remarkably intricate journey. Recent years have witnessed profound advancements in artificial intelligence (AI) technologies, particularly deep learning (DL), which has been progressively impacting multiple facets of drug development. These technologies are accelerating in innovative drug research. However, the high cost associated with acquiring annotated data sets in drug discovery remains a significant impediment to the advancement in this field. Recently, the rapid evolution of unsupervised learning frameworks, epitomized by BERT1 and GPT2, has introduced unsupervised chemical and biological pre-training models across disciplines such as chemistry3,4,5,6,7,8,9,10,11,12, and biology13,14,15,16. These models undergo large-scale unsupervised training to learn representations of small molecules or proteins, subsequently fine-tuned for specific applications. By leveraging unsupervised learning on large-scale datasets, these pre-training models effectively addresses the challenges associated with sparse labeling and suboptimal out-of-distribution generalization, leading to improved performance17.
Large-scale molecular pre-training models can be broadly categorized into two main groups: models based on chemical language and models utilizing molecular graphs. First, chemical language models encode molecular structures using representations such as simplified molecular input line entry system (SMILES)18 or self-referencing embedded strings (SELFIES)19. They employ training methodologies akin to BERT or GPT, well-established in natural language processing (NLP). Notable examples include SMILES-BERT20, MolGPT21, Chemformer22, and Multitask Text and Chemistry T523, which exhibit architectural similarities to universal or general NLP models such as LLaMA24.
Second, graph-based molecular pre-trained models exhibit higher versatility. They represent molecules in a graphical format, with nodes for atoms and edges for chemical bonds. Pre-training methodologies include various techniques, such as random masking of atom types, contrastive learning, and context prediction25,26,27. Unlike language-based models, graph-based molecular pre-trained models inherently incorporate geometric information, as demonstrated by methods like GEM28 and Uni-Mol29.
Despite their advancements, both classes of models exhibit distinct limitations. Large-scale molecular pre-training models based on the chemical language face a significant constraint in their inability to inherently process 3D structural information, which is pivotal for determining the physical, chemical, and biological properties of molecules28,29. Consequently, these models are inadequate for downstream tasks that involve 3D structures, such as molecular conformation generation and 3D structure-based drug design. In contrast, graph-based molecular pre-trained models can effectively incorporate 3D information. However, existing approaches primarily focus on learning molecular representations for property prediction rather than molecular generation. Moreover, integrating these models with universal NLP models presents considerable challenges. As a result, a comprehensive model capable of addressing all drug design tasks remains elusive. Addressing the limitations of these two model types to develop a pre-trained model suitable for all drug design scenarios, and easily integrable with existing general large language models, is a pressing need.
The emergence of universal artificial intelligence offers opportunities in this domain. By leveraging vast amounts of data, these models acquire expert knowledge across various fields, providing valuable assistance to practitioners2,24,30,31. Recent studies suggest that GPT-4 demonstrates a profound understanding of key concepts in drug discovery, including therapeutic proteins and the fundamental principles governing the design of small molecule-based and other types of drugs. However, its efficacy in specific drug design tasks, such as de novo molecule generation, molecular structure alteration, drug-target interaction prediction, molecular property estimation, and retrosynthetic pathway prediction, requires further refinement32. Nevertheless, the application of a token-based approach by the above models to handle continuous spatial data is particularly noteworthy.
Building on this concept, Born et al. introduced the Regression Transformer33, which integrates regression tasks by encoding numerical values as tokens. Nonetheless, this method overlooks the intricate 3D structural complexities of molecules. Additionally, Flam-Shepherd and Aspuru-Guzik proposed directly tokenizing 3D atomic coordinates (XYZ) to represent molecular 3D structures34. Concurrently, the BindGPT framework employs a similar approach to generate molecular structures and their corresponding 3D coordinates35. While the performance of these models still necessitates enhancement, both approaches have exhibited promising outcomes in relevant drug design tasks. These results highlight the potential of large models to grasp the semantics of numerical values and affirm the feasibility of employing token-only models to handle continuous data. However, directly training language models on Cartesian coordinates of atoms presents unique challenges. Specifically, for larger molecules, the extensive XYZ coordinates can result in excessively long sequences, complicating the model’s learning process. Furthermore, achieving invariance through random translation and rotation does not confer equivariance.
In this work, to overcome the limitations of current models, we present Token-Mol, a large-scale language model for molecular pre-training. To enhance compatibility with existing general models, we employ a token-only training paradigm, recasting all regression tasks as probabilistic prediction tasks. Token-Mol is constructed with a Transformer decoder architecture, integrating essential 2D and 3D structural information via SMILES and torsion angle tokens. Furthermore, we utilize a random causal masking strategy during pre-training, leveraging a combination of Poisson and uniform distributions to stochastically mask training data. This strategy enhances the model’s fill-in-the-blank generation capability, increasing its adaptability to a wide range of downstream tasks. To address the token-only model’s limited sensitivity to numerical values, we introduce a Gaussian cross-entropy (GCE) loss function, replacing the traditional cross-entropy loss. This innovative loss function assigns weights to each token during training, enabling the model to learn the relationships between numerical tokens. Additionally, Token-Mol demonstrates exceptional compatibility with other advanced modeling techniques, including fine-tuning and reinforcement learning (RL). This integrative capability facilitates the further optimization of its performance in downstream tasks, thereby enhancing its utility in various applications. To validate the capabilities of Token-Mol, we conduct comprehensive assessments across molecular conformation generation, property prediction, and pocket-based molecular generation tasks. In the molecular conformation generation task, Token-Mol outperforms existing state-of-the-art methods, achieving over 10% and 20% across various metrics on two datasets, respectively. In the molecular property prediction task, Token-Mol achieves an average improvement of 30% in regression tasks compared to token-only models. In the pocket-based molecular generation task, Token-Mol not only achieves molecules with Vina scores comparable to those produced by state-of-the-art models, but also improves drug-likeness (QED) and synthetic accessibility (SA) by approximately 11% and 14%, respectively. To further validate the generalization capability of Token-Mol, we conduct tests in real-world drug design scenarios. Notably, the drug-like molecules generated by Token-Mol demonstrate a 1-fold increase in average success rate across the evaluations on 8 different targets. Furthermore, the integration of RL into Token-Mol effectively enhances the performance of specific downstream tasks within more realistic scenarios, providing an advantage over large models based on geometric graph neural networks for 3D tasks. Finally, we demonstrate Token-Mol’s seamless integration with general large language models through a simple dialogue example. The aforementioned findings highlight the inherent potential of Token-Mol, presenting an outlook on standardizing AI models for drug design.
Results
The overview of Token-Mol
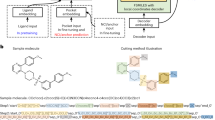
The comprehensive workflow of Token-Mol is illustrated in Fig. 1. The initial phase involves pre-training on the dataset (Fig. 1a) through random causal masking. Subsequently, the model undergoes fine-tuning on customized datasets tailored to specific downstream tasks, including conformation generation, pocket-based molecular generation, and prediction on multiple properties (Fig. 1b). For regression tasks, the GCE loss function (Fig. 1c) is utilized during the fine-tuning process. Furthermore, the performance for specific downstream tasks can be further optimized using reinforcement learning.
The preprocessing of the pretraining dataset holds crucial significance in this context. As shown in Fig. 1a, a depth-first search (DFS) traversal is conducted on the entire molecule in the standard SMILES format to extract the embedded torsion angles within the molecular structure. Following this, each extracted torsion angle is assimilated as a token appended to the SMILES string. Throughout the pretraining phase, random causal masking based on causal regression is implemented. After pretraining, fine-tuning is carried out across downstream tasks. Importantly, the task prompts are specifically designed for the construction of a dialogue system, as indicated by the highlighted yellow box in Fig. 1a. This feature highlights a key advantage of token-only models over other large-scale models: their capability to facilitate real-time interaction. At the end of the Results section, examples will be presented to illustrate this particular advantage.
For the pocket-based molecular generation task, we have introduced pocket encoder and fusion block modules to better incorporate protein pocket information into the model. As depicted in Fig. 1d, we utilized a multi-head condition-attention mechanism to thoroughly incorporate information generated at each autoregressive step into subsequent iterations. This mechanism treats each token generated during autoregression as a prerequisite for further generation, thereby ensuring that the entire query, key, and value matrices originate from the original sequence.
One should note that, in practical scenarios, a lead compound must not only exhibit high affinity for the target but also meet a series of criteria, including high bioactivity and multiple favorable pharmacological properties. This puts higher requirements for pocket-based molecular design tasks, where the integration of receptor-ligand molecule pairs in the training dataset imposes inherent limitations. The model predominantly generates ligand molecules by utilizing information derived from the protein pocket. Consequently, the properties of these generated molecules are heavily influenced by the training data, restricting the explicitly control over their biophysical and chemical properties. These constraints are particularly evident when a precise modulation of molecular properties is desired. Token-Mol, built on an autoregressive language model architecture, where token generation aligns with actions in the RL framework, facilitates the seamless utilization of RL for optimization, thereby ensuring tailored outcomes.
Molecular conformation generation
Molecular conformation is a crucial determinant of the chemical, physical, and biological properties of molecules, underscoring its fundamental importance in structure-based drug design. The integrity and diversity of three-dimensional molecular conformations are essential for various applications in drug discovery, including three-dimensional quantitative structure-activity relationships, molecular docking and thermodynamic calculations. Traditional techniques for obtaining accurate molecular conformations, such as X-ray crystallography and nuclear magnetic resonance (NMR), are either prohibitively expensive or computationally demanding, rendering them impractical for large-scale dataset analysis. The emergence of deep geometric learning has introduced promising alternative methodologies for the generation of molecular conformations34,36,37,38,39,40,41,42,43,44.
In this study, we benchmarked our proposed approach against established baselines using widely recognized conformation generation benchmarks. We employed the dataset utilized by Zhang et al., which includes the dataset from Shi et al. (test set I), comprising 200 molecules, each with fewer than 100 conformations. It is noteworthy that this particular dataset is among the most extensively employed within the conformer generation task. On the other hand, the GEOM-Drug dataset presents a broader range of conformation counts per molecule, from 0 to 12,000. To address this variance, Zhang et al. introduced test set II26, consisting of 1,000 randomly selected molecules with conformation counts distributed similarly to the entire dataset, ranging from 0 to 500.
Our evaluation metrics include both Recall and Precision. Recall measures the diversity of the generated conformations, while Precision evaluates the rationality of the generated conformations. We calculated the mean scores of coverage (COV) and matching (MAT) for both Recall and Precision. COV quantifies the extent to which the quantum computation conformation set covers the generated conformation set within a specified RMSD threshold, with higher values indicating better coverage. Conversely, MAT assesses the similarity between the generated conformations and the quantum mechanical-level training conformations, with lower values suggesting better performance.
Table 1 presents the results for test set I. It indicates that Token-Mol surpasses other SOTA methods in both Precision metrics, resulting in substantial advantages. Notably, Token-Mol achieves notable improvement in the COV Precision (COV-P) metric, outperforming Tora3D by approximately 11%, underscoring the superior quality of molecules produced by Token-Mol relative to alternative methods. However, Token-Mol’s generated conformations exhibit slightly lower Recall performance compared to GeoDiff and Tora3D, positioning it as the second-highest performer overall.
The findings for test set II, depicted in Table 2, reveal Token-Mol’s exemplary performance across all assessment metrics. Remarkably, Token-Mol attains the highest performance in both Precision-based evaluation metrics, COV-P and MAT-P, surpassing other models by approximately 24% and 21%, respectively.
Subsequently, we investigated the relationship between the benchmark performance and the number of rotatable bonds, as illustrated in Fig. 2. Our analysis reveals a clear trend: the performance across all assessment metrics declines as the number of rotatable bonds increases. This decline becomes particularly pronounced when the number of rotatable bonds exceeds 10. Notably, Tora3D exhibits an obvious drop in performance when generating conformations for molecules with a higher number of rotatable bonds. In contrast, Token-Mol demonstrates substantial advantages under these conditions.
Moreover, Token-Mol demonstrates impressive speed. During our evaluation on test set I, utilizing the Tesla V100 for the generation process, Token-Mol required an average of 6.37 seconds to generate all conformations for a single molecule, compared to 8.78 seconds per molecule for Tora3D.
Molecular property prediction
Molecular representation is fundamental to molecular design, as it critically influences the execution of downstream tasks. In this study, we initially assessed the molecular representation capabilities of Token-Mol in the context of molecular property prediction. For a detailed description of the tasks, please refer to the Supplementary Information.
Classification task
For the classification task, we selected six commonly used classification datasets and compared Token-Mol against five representative baselines: XGBoost45 (conventional machine learning), K-Bert46 (sequence-based model), Chemprop47 (graph neural networks), GEM28 (geometry-enhanced graph neural networks), and MapLight+GNN48 (an integrated model combining traditional machine learning with graph neural networks). As outlined in Table 3, Token-Mol demonstrates noteworthy performance across all datasets, outperforming XGBoost and Chemprop in terms of accuracy, albeit marginally trailing behind MapLight+GNN and GEM. Notably, Token-Mol achieves state-of-the-art proficiency on single-task-focused datasets such as BBBP and BACE.
Regression task
We employed a set of six regression datasets for a thorough comparison and analysis. To extend beyond established benchmarks, we introduced the token-only Regression Transformer (RT)33, a model conceptually akin to Token-Mol, to enrich our evaluation framework. Both RT and Token-Mol fully tokenize the input and output, enabling seamless integration with foundational large models, a feature not shared by other models.
A key advantage of token-only models over traditional regression models is their ability to interface seamlessly with large models such as LLaMA, enabling real-time interaction. However, previous models like RT have shown suboptimal performance in prediction tasks, limiting their utility for high-quality interactions. In contrast, Token-Mol treats each numerical value as a single token, rather than decomposing them into multiple tokens like RT. This approach enables one token prediction, thereby accelerating the prediction process. Combined with the GCE, Token-Mol achieves high-quality prediction results. This methodology allows Token-Mol to perform faster and deliver higher prediction quality.
As illustrated in Table 4, Token-Mol’s capabilities in regression tasks are evident, outperforming established benchmarks such as XGBoost, K-Bert, and token-only RT. Notably, Token-Mol consistently surpasses RT across all tasks, showcasing an average performance enhancement of approximately 30%. Particularly remarkable is Token-Mol’s substantial performance boost on the Aqsol dataset, achieving an improvement of around 50%. Additionally, as depicted in Table 5, Token-Mol’s performance closely mirrors that of graph neural network-based models on datasets with large amounts of data, such as Aqsol, LD50, and Lipophilicity. These results collectively underscore the significant potential of Token-Mol in property prediction tasks.
The efficiency of GCE
Token-only generative models conventionally employ cross-entropy loss for regression tasks, but they often exhibit insensitivity to numerical values and fail to capture the relationships between them. To address this issue, we proposed the GCE loss function for regression-related downstream tasks in molecular property prediction. To assess the efficacy of GCE, we conducted ablation experiments to compare models with and without GCE (Table 4). Our results indicate that the absence of GCE notably impairs Token-Mol’s performance across all datasets, with an average RMSE increase of approximately 12%, underscoring the critical role of GCE in regression tasks. Compared to RT, which decomposes individual numerical values into multiple token representations, Token-Mol’s one token prediction approach, enhanced with GCE, demonstrates substantial improvements in both prediction accuracy and efficiency.
Despite the improvements demonstrated by Token-Mol compared to RT, it still exhibits certain limitations relative to other large models based on GNN. This discrepancy is primarily due to the model’s insufficient sensitivity to numerical values. Although we proposed the GCE loss function to address this issue, Token-Mol still lags behind graph neural network-based regression models. Future work will focus on enhancing the model’s performance in regression tasks through approaches such as multi-task prediction and data augmentation.
Pocket-based molecular generation
In modern drug discovery, structure-based drug design holds paramount importance, driving researchers to rapidly identify high-affinity ligands within given protein binding pockets. Hence, pocket-based molecular generation, a method for generating potential ligands for specific pockets, not only avoids computationally intensive physical methods like traditional molecular docking but also broadens the exploration of chemical space. Consequently, it serves as a crucial downstream task to demonstrate the effectiveness of our proposed model. Our goal is to generate ligand molecules tailored to specific protein pockets. To achieve this, as illustrated in Fig. 1d, we amalgamated a pocket encoder and a fusion block. We utilized a pretrained encoder to characterize protein pockets, ensuring its parameters frozen during fine-tuning. Furthermore, we employed condition-attention to integrate both protein and molecule information, mirroring a prompt-like mechanism that incorporates protein pocket information into the ligand molecule generation process. The additional methodological details are outlined in the Methods section.
We compared our model with three popular baseline models in 3D, which is the mainstream method in the pocket-based molecular generation task, namely GraphBP49, Pocket2Mol50, and TargetDiff51. The first two models employ an autoregressive generative graph neural network (GNN) architecture, with Pocket2Mol introducing a geometric deep learning framework that enhances the perception of three-dimensional pocket features. In contrast, TargetDiff adopts a non-autoregressive, probabilistic diffusion model based on an SE(3)-equivariance network. However, since Token-Mol differs from these models with 3D in-situ paradigm by generating only the three-dimensional structure of molecules without simultaneously producing the Cartesian coordinates that represent the spatial relationship of the molecules to the pocket, additional docking is required. Furthermore, these 3D in-situ models have faced some criticism in recent studies52,53. To address this, we additionally employed a 2D-based pocket-based molecular generation model, namely TamGen54, which utilizes a pretrain-finetuning paradigm similar to Token-Mol, involving pre-training on a large dataset of sequence representations of small molecules, followed by fine-tuning based on pocket-ligand pairs, as well as applying the cross-attention mechanism to incorporate pocket information.
Performance on benchmark
We initially evaluated the generalization capability on pocket-based generation (without RL) by the following three criteria: fundamental attributes of the generated molecular sets, binding affinity towards a given pocket, and the physiochemical properties that indicate drug-likeness.
As shown in Table 5, the molecules generated by Token-Mol exhibit satisfactory performance across the entire molecular set. In terms of validity, graph-based models tend to generate some molecules with structural flaws, leading to a decreased validity51. Our experiments partly confirm this issue in several graph-based models, excluding Pocket2mol. Although Token-Mol is a language model, inaccuracies in predicting token counts or values pertaining to torsion angles during autoregressive generation can yield invalid structures. Regarding the diversity, Token-Mol achieves a comparable result than baseline models in the internal diversity metric, while obtaining a relatively moderate results in the #Circle metric which is more sensitive to chemical space coverage.
However, for pocket-based molecular generation, the essence lies in learning how to generate molecules within a specific constrained chemical space55. An ideal molecular generation model should balance and weigh both novelty and similarity to known molecules. Consequently, we also compared the similarity of the generated molecules to the training set and the original ligands in the test targets. The results obviously exhibit that graph-based models exhibit relatively poor similarity, while sequence-based models demonstrate nearly similar levels of similarity. From the perspective of overall similarity and diversity, Token-Mol achieves desirable similarity over 0.1 to training set and the original ligands in the unseen pockets while maintaining adequate diversity, reaching a better performance among a variety of models.
Binding affinity is a crucial metric in measuring the capabilities of pocket-based generation models. Consistent with established practices, we employ the Vina score as the proxy measure of binding affinity. We first probed into the ability to enrich high-affinity molecules, with the Vina score of the original ligands in the test set pockets as references. On average, approximately 47.2% of the molecules generated by Token-Mol demonstrated higher affinity, surpassing those produced by baseline models. We further explored the overall affinity distribution of generated molecules (Fig. 3a and Supplementary Table 1). From both the median and mean perspectives, the performance of the Token-Mol did not obviously inferior from each optimal value. When viewed from the perspective of the entire distribution, there was also no statistically significant difference in the Vina score distribution of the molecules generated by Token-Mol compared to all the baseline models. Considering the above, it can be concluded that the Token-Mol is capable of generating molecules with binding affinities comparable to those produced by specialized models through fine-tuning or training from scratch. Even though there is no statistical difference, it can be observed that the Vina score distribution of two graph-based models, Pocket2Mol and TargetDiff, extend into the region of value less than −10, which is considered to indicate good affinity. However, many of these results are possibly outliers caused by hallucinations56, displaying low Vina scores but containing obvious structural anomalies that render them unsuitable as drug candidates in reality. These concerns are further explored in the section Pocket-based generation on real-world targets.
a Comparison of the average molecular properties distribution in the test set pockets (n = 77) for the molecules generated by Token-Mol and other baseline models (two models have different sample sizes due to the failed generation: GraphBP, n = 53; TargetDiff, n = 74). For monotonic metrics, significance markers have been noted with Token-Mol serving as the reference group, while the light blue area indicates the ideal range for interval metrics. A detailed description of the metrics can be found in the Benchmark of Methods section. The data are shown with box plots, which display the median at the center line, upper and lower quartiles as box limits, and 1.5x interquartile range as whiskers. b Independent distributions of all detectable torsion angles for each model, where n represents the number of detected torsion angles. c Distributions of frequently occurring torsion angles (n = 48) that can be jointly detected in the selected models. In (a) & (c), significance tests were analyzed with a two-sided Mann-Whitney U test, p-values adjusted for multiple comparisons using the Bonferroni correction. Other details are described in the Methods section. All experimental groups were independently compared to the control group (Token-Mol), detailed p-values can be found in Supplementary Table 9. *p < 0.05, **p < 0.01, ***p < 0.001, ****p < 0.0001. Source data are provided as a Source Data file.
Physiochemical properties of molecules play a pivotal role in drug-likeness of drug candidates. In this regard, Token-Mol significantly outperforms the graph-based models in generating molecules with better QED and SA score, exceeding 5 ~ 10% benchmarks, thereby demonstrating its proficiency in creating more drug-like molecules. Compared to the sequence-based model TamGen, Token-Mol shows no statistical difference in QED but performs worse in synthetic accessibility. We analyze these two metrics fundamentally, focusing on molecular structure (Supplementary Table 3). TamGen incorporates a VAE-based contextual encoder sampling the corresponding ligands within the pocket54, resulting in generated molecular structures that closely resemble the originals, which aligns with previous observations of the model’s poor molecular diversity. We suppose that this mechanism enables the generated molecules to exhibit more reasonable structures, particularly in substructure features. Since the penalty terms contributing to the SA Score, such as the number of chiral centers, ring and macrocyclic structure are quite similar between Token-Mol and TamGen, the significant difference could chiefly arises from the fragments term that constitutes the main components of the SA score57: From TamGen, approximately 10% fewer substructure features are extracted compared to those from Token-Mol. Moreover, the sampling of known ligand information in TamGen may lead to the incorporation of more common fragments, which could subsequently result in a lower SA score for the generated molecules.
Additionally, analysis from the perspective of molecular structural information yields other interesting conclusions: Token-Mol incorporates three-dimensional information through torsional angles, enriching the number of torsional angles and rotatable bonds. This may allow the generation of more flexible ligands that can better fit certain uniquely shaped pockets, as well as increasing molecular diversity. Compared to TamGen which is also sequence-based, Token-Mol does not exhibit distinct differences in other structural features while incorporating 3D information. For instance, the proportion of macrocyclic structures or fused ring systems is much lower in Token-Mol than in graph-based baseline models, and it is these structural features that enhance the performance of Token-Mol in terms of QED and SA scores. The capabilities of Token-Mol in molecular structure provides a potential third pathway for molecular representation paradigms, bridging the gap between 2D sequence-based and 3D graph-based approaches, and holds promise for overcoming some inherent limitations of both methods.
In the three additional physicochemical properties closely related to drug-likeness, the overall distributions of molecules generated by Token-Mol for LogP and molecular weight entirely fall within the ideal range. Compared to the results from other models, Token-Mol exhibits a moderate distribution position and range. The metric TPSA determines the oral bioavailability and membrane permeability of molecules58, with values below 140 Å2 for cell membrane traversal and below 90 Å2 for blood-brain barrier penetration. The TPSA distribution of molecules generated by Token-Mol falls within the range of 70-100 Å2, which is more reasonable compared to other baseline models, suggesting superior absorption and potential for further drug discovery in central nervous system diseases59.
Beyond metrics such as binding affinity and molecular properties, the fidelity of torsion angles within generated molecules needs to be considered. Torsion angles will be used as an indicator to evaluate the reasonableness of the initial conformation. A molecule with torsion angle distribution closer to that of the ground truth molecule suggests that its conformation is more likely to be closer to the real molecule and does not violate inherent physical constraints. Moreover, excessively twisted torsion angles in the initial conformation can induce the conformation’s energy to become trapped in local minima during molecular docking, making it difficult to escape and causing deviations in the docking results. Therefore, reasonable torsion angles are also beneficial for virtual screening based on docking.
Our analysis involved the examination of torsion angles within the 3D conformations of approximately 100,000 molecules from the training set in CrossDocked2020 dataset as a reference (Supplementary Fig. 1), we extracted a total of 273 different types of torsion angle distributions. Subsequently, we curated a subset of torsion angles, characterized by their abundance and non-random distribution, enabling an in-depth comparative analysis. Jensen-Shannon divergence (JSD) is used to assess the disparity between the torsion angle distributions in the test set and those of the molecules generated by the models.
We first conducted a comprehensive evaluation to examine all detectable dihedral angles. For the TamGen, the conformations we used were obtained using the ETKDG method from RDKit, which is a widely used conformer generation algorithm that incorporates torsion angle preferences derived from experimental data to refine the initial conformations generated by distance geometry methods60. In addition, utilizing ETKDG ensures a fair comparison with Token-Mol, as our approach also derives the initial conformations from ETKDG, followed by a subsequent refinement with the generated torsion angle tokens.
However, independent assessments of the torsion angle distributions for molecules generated by each model (Fig. 3b) indicate that Token-Mol may capture torsion angles that occur very infrequently in the reference molecular set, achieving approximately 90% recovery for these torsion angles, while the majority of baseline models fell around 60%-80%. This discrepancy of recovery presents a challenge for making fair comparisons of the overall distribution landscape of all detectable torsion angles between each model. Additionally, it explains why the distribution of Token-Mol exhibits outliers with JSD greater than 0.4. Since the model directly learns the numerical distribution of torsion angles, it may struggle to accurately capture the distributions of less frequently occurring torsion angles, resulting in performance that is inferior to the experimentally based ETKDG method.
While in the more common torsion angles, the advantages of learning the numerical distribution of dihedral angles are clearly evident. We selected 48 frequently occurring torsion angles that were present in molecules generated by all the selected models, with each angle appearing more than 1,000 times. This indicates that these torsion angles exist in at least 1% of the reference molecules. We plotted the distribution of these torsion angles (Fig. 3c). From the plots, it is evident that Token-Mol exhibited significantly lower JSD values for these frequently occurring torsion angles compared to the other models. This suggests that Token-Mol can more effectively learn the numerical information associated with torsion angles that occur with sufficient frequency, aligning with our initial intent to use torsion angles as a representation of molecular three-dimensional information.
Eventually, we calculated the average molecular generation time for each model. A faster generation speed may significantly boost researchers’ efficiency by facilitating the acquisition of a more diverse array of molecules in a shorter timeframe and by speeding up the processes of screening and validating the generated compounds. This efficiency also reduces the demand for computational resources, enabling researchers with limited resources to effectively utilize the model.
To ensure a fair comparison, we measured the cumulative time spent by each model in sampling pockets and generating molecules until an output file (in sdf/mol2 format) was obtained. As shown in Supplementary Table 13, when compared to models utilizing geometric deep learning frameworks, Token-Mol demonstrated a remarkably higher generation speed, averaging approximately 35 times faster for individual molecules. This efficiency stems from the different methodologies adopted by competing models. For instance, Pocket2Mol necessitates extensive sampling of molecular objects, excluding invalid or duplicated molecules to maintain diversity and validity. Similarly, TargetDiff requires performing thousands of rounds of sampling on the atoms within the pocket before molecular generation, ensuring high-quality outputs but significantly impeding the generation process for both models. In comparison to TamGen, which is also based on large language models, Token-Mol’s generation speed is relatively less competitive. We attribute this to differences in model architecture. Token-Mol requires the computation of multi-head conditional attention in the fusion block during each inference, which affects the inference speed. Compared to TamGen, Token-Mol also requires additional inference for the torsion angle tokens, which necessitates longer sequence lengths and a larger vocabulary. These factors contribute to an increase in inference time. Additionally, TamGen is developed using the Fairseq toolkit, and the differences in model encapsulation may further contribute to variations in inference speed.
Drug design for real-world targets
To evaluate the generatability of models in designing drug candidates for real-world therapeutic targets, we selected 8 targets from three important protein families, namely kinases, G-protein coupled receptors (GPCRs) and viral proteins, which had been widely studied in structure-based drug design61,62,63 and molecular generation64,65,66,67. Specially, our selection includes a unique dimeric pocket from Programmed cell death 1 ligand 1 (PD-L1), aiming to explore the models’ capability in designing small-molecule modulators for protein-protein interactions.
To mimic a realistic drug discovery scenario, we designed a process similar to virtual screening. This involved generating an equal number of molecules targeting various receptors, followed by performing molecular docking to identify high-affinity candidates. Subsequently, we filtered these candidates based on their QED and SA Scores. Our goal was to produce potent drug-like molecules that possess high affinity to the target, excellent drug-likeness, and favorable synthetic accessibility. To this end, we set criteria that a potent drug-like molecule should simultaneously satisfy Vina Score lower than the average Vina Score of reference molecules from its corresponding target (Supplementary Table 7), QED of at least 0.5, and SA Score not exceeding 5.0.
As shown in Supplementary Table 15, our approach generated potent drug-like molecules across all targets, a capability that none of the baseline models achieved. Approximately 20% of the generated molecules met this criterion, with six out of eight targets achieving optimal or second-best proportions. Further analysis of the distributions of Vina Scores and QED (Supplementary Fig. 2, Supplementary Table 4) for the molecules generated by those models reveals that Token-Mol not only produces molecules with high affinity but also ensures they possess desirable properties. This aligns with the results for our test sets, suggesting that our model is capable of identifying promising lead compounds in real-world drug discovery scenarios.
From the perspective of the targets, one factor influencing the results above is that the selected pockets do not all bind molecules with high affinity for the respective targets, as the input pocket centers for molecular generation and the docking grid centers depend on the original ligands. For instance, in the case of DDR1, the original ligand is a low-affinity hit fragment identified through fragment screening68. Therefore, most methods, including Token-Mol, encountered challenges with this target, while TamGen may have achieved optimal results by sampling the original fragments. TamGen also gained advantages in several target pockets with high-affinity original ligands, with the proportion of drug-like molecules being several times higher than that of Token-Mol.
However, our analysis revealed a strong positive correlation between the proportion of drug-like molecules generated by TamGen and the pIC50 values of the original ligands, with a Pearson correlation coefficient of 0.81, while other methods scored below 0.5 (Supplementary Table 8). This does not reflect real drug discovery scenarios, especially when facing targets without reported high-affinity ligands. In such cases, the generated pocket structures may only contain natural ligands, low-affinity ligands obtained through simple screening, or even computational structures without ligands. TamGen’s approach can even be misled. For example, in the case of 3CLPro, the original high-affinity ligand within the pocket is covalent binding, while the actual affinity of the non-covalent, structurally similar ligand telaprevir is 18 μM69,70. In contrast, our method performed exceptionally well for this target, with approximately 25% of the generated molecules surpassing the average affinity of reference ligands while maintaining excellent drug-like properties. Overall, although Token-Mol did not achieve the best results across all targets, it demonstrated stable generalizability, generating an acceptable proportion of promising molecules for unseen targets, showcasing its potential for application in real drug discovery scenarios.
Furthermore, to evaluate the gains of RL within this model framework, we selected cyclin-dependent kinase 2 (CDK2), representing kinases, and the adenosine A2A receptor (ARA2A), representing GPCRs, as two moderately performing targets from two significant families. As shown in Fig. 4, the molecules generated by Token-Mol exhibit favorable drug-likeness, synthesizability, and promising affinity within the target pockets of two proteins that exhibit significant structural and functional differences. These molecules possess more rational structures compared to those generated by other models and display distinct scaffolds between the two different targets.
Comparison between (a) structures and binding modes, and (b) related molecular properties of drug-like molecules with the highest affinity generated for CDK2 and ARA2A by the Token-Mol and baseline models. The detailed information of molecular properties is presented in Supplementary Table 5.
Among the molecules generated by other baseline models, those produced by GraphBP exhibit distorted conformations, while those by Pocket2Mol are simple aromatic ring derivatives and exhibit minimal differences between the two targets. Similar phenomena can also be observed in the molecules generated by the aforementioned two models in other use cases (Supplementary Fig. 3). For the molecules generated by TamGen, the molecule generated to CDK2 is a widely reported pan-JAK inhibitor, with multiple JAK family protein structures containing this ligand available in the PDB database71. Although this molecule does exhibit weak activity against CDK272, it is difficult to ascertain whether the model accurately generated the specific molecule or if it simply overfitted and output a molecule present in the training set. While in the case of ARA2A, the generated molecule is a simple amino acid derivative, as it references the original ligand with a similar low molecular weight. As for TargetDiff, while the molecules demonstrate favorable results in terms of QED and Vina score, it is noteworthy that molecules for two targets contain tricyclic scaffolds and 7-membered cyclic groups, which are challenging to synthesis. This can explain why the molecules generated by TargetDiff have higher Vina scores in the former test, as these groups with large volume occupy as much space as possible within the pocket, creating more hydrophobic contacts. The predicted binding modes in the two selected cases exhibit that, as the molecules generated by Token-Mol fit the shape of the pocket cavity more precisely, whereas those generated by other baseline models only occupy part of the pocket cavity.
To further demonstrate Token-Mol’s capability to generate molecules that resemble real-world ligands, we calculated the similarity of Bemis-Murcko scaffold73 and Fréchet ChemNet Distance74 (FCD) between the molecules generated by Token-Mol and other baseline models and the reference molecules (Supplementary Table 6). The results indicate that while TamGen achieved the highest scaffold similarity for most targets by generating molecules based on the original ligands as references, Token-Mol produced molecules with greater similarity across all tested targets in a series of models that were not constrained by this reference condition. Despite TamGen excelling in scaffold similarity, it did not completely outperform Token-Mol in the FCD comparison, which assesses chemical and biological feature similarities. In contrast, Token-Mol secured higher FCD rankings across most targets, underscoring its advantage in overall similarity. Notably, molecules generated by Token-Mol maintain an acceptable similarity to known ligands while also preserving good diversity, offering hope for the discovery of novel chemical entities in real-world targets.
Simultaneously, we chose ARA2A as the target to visualize the similarity between ligands and generated molecules. We selected several molecules from Token-Mol and TargetDiff that exceeded the average Vina score and QED thresholds of reference molecules (Supplementary Table 7) against ARA2A for display. We present six real ligands of ARA2A, including agonists and antagonists (Supplementary Fig. 4). Notably, adenosine, the leftmost ligand, serves as the natural ligand of ARA2A and contains a purine scaffold. The other discovered ARA2A ligands all possess a nitrogen heterocyclic core as their scaffold, similar to purine, which can be monocyclic, bicyclic, or tricyclic75. From the perspective of medicinal chemists, for the antagonists, which are majority of ARA2A ligands, their structure-activity relationship (SAR) and co-crystallized structures indicate that, in addition to the nitrogen heterocyclic scaffold, there are aromatic rings such as furan, thiophene, or benzene directly connected to the scaffold or located one or two carbon atoms away from it76. These aromatic groups can penetrate more deeply into the internal space of the orthosteric pocket, facilitating hydrophobic interactions with the surrounding lipophilic residues77,78, thereby enhancing the ligand’s affinity for the receptor and enabling strong competition with the natural ligand.
Among the molecules generated by Token-Mol, it can be observed that most contain monocyclic or bicyclic nitrogen heterocyclic scaffolds resembling real-world ligands, whereas those generated by TargetDiff differ obviously from real-world ligands. Furthermore, these molecules with nitrogen heterocyclic scaffolds possess aromatic rings, such as benzene or pyrazole, directly connected to the scaffold. However, we conducted an in-depth analysis of the binding modes of these four ligands, which feature scaffolds similar to those of real ligands. The results demonstrate (Supplementary Fig. 8) that these four molecules do not achieve optimal recovery rates for key interactions, for instance, hydrogen bonds with N253 and E169 and π-π stacking interactions with F168. Most of them only formed interactions with either N253 or F168, while only one molecule exhibits interactions with both residues. This indicates that although our model achieved better results in terms of ligand similarity compared to other models, the target-specific interactions were not well reproduced. One reason for this is the inherent limitations of the docking algorithm used, which leads to discrepancies between the predicted binding poses and the actual ones. On the other hand, the model still has some shortcomings in utilizing information about the protein pocket, which remains a key area for improvement for our model and future pocket-based molecular generation approaches.
Further optimization with reinforcement learning
The content above has already demonstrated that Token-Mol can generate molecules with high drug-likeness, ease of synthesis, and rational structures in the pockets of given targets. However, when compared to the expert models like TargetDiff for pocket-aware generation, the molecules generated by Token-Mol still exhibit lower affinity to pockets from the test set and selected real-world targets (Supplementary Tables 1 and 2). To address this, we employed a reinforcement learning approach proposed by Olivecrona et al.79 to optimize the affinity of generated molecules for specific target pockets. Within this framework, constraints such as conformational clash and drug-likeness are enforced to ensure that the molecules maintain desirable properties. This strategy aims to maximize affinity for target pockets while preserving the excellent molecular properties demonstrated by the model, as detailed in the Methods section. Notably, optimizing geometric graph-based models such as TargetDiff is challenging due to their high complexity, and RL has not yet been applied to these models for 3D pocket-based molecular generation.
We conducted a total of 1,000 steps of reinforcement learning optimization on CDK2 and ARA2A, the two targets used for demonstration in the previous section. Throughout the reinforcement learning process, we recorded the average values of key metrics at each step (Fig. 5a). It can be observed that during the training of the two targets, the reward score essentially converged within 1,000 steps, indicating the stabilization of the agent model’s training. Regarding our primary optimization objective, the Vina score, the average value is optimized from around −8 to approximately −9.5, with no apparent oscillations observed after convergence. As for QED, which serves as a constraint condition, although the reward term in the reward function is binary rather than positively correlated with QED, it was found that the QED value initially increased and then converged as the reinforcement learning steps increased for both targets, suggesting that QED is also optimized under the set reward function. Although different trends were observed in the SA score during the reinforcement learning process for the two targets, the results remained below the threshold of 5, consistent with our previous tests (Supplementary Fig. 5) that focused solely on affinity optimization. These trends demonstrate that our model can achieve optimization in molecule generation tasks for specific target pockets through reinforcement learning under constraints.
a Key metrics such as reward score, Vina score, QED, and SA score during the process of RL. The 2D structure of molecules from the different stages in the RL are also displayed. b The binding modes of selected molecules predicted with QVina2. c Change trends in the predicted affinities of selected molecules for their respective targets using different docking methods. Source data in (a) are provided as a Source Data file.
Additionally, we selected molecules from the first step, the last step, and step before the convergence of the reward score, showcasing the molecule with the highest affinity in those steps (Fig. 5a). From the perspective of specific molecules, it is obvious that the molecular scaffolds undergo substantial changes at different training stages, and the occurrence of unreasonable structures such as tricyclic structures or seven-membered ring groups also decreases. For their binding modes (Fig. 5b), it can be seen that the scaffold gradually fits into the pocket, which explains the gradual improvement of the Vina score during the training process.
Furthermore, to reduce the bias introduced by a single docking method, we conducted additional docking tests using Glide80 and Surflex-dock81 for the molecules presented in Fig. 5c, and the results demonstrate that reinforcement learning indeed optimized the molecules’ affinity for the targets. In the case of CDK2, the docking scores (i.e., the predicted affinities) obtained from all three methods improved as the training steps increased. In ARA2A, a similar trend was observed, with the exception of Glide. Overall, in both targets, the molecules obtained after training convergence achieved the best results across all three docking methods, further confirming the capability of reinforcement learning to optimize the affinity of generated molecules for the target pockets.
Chat to Token-Mol
Token-Mol’s token-only framework confers a significant advantage over traditional regression models by enabling the seamless integration of cutting-edge large-scale model techniques, including prompt learning, mixture of experts (MoE)82, and retrieval-augmented generation (RAG)83. In this context, we demonstrate an instance of prompt learning.
To illustrate this capability, we present several straightforward dialogue use cases. By employing prompt learning, we can control the execution of tasks such as property prediction mentioned in this study. Initially, we insert specific prompts, such as “Predict ESOL” to fine-tune the model. As shown in Supplementary Fig. 6, this enables direct interaction with the model post-prompting, allowing users to request predictions of different molecular properties. In this example, we queried various properties of different molecules, and Token-Mol successfully provided the corresponding predictions. This demonstrates the potential of Token-Mol for engaging in meaningful dialogues with chemists. Users may provide molecular conformations, but since Token-Mol can generate the corresponding conformations, the final output will include only the predicted target properties.
Additionally, future iterations can incorporate RAG. When querying Token-Mol about a specific property of a molecule, the system employs vector search based on embeddings to convert the query into a vector. This vector is then matched with highly relevant vector descriptions from a database to provide contextual information. The query, along with the retrieved context such as spatial structure information and other relevant properties, is then input to Token-Mol, which then generates the answer.
The aforementioned example highlights the unique of token-only models to seamlessly integrate with general models, a capability that is not exhibited by regression models.
Discussion
This study proposes Token-Mol, the inaugural token-only, extensive pre-trained language model tailored for drug design. Rooted in the GPT framework, Token-Mol integrates random causal masking to enhance its flexible applicability across diverse drug design tasks. Additionally, we propose the Gaussian cross-entropy loss function to foster improved acquisition of continuous spatial information throughout model training, thereby notably reinforcing its performance in regression tasks. Furthermore, through the integration of RL, Token-Mol achieves expedited optimization towards predetermined objectives in specific tasks, aiming to achieve desired outcomes efficiently. To substantiate these capabilities, we conducted assessments across three pivotal drug design tasks.
In the pocket-based generation task, Token-Mol achieves results close to expert models in the pocket-based generation task and obtains optimal results in terms of drug-likeness and synthesizability of molecules. Benefit from the rapid inference of the language model, Token-Mol can generate molecules within the pocket in a shorter time. Additionally, tests on specific real-world targets have also demonstrated that our model can obtain molecules with excellent affinity, drug-likeness, and synthesizability under various conditions simulating real-world virtual screening with a higher proportion. For specific optimization goals in the specific targets, we performed reinforcement learning, and the results also proved that Token-Mol can achieve optimization under constraint conditions, demonstrating the broad application potential of our model.
We subsequently evaluated its capability in molecular conformation generation. Token-Mol demonstrated superior performance relative to other SOTA models, exceeding their performance by approximately 24% in COV-P and 21% in MAT-P. Notably, Token-Mol exhibited improved efficacy in molecules with a higher number of rotatable bonds.
Lastly, we assessed its performance in molecular property prediction tasks. Leveraging the advantages of the Gaussian cross-entropy loss function, Token-Mol demonstrated accuracy on par with state-of-the-art models. In regression tasks, Token-Mol outperformed the token-only model RT by approximately 30% and surpassed existing sequence-based methods, approaching the performance of GNN-based methods.
Meanwhile, Token-Mol demonstrates the ability to simplify complex problems, capitalizing on the inherent advantages of large language models. This proficiency is particularly pronounced in sophisticated tasks such as pocket generation, where Token-Mol achieves a good balance of speed and efficacy. Notably, in comparison to the state-of-the-art model TargetDiff, Token-Mol’s inference speed is 35 times faster.
While Token-Mol demonstrates considerable potential, several areas require further enhancement. In this study, we evaluated its performance on only three representative downstream tasks, leaving many others unaddressed. The molecular diversity within the pre-training data is also limited. In comparison to most of the expert models cited in the references, Token-Mol features a larger number of parameters. This relatively substantial model size may impose certain limitations on its deployment and application. However, we believe that the multitasking flexibility afforded by the pre-training and fine-tuning paradigm for the backbone model allows Token-Mol to achieve a favorable balance between size and application potential. Nonetheless, this also poses challenges for the iterative development of larger-scale models in the future.
Future research will focus on optimizing Token-Mol by expanding the training dataset and developing specific components tailored to particular downstream tasks. Comprehensive evaluations across a broader range of drug design tasks will be conducted. Additionally, we aim to integrate Token-Mol with general artificial intelligence models, utilizing techniques from various large language models such as prompt learning, MoE, and RAG. This integration will facilitate direct interaction between researchers and Token-Mol through conversational interfaces, enhancing its role as a research assistant.
In summary, this study presents a token-only foundational model for drug design, introducing the initial version of Token-Mol. Its development offers an approach towards unifying AI drug design models, paving the way for comprehensive drug design using a single foundational model.
Methods
Model architecture
Backbone
Token-Mol is structured with 12 layers of Transformer decoders, each equipped with 8 attention heads. Employing autoregressive approach, Token-Mol predicts both the 2D and 3D structures of molecules while explicitly representing them. To ensure data integrity during autoregressive training and inference, masking matrices are employed to conceal unencoded segments, thus preventing information leakage. The multi-head attention mechanism, integral to the Transformer architecture, empowers Token-Mol to simultaneously attend to diverse subspaces of the input, facilitating the capture of richer information. Within this mechanism, each attention head learns a unique set of weights to compute attention scores for different positions in the input sequence, facilitating the calculation of the input sequence’s representation. By harnessing parallel computation across multiple attention heads, Token-Mol gains the capacity to interpret the input sequence from various perspectives, consequently enhancing its representational capability and generalization performance. The attention mechanism is shown in Eq. 1:
where \(Q\), \(K\), and \(V\) represent the query, key, and value matrices, respectively, and \({d}_{k}\) is the dimension of \(K\).
To indicate the beginning or end of the sequence during sampling, it is necessary to define a start token and an end token, denoted as “<|beginoftext | >” and “<|endofmask | >”, respectively. During the training, the “<|beginoftext | >” token is concatenated to the sequence as the input. The objective during the training phase is to minimize the negative log-likelihood, as shown in Eq. 2:
During the generation phase, molecular strings are generated using an autoregressive approach based on smiles, which are then concatenated together as shown in Eq. 3:
Gaussian cross-entropy (GCE) loss function
Language models commonly employ the cross-entropy loss function as their primary loss function. The cross-entropy loss function is generally utilized to quantify the disparity between the probability distribution produced by the model and the actual labels. Assuming a classification problem, for each sample, the model outputs a probability distribution indicating the likelihood of the sample belonging to each class. The genuine labels, on the other hand, are one-hot encoded vectors representing the class to which the sample belongs. The cross-entropy loss function is employed to measure the dissimilarity between the probability distribution produced by the model and the genuine labels. In the context of language models, the specific equation for calculating the cross-entropy loss function is as follows:
Here, \(m\) represents the batch size, and \(n\) denotes the length of each data point. \({y}_{{ij}}\) signifies the j-th element of the true label for the i-th data point (taking values of 0 or 1), and \(q({x}_{{ij}})\) represents the j-th element of the probability distribution output by the model. A lower cross-entropy loss indicates a closer resemblance between the model’s output probability distribution and the true labels, thereby reflecting better model performance.
However, the conventional employment of the cross-entropy loss function is primarily confined to discrete category prediction tasks, rendering it inadequate for continuous value prediction endeavors such as regression. In our investigation, we encounter a spectrum of tasks encompassing both classification, exemplified by SMILES strings, and regression, including torsion angles and molecular property prediction. In response to this challenge, the regression transformer disassembles each digit of continuous numerical values into distinct tokens and incorporates specialized numerical embeddings. Nonetheless, their methodology does not fundamentally rectify the issue, as it neglects to facilitate the model’s comprehension of the relative magnitude relationships inherent in numerical values. Notably, the model uniformly assigns loss values in the event of inaccurate predictions, irrespective of the predicted token. For instance, if the label denotes a torsion angle of \(\pi\), erroneous predictions of 3 or 0 result in identical loss values.
To surmount this constraint, we propose the GCE loss function tailored specifically for regression tasks. As shown in Fig. 1, for each prediction, we construct a Gaussian distribution centered around the label’s value, thereby adjusting the probabilities of surrounding tokens from their original values of 0 to correspond with the Gaussian distribution. Consequently, in Eq. 5, where \(({px}_{{ij}})\) is initially denoted as either 0 or 1, we modify it to signify a Gaussian distribution centered around the label’s value, thereby effectively mitigating the issue. The GCE loss function is defined as:
Through the implementation of this configuration, tokens in proximity to the label are allocated greater weights, whereas tokens distanced from the label receive diminished weights. This methodology facilitates the comprehensive learning of relationships between numerical values by the model.
Pocket encoder and fusion block
We utilized the protein pocket encoder trained by Odin et al.65, maintaining its parameters frozen throughout the training process. To merge the information derived from the pocket encoder with the existing molecule information within the model, we employed a multi-head condition-attention mechanism. Diverging from traditional cross-attention mechanisms, our approach involved the adoption of a multi-head condition-attention mechanism to fully integrate the information generated at each autoregressive step into subsequent generations. This mechanism treats each token produced during autoregression as a prerequisite condition for iterative generation. Consequently, the entire query, key, and value matrices stem from the original sentence itself. Particularly, as shown in Fig. 1c, this condition-attention fundamentally regards protein information as prompt data, enabling the model to analyze the interaction between protein information and previously generated tokens.
Reinforcement learning
REINFORCE84, an RL algorithm based on policy gradients, utilizes Monte Carlo methods to determine the optimal policy, and it has been applied in various molecular generation methods79,85,86,87. In this work, we used its variant REINVENT79 algorithm to optimize the model. We aim to optimize the pre-trained model parameter \(\theta\) for the task of generating molecular sequences, so that the optimized model can generate molecules with desired properties, as shown in Eq. 6:
The presented formula elucidates the policy \({\pi }_{\theta }\) as contingent upon model parameters \(\theta\), with τ delineating a trajectory spanning states \({s}_{t}\) and actions \({a}_{t}\) from the initial time step \(t=0\) to the terminal step \(t=T\). The action probabilities of a sequence \(A\) are defined as \(P\left(A\right)={\prod }_{t}^{T}{\pi }_{\theta }\left({a}_{t} | {s}_{t}\right)\), and \(\log {\pi }_{\theta }\left({a}_{t} | {s}_{t}\right)\) represents the sum of the log probabilities of each action given the prior state. According to the REINFORCE, the objective function can be derived as follows:
The reward at \(t\) within the trajectory is designated as \(r\left({s}_{t},{a}_{t}\right)\). Equation 8 concisely portrays the aggregate reward accumulation from time step \(t\) to the final state, encapsulating the core essence of the trajectory’s reward accumulation dynamics.
Within the molecular generation realm, computing \(G\left({s}_{t},{a}_{t}\right)\) for each step in a trajectory, corresponding to incomplete molecules, proves impracticable given the inability to reliably estimate the total molecule score from its constituent fragments alone. This scenario converges with the sparse reward paradigm prevalent in reinforcement learning. To surmount this challenge and enable the deployment of the REINFORCE algorithm in this context, we advocate for equating the complete molecule score with the score at each step, thereby reformulating \(J(\theta )\) as:
In REINVENT, two policies are defined: the Prior policy and the Agent policy, with their respective action probabilities denoted as \({P\left(A\right)}_{{Prior}}\) and \({P\left(A\right)}_{{\mathbb{A}}}\). An augmented likelihood is introduced as \(\log {P(A)}_{{\mathbb{U}}}={P\left(A\right)}_{{Prior}}+\sigma {{{\mathcal{R}}}}\left(A\right)\), where \({{{\mathcal{R}}}}\left(A\right)\) represents the reward of sequence A. The expression for \(G\left(A\right)\) is restructured to \({[\log {P\left(A\right)}_{{\mathbb{A}}}-\log {P\left(A\right)}_{{\mathbb{U}}}]}^{2}/\log {P\left(A\right)}_{{\mathbb{A}}}\). Consequently, the \(J\left(\theta \right)={[\log {P\left(A\right)}_{{\mathbb{A}}} -\log {P\left(A\right)}_{{\mathbb{U}}}]}^{2}\).
Reward function
To optimize affinity, the reward function is designed to prioritize molecules that meet a promising Vina score. Molecules that exceed the affinity threshold and comply with the QED constraints receive additional rewards. Molecules that do not meet the affinity threshold or are non-compliant are penalized. Thus, the reward function \({{{\mathcal{R}}}}\left(m\right)\) is described as Eq. 10:
where m is molecule; Vina(m) represents Vina score, where a smaller value is preferable; init is the threshold value of Vina score, which is set as −8. To avoid the issue of sparse rewards, we have imposed a reward weight ω, set as 5, and a proper penalty term set as 0.1 for molecules which do not meet the threshold of Vina score. \({\theta }_{{{{\rm{qed}}}}}\) is a reward term for molecules that comply with the restraint of QED, describe as Eq. 11:
Random causal masking
The conventional left-to-right causal masking method exclusively relies on the context preceding the generated tokens, thereby proving inadequate for accomplishing the infilling task. To enhance the adaptability to a wider array of downstream tasks, we opted to train it using random causal masking88,89 in lieu of the left-to-right causal masking.
Throughout the training process, we commence by sampling the number of mask spans from a Poisson distribution centered around a mean of 1, while enforcing a limit that confines the count of mask spans within the range of 1 to 6. Following this, we employ random sampling to establish the length of each span. The locations of the masks are identified using placeholders denoted as “<|mask:k | >”, with “k” signifying the index of the specific mask span. Subsequently, the content subjected to masking is affixed to the sequence’s end, preceded by the “<|mask:k | >” prefix. In the inference phase, a sequence incorporating placeholders “<|mask:k | >” is presented as the contextual input, complemented by the addition of “<|mask:k | >” at the sequence’s conclusion to steer the model’s generation of content for the “<|mask:k | >” segments.
Benchmark
Molecular conformer generation
COV and MAT scores are fundamental metrics utilized as benchmarks in the Conformer generation task, extensively employed across conformer generation endeavors. COV and MAT metrics are further categorized into Recall and Precision measures. Recall is defined as:
where \({S}_{g}\) denotes the ensemble of generated conformations, while \({S}_{r}\) represents the ensemble of true conformations. \(C\) and \(\hat{C}\) represent individual conformations from the sets of true and generated conformations, respectively, with \(\delta\) acting as the threshold, set at 1.25 Å. The COV metric evaluates the percentage of structures in one set that are encompassed by another set, where inclusion indicates that the RMSD between two conformations falls below a specified threshold \(\delta\). Conversely, the MAT scores gauge the average RMSD between conformers in one set and their nearest counterparts in another set. Precision, as described in the provided equation, interchanges \({S}_{g}\) and \({S}_{r}\). Consequently, while Recall entails comparing each true conformation with all generated conformations, Precision involves comparing each generated conformation with all true conformations. Precision typically accentuates quality, while Recall is more concerned with diversity.
Pocket-based molecular generation
Unless otherwise specified, the following molecular descriptors and molecular fingerprints are calculated using RDKit (version 2022.09.1).
Valid
Validity of the generated 3D structure, calculated as the proportion of 3D structures that can be translated into canonical SMILES.
IntDiv
Internal diversity90, an assessment of the distinctiveness of molecules within a molecular set, calculated using Tanimoto distance based on ECFP4 fingerprints91,92, which can be described as:
where \({{{\mathcal{S}}}}\) is the generated molecules set, \(d\) is Tanimoto distance, which is defined as 1 minus the Jaccard similarity coefficient calculated using molecular fingerprints.
#Circle
a locality-based chemical space coverage measure93. Described as:
where \(t\) is a distance threshold set as 0.75. \({{{\mathcal{C}}}}\) is a subset of \({{{\mathcal{S}}}}\), containing a specific molecule x and it’s non-neighboring molecules. Due to the sensitivity of this metric to the number of generated molecules \(\left|{{{\mathcal{S}}}}\right|\) and the varying counts of available molecules produced by different models for a given target, this value is calculated by randomly selecting 80 molecules for each target.
Simi
Jaccard similarity between two molecular sets, as mentioned above.
Vina score
The binding energy of ligands to protein pockets by using QVina294.
Higher score
The average ratio of generated molecules exceeding the original molecule within each pocket.
MW
Molecular weights. the optimal range is between 100 and 60095.
TPSA
topological polar surface area96, the optimal range is between 0 and 14058.
LogP
The octanol-water partition coefficient, typically falls within the range of −0.4 to 5.6 for the majority of druglike compounds97.
Lipinski
Lipinski’s rule-of-five98, which consists of the following criteria: the molecular weight of the compound is less than 500 Daltons; the number of hydrogen bond acceptors in the compound’s structure (including hydroxyl and amino groups) does not exceed 5; the number of hydrogen bond donors in the compound does not exceed 10; the logarithm of the compound’s logP falls within the range of −2 to 5. the number of rotatable bonds in the compound does not exceed 10.
QED
Quantitative estimation of drug-likeness99, subsequent researchers have normalized the properties of Lipinski’s rule-of-five into continuous values ranging from 0 to 1, where higher values indicate higher drug-likeness of molecules.
SA score
Synthetic accessibility score57, the SA score represents the synthesis accessibility of molecules and is designated on a scale of 1 to 10, based on chemical expertise. A higher value indicates greater difficulty in synthesis.
Significance tests
All significance tests were conducted using the Mann-Whitney U test with SciPy 1.10.0100 and adjusted for multiple comparisons using the Bonferroni correction with statsmodels101. Prior to performing these tests, the Kolmogorov-Smirnov test was used to confirm that the data groups did not conform to a normal distribution.
Molecular property prediction
During the evaluation, we employ greedy decoding for property prediction. Each method is run independently three times, and the average and standard deviation are reported. We utilize the area under the receiver operating characteristic curve (ROC-AUC)102 metric to evaluate the classification datasets. For the regression datasets, root mean square error (RMSE) is used to quantify the average difference between predicted values and actual values, which is often applied in regression analysis.
For information regarding the model size of all baseline models in the benchmark, please refer to Supplementary Table 12.
Dataset
Pretraining
The pretraining dataset is sourced from the geometric ensemble of molecules (GEOM) dataset, which includes conformers for 317,000 species, augmented with experimental data spanning biophysics, physiology, and physical chemistry domains103. These conformers are generated using sophisticated sampling methods coupled with semi-empirical density functional theory (DFT). Following this, data curation procedures are implemented to exclude molecules containing heavy metals, lacking torsions, or test molecules. Subsequently, each molecule underwent pre-training with a maximum of 30 conformers, yielding a final dataset containing 8,452,080 entries.
Pocket-based molecular generation
The dataset utilized for pocket-based generation is the same as existing work, which is an open-available dataset consisted of over 20 million of pose pairs from nearly 20,000 protein-ligand complexes from CrossDock2020104. Following the protocol outlined in previous studies50,65, we discarded all poses with an RMSD greater than 2 Å, and additionally partitioned the dataset into training and testing sets based on a principle of sequence similarity less than 40%, ensuring a fairer evaluation of the generalizability to unknown pockets. Additionally, we excluded protein-ligand pairs which ligand lacked torsion angles from the dataset, resulted in slightly smaller training and testing sets compared to several models we mention subsequently.
The real-world targets’ structure are download from RCSB PDB105, and reference molecules corresponding to each targets are collected from ChEMBL30 database106. Molecules with a Kd or Ki value less than 1,000 nM for a given target are considered active, counting into the reference sets. If the number of molecules meeting this criterion is low, molecules with an IC50 value less than 1,000 nM are also included in the reference sets. The collected molecules are deduplicated based on SMILES and molecules containing salts are removed.
Molecular conformation generation
We performed fine-tuning using datasets consistent with those utilized in earlier studies34,38,40,42. For the test set, we employed a dataset akin to Tora3D26. Test set I contains 200 molecules, each with fewer than 100 conformations. Test set II comprises 1,000 randomly selected molecules with conformation counts distributed similarly to the entire dataset, spanning from 0 to 500.
Molecular property prediction
We assembled a comprehensive collection of 12 datasets sourced from MolecularNet107 and therapeutics data commons (TDC)108, accompanied by comprehensive datasets descriptions provided in the Supplementary. Drawing upon MolecularNet’s established status as a primary benchmark for molecular property prediction, our selection comprised six classification datasets and three regression datasets. Furthermore, within TDC, widely acclaimed as the premier public benchmark for ADMET analysis, we specifically identified three datasets characterized by relatively homogeneous data distributions. Each dataset underwent three random partitions following the 8:1:1 ratio for testing.
Data availability
The datasets utilized in our study are as follows: The GEOM dataset is available at https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/JNGTDF. For pocket-based molecular generation dataset is provided at https://zenodo.org/records/15194424. The molecular conformation generation, the dataset can be accessed at https://github.com/zimeizhng/Tora3D. Lastly, the datasets for property prediction are available at https://moleculenet.org/datasets-1 and https://tdcommons.ai/single_pred_tasks/adme/. Source data are provided with this paper.
Code availability
The code used in the study is publicly available from the GitHub repository (https://github.com/jkwang93/Token-Mol) or Zenodo (https://doi.org/10.5281/zenodo.1511068).
References
Devlin, J., Chang, M.-W., Lee, K. & Toutanova, K. BERT: Pre-training of deep bidirectional transformers for language understanding. In: Proceedings of the 2019 conference of the North American chapter of the association for computational linguistics: human language technologies, volume 1 (long and short papers) (2019).
Radford, A., Narasimhan, K., Salimans, T. & Sutskever, I. Improving language understanding by generative pre-training. https://openai.com/index/language-unsupervised (2018).
Chithrananda, S., Grand, G. & Ramsundar, B. ChemBERTa: large-scale self-supervised pretraining for molecular property prediction. arXiv preprint, arXiv:2010.09885 (2020).
Rong, Y. et al. Self-supervised graph transformer on large-scale molecular data. In Proceedings of the 34th international conference on neural information processing systems (2020).
Kim, H., Lee, J., Ahn, S. & Lee, J. R. A merged molecular representation learning for molecular properties prediction with a web-based service. Sci. Rep. 11, 11028 (2021).
Liu, S. et al. Pre-training Molecular Graph Representation with 3D Geometry. In International Conference on Learning Representations (2022).
Wang, Y., Wang, J., Cao, Z. & Barati Farimani, A. Molecular contrastive learning of representations via graph neural networks. Nat. Mach. Intell. 4, 279–287 (2022).
Ross, J. et al. Large-scale chemical language representations capture molecular structure and properties. Nat. Mach. Intell. 4, 1256–1264 (2022).
Zeng, X. et al. Accurate prediction of molecular properties and drug targets using a self-supervised image representation learning framework. Nat. Mach. Intell. 4, 1004–1016 (2022).
Li, H. et al. A knowledge-guided pre-training framework for improving molecular representation learning. Nat. Commun. 14, 7568 (2023).
Lin, X. et al. PanGu Drug Model: learn a molecule like a human. Sci. China Life Sci. 66, 879–882 (2023).
Ying, C. et al. Do transformers really perform bad for graph representation? In Proceedings of the 35th International Conference on Neural Information Processing Systems. (2024).
Shuai, R. W., Ruffolo, J. A. & Gray, J. J. IgLM: Infilling language modeling for antibody sequence design. Cell Syst. 14, 979–989.e974 (2023).
Nijkamp, E., Ruffolo, J. A., Weinstein, E. N., Naik, N. & Madani, A. ProGen2: Exploring the boundaries of protein language models. Cell Syst. 14, 968–978.e963 (2023).
Ferruz, N., Schmidt, S. & Höcker, B. ProtGPT2 is a deep unsupervised language model for protein design. Nat. Commun. 13, 4348 (2022).
Rives, A. et al. Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. Proc. Natl Acad. Sci. USA 118, e2016239118 (2021).
Xia, J., Zhu, Y., Du, Y. & Li, S. Z. A systematic survey of chemical pre-trained models. In Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence (2023).
Weininger, D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Computer Sci. 28, 31–36 (1988).
Krenn, M., Häse, F., Nigam, A., Friederich, P. & Aspuru-Guzik, A. Self-referencing embedded strings (SELFIES): a 100% robust molecular string representation. Mach. Learn.: Sci. Technol. 1, 045024 (2020).
Wang, S., Guo, Y., Wang, Y., Sun, H. & Huang, J. SMILES-BERT: large scale unsupervised pre-training for molecular property prediction. In Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics. ACM (2019).
Bagal, V., Aggarwal, R., Vinod, P. K. & Priyakumar, U. D. MolGPT: molecular generation using a transformer-decoder model. J. Chem. Inf. Modeling 62, 2064–2076 (2022).
Irwin, R., Dimitriadis, S., He, J. & Bjerrum, E. J. Chemformer: a pre-trained transformer for computational chemistry. Mach. Learn.: Sci. Technol. 3, 015022 (2022).
Christofidellis, D. et al. Unifying molecular and textual representations via multi-task language modelling. In International Conference on Machine Learning. (PMLR, 2023).
Touvron, H. et al. Llama 2: Open foundation and fine-tuned chat models. arXiv preprint, arXiv:2307.09288 (2023).
Hu, W. et al. Strategies for pre-training graph neural networks. In International Conference on Learning Representations (2020).
Rong, Y. et al. Self-supervised graph transformer on large-scale molecular data. In Advances in Neural Information Processing Systems (2020).
Xia, J. et al. Mole-BERT: rethinking pre-training graph neural networks for molecules. In International Conference on Learning Representations (2023).
Fang, X. et al. Geometry-enhanced molecular representation learning for property prediction. Nat. Mach. Intell. 4, 127–134 (2022).
Zhou, G. et al. Uni-Mol: A universal 3d molecular representation learning framework. In International Conference on Learning Representations (2023).
Team, G. et al. Gemini: A family of highly capable multimodal models. arXiv preprint, arXiv:2312.11805 (2023).
Team, G. et al. Gemini 1.5: Unlocking multimodal understanding across millions of tokens of context. arXiv preprint, arXiv:2403.05530 (2024).
Research AI4Science, M. & Azure Quantum, M. The impact of large language models on scientific discovery: a preliminary study using GPT-4. arXiv preprint, arXiv:2311.07361 (2023).
Born, J. & Manica, M. Regression Transformer enables concurrent sequence regression and generation for molecular language modelling. Nat. Mach. Intell. 5, 432–444 (2023).
Flam-Shepherd, D. & Aspuru-Guzik, A. Language models can generate molecules, materials, and protein binding sites directly in three dimensions as XYZ, CIF, and PDB files. arXiv preprint, arXiv:2305.05708 (2023).
Zholus, A. et al. BindGPT: A scalable framework for 3D molecular design via language modeling and reinforcement learning. In Proceedings of the AAAI Conference on Artificial Intelligence (2025).
Mansimov, E., Mahmood, O., Kang, S. & Cho, K. Molecular geometry prediction using a deep generative graph neural network. Sci. Rep. 9, 20381 (2019).
Simm, G. N. C. & Hernández-Lobato, J. M. A generative model for molecular distance geometry. In Proceedings of the 37th International Conference on Machine Learning. (PMLR, 2020).
Xu, M., Luo, S., Bengio, Y., Peng, J. & Tang, J. Learning neural generative dynamics for molecular conformation generation. In International Conference on Learning Representations (2021).
Xu, M. et al. An end-to-end framework for molecular conformation generation via bilevel programming. In International conference on machine learning. (PMLR, 2021)
Xu, M. et al. GeoDiff: a geometric diffusion model for molecular conformation generation. In International Conference on Learning Representations (2022).
Jing, B., Corso, G., Chang, J., Barzilay, R. & Jaakkola, T. Torsional diffusion for molecular conformer generation. In Advances in Neural Information Processing Systems (2022).
Zhang, Z. et al. Tora3D: an autoregressive torsion angle prediction model for molecular 3D conformation generation. J. Cheminformatics 15, 57 (2023).
Ganea, O.-E. et al. GeoMol: torsional geometric generation of molecular 3D conformer ensembles. In Advances in Neural Information Processing Systems (2021).
Zhang, H. et al. SDEGen: learning to evolve molecular conformations from thermodynamic noise for conformation generation. Chem. Sci. 14, 1557–1568 (2023).
Chen, T. & Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining. (ACM, 2016).
Wu, Z. et al. Knowledge-based BERT: a method to extract molecular features like computational chemists. Briefings in Bioinformatics 23 (2022).
Heid, E. et al. Chemprop: A machine learning package for chemical property prediction. J. Chem. Inf. Modeling 64, 9–17 (2024).
Notwell, J. H. & Wood, M. W. ADMET property prediction through combinations of molecular fingerprints. arXiv preprint, arXiv:2310.00174 (2023).
Liu, M., Luo, Y., Uchino, K., Maruhashi, K. & Ji, S. Generating 3D molecules for target protein binding. In Proceedings of the 39th International Conference on Machine Learning. (PMLR, 2022).
Peng, X. et al. Pocket2mol: efficient molecular sampling based on 3 d protein pockets. In International Conference on Machine Learning. (PMLR, 2022).
Guan, J. et al. 3D equivariant diffusion for target-aware molecule generation and affinity prediction. In The Eleventh International Conference on Learning Representations (2023).
Zheng, K. et al. Structure-based drug design benchmark: Do 3d methods really dominate? In ICML 2024 AI for Science Workshop (2024).
Liu, H. et al. How good are current pocket-based 3D generative models?: The benchmark set and evaluation of protein pocket-based 3d molecular generative models. Journal of Chemical Information and Modeling (2024).
Wu, K. et al. TamGen: drug design with target-aware molecule generation through a chemical language model. Nat. Commun. 15, 9360 (2024).
Chan, L., Kumar, R., Verdonk, M. & Poelking, C. A multilevel generative framework with hierarchical self-contrasting for bias control and transparency in structure-based ligand design. Nat. Mach. Intell. 4, 1130–1142 (2022).
Renz, P., Van Rompaey, D., Wegner, J. K., Hochreiter, S. & Klambauer, G. On failure modes in molecule generation and optimization. Drug Discov. Today.: Technol. 32-33, 55–63 (2019).
Ertl, P. & Schuffenhauer, A. Estimation of synthetic accessibility score of drug-like molecules based on molecular complexity and fragment contributions. J. Cheminformatics 1, 8 (2009).
Veber, D. F. et al. Molecular Properties That influence the oral bioavailability of drug candidates. J. Medicinal Chem. 45, 2615–2623 (2002).
Hitchcock, S. A. & Pennington, L. D. Structure−brain exposure relationships. J. Medicinal Chem. 49, 7559–7583 (2006).
Riniker, S. & Landrum, G. A. Better informed distance geometry: Using what we know to improve conformation generation. J. Chem. Inf. Modeling 55, 2562–2574 (2015).
Liu, S. et al. Discovery of Novel Benzo[4,5]imidazo[1,2-a]pyrazin-1-amine-3-amide-one derivatives as anticancer human A2A adenosine receptor antagonists. J. Medicinal Chem. 65, 8933–8947 (2022).
Clyde, A. et al. High-throughput virtual screening and validation of a SARS-CoV-2 main protease noncovalent inhibitor. J. Chem. Inf. Modeling 62, 116–128 (2022).
Sun, C. et al. Novel small-molecule PD-L1 Inhibitor Induces PD-L1 internalization and optimizes the immune microenvironment. J. Medicinal Chem. 66, 2064–2083 (2023).
Zhang, O. et al. Learning on topological surface and geometric structure for 3D molecular generation. Nat. Computational Sci. 3, 849–859 (2023).
Zhang, O. et al. ResGen is a pocket-aware 3D molecular generation model based on parallel multiscale modelling. Nat. Mach. Intell. 5, 1020–1030 (2023).
Zhavoronkov, A. et al. Deep learning enables rapid identification of potent DDR1 kinase inhibitors. Nat. Biotechnol. 37, 1038–1040 (2019).
Li, S. et al. LS-MolGen: Ligand-and-structure dual-driven deep reinforcement learning for target-specific molecular generation improves binding affinity and novelty. J. Chem. Inf. Modeling 63, 4207–4215 (2023).
Murray, C. W. et al. Fragment-based discovery of potent and selective DDR1/2 inhibitors. ACS Medicinal Chem. Lett. 6, 798–803 (2015).
Qiao, J. et al. SARS-CoV-2 Mpro inhibitors with antiviral activity in a transgenic mouse model. Science 371, 1374–1378 (2021).
Kneller, D. W. et al. Malleability of the SARS-CoV-2 3CL Mpro active-site cavity facilitates binding of clinical antivirals. Structure 28, 1313–1320.e1313 (2020).
Williams, N. K. et al. Dissecting Specificity in the janus kinases: The Structures of JAK-specific inhibitors complexed to the JAK1 and JAK2 protein tyrosine kinase domains. J. Mol. Biol. 387, 219–232 (2009).
Thompson, J. E. et al. Photochemical preparation of a pyridone containing tetracycle: A jak protein kinase inhibitor. Bioorg. Medicinal Chem. Lett. 12, 1219–1223 (2002).
Bemis, G. W. & Murcko, M. A. The properties of known drugs. 1. Molecular frameworks. J. Medicinal Chem. 39, 2887–2893 (1996).
Preuer, K., Renz, P., Unterthiner, T., Hochreiter, S. & Klambauer, G. Fréchet chemnet distance: A metric for generative models for molecules in drug discovery. J. Chem. Inf. Modeling 58, 1736–1741 (2018).
Baraldi, S. et al. In The Adenosine Receptors. (eds. P. A. Borea, K. Varani, S. Gessi, S. Merighi & F. Vincenzi) 91-136 (Springer International Publishing, Cham; 2018).
Yu, F., Zhu, C., Xie, Q. & Wang, Y. Adenosine A2A receptor antagonists for cancer immunotherapy. J. Medicinal Chem. 63, 12196–12212 (2020).
Spinaci, A. et al. In purinergic receptors and their modulators. (eds. V. Colotta & C. T. Supuran) 101-141 (Springer International Publishing, Cham; 2023).
Jaakola, V.-P. et al. The 2.6 angstrom crystal structure of a human A2A adenosine receptor bound to an antagonist. Science 322, 1211–1217 (2008).
Olivecrona, M., Blaschke, T., Engkvist, O. & Chen, H. Molecular de-novo design through deep reinforcement learning. J. Cheminformatics 9, 48 (2017).
Friesner, R. A. et al. Glide: A new approach for rapid, accurate docking and scoring. 1. Method and assessment of docking accuracy. J. Medicinal Chem. 47, 1739–1749 (2004).
Spitzer, R. & Jain, A. N. Surflex-dock: Docking benchmarks and real-world application. J. Computer-Aided Mol. Des. 26, 687–699 (2012).
Jacobs, R. A., Jordan, M. I., Nowlan, S. J. & Hinton, G. E. Adaptive mixtures of local experts. Neural Comput. 3, 79–87 (1991).
Lewis, P. et al. Retrieval-augmented generation for knowledge-intensive NLP tasks. In Proceedings of the 34th International Conference on Neural Information Processing Systems. (PMLR, 2020).
Williams, R. J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 8, 229–256 (1992).
Popova, M., Isayev, O. & Tropsha, A. Deep reinforcement learning for de novo drug design. Sci. Adv. 4, eaap7885 (2018).
Wang, J. et al. Multi-constraint molecular generation based on conditional transformer, knowledge distillation and reinforcement learning. Nat. Mach. Intell. 3, 914–922 (2021).
Wang, J. et al. Molecular generation with reduced labeling through constraint architecture. J. Chem. Inf. Modeling 63, 3319–3327 (2023).
Aghajanyan, A. et al. CM3: A Causal masked multimodal model of the internet. arXiv preprint, arXiv:2201.07520 (2022).
Fried, D. et al. InCoder: A generative model for code infilling and synthesis. In The Eleventh International Conference on Learning Representations (2023).
Polykovskiy, D. et al. Molecular Sets (MOSES): A benchmarking platform for molecular generation models. Frontiers in Pharmacology 11 (2020).
Rogers, D. & Hahn, M. Extended-connectivity fingerprints. J. Chem. Inf. Modeling 50, 742–754 (2010).
Bajusz, D., Rácz, A. & Héberger, K. Why is Tanimoto index an appropriate choice for fingerprint-based similarity calculations? J. Cheminformatics 7, 20 (2015).
Xie, Y., Xu, Z., Ma, J. & Mei, Q. How much space has been explored? measuring the chemical space covered by databases and machine-generated molecules. In The Eleventh International Conference on Learning Representations (2023).
Alhossary, A., Handoko, S. D., Mu, Y. & Kwoh, C.-K. Fast, accurate, and reliable molecular docking with QuickVina 2. Bioinformatics 31, 2214–2216 (2015).
Shultz, M. D. Two decades under the influence of the rule of five and the changing properties of approved oral drugs. J. Medicinal Chem. 62, 1701–1714 (2019).
Ertl, P., Rohde, B. & Selzer, P. Fast calculation of molecular polar surface area as a sum of fragment-based contributions and its application to the prediction of drug transport properties. J. Medicinal Chem. 43, 3714–3717 (2000).
Ghose, A. K., Viswanadhan, V. N. & Wendoloski, J. J. A knowledge-based approach in designing combinatorial or medicinal chemistry libraries for drug discovery. 1. A qualitative and quantitative characterization of known drug databases. J. Combinatorial Chem. 1, 55–68 (1999).
Lipinski, C. A., Lombardo, F., Dominy, B. W. & Feeney, P. J. Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Adv. Drug Deliv. Rev. 23, 3–25 (1997).
Bickerton, G. R., Paolini, G. V., Besnard, J., Muresan, S. & Hopkins, A. L. Quantifying the chemical beauty of drugs. Nat. Chem. 4, 90–98 (2012).
Virtanen, P. et al. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods 17, 261–272 (2020).
Seabold, S. & Perktold, J. Statsmodels: econometric and statistical modeling with python. SciPy 7, 92–96 (2010).
Bradley, A. P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 30, 1145–1159 (1997).
Axelrod, S. & Gómez-Bombarelli, R. GEOM, energy-annotated molecular conformations for property prediction and molecular generation. Sci. Data 9, 185 (2022).
Francoeur, P. G. et al. Three-dimensional convolutional neural networks and a cross-docked data set for structure-based drug design. J. Chem. Inf. Modeling 60, 4200–4215 (2020).
Burley, S. K. et al. RCSB protein data bank (RCSB.org): delivery of experimentally-determined PDB structures alongside one million computed structure models of proteins from artificial intelligence/machine learning. Nucleic Acids Res. 51, D488–D508 (2022).
Zdrazil, B. et al. The ChEMBL Database in 2023: a drug discovery platform spanning multiple bioactivity data types and time periods. Nucleic Acids Res. 52, D1180–D1192 (2023).
Wu, Z. et al. MoleculeNet: a benchmark for molecular machine learning. Chem. Sci. 9, 513–530 (2018).
Huang, K. et al. Therapeutics data commons: Machine learning datasets and tasks for drug discovery and development. In Thirty-fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 1) (2021).
Liu, Q., Allamanis, M., Brockschmidt, M. & Gaunt, A. Constrained graph variational autoencoders for molecule design. In Advances in neural information processing systems (2018).
Shi, C., Luo, S., Xu, M. & Tang, J. Learning gradient fields for molecular conformation generation. In International conference on machine learning. (PMLR, 2021).
Acknowledgements
This work was financially supported by National Key Research and Development Program of China (2022YFF1203003 to Y.K.), National Natural Science Foundation of China (22220102001 to T.H, 22303083 to J.W., 81973281 and 82373791 to Y.K.), China Postdoctoral Science Foundation (2023M733128 and 2023TQ0285 to J.W.), Postdoctoral Fellowship Program of CPSF (GZB20230657 to J.W.), and Scientific Research Fund of Zhejiang Provincial Education Department (Y202457041 to R.Q.). We appreciate Dr Liwei Liu and Dr Xiaozhe Wan, at the Advanced Computing and Storage Laboratory, Central Research Institute, Huawei Technologies Co., Ltd., for their invaluable discussions and collaborative spirit throughout this research.
Author information
Authors and Affiliations
Contributions
Y.K., C.-Y.H., and T.H. designed the research study. J.W. developed the method and wrote the code. J.W., R.Q., M.W., M.F., D.J., X.Z., H.Z., J.G. collected the data, J.W., R.Q., M.W., M.F., Yangyang Zhang, G.L., Q.S., Q.G. performed the analysis. J.W., R.Q., M.W., M.F., Yangyang Zhang, Zhourui Wu, Y.K., C.-Y.H., and T.H. wrote the original draft. J.W., R.Q., M.F., Yuchen Zhu, C.S., O.Z., Zhenxing Wu, T.H., C.-Y.H., and Y.K. wrote the review and editing, all authors read and approved the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Jannis Born, Marcos Quiles and Morgan Thomas for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Wang, J., Qin, R., Wang, M. et al. Token-Mol 1.0: tokenized drug design with large language models. Nat Commun 16, 4416 (2025). https://doi.org/10.1038/s41467-025-59628-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-59628-y