Introduction

The spontaneous Hall effect, one of the most preferred methods for reading out spin polarization in metallic ferromagnets, has been discovered for over a century and is considered a hallmark of long-range ferromagnetism1. However, it was only in recent decades that scientists recognized the physical origin of the anomalous Hall value, specifically the Berry curvature and broken time-reversal symmetry1. The profound understanding naturally leads to the prediction of spontaneous anomalous Hall effect (AHE) and topological Hall effect (THE) in antiferromagnets with nontrivial spin textures2,3,4,5,6, where zero net magnetization is strongly favorable for realizing next-generation ultra-compact spintronic devices7. Soon after the theoretical predictions, AHE was observed experimentally in antiferromagnetic manganese compounds such as \({{{{\rm{Mn}}}}}_{3}{{{\rm{Sn}}}}\)8 and Mn3Ge9. Within these hexagonal materials, the cluster magnetic octupole serves as the order parameter responsible for breaking time-reversal symmetry and facilitating the stabilization of Weyl fermions near the Fermi level10. Additionally, this cluster magnetic octupole can also be flipped by an external field, resembling the flipping of magnetic moments.

Even more intriguing is the extension of AHE studies to two-dimensional (2D) antiferromagnets to explore topologically nontrivial energy bands and spin textures3,11,12,13,14,15,16. Recently, the intercalating 3d magnetic atoms between layers of van der Waals transition metal dichalcogenide (TMDC) has opened up a new route to construct quasi-2D antiferromagnets with various spin configurations and functionalities. For example, a one-dimensional chiral magnetic soliton lattice is reported in Cr1/3NbS217. Electrical switching18 and exchange bias19 are reported in Fe1/3NbS2, where antiferromagnetic and frustrated spin-glass orders coexist and are evidenced to be coupled19. Among these intercalated compounds, CoxNbS2 is well-known for its unexpectedly large AHE value, approaching the quantized conductance value of e2/h per layer20,21,22. According to the angle-resolved photoemission spectroscopy (ARPES) measurements, the intercalated Co2+ cations serve to break the inversion symmetry and shift the Fermi level of NbS2, resulting in extra electronic bands that possibly contribute to AHE23,24,25. The anomalous transport behavior is, therefore, sensitively determined by the stoichiometric composition x with an idealized value of 1/326.

Despite extensive studies on this promising material, the spin configuration of Co1/3NbS2 and the origin of AHE remain controversial. The earliest neutron diffraction results were fitted with multi-domain structures of collinear single q, with six symmetry-related in-plane q sharing equal weights27. However, this collinear structure is generally incompatible with the large AHE observed afterward. To account for the AHE value, Zhang et al. attributed it to the large hidden Berry curvature due to the chiral Dirac-like fermions28. On the other hand, Šmejkal, et al. proposed a picture of the crystal Hall effect29, where magnetic orbitals rather than ordered spins break time-reversal symmetry, giving rise to spontaneous Hall signals. Lu, et al. further pointed out that the spins of Co1/3NbS2 in the bc-plane are nearly anti-parallel, but the spins in adjacent ab-planes are alternately tilted30, which can quantitatively reproduce the AHE value. Meanwhile, Tenasini, et al.21 validated the previous neutron scattering results but proposed a non-coplanar single-domain multi-q magnetic structure to fit the data. The uncompensated k-space Berry curvature in non-coplanar structure can explain the large AHE and is supported by first-principles calculations31,32. Furthermore, Takagi et al. performed polarized neutron scattering experiments and determined an all-in-all-out type non-coplanar magnetic order. They claimed that the AHE can be explained in terms of the topological Hall effect originating from a fictitious magnetic field associated with the scalar spin chirality33. Most recently, Dong et al. employed Mössbauer spectroscopy to reveal the hyperfine magnetic field for the different Co2+ ions and validated the triple-q magnetic order34.

Taken together, the controversial spin configuration has presented significant challenges in determining the physical origin of the prominent spontaneous Hall effect in Co1/3NbS2, and therefore the future applications in AFM spintronics. In this work, we bypassed the specific magnetic order and developed a series of phenomenological pictures to elucidate the mechanism of AHE and magnetic reversal behaviors with the assistance of magnetic, transport, thermoelectric, and reflective magnetic circular dichroism (RMCD) measurements. By analyzing the thermoelectric and transport data, we evidenced that the anomalous Hall conductivity of Co1/3NbS2 is independent of carrier relaxation time, suggesting an intrinsic k-space origin of Berry curvature. In exfoliated Co1/3NbS2, we observed a large RMCD signal below the Néel temperature and directly visualized its magnetic domains via RMCD mapping. Combined with transport measurements, we verified that the magnetic reversal in bulk Co1/3NbS2 initiates within inner domains and is accompanied by the propagation of domain walls, while the reversal of 2D flakes is determined by the depinning of the surface domain wall. This discrepancy accounts for the significant variation in the coercive field between bulk and 2D samples, along with the distinct training effects. Our findings provide a comprehensive understanding of the anomalous Hall and the magnetic reversal behaviors in Co1/3NbS2, which is crucial for establishing the physical framework of 2D non-collinear antiferromagnets and advancing the non-collinear antiferromagnetic spintronic applications.

Results and discussion

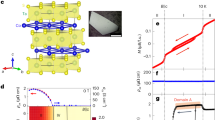
Co1/3NbS2 single crystals were synthesized via the chemical vapor transport (CVT) technique (see Methods Section), and Fig. 1a shows the crystal structure viewed along the axis perpendicular to the bc-plane. Ideally, Co2+ cations reside only at 2c Wyckoff sites, resulting in an inversion symmetry broken superstructure with a space group of P6322 and a lattice constant \(\sqrt{3}\) times that of NbS2. Fig. 1b shows the out-of-plane magnetization of bulk crystals. The apparent kinks at 28.3 K signify the Néel temperature (TN), consistent with previous reports20,35. The magnetization of Co1/3NbS2 below TN is composed of a tiny rectangular hysteresis loop and a linear canting background (Fig. S1, Supplementary Information). The tiny ferromagnetic component along the c-axis results in the abrupt increase of susceptibility at TN in the 0.1 T field cooling (FC) curve, while the linear background is responsible for nearly the same trend in the zero field cooling (ZFC) and 3 T FC curves (Fig. 1b). The measured magnetic moment is more than three orders of magnitudes smaller than the spin moment of Co2+ ions (3.87 μB)27, indicating that Co1/3NbS2 established a long-range antiferromagnetic ground state below TN.

Fig. 1: Basic characterizations of Co1/3NbS2.
figure 1

a The crystal structure of Co1/3NbS2 viewed along the axis perpendicular to the bc-plane. b The measured temperature-dependent out-of-plane susceptibility of single crystal Co1/3NbS2 bulk with ZFC, 0.1 T FC, and 3 T FC. c RMCD signal versus temperature of an exfoliated Co1/3NbS2 flake with a thickness of  ~130 nm. The error bars for each data point were obtained by calculating the standard deviation of 150 consecutive measurements. Red hatching highlights the phase transition, which is used to guide the eye. d Transverse resistivity ρyx versus out-of-plane magnetic field of device 1 at different temperatures, where the anomalous and ordinary Hall coefficients can be extracted.

Full size image

We note that most non-collinear antiferromagnets exhibit tiny net magnetic moments and hysteresis loops resembling those of ferromagnetic materials10,36. However, the ferromagnetic moment is not the primary order parameter responsible for breaking time-reversal symmetry and inducing Berry curvature. Instead, it is a measurable quantity coupled with the real order parameter, such as the magnetic multipole moment37, or spin chirality36, which is the possible case in Co1/3NbS2. In the following, we denote the hidden order parameter in Co1/3NbS2 as M. We first conducted RMCD measurements on exfoliated Co1/3NbS2 flakes to characterize the magnetism of the 2D flakes. After 6 T FC, the exfoliated flake exhibits a distinct RMCD signal of  ~0.12% below the TN. (Fig. 1c). Two points need to be emphasized here. Firstly, the magneto-optical signal in Co1/3NbS2 is comparable to that observed in many 2D ferromagnetic materials38,39, but the net moment is only about 1/1000 of theirs. Secondly, a similar RMCD signal was also observed in the ground state of the sister compound Co1/3TaS2, where a magnetic phase with a much larger magnetic moment hardly generates any RMCD signal (see detailed discussion in Fig. S2, Supplementary Information). Therefore, the contribution of the net magnetization to the RMCD signal in Co1/3NbS2 can be ruled out. Such a significant RMCD value most likely arises from the large transverse optical conductivity caused by the Berry curvature40,41,42,43,44,45. Fig. 1d shows the temperature-dependent Hall measurements of an exfoliated Co1/3NbS2 flake with a thickness of  ~125 nm (labeled as device 1). A large AHE can be observed, and the coercive field Hc increases sharply with decreasing temperature, indicating an extremely large magnetic anisotropy. Both the anomalous and ordinary Hall coefficients can be obtained through the measurements and will be discussed in detail later.

The temperature dependence of the longitudinal and transverse resistivity, ρxx and ρxy, is shown in Fig. 2a. ρxx shows typical metallic behavior, as its value decreases with temperature and drops more sharply after an obvious kink at TN. This may be because electron scattering decreases in the long-range magnetic order; in other words, the relaxation time τ becomes longer. On the contrary, ρxy exhibits a sharp increase upon establishing magnetic order and reaches a plateau afterward, showing no signs of decrease with decreasing temperature. This seems incompatible with the decrease of ρxx with temperature. In a general sense, the transverse resistivity \({\rho }_{xy}^{A}\) scales with ρxx in a power law1:

$${\rho }_{xy}^{A}=\lambda M{\rho }_{xx}^{n}$$
(1)

where M is the order parameter, and λ is a temperature-independent scaling factor (see detailed discussions in Note S2, Supplementary Information). n is the power constant depending on the Hall mechanism, which is typically observed to take one of three distinct values. The real-space Berry curvature mechanism, where the fictitious field generated from the spin chirality induces the transverse velocity, leads to \({\sigma }_{xy}^{A}\propto {\tau }^{2}\) and n = 046,47. On the other hand, the k-space Berry curvature mechanism, where the topological nontrivial bands induce the transverse velocity, leads to \({\sigma }_{xy}^{A}\propto {\tau }^{0}\) and n = 248. Besides, the skew scattering mechanism by thermally fluctuating spin clusters may also contribute to an AHE in non-coplanar magnets49,50, leading to \({\sigma }_{xy}^{A}\propto {\tau }^{1}\) and n = 151,52, but generally does not scale with M. Due to the fact that the conductivity of Co1/3NbS2 is far from the high-conductivity range where extrinsic skew scattering is applicable51, nor does the spontaneous Hall signal evince any phenomena consistent with the skew scattering by thermally fluctuating spin clusters49,50,51,52, we can exclude the possibility of the skew scattering mechanism and confine the origin of the spontaneous Hall effect to be either real-space or k-space Berry curvature. According to Eq. (1), the monotonic increase of \({\rho }_{xy}^{A}\) at low temperatures implies that the value of M continues to increase after the formation of the antiferromagnetic order. As a result, the transverse conductivity \({\sigma }_{xy}=\frac{-{\rho }_{xy}}{{\rho }_{xx}^{2}+{\rho }_{xy}^{2}}\) extracted at temperatures below TN keeps increasing without showing an obvious sign of saturation. Similar behavior is observed in all devices we measured (Figs. S3, 4 and Table S1, Supplementary Information), with a maximum Hall angle of  ~0.014, comparable to other 2D ferromagnetic materials10,53.

Fig. 2: Electrical transport and thermoelectric measurements of Co1/3NbS2.
figure 2

a Temperature-dependent longitudinal and transverse resistivity. b Temperature-dependent Seebeck coefficient of Co1/3NbS2. The inset shows the optical image of the device used for electrical transport and thermoelectric measurements. The scale bar is 20 μm. The sign change in temperature of Sxx is indicated by the red arrow. c Nernst coefficient Sxy versus magnetic field at different temperatures. The temperatures are calibrated to be the actual temperature under the heating current. d Temperature-dependent Sxy of Co1/3NbS2. Open circles are experimental data. The solid blue line represents the best fit using the Mott relation with n = 2.22. The dashed green curve is the best fit with 0. All data were obtained after  ±4 T FC, followed by (anti)symmetrization processing.

Full size image

To elucidate the scaling behavior between ρxx and ρxy, together with the origin of AHE, we measured the thermoelectric coefficients of Co1/3NbS2. Distinct from charge transport, thermoelectric signals detect the flow of entropy and thus serve as sensitive probes of the electronic properties of Fermi surfaces, especially the Berry curvature54,55. The inset of Fig. 2b shows the optical image of thermoelectric device 1. To generate a temperature gradient ∇ T, a heater at one side of the device is heated by driving an a.c. current. The actual temperature and temperature gradient are calibrated by four-probe resistance measurements of the temperature sensors placed on both sides of the sample, and the Seebeck and Nernst signals are obtained by measuring the 2ω voltage signals of the source-drain and Hall electrodes of the sample. The detailed process of temperature calibration is discussed in Figs. S5, 6, Supplementary Information. As shown in Fig. 2b, the Seebeck coefficient, Sxx, is negative at high temperatures and becomes positive below  ~25 K, in good accordance with the measurements for bulk crystals56. The hysteresis loops of Nernst coefficient Sxy can be observed below TN (Fig. 2c), and the value of which reaches as large as 0.3 μV/K at low temperatures (Fig. 2d). Similar behaviors are reproducible in all samples we measured (Fig. S3, Supplementary Information).

We note that the sign change of Sxx should not be attributed to the phonon-drag effect, since the temperature is much lower than the expected value of θD/556,57,58 (θD is the Debye temperature). Neither the ρxy or Sxy signals exhibit any abnormal changes around 25 K, ruling out the possibility of a complete change in carrier type. We can obtain the effective carrier concentration by a linear fit of the ordinary Hall effect extracted from Fig. 1d (Fig. S8, Supplementary Information). The ordinary Hall effect indicates that the material is p-type conduction and the hole concentration decreases with decreasing temperature, which is consistent with previous reports20,21, but incompatible with the trend of Sxx turning from negative to positive. These observations lead to the conclusion of the coexistence of hole and electron carriers in this material. The ordinary Hall effect is mainly contributed by hole carrier, which is the majority carrier provided by the NbS2 bands23. In contrast, the Sxx signal is dominated by the electron band near the Fermi level, which results from the intercalated Co2+ cations23. Sxx should approach zero at low temperatures as the entropy should vanish at T → 0, but the contribution of holes gradually constitutes a larger proportion and exceeds that of electrons, resulting in the sign change from negative to positive. Consequently, the sign change of Sxx may indicate a smooth electronic transition or magnon drag effect, which is also manifested in the temperature-dependent carrier concentration (Fig. S8, Supplementary Information). The overall hole concentration kinks between 20 and 25 K and stops decreasing at lower temperatures, consistent with the trend of Sxx. Differently, due to the absence of sign change in ρxy and Sxy, we can conclude that only one type of carrier, presumably the electrons, contributes to AHE and ANE. The sign change of Sxx and finite Sxy naturally leads to a divergent Nernst angle by \({\theta }_{N}=\frac{{S}_{yx}}{{S}_{xx}}\). As a comparison, the maximum Nernst angle at the lowest measurement temperature of the devices reaches 0.12, and the ratio between anomalous Nernst coefficient to the spontaneous magnetization Syx/M reaches \(1{0}^{3}\,\mu {{{\rm{V}}}}\cdot {{{{\rm{K}}}}}^{-1}\cdot {({\mu }_{{{{\rm{B}}}}}/{{{\rm{f}}}}.{{{\rm{u}}}}.)}^{-1}\) (Table S1, Supplementary Information). These values are much larger than the common FM metals59,60,61 and comparable to other topological materials62,63,64.

In addition to electrical transport, thermoelectric measurements provide us with another degree of freedom to explore the underlying mechanism of AHE. By definition, the Seebeck coefficient is related to other transport parameters by:

$${S}_{yx}=\frac{1}{{\sigma }_{xx}}\left({\alpha }_{yx}+{\sigma }_{yx}{S}_{xx}\right)$$
(2)

Additionally, the Mott relation describes the relationship between αxy and σxy by \({\alpha }_{xy}=\frac{{\pi }^{2}{k}_{B}^{2}T}{3e}{\left.\left(\frac{\partial {\sigma }_{xy}}{\partial \varepsilon }\right)\right| }_{{\varepsilon }_{F}}\), which is applicable to both the k-space and real-space mechanisms59,65,66,67. In light of the overwhelming evidence from recent experiments31,32,33,34, which have consistently demonstrated the all-in-all-out non-coplanar structure of Co1/3NbS2, the spontaneous Hall effect can originate from either the k-space or the real-space Berry curvature47,66. However, assuming that the real-space Berry curvature is responsible for the spontaneous Hall effect, according to the Mott relation, both the ordinary linear part and the spontaneous topological Nernst effect should be proportional to the resistivity counterpart by ref. 65:

$$\frac{{\rho }_{H}^{T}}{{\rho }_{H}^{O}}=\frac{{b}_{z}}{{\mu }_{0}H}\approx \frac{{S}_{xy}^{T}}{{S}_{xy}^{O}}$$
(3)

Where bz is the fictitious field generated by the non-coplanar spin texture. A detailed derivation procedure is presented in Note S1, Supplementary Information. Nevertheless, as shown in Figs. 1d, 2c, the ordinary Hall effect is comparable in magnitude to the spontaneous Hall effect, while the ordinary Nernst effect is almost absent in the Sxy − B curve, contradicting to Eq. (3). Therefore, the real-space contribution to the spontaneous Nernst effect can be considered negligible, with the k-space Berry curvature contribution dominating in the spontaneous Hall and Nernst effect. This conclusion can be further validated by fitting the temperature-dependent spontaneous Nernst effect based on the Mott equation. Substituting Eq. (1) into the Mott relation and combining Eq. (2), we can eliminate the common factor M and obtain the modified Mott relation containing only four transport parameters59,68:

$${S}_{xy}=\frac{{\rho }_{yx}}{{\rho }_{xx}}\left(T\frac{{\pi }^{2}{k}_{B}^{2}}{3e}\frac{{\lambda }^{{\prime} }}{\lambda }-(n-1){S}_{xx}\right)$$
(4)

where λ is the same parameter as in Eq. (1), and \({\lambda }^{{\prime} }\) is the energy derivative of λ. Both of them should be constants. The detailed derivation procedure is presented in Note S2, Supplementary Information). These two equations verify the Mott relation and determine the exponent n without including the temperature-dependent order parameter. The best-fit parameters give n = 2.22 (Fig. 2d), which is close to n = 2 rather than 0 (deviating significantly from the experimental data as shown by the dashed red and green curve in Fig. 2d). This n value indicates that the anomalous Hall conductivity in Co1/3NbS2 is independent of the relaxation time τ, characteristic of the k-space Berry curvature mechanism.

Theoretically, the origin of the spontaneous Hall effect in non-coplanar magnets depends on the relative size of the skyrmion λsk to the carrier mean free path lmfp47,66,69. For large λsk and short lmfp, the real-space fictitious field contribution dominates for the \({\sigma }_{xy}^{A}\), while for small λsk and long lmfp, the k-space picture holds. The optimal \({\lambda }_{sk}^{*}\) where the real-space and k-space Berry curvatures have similar orders of contribution and the \({\sigma }_{xy}^{A}\) peaks can be estimated by \({\lambda }_{sk}^{*} \sim \sqrt{{\mu }_{mob}\frac{h}{e}}\). Here, μmob is the carrier mobility47. Using the ordinary Hall measurement in Fig. S8 in the Supplementary Information, we can extract the μmob of device 1 to be  ~5 cm2/(V ⋅ s), and estimate the \({\lambda }_{sk}^{*}\) to be  ~1.5 nm, larger than the atomic-scale skyrmion size of  ~0.6 nm, confirming that the anomalous Hall conductivity in Co1/3NbS2 belongs to the k-space region (see detailed discussions in Note S3, Supplementary Information). Similar fitting results for device 2 and the discussions on the phenomenological principles of the fitting are presented in Fig. S7, Supplementary Information. Our conclusion based on exfoliated Co1/3NbS2 flakes is consistent with the thermoelectric measurements on the bulk counterpart, where gapped nodal planes are proposed to account for the k-space spontaneous Hall and Nernst effect69.

Now we have phenomenologically understood the physical origin of the spontaneous Hall effect, we turn to the magnetic domains and magnetic reversal behavior to construct a comprehensive picture in Co1/3NbS2. We have shown in Fig. 1c the order parameter in Co1/3NbS2 can be resolved by the RMCD signal. Therefore, by scanning the entire flake (with a laser spot size of  ~1.5 μm), we can obtain the spatially resolved RMCD signals and therefore detect the domain structure of the exfoliated samples, as shown in Fig. 3. Optical and atomic force microscopy height images of the same exfoliated flake, together with the single-point RMCD signal versus temperature after  ±6 T FC can be seen in Fig. S9, Supplementary Information. The main observations are listed below. First, after ZFC (Fig. 3a), the RMCD signal exhibits clear spatial variation between  ±0.4%, consistent with the RMCD values after FC (Fig. S9c, Supplementary Information). This mapping unambiguously demonstrates a multi-domain structure with a domain size of several μm, which is also manifested in the initial magnetization in AHE measurements (Fig. 4e). After 6 or  −6 T FC, the whole sample exhibits a homogeneous but opposite RMCD signal (Fig. 3b, c), showing a single-domain structure. The extremely large values at the edges of the sample are artifacts due to the protrusion of the exfoliated sample and do not contain useful information, as indicated in Fig. S9b, Supplementary Information. We then performed another ZFC measurement, and the domains were completely redistributed (Fig. 3d), implying that the domain structure was randomly formed upon each cooling from a higher temperature. Line cuts from the four mappings are shown in Fig. S9d, Supplementary Information. The domains after different cooling processes exhibit similar RMCD values, confirming the reliability of our measurements.

Fig. 3: RMCD mapping of exfoliated 100-nm-thick Co1/3NbS2 flake at 2 K.
figure 3

a RMCD mapping after the first ZFC. b, c RMCD mappings after 6 T (b) and  −6 T (c) FC. d RMCD mapping after the second ZFC.

Full size image
Fig. 4: Magnetic reversal behaviors.
figure 4

a Anomalous Hall effect under different field angles. The sample lies in the x−y plane and the magnetic field H rotates from the z axis to an in-plane axis. θ is the angle between H and the z axis, as illustrated in the inset of (c). The curves are obtained at 29 K in a 120- nm-thick Co1/3NbS2 device, labeled as device 2, while the dashed curves are obtained at 27 K from a bulk Co1/3NbS2 device. Each curve is normalized to 0°, zero-field anomalous Hall voltage \({V}_{0}^{H}\), and shifted vertically for a clear view. b Coercive field Hc of device 2 and the bulk sample as a function of θ, extracted from (a). Hc is defined as the intercept of \({\rho }_{yx}^{A}\) on the H axis taken from (a). The dashed red line represents the fit of the Kondorsky model. c The reciprocal of the AHE slope at Hc, defined as \({s}^{H}=| dH/d({V}^{H}/{V}_{0}^{H})|\), as a function of θ, extracted from (a). d \({\rho }_{yx}^{A}\) during several consecutive magnetic field sweeps at 27.5 K, obtained from device 2. Hc decreases as the number of sweeps increases. The green circles and dashed lines plot the decreasing Hc versus the number of sweeps N, while the yellow circles and dashed lines plot the Hc extracted from six initial sweeps after cooling down from 50 K. e \({\rho }_{yx}^{A}\) during several consecutive magnetic field sweeps at 27 K, obtained from the bulk sample. The sample was cooled down from 50 K with zero field, and the field sweeps begin with an initial magnetization process from 0 T to  −4 T. f The exchange bias field μ0Heb versus N after the positive and negative initial magnetization process.

Full size image

To date, only very few studies have reported the direct observation of non-collinear antiferromagnetic domains41,70,71,72. Nevertheless, despite their invisible nature, the non-collinear domains often significantly determine the magnetic reversal and transport properties of the material73,74,75. To elucidate the magnetic reversal model, we measured the AHE hysteresis loops for different magnetic field orientations, as shown in Fig. 4a. The solid lines represent the AHE of a 120-nm-thick Co1/3NbS2 device (device 2) at 29 K, while the dashed lines represent that of the bulk Co1/3NbS2 at 27 K. As the field rotates from the out-of-plane axis to an in-plane axis, the coercive field Hc monotonically increases. Both the bulk and 2D samples exhibit well-fitted Hc values using the function \(1/\cos \theta\) (Fig. 4b), while the AHE value remains nearly constant. These phenomena suggest that the magnetic reversal in Co1/3NbS2 follows the Kondorsky model76. In particular, the energy cost of domain wall propagation is much lower than that of coherent domain rotation, so Hc is determined by the competition between Zeeman energy and the domain nucleation or the domain wall depinning energy. These observations are consistent with the observed sharp increase in Hc as the temperature decreases (Fig. S10, Supplementary Information) and the presence of multi-domain structures (Fig. 3).

Despite the similar trend of Hc − θ, the actual magnetic reversal processes differ significantly between the 2D and bulk samples. It is worth noting that at the same temperature, the Hc of the 2D sample is significantly larger than that of the bulk sample (Fig. S10, Supplementary Information). The variation in the magnetic anisotropy energy after mechanical exfoliation alone cannot account for this difference, indicating a strong pinning effect in 2D samples. As shown in Fig. 4a, the magnetic reversal of device 2 exhibits a slow ramping behavior, while the bulk sample shows a steep jump accompanied by a long tail. The AHE shape of the bulk is consistent with the M − H curves (Fig. S1, Supplementary Information), suggesting that the AHE can effectively describe the entire sample’s reversal process. Based on the above observations, we can infer that the magnetic domains in 2D samples are strongly pinned and nearly uncorrelated with each other. The depinning energy of the domain wall is randomly distributed within a certain range, and when the Zeeman energy provided by the external field surpasses the energy barrier, the corresponding domain undergoes reversal. In other words, the domain walls are often pinned and therefore propagate at an extremely low velocity. Under this hypothesis, when the field rotates from the out-of-plane axis to the in-plane axis, the Hc of all the domains should follow the \(1/\cos \theta\) rule, where the width of the Hc distribution will also depend on the field angle as \(1/\cos \theta\). In Fig. 4c, we extracted the reciprocal of the AHE slope at Hc, defined as \({s}^{H}=| dH/d({V}^{H}/{V}_{0}^{H})|\). The sH of the 2D sample can be well-fitted by the \(1/\cos \theta\) function, perfectly confirming our conjecture. In contrast, the reversal of the bulk sample manifests as a sharp initial step even when the field is directed close to the in-plane direction. The extracted sH remains close to zero, implying that the reversal in the bulk sample can be described by domain nucleation followed by rapid propagation of the domain walls throughout the sample. The long tail observed at the end of the reversal likely originates from surface-pinned domains, since all 2D samples exhibit strong pinning behavior. The slight increase in sH at large θs may arise either from the broadening of the tail or the reduction of domain wall velocity under in-plane fields.

Now we can establish a comprehensive understanding of magnetic reversal in Co1/3NbS2. Inside the bulk of Co1/3NbS2, there may exist a distinct type of domains, referred to as the interior nucleus. These domains have remarkably low nucleation fields and always flip first upon each reversal, and their nucleation fields determine the bulk Hc. In contrast, surface domains are strongly pinned and resistant to reversal by the interior domain wall. A larger Zeeman energy is required for the propagation of the surface domain walls. Due to the fact that the size of magnetic domains is on the order of  ~μm (Fig. 3), much larger than the thickness of 2D flakes, only surface domains exist in 2D samples, and their Hc is determined by the domain wall depinning field. This explains the significantly larger Hc in 2D samples (Fig. S10, Supplementary Information). The reversal process in Co1/3NbS2 differs significantly from the previous reported 2D magnetic materials77,78,79 or Mn-based topologcial antiferromagnets72,74. Generally, the vanishing net magnetization in antiferromagnets does not tend to induce the formation of domains within their interiors. Instead, the domains usually nucleate at the surface due to the demagnetization energy or surface inhomogeneity, so reversal often starts from the surface and gradually occupies the center of the sample72,74, which is opposite to the case of Co1/3NbS2.

The unusual domain reversal behavior in Co1/3NbS2 also gives rise to the abnormal training effects of Hc. As depicted in Fig. 4e, f, the bulk Co1/3NbS2 exhibits an intrinsic exchange bias effect26. The sign of the exchange bias field Heb (defined as \(({H}_{c}^{up}+{H}_{c}^{down})/2\)) is opposite to the first polarization state reached after each cooling. In more detail, Heb is negative when the initial magnetization sweep ranges from 0 T to 4 T, and positive when the initial magnetization sweep ranges from 0 to  −4 T. Furthermore, if the sample is cooled with a finite external field, Heb is also opposite to the sign of the external field (Fig. S11, Supplementary Information). The exchange bias effect exhibits a rapid training effect, as Heb approaches zero during the second sweep, shown in Fig. 4f. We have demonstrated that the Hc of bulk Co1/3NbS2 is determined by the flip of the interior nucleus. Phenomenologically, we can deduce that a special type of inhomogeneity resisting domain wall propagation is created after each cooling, so that the initial Hcs are determined by the domain wall depinning field. After undergoing the two opposite domain wall propagation processes, the spin texture is quickly homogenized, and the domain wall can move freely after nucleation. In comparison, the 2D Co1/3NbS2 exhibits a completely different training effect. Figure 4d shows the 2D plot of \({\rho }_{yx}^{A}\) as a function of magnetic field and sweeping number N at 27.5 K. The green dashed line illustrates the relationship between the extracted Hc and N, which drops sharply over the first few sweeps and continues to exhibit a decreasing trend. Nevertheless, the positive and negative Hc values remain symmetric, and no exchange bias effect was observed. Six consecutive sweeps reduce Hc in device 2 by 28%. Moreover, Hc can be set back to the initial value by raising the temperature above TN and cooling back to 27.5 K, which we call the initialization process. We raised the temperature to 50 K and then cooled it back, and then directly carried out the AHE measurement. The initialization process was also repeated six times, and the six extracted Hc are plotted in the yellow dashed line in Fig. 4d, exhibiting consistent values with perfect reproducibility. This training effect can also be repeated in all the 2D devices we measured (Fig. S12, Supplementary Information). Based on our previous understanding, the surface inhomogeneity induced by the initialization process gradually relaxed during the slow domain wall propagation process, consistent with the strong pinning effect from the surface. The exchange bias and training effect in both bulk and 2D Co1/3NbS2 provide us with a useful tool to manipulate the AHE of the non-collinear antiferromagnetic states simply by continuously sweeping the external field. Information regarding the coercive field Hc will be memorized and can be erased after raising the temperature above TN and cooling again.

In summary, we developed a series of phenomenological pictures to elucidate the mechanism of AHE and magnetic reversal behaviors in Co1/3NbS2. We investigated the large AHE, ANE, and the magnetic domain-related behavior in exfoliated flakes. The analysis of the temperature- and field-dependent transport along with thermoelectric coefficients based on the Mott relation indicates an intrinsic k-space Berry curvature origin of the spontaneous Hall effect. Additionally, a substantial reflective magnetic circular dichroism (RMCD) signal was observed, enabling the visualization of magnetic domains via RMCD mapping. Combined with transport measurements, we elucidated the mechanism of magnetic reversal in the Co1/3NbS2 samples and explained the distinct Hc values and training effect between the bulk and 2D samples. Our work probes the intrinsic Berry curvature and provides an explicit picture of AHE and magnetic reversal mechanism in Co1/3NbS2 without including its controversial magnetic order. This information is essential for the development of future spintronic devices such as the all-antiferromagnetic 2D spin valves, antiferromagnetic spin-orbit torque devices, etc.

Methods

Crystal growth and magnetic characterizations

High-quality Co1/3NbS2 single crystals were grown by the chemical vapor transport method. Co, Nb, and S powders with a ratio of 1:3:6 were sealed in a quartz tube, then put into a furnace, heated to 800 °C, and kept for 5 days to prepare polycrystalline precursor. The resulting powders (1 g) and transport agent iodine (15 mg/cm3) were then sealed in a quartz tube to grow single crystals with a temperature gradient set between 950 °C (source) and 850 °C (products) for 10 days. Finally, hexagonal plate-shaped single crystals were obtained, which are easy to exfoliate. The thickness of the ultrathin samples was verified by the atomic force microscopy characterization using an Oxford Cypher S system in tapping mode. Magnetization measurements were performed by standard modules of a Quantum Design PPMS.

Electrical and thermoelectric measurements

Metal contact electrodes of Cr/Au (10/80 nm) were defined using electron beam lithography, electron beam evaporation, and lift-off processes on the exfoliated flakes. The devices were then loaded into a physical property measurement system (Cryomagnetics) with a magnetic field up to 14 T. AC voltage measurements were performed with Stanford Research SR830 lock-in amplifiers using the standard four-point method. ρxx and ρxy were measured under an a.c. current of 10 μA at 17.777 Hz, while Sxx and Sxy were measured under an a.c. heater current of 5–10 mA at 3.777 Hz. Temperature perturbation was calibrated by the four-probe resistances of the thermocouples. Details of thermoelectric measurements and temperature calibration are presented in Figs. S5, 6, Supplementary Information, and the following discussions.

RMCD measurements

The RMCD measurements were performed based on the Attocube closed-cycle cryostat (attoDRY2100) down to 1.6 K and up to 9 T in the out-of-plane direction. The linearly polarized light of the 633-nm HeNe laser was modulated between left and right circular polarization by a photoelastic modulator (PEM) and focused onto the sample through a high numerical aperture (0.82) objective. The reflected light was detected by a photomultiplier tube (THORLABS PMT1001/M). The magnetic reversal under the external magnetic field was detected by the RMCD signal determined by the ratio of the a.c. component of PEM at 50.052 kHz and the a.c. component of the chopper at 779 Hz (detected by a two-channel lock-in amplifier, Zurich HF2LI). RMCD mapping was implemented by moving the piezo sample stage.