Introduction

Quantum bits (qubits) are inherently susceptible to various types of errors, necessitating the implementation of quantum error correction (QEC) to build logical qubits for the realization of fault-tolerant quantum computers1,2. The surface code is one of the promising fault-tolerance error correction schemes that leverages the topological properties of a qubit system to tolerate arbitrary local errors3. Along this direction, small-scale multiqubit correlated errors can be alleviated by the optimization of error correction methods or the allocation of more physical qubits4,5. However, for large-scale correlated errors, the effectiveness of these strategies diminishes since the presence of non-local correlated errors can disrupt the topological properties, thereby posing significant challenges to QEC6,7,8.

For the superconducting qubits, it is found that the high-energy particles, like cosmic-ray muons and γ-rays, can significantly limit the qubit coherence times by elevating the quasiparticle (QP) density9,10. Correlated offset-charge jumps and energy relaxation errors have been observed, which are explained via numerical simulations as arising from QP bursts induced by muons and γ-rays11,12. Moreover, large-scale correlated errors have been demonstrated in Google’s Sycamore superconducting processor by monitoring multiqubit simultaneous energy relaxations13, and the detection of coincident events of cosmic-ray muons and correlated errors in superconducting qubits is also reported14. These works show that the correlated errors can be caused by QP bursts arising mainly from muon and γ-ray radiations15, and it is imperative to identify these particles and better understand their impact on the superconducting processor.

Here, we present an experimental study of large-scale QP bursts and correlated errors induced by cosmic-ray muons and γ-rays on a 63-qubit superconducting processor (see the left panel of Fig. 1a and Methods), by continuously monitoring multiqubit correlated charge-parity jumps and bit flips, while at the same time recording the muon events via two muon detectors located beneath the sample box in the dilution refrigerator (see the right panel of Fig. 1a). We are able to separate the contributions from muons and γ-rays and observe strong coincidences between QP bursts and muon events. The occurrence time of muon-induced bit flips, estimated to be 25 minutes, remains too short to execute a QEC algorithm effectively, which typically needs operation times on the order of several hours16,17. Moreover, we find nearly identical reduction rates of QP bursts and γ-ray events when a lead (Pb) shield is used. The percentages of QP bursts by muons and γ-rays are found to be 18.4% and 81.6%, respectively.

Fig. 1: Device and QP burst detection.
figure 1

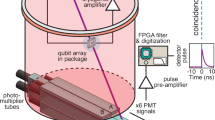
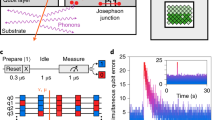
a Left: the optical image of the device with a bottom carrier chip and a top qubit chip containing 63 qubits and 105 couplers. The circuits on the half-transparent qubit chip are, on the back side, seen as a grid image, and color circles are added at the nodes to indicate qubits. 31 qubits in yellow are selected for measurement and 1 qubit in orange for QP injection. Right: Schematic of zoomed-in side view near a single qubit. (The sapphire carrier chip is in good thermal contact with the copper sample box on the periphery, here they are shown in direct contact under qubit area for simplicity). High-energy particles, such as muons (μ) and gamma-rays (γ), generate nonequilibrium phonons that break Cooper pairs thus causing QP bursts. Phonons can also be generated from the recombination of injected QPs. Two muon detectors, MDA and MDB, are located at the bottom of the copper sample box to detect muons that traverse through the device, sample box, and detectors. b Ramsey-based sequence for measuring the charge-parity state (violetred “e" for even state and gold “o" for odd state) of a qubit with the corresponding evolution of the qubit state on the Bloch sphere. c Sequence for measuring the charge-parity state using microwave control (XY), readout, and qubit frequency control (Z). The qubit frequency can be tuned to the idle point, readout point, reset point, and charge-sensitive point for qubit state control, measurement, initialization, and charge parity mapping, respectively. d Illustration of a typical QP burst. Charge-parity states of all selected qubits (Q0 to Qn) are continuously monitored with a period of 5.6 μs. The QP bursts induced by μ or γ are identified when there is a multiqubit simultaneous charge-parity jump (MQSCPJ).

Full size image

We also find that QPs in our case decay two to three orders of magnitude faster compared to the case in Google’s experiment13. We attribute this to the increased QPs trapped in the aluminum (Al) films of the qubit tunnel junctions. The Al films have a smaller energy gap than that of the tantalum (Ta) films, which are in contact and serve as the capacitor pads, thereby forming QP traps. Our work shows that the sensitivity of charge-parity jump to QP burst is much higher than bit flip. By monitoring the charge-parity jump, using QP traps, and reducing the area of ground Ta films, the superconducting qubits could be used for the detection of cosmic-ray particles and dark matter18,19,20,21 over a wide energy range.

Results

Device and QP burst detection

Figure 1a shows the photograph of the device used in our experiment (left) and the basic process of QP bursts generated by high-energy particles (right). The device contains 63 flipmon qubits and 105 couplers22,23, which are composed of Ta capacitor pads, indium (In) bumps, and Al Josephson junctions (see also Methods and Supplementary Information). The muons or γ-rays traverse through the sapphire substrate and generate nonequilibrium phonons, which propagate throughout the substrate, transferring energy to superconducting films. During the process, Cooper pairs can be broken, thus generating excess QPs on a large scale (QP burst). QP tunneling across the qubit’s Josephson junctions, with rate linearly increasing with the QP density24,25,26,27, leads to correlated errors. Previous works have studied the impact of high-energy particles by monitoring the energy relaxation times9,11,13, which involves a bit-flip process assisted by QP tunneling28. In this work, we also use a technique of monitoring the charge-parity change when QPs tunnel. Since the charge parity will change immediately if the number of tunneling QPs is odd, this technique has a much higher sensitivity to QP bursts. Theoretical estimation indicates that the probability of charge-parity change due to QP tunneling is approximately 20-80 times higher than the bit-flip probability 25.

The charge-parity state of a single transmon qubit can be measured using the Ramsey-based sequence29, shown in Fig. 1b, which allows the mapping of the charge-parity state (even or odd) onto the qubit eigenstate (\(\left\vert \right.0\left.\right\rangle\) or \(\left\vert \right.1\left.\right\rangle\)). The qubit exhibits different frequencies depending on its charge-parity state, with a frequency difference 2Δf. A π phase difference between the even and odd charge-parity states can be accumulated after an evolution time of 1/(4Δf). To accumulate a fast phase difference, it is necessary to reduce the ratio of Josephson energy (EJ) to charging energy (EC) of the qubit30. However, doing so moves the qubit away from the transmon regime, which could decrease the qubit performance.

We select 31 qubits exhibiting readout fidelities above 90% for the experiment and one additional qubit for QP injection. Each qubit spectrum is engineered with a higher (7.1 GHz) and a lower (3 GHz) sweet spot by using asymmetrical qubit Josephson junctions, resulting in larger and smaller EJ/EC ratios. As shown in Fig. 1c, we are able to achieve high-fidelity gate operations at the higher sweet spot with EJ/EC ≈ 83 and Δf ≈ 68 Hz (idle point) and fast charge-parity mapping at the lower sweet spot with EJ/EC ≈ 16.5 and Δf ≈ 11 MHz (charge-sensitive point). We also achieve fast qubit reset by tuning the qubit frequency to match the readout resonator frequency (4.3 GHz) and high qubit-readout fidelity by adjusting the qubit frequency (6 GHz) to maximize readout efficiency. Overall, the Ramsey-based sequence can be repeatedly executed in 5.6 μs, enabling continuous monitoring of the charge-parity state of the qubit.

We explore QP bursts from the high-energy particles by monitoring the multiqubit simultaneous charge-parity jumps (MQSCPJ). As illustrated in Fig. 1d, the initial parity state of each qubit is random but stabilizes during subsequent measurements, showing a stable parity behavior. However, when a QP burst occurs, charge-parity jumps across multiple qubits are observed, showing an unstable parity behavior. After the relaxation of the QP burst, all qubits return to stable parity behavior. Note that the correlated phase error induced by charge-parity jump is negligible in transmon qubits with a large ratio of EJ/EC30. However, the correlated bit-flip error across multiple qubits induced by QP burst is not negligible and poses a significant obstacle to quantum error correction. Below, we measure the multiqubit simultaneous bit flips (MQSBF), similar to the case in Ref. 13, to evaluate correlated errors. We will show that while bit flips are closely related to correlated errors, charge-parity jumps are more sensitive to QP burst, thus providing a promising method for cosmic-ray particle detection.

Comparison of MQSCPJ and MQSBF

We compare the two detection methods of MQSCPJ and MQSBF. To this end, we use an injection qubit (see Fig. 1a) to produce nonequilibrium QPs31 (see also Methods). For each injection power, we measure the average time of charge-parity jump (τ) and bit flip (T1) of each qubit. As shown in the inset of Fig. 2a, τ can be determined from the power spectral density of the time evolution of charge parity obtained by continuously performing the charge-parity measurement sequence in Fig. 1c. τ is found to be 2.4 ms (green) at an injection power of -15 dBm and 0.5 ms (orange) at 15.4 dBm, respectively. Similarly, in the inset of Fig. 2b, by fitting the qubit energy relaxation, T1 is found to be 10.6 μs (green) and 6.8 μs (orange) at the injection powers of −15 dBm and 24 dBm, respectively. Figure 2a and b display the average values of τ and T1 for all selected qubits as a function of injection power, normalized to the value at the injection power of −20 dBm. We find that T1 for each qubit remains unchanged until the injection power reaches approximately 22 dBm, while τ undergoes a noticeable change at an injection power of around 4 dBm. This power level, very likely, corresponds to the voltage across the qubit junctions exceeding the gap voltage, so QPs start to be generated. The injected QPs immediately cause noticeable changes of MQSCPJ but not of MQSBF.

Fig. 2: Response of charge-parity jump and bit flip to QP burst.
figure 2

a Average time of charge-parity jump (τ) versus QP injection power for all selected qubits, normalized to the value at  −20 dBm. Data with different darkness is for different qubits. The power spectral densities (PSD) of the charge-parity time evolution for two injection powers indicated by green and orange squares are shown in the inset, which are used to extract τ. As the injection power increases to approximately 4 dBm, τ starts to decrease. b Normalized average time of bit flip (T1) versus QP injection power. The qubit energy relaxations for two injection powers, indicated by green and orange squares, are shown in the inset, which is used to determine T1. T1 is seen to decrease at the injection power of approximately 22 dBm. Source data is provided as a Source Data file.

Full size image

QP bursts induced by muons

We are able to observe the coincidences of QP bursts and muon events by continuously monitoring MQSCPJ or MQSBF, and at the same time recording muon events by muon detectors. Employing two muon detectors (see Fig. 1a) makes it possible to distinguish signals induced by muons from those by γ-rays, as the latter is unlikely to produce simultaneous responses on both detectors, a criterion we use to identify muon events. Each muon detector has a plastic scintillator serving as the detection medium, along with a silicon photo-multiplier tube for signal collection. After the amplification at room temperature, the signal can be captured in a continuous acquisition mode by a data acquisition card.

The measured MQSCPJ and MQSBF signals are found to have background noises that are mainly caused by limited qubit operation and readout fidelities. To reduce the background noise in the MQSCPJ experiment, we smooth the continuous-monitored charge-parity data for each qubit through convolution with a square window of length 20 sampling points. We calculate the charge-parity jumps for each qubit and average the results across all the selected qubits, which is defined as the smoothed MQSCPJ ratio (see Methods for details). In the MQSBF experiment, we calculate the ratio of the number of error qubits to the total number of selected qubits and convolve with a Gaussian window of length sigma about 10 sampling points, which is defined as the smoothed MQSBF ratio (see Methods for details).

Figure 3a shows the typical time series of the smoothed MQSCPJ ratio for a time period up to  ~599 s. Clear peaks from QP bursts above the threshold value of 0.31, corresponding to the noise level are observed. The representative time slices of a single QP burst and muon events recorded by both MDA and MDB are shown in Fig. 3b and c, respectively. The coincidence of QP burst and muon events is confirmed since the peaks fall within the time window of 100 μs. Statistically, if QP burst and muon events are completely uncorrelated, the probability of one coincidence within the duration of  ~599 s is (41 × 127)/(599 s/100 μs)  ≈ 8.7 × 10−4. However, 10 coincident events are identified, as indicated by the vertical dashed lines in Fig. 3a, providing strong evidence of these QP bursts being induced by muon events. In Fig. 3a, we can see 41 QP bursts and 127 muon events. Additional QP bursts other than the coincident ones should be induced by γ-rays (see below), while additional muon events are expected, considering that the detector area is larger than the area of the qubit chip.

Fig. 3: QP bursts by muons and γ-rays.
figure 3

a Smoothed MQSCPJ ratio PMQSCPJ(blue lines, left scale) in a time period of  ~599 s. The horizontal dashed line indicates a threshold of 0.31 above which the MQSCPJ peaks correspond to QP bursts. Thin green and pink lines are the voltage signals of MDA and MDB (right scale). In all, 41 QP bursts and 127 muon events are detected, and 10 coincident events (marked by vertical dashed lines) are identified from the simultaneous appearance of MQSCPJ, MDA, and MDB signals as shown in b, c near tx ~ 464 s. d Smoothed MQSBF ratio PMQSBF measured over 22,400 s with a threshold of 0.21. In all, 75 QP bursts, 4751 muon events (not shown due to overcrowding), and 12 coincident events are detected. e, f Histograms of the time intervals between neighboring coincident events (light blue bars) and QP bursts (blue bars) for MQSCPJ and MQSBF experiments, respectively. Lines are the corresponding exponential fits. g, h Averaged dynamic processes starting from each coincident events for MQSCPJ and MQSBF ratios, respectively. The error bars represent the standard deviations of the PMQSCPJ and PMQSBF for the coincident events. Lines are the exponential fits yielding the recombination times of 36 ± 3 μs and 21 ± 2 μs. To better describe the rapid process, the length of the smoothing window used in g is 2 sampling points, while no smoothing window is used in h. Source data are provided as a Source Data file.

Full size image

In the MQSBF experiment, we observe 75 QP bursts and 4751 muon events over a time duration of 22,400 s, as shown in Fig. 3d. A much longer time range is used since the number of QP bursts measured by MQSBF becomes much smaller. Because of this, Fig. 3d does not show the overcrowded detector signals of MDA and MDB. In the figure, 12 coincident events are observed as indicated by the vertical dashed lines. The uncorrelated hypothesis gives the probability of one coincidence within the duration of 22,400 s is 1.6 × 10−3, which again confirms that these coincident QP bursts are induced by muon events.

We repeat the MQSCPJ experiments and exponentially fit the histograms of the time intervals between neighboring events to yield the average occurrence times of 12.7 ± 0.4 s for all QP bursts, 67 ± 3 s for muon-induced QP bursts, which are presented in Fig. 3e. Taking into account the size of our qubit chip (15 × 15 mm2), we can calculate a coincidence occurrence rate of 0.40 ± 0.02 min−1cm−2. Since muon events affect a limited area on the qubit chip32, the rate may be underestimated (Supplementary Information). Similarly, the repeated MQSBF experiments give the average occurrence times of 386 ± 19 s for all QP bursts, 1500 ± 173 s for muon-induced QP bursts, as shown in Fig. 3f. The times are too short for QEC, which typically needs operation times on the order of hours 16,17.

QP bursts induced by γ-rays

In Fig. 3a and d, we see that the number of QP burst peaks exceed those in coincidence with muon detector signals. These additional peaks should be induced by γ-rays. To further see the impact of the γ-rays, we use a γ-ray detector and a Pb shield with a thickness of 1 cm that can be placed around the outer vacuum chamber (OVC) of the refrigerator to reduce the γ-ray radiation (see Fig. 4a). Figure 4b shows an average occurrence time of 4.48 s (6.39 s) without (with) the Pb shield, indicating a shielding efficiency of (1/4.48–1/6.39)  × 4.48 = 29.9%  ± 1.5%. However, it shows almost no effect on the muon events with an average occurrence time of 4.74 s (4.78 s) without (with) Pb shield, as depicted in Fig. 4c, which corresponds to a muon flux of 0.506  ± 0.004 min−1cm−2 when considering the area of the plastic scintillator of 5 × 5 cm2 (Supplementary Information).

Fig. 4: Separation of the events induced by muons and γ-rays.
figure 4

a Schematic of the outer vacuum chamber (OVC) of the refrigerator with (on) and without (off) Pb shield. b, c Probability of time intervals between neighboring events of the γ-ray detector and muon detectors with and without Pb shield. All solid lines are exponential fits to give τon or τoff. d The QP burst event occurrence time τMQSCPJ is measured with and then without Pb shield, and the cycle is repeated 5 times to give an average value of 16.7 ± 0.4 s (12.3 ± 0.6 s) for Pb shield on (off). Source data is provided as a Source Data file.

Full size image

To eliminate random fluctuations, we measure MQSCPJ and collect hundreds of events with the shield off, followed by the shield on, and repeat this cycle five times. As shown in Fig. 4d, the average values are 16.7  ± 0.4 s (12.3  ± 0.6 s) with shield on (off), indicating the average occurrence time apart from muon-induced QP bursts is 1/(1/16.7–1/67) s = 22.2  ± 0.8 s with shield on, and 1/(1/12.3–1/67) s = 15.1  ± 0.9 s with shield off. Thus, the shielding efficiency detected by MQSCPJ is (1/15.1–1/22.2)  × 15.1 = 32%  ± 5%, which is close to the efficiency of 29.9% detected by the γ-ray detector. So, apart from muons, QP bursts are primarily induced by γ-rays15, with a ratio of approximately (1/12.3–1/67) × 12.3 = 81.6%  ± 1.2%.

QP trapping and particle detection

To see the dynamical behavior of the QP bursts induced by muon events, we look at the processes starting from each coincident points (indicated by vertical dashed lines in Fig. 3) and average the corresponding coincident events. The results are shown in Fig. 3g and h for MQSCPJ and MQSBF experiments, respectively. We fit the tails of the averaged events and determine the recombination times to be 36 ± 3 μs and 21 ± 2 μs, respectively. The recombination times are roughly two to three orders of magnitude shorter than that observed in Google’s Sycamore processor13, which should result largely from the increased QP density and QP trapping in the Al films of the qubit tunnel junctions. As can be seen in Fig. 1a and 5 below in Methods, the Al films are in contact with the Ta films serving as the qubit capacitor pads. Hence, the Al films having a smaller energy gap act as QP traps that accumulate QPs. Since the QP recombination rate is proportional to the QP density12,13,33,34 which also increases the tunneling rate35, they lead to shorter recombination times (Fig. 3g and h).

Fig. 5: False-color SEM images near the center of a qubit.
figure 5

a Qubit chip. b Carrier chip. c Zoomed-in view of the SQUID structure.

Full size image

Specifically, the muons first deposit energy in the qubit chip (substrate), which is transferred to the Ta films as phonons near the Debye energy of  ~20.7 meV. The Ta films have an energy gap of  ~0.69 meV, so a number of Cooper pairs are broken leading to QP bursts. The QPs will scatter, quickly relax to the gap edge, diffuse into the Al films with a smaller gap of  ~0.18 meV, and be trapped. Though the superconducting device has a complex structure with a carrier chip connected via In bumps13,22,23, the present situation is simpler since In bumps have a gap of  ~ 0.51 meV and QP diffusion to the Ta pads with a larger gap can be ignored.

The sensitivity of charge-parity jump to QP burst is much higher than that of bit flip, since the former occurs whenever odd number of QPs tunnel while the latter has a much smaller probability requiring energy conservation28. The present method using MQSCPJ may therefore be applied for the detection of cosmic-ray and dark matter particles over a wide energy range, which has recently received increasing interest18,19,20,21. With this method, the detection starts with the absorption of the energy of the particles that penetrate the qubit chip (substrate). The conversion of the energy to more QPs close to the tunnel barrier and highly detectable tunneling events are the key to high detection efficiency. Estimations considering MQSCPJ, QP trapping, and reduction of ground Ta film area show that the detection could be effective when the energy deposited in the substrate is tens of meV and above (Supplementary Information), or for particles roughly with energies of sub-keV up to GeV. The threshold energy may vary depending on the absorption coefficient of the substrate. For dark matter particles with low coefficient36, the threshold is on the order of tens of keV, which is below the threshold of MeV of the presently available detectors. The method should also be applicable for the detection of far-infrared photons if they are directed to the qubit chip19,37.

Discussion

We have provided direct evidence of QP bursts and correlated errors induced by muons and γ-rays, and successfully separated their contributions in the superconducting qubits. We find that the correlated charge-parity jumps occur more frequently than the correlated bit flips, which may also have an impact on topologically protected Majorana qubits, since they would not survive a charge-parity jump event 38,39,40.

The occurrence time of charge-parity jumps induced by muons is found to be 67 seconds, while that of bit flips is 25 minutes, which remains too high for the implementation of QEC. One effective mitigation approach is to conduct the experiment deep underground41,42. However, such an approach would require high costs. Several methods propose using low-gap superconductor or normal metal as quasiparticle43,44 and phonon45 traps, employing gap engineering46, and suppressing the phonon transport47, in order to mitigate correlated errors. On the ground, Pb shields can be used to effectively reduce the impact of the γ-rays but not of the cosmic-ray muons. We have shown that muon detectors can operate within the refrigerator, which enables the development of muon detection arrays for the identification of the occurrence and location of muon-induced QP bursts. This can be used to build QEC circuits around the correlated error and drop a section of the device or chiplet out of the QEC protocol 16,48.

Also, the present method of monitoring multiqubit simultaneous charge-parity jumps shows high sensitivity to QP burst and has the potential for application in cosmic-ray and dark matter particle detection in the future18,19,20,21.

Methods

Device and fabrication

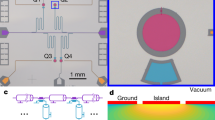
Our device consists of 63 flipmon qubits and 105 couplers. The topology, design parameters, and fabrication techniques are described elsewhere22,23. As is shown in Fig. 1a, the 15 × 15 mm2 qubit chip is precisely aligned and integrated with the larger 30 × 30 mm2 carrier chip using indium bumps. The vacuum gap between these two chips is about 10 μm. The flipmon qubits feature a floating design, where one capacitor pad is on the qubit chip. The other capacitor pad is largely located on the carrier chip, with a smaller portion on the qubit chip, and the two parts are electrically connected via indium bumps. Detailed views of a flipmon qubit on the qubit and carrier chips are shown in Fig. 5a and b. The capacitor pads are made from 200 nm thick layers of Ta and 36 nm thick layers of Al. Two capacitor pads are electrically connected with a SQUID (superconducting quantum interference device) which is prepared using the Dolan-bridge shadow evaporation technique. The two aluminum layers used for the Dolan bridge have thicknesses of 17 nm and 19 nm, respectively. The total areas of the larger capacitor pad on the qubit chip made from Ta and Al are about 63236 μm2 and 87 μm2, respectively. Components around the qubit center include the couplers (green), air bridges (orange), and a readout pad (purple). The couplers mediate qubit-qubit interactions, while the air bridges ensure robust electrical connections. Fig. 5c further magnifies the SQUID region (blue), showing its detailed structure. The SQUID loop enables frequency tunability of the qubit by controlling the magnetic flux.

Charge-parity jump rate vs bit-flip rate

The charge-parity jump rate Γe→o divided by bit-flip rate Γ1→0 is given by25:

$$\frac{{\Gamma }_{{\mbox{e}}\to {\mbox{o}}}}{{\Gamma }_{1\to 0}}=\frac{{E}_{J}({\phi }_{1}){e}^{\frac{{f}_{eo}({\phi }_{1})}{2T}}{K}_{0}\left(\frac{{f}_{eo}({\phi }_{1})}{2T}\right){\omega }_{p}({\phi }_{2})\left({\omega }_{p}^{2}(0)-{\omega }_{p}^{2}({\phi }_{1})\right)}{{E}_{J}({\phi }_{2}){e}^{\frac{{\omega }_{p}({\phi }_{2})}{2T}}{K}_{0}\left(\frac{{\omega }_{p}({\phi }_{2})}{2T}\right){E}_{C}\left({\omega }_{p}^{2}(0)+{\omega }_{p}^{2}({\phi }_{2})\right)},$$
(1)

where ϕ1 and ϕ2 represent the normalized fluxes at which the charge-parity jump and bit-flip experiments are performed. EJ, ωp and feo denote the flux-dependent Josephson energy, plasma oscillation frequency, and the frequency difference between even and odd charge-parity state, respectively. EC is the charging energy. T is the effective temperature of qubit. K0 is the modified Bessel function of the second kind. In our experiment, we have ϕ1 = 0.5, ϕ2 = 0, EJ(0.5) = 4.719 GHz, EJ(0) = 23.8 GHz, ωp(0) = 7.379 GHz, ωp(0.5) = 3.286 GHz, feo(0.5) = 11 MHz, EC = 0.286 GHz, and T ~ 40 mK, which approximately give a ratio of Γe→o/Γ1→0 = 18.

QP injection

As shown in Fig. 1a, we select a qubit (orange) as an injection qubit to inject QPs31. A microwave switch is placed at the output of a microwave source (with maximum power of 25 dBm) to generate a strong microwave pulse with the frequency set to the bare frequency of the qubit resonator (~4.25 GHz). With this, we generate and store photons of sufficient number, which create an oscillating voltage across the qubit Josephson junctions. When the voltage exceeds the gap voltage, a number of QPs are generated. These nonequilibrium QPs will recombine into Cooper pairs or relax to lower energy levels, producing a number of phonons that propagate throughout the substrate and break Cooper pairs leading to QP bursts, similar to the QP burst process induced by muons and γ-rays.

Generally, the intensity of the produced QP bursts increases with increasing power of the injected microwave pulse. By varying the injection power, we can control the QP burst intensity and perform the charge-parity jump and bit-flip measurements.

QP burst detection by MQSCPJ and MQSBF

The key point of detection is the ability to convert or transduce a physical process into a measurable signal, which can be processed, analyzed, and interpreted. Here, we detail how to calculate and analyze the response of MQSCPJ and MQSBF to QP bursts while taking account of system noise. Since only a few QP tunnelings occur in each qubit during a QP burst that lasts only tens of microseconds, it is challenging to distinguish a QP burst from the background noise of QP tunneling using only a single qubit. Therefore, we consider QP tunneling occurring simultaneously across multiple qubits to reliably confirm the occurrence of a QP burst.

For the MQSCPJ experiment, we continuously monitor the charge parity of each selected qubit, recording the resulting data as a sequence of 0’s and 1’s. Charge parity jumps are characterized by transitions between 0 and 1. This raw data also contain random noise due to the operation and readout errors of the qubits. Therefore, convolving the raw data with a square window is well suited to suppress the noise while having little effect on the charge-parity jump behavior. The window length is set to 20 sampling points (112 μs), which is approximately three times the recombination time of QP burst in our device. This duration is also much shorter than the average interval between QP bursts (12.3 s). To further enhance the signal-to-noise ratio of the QP burst, we average the smoothed data across multiple qubits to identify the burst event, which is defined as smoothed MQSCPJ ratio (PMQSCPJ):

$${P}_{{{\rm{MQSCPJ}}}}(n)=\frac{1}{M}{\sum }_{m=1}^{M}\left(0.5-\left| {\sum }_{\tau=1}^{L}{f}_{L}(\tau ){d}_{m}(n-\tau )-0.5\right| \right),$$
(2)

where M is the number of selected qubits, fL(τ) is a normalized square window function with length L, and d is the raw data.

For the bit-flip experiments, we continuously monitor the state of each selected qubit. The qubit state typically remains at \(\left\vert \right.1\left.\right\rangle\) but occasionally undergoes flip to \(\left\vert \right.0\left.\right\rangle\) due to QP bursts. After the relaxation of the QP bursts, the qubit state returns to \(\left\vert \right.1\left.\right\rangle\). We first average the raw data across multiple qubits, then considering the operation and readout errors as in the MQSCPJ experiment, we smooth the raw data by convolving with a Gaussian window with a sigma length of 10 sampling points (56 μs) to have the smoothed MQSBF ratio:

$${P}_{{{\rm{MQSBF}}}}(n)={\sum }_{\tau=-4L}^{4L}{f}_{L}(\tau )\left(\frac{1}{M}{\sum }_{m=1}^{M}\left(1-{d}_{m}(n-\tau )\right)\right),$$
(3)

where M is the number of qubits used, fL(τ) is a normalized Gaussian window function with a sigma length L, and d is the raw data.

The choice of detector threshold is another key point. We set threshold values conservatively in the MQSCPJ and MQSBF experiments, which almost eliminates the concerns about QP bursts caused by long-term random fluctuations. The thresholds are set to 6 (6.6) sigma deviation of the mean value of the smoothed MQSCPJ (MQSBF) ratio in the duration of  ~ 599 s (22,400 s).