Introduction

The one-dimensional sp1 hybridized carbon allotrope, carbyne, is a periodic linear carbon chain, with alternating triple-single bond geometry, owing unique properties independent of its length1. Theoretically, freestanding carbyne in vacuum is used as the simplest toy model for phonons and one dimensional metal-semiconductor transitions2. Carbyne is also known to be the strongest Raman scatterer3, and it is predicted to be the strongest material in terms of traction4. Experimentally, however, in contrast to studies of polyenes5,6, bulk carbyne has remained elusive for >125 years. Only in 2016 linear carbon chains up to 1 micron length7 were verified inside carbon nanotubes. The encaging nanotube host solely defines the properties of the chain7,8,9,10,11. Hence, this coaxial one dimensional carbon hybrid structure is named confined carbyne (CC), a new carbon allotrope7,10. It is distinctively different to polyynes, where all properties9,11,12,13,14,15 are defined by the environment, bond length alternation (BLA) and total chain length16,17,18. Growing carbyne inside nanotubes comes with severe modifications in the nanotube related G-modes as additional shoulders7,10,19,20,21. These new features have never been analyzed nor explained and appear whenever the confinement is strong. Their visibility in the Raman spectrum depends severely on the overall filling yield and the diameter distribution of the precursor material. The satellites progressively disappear with decreasing interaction and increasing radius, as confirmed by a recent work showing absent satellites for a hosting SWCNT of 1nm diameter18. In contrast to freestanding carbyne, the confined carbyne interacts strongly with the hosting tube, complicating the theoretical analysis11,13,15,22. State-of-the-art ab-initio calculations have shown23 that, anharmonicity as well as the dielectric environment play a crucial role in describing the vibrational properties of free-standing carbyne. Whenever the confinements interaction is strong enough, these satellites are observed. Standard density functional theory (DFT)24 calculations in the harmonic approximation fail to describe the phonons inside carbyne and a surrounding nanotube can not be mimicked by a dielectric environment alone.

In this letter we use the templated growth of confined carbyne inside arc-discharge nanotubes with a narrow diameter distribution to unravel the unique resonance Raman fingerprint of CC inside DWCNTs. The spectral response is distinctively different from those of individual carbon nanotubes and carbyne, previously evaluated within the harmonic approximation. Here we show that confined carbyne hosts an apparent paradox: the tube and the chain are electronically decoupled and nevertheless the vibrational states are strongly altered by many body effects beyond the harmonic approximation. This large phonon-phonon scattering is surprisingly sufficient to explain the unconventional resonant spectra of this coaxial one dimensional interface. CC@DWCNT is an archetypical reference system to study the effect of phonon–phonon interactions in hybrid systems.

Results

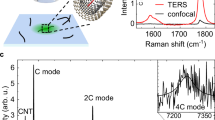
To introduce the changes in the complete Raman response by our templated growth of confined carbyne, we show the spectra of CC@DWCNT with an unfilled DWCNT reference prior to the carbyne growth in Fig. 1.

Fig. 1: On resonance Raman spectrum of double walled carbon nanotubes (DWCNTs) and confined carbyne (CC) grown inside the same DWCNT measured with a 2.18 eV laser and normalized to the same laser power.
figure 1

A sketch of carbyne confined (CC) inside a DWCNT (a) in black and an unfilled DWCNT (b) in gray is linked to the corresponding spectra of the designated colors. The red arrow points to the LO-CC line associated to the encapsulated carbyne (red atoms in (a)). The radial breathing modes (RBM) reveal the same diameter distribution. For the CC@DWCNT hybrid structure the LO mode of CC is strongly resonance enhanced. Interestingly, the nanotube modes of the DWCNTs are strongly altered by the carbyne growth which manifests in both the G-mode and the defect related D mode as well as its 2D overtone, showing pronounced shoulders highlighted in red.

Full size image

The radial breathing modes (RBMs) reveal the same diameter distribution of both filled and unfilled DWCNTs (later analyzed in Fig. 2e). For the CC@DWCNT hybrid structure the LO-mode of CC is strongly resonance enhanced. Interestingly the resonance Raman fingerprint of confined carbyne comes concomitant with new features which are only present in the CC@DWCNT hybrid system. Both the G-mode and the defect related D-mode and its overtone (2D-mode) show pronounced shoulders. In this letter, we quantitatively explain all spectral features of this unique hybrid system by comprehensive experimental and theoretical investigations. Confined carbyne turns out to be a strongly anharmonic one dimensional hybrid system, where the interaction between phonons causes a dramatic change of their energy spectrum. The concomitant theory suggests vanishing charge transfer, yet strong phonon-phonon interactions. Bulk confined carbyne turns out to be an archetypical example of strong anharmonicities affected by interfaces of hybrid structures. In order to grow CC@DWCNT with a well defined geometry, we used arc discharge SWCNT25,26 with a narrow Gaussian diameter distribution of d = 1.36 ± 0.08 nm (see Fig. 2a) as templates. They are filled with C60 molecules to form peapods. DWCNTs with inner tubes of \(d=\left(0.6\right.\) to \(\left.1.0\right)\) nm diameter are then formed by a one-step annealing27 (see Fig. 2b). CC@DWCNT was then grown via a two step process described in detail in ref. 19,28. Further information can be found in the Methods section.

Fig. 2: Raman spectra of confined carbyne grown from C60 filled nanotubes of narrow diameter distribution of 1.36  ± 0.08 nm.
figure 2

a Shows the C60 filling yield of nanotubes with diameter around 1.36 Å together with a sketch of the C60 filling. b Indicates the diameter distribution of the inner tubes grown from the C60 together with a sketch of the formation of the inner tubes. c Shows the LO-frequency of the carbyne with respect to the inner wall diameter assigned from 8 together with a sketch of the carbyne filled DWCNTs. Figure (d) shows the resonance Raman spectra of CC for 1.96 eV (red) and 2.18 eV (black) laser. The spectra featuring the CC-LO were decreased by the displayed factor for comparability. e Displays a line-shape analysis of the RBMs (eI) and (eII) of the 2.18 eV spectrum of figure (d) together with a sketch indicating the associated diameters. f Shows the carbyne LO-mode of the resonance Raman spectrum depicted in (d) obtained with a laser energy of 2.18 eV together with a sketch indicating the LO-modes of carbyne inside two different nanotubes.

Full size image

The observed LO-modes of CC ranges from 1790–1850 cm−1 for different laser excitation energies (see Figs. 2d and 3b). They can be assigned to inner tube diameters between 0.6 and 0.9 nm (see Fig. 2c) from direct near field measurements8 and the line shape analysis from bulk samples29. The corresponding major components of the LO-CC line around 1826 cm−1 and 1846 cm−1, shown in Fig. 2f, are assigned to CC in inner-tubes between 0.73 and 0.77 nm11.

The spectra shown in Fig. 2d highlight the new vibrational modes appearing as interaction peaks located around 1630 cm−1 and around 1540 cm−1 in the region of the DWCNT G-band and additional shoulders in the 2D response. These peaks can not be seen in carbon nanotubes of any sort. Also, regarding the Raman active carbyne modes, only the LO CC-mode is symmetry allowed. A defect induced symmetry break, which would make certain modes such as the longitudinal acoustic (LA) mode of CC outside of Γ Raman active, is discussed in Supplementary File and shown in Supplementary Fig. 7 and can be ruled out. These features being in fact a consequence of the carbyne being present in the tube can be seen in the sonication experiment shown in the Supplementary Figs. 1–4 as well as in ref. 19 which display a direct correlation between the CC yield and the additional shoulders. It shows a systematic decrease of these additional peaks together with the diminishing of the CC-mode via a destruction of the CC by subsequent sonication, finally yielding pristine defective DWCNT.

In order to analyze the resonance Raman behavior of these additional features we performed measurements at different laser energies. The results are shown in Fig. 3. The coupled modes are highlighted by the difference to the pristine DWCNT as red and blue areas in the inset (a)I and (c)I of Fig. 3. The CC coupled G+ and G- bands of Fig. 3a show a distinctively different resonance behavior than the CC-LO mode shown in Fig. 3b. In other words: The interaction induced shoulders around the G-line change differently in their absolute intensity than the LO-CC mode does for varying laser energies. Similar behavior holds for the dispersive 2D line (Fig. 3c). The corresponding line shape analysis can be seen in the Supplementary Fig. 5.

Fig. 3: Raman spectra of CC and unfilled DWCNTs for different laser excitations.
figure 3

a Shows the G line of CC and the contribution of the corresponding unfilled DWCNTs as dark area. The inset (aI) in the upper side of (a) highlights the difference of the filled and unfilled system by a line shape analysis including the high energy (blue) and low energy (red) coupled modes in the G-band, respectively. b Shows the resonance behavior of the different components of the CCs LO-mode. Note that for the IR-laser radiation (1.17 eV) no LO-mode of the CC is in resonance, while the associated interaction features around the G-line (shown in (a)) are in resonance. c Shows the corresponding 2D bands of the CC and the unfilled system. As expected a clear laser energy dependent dispersion is observed concomitantly to additional shoulders in the CC filled DWCNT. The inset (cI) in the upper side of (c) highlights the difference of the filled and unfilled system by a line shape analysis including also dispersive high energy (blue) and low energy (red) shoulders in the 2D, respectively.

Full size image

The interaction features of the 2D-line mirrors the ones of the G-line for energies above 2.41 eV. The D- and 2D-lines resonance follows the direct electronic excitation energies of the tubes. Their new interaction features are visible for all investigated laser energies and follow the trend of the 2D-line. Indeed, even if the CC mode is completely out of resonance, as for the NdYaG IR-laser of 1.17 eV excitation energy, the resonance of the interaction related additional modes are still present (see yellow curve of Fig. 3).

Since the new features around the G-line and 2D-line are vibrations of the tube-chain hybrid system, they can be evaluated by an analysis of the ion dynamics. The resonance behavior of a solid state system is connected to its possible excitations. Both can be simulated on ab-inito level by DFT. We will assume here that the outer tube only serves as a stabilizer and the interaction appears mainly between the inner tube and the carbyne.

Concerning DFT calculations, we focus our analysis on the [5,5] metallic nanotube due to the reduced number of atoms in the unit cell. The tube was stretched by 0.06 Å in axial direction to ensure a commensurate unit cell. The overall geometry was relaxed to minimize the total energy of the carbyne in combination with the interaction energy (For further information see Supplementary Note 4).

Reproducing the main features such as the CC-LO-mode of the bulk confined carbyne system proves to be challenging22. It is however possible to reproduce this eigenfrequency at 1860 cm−1 balancing Hartree Fock-exchange30 \({E}_{x}^{HF}=0.3\) and range separated screening HFSCREEN = 0.0731. These parameters differ for semiconducting and metallic nanotubes which underlines the strong impact of the electronic environment.

For illustration the harmonic eigenfrequencies ωm(Γ) of the CC@[5,5] system, which imply a change of polarizability, are plotted utilizing a simple approximation for the Raman tensor (see Supplementary Note 5). This quick estimation is compared to the experimental Raman spectrum of Fig. 3 and below (see Fig. 4a).

Fig. 4: DFT analysis regarding vibrational properties and charge transfer of CC.
figure 4

a Shows a direct comparison of the Γ phonons of the CC@[5,5] system obtained by the harmonic approximation from DFT (in red) together with the experimental Raman spectrum of CC@DWCNTs measured with a 568 nm laser (blue). The gray dashed lines in (a) show the individual modes ωn(Γ) forming the spectrum (in red). Figure (b) shows the convergence of the LO-mode of the chain with increasing k-mesh for different sized supercells together with a sketch illustrating this vibration. Figure (c) shows the Joined Density of States (JDOS) of the isolated carbyne (blue) and the [5,5] tube system (black) together with the resonance behavior of the interaction features of the G line displayed in Fig. 3a and the carbynes LO mode from Fig. 3b marked by crosses (x). The experimental values (x) are relative values of the intensities of the corresponding feature (CC-line and interaction features) with respect to the G-line intensity (ICC/IG). They are scaled by 1.3 (blue) and 0.5 (black) respectively for comparison to account for the resonance. The JDOS is normed such that \(\int_{1}^{3}JDOS(E)dE\) = 1. d Shows the geometry and charge density of the [5,5] and CC@[5,5] system obtained from DFT and the associated charge transfer.

Full size image

From our charge transfer32 evaluation illustrated in Fig. 4d we conclude that only very small charge carrier rearrangement of 0.01 electrons per primitive CC unit cell from the [5,5] nanotube onto the chain is present. This is in agreement to previous charge transfer analysis22. We therefore safely conclude that charge transfer is not the main player of the chain tube interaction. In the classical charge transfer picture the carybne and the tube are almost isolated from each other. Nevertheless, the chain interacts strongly with the surrounding tube by electrostatic and Hartree-Fock like interactions. This external potential onto the chain changes its potential energy surface and leads to softer force constants  → downshift of the CC-LO mode.

This is perfectly in line with the experimental observations shown in Fig. 3. Assuming that the Raman tensor of the phonon modes doesn’t change with the laser-excitation energy, the joined density of states (JDOS) describes the possible electronic excitations and so can be used to approximate the resonance behavior. When comparing the JDOS of the isolated systems (chain and tube) to the resonance of the interaction peaks from Fig. 3a and the CC-LO mode from Fig. 3b we find quantitative agreement (see Fig. 4c). Note that this is not the case if we compare it to the JDOS of the combined system where excitations between tube and chain are allowed (see Supplementary Fig. 6). This indicates that electronic excitations between the two subsystems do not occur.

While the peak positions in the spectra of Fig. 4a compare quite well, the interaction states around the G line shown in Fig. 3a, are not described by the harmonic approximation (see Fig. 4a). The dynamical matrix reveals no vibrational states where chain and tube oscillate collectively. Also no Γ-mode of the tube or carbyne resembles the frequency of the interaction features.

Since these new features seen in the Raman spectrum are real Raman active vibrational states of the combined CC@CNT hybrid system, we have to improve on the description of the vibrational states. The experiment as well as DFT conclude that the two systems act isolated in a classical electronic picture. Still there is a coupling affecting the vibrational spectrum. A direct improvement on this is including anhamonicity and scattering from different phonons. Therefore we use these results as a basis for the stochastic self consistent harmonic approximation (SSCHA)33. The SSCHA approach evaluates the free energy and related objects such as the free energy Hessian D(q) at finite temperature. It incorporates phonon-phonon interactions and can be evaluated in a dynamic formalism to simulate the cross section of inelastic scattering processes33,34.

We evaluate the D(q) in two limits, called the bubble approximation D3 and the full self energy D4. In practice this is evaluated in a Green’s function formalism and the related objects are the response functions χ yielding the spectral functions \({\sigma }_{{D}^{(3)}}\) and \({\sigma }_{{D}^{(4)}}\). The D4 was here evaluated in the time dependent SSCHA formalism35. By allowing a mixing of phonons in the expression of the corresponding self energy36, the vibrational spectrum splits up and new features emerge which are referred as satellites. These satellites are the direct consequence of the dynamic interaction of the phonons from the entire system.

The results evaluated for the D(4) are depicted in Fig. 5a in comparison to the resonant Raman spectra of the CC@DWCNT and the unfilled DWCNT at 2.18 eV, respectively. The G- mode (in red) is shifted by about 130 cm−1 using the observed Grüneisen parameter for uniaxial strain37 to compensate for the stress onto the [5,5] tube by 4.4% applied in the calculations to get a commensurate structure. The G + mode (in blue) is not affected by the strain. The non-shifted calculations together with the free energy Hessian frequency in the static limit Gs are displayed in Supplementary Fig. 9a, b. The relative splitting of the observed shoulders agrees well with the experiment. Both G+ and G- state build up satellites which follow the trend of the interaction features of the experiment. The total spectral function obtained by the theory underestimates all modes systematically by about 30 cm−1. The overall red-shift of the theoretical spectrum can be ascribed to the exchange correlation functional used in the calculation. The different levels of approximations can be seen in the phonon dispersion of Supplementary Fig. 9. The LO mode of the carbyne (green) is especially influenced by the anharmonicity. The D(4) correction downshifts the LO mode to 1753 cm−1 and introduces a major satellite at 1630 cm−1 as a consequence to the phonon-phonon scattering with the tubes G-line states. This satellite also occurs for the calculation of the CC@[10,0] system displayed in Supplementary Fig. 10. Also the full width half maximum matches the experimental interaction feature. Apart from the satellites of the CC-LO mode, the D(4) essentially corrects all modes by an up-shift of roughly 20 cm−1 in contrast to the D(3).

Fig. 5: Results of the SSCHA analysis in direct comparison to the experimental Raman spectrum obtained for the 2.18 eV laser.
figure 5

a Shows the spectral function on D(4) level of the CC systems G − (red), G + (blue) and LO-carbyne mode (green) evaluated at Γ (σ(k = 0)) in comparison to the resonance Raman spectra of the CC@DWCNT (black) and the unfilled DWCNT (gray) at 2.18 eV, respectively. The G- mode was shifted by about 130 cm−1 using the observed Grüneisen parameter for uniaxial strain37 to compensate for the uniaxial strain of the [5,5] tube by 4.4 % applied in the calculations in order to get a commensurate structure. The G + mode in blue is not affected by the strain. b Shows the spectral weight σD4 of the LO-mode of the carbyne in the full dynamic approximation, in green, together with the frequency of the static limit Gs in gray. The associated polarization vector of Gs is indicated by the red arrows in the geometry sketch, showing the CC-LO-mode. c Shows the spectral function σD3(k = 0.298[2π/a]) in the bubble approximation of the CC@[5,5] system, which corresponds to an electronic excitation energy of 2.18 eV (in yellow), together with the 2D resonance Raman profile of the CC (black) and unfilled DWCNT system (gray) measured with the 2.18 eV laser. The 2D resonance Raman profile of the CC system (black) also includes the line shape analysis using the predicted 6 phonon branches (blue,gray and red underlying curves). The evaluated maxima of the red and blue-shifted shoulders are marked by the red and blue crosses (x), respectively. Again for the χD3 the contributions emerging from the G- modes, the frequency shift by uniaxial strain was taken into account.

Full size image

In order to further support the explanation with anharmonic phonon-phonon interactions we also analyzed the D and 2D-mode. Its resonance is connected to the vertical excitation energy of the electrons at the associated k-point. The spectral function \({\sigma }_{{D}^{(3)}}(k)\) of the CC@[5,5] system shows the possible vibrational states at the associated reciprocal vector k, including anharmonicities up to 3-phonon vertices (see Fig. 6a). Choosing the k point such that the associated vertical excitation energy matches the laser energy, we meet the double resonance criterion38. These k-points relate to excitation energies of (1.17 –2.71 eV) and are highlighted for the [5,5]-CNT by the green rectangle in Fig. 6a. Figure 5c compares \({\sigma }_{{D}^{(3)}}({{\bf{k}}})\) of the CC@[5,5] system (yellow), at (k = 0.298[2π/a]) corresponding to a electronic excitation energy of 2.18 eV, together with the 2D resonance Raman profile of the CC filled (black) and unfilled (gray) DWCNT system measured at 2.18 eV laser. The 2D resonance Raman profile of the CC system includes the line shape analysis and depicts the centers of the main features by crosses (x).

Fig. 6: Spectral function indicating the 2D modes from bubble approximation of the CC system.
figure 6

a shows the spectral function obtained in the bubble approximation in the dynamical limit (color gradient) and the Fourier interpolated static branches as dashed lines for the first BZ. The color code displays the spectral weight of each k-point, such that ∑nσD3(k)n = N where n is given by the energy spacing and N the number of vibrational modes. The green rectangle (aI) shows the k-point region corresponding to the laser excitation energies of the experiment. All phonon-branches contributing to the defect line are found within 1130–1400 cm−1. The 2D line, its corresponding overtone, is located at twice this frequency, following the double resonance process. The drawn dashed lines (red and blue) inside (aI) highlight the branches emerging from the G+(blue) and G-(red) bands responsible for the D-line and the associated 2D-line dispersion. The middle (b) shows the spectral function evaluated at the q-points where the direct excitation energy of the electronic dispersion of the [5,5] nanotube equals the laser energy. The G- branches in (b) are stress corrected by the uniaxial Grüneisen parameter37. The black dashed and dotted lines connecting (aI) and (b) indicate the change of the frequency range due to the stress correction and doubling in frequency by the “D → 2D” label. The maxima of the individual branches are marked by dots in (b). The right (c) shows the position of the maxima of the calculated spectral function corresponding to the D and 2D line as evaluated from (b) as dots together with the experimental ones obtained from Fig. 3c marked as crosses. Linear fits of the theoretical results are shown as dashed lines. Additionally the measured 2D line frequencies of unfilled DWCNTs with the same diameter distribution from ref. 25 are shown as solid gray lines for the inner (flat dispersion) and outer tubes (steep dispersion) as reference.

Full size image

The contributions of the G-branches (marked by the red dashed lines in Fig. 6a are again stress corrected). The comparison to the experimental spectra of Fig. 5b has to be taken with great care since the effects of the Raman tensor were not included. Generally there is no existing theory linking satellites to neither on- nor off-resonance Raman intensities. The satellites around the G line and the relative positions of the vibrational states are, however, in excellent agreement with the experiment. The fact that also the theoretical coupled vibrational modes of the tube follow the main features of the experimental 2D line strengthen the conclusion of interpreting the interaction features as coupled modes.

Figure 6c shows an analysis of the measured dispersion of the 2D line in CC@DWCNTs and in DWCNT (crosses) in comparison to the simulated results of the laser energy dependent spectral function (solid circles) from Fig. 6b using the mean value of the maxima.

Just as the satellites of the G-line at k = Γ, we can assign the interaction states of the 2D line appearing in the Raman experiment of Fig. 3c to satellites emerging from the phonon branches of G+ and G- at the associated k-point in Fig. 6b, c. Figure 6c shows the comparison of the peak positions of the theory and experiment as a function of the excitation energy. The excellent agreement for both the G+, G- and 2D peaks for all excitation energies validate our interpretation of the spectra and, moreover, validates the approximation of identifying the resonant features from the SSCHA spectral function. The contribution of the 2D-line from the unfilled DWCNT, as revealed by the line shape analysis depicted in Fig. 5c, is indicated as black crosses in Fig. 6c and compared to the 2D-line of unfilled DWCNTs from a previous analysis25 shown as gray solid line and gray area. The simulated results display interacting vibrational modes of the tube with the entire CC system. This is in agreement to the experiment which concludes that the resonance behavior of the interaction features follows the electronic excitations of the tube. The features of the G-line associated shoulders shown in Fig. 5 as well as the interaction peaks around the D and 2D-line depicted in Fig. 6 and the LO-CC mode can be reproduced with remarkable agreement by treating the CC@CNT system explicitly and including anharmonic many body effects. The interaction features are satellites of the G-line of the tube which emerge from the phonon-phonon interaction of the entire coupled system.

A major application of confined carbyne is related to the enormous resonance enhancement of the CC-LO mode, making it a perfect choice for contact free nanoscale sensing. For instance using individual carbyne chains as nanoscale temperature sensors7,39. A bulk yield synthesis of defined CC is crucial for reproducible and efficient sensing. The current publication provides a pathway towards a fast and efficient optimization of confined carbyne synthesis19.

In summary we have proven that confined carbyne can be described as a weakly coupled one dimensional van der Waals herterostructure with an electronic energy spectrum mainly consisting of a superposition of the isolated sub systems. The vibrational spectrum however is strongly coupled via anharmonicities, elevating phonon-phonon interactions to a leading order term. The surrounding tube can not be mimicked by a simple dielectric environment, but has to be addressed explicitly, yielding vast differences in the vibrational spectrum regarding chirality and electronic structure of the hosting tube. While the experimental analysis of anharmonicities is mostly limited to overtones, in confined carbyne the anharmonic interaction lead to strong satellites directly measurable in the Raman response. Hence confined carbyne acts as toy model to describe coupled phonons in one dimensional systems and offers vast future applications for theoretical modeling of basic physical principles.

Methods

Controlled growth of confined carbyne

In order to grow CC@DWCNT hybrids with a well defined inner tube diameter distribution, we used arc discharge SWCNT25,26 with a narrow Gaussian diameter distribution of d = 1.36 ± 0.12 nm.

All the metallicity-sorted SWCNTs were first annealed in air for opening the caps. Subsequently the the precursor (commercial C60 molecules without further purification) was sealed and filled into the opened SWCNTs inside a glass vial under vacuum (10-6 mbar). The sealed vial was heated at 450 °C for 3 days to form peapods. After filling, the SWCNTs were washed by toluene (99%) three times for dissolving the residual C60 attached on the surface.

The C60 filled SWCNTs were annealed at 1300 °C for 1 h to transform the C60 molecules into inner tubes of a diameter between 0.6 and 1 nm with a maximum yield around 0.78 nm. This is the ideal diameter for high yield of CC growth10.

CC@DWCNT was grown via a two step process described in detail in refs. 19,28. After the annealing at 1300 °C the DWCNTs are annealed again. The highest yield of CC@DWCNT hybrids was achieved by annealing at 1560 °C for 1 h to synthesis confined carbyne. The Raman spectra of the C60 filled precursor CNTs is provided as source material.

Resonance Raman spectroscopy

The samples were measured by Raman spectroscopy (LabRAM, Horiba) with excitations at laser wavelengths of 458, 488, 532, 568, 633 nm and by Fourier transform Raman spectroscopy (MultiRAM, Bruker) with a 1064 nm laser. All the spectra were measured using a 50x objective with a laser power of 0.5 mW and a measuring time of 20 s together with 20 repetitive cycles.

For the sonication experiment the CC was sonicated in ethanol and then dropcasted on a TEM-grid.

DFT calculations

For the calculations of the CC@[5,5] system the VASP40 code was utilized together with a pseudopotential41, hybrid functionals featuring HF-exchange30 and range separated screening31.

To avoid interactions in the non-periodic directions the unicell size was extended to 15 Å which gives 8 Å of vacuum between the closest neighboring atoms. Within the CC@[5,5] system there are 22 atoms per primitive unitcell. The unitcell-size was adjusted to minimize the energy of the carbyne system together with the tube-chain interaction energy (see Supplementary Note 4 for more details).

The phonon eigenvectors and the corresponding eigenfrequencies within the harmonic approximation are calculated using the finite difference method using a displacement of POTIM = 0.015 Å implemented in VASP. The functional utilized AXX = 30% HF-exchange and a range separated screening of HFSCREEN = 0.07 on a 60 kpc grid on (1 × 1 x 2) supercell.

The energies and forces of the single scf calculations for the training data of the SSCHA were obtained using AXX = 30 % HF-exchange and a range separation of HFSCREEN = 0.07 on a 30 kpc grid on (1 × 1 x 5) supercell.

Images of geometries and charge densities were created using VESTA42.

SSCHA calculations

For the SSCHA algorithm the two GAP potentials described in the Supplementary Note 9 and in methods section below were utilized to calculate the corresponding energies and forces. They were utilized through the Python ASE platform, that includes the python interface of the QUIP library43,44,45.

The structural relaxation as well as the calculation of the free energy Hessian was was performed utilizing a custom fitted Potential (see Section "Machine learning potential" and Supplementary Note 9). The meaningful factor was set to 0.2 and the temperature was set to T = 7 K to perform the free energy relaxation. The free energy Hessian needs at least 60000 configurations to converge the static frequency of the LO mode. For the dynamic correction the smearing parameter δsm = 2 cm−1 was chosen. The spectral function was evaluated on 200 irreducible q-points with a grating of 0.5 cm−1 which were than interpolated on a finer grid.

Machine learning potential

Gaussian approximation potentials (GAP) were chosen as a platform for machine learning the potential energy surface of CC@CNT46. The GAP potential was fitted using the smooth overlap of atomic orbitals (SOAP) as only descriptor47. A set of 1320 randomly displaced hybrid-DFT calculations were split up into training and validation sets of 1200 and 120 configurations, respectively. Further information regarding the training can be found in the Supplementary Note 4.

The generation of the potentials was highly nontrivial, since very low errors on the energies and forces are required to obtain reasonable second energy derivatives. A detailed discussion can be found in the Supplementary Note 9. In total 2 potentials were used, one overall potential and one with a refined accuracy in the axial direction. SOAP cutoffs were set to 4.5 Å for both potentials, together with a total of 35,000 sparse points for the general and 10,000 sparse points for the axial force refined potential. Both potentials used 12 radial and 10 angular basis functions.