Introduction

A major obstacle to scaling up quantum computers is noise, which causes logical errors and prevents the reliable execution of quantum algorithms. Quantum error correction (QEC) provides a path toward fault-tolerance1,2,3,4, but this typically comes at the cost of significant resource overhead, often requiring hundreds of physical qubits per logical qubit5,6,7,8,9. Bosonic codes offer a hardware-efficient alternative to multi-qubit QEC codes by redundantly encoding quantum information in the large Hilbert space of a harmonic oscillator10,11,12,13,14,15. These codes have been employed to achieve landmark experimental demonstrations, including beyond break-even QEC of quantum memories16,17,18,19 and fully-autonomous QEC protocols20,21,22. However, these experiments rely on an ancilla qubit to control the oscillator and perform quantum error correction, such that errors on the ancilla can propagate to the logical qubit, limiting its lifetime.

In circuit quantum electrodynamics23,24 these realizations of bosonic codes typically use a microwave cavity as the oscillator and a transmon as the ancilla. The two are coupled dispersively, and since this dispersive interaction is transparent to transmon phase-flip errors, these QEC protocols are usually only sensitive to transmon bit-flip errors. Although fault-tolerant error syndrome measurements have been experimentally demonstrated using a transmon ancilla25, another approach to achieving fault-tolerance is to use a biased-noise qubit as an ancilla for bosonic codes26. Ideally, the error channel of such an ancilla should be dominated by phase flips, with a negligible rate of bit flips compared to other rates in the system.

The Kerr-cat qubit (KCQ) has the potential to be exactly such an ancilla due to its promise of an exponential noise bias27. Recent experimental realizations of KCQs have reached a strong noise bias of about 100028,29,30 (corresponding to a bit-flip lifetime of  ~ 1 ms and phase-flip lifetime of  ~ 1 μs), and although these are not as large as we expect from theory, there are many possible methods for further improvement31,32,33,34,35,36. With a strong noise bias and fast single-qubit gates29,37, the only remaining ingredient for using the KCQ as an ancilla for bosonic codes is a coherent entangling operation between the KCQ and an oscillator that enables the measurement of error syndromes, which to date has not been demonstrated.

In this work, we experimentally demonstrate a coherent parametrically-driven conditional displacement (CD) gate between a KCQ and a high-quality-factor microwave cavity, where the cavity is displaced in one of two directions depending on the state of the KCQ. Combined with single-qubit gates on the KCQ, this CD gate enables universal quantum control of the cavity38. We use this CD gate to measure the decoherence of the cavity in the presence of the KCQ and discover excess cavity dephasing due to heating of the KCQ into excited states, an effect that was not previously predicted. However, by engineering frequency-selective dissipation to counteract this heating31, we are able to eliminate this dephasing up to the precision of our measurements. This lack of dephasing indicates that the two systems do not entangle unless we are actively driving their interaction, demonstrating a high on-off ratio of control. Our results pave the way toward using the Kerr-cat as an ancilla for fault-tolerant syndrome measurements of bosonic codes26, in particular the Gottesman-Kitaev-Preskill code11 whose error syndromes can be mapped to an ancilla via CD gates39,40,41.

Results

The KCQ consists of the degenerate ground state manifold of the Hamiltonian

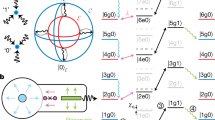
$${H}_{{{{\rm{KCQ}}}}}/\hslash=-K{a}^{{{\dagger}} 2}{a}^{2}+{\epsilon }_{2}{a}^{{{\dagger}} 2}+{\epsilon }_{2}^{*}{a}^{2},$$
(1)

where a is the annihilation operator of the Kerr-oscillator mode, K is the Kerr nonlinearity of the mode, and ϵ2 is the strength of the squeezing drive. This computational subspace is spanned by the orthornormal even- and odd-parity cat states \(\left\vert {{{{\mathcal{C}}}}}_{\alpha }^{\pm }\right\rangle={{{{\mathcal{N}}}}}_{\alpha }^{\pm }(\left\vert+\alpha \right\rangle \pm \left\vert -\alpha \right\rangle )\) (with normalization \({{{{\mathcal{N}}}}}_{\alpha }^{\pm }=1/\sqrt{2\left(1\pm {e}^{-2{\alpha }^{2}}\right)}\))27, where \(\alpha=\sqrt{{\epsilon }_{2}/K}\) is assumed to be real without loss of generality. This gives rise to the Bloch sphere depicted in Fig. 1a. These cat states \(\left\vert {{{{\mathcal{C}}}}}_{\alpha }^{\pm }\right\rangle\) form the X basis of the KCQ, while the parity-less cats \(\left\vert {{{{\mathcal{C}}}}}_{\alpha }^{\pm i}\right\rangle={{{{\mathcal{N}}}}}_{\alpha }^{\pm }(\left\vert+\alpha \right\rangle \pm i\left\vert -\alpha \right\rangle )\) form the Y basis. The Z basis consists of the even and odd superpositions of \(\left\vert {{{{\mathcal{C}}}}}_{\alpha }^{\pm }\right\rangle\), which are approximately equal to the coherent states \(\left\vert \pm \alpha \right\rangle\) for large α. The noise bias of the KCQ comes from the metapotential associated with HKCQ26,42: it has a double-well structure with two global minima (corresponding to the coherent states) separated by a potential barrier37. Dephasing of the Kerr-oscillator causes tunneling events between the wells, corresponding to bit-flip errors, which are exponentially suppressed by a factor \(2{\alpha }^{2}\exp (-2{\alpha }^{2})\) due to the height of the potential barrier33. On the other hand, photon-loss events in the Kerr-oscillator cause the cat states to change parity, corresponding to phase-flip errors, which are linearly amplified by a factor 2α2 due to the average number of photons in the coherent states13,27,28,37.

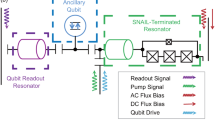
Fig. 1: Kerr-cat qubit Bloch sphere and experimental schematic.
figure 1

a Bloch sphere of the Kerr-cat qubit (KCQ). b Schematic of the experimental setup for coupling a KCQ (realized in a SNAIL mode, pink) to a high-Q storage cavity. The active modes of the system are the storage mode, the readout mode and the SNAIL (Superconducting Nonlinear Asymmetric Inductive eLement)43 -- 45 mode, whereas the buffer modes are used to facilitate parametric drives to the SNAIL, in particular the CQR (cat qubit readout) drive, the CD (conditional displacement) drive and the squeezing drive.

Full size image

Following previous demonstrations28,29,33,37, we experimentally realize the KCQ by squeezing a capacitively-shunted Superconducting Nonlinear Asymmetric Inductive eLement (SNAIL)43,44,45. The SNAIL is a flux-tunable circuit described by the Hamiltonian \({H}_{{{{\rm{SNAIL}}}}}/\hslash={\omega }_{a}({\Phi }_{{{{\rm{ext}}}}}){a}^{{{\dagger}} }a+{g}_{3}({\Phi }_{{{{\rm{ext}}}}}){(a+{a}^{{{\dagger}} })}^{3}+{g}_{4}({\Phi }_{{{{\rm{ext}}}}}){(a+{a}^{{{\dagger}} })}^{4}\), where g3 and g4 are the third and fourth order nonlinearities of the SNAIL, and Φext is the external flux threading the SNAIL. The KCQ Hamiltonian in Eq. (1) is obtained as the static effective Hamiltonian of the system when we apply a squeezing drive to the SNAIL at frequency ωs = 2ωa. A continuous σz(θ) rotation of the KCQ is realized by driving the SNAIL at its resonant frequency ωs/2 = ωa, while a discrete σx(π/2) rotation is realized by turning off the squeezing drive and allowing the SNAIL mode to evolve under its bare Kerr-nonlinear Hamiltonian for time TK = π/K37,46. Together, these rotations enable universal single-qubit gates on the KCQ. To read out the logical information stored in this qubit, we use a process called cat-qubit readout (CQR)37, which involves parametrically driving a beam-splitter interaction between the SNAIL circuit and a readout cavity (frequency ωr and mode operator r) at the difference frequency ωr − ωs/2 while stabilizing the KCQ. After projecting the Hamiltonian of this interaction onto the computational basis of the KCQ, it takes the form of a conditional displacement of the readout cavity HCQR = gCQR(r + r†)σz37, such that measuring the phase of the radiation leaking out of the readout cavity constitutes a readout of the KCQ along its Z axis.

The same conditional displacement interaction can be activated between the KCQ and a high-Q storage cavity (frequency ωb and mode operator b) by driving the SNAIL at the difference frequency ωb − ωs/2. For clarity, we reserve the acronym CD for the conditional displacement interaction between the KCQ and the high-Q cavity. While driving this beamsplitter interaction at a rate gBS, the static effective Hamiltonian of the system in the rotating frame of the SNAIL and the storage cavity takes the form37

$$H/\hslash={H}_{{{{\rm{KCQ}}}}}/\hslash -{\chi }_{ab}{a}^{{{\dagger}} }a{b}^{{{\dagger}} }b+{g}_{{{{\rm{BS}}}}}{a}^{{{\dagger}} }b+{g}_{{{{\rm{BS}}}}}^{*}a{b}^{{{\dagger}} },$$
(2)

where χaba†ab†b is the parasitic cross-Kerr interaction and \({g}_{{{{\rm{BS}}}}}{a}^{{{\dagger}} }b+{g}_{{{{\rm{BS}}}}}^{*}a{b}^{{{\dagger}} }\) is the beamsplitter interaction. Assuming that the KCQ remains in its degenerate ground state manifold, we project onto the cat-qubit subspace with the projector \({{{{\mathcal{P}}}}}_{{{{\mathcal{C}}}}}=\left\vert {{{{\mathcal{C}}}}}_{\alpha }^{+}\right\rangle \langle {{{{\mathcal{C}}}}}_{\alpha }^{+}|+| {{{{\mathcal{C}}}}}_{\alpha }^{-}\rangle \left\langle {{{{\mathcal{C}}}}}_{\alpha }^{-}\right\vert\) and obtain

$${H}_{{{{\rm{int}}}}}/\hslash= {g}_{{{{\rm{BS}}}}}\alpha \left(\left({b}^{{{\dagger}} }+b\right){\sigma }_{z}+i{e}^{-2{\alpha }^{2}}\left({b}^{{{\dagger}} }-b\right){\sigma }_{y}\right)\\ - {\chi }_{ab}{\alpha }^{2}{b}^{{{\dagger}} }b\left({\mathbb{1}}-2{e}^{-2{\alpha }^{2}}{\sigma }_{x}\right).$$
(3)

See Supplementary Information Section I for more details on this derivation. In general, the cross-Kerr interaction will lead to dephasing of the storage cavity due to photon shot noise in the SNAIL. As we increase α, however, the entangling term proportional to b†bσx becomes exponentially suppressed such that the cross-Kerr interaction simplifies into a Stark shift, thereby preventing KCQ-cavity entanglement during idling time. This feature is crucial for engineering an ancilla with a large on-off ratio of cavity control, where the interaction between the ancilla and the cavity is only activated via a driven parametric process.

In the limit of α ≫ 1, Eq. (3) simplifies to a conditional displacement interaction and a Stark shift given by

$${H}_{{{{\rm{int}}}}}/\hslash \approx {g}_{{{{\rm{BS}}}}}\alpha \left({b}^{{{\dagger}} }+b\right){\sigma }_{z}-{\chi }_{ab}{\alpha }^{2}{b}^{{{\dagger}} }b.$$
(4)

By tracking this Stark shift and evolving for time t = β/(2gBSα), we realize the conditional displacement unitary \({{{\rm{CD}}}}(\beta )={{{\rm{D}}}}(-\beta /2)\left\vert -\alpha \right\rangle \left\langle -\alpha \right\vert+{{{\rm{D}}}}(+\beta /2)\left\vert+\alpha \right\rangle \left\langle+\alpha \right\vert\), where \({{{\rm{D}}}}(\beta )=\exp (\beta {b}^{{{\dagger}} }-{\beta }^{*}b)\) is the displacement operator and the conditional displacement rate gCD = 2gBSα is enhanced by having more photons in the KCQ. Together with the single qubit gates on the KCQ, this conditional displacement gate enables universal control of the system38.

A schematic of our experimental setup is shown in Fig. 1b. It consists of a sapphire chip sandwiched between two 3D superconducting microwave post cavities machined out of high-purity aluminum47. On the sapphire substrate we fabricated tantalum-based superconducting circuits48,49, which capacitively couple to the 3D cavities via waveguide tunnels. The active modes of our system are the on-chip SNAIL mode (ωa = 2π × 4.00 GHz), the fundamental mode of the 3D storage cavity (ωb = 2π × 7.02 GHz) and the first harmonic of the 3D readout cavity (ωr = 2π × 9.36 GHz). The remaining modes in our system are buffers for delivering parametric drives to the SNAIL; they are essentially Purcell filters, designed to be detuned from the desired drive frequency by about 50 MHz50. These buffer modes are the on-chip stripline resonator for delivering the CQR drive (ωCQR = ωr − ωs/2 = 2π × 5.36 GHz), the on-chip stripline resonator for delivering the squeezing drive (ωs = 2ωa = 2π × 8.00 GHz), and the fundamental frequency of the 3D readout cavity used for delivering the CD drive (ωCD = ωb − ωs/2 = 2π × 3.02 GHz). Magnetic flux is delivered to the SNAIL with a solenoid (consisting of a copper coil wound with superconducting NbTi wire) and an on-chip superconducting flux transformer50. For all of our experiments we operate the SNAIL at a flux-bias point of Φext = 0.32Φ0, where the SNAIL circuit has appreciable g3 and g4 values51, and the frequency conditions of the various parametric processes are reasonably close to their buffer modes. See Supplementary Information Section II for more detail on the experimental apparatus and the fabrication process.

With this experimental setup, we have demonstrated KCQ gates and readout following ref. 37 (see Supplementary Information Section IV), as well as characterized both the bare SNAIL lifetimes and the KCQ lifetimes. In particular, the SNAIL has an energy relaxation lifetime T1,a = 16.0 ± 0.4 μs and a Ramsey coherence lifetime T2,a = 7.2 ± 0.1 μs. For our standard cat size of α2 = 4 that is used throughout this manuscript, the KCQ has a coherent state lifetime TZ = 147 ± 4 μs and a cat state lifetime TX,Y = 2.32 ± 0.04 μs. The σx(π/2) rotation, realized by free evolution of the SNAIL under its Kerr nonlinearity, takes TK = 272 ns corresponding to K/2π = 0.93 ± 0.03 MHz. Additional information on our system characterization can be found in Section IV of the Supplementary Information.

To demonstrate a coherent conditional displacement interaction between the storage cavity and the KCQ, we perform characteristic function (CF) tomography on the storage cavity using the KCQ38,40,41. The characteristic function is defined as \({{{\mathcal{C}}}}(\beta )=\langle {{{\rm{D}}}}(\beta )\rangle\), and it can be measured by initializing the KCQ in the \(\left\vert {{{{\mathcal{C}}}}}_{\alpha }^{\pm i}\right\rangle\) state, performing CD(β), and measuring the KCQ along its X and Y axes. The principle of this measurement is that when implementing a conditional displacement CD(β) between the KCQ and the storage cavity, the KCQ rotates about its z-axis by an amount that encodes the phase of the displacement operator, such that 〈D(β)〉 = ± 〈σy〉 ∓ i〈σx〉, where the signs are determined by the choice of initial state.

To perform CF tomography, we follow the pulse sequence depicted in Fig. 2a. First, we prepare a coherent state of amplitude 1 in the storage cavity by driving the cavity resonantly with a Gaussian pulse (duration 480 ns). At the same time, we prepare a parity-less cat state \(\left\vert {{{{\mathcal{C}}}}}_{\alpha }^{\pm i}\right\rangle\) in the KCQ by ramping up the squeezing drive (duration 2 μs), projecting into a coherent state with a CQR measurement (duration 2.5 μs), and performing a σx(π/2) gate (duration 272 ns). Next, we implement a conditional displacement gate CD(β) with varying amplitude and phase of β (duration 348 ns, corresponding to the rate gCD/2π = 6.18 ± 0.06 MHz). Finally, we repeat the experiment multiple times, measuring the KCQ along the X and Y axes to determine the real and imaginary parts of the characteristic function; to measure along the Y axis we perform a σx(π/2) gate followed by a CQR measurement (duration 2.5 μs), whereas to measure along the X axis we prepend this sequence with a σz(π/2) gate (duration 80 ns). The results of this measurement are shown in Fig. 2b. The contrast of the CF tomography is limited by photon-loss errors in the SNAIL during the σx(π/2) rotation. Aside from reduced contrast, we find excellent agreement between our experimental results and theoretical predictions. Furthermore, the fact that we are able to imprint the phase associated with the displacement operator onto the equator of the KCQ demonstrates the coherence of the CD gate, which we are able to observe due to the CD rate gCD being faster than all decoherence rates in our system. Combined with single-qubit gates on the KCQ, this CD gate enables universal quantum control of the cavity38.

Fig. 2: Cavity state tomography with a Kerr-cat qubit.
figure 2

a Gate sequence (upper) and pulse sequence (lower) for performing characteristic function tomography of a coherent state of amplitude 1 in the storage cavity with the KCQ. The pulse lengths are not to scale. b Experimental (upper) and theoretical (lower) characteristic function tomography of a coherent state with amplitude 1 in the cavity, demonstrating the coherence of the conditional displacement interaction. Note that the characteristic function of a coherent state \(\left\vert \eta \right\rangle\) is given by \({{{\mathcal{C}}}}(\beta )=\exp (-| \beta {| }^{2}/2)\exp (\beta {\eta }^{*}-\eta {\beta }^{*})\), where the second exponential term provides the interference fringes observed in the plot. This expression originates from the geometric phase associated with displacements according to \(D(\eta )D(\beta )=\exp (2iA)D(\beta )D(\eta )\) with \(A={{{\rm{Im}}}}[\eta {\beta }^{*}]\).

Full size image

In order to use this platform for bosonic quantum error correction, we need to demonstrate the ability to maintain storage coherence while establishing a KCQ in the SNAIL. From Eqs. (3) and (5), we expect the storage dephasing due to SNAIL photon shot noise to be suppressed as we increase α2, which we can verify experimentally by measuring the energy relaxation rate and dephasing rate of the storage cavity in the presence of a KCQ with varying size α. As a first step, we develop a method of measuring the storage coherences that is amenable to our experimental setup.

Similar to other approaches17,38,40,41,52, we measure T1 and T2 of the storage cavity by restricting the cavity to its Fock-qubit subspace (spanned by \(\left\vert 0\right\rangle\) and \(\left\vert 1\right\rangle\), with Pauli operators X, Y, and Z), preparing the state \(\left\vert+Y\right\rangle=(\left\vert 0\right\rangle+i\left\vert 1\right\rangle )/\sqrt{2}\), and measuring 〈X(t)〉, 〈Y(t)〉 and 〈Z(t)〉 while the cavity state decays. Our control sequence for this measurement is shown in Fig. 3a. To prepare the \(\left\vert+Y\right\rangle\) state in the storage we first excite the SNAIL to the \((\left\vert g\right\rangle+i\left\vert e\right\rangle )/\sqrt{2}\) state with a square pulse of duration 1.1 μs, after which we drive a beamsplitter interaction at ωb − ωa for 1.5 μs to swap the SNAIL state into the storage cavity. The square pulse of duration 1.1 μs is designed such that its frequency distribution is a sinc function with a notch at the anharmonicity of the SNAIL, thereby minimizing leakage of the SNAIL to its \(\left\vert f\right\rangle\) state. To measure 〈X(t)〉, 〈Y(t)〉 and 〈Z(t)〉 we use a method adapted from ref. 52: assuming we remain in the Fock-qubit subspace of the storage cavity, these Pauli expectation values can be determined by measuring the characteristic function \({{{\mathcal{C}}}}(\beta )\) at the four points \(\beta=0,\sqrt{2},\sqrt{2}i,-\sqrt{2}i\). See Supplementary Information Section VII for more detailed information.

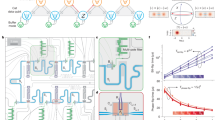
Fig. 3: Cavity lifetime measurement with a Kerr-cat qubit.
figure 3

a Pulse sequence for storage cavity lifetime measurements. We prepare a \((\left\vert 0\right\rangle+i\left\vert 1\right\rangle )/\sqrt{2}\) state in the storage, wait a variable time t, and perform characteristic function tomography at specific values of β to reconstruct the expectation values of the Pauli operators of the storage Fock qubit (spanned by the \(\left\vert 0\right\rangle\) and \(\left\vert 1\right\rangle\) states). b Measured (upper) and predicted (lower) characteristic function (CF) of the \((\left\vert 0\right\rangle+i\left\vert 1\right\rangle )/\sqrt{2}\) state prepared in the storage cavity. The four points in the plot are the values of β at which we sample the CF in order to measure the Pauli expectation values of the Fock qubit in the storage cavity. c Evolution of the expectation values 〈X〉, 〈Y〉 and 〈Z〉 of the storage Fock qubit as a function of time, from which we can determine T1 = 204 ± 9 μs and T2 = 381 ± 8 μs. The fits are displayed in solid lines.

Full size image

The experimentally measured 〈X(t)〉, 〈Y(t)〉 and 〈Z(t)〉 are shown in Fig. 3c, where the decay of 〈Z(t)〉 tells us T1 = 204 ± 9 μs and the ring-downs of 〈X(t)〉 and 〈Y(t)〉 tell us T2 = 381 ± 8 μs, corresponding to a pure dephasing rate Γϕ = (5.7±2.8 ms)−1. Bare microwave cavities have minimal intrinsic dephasing25,49,53,54,55, so we expect this dephasing to be dominated by heating in the SNAIL coupling to the storage cavity via the cross-Kerr interaction, which we verify experimentally by measuring the thermal population of the SNAIL. Owing to the low contrast of SNAIL dispersive readout, we cannot carry out this measurement directly (see Supplementary Information Section III for details). To get around this limitation, we map the thermal population of the SNAIL into the storage by swapping their states (via a beam-splitter interaction, see Supplementary Information Section X for details) after the system reaches thermal equilibrium, and then perform CF tomography on the storage. The width σth of the resulting Gaussian is related to the thermal population in the storage according to \({\sigma }_{{{{\rm{th}}}}}=1/\sqrt{2{n}_{{{{\rm{th}}}}}+1}\). We find nth = 2.8 ± 0.5%, corresponding to an induced dephasing rate56 of Γϕ = (7.3±1.3 ms)−1, which agrees with our direct measurement of the storage dephasing rate. It is important to note that this method assumes that the storage cavity at 7 GHz has a much lower thermal population than the SNAIL at 4 GHz, but the fact that these two independent measurements of the storage dephasing rate agree with one another is consistent with this assumption.

With this technique for characterizing the storage lifetimes, we can investigate the effect of the second term of Eq. (3),

$${H}_{\chi }/\hslash=-{\chi }_{ab}{\alpha }^{2}{b}^{{{\dagger}} }b\left({\mathbb{1}}-2{e}^{-2{\alpha }^{2}}{\sigma }_{x}\right),$$
(5)

which arises from the cross-Kerr interaction between the SNAIL and the storage cavity with χab/2π = 2.91 ± 0.03 kHz (see Supplementary Information Section VIII for our cross-Kerr characterization details). The first term is a Stark shift of the storage due to photons in the KCQ, which can be tracked in software. The second term corresponds to a residual cross-Kerr interaction between the KCQ and the storage, where the strength of the interaction peaks at α2 = 1/2 and is then exponentially suppressed with the number of photons α2 in the KCQ. Under this interaction, parity flips in the KCQ (due to photon shot noise in the SNAIL) induce dephasing in the storage, just as SNAIL heating gave rise to storage dephasing in the previous measurement. When we increase the size of the KCQ, this dephasing is exponentially suppressed, keeping the KCQ disentangled from the storage and preserving the coherence of the storage cavity. To examine this effect experimentally, we modify our previous measurement by stabilizing a KCQ with varying size α while we idle the storage cavity (pulse sequence depicted in Fig. 4a). Then we measure 〈X(t)〉, 〈Y(t)〉 and 〈Z(t)〉 of the storage cavity using the method discussed above and shown in Fig. 3. The result of this measurement is shown in Fig. 4b. As α increases from zero, the cavity experiences more dephasing, causing T2 to decrease. Upon reaching half a photon in the KCQ, we observe maximum storage dephasing and a subsequent revival of storage T2 as α increases, indicating suppression of photon shot noise as predicted in Eq. (5). However, the revival does not continue all the way to T2 = 2T1, which corresponds to the region colored in light green in Fig. 4(b). This additional channel of dephasing in the storage cavity is due to heating in the KCQ, as we will demonstrate.

Fig. 4: Cavity lifetime in the presence of a Kerr-cat qubit.
figure 4

a Pulse sequence measuring storage cavity T1 and T2 in the presence of a KCQ. b Measurement results for storage dephasing in the presence of a KCQ with varying size α. The blue circles are measured without cooling the KCQ, the orange squares are measured with active cooling via frequency-selective dissipation (FSD), and the error bars are one standard deviation. The purple line serves as a guide to the eye for our results, assuming a pure dephasing rate of the storage proportional to \({\chi }_{{{{\rm{eff}}}}}^{2}\) according to Fermi’s golden rule, where \({\chi }_{{{{\rm{eff}}}}}(\alpha )=2{\alpha }^{2}{\chi }_{ab}\exp \left(-2{\alpha }^{2}\right)\) is the effective cross-Kerr strength. The green region is our one standard deviation confidence interval of the storage 2T1 we obtain from these measurements, taken over a one-month period, corresponding to 435 ± 17 μs. c Schematic representation of the metapotential and the lowest-lying energy levels of a KCQ with ncat = 4. We dissipate the excited state population of the KCQ into the readout cavity via a three-wave mixing process. (d) CQR I/Q signal histograms (upper panel) and their marginals along the I quadrature (lower panel) of the KCQ with artificially-induced heating before (left) and after (right) FSD. See Supplementary Information Section XII for more information.

Full size image

To illustrate the physics of the storage dephasing, we consider a KCQ with α = 2, the potential energy and eigenstates of which are shown in Fig. 4(c). The states at the minima are the degenerate ground states of the metapotential, forming the computational subspace of the KCQ, whereas the first excited states are non-degenerate excited states outside of the wells. These excited states have different average photon number than the ground states, and therefore cause different Stark-shifts of the storage cavity (see Supplementary Information Section I for details). Without heating, the KCQ would stay in the degenerate ground states and remain disentangled from the storage cavity. With heating, indicated by the dotted red arrows, the KCQ would transition from the ground states to the excited states, dephasing the storage cavity.

One way to mitigate this dephasing is through a frequency-selective dissipation (FSD) of the excited state population of the KCQ31. The idea is to dissipate excited state population through a lossy mode without affecting the ground state manifold. Whereas ref. 31 proposed using filter modes that are on resonance with the energy gap of the KCQ, here we use the three-wave mixing capability of our SNAIL to hybridize the first excited state manifold of the KCQ with the readout cavity. This method is convenient to perform in our setup, as the beamsplitter interaction required by this process is our built-in CQR interaction with a detuning, giving us ωFSD = ωr − ωs/2 + ωgap. We calibrate the energy gap ωgap/2π = 12.5 MHz at α = 2 by performing spectroscopy on the excited states of the KCQ (see Supplementary Information Section IV D for details). To calibrate the amplitude of the FSD drive, we need a way to measure the population of the excited state manifold. Due to the fact that the CQR drive does not displace the readout cavity when the KCQ is in an excited state outside of the wells, the center blob in the I/Q plane of the CQR signal correlates with the total excited state population (see Supplementary Information section XII A for more details). We set the FSD amplitude to the value that minimizes this signal, as is shown in Fig. 4(d).

With the FSD, we can experimentally verify that the storage dephasing is due to KCQ heating. To do so, we repeat the previous measurement shown in Fig. 3 at α2 = 2.0, 2.7, 3.4 and 4.1, except now we apply the FSD drive to the KCQ during the storage idling time. As shown in Fig. 4b, the active cooling on the KCQ improves T2 of the storage cavity to a level consistent with zero dephasing, up to the precision of our measurement, while T1 of the storage cavity is unaffected. Based on the error bars of these measurements of T1 and T2, we estimate the upper bound of the residual dephasing rate in the storage cavity to be (27 ms)−1.

In addition to verifying the origin of the storage dephasing, this result validates the interaction Hamiltonian (Eq. (3)) between the storage and the KCQ: for sufficiently large cats, the storage and the KCQ do not entangle, provided that the KCQ stays in its computational manifold. Furthermore, the fact that the two systems do not entangle unless we are actively driving their interaction demonstrates a high on-off ratio of control. To quantify this ratio, we assume there exists a residual interaction \({\chi }_{{{{\rm{res}}}}}{b}^{{{\dagger}} }b{\sigma }_{x}\) between the storage cavity and the KCQ, giving rise to residual dephasing consistent with our measurement precision. Based on our bound for the residual dephasing rate, we can bound \({\chi }_{{{{\rm{res}}}}}/2\pi < 1\) kHz, yielding a bound on the on-off control ratio of \({g}_{{{{\rm{CD}}}}}/{\chi }_{{{{\rm{res}}}}} > 6000\) (see Supplementary Information Section IX for the corresponding analysis). We emphasize that these are conservative bounds limited by our measurement precision, and based on the assumption that FSD removes all the excited state population.

Discussion

We note that the origin of the KCQ heating is a subject of ongoing research. In addition to the cavity dephasing that we observe, this heating causes the staircase-like pattern in the coherent state lifetime of the KCQ that is observed as the squeezing drive strength is increased28,29,30,36 (also see Supplementary Fig. 8(f)). Although we understand the qualitative features of this staircase, we do not yet have a quantitative understanding of the KCQ lifetimes in terms of the underlying physical error rates of the SNAIL.

In summary, we have experimentally realized a coherent parametrically-driven CD gate between a KCQ and a high-quality-factor storage cavity that, combined with single-qubit KCQ gates, enables universal quantum control of the cavity38. By actively cooling the KCQ we were able to prevent the two systems from entangling during idling time, thereby demonstrating a high on-off ratio of control. The operations we have demonstrated constitute all the necessary ingredients for stabilizing Gottesman-Kitaev-Preskill codewords in the storage cavity11,39,40, paving the way towards fault-tolerant quantum error correction of this code26. To achieve this, we need to implement a higher quality σx(π/2) Kerr-cat rotation, for instance by improving the coherence of the SNAIL or by using alternative strategies for realizing this rotation27,29,57. In addition to performing fault-tolerant syndrome measurements of bosonic codes, the experimental platform we developed for coupling a Kerr-cat to a cavity could be useful for realizing error-transparent gates in hybrid discrete/continuous variable systems58. Finally, our understanding of the Kerr-cat-induced cavity dephasing and its mitigation with active cooling will be important for other experiments in which Kerr-cats are coherently coupled to other systems59,60.