Introduction

Current-driven domain wall (DW) dynamics in magnetic thin films with perpendicular magnetic anisotropy (PMA) is of great interest for spintronic logic and memory applications, including racetrack memory1,2. The most efficient means of current-driven DW displacement is through spin–orbit torque (SOT), in which a spin current is injected from a heavy metal layer in contact with the magnetic film. SOT-driven DW motion can be well understood in the framework of the one-dimensional model3,4,5,6,7,8 which describes the DW structure with a single angular variable that spans the whole wall volume: the in-plane (IP) orientation of local magnetization, in other words, the Néel component of the wall. The SOT-driven velocity is proportional to this Néel component, which is usually stabilized by an interfacial DMI (iDMI)5,7,8,9, and the direction of the DW motion is set by the DW chirality, which is fixed in materials with strong iDMI. A practical scheme for stabilizing degenerate Néel DWs of either chirality in the remanent state, and for fast and reliable switching of the chirality on demand, has been lacking. While gate control of DW chirality by changing the sign of iDMI has been demonstrated10, challenges that exist include long gating times, volatility of the gated state, and the irreversible modification of the energy landscape upon gating.

Here, we present a (110)-oriented EuIG thin film with PMA, which exhibits a novel field-free SOT-driven DW motion resulting from stabilization of the Néel component of the DW. The film, while OOP magnetized, has a strong IP uniaxial anisotropy, and the Néel character of the DW is stabilized by aligning the direction of the DW normal with the easy IP direction in DW tracks fabricated along the easy IP direction. Lacking the symmetry breaking of iDMI, this system exhibits bistability of Néel DWs with either chirality, and enables the chirality to be switched with an IP magnetic field. We show that the two stable chiralities are separated by an energy barrier that is large compared to the thermal energy, which allows the chirality to encode information in a nonvolatile manner. We further show that chirality switching occurs through the nucleation and propagation of Bloch lines (BLs), whose nucleation energy we extract for the first time by measuring the dependence of the chirality reversal on the magnitude and timescale of magnetic field pulses. We investigate the flow regime of SOT-driven motion of the IP anisotropy-stabilized Néel DWs, which exhibits a non-monotonic dependence on current density as a result of the competition between the effective fields from SOT and IP anisotropy, and we further explore the potential implementation of random number generation based on DW chirality switching. This scheme provides a new degree of freedom to individually program the chirality and direction of motion of DWs in a racetrack, opening up novel possibilities for spintronic device designs.

Results

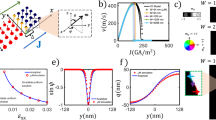
A EuIG film with a thickness of 12 nm was epitaxially grown on a (110)-oriented gadolinium gallium garnet (GGG) substrate using pulsed laser deposition. The film is perpendicularly magnetized (lowest energy axis normal to the film plane and remanent magnetization oriented out-of-plane (OOP) [110]) due to a dominant magnetoelastic anisotropy resulting from the lattice mismatch between the GGG substrate (lattice parameter 12.376 Å) and the EuIG film (12.498 Å)11 combined with positive magnetostriction coefficients λ111 and λ100. In addition, the reduced IP symmetry compared to more common (111)-oriented garnet films results in a uniaxial anisotropy within the film plane12, with the IP lowest energy axis oriented along [\(\bar{1}1\)0] (defined as the \(\hat{{{\bf{x}}}}\)-axis). The anisotropy landscape is hence biaxial and can be parameterized as \(K\left(\theta,\phi \right)={K}_{u,{{\rm{OOP}}}}^{{{\rm{eff}}}}{\sin }^{2}\theta {\cos }^{2}\phi+{K}_{u,{{\rm{IP}}}}{\sin }^{2}\theta {\sin }^{2}\phi\), where \(\theta\) is the polar angle measured from [110] (defined as the \(\hat{{{\bf{z}}}}\)-axis) and \(\phi\) the azimuthal angle measured from the [\(\bar{1}\)10] axis. Here, the OOP anisotropy, \({K}_{u,{{\rm{OOP}}}}^{{{\rm{eff}}}}\), defines the effective anisotropy within the \(\hat{{{\bf{x}}}}\)-\(\hat{{{\bf{z}}}}\) plane normal to the film plane, including demagnetizing effects, and \({K}_{u,{{\rm{IP}}}}\) corresponds to anisotropy within the \(\hat{{{\bf{x}}}}\)-\(\hat{{{\bf{y}}}}\) film plane.

To quantify \({K}_{u,{{\rm{OOP}}}}^{{{\rm{eff}}}}\) and \({K}_{u,{{\rm{IP}}}}\), we performed spin-Hall magnetoresistance (SMR) measurements13 on a patterned EuIG/Pt (4 nm) Hall cross to probe the equilibrium magnetization direction as a function of applied field H along the principal anisotropy axes, [110], [\(\bar{1}\)10] and [001], i.e., \(\hat{{{\bf{z}}}}\), \(\hat{{{\bf{x}}}}\), \(\hat{{{\bf{y}}}}\) (Fig. 1a). The square hysteresis loop along [110] shows that the film has PMA and the difference of the IP saturation field along [\(\bar{1}\)10] and [001] indicates the presence of an IP anisotropy. Fitting a macrospin model to the experimental data12 and using the measured saturation magnetization \({M}_{s}\) = 77 emu/cm3, we extracted \({K}_{u,{{\rm{OOP}}}}^{{{\rm{eff}}}}\) = 1.08\(\times\)105 erg/cm3 (10.8 kJ/m3) and \({K}_{u,{{\rm{IP}}}}\) = 1.96\(\times\)105 erg /cm3 (19.6 kJ/m3), with corresponding anisotropy fields \({H}_{k,{{\rm{OOP}}}}^{{{\rm{eff}}}}\) = 2810 Oe and \({H}_{k,{{\rm{IP}}}}\) = 5100 Oe, respectively. The anisotropy landscape (Fig. 1b) hence favors OOP domains with DWs whose spin rotation is confined to the \(\hat{{{\bf{x}}}}\)-\(\hat{{{\bf{z}}}}\) plane (Fig. 1bi) due to the large anisotropy within the film plane (Fig. 1bii), evidenced by X-ray magnetic circular dichroism photoemission electron microscopy (XMCD-PEEM) measurements showing OOP domains with spins at the center of DWs aligned along the IP easy \(\hat{{{\bf{x}}}}\)-axis (Supplementary). Contributions to the anisotropy landscape include magnetoelastic anisotropy (\({K}_{{{\rm{ME}}},{{\rm{OOP}}}}\) ~ 4\(\times\)104 erg/cm3, \({K}_{{{\rm{ME}}},{{\rm{IP}}}}\) ~ 2 − 4\(\times\)105 erg/cm3), magnetostatic (shape) anisotropy (\({K}_{{{\rm{MS}}},{{\rm{OOP}}}}\) ~ −4\(\times\)104 erg/cm3), surface anisotropy (\({E}_{{{\rm{surface}}},{{\rm{IP}}}}\) ~ 8\(\times\)10−2 erg/cm2, \({E}_{{{\rm{surface}}},{{\rm{OOP}}}}\) ~ 3\(\times\)10−3 erg/cm2), and magnetocrystalline anisotropy (\({K}_{1}\) ~ −3.8\(\times\)104 erg/cm3)12.

Fig. 1: Magnetic characterization and DW structure of the film.
figure 1

a SMR data and modeled fit to extract the anisotropy energies. Transverse Hall resistances (\({R}_{{{\rm{H}}}}\)) are measured as a function of applied field (\(H\)) along IP easy (IPE), IP hard (IPH), and OOP directions, corresponding to [\(\bar{1}\)10] (defined as \(\hat{{{\bf{x}}}}\)), [001] (defined as \(\hat{{{\bf{y}}}}\)), and [110] (defined as \(\hat{{{\bf{z}}}}\)) directions, respectively. The square hysteresis loop (green circles) indicates that the lowest anisotropy energy axis is OOP, [110], and the slope originates from the ordinary Hall effect. A zoomed-in plot of the OOP hysteresis loop with a field range of \(\pm\)2000 Oe is shown in the inset. The OOP anisotropy energy density, \({K}_{u,{{\rm{OOP}}}}^{{{\rm{eff}}}}\) is extracted from the saturation field, \({H}_{k,{{\rm{OOP}}}}^{{{\rm{eff}}}}\) of the [\(\bar{1}\)10] data (yellow circles). The IP anisotropy energy density, \({K}_{u,{{\rm{IP}}}}\) is extracted from \({H}_{k,{{\rm{IP}}}}\), the difference between the saturation fields of the [001] (blue circles) and [\(\bar{1}\)10] data. The red solid curves are modeled fits to the experimental data, which give \({H}_{k,{{\rm{OOP}}}}^{{{\rm{eff}}}}\) = 2810 Oe and \({H}_{k,{{\rm{IP}}}}\) = 5100 Oe. A schematic of the Hall cross device, along with the \(\hat{{{\bf{x}}}}\), \(\hat{{{\bf{y}}}}\), \(\hat{{{\bf{z}}}}\) coordinate system throughout this paper, is shown in the inset. b Surface plot of the measured anisotropy landscape. The energy density along the lowest energy axis, [110], is taken as the zero reference. (i) Polar plot of the projected energy density landscape on the (001) vertical plane. (ii) Polar plot of the projected energy density landscape on the (110) film plane. c Schematics of DW track configuration for Néel wall stabilization and of fully Néel CCW and CW DW spin structures stabilized in the film by the strong IP anisotropy corresponding to the wall center spins oriented to the left (red arrow) and to the right (blue arrow) for up-down and down-up walls.

Full size image

We utilized the IP anisotropy to stabilize Néel DWs by patterning magnetic racetracks parallel to the \(\hat{{{\bf{x}}}}\)-axis, such that the IP easy axis coincides with the normal of the track-confined DW (Fig. 1c). Spins at the center of the DW are stabilized by IP anisotropy to orient parallel (blue arrow) or antiparallel (red arrow) to the IP easy axis (\(\hat{{{\bf{x}}}}\)-axis). The parallel case gives rise to a clockwise (CW) up-down Néel wall and a counterclockwise (CCW) down-up Néel wall, while the antiparallel case gives rise to a CCW up-down Néel wall and a CW down-up Néel wall. Generally, an effective field exceeding the DW shape anisotropy field \({H}_{{{\rm{shape}}}}=\frac{t{\mathrm{ln}}2{M}_{s}}{\pi {\triangle }_{{{\rm{DW}}}}}\) is required to ensure fully Néel DWs14. Here, \(t\) is the film thickness, \({\triangle }_{{{\rm{DW}}}}=\sqrt{A/{K}_{u,{{\rm{OOP}}}}^{{{\rm{eff}}}}}\) is the DW width, and A is the exchange constant. We estimate a threshold \({H}_{{{\rm{shape}}}}\) = 138 Oe required to stabilize Néel DWs15,16,17 (Fig. 1c), and since \({H}_{k,{{\rm{IP}}}}\) far exceeds this threshold, we expect rigid Néel DWs in this system. The DW anisotropy, also referred to as DW stiffness, controls the SOT-driven behavior in the flow regime and is given by \({H}_{K,{{\rm{DW}}}}={H}_{k,{{\rm{IP}}}}-{H}_{{{\rm{shape}}}}\) = 5000 Oe.

Racetracks were fabricated from a EuIG/Pt (4 nm) bilayer (see Methods), in which the Pt overlayer was used to generate current-induced SOT. The direction of SOT-driven DW motion depends on the DW chirality, providing a convenient means to probe the internal DW configuration. Figure 2 shows wide-field magneto-optical Kerr effect (MOKE) images of field-free current-driven DW displacement as the DW chirality was toggled using an IP magnetic field. First, a CCW DW was initialized by preparing an up-down DW and applying a field \({H}_{x}^{{{\rm{set}}}}\) along \(-\hat{{{\bf{x}}}}\) (“left”) to set the internal orientation (see Methods). A current pulse was then applied to trigger displacement via DW creep. The SOT-driven DW motion (Fig. 2b) was antiparallel to the charge current, as expected when Pt is on top18. In Fig. 2c, d, a displacement current pulse was then injected after applying an IP field along \(+\hat{{{\bf{x}}}}\) (“right”) and \(-\hat{{{\bf{x}}}}\), respectively, which toggled the direction of current-driven displacement in a manner consistent with chirality reversal. Performing the same procedure on a down-up wall gives the opposite direction of current-driven motion. We conclude that Néel DWs of either chirality are stable at equilibrium.

Fig. 2: Wall chirality switching by Hx pulse.
figure 2

a–d Wide-field MOKE images of a DW on the racetrack whose edges are denoted by horizontal dashed lines. Dark color corresponds to an up domain and gray corresponds to a down domain. The DW positions in each frame are denoted by white dashed lines. The area to the left of the vertical red dashed line corresponds to the region covered by the contact pad and therefore does not show magnetic contrast. An up-down (down-up) wall is first initialized in the track (a). The arrows on the left of each frame denote the operation sequence of field and current pulses between the previous and the current frames. b–d The DW positions after the corresponding operations, which are denoted on the left of each frame. The DW moment orientation is set to the left by a \({H}_{x}^{{{\rm{set}}}}\) pulse (\(500\) Oe, \(500\) ms), which results in DW motion to the right (left) for a CCW (CW) DW (a–b). The wall chirality is then switched twice by \({H}_{x}^{{{\rm{sw}}}}\) pulse (330 Oe, 1 s) to CW (CCW) and then to CCW (CW), which results in DW motion to the left (right) and then to the right (left) (b, c and c, d). The current pulse used to drive the DW is fixed at \(1.33\times {10}^{11}{{\rm{A}}}/{{{\rm{m}}}}^{2}\), 10 ms.

Full size image

To quantify the DW configurational stability, we first determined the critical field \({H}_{x,c}^{{{\rm{sw}}}}\) required for chirality switching. We adopted a measurement protocol in which we first initialized the internal moment of an up-down DW to point either “left” or “right.” We then applied a field pulse \({H}_{x}^{{{\rm{sw}}}}\) with 1 s pulse width antiparallel to the DW moment, followed by a current pulse to probe the direction of current-driven displacement. For each \({H}_{x}^{{{\rm{sw}}}}\) amplitude, we repeated the sequence 100 times to determine the switching probability. In Fig. 3, the blue (red)-colored branches plot the probabilistic DW moment orientation as a function of \({H}_{x}^{{{\rm{sw}}}}\), corresponding, to initially-“right” and “left” states, respectively. The threshold \({H}_{x,c}^{{{\rm{sw}}}}\) to achieve 50% switching probability is symmetric within experimental uncertainty, which implies that the influence of DMI, which would prefer one chirality over the other, is negligible compared with the effect of the IP anisotropy. This finding is consistent with other works, which find negligibly small DMI effective fields in epitaxial rare-earth garnet films with thickness >10 nm16. The non-zero DW motion velocity in the absence of DMI aligns with a recent prediction19 in systems with orthorhombic anisotropy.

Fig. 3: Magnetic hysteresis of a Néel DW.
figure 3

The probabilistic DW moment orientation is measured through DW motion as a function of the IP field pulse amplitude \({H}_{x}^{{{\rm{sw}}}}\). The width of the \({H}_{x}^{{{\rm{sw}}}}\) pulse is 1 s. The lower (upper) range denoted by “Left” (“Right”) represents a 100% probability of measuring DW motion corresponding to a left (right)-oriented DW. On the negative \({H}_{x}^{{{\rm{sw}}}}\) branch (red circles), the DW moment orientation is initialized to the right with a 500 Oe, 500 ms IP initialization field pulse. On the positive \({H}_{x}^{{{\rm{sw}}}}\) branch (blue circles), the DW moment orientation is initialized to the left with a 500 Oe, 500 ms IP initialization field pulse. Orange solid curves are error functions fitted to the measured data, from which we obtain \({H}_{x,c}^{{{\rm{sw}}}}\), which is the critical field amplitude, corresponding to a 50% success rate of switching the DW chirality. We extract the DW coercive field from the width of the fitted hysteresis loop, \({H}_{c,{{\rm{DW}}}}\) = 160 \(\pm\) 32 Oe, and the DMI field from the lateral shift \({H}_{D}\) = 11 \(\pm\) 32 Oe.

Full size image

The probabilistic nature of the DW chirality switching suggests a thermally activated process, which depends on both the energy barrier landscape and the timescale. In Fig. 4a, we plot a family of curves showing the chirality switching probability \({P}^{{{\rm{sw}}}}\) versus applied field \({H}_{x}^{{{\rm{sw}}}}\) for various field pulse widths, \({\tau }^{{{\rm{sw}}}}\). We observe an inverse linear relationship between \({H}_{x,c}^{{{\rm{sw}}}}\) and \({\mathrm{ln}}{\tau }^{{{\rm{sw}}}}\) (Fig. 4b), which is well-fitted by a phenomenological model describing activation over an intrinsic barrier \({E}_{a}^{0}\) modulated by a Zeeman energy term \(\Delta {E}_{a}=p{H}_{x}^{{{\rm{sw}}}}\), i.e., \({\tau }^{{{\rm{sw}}}}={\tau }_{0}{e}^{({E}_{a}^{0}-p{H}_{x}^{{{\rm{sw}}}})/{kT}}\). Here, \({\tau }_{0}\) is a characteristic timescale, \(k\) is the Boltzmann constant, \(T\) is the temperature, and \(p\) is a proportionality factor. Figure 4b can therefore be understood as the phase diagram for DW chirality switching, with red (blue) shaded area well below (above) the line representing deterministic switching (unchanged orientation). The gray-shaded area around the line corresponds to the probabilistic switching regime.

Fig. 4: Wall chirality switching behavior and its dependence on IP field pulse width and amplitude.
figure 4

a Example line scans of the probability of successfully switching the wall chirality, \({P}^{{{\rm{sw}}}}\), as a function of the switch pulse amplitude \({H}_{x}^{{{\rm{sw}}}}\) at different pulse widths \({\tau }^{{{\rm{sw}}}}\). With the DW initialized to be CCW for an up-down wall, an IP field pulse with pulse width \({\tau }^{{{\rm{sw}}}}\) and pulse amplitude \({H}_{x}^{{{\rm{sw}}}}\) is applied to switch the DW to CW. Solid lines are error functions fitted to the experimental data. b Phase diagram for wall chirality switching. \({\mathrm{ln}}({\tau }^{{{\rm{sw}}}}(s))\) is plotted against the threshold pulse amplitude, \({H}_{x,c}^{{{\rm{sw}}}}\) which are extracted from the error function fit to each line scan. Error bars plotted are obtained from the fit. The red solid line is a linear fit to the plotted data, showing the negative correlation between pulse amplitude and width required for switching the DW chirality. In the red (blue) colored region, switching (not switching) events occur deterministically. In the gray-colored region, switching occurs probabilistically. c Global fitting using the expression \({\mathrm{ln}}\left(\right.-{\mathrm{ln}}\left(1-{P}^{{{\rm{sw}}}}\right)-{\mathrm{ln}}{\tau }^{{{\rm{sw}}}}=\frac{p{H}_{x}^{{{\rm{sw}}}}}{{kT}}+{\mathrm{ln}}\nu -\frac{{E}_{a}^{0}}{{kT}}\) to extract the energy barrier for DW chirality switching, \({E}_{a}^{0}\) and the lowering of the energy barrier by the applied IP field, \(p{H}_{x}^{{{\rm{sw}}}}\).

Full size image

More rigorously, we model \({P}^{{{\rm{sw}}}}\) as a function of \({\tau }^{{{\rm{sw}}}}\) and \({H}_{x}^{{{\rm{sw}}}}\) by considering the rate of successful activation over the energy barrier, \(\Gamma \left({H}_{x}^{{{\rm{sw}}}}\right)=\nu {e}^{-\frac{{E}_{a}\left({H}_{x}^{{{\rm{sw}}}}\right)}{{kT}}}=\nu {e}^{-\frac{{E}_{a}^{0}}{{kT}}}{e}^{\frac{p{H}_{x}^{{{\rm{sw}}}}}{{kT}}}\), where \(\nu\) is the attempt frequency. The IP field pulse lowers the energy barrier in proportion to \({H}_{x}^{{{\rm{sw}}}}\), and therefore exponentially increases \(\Gamma\) at fixed T. The switching probability can be written \({P}^{{{\rm{sw}}}}({\tau }^{{{\rm{sw}}}},{H}_{x}^{{{\rm{sw}}}})=1-{e}^{-{\tau }^{{{\rm{sw}}}}\Gamma \left({H}_{x}^{{{\rm{sw}}}}\right)}\), which exponentially approaches unity as \({\tau }^{{{\rm{sw}}}}\) and \({H}_{x}^{{{\rm{sw}}}}\) increase. By fitting the experimental data to the model rewritten as \({\mathrm{ln}}\left(-{\mathrm{ln}}\left(1-{P}^{{{\rm{sw}}}}\right)-{\mathrm{ln}}{\tau }^{{{\rm{sw}}}}=\frac{p{H}_{x}^{{{\rm{sw}}}}}{{kT}}+{\mathrm{ln}}\nu -\frac{{E}_{a}^{0}}{{kT}}\right.\) (see Methods), we can extract \({E}_{a}^{0}\) and \(p\). Fitting the full data set from Fig. 4a, plotted in this way (Fig. 4c), yields \(\frac{p}{{kT}}=0.031\pm 0.002\) Oe-1 and \({\mathrm{ln}}\nu -\frac{{E}_{a}^{0}}{{kT}}=-3.01\pm 0.42\). Approximating \(\nu\) by 1 GHz20,21, we estimate the intrinsic energy barrier as \({E}_{a}^{0}\) = (23.0 \(\pm\) 0.4) \({kT}\) = 0.61 \(\pm\) 0.01 eV. Since \(\nu\) varies with the effective field and damping parameters22, a range of values from 0.1 to 10 GHz can be feasible23,24,25, which increases the uncertainty \({E}_{a}^{0}\) = (23.5 \(\pm\) 3) \({kT}\) = 0.61 \(\pm\) 0.07 eV.

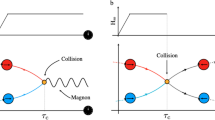
The switching threshold in Fig. 4b is much smaller than the IP anisotropy field, which suggests an incoherent (heterogeneous) reversal process within the DW in contrast to a coherent rotation. More specifically, Néel wall switching takes place through the nucleation of an opposite chirality DW segment and the subsequent propagation of BLs that are spin textures separating Néel wall segments with opposite chirality26 (Fig. 5a), analogous to incoherent magnetization reversal through nucleation of domains followed by propagation of DWs27. More concisely, the reversal process of these Néel walls occurs through the nucleation and propagation of BLs. BLs are shown to exist in our films using XMCD-PEEM imaging (Fig. 5b), and the propagation of BLs in rare-earth iron garnets has been reported28. BLs are known to exhibit a high mobility in garnet films28. Once nucleated, they readily propagate across the track width within the time frame of the IP field pulse, in other words, the DW chirality reversal process is nucleation-limited. Therefore, the energy barrier \({E}_{a}\) for the reversal process corresponds to the nucleation of BLs.

Fig. 5: Néel wall chirality switching by BL nucleation and propagation.
figure 5

a Schematic illustration of the wall chirality switching process (top view) under the IP field \({H}_{x}\). A, Initial state of a purely Néel wall oriented to the left. B, The wall with a BL nucleated under the driving force \({H}_{x}\). C, The switched region (blue) grown under \({H}_{x}\) by BL propagation. D, The wall becomes fully Néel to the right after the switched region expands across the entire wall. b An XMCD-PEEM image of two DWs with opposite spin orientations intersecting, where a 180° BL exists to maintain spin continuity. The spin orientation at the center of the DW is indicated by arrows. X-ray direction is aligned with the IP easy axis such that spin orientation at the center of DW gives maximum contrast (white contrast for parallel and dark contrast for antiparallel with the IP easy axis). The film image is 37 nm in thickness with a similar anisotropy landscape. Details of imaging conditions are discussed in the Supplementary. c Potential energy landscape for the BL nucleation process (A → D). The driving force from \({H}_{x}\) is denoted by 2\(\delta\). The energy barrier is denoted by \({E}_{a}\), and the lowering of the energy barrier by \({H}_{x}\) is denoted by \(\Delta {E}_{a}\).

Full size image

To understand \({E}_{a}^{0}\) in terms of this process (Fig. 5a), consider a homogeneous Néel DW oriented to the left (red color arrows, frame A). An applied field \({+H}_{x}\) favors spins oriented to the right, which tends to nucleate a 360° BL (i.e., a pair of 180° BLs, blue color arrows) in the DW (frame B). In the presence of \({H}_{x}\), the rightward-oriented region then grows rapidly, with the two 180° BLs moving away from each other (frame C). Eventually, the rightward-oriented region grows to span the entire DW, resulting in a wall that is fully Néel and oriented to the right (blue color arrows, frame D). Another possible process is that instead of nucleating a 360° BL at the center of the wall (frame B), a 180° BL nucleates at the track edge where defects and local spin misalignments exist. Both processes are feasible. While edge nucleation is energetically favored, center nucleation is statistically favored by a factor given by the center-to-edge area ratio of \(\frac{w}{{\Delta }_{{{\rm{DW}}}}}\sim {10}^{3}\), where \(w\) is the track width.

We schematically consider the potential energy landscape for process A → D in Fig. 5c. State B represents an intermediate state with maximum energy. The energy barrier is denoted by \({E}_{a}\). With no applied field, A0 and D0 are degenerate in energy, and the energy barrier (the difference between state A0 and state B0) is \({E}_{a}^{0}\), representing the exchange and anisotropy energy penalty imposed by forming a 360° BL. With finite \({H}_{x}\) favoring a DW with internal spins oriented to the right, the Zeeman term lifts the energy for state A and lowers the energy for state D by the same amount, \(\delta\), creating a driving force for DW chirality switching A → D. The Zeeman term raises the energy for state A more than state B, effectively lowering the energy barrier by \(\Delta {E}_{a}=-{\mu }_{0}{M}_{S}{\int }_{{{\rm{DW}}}}\left({{{\bf{m}}}}_{{{\bf{A}}}}-{{{\bf{m}}}}_{{{\bf{B}}}}\right)\bullet {{{\bf{H}}}}_{{{\bf{x}}}}{{\rm{d}}}{{\bf{V}}}\doteq {\mathrm{ln}}\left(1+{e}^{{d}_{{{\rm{BL}}}}/{\triangle }_{{{\rm{BL}}}}}\right)\pi t{\triangle }_{{{\rm{DW}}}}{\triangle }_{{{\rm{BL}}}}{\mu }_{0}{M}_{S}{H}_{x}\) (see Methods), where \({\triangle }_{{{\rm{BL}}}}\) is the 180° BL width, \({d}_{{{\rm{BL}}}}\) is the distance between the nucleated BLs (length of the nucleated DW segment) and the integration is over the DW volume. The lowering of the energy barrier is \(\Delta {E}_{a}\propto {H}_{x}\), with the proportionality factor \(p\doteq {\mathrm{ln}}(1+{e}^{{d}_{{{\rm{BL}}}}/{\triangle }_{{{\rm{BL}}}}})\pi t{\triangle }_{{{\rm{DW}}}}{\triangle }_{{{\rm{BL}}}}{\mu }_{0}{M}_{S}\). The equilibrium BL width is given by \({\triangle }_{{{\rm{BL}}}}=\sqrt{\frac{A}{{K}_{u,{{\rm{IP}}}}-{H}_{{{\rm{shape}}}}{M}_{s}/2}}=\) 14.8 nm26. Using the fitted value for \(p\) obtained above, we estimate \({d}_{{{\rm{BL}}}}\,\)= 18.5 nm, which is on the order of the exchange length. For edge nucleation, the proportionality factor changes to \(p\doteq {\mathrm{ln}}\left(1+{e}^{2{d}_{{{\rm{BL}}}}/{\triangle }_{{{\rm{BL}}}}}\right)\frac{\pi }{2}t{\triangle }_{{{\rm{DW}}}}{\triangle }_{{{\rm{BL}}}}{\mu }_{0}{M}_{S}\), which gives \({d}_{{{\rm{BL}}}}\,\)= 21.9 nm. The assumption of center or edge nucleation does not affect the qualitative phenomena but only leads to quantitative modifications to the extracted nucleation length.

Néel walls stabilized by IP anisotropy behave differently from Néel walls stabilized by DMI in their current-driven motion in the flow regime because of the functionally different torques applied to the DW. Figure 6a shows the linear motion of the DW under a nanosecond current pulse from which the DW velocity \(v\) is extracted. We investigate the SOT-driven dynamics by studying the dependence of the DW motion velocity on IP field \({H}_{x}\) (Fig. 6b) and current density \(j\) (Fig. 6c). While the effective field from DMI is unidirectional, the IP anisotropy field is uniaxial. DMI stabilizes one chirality of DW, with the chirality determined by the sign of DMI, and it acts to introduce a horizontal shift of the \(v\) curves such that the velocity is non-zero at zero field7,9. IP anisotropy field stabilizes both CW and CCW chiralities. Therefore, at an IP field greater than the wall chirality switching field, the DW motion direction is determined by the IP field polarity and positive and negative IP fields increase the DW velocity symmetrically (Fig. 6b). DW velocity shows a non-monotonic dependence on the current density \(j\) (Fig. 6c). Above a depinning threshold current density of \({j}_{0}=2\times {10}^{11}{{\rm{A}}}/{{{\rm{m}}}}^{2}\), the DW velocity firstly increases linearly with current density with a mobility \(\mu=\frac{\left|v\right|}{j-{j}_{0}}=\frac{\pi }{2}\frac{{\Delta }_{{{\rm{DW}}}}{M}_{s}\chi }{{\alpha }_{{{\rm{eff}}}}\delta S}=50({{\rm{m}}}/{{\rm{s}}})/({10}^{11}{{\rm{A}}}/{{{\rm{m}}}}^{2})\). As current density continues to increase, the DW velocity deviates from the linear dependence, reaching a peak at \(7\times {10}^{11}{{\rm{A}}}/{{{\rm{m}}}}^{2}\), beyond which increasing current density decreases the DW velocity.

Fig. 6: SOT-driven motion of DW stabilized by IP anisotropy.
figure 6

a Example of sequential images of the DW position captured after applying a current pulse between each frame (with pulse width 12 ns and pulse amplitude 9.2\(\times {10}^{11}{{\rm{A}}}/{{{\rm{m}}}}^{2}\)) without an external field. b DW velocity \(v\) plotted as a function of the IP field \({H}_{x}\) for three selected current densities, corresponding to the low (4.9\(\times {10}^{11}{{\rm{A}}}/{{{\rm{m}}}}^{2}\)), intermediate (6.2\(\times {10}^{11}{{\rm{A}}}/{{{\rm{m}}}}^{2}\)), and high (12.8\(\times {10}^{11}{{\rm{A}}}/{{{\rm{m}}}}^{2}\)) current density regime, respectively. Error bars in DW velocity are obtained from the linear fit of DW displacement to pulse number. c DW velocity \(v\) plotted as a function of the current density under zero field. Experimental data points are plotted as black circles, and the solid red curve represents the fit to the analytical 1D DW model (see Methods). Dashed gray plots represent the analytical model with the two limiting cases of infinitely large IP anisotropy field (\({H}_{k,{IP}}\to \infty\)) and a \(50{{\rm{Oe}}}\) DMI field with zero IP anisotropy field (\({H}_{k,{IP}}=0{{\rm{Oe}}}\), \({H}_{D}=50{{\rm{Oe}}}\)), while other parameters are kept the same as the fit. d Calculated DW internal magnetization angle \(\psi\) from the analytical models for the fit (red), the two limiting cases \({H}_{k,{IP}}\to \infty\) and \({H}_{k,{IP}}=0{{\rm{Oe}}}\), \({H}_{D}=50{{\rm{Oe}}}\) (dashed gray).

Full size image

The current density dependence of DW velocity can be well described by a 1D DW model29,30 (see Methods) as shown by the modeled fit plotted in red (Fig. 6c, d). The Néel component is represented by \(\cos \psi\), where \(\psi\) is the DW internal magnetization angle. \(\psi={0}^{\circ }\) corresponds to a pure Néel wall and \(\psi={90}^{\circ }\) corresponds to a pure Bloch wall. The SOT-driven motion is most efficient for a Néel wall. The equilibrium DW angle \(\psi\) is determined by the competition between the effective field from the current-induced SOT, which favors the Bloch character and the IP anisotropy field, which acts as a stiffening field to favor the Néel character. Application of the IP field \({H}_{x}\) increases the DW velocity as it strengthens the IP anisotropy field to increase the DW Néel component (Fig. 6b).

To understand the dynamics, we consider the DW velocity (Fig. 6c) and DW character (Fig. 6d) at different current densities. The linear component at low current densities corresponds to the DW being largely Néel. In the limit of an infinitely large IP anisotropy field (\({H}_{k,{{\rm{IP}}}}\to \infty\)), the DW stays Néel independent of current density, and the velocity vs. current density remains linear. In our case, where the \({H}_{k,{{\rm{IP}}}}\) is finite, the SOT effective field dominates at high current densities, and the velocity decreases with current density as the DW gains an increasingly Bloch character. The deviation of experimental data from the analytical model at high current densities (above the peak velocity) is a result of a transient behavior as the current changes the DW character, as illustrated in previously reported micromagnetic simulations29. As shown by the dashed plot for a typical DMI field of \({H}_{D}=50{{\rm{Oe}}}\)4,15,16 in the absence of an IP anisotropy, the presence of an IP anisotropy increases the DW peak DW velocity by ten times because of the smaller DW canting at current densities below \(8.5\times {10}^{11}{{\rm{A}}}/{{{\rm{m}}}}^{2}\).

The peak velocity corresponds to a DW angle of \(\psi={45}^{\circ }\) (Fig. 6c, d) because the internal torque on the DW is maximized at this angle. Further increase in current density leads to a decline in velocity until the velocity reaches zero when the DW becomes fully Bloch. As shown in Eq. M4, the peak velocity is determined by the DW stiffness (\({H}_{K,{{\rm{DW}}}}\)) and width (\({\Delta }_{{{\rm{DW}}}}\)) and the effective gyromagnetic ratio (\({\gamma }_{{{\rm{eff}}}}=\frac{{M}_{s}}{\delta S}\)), and the corresponding current density is determined by the effective damping (\({\alpha }_{{{\rm{eff}}}}\)) and the spin-Hall efficiency (\({\chi }_{0}\)) as discussed in the Supplementary. The peak velocity can therefore be further increased by tuning the anisotropy landscape, specifically, increasing the DW stiffness and decreasing the PMA strength (to increase DW width) through tuning temperature and film thickness31, or increasing the effective gyromagnetic ratio by tuning rare-earth composition or temperature to near angular momentum compensation \((\delta S=0)\).

Discussion

The extracted energy barrier \({E}_{a}^{0}\) = (23.5 \(\pm\) 3)\({kT}\) = 0.61 \(\pm\) 0.07 eV for Néel wall chirality reversal is significantly larger than the thermal excitation at room temperature, making pure Néel walls (left- or right-oriented) thermodynamically stable states at room temperature. The energy barrier can be increased further through materials optimization, such as increasing the IP anisotropy via the film thickness and composition12,32. The bistability of the two DW states, together with the nanometer length scale of DWs, suggests the possibility of high-density nonvolatile memory storage, where the binary bits can be encoded as the wall chiralities. Local fields such as the Oersted field of a thin current-carrying line5, for instance, can be used to individually program the wall polarity. Read-out of the DW chirality can be carried out either through a magnetic tunnel junction (MTJ) with an IP fixed layer33,34, or through the direction of the current-driven DW motion illustrated in this work. While the insulating nature of EuIG makes it MTJ integration challenging, possible schemes to incorporate MTJ readout could include exchange coupling35,36,37 the magnetization in garnet with a conductive metallic ferromagnet free layer or increasing garnet conductivity through doping38,39. Engineering similar anisotropy landscapes in metallic ferromagnets is also an important pathway to generalize the bistable Néel walls demonstrated in this work through controlled deposition40,41 or nanofabrication42,43 to introduce IP anisotropy.

In addition, probabilistic computing44 can be potentially implemented using the thermally assisted energy barrier-crossing process to switch between DW chirality states. As an example, using \(n\) walls initialized to the left and a pair of (\({H}_{x,c}^{{{\rm{sw}}}}\), \({\tau }^{{{\rm{sw}}}}\)) parameters corresponding to a 50% success rate, random number generation from 1 to \({2}^{n}\) can be generated and stored as nonvolatile bits. We present a proof-of-principle demonstration of a two-bit random number generator using two parallel tracks on a multiwire device (Fig. 7). The switching of DW chirality, which is read out through the current-driven DW motion direction, is encoded as 0 and 1. As shown in the frames in Fig. 7a, which are obtained by taking the difference between the images before and after the current injection, the black and white boxed regions represent a successful switch (1) and an unsuccessful switch (0) of the DW chirality. With the postselection of events corresponding to a ~50% success rate on each track, we generate a histogram of the occurrence of the four possible states, 00, 01, 10, and 11, shown in Fig. 7b. The probability of observing each state is equal, which demonstrates the feasibility of random number generation using the proposed scheme. With further automation and optimization of multiwire devices, this can be easily scaled to larger bit numbers.

Fig. 7: Demonstration of a two-bit random number generator.
figure 7

a Examples of two-bit states represented by the DW motion direction on two DW tracks. Each image is obtained from the difference between the image taken before and after a creep current pulse. The red crosses mark the horizontal and vertical position of a DW track. Black in the boxed area represents a successful switching of DW chirality by \({H}_{x}^{{{\rm{sw}}}}\) encoded as 1, whereas white indicates that the DW chirality remains the same as that set by the field pulse, \({H}_{x}^{{{\rm{set}}}}\), encoded as 0. The four images shown therefore represent 00, 01, 10, and 11, respectively, as labeled next to each image. b Histogram for each two-bit state.

Full size image

BLs, for which the nucleation and propagation are critical to the thermally activated DW chirality reversal described in this work, have been investigated for their potential applications as memory storage bits in the context of vertical Bloch lines (VBLs)45. Other scientifically interesting possibilities for BLs have also been proposed, such as topologically protected DW skyrmions in the form of BLs in systems with DMI46, and BLs in antiferromagnets with IP anisotropy as analogs of fluxon states in Josephson junctions47. The BL width (~10 nm) and energy (~10 \({kT}\)) from micromagnetic simulations reported in the literature (at zero DMI)46 also agree with the order of magnitude estimated in this work.

In conclusion, the demonstration of bistable DW chirality states in a perpendicularly magnetized thin film with an IP anisotropy, as well as their controlled reversal using IP field pulses and readout using current pulses, could inspire many future spintronic devices, such as DW chirality-based logic and storage devices, probabilistic computing devices, etc. The study of the DW reversal statistics also allows for the extraction of BL parameters, which are of scientific importance but are difficult to directly probe because of the nanometer size of BLs.

Methods

Materials growth and characterization

The 12 nm EuIG thin film was grown on a GGG (110) substrate (MTI Corporation) by pulsed laser deposition with a Compex Pro 248 nm wavelength KrF excimer laser operated at an energy of 350 mJ and a repetition rate of 10 Hz. The target used was a commercially available EuIG target (Furuuchi) with a 99.99% elemental purity. The deposition was performed at a substrate heater temperature setpoint of 900 °C, which corresponds to 700 °C at the substrate and an O2 pressure of 150 mTorr with a chamber base pressure of 5 × 10−6 Torr. The film thickness and strain state were determined by fitting to data from high-resolution X-ray diffraction (HRXRD) measurements of the (440) reflection on a Bruker D8 HRXRD instrument. The saturation magnetization was determined to be \(77\pm 8\) kA/m from vibrating sample magnetometry measurements (VSM) on a thickness series of EuIG films from 5 to 50 nm grown under the same conditions.

Device patterning

About 4 nm Pt was sputtered on EuIG(12 nm)/GGG(110) from a 1-inch Pt target using a d.c. sputter system with an Ar pressure of 3 mTorr and a base pressure of 5 × 10−8 Torr. Hall crosses with a typical active area dimension of 100 × 100 μm were patterned with standard photolithography and ion milling. The current arm of the device was aligned to 45 degrees from the IP principal anisotropy axes to maximize the IP signal. DW motion tracks were patterned using electron beam lithography and ion milling to minimize line edge roughness. DW tracks were patterned parallel to the IP easy axis for the DW to have a Néel character stabilized by IP anisotropy. A multiwire design with ten parallel 5 \(\times\) 50-μm tracks on a single device was used to acquire more statistics during a single measurement. Second-layer Ta (6)/Au (150) contacts were patterned to enhance current density uniformity and wire-bonding repeatability via lift-off.

SMR measurements

SMR measurements shown in Fig. 1a were performed at room temperature on a custom-built transport measurement setup. The current was applied through an SR830 lock-in amplifier at a frequency of 9.973 kHz and a voltage amplitude of 5 V. Device resistance was typically 100 Ω. A 10 kΩ resistor was connected in series to provide a stable current source of 0.5 mA. The transverse voltage was differentially fed back to the lock-in amplifier. The Hall magnetoresistance, \({R}_{{\mbox{H}}}\) can be expressed in Eq. 1, where \({\phi }_{I}={45}^{\circ }\), \({R}_{{\mbox{SMR}}}\) and \({R}_{{\mbox{SMR}},{\mbox{AHE}}}\) are the changes in \({R}_{{\mbox{H}}}\) as a function of the IP and OOP magnetization components, respectively, arising from the SMR effect, and \({R}_{{\mbox{OHE}}}\) is the magnetoresistance from the ordinary Hall effect.

$${R}_{{\mbox{H}}}={R}_{{\mbox{SMR}},{\mbox{AHE}}}\cos \theta+{R}_{{\mbox{SMR}}}{\sin }^{2}\theta \sin 2\left(\phi -{\phi }_{I}\right)+{R}_{{\mbox{OHE}}}{\mu }_{0}{H}_{3}$$
(1)

Wide-field MOKE measurements

The sample magnetization was probed using the polar MOKE, with the Kerr rotation and ellipticity revealing the local magnetization. The measurements were performed on our custom-built, 3-axis wide-field Kerr microscope with independent OOP and IP magnetic field control. Kohler illumination was used with a 10× objective. The light source was a 456.6 nm wavelength LED.

All experiments are performed on 5-µm-wide racetracks. An up-down DW was first initialized on the track. A field pulse \({H}_{x}^{{{\rm{set}}}}\) of 500 Oe, 500 ms is applied along the track, sufficient to orient the DW moment parallel to the field direction. A subsequent field pulse of pulse height \({H}_{x}^{{{\rm{sw}}}}\) and pulse width \({\tau }^{{{\rm{sw}}}}\) is then applied in the opposite direction to toggle the DW moment orientation. Pulse amplitude is varied within a range from 0 to 370 Oe and pulse width from 150 μs to 1 s. A creep current pulse of 1.33 × 1011 A/m2, 10 ms is subsequently applied to drive the DW, and the resulting wall position is recorded. The wall chirality is inferred from the wall motion direction to determine whether the field pulse (\({H}_{x}^{{{\rm{sw}}}}\), \({\tau }^{{{\rm{sw}}}}\)) has successfully toggled the wall chirality. Each probability data point is calculated from approximately 100 repeats of the abovementioned sequence.

Variations in the absolute value of the DW displacement for different pulses are attributed to the creep nature of the DW motion. In the creep regime, the wall dynamics are strongly affected by disorder and pinning and are therefore not expected to be fully deterministic or reproducible. We have chosen to use a low current in the creep regime to probe the DW chirality because the current itself will not disturb the wall configuration, whereas fast DW motion in the flow regime might lead to a canting of wall moments. The lower current also leads to much less Joule heating, which agrees with our assumption of room temperature in the DW chirality switching process. For a 10-µm-wide track, we estimated a temperature rise of 30 K at 1.33 × 1011 A/m2 and 70 K at 2 × 1011 A/m2 by measuring the longitudinal resistance.

DW motion velocity measurements are performed using a custom-built nanosecond pulse generation setup. For each velocity measurement, 10 consecutive current pulses of 12 ns in duration are applied, and the wall position before and after each pulse is obtained by fitting to the DW profile function. The velocity is extracted from a linear fit of the wall displacement and pulse number.

IP field pulse generation

IP field pulses with pulse width between 150 μs and 5.2 ms were produced with a custom-built air coil electromagnet with an inductance of 130 μH. A current limiting resistor of 5 k\(\Omega\) is connected in series, giving a rise time of 72 μs. For pulse widths between 37 ms and 1 s, a commercial GMW electromagnet with field feedback was used to produce the IP field pulses. With the iron core removed, the field rise rate is 20 Oe/ms. The applied field is calibrated with a Gauss meter placed near the sample position.

Model for DW chirality switching through thermally activated barrier crossing

We consider the rate of BL nucleation using standard nucleation theory. The frequency of successful attempts is \(\Gamma \left({H}_{x}^{{{\rm{sw}}}}\right)=\nu {e}^{-\frac{{E}_{a}\left({H}_{x}^{{{\rm{sw}}}}\right)}{{kT}}}=\nu {e}^{-\frac{{E}_{a}^{0}}{{kT}}}{e}^{\frac{p{H}_{x}^{{{\rm{sw}}}}}{{kT}}}\), where \(\nu\) is the total attempt frequency which can be approximated by the precessional frequency; \({E}_{a}\) is the nucleation energy barrier which consists of the intrinsic nucleation energy barrier of a BL, \({E}_{a}^{0}\), and the lowering of the energy barrier by an applied field, \(\Delta {E}_{a}=p{H}_{x}^{{{\rm{sw}}}}\) with \(p\) the proportionality factor; \(k\) is the Boltzmann constant and \(T\) is the temperature.

The rate equation can therefore be written as \(\frac{d{P}^{{{\rm{sw}}}}}{{dt}}=\Gamma (1-{P}^{{{\rm{sw}}}})\), where \({P}^{{{\rm{sw}}}}\) is the probability of DW chirality switching. Here, we neglect the rate of reversing the nucleation because nucleated BLs propagate with a negligible energy barrier. With the boundary conditions \({{P}^{{{\rm{sw}}}}|}_{{\tau }^{{{\rm{sw}}}}=0}=0\) and \({{P}^{{{\rm{sw}}}}|}_{{\tau }^{{{\rm{sw}}}}=\infty }=1\), the DW chirality switching probability can be written as \({P}^{{{\rm{sw}}}}\left({H}_{x}^{{{\rm{sw}}}},{\tau }^{{{\rm{sw}}}}\right)=1-{e}^{-{\tau }^{{{\rm{sw}}}}\Gamma \left({H}_{x}^{{{\rm{sw}}}}\right)}\), i.e., \({\mathrm{ln}}\left(-{\mathrm{ln}}\left(1-{P}^{{{\rm{sw}}}}\right)-{\mathrm{ln}}{\tau }^{{{\rm{sw}}}}=\frac{p{H}_{x}^{{{\rm{sw}}}}}{{kT}}+{\mathrm{ln}}\nu -\frac{{E}_{a}^{0}}{{kT}}\right.\), which is the equation used for global fitting. The gradient of LHS vs \({H}_{x}^{{{\rm{sw}}}}\) corresponds to \(\frac{p}{{kT}}\), and the y-intercept corresponds to \({\mathrm{ln}}\nu -\frac{{E}_{a}^{0}}{{kT}}\).

Calculation of the change in nucleation energy barrier

We start with the definition of the change in nucleation energy barrier \(\Delta {E}_{a}\) when an IP field is applied:

$$\Delta {E}_{a}=-{\mu }_{0}{M}_{S}\int\limits_{DW}({{{\bf{m}}}}_{{{\bf{A}}}}-{{{\bf{m}}}}_{{{\bf{B}}}})\cdot {{{\bf{H}}}}_{{{\bf{x}}}}d{{\bf{V}}}$$
(2)

The profile of an up-down wall without and with a BL can be well approximated by the Walker ansatz31 (the spin structure is assumed to be homogeneous along \(\hat{{{\bf{z}}}}\)):

$$\theta \left(\hat{x},\hat{y}\right)=2{\tan }^{-1}\exp (\hat{x}/{\triangle }_{{DW}})$$
(3a)
$$\phi (\hat{x},\hat{y})=\left\{\begin{array}{r}\pi,\\ -2{\tan }^{-1}\exp (\, \hat{y}/{\varDelta }_{{{\rm{BL}}}}),\end{array}\begin{array}{l}\,state\,A\\ \,state\,B\end{array}\right.$$
(3b)

where \(\theta\) is the polar angle of local magnetization orientation \({{\bf{m}}}\) at position \(\left(\hat{x},\hat{y}\right)\) and \(\phi\) is the azimuthal angle with respect to the \(\hat{{{\bf{x}}}}\) direction. The zero point of \(\left(\hat{x},\hat{y}\right)\) is defined as the center of the DW and the center of the 180° BL. The same profile as the DW can be used to describe the BL26. For the case of center nucleation, two 180° BLs are formed, separated by a distance \({d}_{{{\rm{BL}}}}\). For edge nucleation, one 180° BL is formed, separated from the edge by distance \({d}_{{{\rm{BL}}}}\). Integration over the DW profile in Eq. 2 gives the following expression for \(\Delta {E}_{a}\).

$$\Delta {E}_{a}=\left \{\begin{array}{c}{\mathrm{ln}}\left(1+{e}^{\frac{{d}_{{{\rm{BL}}}}}{{\varDelta }_{{{\rm{BL}}}}}}\right)\pi t{\varDelta }_{{{\rm{DW}}}}{\varDelta }_{{{\rm{BL}}}}{\mu }_{0}{M}_{S}{H}_{x},\,center\,nucleation\\ {\mathrm{ln}}\left(1+{e}^{\frac{2{d}_{{{\rm{BL}}}}}{{\varDelta }_{{{\rm{BL}}}}}}\right)\frac{\pi }{2}t{\varDelta }_{{{\rm{DW}}}}{\varDelta }_{{{\rm{BL}}}}{\mu }_{0}{M}_{S}{H}_{x},\,edge\,nucleation\end{array}\right.$$
(4)

SOT-driven DW motion model

The DW velocity \(v\) and its azimuthal angle \(\psi\) defined from \(\hat{{{\bf{x}}}}\)-axis in the \(\hat{{{\bf{x}}}}-\hat{{{\bf{y}}}}\) plane can be determined by solving the coupled equations in Eq. 5, where \(Q=1\) for up-down wall, \({\chi }_{0}\) is the spin-torque efficiency and the DW anisotropy field \({H}_{K,{{\rm{DW}}}}={H}_{k,{{\rm{IP}}}}-{H}_{{{\rm{shape}}}}\).

$$\left\{\begin{array}{c}{\alpha }_{{{\rm{eff}}}}\delta S\frac{v}{{\Delta }_{{{\rm{DW}}}}}=-\frac{\pi }{2}Q{M}_{s}{\chi }_{0}j\cos \psi \hfill \\ Q\delta S\frac{v}{{\Delta }_{{{\rm{DW}}}}}=\frac{\pi }{2}{M}_{s}\left({H}_{x}-Q{H}_{D}\right)\sin \psi+{M}_{s}{H}_{K,{{\rm{DW}}}}\sin \psi \cos \psi \end{array}\right.$$
(5)

With the following definitions for the net spin density \(\delta S\) and the effective damping \({\alpha }_{{{\rm{eff}}}}\) in terms of the magnetization (\({M}_{1}\) and \({M}_{2}\)), gyromagnetic ratio (\({\gamma }_{1}\) and \({\gamma }_{2}\)), and spin density (\({S}_{1}\) and \({S}_{2}\)) on each sublattice and the intrinsic Gilbert damping \({\alpha }_{0}\).

$$\left\{\begin{array}{c}\delta S=\frac{{M}_{1}}{{\gamma }_{1}}-\frac{{M}_{2}}{{\gamma }_{2}}={S}_{1}-{S}_{2}\\ {\alpha }_{{{\rm{eff}}}}=\frac{{\alpha }_{0}\left({S}_{1}+{S}_{2}\right)}{{S}_{1}-{S}_{2}}\hfill\end{array}\right.$$
(6)