Introduction

As a primary source of OH radicals in the atmosphere, HONO (Nitrous acid) promotes the formation of secondary aerosol and ozone by affecting atmospheric oxidative capacity (AOC)1. The heterogeneous reaction of NO2 on various surfaces is a crucial source of HONO, in particular, during particulate matter (PM) pollution events2. However, its contribution is still controversial, with substantial discrepancies among different studies. For instance, Zhang et al.2 reported that heterogeneous conversion of NO2 on PM surfaces is the most important source of HONO, accounting for over 70% in Beijing. In contrast, Zhang et al.3 and Xuan et al.4 found that heterogeneous reaction of NO2 on ground surfaces accounted for 42% and 85.6% of the HONO, respectively, as the dominant source in Hong Kong and Beijing. Vertical measurements further indicate that ground surfaces often dominate the heterogeneous conversion of NO25. However, some studies argued that heterogeneous reactions were less significant compared to direct emissions6,7, contributing only 5–8% to HONO sources8. An important reason leading to these discrepancies, even exceeding 90%, is the variability in the uptake coefficient (γNO2) used in parameterization schemes for budget analysis of HONO9,10.

Current models typically use the γNO2 on model particles in laboratory studies11,12,13 or that derived from short-term field observations9,10,14. As shown in Supplementary Table 1, the γNO2 values vary greatly, from 10−9 to 10−4, on different types of surfaces. It spans several orders of magnitude even if measured on the same type of interface. In addition, the γNO2 greatly depends on relative humidity (RH), light intensity, and concentrations of NO2 and co-existing pollutants. Liu et al.15 found that the initial γNO2 on kaolinite and hematite decreased exponentially accompanied by an increase in HONO yield as RH increased. Stemmler et al.16 and Han et al.17 demonstrated that light irradiation significantly enhances the heterogeneous conversion of NO2 to HONO on humic acid surfaces, increasing γNO2 by up to 23 times. Liu et al.18 and Gao et al.19 observed that high NO2 concentrations partially inhibited the γNO2 owing to surface saturation according to the Langmuir-Hinshelwood mechanism, measured using a flow tube at NO2 concentrations close to ambient values, whereas, high NO2 concentrations facilitate the uptake of NO2 measured using a Diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS)19. Additionally, Ma et al.20 and Zhang et al.21 found that SO2 significantly enhanced γNO2 on MgO and diesel black carbon. Xia et al.22 also observed that CO2 promotes the heterogeneous conversion of NO2 to HONO on the surfaces of glass tubes. NH3 has also been found to significantly promote the heterogeneous conversion of NO223. Currently, it is a big challenge to parameterize the γNO2 in models based on laboratory studies because of the great discrepancy in the conditions between experiments and real atmospheres as well as the dynamic variations of multiple factors affecting the γNO2. Thus, the γNO2 on authentical PM is more reasonable and credible for HONO budget analysis, while it remains unclear, despite few studies having reported the γNO2 on authentic dust surfaces based on short-term observations24. The γNO2 derived based on field observations, ranging from 1 × 10−6 to 7.6 × 10−5 (Supplementary Table 1), should better reflect the real atmospheric conditions including particle composition, levels of gas-phase pollutants, and meteorological parameters than that derived based on laboratory studies. However, the representativeness of those reported γNO2 based on short-term field observations is required to be verified using long-term continuous observation data. In addition, heterogeneous reactions are closely linked to the chemical composition of particles25. As the air quality characterized by PM2.5 (with aerodynamic diameter less than 2.5 μm) has improved significantly in China since 2013, the changes in the chemical composition of PM2.5, such as a decrease in sulfate and an increase in nitrate proportions26, should have a possible influence on the γNO2. Unfortunately, it is unknown how the γNO2 responds to the improvement of air quality due to the lack of long-term continuous observations on HONO formation.

In this study, a continuous dataset of γNO2 on ambient PM is obtained in Beijing based on comprehensive observations of pollutants (e.g., HONO, NO2, aerosol components) and meteorological parameters from 2019 to 2023. The driving factors for γNO2 evolution have been investigated using a random forest model combined with Shapley additive explanations (SHAP). The dependence of γNO2 on the crucial chemical composition of PM is analyzed in detail. These results not only provide a precious kinetic dataset of γNO2 to form HONO on ambient aerosols but also offer insights into the HONO sources and complex air pollution in future emission reduction scenarios.

Results and Discussion

HONO concentration and the γNO2 to form HONO

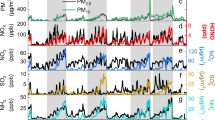
Figure 1a, b present the time series of HONO concentrations and the corresponding γNO2 to form HONO during the observations. The time series of NO2, T, RH, PM2.5, (NH4)2SO4 (AS), NH4NO3 (AN), pH, and Aerosol liquid water content (ALWC) are shown in Supplementary Fig. 1. HONO concentrations fluctuate between 0.01 and 17.4 ppb, with an average of 0.97 ± 0.94 ppb. This is lower than the annual average of 1.15 ppb in Jinan27, but higher than the 0.69 ppb observed in Nanjing14, and comparable to that (0.92 ppb) recorded in Shanghai28. As shown in Fig. 1c and Supplementary Table 1, the mean γNO2 is 2.27 ± 2.58 × 10−6, comparable to the values reported in some laboratory studies, e.g., 1.7 ± 0.14 × 10−6 on humic acid surfaces17 and 4.6 ± 1.0 × 10−6 on real dust surfaces at 90% RH18. However, it is higher than those measured γNO2 over kaolinite (1.4 ± 0.10 × 10−7), but much lower than the γNO2 observed on deliquesced NaCl (2.8 − 3.7 × 10−4)29, NaCl solutions (1 × 10−4)30, dry NaCl (6 × 10−5)31 and CaO (2.2 × 10−5)32. The γNO2 values are comparable with those derived from previous field observations, ranging from (1.0-3.0) × 10−6 on PM2.5 and (1.3 × 10−6) on the ground surfaces in Beijing9,10, but slightly lower than those observed in Svalbard and Shijiazhuang (5.9 − 6.4 × 10−6)33,34, and much lower than those (0.69 − 1.4 × 10−5) in Nanjing14. As shown in Supplementary Fig. 2, the derived γNO2 on ambient aerosol particles across short-term campaign observations varies greatly, whereas most of those γNO2 values are in the range of this study. The differences between this study and previous ones likely stem from the distinction between real ambient particles and model particles, as well as from the variability in precursor concentrations, chemical composition, RH, etc. between short-term and long-term observations. This highlights the importance of studying the long-term characteristics of γNO2 in the atmosphere.

Fig. 1: Long-term variations of HONO concentration and γNO2 in Beijing from January 2019 to January 2024.
figure 1

a Time series of HONO and b time series of γNO2; c The γNO2 on different reaction surfaces reported in the literature and derived in this study; d The annual variations of HONO concentration and γNO2. The center lines in the box plots represent the median; the red dots indicate the mean; the whiskers mean 1.5 times the interquartile range (IQR); and the boxes span the 25th to 75th percentiles.

Full size image

Figure 1d illustrates the interannual variations of HONO and γNO2, both of which exhibit clear annual trends. The HONO concentration decreased from 1.26 ± 1.16 ppb in 2019 to 0.81 ± 0.76 ppb in 2022, with a slight increase to 0.99 ± 0.91 ppb in 2023 (Supplementary Table 3). Interestingly, γNO2 shows a consistent decline from 2019 to 2023, with annual γNO2 were 3.07 ± 5.99 × 10−6, 2.27 ± 4.03 × 10−6, 1.69 ± 3.19 × 10−6, 2.05 ± 4.19 × 10−6, and 1.43 ± 3.22 × 10−6, respectively. The corresponding HONO formation rate from the NO2 heterogeneous reaction on aerosol surfaces also decreased annually, showing a reduction of over 70% from 2019 to 2023 (Supplementary Fig. 3) although the absolute values were lower than most of those in previous studies calculated based on larger γNO2 values (Supplementary Table 1). The decline trends of both HONO concentration and γNO2 are also confirmed after the missing data have been accounted for. Supplementary Fig. 4 shows the clear seasonal variation of HONO and γNO2. The highest HONO concentrations were observed in spring (1.30 ± 1.21 ppb) and winter (1.30 ± 1.12 ppb), followed by autumn (1.04 ± 0.82 ppb), with the lowest in summer (0.97 ± 0.81 ppb). For γNO2, the highest value (4.16 ± 7.09 × 10−6) was observed in summer, followed by spring (2.50 ± 4.57 × 10−6), winter, and autumn (1.80 ± 3.64 × 10−6 and 1.17 ± 2.04 × 10−6, respectively).

We binned the γNO2 according to different levels of NO2, pH, PM2.5, and RH to examine how it varies with those parameters. As shown in Supplementary Fig. 5, γNO2 displays a clear decreasing trend as NO2 concentration increases, which is consistent with laboratory findings17. Notably, NO2 suppresses γNO2 after the particle surface adsorption sites become saturated. This suggests that, in real-world environments, reactive sites on particle surfaces should be limited or typically saturated. In Supplementary Fig. 5b, γNO2 decreases significantly with increasing pH, likely due to reduced acidity, which lowers the conversion of aqueous nitrites to gaseous HONO and inhibits NO2 hydrolysis35. Furthermore, as pollution levels of PM2.5 rise, γNO2 shows a clear downward trend. This may be attributed to changes in the specific surface area resulting from increased particulate matter, or alterations in the chemical composition and physicochemical properties of the particles under serious pollution conditions. Previous studies have shown that γNO2 increases with RH on model particles15,18. However, in our observations, γNO2 did not exhibit the expected response to RH. This discrepancy may stem from the fact that field observations reflect real particle surfaces, which are more complex than the model particles used in laboratory studies. Interestingly, the HONO concentration increased in 2023, accompanied by a decrease in pH value and a decline of HONO production yield from heterogeneous reactions of NO2 on particle surfaces (Supplementary Fig. 3). This suggests heterogeneous reactions of NO2 on particle surfaces might be a minor source of HONO, whereas other sources, such as direct emissions, might be more important to atmospheric HONO in Beijing. This is consistent with the increase in transport and other economic activities after the relaxation of epidemic control at the end of 2022 in Beijing. In this case, heterogeneous reactions on particle surfaces may not be the dominant source of HONO. Overall, the composition and physicochemical properties of PM2.5, along with humidity and NO2, likely exert complex influences on the NO2 uptake kinetics in the atmosphere. However, due to the nonlinear interactions among these variables, it is a challenge to precisely reveal their complicated relationships.

Dominant factors affecting the γNO2

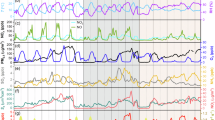
As mentioned earlier, potential factors influencing γNO2 on particle surfaces include light intensity, RH, T, NO2, coexisting SO2, NH3, NO, and particle pH. A random forest model was employed to examine their effects on nocturnal γNO2. Additionally, ALWC better reflects the hydration state of both the surface and interior of particles compared to RH, which is a more general environmental parameter. Therefore, ALWC rather than RH is used as an input variable. In summary, the model input includes T, pH, ALWC, NO2, NO, SO2, and NH3, all of which may influence the γNO2. As shown in Fig. 2a, b, the nocturnal γNO2 predicted by the Random Forest (RF) model closely matches the calculated γNO2, with an R2 of 0.93. The SHAP algorithm was used to quantitatively assess the contribution of each factor to the γNO2. Briefly, a larger SHAP value of a feature indicates a higher contribution to the γNO2 variation. Thus, we obtained the relative importance (the mean of absolute SHAP values) of various factors affecting γNO2.

Fig. 2: Performance of the Random Forest (RF) model for predicting γNO2 and the relative importance of individual factors.
figure 2

a The linear relationship between the observed γNO2 and the predicted γNO2; b The time series of the observed and the predicted γNO2; c The relative importance of each factor for the γNO2; d The SHAP (Shapley additive explanations) value of each feature variable, T: Temperature; ALWC: Aerosol Liquid Water Content.

Full size image

As shown in Fig. 2c,d, NO2 has the largest SHAP value and the highest relative importance. Changes in NO2 concentration influence the availability of active sites on the particle surface, shift the reaction equilibrium, and directly alter the uptake coefficient. pH is the second most important factor, as indicated by both its relative importance and SHAP value. It can alter reaction pathways, product stability, surface properties (such as charge and active sites), and interactions with other gases, all of which significantly influence the γNO2, making pH crucial to γNO2. For example, Kim et al.36 found that changes in soil pH can significantly affect HONO emissions. Liu et al.37 showed that a decrease in aerosol pH enhances the uptake coefficient of NH3. Bao et al.38 demonstrated that acidic protons are crucial for HONO formation during the photochemical aging of PM2.5. Similarly, Zhang et al.39 highlighted the promotion effect of acidic protons on HONO formation during the oxidation of SO2 by nitrates on mineral dust. NO affects γNO2 by altering the gas-phase concentration of NO2. Liu et al.40 found that NO adsorbs on the surfaces of metal oxide catalysts, competing with SO2 for active sites. This suggests that NO may similarly compete with NO2 for adsorption in the atmosphere, thereby affecting γNO2. Additionally, SO2 and NH3 can not only compete with NO2 for surface active sites but also alter the particle acidity41,42. Both SO2 and NH3 can react with NO2, impacting the NO2 uptake process21,43. Previous studies have highlighted the role of RH in the heterogeneous conversion of NO2 to HONO15,24. Aerosol liquid water acts as a reaction medium. It can promote NO2 interaction with water and other substances, modify particle surface properties, enhance the interaction between NO2 and active sites, and influence the chemical equilibrium, thereby affecting γNO217.

Although laboratory studies have shown minimal effects of temperature on γNO217, our results suggest that temperature does affect the uptake of NO2 in the real atmosphere, but is less important compared to chemical factors. Firstly, higher temperatures can accelerate related chemical reactions, allowing more NO2 to participate in surface reactions. Secondly, the temperature may affect particle surface properties and product stability, influencing the γNO244. Although NO2 is the primary factor influencing γNO2, its concentration is mainly determined by emissions and meteorological conditions, making it a relatively straightforward factor. It is important to note that annual mean concentrations of NO2 in Beijing were 18.9 ± 14.4, 15.5 ± 12.8, 19.4 ± 13.2, 12.2 ± 10.1, and 13.6 ± 10.7 ppb, respectively, from 2019 to 2023. This suggests that a downtrend of NO2 should facilitate the uptake of NO2, while it is in contrast with the decreased γNO2. These results imply that NO2 should not likely be the driving factor for the observed decrease in γNO2 despite NO2 showing the highest relative importance. Instead, this decline is likely due to annual variations in pH, the second most important factor, as shown in Supplementary Fig. 6. pH is influenced by factors such as particle composition, adsorbed gases, RH, and chemical reactions with other substances. To investigate the underlying causes of the pH dependence of γNO2, we further analyze the driving factors of the annual increase in the aerosol pH in the following section.

Characteristics of aerosol pH in Beijing from 2019 to 2023

As shown in Supplementary Fig. 1b, aerosol pH ranges from 1.5 to 6.6, with a mean of 3.7 ± 0.87, which is comparable to that reported at Mountain Tai (3.6)45 and Beijing (3.8)46, but lower than that in Zhengzhou (4.5)47 and Xi’an (5.0)48. It is slightly higher than values in Shanghai (3.1–3.3)49. As shown in Supplementary Table 3, aerosol pH shows significant interannual variation (P < 0.05), with annual mean values increasing from 3.54 in 2019 to 3.87 in 2023. This is consistent with the yearly changes in aerosol pH reported in Shanghai (2011-2019) with an increased rate of 0.19 per year49. Aerosol pH also exhibits distinct seasonal variation, with a maximum in winter (4.84 ± 0.68), followed by spring (4.09 ± 0.64), autumn (3.99 ± 0.72), and summer (3.13 ± 0.62) (Supplementary Table 4). The pH values observed in this study show a similar seasonal variation, i.e., 4.5 ± 0.7 (winter) > 4.4 ± 1.2 (spring) > 4.3 ± 0.8 (autumn) > 3.8 ± 1.2 (summer), observed between 2016 and 2017 (around 7 months) in Beijing46 and Shanghai49. Whereas, slight differences are observed among different seasons. These discrepancies may stem from differences in the data collection periods (7 months vs. 5 years) and changes in air pollution levels. This seasonal variation is primarily driven by temperature, as the dissociation rate constants of acids to release H+ in aerosols increase exponentially with temperature44.

To further investigate the crucial chemical factors affecting pH, a random forest model was used to analyze the feature importance and SHAP values of different variables. As shown in Fig. 3a, b, the model well predicts aerosol pH, with an R2 of 0.99. Figure 3c, d reveal that temperature is the most important factor affecting aerosol pH, with the highest relative importance. This is consistent with the fact that the rate constant of the dissociation reaction of acids to release H+ is exponentially dependent on the reciprocal of temperature50. NH4NO3 (AN) and (NH4)2SO4 (AS) rank as the second and third most vital factors, even surpassing the impact of RH. Although the relative importance of individual metal cations is low, their collective contribution cannot be ignored. For instance, Ca2+ ranks fifth, consistent with the findings of Wang et al.51. It should be noted that organic compounds were not considered in our calculation of aerosol pH. The omission of organic acids in the ISORROPIA II model may underestimate aerosol acidity, while previous research suggests that the impact of organic matter on aerosol pH is quite small37.

Fig. 3: Performance of the Random Forest (RF) model for predicting aerosol pH and the relative importance of individual factors.
figure 3

a The linear relationship between the aerosol pH calculated with the ISORROPIA II model and the predicted values by the RF Model; b The time series of aerosol pH; c The relative importance of each factor for aerosol pH, T: Temperature; AN: NH4NO3; AS: (NH4)2SO4; RH: Relatively Humidity; OA: Organic Aerosol; d The SHAP (Shapley additive explanations) value of each feature variable.

Full size image

To further assess the roles of NH4NO3 and (NH4)2SO4 in aerosol pH, the ISORROPIA II model was run with NH4NO3 and (NH4)2SO4 removed separately from the input files. When (NH4)2SO4 was subtracted, the pH ranged from 1.5 to 6.7 with an average of 4.0 ± 0.79, showing an increase in pH of ~0.26. Conversely, removing NH4NO3 resulted in a lower mean pH of 3.4 ± 0.89, with a decrease of ~0.36. Supplementary Fig. 7a illustrates the opposite effects of the subtraction of (NH4)2SO4 and NH4NO3 on pH. Since the complementary relationship between NH4NO3 (AN) and (NH4)2SO4 (AS) on aerosol pH, AN/(AN + AS), i.e., the fraction of NH4NO3 in SNA (i.e., AS + AN), is a better indicator than its concentration for understanding the long-term variation of aerosol pH. As shown in Supplementary Fig. 6, both aerosol pH and AN/(AN + AS) exhibit rising interannual trends. Notably, although the temperature has the largest relative importance or SHAP value (Fig. 3c) due to the seasonal variation of T, it shows a stable interannual trend. This indicates that temperature is unlikely to drive the increase in aerosol pH from 2019 to 2023. Instead, it predominantly drives seasonal variations of aerosol pH, as reflected in the lowest aerosol pH observed during the summer (Supplementary Fig. 8). The observed annual increase in aerosol pH can be mainly attributed to the rising AN/(AN + AS) ratio because NH4NO3 (AN) and (NH4)2SO4 (AS) are the second and third most important factors affecting aerosol pH, respectively, as shown in Supplementary Fig. 6. This is in agreement with other studies highlighting the critical role of (NH4)2SO4 and NH4NO3 in the physicochemical properties of particulate matter37,52,53. In addition, as shown in Supplementary Fig. 9a, the mean pH in the same month (October) from 2019 to 2023 shows significant differences among different years at a 0.05 level, while the mean temperature does not exhibit significant changes, to decrease the contribution of temperature to aerosol pH. This is well consistent with the single-factor analysis results that temperature is the dominant factor affecting ΔpH among different seasons (Supplementary Fig. 9c), while the chemical composition is the dominant one between different years (Supplementary Fig. 9b).

The mechanism of (NH4)2SO4 and NH4NO3 affecting γNO2

ALWC and aerosol pH are key parameters influencing secondary aerosol formation by altering the phase of gaseous precursors and the rates of related chemical reactions54. As discussed in Section 3.2, the annual increase in aerosol pH contributed to the decline in γNO2, with changes in the relative proportions of NH4NO3 and (NH4)2SO4 being the primary drivers of pH variation. Figure 4a shows the probability density plot of aerosol pH as a function of the NH4NO3 (AN) proportion in SNA, highlighting the significant impact of NH4NO3 and (NH4)2SO4 on aerosol pH. Figure 4b shows that the mean aerosol pH increases from 2.68 to 4.31, with the median pH increasing from 2.54 to 4.31 as the NH4NO3 fraction in SNA rises from less than 50% to higher than 85%. ALWC also increases with the rise in the NH4NO3 proportion, though a decline occurs when the NH4NO3 proportion exceeds 85%. This drop is due to ALWC being more influenced by the absolute concentrations of NH4NO3 and (NH4)2SO4, whereas pH is primarily regulated by their relative proportions. Consistent with pH, the annual variation in the AN/(AN + AS) ratio shows a clear upward trend (P < 0.05), increasing from 59 ± 24% to 73 ± 21% (Supplementary Table 3).

Fig. 4: Dependence of aerosol pH and γNO2 on the fraction of NH4NO3 in SNA.
figure 4

a Probability density plot of aerosol pH as a function of AN/(AN + AS), AN: NH4NO3; AS: (NH4)2SO4; ALWC: Aerosol Liquid Water Content; SNA: AS + AN; b Box plots of aerosol pH and ALWC according to binned AN/(AN + AS); c Probability density plot of log10(γNO2) as a function of AN/(AN + AS); d Box plots of γNO2 according to binned AN/(AN + AS). Since the concentration of AN (14 ± 17 µg m-3) is much higher than that of AS (4.9 ± 6.3 µg m−3), date points with AN/(AN + AS) less than 50% are grouped into a single bin and to ensure the data size in each bin being generally identical. The center lines in the box plots represent the median; the red dots indicate the mean; the whiskers mean 1.5 times the interquartile range (IQR); and the boxes span the 25th to 75th percentiles.

Full size image

Figure 4c, d show the dependence of the γNO2 on the NH4NO3 (AN) fraction. As the proportion of NH4NO3 relative to SNA increases in the particles, the mean γNO2 decreases from 4.17 ± 7.19 × 10−6 to 1.76 ± 4.24 × 10−6, with the median value dropping from 1.73 × 10−6 to 7.42 × 10−7, representing a reduction of about 58%. The annual variation in AN/(AN + AS) contrasts with the decline in γNO2. Similarly, the seasonal variation of AN/(AN + AS) is opposite to that of γNO2, further reflecting the influence of NH4NO3 and (NH4)2SO4 on γNO2. On one hand, the acidity of NH4NO3 is weaker than that of (NH4)2SO452. On the other hand, NH4NO3 has a lower deliquescence RH, facilitating water uptake at moderate RH, than (NH4)2SO4. As shown in Fig. 4b, the ALWC increases as a function of the AN/(AN + AS). The dilution effect should also contribute to the increase in aerosol pH55. Thus, the decreased γNO2 on ambient aerosol surfaces is attributed to both the weak acidity of NH4NO3 and the enhanced water uptake ability as the NH4NO3 fraction in SNA increases. It should be noted that there are some gaps between the mean values and median values of both ALWC and γNO2 in Fig. 4 due to the skewed distribution of the datasets. The dependence of ALWC or γNO2 on the AN/(AN + AS) is significant at a 0.05 level according to a Mann-Whitney U test.

In summary, we propose that the increase in the proportion of NH4NO3 to (NH4)2SO4 + NH4NO3 in particles drives an annual rise in pH in Beijing, which in turn reduces the heterogeneous uptake kinetics of NO2 to HONO on the particle surfaces. This aligns with previous studies showing that aerosol acidity can influence the uptake of gaseous precursors onto particle surfaces and the rates of related chemical reactions, thereby affecting secondary aerosol formation37,56. This study is crucial for understanding how changes in physicochemical properties of aerosol particles, such as acidity and ALWC, due to shifts in particle composition, impact the heterogeneous conversion of NO2 to HONO. It also offers valuable insights into the HONO budget, atmospheric oxidizing capacity, and the mechanisms of secondary pollutant formation under future emission-reduction scenarios.

Implications

This study demonstrates a notable increase in the NH4NO3 fraction over the past few years. This shift has driven a rise in aerosol pH, which in turn led to a significant decrease in γNO2, a key parameter for HONO formation. Despite the reduction in sulfate and nitrate concentrations due to pollution control measures, changes in aerosol composition continue to influence key physicochemical properties such as pH and ALWC, affecting multiphase aerosol chemistry. Our findings challenge the use of fixed γNO2 values in HONO budget models, highlighting the limitations of laboratory-based kinetics in real-world conditions. As HONO is a primary source of atmospheric OH radicals, which govern the AOC, understanding these complex interactions is critical for accurately modeling urban air chemistry. These insights underscore the importance of incorporating aerosol composition changes and pollution control strategies into future research and policymaking to better manage secondary pollutant formation and improve urban air quality.

Methods

Field observations

The observations were conducted on the rooftop of a teaching building, ~18 meters above ground level, at the west campus of Beijing University of Chemical Technology (39.93°N, 116.28°E). The observation station is a typical urban station and is located at the intersection of the West 3rd Ring Road and the Zizhuyuan Road in Beijing57. The observation period spanned from January 1, 2019, to December 31, 2023. HONO was measured using a homemade Water-based Long-Path Absorption Photometer (LOPAP, Institute of Chemistry, Chinese Academy of Sciences), which has been proven to be stable and reliable for HONO measurements in previous field measurements6,58. Briefly, gas-phase HONO absorbed by deionized water (≥18.2 MΩ) in a stripping coil reacts with N-(1-naphthyl) ethylenediamine-dihydrochloric acid (0.077 mmol L−1) in an acidic solution (2 mmol L−1 sulfanilamide in 0.12 mol L−1 HCl) to form an azo dye, which is measured at 550 nm using a spectrometer with a Liquid Waveguide Capillary Cell (LWCC-3250, WPI, USA). The sampling rate was 1 L min−1 controlled by a mass flow meter and diaphragm pump, while the absorption liquid flow rate was 0.5 mL min−1 controlled by a peristaltic pump. The detection limit of the LOPAP is 0.01 ppb for a 60 s sampling duration. Calibration with nitrite standard solution was carried out every three weeks, and zero drift was checked with zero air every 24 h. The status of the LOPAP is stable through five-year observation as shown in Supplementary Fig. 10. PM2.5 mass concentrations were obtained from the China National Environmental Monitoring Center (http://www.bjmemc.com.cn/) and averaged across the three nearest monitoring stations to the BUCT site, i.e., Guanyuan (39.94°N, 116.36°E), Wanshouxigong (39.87°N, 116.37°E), and Wanliu (39.99°N, 116.32°E)59. Water-soluble ions in PM2.5 and Gaseous ammonia (NH3) were measured online using a Monitor for Aerosols and Gases in Air (MARGA, 2060 R)37. NO2 and SO2 were detected using commercial analyzers (Thermo Scientific 42i and 43i). Organic aerosols (OA) were measured with a Time-of-Flight Aerosol Chemical Speciation Monitor (ToF-ACSM). Dust concentrations were calculated based on the method reported by Liu et al.60. Organic carbon (OC) and element carbon (EC) were measured using an OC/EC analyzer (Sunset OCEC Model-4). Metal elementals (Si, Cl, Al, K, Ca, Ti, Cr, Mn, Fe, Ni, Cu, Zn, As, Pb, etc.) were analyzed with a heavy metal analyzer (XHAM-2000A). Temperature (T) and RH were monitored with a weather station (AWS 310, Vaisala). Detailed descriptions of the site and data quality control were provided in previous studies57. All instruments and their detection limits are listed in Supplementary Table 2.

Data process

The heterogeneous conversion of NO2 to form HONO at night is considered a pseudo-first-order reaction. Similar to previous studies2,10,13, the reaction rate constant (khet, s−1) is calculated based on the conversion of NO2 during a given period (from time t1 to t2), as shown in Eq. (1),

$${k}_{{het}}=\frac{{c}_{{HONO},{corr},{t}_{2}}-{c}_{{HONO},{corr},{t}_{1}}}{\overline{{c}_{{NO}2}}\times ({t}_{2}-{t}_{1})}$$
(1)

where \(\bar{{c}_{{NO}2}}\) (ppbv) is the mean concentration of NO2 between t1 and t2, and cHONO,corr (ppbv) represents the HONO concentration related to secondary conversion, obtained by subtracting the directly emitted HONO, as shown in Eq. (2)2. To prevent underestimating the secondary formation of HONO, we set an emission factor of 0.005 as the lower limit61.

$${c}_{{HONO},{corr}}={c}_{{HONO}}-0.005\times {c}_{{{NO}}_{X}}$$
(2)

Besides heterogeneous reactions of NO2 on particles, photolysis of nitrate and photo-enhanced heterogeneous reactions of NO2 complicate the daytime formation of HONO. Thus, we only focus on the nocturnal γNO2 to form HONO on particle surfaces when UVB is less than 0.01 W m−2 14. It is derived according to Eqs. (3) and (4),

$${\gamma }_{{{NO}}_{2}}=\frac{4\times {k}_{{het},{aerosol}}}{{A}_{s}\times \omega }=\frac{4\times {k}_{{het},{aerosol}}}{{A}_{s}\times \sqrt{\frac{8{RT}}{\pi M}}}$$
(3)
$${k}_{{het},{aerosol}}={k}_{{het}}\times \frac{{A}_{s}}{\left({A}_{s}+\frac{\delta }{H}\right)}$$
(4)

where khet,aerosol is the heterogeneous rate constant of NO2 on aerosol surfaces, calculated based on the fraction of aerosol surface area concentration in the total surface area concentration (both ground and aerosol surfaces) and the khet10. As is the surface area concentration of the PM2.5 surface (m2 m−3)13, \(\omega\) is the average molecular velocity (m s⁻1). R is the ideal gas constant (J K−1·mol−1), T is the air temperature (K), and M is the molecular weight of NO2 (kg mol−1). δ is the surface roughness, in this study, we used 3.85 13. H is the planetary boundary layer height (m). The production rate of HONO via heterogeneous reaction is calculated according to Zhang et al.10.,

$${P}_{{HONO}}=3600\times {k}_{{het},{aerosol}}\times {Y}_{{HONO}}\times {c}_{{{NO}}_{2}}$$
(5)

where YHONO is the HONO yield (0.5), cNO2 is the concentration of NO2 (ppbv).

The mass concentration of (NH4)2SO4 and NH4NO3 in PM2.5 were reconstructed using the concentrations of water-soluble ions and the Ion Balance (IB) method, based on ion thermodynamic equilibrium. First, the molar ratio of NH4+ to SO42− (RNH4+/SO42-) was calculated. If 0 < RNH4+/SO42- < 1, NH4+ exists as H2SO4 and NH4HSO4. If 1 < RNH4+/SO42- < 2, NH4+ exists as (NH4)2SO4 and NH4HSO4. If RNH4+/SO42- > 2, a part of NH4+ exists as NH4NO3 and NH4Cl, in addition to (NH4)2SO4. The remaining NO3− is assumed to be NaNO3. Additionally, Ca2+ and Mg2+ are considered to exist as CaSO4 and MgSO4, thus the RNH4+/SO42- was calculated using the remaining SO42− concentration after neutralization by Ca2+ and Mg2+.

ALWC and pH were calculated using the ISORROPIA II model based on the concentrations of particulate water-soluble ions, gaseous NH3, HNO3, and HCl, as well as T and RH. The model was run in “forward” mode, assuming the aerosol system was in a metastable state, to calculate the mass concentration of H+ (cH+, μg m−3) and ALWC. Aerosol pH was calculated using the following formula,

$${{{\rm{pH}}}}=-{\log }_{10}\frac{1000{\gamma }_{{H}^{+}}{c}_{{H}^{+}}}{{ALWC}}$$
(6)

where γH+ is the activity coefficient of H+, assumed to be 1.0 based on the literature. Due to large uncertainties in ALWC calculations at RH < 35%62, only ALWC and pH for RH > 35% are discussed in this study.

The random forest (RF) model, a widely used and powerful machine learning algorithm with broad applications including atmospheric sciences63, was used to identify crucial factors influencing aerosol pH and γNO2. The model was fed by trace gases (NO2, NO, NH3, SO2), meteorological parameters (RH and T), chemical components, and properties of aerosol (NH4NO3, (NH4)2SO4, Ca2+, Mg2+, Na+, K+, Cl−, OA, Dust, pH, and ALWC). The inputs were randomly divided into a training set (80%) and a test set (20%). To reduce overfitting and improve model generalization, we optimized the number of decision trees to minimize variance and bias. A 10-fold cross-validation (CV) and grid search were performed to enhance prediction stability through random sampling and feature selection. Model performance was evaluated using the correlation coefficient (R2), root-mean-square error (RMSE), and mean absolute error (MAE). The contributions of these driving factors to pH and γNO2 were quantified using Shapley Additive Explanations (SHAP) values. Details of the parameters, evaluation metrics, and other specifications of the RF model are shown in the SI.