Abstract
Multimode optical fibers represent the ideal platform for transferring multidimensional light states. However, dispersion degrades the correlations between the light’s degrees of freedom, thus limiting the effective transport of ultrashort pulses between distant nodes of optical networks. Here, we demonstrate that tailoring the spatiotemporal structure of ultrashort light pulses can overcome the physical limitations imposed by both chromatic and modal dispersion in multimode optical fibers. We synthesize these light states with predefined spatial and chromatic dynamics through applying a sequence of transformations to shape the optical field in all its dimensions. Similar methods can also be used to overcome dispersion processes in other physical settings like acoustics and electron optics. Our results will enable advancements in laser-based technologies, including multimode optical communications, imaging, ultrafast light-matter interactions, and high brightness fiber sources.
Similar content being viewed by others
Introduction
The combination of spatiotemporal light beam synthesis and sophisticated multimode waveguides raises the intriguing possibility of harnessing ultrashort light pulses with rich dynamics in a variety of applications. Yet, an optical pulse that originally exhibits precise spatiotemporal correlations prior to transmission through a medium invariably loses its initial state due to effects arising from dispersion. Specifically, the spatial and chromatic constituents of light travel at different speeds, leading to undesirable aberrations in the overall pulse structure. Consequently, controlling the energy distribution contained in optical pulses as they traverse multimode channels presents a formidable challenge. This affects diverse technological areas such as ultrafast optics, fiber lasers, communications, and custom light delivery. Addressing this problem using richer pulse light configurations in multimode environments will facilitate investigations of fundamental phenomena such as multimode multicolor solitons1, spatiotemporal probing, and coherent control of ultrafast light-matter interactions2,3,4. Recent work on space-time beams incorporates nonseparable spatiotemporal states via generation of localized wavepackets with controllable group velocity5,6, spatiotemporal orbital angular momentum (OAM) dynamic beams2,7,8,9,10,11,12, and toroidal vortices13,14. Additionally, major experimental efforts have led to spatiotemporal focusing using pulsed laser sources15,16,17,18,19, combination of spatial modes in continuous-wave conditions20, excitation of supermodes in unbounded planar waveguides21, and fiber optics22,23, even experimental propagation of transverse OAM structures in few-mode fiber24. This, in turn, sparked a surge of numerical studies proposing the generation of guided space-time wavepackets in integrated photonics25, suggesting how to categorize and synthesize space-time wavepackets26 and exploring space-time beams coupling in multimode waveguides27,28. In the context of imaging systems, of special interest are multimode optical fibers, which many consider to be the probe of choice in terms of examining the interior of living organisms and tissues29,30, and observing the intricate details of biological systems31,32. Admittedly, to faithfully retrieve the optical information and to diminish the detrimental effects of random scattering and dispersion, most methods require prior knowledge of the light scrambling processes by either computing and measuring the transmission matrix20,22,33,34,35, or by learning the output speckle patterns36,37,38,39,40,41,42,43,44. Indeed, previous investigations have reported on compensation of modal dispersion by controlling time-varying principal modes via feedback45 and the compensation of chromatic dispersion by modal dispersion46.
Notwithstanding these advancements, uncontrolled dispersion effects on spatiotemporal pulses in multimode optical fibers continue to limit the ultimate performance of these technologies34. Leveraging our previous free-space spatiotemporal pulse synthesis framework11, we now investigate its implementation within multimode fiber environments, a pivotal advancement for the practical deployment of ST pulse-based systems. We achieve this by manipulating the spatiotemporal degrees of freedom (DOF) of ultrashort light pulses prior to propagation through multimode optical fibers. Specifically, we delivered spatiotemporal optical pulses at ~1 μm wavelength through a 2 m-long multimode optical fiber with high fidelity, thereby demonstrating the capability of our system to mitigate both chromatic and modal dispersion.
Results
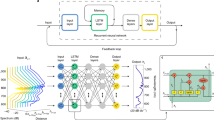
In Fig. 1, we illustrate this concept and our experimental setup. The first element in our arrangement is a laser source generating a discrete array of evenly spaced pulses with pulse duration of 180 fs centered at a wavelength of λ = 1030 nm with 6.4 nm bandwidth full-width at half-maximum (FWHM), Fig. 1b. We split the pulse train to generate a reference beam and a signal beam. On the reference beam, we insert a delay line to vary the path length, so we can perform holographic interference to examine the output beam. On the other hand, a reconfigurable space-time (ST) module allows us to readily program the spatiotemporal structure of the signal beam and then precisely couple it into a multimode fiber. The temporal stage of the ST module consists of a two-dimensional (2D) Fourier transform pulse shaper that controls the spectral content (eigenfrequencies) of the signal pulse and a diffraction grating that decomposes the light pulse into its constituent wavelengths. A cylindrical lens projects the pulse onto a two-dimensional (2D) spatial light modulator (SLM). Crucially, as different wavelengths impinge upon the horizontal axis of the SLM, the spectral/temporal shaping of the signal beam takes place along the horizontal direction. That is, the horizontal axis of our SLM is calibrated to imprint a particular phase pattern on each wavelength component, while the vertical axis is configured to steer the spectrally modulated pulses towards predefined positions before entering the spatial stage of our ST module (see Supplementary Section I, Supplementary Fig. 1). A dual-lens telescope adjusts the beam size prior to the spatial transformations. The spatial stage consists of a multi-plane light conversion (MPLC) system, which adiabatically transforms the spatial profile of the input field into specific mode functions. The MPLC consists of a second SLM and a mirror parallel to each other such that the input beam acquires the phase morphology of six holograms upon bouncing back and forth at six different positions on the SLM (see Supplementary Section I, Supplementary Figs. 2 and 3). Altogether, this optical configuration allows full control of the temporal and spatial DOF of the pulsed field. To demonstrate the capability of our system, we prepare light states with intricate structures and propagate them through a graded index multimode optical fiber. Specifically, we synthesize a single-polarization optical field represented by the spatiotemporal function
a A light pulse \({E}_{{in}}\left(x,y,t\right)\) with a specific spatiotemporal correlation defies modal and chromatic dispersion after propagating in a multimode optical fiber, enabling controllable correlations between the various DOFs, \({E}_{{out}}\left(x,y,t\right)\). b A femtosecond pulse is divided into a signal and a reference beam using a half-wave plate (\(\lambda /2\)) and a polarization beam splitter (PBS). The signal pulse undergoes a series of transformations in an ST synthesis module (green background). Initially, a spectral/temporal stage manipulates the signal pulse. At this stage, a 2D Fourier transform pulse shaper tailors the frequency components of the pulse. Next, a multi-plane light conversion system (MPLC) quasi-adiabatically molds the spatial phase and intensity profiles of the wavepacket. The synthesized ST optical field then couples to 2 m of graded index fiber (GIF). Finally, a frequency-resolved tomographic interrogation module (yellow background) analyzes the output light. A CCD records the holographic interference pattern between the reference and signal wave in an off-axis geometry. A time delay on the reference arm scans the time dimension \(\tau\). We controllably tilt a bandpass filter (SF) to discriminate the chromatic components of the pulse. To filter the pulse polarization, we use a tunable polarization filter composed of a half-wave plate (\(\lambda /2\)) and a polarization beam splitter (PBS). Supplementary Sections I–IV provide more details about the ST synthesis module and interrogation module.
Physically, Eq. (1) describes an entangled (nonseparable) optical field formed by a coherent superposition of complex time-varying functions, \({F}_{m,n,k}\left(t\right){{{{\rm{e}}}}}^{{{{\rm{i}}}}{\Psi }_{m,n,k}\left(t\right)}\), that modulate a set of carrier signals of frequency \({\omega }_{k}\left(t\right)\), each one exhibiting an instantaneous spatially structured Hermite-Gauss profile, \(H{G}_{m,n,k}\left(x,y\right)\), and a spatial phase \({\varphi }_{m,n,k}\), where (m,n) are the indices of the transverse spatial modes. Notice, even though Eq. (1) describes a coherent superposition of products involving spatial and temporal functions, in general, it cannot be expressed as a single product. Therefore, the generated optical fields are instances of the so-called classically entangled light states47.
For our experiments, we use a 2 m-long graded index optical fiber with a diameter of 11 μm and a refractive index contrast ∆ = 16 × 10−3. This fiber supports six linearly polarized (LP) modes at the central wavelength of our source (λ = 1030 nm) (see Supplementary Section II, Supplementary Fig. 4). To examine the multidimensional composition of the optical fields, we use a spectrally resolved holographic technique. This allows us to extract the instantaneous complex spatial composition (amplitude and phase) of each spectral component. To achieve this, we record the interference pattern between the signal and reference beams with a charge-coupled device (CCD) camera in an off-axis geometry (Supplementary Section III, Supplementary Fig. 5). By adjusting the time delay of the reference beam, we reconstruct the signal wave dynamics. In addition, we discriminate the spectral components of the spatiotemporal field by controllably tilting a narrow bandpass filter (see Supplementary Section IVa, Supplementary Fig. 6). Furthermore, we access and examine the output polarization light state by employing a tunable polarization filter (see Supplementary Section IVb, Supplementary Fig. 7).
To benchmark the performance of our system, we first characterize the response of the fiber by individually exciting each of the first three supported modes \(\left(L{P}_{01},L{P}_{11x},L{P}_{11y}\right)\) without altering the spectrotemporal properties of the source pulse, Fig. 2. To do so, we shape the spatial profile of the input pulse to match the HG modes \(\left({{HG}}_{00},{{HG}}_{01},{{HG}}_{10}\right)\), which coincide with the LP modes in graded index fibers. In Fig. 2a, c, e, we present the iso-intensity surfaces of the output fields reconstructed for all chromatic components at each specific time and realization. To characterize the complex structure of the ST optical fields, we analyze the generated configuration using spatial, temporal, and frequency-resolved measurements. To visualize the impact of chromatic and modal dispersion on the transmitted pulses, we generate the spectrotemporal maps shown in Fig. 2b, d, f. Here, each pixel represents the retrieved instantaneous field at a particular wavelength, expressed in terms of the spatial Laguerre–Gaussian (LG) basis, see insets Fig. 2b, d, f. Using this LG mode representation, we color-code the angular momentum exhibited by the output fields, \({{\ell}}_{1}=1\,\)(cyan), \({{\ell}}_{0}=0\) (magenta), and \({{\ell}}_{-1}=-1\) (yellow), where any superposition of these modes is represented by a single color, creating an CMY additive color model (Supplementary Section V, Supplementary Figs. 8, and 9). Typically, in the absence of dispersion, every pulse component, modal and chromatic, travels at the same velocity. However, after propagation through the fiber, modal dispersion causes each mode comprising the pulse to emerge at a different time, producing relative delays along the time axis of the maps. We observe that the spatial mode with no vorticity \({\ell}{=}0\) is the fastest, followed by the modes with OAM \({\ell}{=}{{{\mathscr{+}}}}1\) and \({\ell}{=}{{{\mathscr{-}}}}1\), respectively. The physical cause behind these delays is that, in practice, optical fiber modes with OAM exhibit different propagation constants. Additionally, chromatic dispersion produces a positive chirp in the pulses, which appears as a positive slope in the spectrotemporal maps. It is also worth mentioning that no pulse spectral broadening or central wavelength shift was observed in our experiments.
a, c, e Measured iso-intensity surfaces of the pulsed field when we excite individually each one of the first three supported modes \(\left({{HG}}_{00},{{HG}}_{01},{{HG}}_{10}\right)\). b, d, f Color-coded modal decomposition maps after projecting the field onto a set of Laguerre–Gaussian (\({LG}\)) modes, in this map each ‘pixel’ corresponds to the spatial distribution of the amplitude and phase, measured at a specific time and wavelength. Each mode of this basis is associated with an \({CMY}\) color (\({{\ell}}_{-1}=-1\,\)(yellow), \({{\ell}}_{0}=0\) (magenta), and \({{\ell}}_{1}=1\) (cyan)). Note that the presence of only one color in each panel indicates mode purity. We observe that the spatial mode with vorticity \({\ell}{=}0\) is the fastest, followed by the modes with OAM \({\ell}{=}{{{\mathscr{+}}}}1\) and \({\ell}{=}{{{\mathscr{-}}}}1\), respectively. Chromatic dispersion produces a delay in the spectral components of the pulse, which appears as a positive slope in the shape. In the insets, we present a detailed view of the spatial structure of the propagated pulses.
Further supporting data can be found in Supplementary Section VI, Supplementary Fig. 10 presents additional measurements for the generated ST wavepackets for both polarizations, and Supplementary Fig. 13 displays maps of amplitude spatial distribution.
To highlight the combined effect of modal and chromatic dispersion on the spatiotemporal pulses, we propagate an optical field composed of all three accessible spatial modes \(\left(L{P}_{01},L{P}_{11x},L{P}_{11y}\right)\) that preserve the spectral and temporal properties of the source pulse. In Fig. 3a, we display the measured iso-intensity surface of the propagated field. The spectrotemporal map in Fig. 3b depicts the aberrations in the overall pulse structure. The three modes are delayed relative to one another as a consequence of modal dispersion, while also acquiring positive chirps (represented as positive slopes) as a result of chromatic dispersion. In Fig. 3c, we present intensity distributions associated with the selected sections of the measured spectrotemporal map.
Measured iso-intensity of a a wavepacket composed of our three accessible spatial modes coupled together \(\left({{HG}}_{00},{{HG}}_{01},{{HG}}_{10}\right)\). c A field structure made up of our three spatial modes appropriately delayed to exit the fiber concurrently. e A single spatiotemporal entity comprised of spatial modes \({{HG}}_{00}\) and \({{HG}}_{01}\) allocated in different sections of the pulse spectrum. Color-coded modal decomposition maps where each ‘pixel’ depicts the complex (amplitude/phase) spatial distribution measured at a specific time and wavelength, displaying b three \({HG}\) mode elements delayed due to modal dispersion and positively chirped because of chromatic dispersion. d Our three \({HG}\) modes arriving simultaneously with positive chirp. f A pulse structure featuring two different topological charges, with vorticity value \({\ell}{=}0\) in the longer wavelengths and \({\ell}{=}{{{\mathscr{+}}}}1\) in the shorter wavelengths. In the insets, we present the spatial intensity structure of the wavepackets.
We now show that we can readily manipulate the spatiotemporal structure of the input pulse to negate the effects of dispersion and to eliminate the relative modal time delays. During the first experimental trial, we counteract the effects of modal dispersion in the fiber by fine-tuning the timing between three input modes \(\left({{HG}}_{00},{{HG}}_{01},{{HG}}_{10}\right)\). To achieve this, we synthesize a train of three pulses, each assigned a different spatial profile/mode and corresponding propagation constant, with time offsets selected such that they temporally overlap at the fiber output. We delay the \({{HG}}_{01}\) and \({{HG}}_{10}\) modes with respect to the \({{HG}}_{00}\) mode by 1.15 ps and 0.62 ps, respectively. To do so, we apply a linear phase sweep onto the pulse spectrum using the SLM in the Fourier transform pulse shaper, which corresponds to a temporal shift. Figure 3c depicts the experimentally measured iso-intensity surface of the output field. In Fig. 3d, we display the field’s modal composition in the color-coded map. The chromatic superposition of cyan (\({{\ell}}_{+1}=+ 1\)), magenta (\({{\ell}}_{0}=0\)), and yellow (\({{\ell}}_{-1}=-1\)) creates a uniform whitish color in the spectrotemporal map (Fig. 3e), indicating that the three modes exit the fiber simultaneously. In the inset of Fig. 3d, we present the spatial mode composition of the field retrieved from the white pixel-squared region.
In a second experiment, we generate a single pulse structure by allocating different modes at different parts of the spectrum, assigning the \({{HG}}_{00}\) mode at longer wavelengths of the pulse, while designating the \({{HG}}_{01}\) mode at a shorter wavelength, such that the combination produces a monolithic spatiotemporal entity at the fiber output. In other words, we compensate chromatic dispersion by properly manipulating the modal dispersion that the pulse is expected to experience during propagation. To implement such a structure, we seize the fact that (i) the \({{HG}}_{00}\) mode travels faster than \({{HG}}_{01}\) mode in the fiber (due to modal dispersion) and that (ii) longer wavelengths propagate faster than shorter ones (due to chromatic dispersion). The iso-intensity surface corresponding to this case is shown in Fig. 3e. Figure 3f displays the composition of this spatiotemporal pulse, where the magenta and cyan colors represent the two different angular momentum states, OAM value \({\ell}{=}0\) at the longer wavelengths and \({\ell}{=}{{{\mathscr{+}}}}1\) at the shorter wavelengths, both emerging simultaneously. In the insets of Fig. 3f, we show the spatial intensity distribution of the field corresponding to the white square regions.
Complementary results are also shown in Supplementary Section VI, Supplementary Figs. 11 and 14. Here, we present additional measurements for the generated ST wavepackets for both polarizations and maps of amplitude spatial distribution, respectively.
To further illustrate the capabilities of our system, we next proceed to counterbalance the effects of both modal and chromatic dispersion simultaneously. The first pulsed field we synthesize for this set of experiments exhibits a cylindrical-like spatial composition with negative vorticity \(({l}_{-1}=-1)\), which possesses a positive cubic chromatic function. In order to generate this spatial structure, we employ 2 of the 3 spatial modes available in our ST synthesis module, that is \({{HG}}_{01}\) and \({{HG}}_{10}\) modes. Initially, we delay the \(H{G}_{01}\) mode with respect to the \(H{G}_{10}\) mode by 0.5 ps to compensate for chromatic dispersion. Furthermore, (i) we correct for the chirp induced by the fiber propagation and (ii) we tailor the instantaneous frequency of the pulses corresponding to \(H{G}_{01}\) and \(H{G}_{10}\) modes with a third-order function. The measured iso-intensity profile for this field is depicted in Fig. 4a, while Fig. 4b depicts the corresponding spectrotemporal configuration, which resembles a parabolic function and provides evidence of the positive third-order frequency function imposed in the spectral phase of the field. The beam vortex attributes, intensity and phase, taken at the region enclosed by the white square in the spectrotemporal map, are shown in Fig. 4c.
Measured iso-intensity of the wavepackets. a A pulsed field displaying spatial negative vorticity (\({\ell}{=}{{{\mathscr{-}}}}1\)). d A train of three pulses, each with different spatial mode structure, matching the first three \({LP}\) modes guided in fiber. Here, instead of the natural arrival time, we set the temporal order of the modes ad libitum. Color-coded modal decomposition maps after projecting the field onto a set of Laguerre–Gaussian (LG) modes displaying. b Our pulse with vorticity \({\ell}{=}{{{\mathscr{-}}}}1\), (yellow color). It’s important to note that the cubic spectral function is manifested as a parabola-like shape. e The spectral function is fashioned on each element of the train of pulses, a cubic spectral function on the \({{LP}}_{11x}\) mode, no frequency chirp on the \({{LP}}_{11y}\) mode, a negative quadratic spectral function on the \({{LP}}_{01}\) mode. In (c, f), we depict the spatial profile intensity of selected regions of the spatiotemporal structures.
To provide more compelling evidence of simultaneous compensation for chromatic and modal dispersion, we prepared an entangled three-pulse train using our 3 available spatial modes \(\left({{HG}}_{00},{{HG}}_{01},{{HG}}_{10}\right)\), each pulse exhibiting a particular spatial Hermite-Gauss mode and different spectral chirp, see Fig. 4d, e, f. We use our ST pulse synthesizer to generate a train of three pulses where: On the first pulse, we imprint the spatial HG00 mode with a second-order spectral function, in the second pulse, we mold the HG01 mode with a third-order function, while in the third pulse we impose an HG10 mode with no modulation. Our three spatial structures are allocated at different times, swapping the characteristic arrival time of the guided modes, we delay the HG01 by 4.6 ps and the HG10 by 3.1 ps, both with respect to the HG00 pulse. This pulsed field, when captured at a specific propagation distance, z = z0, is analytically described by the spatiotemporal superposition \(E\left(x,y,t\right)={A}_{00}{e}^{-{\left(\frac{t-{\tau }_{00k}}{{\sigma }_{00k}}\right)}^{2}}{e}^{i{\beta }_{{{\mathrm{0,0}}},k}{t}^{2}}{e}^{i{\omega }_{k}t}{{HG}}_{00}(x,y)+{A}_{01}{e}^{-{(\frac{t-{\tau }_{01k}}{{\sigma }_{01k}})}^{2}}{e}^{i{\beta }_{{{\mathrm{0,1}}},k}{t}^{2}}{e}^{i{\omega }_{k}t}{{HG}}_{01}\left(x,y\right)+{A}_{10}{e}^{-{\left(\frac{t-{\tau }_{10}}{{\sigma }_{10}}\right)}^{2}}{e}^{i{\omega }_{k}t}{{HG}}_{10}\left(x,y\right)\), which evidently is nonseparable.
In Fig. 4d we present the corresponding iso-intensity surfaces displaying the spatial patterns of the LP modes in the predefined temporal order. We tailor the first element to exhibit positive vorticity \(\left({{\ell}}_{1}=1\right)\) and a negative cubic chromatic function (parabolic-like shape pointing to the left of the map). The second pulse has negative vorticity \(\left({{\ell}}_{-1}=-1\right)\) and a constant phase. The third element has no vorticity \(\left({{\ell}}_{0}=0\right)\) and a negative quadratic chromatic function (negative slope). Notice, the chromatic function imprinted on the modes was chosen arbitrarily, and their realization is meant to demonstrate the potential of our system to manipulate the spectral content of the constituent modes. Figure 4e shows the imposed frequency functions for each component. The spatial profiles in Fig. 4f demonstrate the transition of the LP mode content across different spectral/temporal regions. These results clearly demonstrate that our platform can establish a new design paradigm for ultrafast fiber applications and fiber amplifiers.
Supplementary Section VI provides extended characterization in Supplementary Figs. 12 and 15, presenting additional measurements for the generated ST wavepackets for both polarizations and maps of amplitude spatial distribution, respectively.
Despite the outstanding capabilities of our system, there are limitations in the fiber length that our system can compensate for. Let us elaborate, when a pulse traverses an optical fiber of length L, it acquires a spectral phase \(\phi \left(\omega \right)=-\beta \left(\omega \right)L\)48. Accordingly, to compensate the expected group velocity dispersion (GVD), we must counterbalance the nonlinear terms \({\phi }_{2}{\left(\omega -{\omega }_{0}\right)}^{2}/2\) and \({\beta }_{2}{\left(\omega -{\omega }_{0}\right)}^{2}L/2\), where ϕ2 and β2 are the second-order terms in the Taylor expansion of the spectral phase and the fiber propagation constant, respectively. For silica at λ = 1030 nm, we obtain \({\beta }_{2}=18.973{{fs}}^{2}/{mm}\), which corresponds to a maximum phase delay \({\phi }_{2}\approx 1.82\times {10}^{5}\,{{fs}}^{2}\). This is the maximum spectral phase that can be attained by our system, and it is enough to compensate for chromatic dispersion in a graded index fiber of approximately 9 m. In principle, it is possible to compensate for dispersion for longer fiber lengths by using a cascade pulse-shaping system, where each stage can gradually correct for a certain amount of dispersion. Additionally, our system can be adapted to operate with dual-polarization optical fields. To do so, we would need to upgrade the current SLMs to implement polarization-insensitive spatial light modulations in the Fourier transform pulse shaper and the MPLC49,50,51. Looking forward, the dispersion compensation techniques employed here can serve as a basis to explore the robustness of spatiotemporal wavepackets to the effects of external perturbations of the multimode fiber. This will open an opportunity to find the dispersion regimes, as we have done in the cases considered here, and generate spatiotemporal wavepackets tailored to endure particular external perturbations.
In summary, we experimentally demonstrated the ability to deliver a rich variety of spatiotemporal states of pulsed light to overcome the adverse effects encountered in a complex environment like a multimode waveguide. Our methodology allows one to synthesize arbitrary multidimensional light pulses in a robust and versatile manner. This has implications for a broad range of applications such as fiber-based multimode imaging systems, long-distance communications, ultrafast light-matter interactions, optical fiber amplifiers, and multidimensional information encoding.
Methods
We employ a pulse laser source centered at ~1030 nm, 180 fs (~6.4 nm FWHM, sech2-shaped pulse) and repetition rate of 40 MHz (Origami NKTPhotonics). We use a half-wave plate (AHWP05M-980 Thorlabs) and a polarization beam splitter (PBS123 Thorlabs) to controllably divide the beam into reference and signal pulses. We temporally modulate the signal pulse train with a two-dimensional Fourier transform pulse shaper in a folded configuration. We use a ruled reflective diffraction grating (1200 grooves⁄mm, Blaze wavelength 1 μm, Thorlabs). A C-coated cylindrical lens with 30 cm focal length (LJ1558RM-B Thorlabs). Additionally, we employ a 1920 × 1080 pixels reflective SLM, pixel size 8 μm (PLUTO-2.1-NIR Holoeye). We direct the modulated pulse coming out of the two-dimensional Fourier transform pulse shaper to the next stage using a 50/50 beam splitter (BS014 Thorlabs). We adjust the size of the field with a two-lens system composed of two C-coated plano-convex lenses, f1 = 3.5 cm (LA1027-C Thorlabs) and f2 = 30 cm (LA1484-C Thorlabs). At the last stage, we spatially engineer the field profile with an MPLC system using a 1920 × 1080 pixels reflective SLM, pixel size \(8\,\mu m\) (PLUTO-2.1-NIR Holoeye), and a squared mirror (PFSQ05-03-P01 Thorlabs).
For our experiments, we use 2-m-long graded index optical fiber home-drawn with a diameter size of \(11\mu m\) and a refractive index contrast ∆n = 16 × 10−3. We wind our fiber on a 20 cm diameter coil. We use a B-coated aspheric lens with 4.6 mm focal length (CFC5A-B Thorlabs) to couple the synthesized fields in our graded index fiber. Finally, we use a B-coated aspheric lens with 11-mm focal length (C397TMD-B Thorlabs) to uncouple the light.
To analyze the spatiotemporal structure of the fields, we use the reference pulse with a controllable time delay. We use a second set of half-wave plates and a polarization beam splitter to adjust the reference pulse’s intensity. We resolve the frequency components of the signal pulse by employing a spectral filter centered at 1047.1 nm, 4 nm FWHM bandwidth (LL01−1047−12.5 Semrock) mounted on a rotation stage (Thorlabs ELL14). We recombined the reference and signal arms using a 50/50 beam splitter (BS005 Thorlabs). We distinguish the polarization state using a system composed of a half-wave plate (AHWP05M-980 Thorlabs) and a polarization beam splitter (PBS053 Thorlabs). Finally, we record the reference and signal interference pattern on a CCD camera 2048 × 1088 pixels, 5.5 μm pixel size (Beamage-3.0 Gentec). In order to capture the dynamics of the field, a linear translation stage driven by an actuator (Z825B Thorlabs). We scan the time dimension by introducing a time delay τ on the reference arm at time steps of ~66.66 ps (20 μm optical path length steps), while we interrogate the frequency components by rotating the spectral filter at angle steps of 0.5°.
Data availability
The authors declare that the data supporting the findings of this study are available via OSF at https://doi.org/10.17605/OSF.IO/H3JXQ.
References
Babin, S. A. et al. Multicolour nonlinearly bound chirped dissipative solitons. Nat. Commun. 5, 4653 (2014).
Rego, L. et al. Generation of extreme-ultraviolet beams with time-varying orbital angular momentum. Science 364, 6447 (2019).
Defienne, H., Barbieri, M., Walmsley, I. A., Smith, B. J. & Gigan, S. Two-photon quantum walk in a multimode fiber. Sci. Adv. 2, e1501054 (2016).
Lib, O., Hasson, G. & Bromberg, Y. Real-time shaping of entangled photons by classical control and feedback. Sci. Adv. 6, eabb6298 (2020).
Kondakci, H. E. & Abouraddy, A. F. Optical space-time wavepackets having arbitrary group velocities in free space. Nat. Commun. 10, 929 (2019).
Yessenov, M. et al. Space-time wave packets localized in all dimensions. Nat. Commun. 13, 4573 (2022).
Hancock, S. W., Zahedpour, S., Goffin, A. & Milchberg, H. M. Free-space propagation of spatiotemporal optical vortices. Optica 6, 1547–1553 (2019).
Chong, A., Wan, C., Chen, J. & Zhan, Q. Generation of spatiotemporal optical vortices with controllable transverse orbital angular momentum. Nat. Photon. 14, 350–354 (2020).
Cao, Q. et al. Sculpturing spatiotemporal wavepackets with chirped pulses. Photon. Res. 9, 2261–2264 (2021).
Chen, L. et al. Synthesizing ultrafast optical pulses with arbitrary spatiotemporal control. Sci. Adv. 8, eabq8314 (2022).
Cruz-Delgado, D. et al. Synthesis of ultrafast wavepackets with tailored spatiotemporal properties. Nat. Photon. 16, 686–691 (2022).
Piccardo, M. et al. Broadband control of topological–spectral correlations in space–time beams. Nat. Photon. 17, 822–828 (2023).
Wan, C., Cao, Q., Chen, J., Chong, A. & Zhan, Q. Toroidal vortices of light. Nat. Photon. 16, 519–522 (2022).
Zdagkas, A. et al. Observation of toroidal pulses of light. Nat. Photon. 16, 523–528 (2022).
McCabe, D. et al. Spatio-temporal focusing of an ultrafast pulse through a multiply scattering medium. Nat. Commun. 2, 447 (2011).
Katz, O., Small, E., Bromberg, Y. & Silberberg, Y. Focusing and compression of ultrashort pulses through scattering media. Nat. Photon. 5, 372–377 (2011).
Hernandez, O. et al. Three-dimensional spatiotemporal focusing of holographic patterns. Nat. Commun. 7, 11928 (2016).
Sun, B. et al. Four-dimensional light shaping: manipulating ultrafast spatiotemporal foci in space and time. Light Sci. Appl. 7, 17117 (2018).
Wei, X. et al. Real-time frequency-encoded spatiotemporal focusing through scattering media using a programmable 2D ultrafine optical frequency comb. Sci. Adv. 6, eaay1192 (2020).
Mounaix, M. et al. Time reversed optical waves by arbitrary vector spatiotemporal field generation. Nat. Commun. 11, 5813 (2020).
Shiri, A., Webster, S., Schepler, K. L. & Abouraddy, A. F. Propagation-invariant space-time supermodes in a multimode waveguide. Optica 9, 913–923 (2022).
Carpenter, J., Eggleton, B. & Schröder, J. Observation of Eisenbud–Wigner–Smith states as principal modes in multimode fibre. Nat. Photon. 9, 751–757 (2015).
Gao, H., Hu, H. & Zhan, Q. Generation and applications of spectral-spatially correlated principal mode in multimode fibers. Optica 11, 205 (2024).
Cao, Q., Chen, Z., Zhang, C., Chong, A. & Zhan, Q. Propagation of transverse photonic orbital angular momentum through few-mode fiber. Adv. Photon 5, 036002 (2023).
Guo, C. & Fan, S. Generation of guided space-time wave packets using multilevel indirect photonic transitions in integrated photonics. Phys. Rev. Res. 3, 033161 (2021).
Béjot, P. & Kibler, B. Quadrics for structuring invariant space−time wave packets. ACS Photonics 9, 2066 (2022).
Jolly, S. W. & Kockaert, P. Coupling to multi-mode waveguides with space-time shaped free-space pulses. J. Opt. 25, 054002 (2023).
Guang, Z. & Zhang, Y. Coupling ultrafast laser pulses into few-mode optical fibers: a numerical study of the spatiotemporal field coupling efficiency. Appl. Opt. 57, 9835–9844 (2018).
Choi, Y. et al. Scanner-free and wide-field endoscopic imaging by using a single multimode optical fiber. Phys. Rev. Lett. 109, 203901 (2012).
Turtaev, S. et al. High-fidelity multimode fibre-based endoscopy for deep brain in vivo imaging. Light Sci. Appl. 7, 92 (2018).
Ohayon, S., Caravaca-Aguirre, A., Piestun, R. & DiCarlo, J. J. Minimally invasive multimode optical fiber microendoscope for deep brain fluorescence imaging. Biomed. Opt. Express 9, 1492–1509 (2018).
Zhao, T. et al. Ultrathin, high-speed, all-optical photoacoustic endomicroscopy probe for guiding minimally invasive surgery. Biomed. Opt. Express 13, 4414–4428 (2022).
Popoff, S. M. et al. Measuring the transmission matrix in optics: an approach to the study and control of light propagation in disordered media. Phys. Rev. Lett. 104, 100601 (2010).
Plöschner, M., Tyc, T. & Čižmár, T. Seeing through chaos in multimode fibres. Nat. Photon. 9, 529–535 (2015).
Mounaix, M., de Aguiar, H. B. & Gigan, S. Temporal recompression through a scattering medium via a broadband transmission matrix. Optica 4, 1289–1292 (2017).
Lerosey, G., Rosny, J. D., Tourin, A. & Fink, M. Focusing beyond the diffraction limit with far-field time reversal. Science 315, 1120–1122 (2007).
Yaqoob, Z., Psaltis, D., Feld, M. S. & Yang, C. Optical phase conjugation for turbidity suppression in biological samples. Nat. Photon. 2, 110 (2008).
Vellekoop, I. M. & Mosk, A. Focusing coherent light through opaque strongly scattering media. Opt. Lett. 32, 2309–2311 (2007).
Čižmár, T. & Dholakia, K. Exploiting multimode waveguides for pure fibre-based imaging. Nat. Commun. 3, 1027 (2012).
Caravaca-Aguirre, A. M., Niv, E., Conkey, D. B. & Piestun, R. Real-time resilient focusing through a bending multimode fiber. Opt. Express 21, 12881–12887 (2013).
Rivenson, Y. et al. Deep learning microscopy. Optica 4, 1437–1443 (2017).
Turpin, A., Vishniakou, I. & Seelig, J. D. Light scattering control in transmission and reflection with neural networks. Opt. Express 26, 30911–30929 (2018).
Zhai, Y. et al. Turbulence aberration correction for vector vortex beams using deep neural networks on experimental data. Opt. Express 28, 7515–7527 (2020).
Zhou, Y. et al. High-fidelity spatial mode transmission through a 1-km-long multimode fiber via vectorial time reversal. Nat. Commun. 12, 1866 (2021).
Shen, X., Kahn, J. M. & Horowitz, MarkA. Compensation for multimode fiber dispersion by adaptive optics. Opt. Lett. 30, 2985–2987 (2005).
Gholami, A., Molin, D. & Sillard, P. Compensation of chromatic dispersion by modal dispersion in MMF- and VCSEL-based Gigabit Ethernet transmissions. IEEE Photon. Technol. Lett. 21, 645–647 (2009).
Forbes, A., Aiello, A. & Ndagano, B. Classically entangled light. Prog. Opt. 64, 99 (2019).
Weiner, A. M. Femtosecond pulse shaping using spatial light modulators. Rev. Sci. Instrum. 71, 1929 (2000).
Liu, J. & Wang, J. Demonstration of polarization-insensitive spatial light modulation using a single polarization-sensitive spatial light modulator. Sci. Rep. 5, 9959 (2015).
Mitchell, KevinJ., Radwell, Neal, Franke-Arnold, Sonja, Padgett, MilesJ. & Phillips, DavidB. Polarisation structuring of broadband light. Opt. Express 25, 25079–25089 (2017).
Fontaine, N. K. et al. Laguerre-Gaussian mode sorter. Nat. Commun. 10, 1865 (2019).
Acknowledgements
This effort was sponsored, in part, by the Army Research Office of Scientific Research (W911NF1710553 and W911NF1910426); NASA (80NSSC21K0624); Department of the Navy, Office of Naval Research, (N00014-20−1-2789); the National Science Foundation (EECS-1711230); the Simons Foundation (733682); the US-Israel Binational Science Foundation (BSF; 2016381). Article processing charges were provided in part by the UCF College of Graduate Studies Open Access Publishing.
Author information
Authors and Affiliations
Contributions
D.C.-D., M.A.B., and R.A.-C. conceived the idea for this work. D.C.-D., M.A.B., and R.A.-C. designed the experimental setup. J.E.A.-L. designed and fabricated the optical fibers. D.C.-D. performed the experiments. D.C.-D., A.P.-L., N.K.F., S.S.E., D.N.C., M.A.B., and R.A.-C. interpreted the results. D.C.-D., A.P.-L., S.S.E., and R.A.-C. co-wrote the manuscript with the input of all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Marco Piccardo and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Cruz-Delgado, D., Antonio-Lopez, J.E., Perez-Leija, A. et al. Spatiotemporal control of ultrafast pulses in multimode optical fibers. Nat Commun 16, 6081 (2025). https://doi.org/10.1038/s41467-025-60615-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-60615-6