Introduction

Animal brains can perform complex computations including sensory processing, motor control, and working memory, as well as higher cognitive functions, such as decision-making and reasoning, in an efficient and reliable manner. At the neural network level, these processes are implemented using a variety of computational primitives that rely on neural dynamics within recurrent neocortical microcircuits1,2,3,4,5,6. Translating the computational primitives observed in the brain into novel technologies can potentially lead to radical innovations in artificial intelligence and edge-computing applications. A promising technology that can implement these primitives with compact and low-power devices is that of mixed-signal neuromorphic systems which employ analog electronic circuits to emulate the biophysics of real neurons7,8,9. As opposed to software simulations, the direct emulation performed by these electronic circuits relies on the use of the physics of the silicon substrate to faithfully reproduce the dynamics of neurons and synapses asynchronously in real time. While systems designed following this approach have the advantage of ultra-low power consumption, they have limitations and constraints similar to those found in biology. These include a high degree of variability, heterogeneity, and sensitivity to noise10,11. Due to these constraints, implementing recurrent networks in silicon with the same stability and robustness observed in biological circuits has remained an open challenge.

Previous studies have already demonstrated neuromorphic implementations of recurrent computational primitives such as winner-take-all or state-dependent networks12,13,14,15. However, these systems required manual tuning and exhibited dynamics that would not always produce stable self-sustaining regimes. Manually tuning on-chip recurrent networks with large numbers of parameters is challenging, tedious, and not scalable. Furthermore, because of cross-chip variability, this process requires re-tuning for each individual chip. Even when a stable regime is achieved with manual tuning, changes in the network conditions (e.g., due to temperature variations, increase or decrease of input signals, etc.) would require re-tuning. Therefore, mixed-signal neuromorphic technology can greatly benefit from automatic stabilizing and tuning mechanisms. While not aiming to remove existing heterogeneities (which are also present in biological systems), we can work with them to manage the challenges imposed by the analog substrate.

Neocortical computations rely heavily on positive feedback through recurrent connections between excitatory neurons, which allows networks to perform complex time-dependent computations and actively maintain information about past events. Recurrent excitation, however, also makes neocortical circuits vulnerable to “runaway excitation” and epileptic activity16,17. In order to harness the computational power of recurrent excitation and avoid pathological regimes, the neocortical circuits operate in an inhibition-stabilized regime, in which positive feedback is held in check by recurrent inhibition18,19,20,21. Indeed, there is evidence that the default awake cortical dynamic regime may be inhibition-stabilized20,22.

It is generally accepted that neocortical microcircuits have synaptic learning rules in place to homeostatically balance excitation and inhibition in order to generate dynamic regimes capable of self-sustained activity23,24,25,26,27. Recently, a family of synaptic learning rules that differentially operate at excitatory and inhibitory synapses has been proposed, which can drive simulated neural networks to self-sustained and inhibition-stabilized regimes in a self-organizing manner28. This family of learning rules is referred to as being “cross-homeostatic” because synaptic plasticity at excitatory and inhibitory synapses is dependent on both the inhibitory and excitatory set-points. Taking inspiration from self-calibration principles in cortical networks, we use these cross-homeostatic plasticity rules to guide neuromorphic circuits to balanced excitatory-inhibitory regimes in a self-organizing manner. We show that these rules can be successfully employed to autonomously calibrate analog spiking recurrent networks in silicon. Specifically, by automatically tuning all synaptic weight classes in parallel, the dynamics of the silicon networks converge to a fully self-sustained inhibition-stabilized regime. The weights and firing rates converge to stable, fixed-point attractors. In addition, the emergent (fast) neural dynamics reach an asynchronous, irregular regime and express the “paradoxical effect”, a signature of inhibition-stabilized networks widely observed in cortical circuits, where an increase in input to the inhibitory population results in a counter-intuitive decrease in its firing response18,20.

The plasticity rules proposed prove resilient to hardware variability and noise, also across different chips, as well as to different parameter initializations. Importantly, we demonstrate that inhibitory plasticity (often neglected in neuromorphic electronic systems) is necessary for successful convergence. We also demonstrate that by utilizing these plasticity rules, multiple, coexisting long-term memories can be maintained within the same network without disrupting the learned dynamics.

This behavior aligns with the previous work on network models crafted to support competition among multiple clusters12,13,14,15,29,30.

From a computational neuroscience perspective, these results validate the robustness of cross-homeostatic plasticity in a physical substrate that presents similar challenges to those of biological networks, unlike idealized digital simulations. From a neuromorphic perspective, this approach provides the community with a reliable method to autonomously and robustly calibrate recurrent neural networks in future mixed-signal analog/digital systems that are affected by device variability (also including memristive devices31,32). This will open the door to designing autonomous systems that can interact in real time with the environment, and compute reliably with low-latency at extremely low-power using attractor dynamics, as observed in biological circuits.

Results

In the cortex, excitatory Pyramidal (Pyr) and inhibitory Parvalbumin-positive interneurons (PV) constitute the main neuronal subtypes and are primarily responsible for excitatory/inhibitory (E/I) balance33. Pyr and PV neurons have different intrinsic biophysical properties: for example, in terms of excitability, PV cells havecontinuous a higher threshold and gain compared to Pyr neurons34.

In our hardware experiments, we reproduce the properties of both Pyr and PV neuron types on a mixed-signal analog/digital Dynamic Asynchronous Neuromorphic Processor, called DYNAP-SE235 (see Fig. 1a), which implements silicon neuron circuits equivalent to the adaptive exponential (AdEx) integrate-and-fire neuronal model. The dynamics of the different neuron classes were reproduced by tuning the refractory period, time constants, spiking threshold, and neuron gain parameters (Table 3, in the Supplementary Material) to match the corresponding biologically measured values (Fig. 1b). We disabled neural spike-frequency adaptation for all the experiments discussed in this article. Since parameters are shared by all neurons in a chip core, we assign each neuron population type to a different core (Fig. 1a). Similarly, weights only depend on neuron type and not on individual neurons, so that we have four parameters for the four weight classes (wee, wei, wie, wii). Even though all neurons in a core share the same parameters, variations in their intrinsic characteristics arise as a result of analog mismatch. For instance, one can observe differences between two excitatory or inhibitory neurons recorded within the same core, as illustrated in Fig. 1c.

Fig. 1: On-chip instantiation and validation of an E–I microcircuit on the DYNAP-SE2 neuromorphic platform.
figure 1

a Image of the DYNAP-SE2 chip, showing the four cores. An E-I network is implemented on chip. Excitatory (Pyr) and Inhibitory (PV) neurons occupy different cores, and are connected by four weight classes, Pyr-to-Pyr (wee), Pyr-to-PV (wie), PV-to-PV (wii), and PV-to-Pyr (wei). b Circuit diagram depicting a DPI neuron, with each component within the circuit replicating various sub-threshold characteristics (such as adaptation, leakage, refractory period, etc.) inherent to an adaptive exponential neuron35. c Neuron membrane potential traces over time as a response to DC injection. Blue traces show two example cells from the excitatory chip core in response to four current levels. Red traces show two sample PV cells from the inhibitory chip core. The relationship between the measured voltage and the internal current-mode circuit output that represents the membrane potential is given by an exponential function that governs the subthreshold transistor operation mode59. In each case, the bottom two traces show neuronal dynamics in the subthreshold range. The top two traces show neuronal dynamics as the membrane potential surpasses the spike threshold (spike added as gray line to indicate when the voltage surpasses threshold). DC injection values are indicated on each trace. d Input-response curves for the resulting Pyr and PV neurons on-chip, averaged over a population of 200 neurons per cell type. The shaded areas encompass  ±1 standard deviations. Inset: zoomed-in view at low firing rates. In (c), it is evident that a higher input current was required to elicit spikes in PV neurons. This phenomenon can be attributed to the higher threshold of PV neurons.

Full size image

Overall, the neural dynamics and the Input-Frequency (FI) curve of the recorded excitatory and inhibitory neurons on chip (Fig. 1c–d) show that the choice of parameters used for the silicon neurons leads to behavior which is compatible with the behavior of biological PV and Pyr cells34.

In the following section, we employ cross-homeostatic plasticity28 to self-tune the connections between PV and Pyr populations so that spontaneous activity in the inhibition-stabilized regime emerges in the network.

The network converges to stable self-sustained dynamics

As an overview of the experimental paradigm, the training procedure begins with random initialization of the network weights. Then, at each iteration, we record the resulting firing rates averaged over 5 repetitions, calculate the weight update following the cross-homeostatic equations for the four weight classes (wee, wei, wie, and wii, eq. (2), see “Methods”) and apply the new weight values to the chip. We conduct 57 trials in this experiment, each with randomized network connectivity and weight initialization, to evaluate the robustness of the proposed cross-homeostasis rule. This paradigm is consistently applied across all training experiments.

Figure 2a illustrates an example of the evolution of firing activity during the course of training for Pyr and PV cells. Starting from a random value determined by the initialization of weights, the average rates converge to their target values. Figure 2b plots the evolution of weights during training. On chip, the weights are controlled by two parameters, a coarse Cw and a fine Fw value (See “Methods”, eq. (5)). On most iterations, only the fine value Fw is updated, but updates to the coarse value Cw occur occasionally. Even though the coarse updates cause abrupt jumps in the weight value (due to the nature of the bias-generator circuit implementation), the cross-homeostatic rule is robust enough to guide the network to a stable regime. Figure 2c shows a raster plot from the network in Fig. 2a, b at a converged state. For an additional example with different weight dynamics see Fig. S2. It should be emphasized that, while an initial “kick” was provided to the network to engage recurrent activity (40 ms at 100 Hz), no further external input was introduced during the trial; hence, any observed spiking activity originates entirely from internal mechanisms.

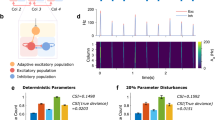
Fig. 2: Cross-homeostasis drives convergence to target firing rates and asynchronous-irregular regime in a E–I network.
figure 2

a A representative trial of the convergence of excitatory (red) and inhibitory (blue) firing rates during learning. The gray dashed lines show the desired set-point targets. b A representative trial (the same as in a) of the convergence of weight values during learning. The plotted value is nominal, inferred from eq. (1) (see “Methods”). c Raster plot exemplifying on-chip firing activity during a single emulation run at the end of training. Both Pyr and PV neurons successfully converge to an asynchronous-irregular firing pattern at the desired population FRs. d Initial and final firing rates across different chips (n = 57, across two chips) and different initial conditions. For each initial condition, network connectivity was randomized. e Left: relationship between the final wee and wei values across different iterations. Orange and green colors correspond to two different chips. Right: same for wie and wii. f Distributions for the 5 ms correlation coefficients between neurons (left) and coefficient of variation (CV2) (right), demonstrating low regularity and low synchrony. The line indicates the mean. The shaded region indicates the standard deviation.

Full size image

When repeating the training process from different initial conditions of randomly sampled weights (see Fig. S1 for the corresponding initialization), the weights converge to different values, which however produce the same desired network average firing rate28. Figure 2d illustrates the rate space with multiple initialization and convergence to respective target set-points (dashed lines). The root mean square error from the target is 0.945 Hz for \(\bar{E}\) and 1.653 Hz for \(\bar{I}\). The converged weight values are approximately aligned to a linear manifold (Fig. 2e), where the sets of excitatory and inhibitory weights wee, wei and wie, wii, are correlated (correlation coefficients and p-values are as follows: wee and wei: ρchip1 = 0.81 and p = 1.55 × 10−06; ρchip2 = 0.88, p = 6.6 × 10−12; wie and wii: ρchip1 = 0.63 p = 0.0009; ρchip2 = 0.75, p = 3.9 × 10−07). This is well aligned with the theoretical solution derived for rate E–I networks at their set-points, when the neuron transfer function is linear or threshold-linear28, eqs. (4, 5). In our case, the linear transfer function assumption does not hold, because the AdEx silicon neuron models saturate at a rate that is inversely proportional to the refractory period parameter. However, the linear approximation holds well in the region of operation forced by the learning rule, set at relatively low firing rates (see Fig. 1d).

The network is in an inhibition-stabilized asynchronous-irregular firing regime

Next we investigated the properties of the final network dynamics after learning. Figure 2c shows a sample of activity of the converged network, as recorded from the chip, in which the excitatory and inhibitory populations exhibit asynchronous-irregular activity patterns. The minimal correlations among neurons (averages 〈ρpyr〉 =  0.037, 〈ρpv〉 = 0.069) serve as evidence of their asynchronous activity (Fig. 2f, left). Irregularity is shown by the coefficient of variation (CV2) of most neurons being close to 1 (averages \(\langle C{V}_{pyr}^{2}\rangle\) = 0.949, \(\langle C{V}_{pv}^{2}\rangle\) = 0.945) (Fig. 2f, right). The CV2 is computed as the variance of the inter-spike interval divided by its squared mean, and equals 0 for perfectly regular firing, and 1 for Poisson firing36. It is worth noting that during the 1-s simulations, we do find instances of synchronization, which can be attributed to the small population size of the network and increased firing rate in comparison to the baseline spontaneous activity. As an average however, we conclude that cross-homeostatic plasticity brings the network to an asynchronous-irregular firing regime, which is typical in realistic cortical networks37.

As further evidence of the inhibition-stabilized regime of the network, we demonstrate the occurrence of the “paradoxical effect” in our deployed network on chip18,20. The paradoxical effect is a hallmark of inhibition-stabilized networks that has been observed in cortical circuits. When inhibitory neurons are excited (either optogenetically in vivo, or via an external current in computational models) their firing rates show a paradoxical decrease in activity during the stimulation, providing clear evidence that that the network is in an inhibition-stabilized regime (Fig. 3a). Analogously, when we inject an external depolarizing pulse to all PV neurons on chip for 0.2 s we observe a decrease in the firing rate of both cell populations for the duration of the stimulus, returning back to the target FR when the stimulus ends (Fig. 3b). Across all 14 iterations we use pairwise t-tests to assess the impact of stimulating PV neurons. For PV neurons, stimulation significantly reduces activity during stimulation compared to pre- and post-stimulation states (p < 10−18 in both cases). Conversely, there is no significant difference between pre- and post-stimulation activity, indicating recovery. Five trials, which were excluded from the analysis, do not exhibit recovery because the activity is entirely suppressed by the strength of the paradoxical effect. A similar trend is observed for Pyramidal neurons (p < 10−20).

Fig. 3: Neuromorphic emulation of the paradoxical effect confirms inhibition-stabilized regime.
figure 3

a The paradoxical effect is a well known phenomena in cortical circuits. In the awake resting cortex of mice (upper figure), when inhibitory neurons are optogenetically activated, their firing rates (in red) show a paradoxical decrease in activity during the stimulation, indicative of an inhibition-stabilized network. Adapted from Sanzeni et al.21. Similar to the experimental case (bottom figure), numerical simulations of firing rate models with sufficient excitatory gain and balanced by inhibition show the paradoxical effect when the inhibitory population is excited via an external current. b The paradoxical effect can be demonstrated in analog neuromorphic circuits by applying a Poisson input of 250 Hz for 200 ms to the inhibitory units of networks converged to self-sustained activity via cross-homeostasis. The resulting decrease in the firing rate of the inhibitory units demonstrates that the on-chip network is in the inhibition-stabilized regime. No. of trials = 14; the shading around the lines represents the standard deviation in firing rate across trials.

Full size image

Inhibitory plasticity is necessary to achieve reliable convergence

The equations for the weights in absence of noise28, eqs. (4, 5) and the experimental results in Fig. 2e indicate that two of the four weight parameters, for example, the inhibitory weights wii and wei, can be chosen arbitrarily, since one can always find a solution by learning the other two. This appears to suggest that homeostatic plasticity of the inhibitory weights might not be required in an ideal case. However, we experimentally show that excitatory plasticity alone is not sufficient to reliably make the network converge in the presence of the noise and non-idealities of the analog substrate (see Fig. 4). In the absence of inhibitory plasticity, both the excitatory and inhibitory populations approach their respective set-points, but they fail to converge to stable activity levels. In addition, the network is in an unstable configuration, as can be seen by the many instances of “exploding” activity that occur during the trial, where the firing rate diverges and is limited only by the saturation of the spiking dynamics. (Fig. 4a). In contrast, the full cross-homeostatic plasticity rule robustly drives the network activity towards the set-points after just a few iterations (Fig. 2a). These results hold for multiple initializations (Fig. 4b), indicating that inhibitory plasticity is necessary for robust convergence.

Fig. 4: Ablation of inhibitory learning results in unstable dynamics and impaired training.
figure 4

a Example network with training results on “fixed” inhibitory synapses. Convergence is impaired if inhibitory plasticity is turned off. Note that during the experiment, the network exhibits “exploding” rates above 300 Hz, corresponding to the neuron’s saturation rates. b Random networks ran with different initialization of all weights (n = 8). The firing rates do not converge to the targets as precisely as in Fig. 2a, having a much higher root mean square error from the target (RMS on \(\bar{E}\): 6.39, on \(\bar{I}\): 35.11).

Full size image

Homeostatic plasticity in inhibitory neurons is less studied than in excitatory neurons24,38, although there is evidence that inhibitory neurons also regulate their activity levels based on activity set-points39,40. Considering our on-chip results, we therefore speculate that homeostatic plasticity in all excitatory and inhibitory connections plays an important stabilization role also in biological systems.

Excitatory plasticity is desirable for reliable convergence and chip resource utilization

Given that inhibitory plasticity seems to be crucial, we next investigated whether excitatory-to-excitatory plasticity is also necessary, providing the fixed value of wee is sufficiently high to generate self-sustained activity. Having wee free from any homeostasis could be beneficial when introducing other forms of plasticity, such as standard associative learning rules (eg. Hebbian learning or spike timing dependent plasticity (STDP)). We thus ran a set of trials with wee plasticity frozen. We find that in most cases, the network is able to converge to stable activity levels at the set-points (Fig. S3). However, because of the fewer degrees of freedom, the rules fail to converge whenever any of the weights reaches their maximum possible value on chip (Fig. S3b). We conclude that although it is possible to operate cross-homeostasis without wee plasticity, it is highly beneficial to maintain all four weight classes plastic for robust convergence across all initial conditions. This is true also when freezing weights other than wee. To confirm these results, we ran multiple simulations on a rate model (see Figs. S5 and S6), freezing different sets of weights. Indeed, our results show that having plasticity in all weight classes allows for robust convergence across a wide range of initial conditions, while such convergence is always partly impaired whenever plasticity is blocked on any weight class.

Despite the above evidence that excitatory-to-excitatory plasticity is highly beneficial, these results do not rule out that alternative forms of homeostasis could still succeed in bringing the network to fully self-sustained regimes without operating on wee. Recently, a set of homeostatic rules operating at the wei and wie weights has been proposed which implement stimulus-specific feedback inhibition consistent with V1 microcircuitry41. The rules proposed by Mackwood and colleagues are simple enough that they can be implemented with our chip-in-the-loop setup, as are the cross-homeostatic plasticity rules (see Methods). In fact, the rule for the wie weight is the same as its cross-homeostatic counterpart. The rule for wei obeys a more classic homeostatic formulation24,42. Unlike cross-homeostasis, these rules only impose an activity set-point for the excitatory population. We decided to test whether, in the absence of external input but with sufficiently high wee, the rules from Mackwood and colleagues could be employed to generate self-sustained dynamics in the inhibition-stabilized regime on chip. The experiments show that, in most cases, the network converges with stable self-sustained dynamics to the established excitatory set-point (Fig. 5a–b). However—as happened when dropping plasticity in some of the cross-homeostatic weights—because of the lower degrees of freedom, the rules fail to converge whenever any of the weights reach their maximum possible value on chip (Fig. S3b). Another disadvantage of employing these rules is the lack of an inhibitory set-point for the I population. Although this could be perceived as advantageous (to keep inhibitory rates free of constraints), in practice the network often converges to very large values of inhibitory rates (in most cases above 100 Hz) (Fig. 5c). These high rates are often un-biological, and not desirable for neuromorphic applications where sparsity and ultra-low power consumption are a constraint.

Fig. 5: Results obtained using Mackwood et al.’s rule.
figure 5

a Convergence of the firing rate to stable self-sustained dynamics. Note that, in this case, there is no inhibitory target. b Convergence of the weight values. wii and wee are fixed and thus do not show any dynamics under this rule. c Initial and final firing rate values over many trial runs. \(\bar{E}\) mostly converges to the target, while, unlike with cross-homeostasis, the final \(\bar{I}\) is left to vary freely (n = 34).

Full size image

In the light of these results we envision cross-homeostatic plasticity as a powerful tool to robustly calibrate neuromorphic hardware, likely after fabrication, into a fully self-sustained inhibition stabilized regime. After initial calibration—which would bring the four weights to a stable low-firing regime across a broad range of initial conditions — the experimenter could choose, for example, to freeze homeostasis on the excitatory weights, or use the rules proposed by Mackwood and colleagues, to allow for more freedom for other plasticity forms.

Multiple sub-networks can be emulated on a single chip

In the network discussed so far, we modeled a single stable fixed point attractor in firing rate space, using an E/I-balanced network. We used 200 out of the 256 neurons available on a single core of our multi-core neuromorphic chip (DYNAP-SE2).

Even though it is still a relatively small-scale network, for computational purposes, having a single attractor formed from 200 neurons is not an optimal utilization of the resources on the chip. Employing smaller networks would allow us to implement multiple attractors on a single chip, whereby each sub-network could represent, for example, a distinct choice in a decision-making task. This could be useful for stateful computations, or, for example, to implement different recurrent layers on a chip43.

Therefore, we also run scaled down variations of the previous network, and assess whether cross-homeostatic plasticity can still bring activity to desired levels. Table 1 summarizes the population count, connectivity scaling, and adjustment in the target firing rate that we adopt for each experiment.

Table 1 Variation in network size, connection scaling, and stable target firing rate (set-points) for reliable self-sustained activity
Full size table

Furthermore, we experiment with implementing multiple copies of these scaled-down networks on the same chip. We create five instances of different E/I networks, each with 50 excitatory and 15 inhibitory neurons. The connectivities within each sub-network are drawn from the same distribution. Each sub-network operates independently, with no interaction between them. The configuration is illustrated in Fig. 6a. To implement this configuration on the chip, we group the excitatory neuron populations into a single core, and use another core for the inhibitory populations. All parameter values, including weights, are shared between sub-networks. The challenge is to check whether homeostatic plasticity leads to convergence for all sub-networks, since the effect of the weights is different for each E/I network due to the inhomogeneity of the chip.

Fig. 6: Simultaneous training of multiple clusters.
figure 6

a Schematic of clusters on the chip. One core contains excitatory populations, and another contains inhibitory populations. We implemented five E/I networks, with each network comprising 50 excitatory and 15 inhibitory neurons. As per table 1, the connection probability within these networks is 0.35. To account for the network’s scaling, we defined higher set-points. Note that these clusters do not interconnect with one another. b Rate convergence for five clusters sharing the same nominal weights. Each color represents one cluster.

Full size image

During the training process, we sequentially stimulate one sub-network at a time during each iteration. We then compute the change in synaptic weights, denoted as Δw, based on the activity of the neuron population within that E/I network. The weight is configured on the chip after each iteration based on the average Δw across all sub-networks. Figure 6b shows that all five sub-networks, with shared weights, can indeed converge to mean firing rate regimes close to the target firing rate.

Neuronal ensembles remain intact under cross-homeostasis

The effect of homeostasis is to maintain a set level of activity in neurons by scaling synaptic efficacy, as done in this work, or by changing the intrinsic properties of the neuron. This raises concerns about the stability-plasticity dilemma, i.e., the competition between the homeostatic stability mechanism and the associative forms of synaptic plasticity that contribute to the formation of functional neural ensembles, as they may counteract each other causing either forgetting or the inability to form new memories. A neural ensemble refers to a group of interconnected neurons—such as those that strengthen their synaptic connections through learning—that collectively contribute to representing a specific memory concept. Typically, neurons forming an ensemble exhibit shared selectivity44,45.

The stability of an ensemble could potentially be affected by the homeostatic scaling process which attempts to equalize the activity levels across the network.

To verify that the cross-homeostatic plasticity used here does not interfere with neural ensembles, we artificially formed a “crafted memory” ensemble in the network, but left it disabled by using the chip’s ability to modulate the shared weight parameters with a 4-bit mask (see “Methods”). Specifically, the ensemble consists of 32 neurons, in which each neuron has a connection probability with other neurons of the same ensemble of 0.5, i.e., five times more than the rest of the network (Fig. 7a). We then manually instantiate the memory in the rest of the network, by properly configuring the weight masking bits, after the homeostatic training process had converged to a steady state (see iteration 250 in Fig. 7).

Fig. 7: Training result with a memory implanted in the network.
figure 7

a Random recurrent E/I network with a neural ensemble (size = 32, green neurons). b Convergence of both excitatory (Pyr) and inhibitory (PV) populations to their respective set-points. A subset of the weights is manually changed to instantiate a new ensemble at iteration 250, well after the network has converged to its set-point. A jump in activity is observed in both Pyr and PV cells due to the presence of the newly implanted memory. c Schematic illustration of the process of re-balancing a weight matrix after implanting a new memory, instantiated as a network of six neurons containing an ensemble of three neurons. This is only indicative, as in the current chip it is not possible to read the weight matrix for visualization. d The nominal weight value for 32 neurons (wee) is increased by 0.0088 μA at the time point highlighted with the dotted line. All weights undergo alteration again to compensate for the presence of the new ensemble, bringing the network back to the set-point after the memory is implanted. However, the memory remains intact, as evidenced by higher recurrent weight (wmemory) compared to the baseline excitatory connectivity (wee).

Full size image

We observe an immediate increase in the overall activity of both excitatory and inhibitory neurons (Fig. 7b) after ensemble implantation, which is however reduced as the homeostatic training continues. The change in weights (Fig. 7c, d) illustrates how inhibitory plasticity (especially wei) compensates for increased activity, bringing the firing rates back to the target point. Because the values of weights within and outside of the ensemble remain differentiated, even after homeostatic plasticity converges, the neural ensemble remains intact and retains its selectivity for the specific feature it represents. We conclude that the cross-homeostatic learning rule brings the activity back to the target while preserving the implanted memory.

Multiple stable ensembles can coexist with emergent sWTA dynamics

The previous results show that a single memory can be implanted and persist in the presence of cross-homeostasis. We extended the model as a proof-of-concept to craft multiple memory clusters with inter-cluster connectivity, and demonstrate to what extent they could be individually recalled. Figure 8a–c illustrates a network with three stable implanted memories. As described in the previous section, after the memory implantation, the firing rates of the network are brought to its original converged state by cross-homeostasis (see Fig. S4). These individual memories can be robustly recalled even when inputs are presented to other memory clusters. Remarkably, these implanted memories exhibit emergent soft-winner-take-all (sWTA) dynamics, where the neural population receiving the strongest stimulus “wins” and exhibits an increased firing rate during recall. This cross-cluster competition arises from lateral inhibition between clusters, as demonstrated in rate-based network simulations (see Fig. S7). Note also how the purple cluster, which presents a higher firing rate upon baseline, is effectively suppressed when the green and orange clusters are maximally activated, further supporting that assemblies are competing via lateral inhibition. Notably, this occurs despite no additional or specific inhibitory motifs were hand-crafted into the network.

Fig. 8: Winner-take-all dynamics with three sub-clusters implanted in the network.
figure 8

a Random recurrent E/I network with three neural ensembles (size = 50, green, orange and purple neurons). The stimulation protocol (top left) shows how different sub-clusters receive inputs over the course of emulation. b Firing rates of all clusters when each cluster is stimulated with either high (300 Hz) or low frequency (60 Hz) inputs. The cluster receiving the high-frequency input dominates the competition. We demonstrate that no special tuning is necessary to achieve this winner-takes-all (WTA) phenomenon. c Raster plot illustrating spike activity for all neurons in different clusters. d Activity in an extended version of the memory network with 10 sub-clusters, each with 20 neurons. Here every cluster is stimulated independently, showing that up to 10 memories can be individually recalled.

Full size image

Cross-homeostasis therefore implicitly implements sWTA dynamics in recurrent networks.

We finally show that the chip supports the implementation of up to 10 coexisting memory clusters that can be robustly recalled independently (Fig. 8d). These networks could be used to implement decision-making processes on chip, along with other interesting computations such as signal-restoration or state-dependent processing. We conclude that cross-homeostatic plasticity not only allows for maintenance of information, but imposes, “for free”, computationally relevant dynamics onto the network.

Discussion

Hardware implementations of spiking neural networks are being proposed as a promising “neuromorphic” technology that can complement standard computation for sensory-processing applications that require limited resource usage (such as power, memory, and size), low latency, and that cannot resort to sending the recorded data to off-line computing centers (i.e., “the cloud”)32,46,47. Among the proposed solutions, those that exploit the analog properties of their computing substrate have the highest potential to minimize power consumption and to carry out “always-on” processing9,48. However, the challenge of using this technology is to understand how to carry out reliable processing in the presence of the high variability, heterogeneity and sensitivity to noise of the analog substrate. This challenge becomes even more daunting when taking into account the variability of memristive devices, which are expected to allow for the storage and processing of information directly on chip49.

In this paper, we show how resorting to strategies used by animal brains to solve the same challenge can lead to robust solutions: we demonstrated that cross-homeostatic plasticity can autonomously bring analog neuromorphic hardware to a fully self-sustained inhibition-stabilized regime, the regime that is thought to be the default state of the awake neocortex19,20,21,22. These are the first results to show how biologically inspired learning rules can be used to self-tune neuromorphic hardware into computationally powerful states while simultaneously solving the problem of heterogeneity and variability in the hardware.

Our results also validate the robustness of the cross-homeostatic plasticity hypothesis28 in a physical substrate that presents similar challenges to those of faced by biological networks. We also highlight the crucial contribution of inhibitory plasticity, specifically, that homeostatic plasticity of inhibitory connections is necessary to maintain stability in both biological and silicon networks. We further show that although not necessary, excitatory homeostatic plasticity is desirable to guarantee convergence across a wide range of initial conditions. Additionally, by comparing our results with those given by using a different learning rule41, we demonstrate that having a set-point for the inhibitory population is also beneficial, in order to keep firing rates within a biological regime. These low firing rates are also technologically relevant, as neuromorphic applications benefit from the sparsity and ultra-low power consumption of networks in this regime.

Notably, we constructed an on-chip stable attractor neural network that effectively maintains a long-term memory represented by a neural ensemble, and demonstrates that multiple networks, each exhibiting fixed-point attractor dynamics, can coexist within the hardware18,37. We show that when embedded into a recurrent network, this stable multi-network implementation presents emergent sWTA dynamics, even though no specific inhibitory connectivity motives have been introduced in the network, unlike in previous work12,13,14,15. Networks with sWTA dynamics can perform numerous computations, including pattern recognition, signal-restoration, state-dependent processing and working memory. Indeed, the type of architecture that emerges after the learning process, with common inhibitory feedback suppressing the different assemblies, is a neuromorphic implementation of the architecture described by Wang and colleagues29,30, which reproduces perceptual decision making in primates. Cross-homeostatic plasticity could thus be used to configure networks with self-generated dynamics that are thought to underlie a number of computations including decision-making, motor control, timing, and sensory integration50,51,52.

By taking inspiration from the self-calibration features of biological networks, we achieve a remarkable level of resilience to hardware variability, enabling recurrent networks to maintain stability and self-sustained activity across different analog neuromorphic chips. Cross-homeostatic plasticity allows us to instantiate neural networks on different chips without the need for chip-specific tuning, thereby addressing the problem of inherent mismatch in analog devices. Such bio-plausible algorithms provide a promising avenue for the development of robust and scalable hardware implementations of recurrent neural networks, while mitigating the challenges associated with the presence of device mismatch in analog circuits.

In short, these results not only provide insights into the underlying mechanisms configuring biological circuits, but also hold great promise for the development of neuromorphic applications that unlock the power of recurrent computations. This research presents a substantial step forward in our understanding of neural dynamics and paves new possibilities for practical deployment of mixed-signal analog/digital neuromorphic processors that compute, like biological neural circuits, with extremely low-power and low-latency using attractor dynamics.

Methods

Neuromorphic hardware: the spiking neural network chip

In this study, we use a recently-developed mixed-signal spiking neural network chip, called the Dynamic Neuromorphic Asynchronous Processor (DYNAP-SE2)35. This chip comprises 1024 adaptive-exponential integrate-and-fire (AdEx I&F) neurons8,53, distributed across four cores. Adaptation, however, is turned off in all experiments discussed in this article. The neuron parameters consist of its spiking threshold, refractory period, membrane time constant, and gain. On hardware, the inputs to each neuron are limited to 64 incoming connections, implemented using differential pair integrator (DPI) synapse circuits54. Each synaptic input can be configured to express one of four possible temporal dynamics (via four different DPI circuits): AMPA, NMDA, GABA-A, and GABA-B. Besides expressing different time constants, the excitatory synapse circuits (AMPA and NMDA) differ in that the NMDA circuit also incorporates a voltage gating mechanism. Similarly, the inhibitory synapses (GABA-A, and GABA-B) differ in their subtractive (GABA-B) versus shunting (GABA-A) effect.

The bias parameters that determine the weights, neuronal and synaptic properties are set by an on-chip digital to analog (DAC) bias-generator circuit55 and are shared globally within each core. For synaptic weights, each core has a shared ‘maximum’ value that can be modulated using a 4-bit masking mechanism35. These parameters are expressed as currents that drive the neuromorphic circuits and are represented internally through a “coarse” and a “fine” value, according to the following equation:

$$I={I}_{C}({C}_{w})\frac{{F}_{w}}{255},$$
(1)

where Fw represents the fine value and Cw the coarse value. The variable IC represents a current estimated from the bias-generator circuit simulations, which depends on Cw as specified in Table 2. We interface to the chip using the “Samna” software35(see section 7), version 0.14.0. All parameters not specified in Tables 1–4 are initialized to their software-defined default value, by the Samna software.

Table 2 Nominal estimated coarse current values from the on-chip bias generator circuit for synaptic weights
Full size table

Before training, the network is initialized with Cw randomly taking a value of 3, 4, or 5, and Fw uniformly distributed between 20 and 200. The corresponding currents will therefore range between 2.7 nA and 1757 nA. We avoided using lower values of Cw because the neuron remains inactive when stimulated with such small current injections. Additionally, initializing all weights with very high values causes the chip to produce too many spikes for the digital interface to the data-logging computer to handle.

Due to device mismatch and variability in the analog circuits, even when many circuits share the same nominal biases, the effective values will vary. On the DYNAP-SE2 and other mixed-signal neuromorphic processors implemented using similar technology nodes and circuit design styles, the coefficient of variation of these parameters is typically around 0.210. The learning rules proposed in this work make these networks robust to variability with these figures, and lead to a stable activity regime.

Network emulation

We create an on-chip E/I network composed of 200 Pyr (excitatory) and 50 PV (inhibitory) neurons. Each neuron type is implemented by tuning the refractory period, time constants, spiking threshold, and neuron gain parameters to match biologically measured values (Fig. 1c,34). However, the neurons’ adaptive behavior is disabled. The two populations are sparsely connected with a 10% connection probability for each pair of neurons (both within population and between populations). Synaptic weights take four sets of values shared globally among all Pyr-to-Pyr (wee), Pyr-to-PV (wie), PV-to-PV (wii), and PV-to-Pyr (wei) connections respectively. All excitatory weights represent synapses modeled as AMPA receptors, and inhibitory weights as GABA-A (somatic). Here, wii and wei are somatic inhibitory connections. Even though the weight parameters are shared, the synaptic efficacy of each synapse is subject to variability due to device mismatch in the analog circuits10.

During training, synaptic weights are adjusted such that the average activity for both Pyr and PV population converge to their respective target firing rates (or set-points), and can thus maintain self-sustained activity in the absence of any external input or bias current. To kickstart activity in the network, we provide a brief 40 ms external input of four spikes at 10 ms intervals to 80% of the Pyr cells, with random delays for each postsynaptic target neuron to introduce temporal sparsity to the initial response of the population. The network is emulated in real-time on the chip (i.e., the dynamics of the analog circuits evolve through physical time reproducing the dynamics of the biological neural circuits). Each iteration runs for 1 s and the spiking activity of the whole network is streamed to a computer, for data logging and analysis purposes.

In the analysis, the network response is measured by calculating the average firing rate of both neural populations, which is then used to calculate the error (i.e., the difference between set-point and actual activity) that drives the weight update (see next section). As we are interested in the network’s self-sustained behavior, we discard the response induced by the transient external input while calculating the firing rates (i.e., we ignore the first 60 ms of activity, which comprises the first 40 ms of external stimulation and an additional stabilization window of 20 ms). During the initial stages of the training procedure, before E/I balance is reached, the network could generate non-sustained bursts of activity. Therefore, we calculate the firing rate by considering only the time window when the neural populations are active, i.e., the in-burst firing rate, as opposed to the average over the whole trial. We empirically find that this choice leads to the desired sustained activity.

Learning rule

To bring the recurrent dynamics to a fully self-sustained inhibition-stabilized regime we employ the recently proposed cross-homeostatic plasticity rule28, which tunes all four synaptic weight classes in parallel.

In classic forms of homeostatic plasticity, both excitatory and inhibitory populations self-regulate calcium levels based on their own activity24,38. In contrast to these classic forms, where a neuron tunes its weights to maintain its own average output of activity (a firing rate set-point), the cross-homeostatic weight update rule aims at bringing the neuron’s presynaptic partners of opposite polarity to an average population firing rate set-point, according to the following equations:

$$\begin{array}{rcl}\Delta {w}_{ee}=+ \alpha \bar{E}(t)({I}_{target}-\bar{I}(t)),\\ \Delta {w}_{ei}=-\alpha \bar{I}(t)({I}_{target}-\bar{I}(t)),\end{array}\qquad \begin{array}{rcl}\Delta {w}_{ie}=-\alpha \bar{E}(t)({E}_{target}-\bar{E}(t)),\\ \Delta {w}_{ii}=+ \alpha \bar{I}(t)({E}_{target}-\bar{E}(t)),\end{array}$$
(2)

where α is the learning rate (α = 0.05), \(\bar{E}(t)\) and \(\bar{I}(t)\) are the measured population firing rates averaged over 1 s during a trial t and Etarget  = 20 Hz, Itarget = 40 Hz are the desired firing rate set-points for the Pyr and PV populations respectively. This type of plasticity can be interpreted biologically as setting a target on the input current that a given neuron receives. For example, an excitatory neuron could have indirect access to the average firing rate of their presynaptic inhibitory neurons based on a running average of the total GABA it receives.

While biologically plausible target activities are typically lower (e.g., 5 Hz for the E population and 14 Hz for the I population as proposed in ref. 28), in our experiments we had to use higher set-point rates to attain reliable behavior, because of the relatively small network size and the low probability of connections used. In Table 1 we quantify the effects of network size and connectivity with additional experiments.

As the weights are shared globally within each population, the learning rules are implemented at the whole population level. Therefore the network maintains a given firing rate at the population level, rather than at the individual neuron level (see28 for a local implementation of the rules). However, the heterogeneity in the analog circuits and their inherent noise produce diverse behaviors among neurons, for example leading some of the neurons to fire intermittently at slightly increased rates (while maintaining the desired set-point firing rate at the full population level). In the following section, we explain the training procedure on the hardware and how the changes in weight Δw are translated to the fine Fw and course Cw synaptic bias parameters on chip.

We further extended our study and implemented the homeostatic rules proposed by Mackwood et al.41. The values for wee and wii remained unchanged during the learning process. We simplified the equations for the other two weights to ensure compatibility with the chip.

$$\Delta {w}_{ei}=+ \alpha \bar{I}(t)(\bar{E}(t)-{E}_{target}),\qquad \Delta {w}_{ie}=+ \alpha \bar{E}(t)(\bar{E}(t)-{E}_{target}),$$
(3)

Chip-in-the-loop training

Although the DYNAP-SE2 chip can be tuned to exhibit biologically plausible dynamics, it does not incorporate on-chip synaptic plasticity circuits that are capable of learning. To overcome this limitation we used a “chip-in-the-loop” learning paradigm: the activity produced by the chip is transmitted to a computer, which analyzes the data in the software and calculates the parameter updates, which are then sent back to the chip.

In particular, the network runs for 1 s on the chip. Each iteration is repeated five times to reduce the influence of noise and obtain more reliable results. The output spikes are sent back to the computer, which averages the results, calculates the appropriate weight update, applies stochastic rounding (see below), and sends the updated weights to the chip for the next iteration (i.e., after five repetitions). After each iteration, we drain the accumulated residual current from both the neuron and synapse circuits. We conclude the procedure after 400 iterations, as we found it to be sufficient for the network to converge to the target firing rates regardless of the initial conditions. Most simulations converge to target firing rate before iteration 200, which shows the long-term stability of the cross-homeostasis rules in a converged network.

For all experiments, we applied the same set of parameters to neurons and synapses at the beginning of the training, with the exception of the random initialization of weights. The training produced stable and reliable activity around the programmed set-points 100% of the time, without having to re-tune any of the neuron or synapse parameters (except the synaptic weights), across multiple days, and for multiple chips.

Stochastic rounding

As the values of the synaptic weight parameters are set by the bias-generator DAC, the weight updates can only take discrete values ΔFw  = 0, ±1, ±2, . . . . For very large learning rates, this could lead to unstable learning, and for very low ones to no changes at all. To overcome the constraints of limited-resolution weight updates, a common strategy used is to use stochastic rounding (SR)56,57. The SR technique consists of interpreting the Δw calculated by the learning rule as a probability to increase or decrease the weight, as follows:

$${{{\rm{SR}}}}(x)=\left\{\begin{array}{ll}\lceil x\rceil \quad &\,{\mbox{with probability}}\,x-\lfloor x\rfloor \\ \lfloor x\rfloor \quad &\,{\mbox{otherwise.}}\hfill\end{array}\right.$$
(4)

where ⌈ ⋅ ⌉ indicates the ceiling operation and ⌊ ⋅ ⌋ the floor operation.

Values for the desired weight updates Δw are given by the learning rules (2) or (3). We also define upper and lower bounds for Fw, respectively F− =  20 and F+ =  250. We then obtain the new coarse and fine values \({C}_{w}^{{\prime} },{F}_{w}^{{\prime} }\) of the weight as follows:

$$\left\{\begin{array}{ll}{C}_{w}^{{\prime} }={C}_{w},\,{F}_{w}^{{\prime} }={F}_{w}+{{{\rm{SR}}}}(\Delta w)\quad &{{{\rm{if}}}}\,{F}_{-}\le {F}_{w}+{{{\rm{SR}}}}(\Delta w)\le {F}_{+}\\ {C}_{w}^{{\prime} }={C}_{w}-1,\,{F}_{w}^{{\prime} }={F}_{+}\quad &{{{\rm{if}}}}\,{F}_{w}+{{{\rm{SR}}}}(\Delta w) < {F}_{-}\\ {C}_{w}^{{\prime} }={C}_{w}+1,\,{F}_{w}^{{\prime} }={F}_{-}\quad &{{{\rm{if}}}}\,{F}_{w}+{{{\rm{SR}}}}(\Delta w) > {F}_{+}.\end{array}\right.$$
(5)

In other words, the fine value is updated with the stochastically-rounded version of Δw; when it exceeds the bound, the fine value is reset to the bound, and the coarse value is changed instead.

Note that this SR strategy is compatible with neuromorphic hardware implementations, as demonstrated in ref. 58. Our setup using a chip-in-the-loop enables the evaluation of different learning mechanisms and the testing of the robustness of different design choices. The design of future on-chip learning circuit can therefore be informed by our results, following a hardware-software co-design approach.