Chaotic information metasurface for direct physical-layer secure communication

Abstract

Wireless information security has garnered significant attention with the ever-increasingly widespread adoption of broadcast wireless communication systems. The utilization of chaotic systems for secure communication methods has become a prominent area of research, given their inherent advantages of high randomness and sensitivity to initial conditions. However, existing chaos-based approaches usually require legitimate receivers to have access to the chaotic system’s parameters as decryption keys, often involving complex operations at the digital level. In this study, we present a novel physical-layer secure communication scheme that relies on an information metasurface whose local reflection properties are dynamically modulated by chaotic patterns. Our approach introduces a “one-time” mixed-pattern generation method that concurrently ensures communication security and transmission efficiency. More importantly, our proposed scheme removes the stringent requirement for decryption operations, enabling the legitimate receiver to directly access the original data while illegitimate receivers receive chaotically encrypted signals. This approach demonstrates significant merits, encompassing high security, a streamlined architecture, and intrinsic backward compatibility. Our innovative strategy provides a renewed perspective for advancing next-generation secure wireless communication systems.

Introduction

In today’s rapidly evolving communication landscape, safeguarding information security has become increasingly crucial, especially with the pervasive adoption of broadcast wireless communication systems¹. For next-generation (6 G) wireless networks, a notable trend is the advancement of smart radio environments that dynamically respond to variable conditions, which can optimize both network performance and user experience². The core of this paradigm is the integration of reconfigurable intelligent surfaces³. These programmable metamaterial platforms⁴, also known as information metasurfaces⁵, consist of two-dimensional arrays of sub-wavelength elements that reflect the electromagnetic signals based on digital coding patterns, such as in-phase or out-of-phase in the binary case. This dynamic capability enables real-time adjustments to signal propagation, resulting in the improvement of signal strength, reduction of interference, and enhancement of overall energy efficiency. However, this advancement also introduces new challenges in physical-layer security, stemming from potential malicious uses of these technologies^6,7,8,9.

Remarkably, as demonstrated hereafter, the integration of information metasurface can also provide an intriguing solution for secure communications, particularly when employed in conjunction with chaotic systems. Chaos, a ubiquitous phenomenon in nature, manifests itself through exponential sensitivity in the evolution of a nonlinear system to initial conditions. This results in long-term algorithmic unpredictability and behavior akin to randomness¹⁰. Owing to these distinctive properties, chaotic systems have become a central focus in research on information encryption and secure communications¹¹. The surge in interest in this area dates back to the 1990s, marked by the seminal discovery of chaos synchronization¹², laying the foundation for various secure communication methods rooted in chaos.

Early communication systems based on chaos relied on coherent detection^13,14,15, wherein chaotic systems generated analog or digital chaotic signals for secure transmission. In these systems, the receiver created a synchronized copy of the chaotic signal to recover the transmitted data. One notable technique was chaos shift keying¹⁴, which utilized two independent chaotic systems at the transmitter. It encoded a binary digital sequence into the transmitted signal using a shift switch. At the receiver, the received signal drove two self-synchronous subsystems, determining the transmission symbol by detecting coherence between the received signal and their output signal. Another approach, known as additive chaotic masking¹⁶, involved introducing an additive chaotic signal into an analog data signal to create the transmitted signal. The receiver reconstructed the chaotic signal through chaos synchronization, extracting analog information by subtracting the chaotic signal from the received signal. While effective in securing against eavesdroppers who lack knowledge of the chaotic system’s parameters, this method had potential security risks due to power variations in the transmitted signal. In a different method called chaotic modulation¹⁷, the analog signal for transmission was directly injected into a chaotic system, modifying its phase space or parameters to generate a chaotic signal containing analog information. Although offering superior performance compared to chaos shift keying and additive chaotic masking, this approach heavily relied on the precise design of the receiver controller.

To overcome the aforementioned limitations, considerable research attention has been directed toward chaos-based communication systems employing non-coherent detection. A key advancement in this domain is the introduction of differential chaos shift keying¹⁸. In this scheme, each symbol period is divided into two slots, encompassing a reference chaotic signal and a data signal. This latter is derived by multiplying a binary sequence {1, −1} with a delayed reference chaotic signal. A shift switch alternates between the reference signal and the data signal to generate the transmission signal. At the receiver, correlation operations are conducted on the received signal and its delayed versions, followed by threshold discrimination to derive the decoded result. This approach has demonstrated robustness against both linear and nonlinear distortions in the channel, due to the simultaneous transmission of the reference chaotic signal and the data signal, overcoming the sensitivity observed in chaos shift keying. Given its outstanding performance, the exploration of various enhanced versions of differential chaos shift keying continues to be a focal point in the realm of chaos-based communication research.

The majority of secure communication methods based on chaos employ encryption at the signal level using chaotic circuits. However, in recent years, there has been a novel exploration of chaos-based secure communication techniques within the radio-frequency (RF) domain, involving the encryption of transmitted data using antenna arrays. In particular, a recent study has proposed chaotic phase modulation within a time-modulated antenna array system¹⁹. This innovative approach employs chaotic sequences in the RF domain to encrypt plaintext sequences, effectively addressing the security vulnerabilities associated with time-modulated antenna array systems. Notably, this method eliminates the need for baseband modulation modules, leading to a simplified hardware architecture.

Generally, the existing chaos-based secure communication methods share a common requirement for the receiver to possess the chaotic system’s parameters for decryption. These parameters are treated as keys and necessitate the secure transmission channels. As a result, these methods fall within the realm of classical cryptography. So far, the field has seen limited exploration of physical-layer secure communication methods that eliminate the need for secret keys. To address this gap, in this study, we introduce a novel scheme based on chaotic information metasurface that operates securely without relying on secret keys. This innovative approach introduces a unique layer of security by actively generating distinct chaotic noise to eavesdroppers based on their orientations, thereby enhancing the overall security of the communication. Importantly, the legitimate receiver can directly receive the intended high-quality data without undergoing any decryption operations. Additionally, the proposed scheme is highly compatible and can be deployed as an independent secure transmission module alongside the transmitter, without disrupting the existing settings of the original transmitter and receiver.

Results

System model

As illustrated in Fig. 1, we examine a scenario where a legitimate transmitter (referred to as Alice) aims to send information wirelessly to a legitimate receiver (referred to as Bob). Meanwhile, there are one or more potential eavesdroppers (labeled as Eve) attempting to eavesdrop on the communication between Alice and Bob. Traditional physical-layer secure transmission approaches, rooted in spatial domain methods, employ multi-antenna transmitters to realize secure beamforming. This strategy aims to maximize the signal energy received by the legitimate receiver, while minimizing the energy received by eavesdroppers in other directions. The goal is to amplify the disparity between the legitimate channel (Alice to Bob) and the wiretap channel (Alice to Eve) by enhancing the signal-to-noise ratio (SNR) at the legitimate receiver and suppressing it at the eavesdropping receivers. However, vulnerabilities arise when eavesdroppers use highly sensitive receivers or the intrinsic noise power of the channel is low, potentially compromising transmission security.

Fig. 1: Conceptual illustration of the proposed physical-layer secure communication scheme relying on the chaotic information metasurface.

With the chaotic information metasurface, the legitimate transmitter Alice transmits unencrypted information to the legitimate receiver Bob, and the eavesdroppers Eve1, Eve2, Eve3… receive chaotically encrypted information.

Our proposed physical-layer secure transmission scheme leverages the information metasurface to establish a backscatter wireless communication channel. This metasurface injects chaotic information into spatio-temporal domain while modulating the spatial distribution of electromagnetic energy. In this approach, the transmitter sends unencrypted signals directly to the metasurface, which employs mixed-chaotic coding patterns optimized to direct the energy efficiently toward the legitimate receiver. To enhance the security, we introduce a “one-time pattern” switching technique independently of the baseband symbol period, leveraging chaotic maps to generate unique coding patterns for each transmission symbol as needed. These patterns render the signal at eavesdroppers, located in unintended directions, indistinguishable from random noise. Importantly, the “one-time pattern” switching can ensure strong resistance to known-plaintext attacks.

For given transmitter (Alice) and receiver (Bob) locations, the information metasurface is divided into two sections: metaA (comprising N_metaA meta-atoms) and metaB (comprising N_metaB meta-atoms). The metaA section is responsible for implementing a static focusing coding pattern C_metaA, which modulates the spatial distribution of electromagnetic energy, ensuring a high SNR for the legitimate receiver, Bob. In contrast, metaB deploys dynamic chaotic coding patterns C_metaB(t) to inject chaotic information and provides spatio-temporal encryption at the physical layer. Under this framework, the metasurface-mediated responses for the Alice-metasurface-Bob and Alice-metasurface-Eve links can be expressed as H_A→B(t) and H_A→E(t) respectively (see the notation in the “Methods” section). Notably, when N_metaA = 0, the metasurface coding pattern is entirely driven by chaos, exhibiting high randomness. Conversely, when N_metaB = 0, the coding pattern becomes purely focused, maximizing Bob’s signal energy and SNR. Importantly, since the static focusing coding pattern (metaA) is applied and the chaotic component (metaB) has minimal impact on the legitimate receiver, Bob receives the signal in its unencrypted form. This eliminates the need for a physical-layer key exchange between Alice and Bob, simplifying the secure transmission process and reducing the risk of key interception. Additionally, Alice and Bob can continue to use their existing transmitter and receiver equipment without any modifications to their modulation and demodulation algorithms, highlighting the seamless compatibility of this scheme with current hardware setups.

The secure transmission of information from Alice to Bob via the chaotic information metasurface occurs in two key stages. Firstly, Alice, the transmitter, performs conventional baseband modulation using standard RF circuits. Next, the information metasurface applies chaotic coding pattern switching, following a “one-time pattern” approach that induces the spatio-temporal modulation. When Alice employs baseband modulation techniques, such as phase shift keying (PSK), the amplitude and phase of the signals received in various directions are influenced by both the transmitted baseband symbol and the metasurface’s coding patterns. These optimized coding patterns ensure minimal noise at Bob’s location, while generating highly random amplitude-phase responses in all other unintended directions, effectively encrypting the signal and securing the transmission.

Generation of chaotic sequence

The coding patterns are switched at discrete time intervals. Specifically, for a given set of discrete time instants t_n and a series of discrete chaotic values x_i, the metasurface coding patterns are generated using the chaotic mapping f_chaos and the coding pattern mapping function g:

$${x}_{i+1}={f}_{{chaos}}\left({x}_{i}\right)$$

(1)

$${\widetilde{\rm{x}}}_{n}=\left({x}_{768n},{x}_{768n-1},{x}_{768n-2},\cdots,{x}_{768n-767}\right)$$

(2)

$${{\mathbf{C}}}_{{\mathbf{metaB}}}\left({t}_{n}\right)=g\left(\widetilde{{{\mathbf{x}}}_{{\mathbf{n}}}}\right)$$

(3)

where C_metaB(t₁), C_metaB(t₂), …, C_metaB(t_n) represent the chaotic coding pattern sequences. In this study, we utilize the commonly employed one-dimensional logistic map¹⁰, expressed as: x_i+1 = μx_i(1 − x_i), where x_i ∈ (0, 1), and μ $\in$ (0, 4] is a system parameter. To ensure that the sequence {x_i} exhibits stable chaotic behavior, the parameter μ should lie within the range (3.5699456, 4], excluding certain isolated intervals known as ‘islands of stability’²⁰. In our chaotic metasurface system, both the parameter μ and the initial value x₁ of each “one-time pattern” are randomly selected within the valid ranges. After that, these chaotic sequences are quantized to produce one-dimensional binary sequences, which are then combined to form two-dimensional, 1-bit metasurface coding patterns. To achieve this, we apply the least significant bit (LSB) method to map the chaotic sequences into two-dimensional metasurface coding patterns. Each group ${\widetilde{{\bf{x}}}}_{{\bf{n}}}$ consists of 768 elements, corresponding to a metasurface coding pattern C_metaB(t_n). Each chaotic value x_i is represented in floating-point notation as [x_i] = 0.a₁a₂…a_k, where a_k denotes the least significant bit. By evaluating the parity of a_k, the chaotic sequence is transformed into a binary sequence, which is then used to generate a two-dimensional coding pattern for the 1-bit quantized metasurface. Further details of the chaotic sequence are provided in Supplementary Note 1.

Chaos-based techniques offer significant advantages over the conventional pseudo-random number generation methods, particularly in terms of unpredictability and sensitivity to initial conditions. For instance, the Mersenne Twister algorithm^21,22,23, commonly used in software applications to generate pseudo-random numbers, can quickly produce extremely long sequences. However, this algorithm poses security risks in scenarios like encrypted communication, as eavesdroppers can potentially predict future sequences by back-analyzing segments of a given length²¹. If such pseudo-random number generation methods are used in the proposed system, an eavesdropper could potentially reconstruct portions of the metasurface coding via channel estimation and subsequently predict future coding states, thereby compromising system security. To mitigate these security vulnerabilities, the chaotic mapping provides a promising approach for generating high-quality pseudo-random numbers in secure communication. Its key characteristics—sensitivity to initial values, unpredictability, and nonlinearity—enhance its ability to safeguard information.

Mixed pattern generation algorithm

As previously discussed, the metasurface coding patterns generated through chaotic mapping and quantization exhibit a high degree of randomness. However, when N_metaA = 0, indicating that the metasurface coding pattern is entirely chaotic, the performance of the backscatter wireless communication link deteriorates, resulting in inefficient transmission towards the legitimate receiver, Bob. Conversely, when N_metaB = 0, the metasurface coding pattern becomes purely focused, ensuring high transmission quality at Bob’s location but lacking the necessary randomness to prevent eavesdropping. Therefore, finding an optimal balance between transmission effectiveness and security through the appropriate allocation and distribution of chaotic coding patterns is critical. To address this challenge, we propose a weight-based mixed coding pattern generation algorithm. Firstly, for given transmitter and legitimate receiver positions, the static focusing coding pattern C_metaA is generated using the modified Gerchberg–Saxton (GS) algorithm^24,25. Next, we compute the normalized weight for each meta-atom to quantify its contribution to the electromagnetic response at Bob’s location. Specifically, for a generic n_th meta-atom, the normalized weight W_n is defined as follows:

$${W}_{n}=\frac{{Re}\left({H}_{A\to M\to B}\right){Re}\left({H}_{A\to n\to B}\right)+{Im}\left({H}_{A\to M\to B}\right){Im}\left({H}_{A\to n\to B}\right)}{{\max }_{i=1,2,\cdots,N}\left(\left[{Re}\left({H}_{A\to M\to B}\right){Re}\left({H}_{A\to i\to B}\right)+{Im}\left({H}_{A\to M\to B}\right){Im}\left({H}_{A\to i\to B}\right)\right]\right)}$$

(4)

where $N$ denotes the total number of meta-atoms, and

$${H}_{A \to M \to B}=\mathop{\sum }\limits_{n \in {metaA}\&{metaB}}\underbrace{{h}_{A \to n \to B}exp (j { \varnothing }_{n}^{A})}_{{H}_{A \to n \to B}}$$

(5)

Here, H_A→M→B and H_A→n→B represent the metasurface-mediated responses of the entire metasurface array and the n_th meta-atom, respectively, when only the static focusing coding pattern ${{C}}_{{metaA}}$ is applied. In our mixed pattern generation algorithm, we first calculate the normalized weight for each meta-atom. Next, for the n_th meta-atom, the coding pertaining to the focusing pattern is retained if the normalized weight W_n exceeds a predetermined threshold τ, otherwise it is replaced with a chaotic one. This process results in the creation of mixed coding patterns, as illustrated in Fig. 2a, b. More details on the mixed pattern generation algorithm are provided in Supplementary Note 2.

Fig. 2: Generation of mixed coding patterns.

a Generation of a mixed pattern by combining a chaotic pattern with a focusing pattern. b Mixed coding patterns at different time steps. c Cylindrical coordinate system utilized. d Normalized amplitude distributions of scattering fields for various values of the mixing factors. $\theta$ and $\varphi$ denote the polar angle and azimuthal angle of points on the observation hemisphere, respectively. e Numerical results of received signals’ constellation diagrams at different azimuth angles, for a mixing factor α = 0.469. The operational frequency is 2.47 GHz, and the normalized standard deviation of noise amplitude σ is set to 2 × 10⁻³.

Next, the values of ${N}_{{metaA}}$ and ${N}_{{metaB}}$ must be balanced. To achieve this, we introduce the mixing factor$\,\alpha \,={N}_{{metaA}}/({N}_{{metaA}}\,+\,{N}_{{metaB}})$. To initially assess the impact of the mixing factor $\alpha$ on the properties of the scattering field properties, we consider a cylindrical coordinate system $(r,\varphi,\,z)$ centered at the origin of the metasurface, as schematized in Fig. 2c. The source antenna is positioned at (1.15 m, 0°, 0 m), while the target focusing position is at (3 m, 0°, −0.34 m). Using Eqs. 11 and 12 from the “Methods” section, we calculate the normalized amplitude distributions of the scattering field over a hemisphere which contains the target focusing position and is centered at the origin$.$ These results, corresponding to different mixing factors as illustrated in Fig. 2d, show that the mixed coding patterns, generated with appropriate mixing factors, can effectively focus electromagnetic energy on the target region, even while a portion of the meta-atoms is used to inject chaotic information. Throughout the paper, we define the normalized standard deviation of noise amplitude relative to the transmitted signal as σ. Figure 2e presents the numerical results in terms of signal constellation diagrams at different azimuth angles, where the mixing factor α is set to 0.469, σ is set to 2 × 10⁻³, and the source antenna sends an 8PSK-modulated signal with a carrier frequency of 2.47 GHz. The results demonstrate that, with an appropriately chosen mixing factor, the chaotic information metasurface can encrypt signals in non-target areas while maintaining signal quality in the target region, as the meta-atoms in the dynamic section are switched according to chaotic mapping. Additional simulation results are presented in Supplementary Notes 3 and 4.

In what follows, we perform a more detailed analysis at the communication system level, considering various parameters such as mixing factors, noise amplitude, and antenna positions. This evaluation enables us to identify the optimal mixing factor under different conditions.

Simulation results

Following the principles outlined, we conduct numerical simulations based on MATLAB, as shown in Fig. 3. Specifically, we assessed the performance of the proposed chaotic information metasurface, which operates in 2.47 GHz, in a single-input-single-output (SISO) channel. In the simulations, the transmitting antenna continuously sends an 8PSK-modulated signal consisting of ${10}^{4}$ samples to the legitimate receiver, while the $32\times 24$ chaotic information metasurface is loaded with chaotic coding patterns to modulate the channel characteristics. Considering that the antennas we used in subsequent experiments exhibit approximately uniform radiation intensity across the 0–180 degrees range, the radiation patterns of the transmitter and receiver is set to constant values. In Fig. 3a, b, the transmitter is located at (1.15 m, 0°, 0 m), and the legitimate receiver is positioned at (3 m, 0°, −0.34 m). In Fig. 3c, d, the transmitter is located at (0.75 m, 0°, −0.57 m), and the legitimate receiver is positioned at (3 m, 0°, 0 m). To directly evaluate the effect of the chaotic information metasurface on modulating channel characteristics, we examine the bit error rate (BER) and assume that the receiver can ideally filter out the interference caused by additive channel noise when determining the decision region using the reference signal.

Fig. 3: Simulation results of physical-layer secure transmission based on the chaotic information metasurface.

a BER for receivers in different positions, when the transmitter and legitimate receiver are located at (1.15 m, 0°, 0 m) and (3 m, 0°, −0.34 m), respectively. b Corresponding efficiency loss and security gain as a function of σ, the normalized standard deviation of noise amplitude, when the transmitter is positioned at (1.15 m, 0°, 0 m), and the legitimate receiver is positioned at (3 m, 0°, −0.34 m). c, d As in panels (a) and (b), respectively, but for transmitter and legitimate receiver located at (0.75 m, 0°, −0.57 m) and (3 m, 0°, 0 m), respectively.

To evaluate the impact of the chaotic information metasurface on communication performance at different receiver locations, receiving antennas are positioned at (3 m, φ, −0.34 m) in Fig. 3a and (3 m, φ, 0 m) in Fig. 3c, with the azimuth angle φ sampled from −90° to 90° in 1° increments. Here, the normalized standard deviation of noise amplitude $\sigma$ is set to $2\times {10}^{-3}$. The simulation explores the relationship between the BER and the azimuth angle φ for different thresholds $\tau$ and mixing factors α applied to the chaotic information metasurface. For comparison, we also present simulation results for cases where the metasurface employs only focusing coding pattern in each subplot.

The results demonstrate that the chaotic information metasurface, when configured with an appropriate mixing factor $\alpha$, effectively degrades the communication quality for illegitimate users at other spatial locations while maintaining satisfactory communication quality for legitimate receivers. The choice of $\alpha$ is critical: a larger mixing factor enhances communication quality for the legitimate receiver but reduces the interference effect on the illegitimate receivers, emphasizing the aforementioned trade-off. The threshold $\tau$ and the corresponding mixing factor $\alpha$ are selected through parameter sweeping. Specifically, the chaotic information system samples candidate thresholds at uniform intervals and selects the highest threshold that maintains the BER of legitimate receiver below the maximum tolerable limit. This process yields the final values τ and α. Further details are provided in Supplementary Note 2.

Additionally, the noise amplitude affects the overall channel response, making the choice of mixing factor also dependent on the noise level. To evaluate the impact of different mixing factors under varying normalized standard deviation of noise amplitude σ, we apply the simulation process outlined earlier. To conveniently quantify the effect of the chaotic information metasurface on both the efficiency and security of communication systems, we introduce two key metrics: efficiency loss L_e and security gain G_s, defined as follows:

$${L}_{e}={{BER}}_{{chaos}}\left({\varphi }_{{{legitimate}}\,{{receiver}}}\right)-{BER}_{{{only}}\,{{focus}}}\left({\varphi }_{{{legitimate}}\,{{receiver}}}\right)$$

(6)

$${G}_{s}={\min }_{{\varphi }_{1}}\left({{BER}}_{{chaos}}\left({\varphi }_{1}\right)\right)-{\min }_{{\varphi }_{2}}\left({{BER}}_{{{only}}\,{{focus}}}\left({\varphi }_{2}\right)\right)$$

(7)

$$\left|{\varphi }_{1}-{\varphi }_{{{legitimate}}\,{{user}}}\right| > {10}^{\circ },\quad \left|{\varphi }_{2}-{\varphi }_{{{legitimate}}\,{{user}}}\right| > {10}^{\circ }$$

(8)

Here, ${{BER}}_{{chaos}}(\varphi )$ and ${{BER}}_{{{only}}\; {\rm{focus}}}(\varphi )$ denote the BER at angle $\varphi$ when the metasurface is loaded with the mixing coding pattern and the focusing coding pattern, respectively. ${\varphi }_{{legitimate\; user}}$ refers to the azimuth angle at which the legitimate receiver is located. The efficiency loss L_e measures the impact of the mixing coding pattern on the communication efficiency for the legitimate receiver. The security gain G_s quantifies the ability of the mixing coding pattern to degrade communication for eavesdroppers located beyond a certain angular deviation from the legitimate receiver’s position. The simulated efficiency loss and security gain for different σ are shown in Fig. 3b, d, for the scenarios in Fig. 3a, c, respectively. Overall, as the normalized standard deviation of noise amplitude σ increases, G_s initially rises and then declines, while L_e generally exhibits a gradual upward trend. An exception occurs in the fourth graph of Fig. 3b, d (τ = 0.9) where only a limited number of static focusing coding patterns are generated by the GS algorithm. Consequently, BER for legitimate receivers exceeds 0.3, making reliable communication nearly impossible, even at lower noise levels.

Experimental results

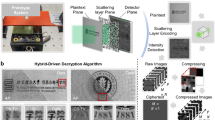
To validate our theoretical and numerical findings, we conduct experimental tests in a real indoor environment using the chaotic information metasurface device and a software-defined radio (Ettus USRP X310) for signal transmission and reception. As shown in Fig. 4a, the chaotic information metasurface is implemented with a $32\times 24$ element 1-bit programmable metasurface operating around 2.47 GHz^25,26. The meta-atom measures 54 × 54 mm² and consists of two substrate layers, as shown in Fig. 4b²⁶. The top layer is made of F4B (with a relative permittivity of 2.55 and a loss tangent of 0.0019), while the bottom layer is FR4 (with a relative permittivity of 4.4 and a loss tangent of 0.03). Each meta-atom is controlled by a SMP1345-079LF positive-intrinsic-negative (PIN) diode, which can be switched between ‘ON’ and ‘OFF’ states. The minimum switching interval for each PIN diode is approximately 2.5 μs. As illustrated in Fig. 4c²⁶, each meta-atom introduces a local phase shift in the reflected electromagnetic wave at the operating frequency, with a phase difference of approximately 180° between the ‘ON’ and ‘OFF’ states, while maintaining nearly identical amplitudes. As a result, this programmable platform can be approximated as an ideal 1-bit phase-shift metasurface. The platform is controlled by a host computer via a field programmable gate array (FPGA), which coordinates command dispatch using a 50 MHz clock signal, and uploads the coding patterns from the host computer using TCP/IP protocol.

Fig. 4: Experimental validation of physical-layer secure transmission based on chaotic information metasurface.

a Prototype of the metasurface and experimental setup. b Geometry of the meta-atom. c Reflection response of the meta-atom. d Measured results of CSI and constellation diagrams comparing the cases where mixed-chaotic and only focusing patterns are employed. The transmitter is positioned at (1.15 m, 0°, 0 m), the legitimate receiver is positioned at (3 m, 0°, −0.34 m), eavesdropper 1 and eavesdropper 2 are located at (3 m, 20°, −0.34 m), (3 m, 40°, −0.34 m), respectively. e As in panels (d), but the transmitter is positioned at (0.75 m, 0°, −0.57 m), the legitimate receiver is positioned at (3 m, 0°, 0 m), eavesdropper 1 and eavesdropper 2 are located at (3 m, 20°, 0 m), (3 m, 40°, 0 m), respectively. f XOR operation of transmit and receive bitstream in different positions for mixed chaotic patterns, for the transmitter positioned at (1.15 m, 0°, 0 m) and the legitimate receiver positioned at (3 m, 0°, −0.34 m). g As in panels (f), but the transmitter is positioned at (0.75 m, 0°, −0.57 m), and the legitimate receiver is positioned at (3 m, 0°, 0 m).

Experimental results under different configurations are presented in Fig. 4d–g to verify the performance of chaotic information metasuface in various aspects. In these experiments, the transmitter sends an 8PSK-modulated signal, which is further modulated by the chaotic information metasurface and received by antennas positioned at different locations. First, as shown in Fig. 4d, e, we compare the channel state information (CSI) and constellation diagrams of the legitimate user and eavesdroppers when the metasurface is loaded with mixed chaotic patterns and only focusing patterns, respectively. Specifically, in Fig. 4d, the transmitter and legitimate user are positioned at (1.15 m, 0°, 0 m) and (3 m, 0°, −0.34 m), respectively. The mixing factor $\alpha$ of the chaotic information metasurface is set to 0.469. In Fig. 4e, the transmitter and legitimate user are positioned at (0.75 m, 0°, −0.57 m) and (3 m, 0°, 0 m), respectively, and the mixing factor $\alpha$ is set to 0.227. Meanwhile, two eavesdroppers are located at azimuthal deviations of 20° and 40° relative to the legitimate user for both Fig. 4d, e. Measurements of CSI show that, when the focus coding is used, the system can significantly increase the signal strength of legitimate user while decreasing that of eavesdropper. However, since the control coding pattern of metasurface is static, the CSI’s phase of eavesdropper remains relatively stable. In this case, the constellation diagram of eavesdropper is still within the noise tolerance of 8PSK demodulation. In contrast, when the mixed chaotic pattern is used, the metasurface works with dynamic chaotic patterns and gives rise to the spatiotemporal-varying CSI, which is responsible for selectively encrypting the eavesdroppers’ channel. As a result, the CSI phase of eavesdropper varies rapidly over time, but the CSI phase of the legitimate user remains relatively stable. Thus, the legitimate user can receive distinguishable 8PSK constellation diagrams, but the eavesdropper fails to do it. The results above demonstrate the differences and advantages of our chaotic information metasurface compared to using only focus coding patterns. To further quantify the performance of chaotic information metasurfaces, the information transmission results for receivers in different positions when using mixed chaotic patterns are provided in Fig. 4f, g. Here, we characterize the result of information transmission with XOR operation, which results in 1 when the receive bit is different from the transmit bit, and 0 otherwise. In Fig. 4f, the transmitter and receivers are positioned at (1.15 m, 0°, 0 m) and (3 m, φ, −0.34 m), respectively, with the azimuth angle φ of the legitimate receiver set to 0°, consistent with the configuration used in the numerical simulations. The mixing factor α of the chaotic information metasurface is set to 0.469. In Fig. 4g, the transmitter and receivers are positioned at (0.75 m, 0°, −0.57 m) and (3 m, φ, 0 m), respectively, and the mixing factor α is set to 0.227. Moreover, the corresponding BER measurements are provided in Table 1.

Table 1 Measured BER performance when employing mixed chaotic patterns and only focusing patterns, where the transmitter sends bitstreams containing $3\times {10}^{3}$ samples and the receivers are located at azimuthal deviations of 0°, ±20° and ±40°, respectively, relative to the legitimate user

Before closing this section, we provide a brief discussion of the system’s peak transmission rate. The peak transmission rate is limited to the minimum switching interval of metasurface to fully utilize the encryption capabilities of the proposed system. Specifically, the symbol period of the system needs to be longer than the minimum switching interval of metasurface to ensure that the metasurface can provide different channel interference for each symbol through pattern switching. The minimum switching interval of metasurface is 2.5 μs, and the system uses 8PSK modulation. Therefore, the peak symbol transmission rate is $\frac{1({\rm{symbol}})}{2.5{\rm{\mu }}{\rm{s}}}=4\times {10}^{5}$ ${\rm{symbol}}\cdot {\rm{Hz}}$, and the corresponding peak of bit transmission rate is $3\frac{{\rm{bit}}}{{\rm{symbol}}}\times 4\times {10}^{5}{\rm{symbol}}\cdot {\rm{Hz}}=1.2\times {10}^{6}$ ${\rm{bit}}\cdot {\rm{Hz}}$.

Discussion

The proposed chaotic information metasurface introduces a novel physical-layer secure communication scheme that operates without secret keys. The transmitter uses a directional antenna aimed at the metasurface, minimizing information leakage through the direct path between the transmitter and receiver. When eavesdroppers, using either conventional antennas or information metasurfaces⁷, are positioned on the same side of the chaotic information metasurface and the transmitter, their ability to intercept signals is significantly disrupted, ensuring security. However, if the eavesdropper is between the transmitter and the chaotic information metasurface, some information leakage may occur. To mitigate this, the transmitter should be placed close to the metasurface, reducing the interceptable area of the direct signal. In cases where this area is sufficiently small, it can be isolated or monitored to prevent eavesdroppers from accessing it.

In summary, our scheme enhances security by ensuring that eavesdroppers receive chaotic noise while the legitimate receiver accesses the original data directly, without decryption. The system is highly compatible with existing setups, and experimental validation with a metasurface operating around 2.47 GHz confirms its effectiveness. This innovative solution offers a promising pathway for advancing secure wireless communication in next-generation networks.

Methods

Signal model of chaotic information metasurface

In a conventional channel model with additive noise, the signals received by the legitimate receiver, Bob, and the eavesdropper, Eve, can be expressed as follows⁷:

$$y\left({{\boldsymbol{r}}}_{{\boldsymbol{B}}}{;t}\right)=\sqrt{{P}_{A}}{x}_{A}\left(t\right){H}_{A\to B}+\sqrt{{P}_{A}}{x}_{A}\left(t\right){h}_{A\to B}+{\epsilon }_{B}$$

(9)

$$y\left({{\boldsymbol{r}}}_{{\boldsymbol{E}}}{;t}\right)=\sqrt{{P}_{A}}{x}_{A}\left(t\right){H}_{A\to E}+\sqrt{{P}_{A}}{x}_{A}\left(t\right){h}_{A\to E}+{\epsilon }_{E}$$

(10)

$${H}_{A\to B}(t)= \sum_{n\in {metaA}}{\underbrace{\frac{\sqrt{{G}_{A}({{\bf{r}}}_{{\bf{n}}}){G}_{n}({{\bf{r}}}_{{\bf{B}}},{{\bf{r}}}_{{\bf{A}}}){G}_{B}({{\bf{r}}}_{{\bf{n}}})\Delta }}{{(4\pi )}^{2}|{{\bf{r}}}_{{\bf{A}}}-{{\bf{r}}}_{{\bf{n}}}||{{\bf{r}}}_{{\bf{B}}}-{{\bf{r}}}_{{\bf{n}}}|}\exp ({jk}(|{{\bf{r}}}_{{\bf{A}}}-{{\bf{r}}}_{{\bf{n}}}|+|{{\bf{r}}}_{{\bf{B}}}-{{\bf{r}}}_{{\bf{n}}}|))}_{{h}_{A\to n\to B}}\exp (j{\varnothing }_{n}^{A}}) \\ +\sum _{n{\in} {metaB}}{\underbrace{\frac{\sqrt{{G}_{A}({{\bf{r}}}_{{\bf{n}}}){G}_{n}({{\bf{r}}}_{{\bf{B}}},{{\bf{r}}}_{{\bf{A}}}){G}_{B}({{\bf{r}}}_{{\bf{n}}})\Delta }}{{(4\pi )}^{2}|{{\bf{r}}}_{{\bf{A}}}-{{\bf{r}}}_{{\bf{n}}}||{{\bf{r}}}_{{\bf{B}}}-{{\bf{r}}}_{{\bf{n}}}|}\exp ({jk}(|{{\bf{r}}}_{{\bf{A}}}-{{\bf{r}}}_{{\bf{n}}}|+|{{\bf{r}}}_{{\bf{B}}}-{{\bf{r}}}_{{\bf{n}}}|))}_{{h}_{A\to n\to B}}\exp }(j{\varnothing }_{n}^{B}(t))$$

(11)

$${{H}}_{{A}\to {E}}\left({t}\right)=\sum _{{n}\in {metaA}}{{h}}_{{A}\to {n}\to {E}}\exp ({j}{\varnothing }_{n}^{A})+\sum _{{n}\in {metaB}}{{h}}_{{A}\to {n}\to {E}}\exp \left(\text{j}{\varnothing }_{n}^{B}\left({t}\right)\right)$$

(12)

$${{{\varnothing }}}_{n}^{A}=f\left({{{C}}}_{{{metaA}}},n\right),{{{\varnothing }}}_{n}^{B}\left(t\right)=f\left({{{C}}}_{{{metaB}}}\left(t\right),n\right)$$

(13)

$${h}_{A\to B}=\frac{\exp \left({jk}\left|{{\boldsymbol{r}}}_{{\boldsymbol{A}}}-{{\boldsymbol{r}}}_{{\boldsymbol{B}}}\right|\right)}{4\pi \left|{{\boldsymbol{r}}}_{{\boldsymbol{A}}}-{{\boldsymbol{r}}}_{{\boldsymbol{B}}}\right|}\sqrt{{G}_{A}\left({{\boldsymbol{r}}}_{{\boldsymbol{B}}}\right){G}_{B}\left({{\boldsymbol{r}}}_{{\boldsymbol{A}}}\right)}$$

(14)

$${h}_{A\to E}=\frac{\exp \left({jk}\left|{{\boldsymbol{r}}}_{{\boldsymbol{A}}}-{{\boldsymbol{r}}}_{{\boldsymbol{E}}}\right|\right)}{4\pi \left|{{\boldsymbol{r}}}_{{\boldsymbol{A}}}-{{\boldsymbol{r}}}_{{\boldsymbol{E}}}\right|}\sqrt{{G}_{A}\left({{\boldsymbol{r}}}_{{\boldsymbol{E}}}\right){G}_{E}\left({{\boldsymbol{r}}}_{{\boldsymbol{A}}}\right)}$$

(15)

where P_A and x_A (t) represent Alice’s radiated power and transmitted data, respectively; H_A→B and H_A→E denote the metasurface-mediated responses of the Alice-metasurface-Bob and Alice-metasurface-Eve links, respectively, while h_A→B and h_A→E refer to the responses of the Alice-Bob and Alice-Eve links, respectively, without the metasurface. The sums are taken over all meta-atoms constituting the metasurface. Moreover, r_A, r_B, r_E, r_n are the positions of Alice, Bob, Eve and the ${n}_{{th}}$ meta-atom, respectively; ${\varnothing }_{n}^{A}$ is the phase response of the n_th meta-atom of the 1-bit programmable metasurface loaded with the static focusing coding pattern C_metaA, and ${\varnothing }_{n}^{B}(t)$ is the phase response of the n_th meta-atom of the 1-bit programmable metasurface loaded with the dynamic chaotic coding pattern C_metaB(t). Specifically, when the bit of the loaded coding pattern (${{C}}_{{metaA}}$ or ${{C}}_{{metaB}}(t)$) is 0 or 1, the corresponding phase response is 0 or 180°, respectively. Moreover, ∆ is the area of the meta-atom; G_A, G_B, G_E, G_n are the power radiation patterns of Alice, Bob, Eve’s antennas and the n_th meta-atom, respectively; ε_B and ε_E indicate additive noise at Bob and Eve, respectively. Their amplitude follows Gaussian distributions, and their phase follows uniform distributions; $j$ denotes the imaginary unit, and k is the free-space wavenumber. Notably, assuming a directional antenna at the transmitter allows neglecting the direct wave components $\sqrt{{P}_{A}}{x}_{A}\left(t\right){h}_{A\to B}$ and $\sqrt{{P}_{A}}{x}_{A}\left(t\right){h}_{A\to E}$. In addition, data and code that support the findings of our work are provided in Source Data and Supplementary Software, respectively.