Introduction

Acid-base chemistry and most biological redox chemistry are closely related to proton transfer (PT) through water, which has been believed to proceed with a structural diffusion mechanism that was firstly proposed by Grotthuss more than two centuries ago1. According to the modern picture of the Grotthuss mechanism, PT in aqueous solution undergoes ultrafast interconversion between the Eigen and Zundel cations, both of which were suggested as the probable states of the hydrated protons by Wicke2 and Zundel3, respectively. While these seminal works settled the foundation of proton dynamics in aqueous solution4,5, intensive structural dynamics in the vicinity of the excess proton seemed to blurred the boundary between Zundel-like and Eigen-like configurations, raising sustained dispute on assessing the importance of the two limiting structures in shaping the behavior of hydrated protons6,7,8,9,10.

Based on the Eigen-Zundel two-structure model, it has been noticed that the experimentally determined relaxation decay of the 1750 cm−1 signature11, along with its intricate coupling with other vibrational frequencies7, cannot be thoroughly interpreted9,11. On the other hand, molecular dynamics (MD) simulations had uncovered a substantial portion of untypical configurations that are intermediate between Zundel and Eigen configurations4,5,9,12,13,14,15,16. By using various specifically designed descriptors to measure the structural deviation from the two limiting structures, many efforts have been made to divide structures into additional classes8,9,15,16,17. However, the unique spectral feature of these intermediating configurations has not been unambiguously captured from the proton-relevant band across 1000-3000 cm−1, raising concerns about the existence of “hidden configurations”.

To decipher the vibrational spectra of hydrated proton in aqueous solution presents significant challenges. Plenty of previous studies simplified the aqueous solution to various static structures of protonated water clusters, and averaging the results to mimic the aqueous spectrum8,9,10,12,17,18,19. This approach establishes the explicit structure-spectroscopy relationship, but is typically unable to account for the anharmonic effects caused by the structural dynamics. While the distinctive spectral signatures emerged above 2000 cm−1 and below 1500 cm−1 has been unambiguously associated with Eigen-like and Zundel-like configurations, respectively, consensus on interpreting the prominent spectral signature near 1750 cm−1 is still absent.

To fully account for the dynamical effect, several vibrational analysis methods based on MD trajectories have been developed, including those involving diagonalizing the velocity covariance matrix20 and the dipole velocity cross-correlation matrices21. However, the methods have some limitations in dealing with aqueous acidic solutions due to the fast transport of the hydrated protons via Grotthuss mechanism, as discussed in the Methods section. Recent studies simulated the vibrational spectrum through the Fourier transform of the autocorrelation function of dipole moment or velocity of aqueous proton13,14. By simulating the vibrational spectra utilizing short time segments of MD trajectory presenting distinct configurational affiliations, the spectrum corresponds to an ensemble of dynamic structures. Thus, one-to-one assigning the vibrational signatures to specific vibrational modes of distinct structures remains an open problem.

In this work, we design an approach that inversely translates spectral signatures back to frequency-specific vibrational movements and re-establishes the linkage between vibrational characteristics and the underlying structural features. This theoretical scheme is combined with the atomic neural network force field (ANNFF) for HCl solutions, which is constructed from the machine learning of the energies and forces computed with the density functional theories (DFT)22. The constructed ANNFF offers excellent reproduction of the radial distribution functions (RDFs) and the proton diffusion coefficient, presented in Supplementary Figs. 1–2 and Supplementary Table 1. The computational scheme is highly efficient to allow for implementing nanosecond scale of MD simulations on highly dilute HCl solutions, with the convenience of eliminating the concentration effect. Based on our vibrational spectrum assignment approach and proton structure decomposition, we unveil a distinct “Intermediate” configuration that bridges the Zundel-like and Eigen-like conformations. These structures are characterized by a proton stretching mode frequency of 1770 cm−1 and comprise a significant 44% of the overall distribution, in comparison to the Zundel-like (28%) and Eigen-like (28%) configurations. Through further research utilizing local electric field analysis and time correlation function analysis, we determine that the Intermediate persists for 51 fs, outlasting both the Zundel-like (25 fs) and Eigen-like (36 fs). The enhanced stability of these intermediate configurations is attributed to the stabilizing effects of the local electric field induced by the surrounding hydrogen-bond (HB) network.

Results and discussion

Devising the vibrational spectrum assignment approach

To overcome the challenge of attributing vibrational signatures to specific vibrational modes of distinct structures in liquids, we develop an integrated approach that reconstructs frequency-specific vibrational vectors through inverse fast Fourier transform (IFFT) of the vibrational density of states (VDOS). While the details of the integrated numerical scheme are introduced in the Methods section, it is outlined as the flowchart shown in Fig. 1, which comprise four distinct steps.

  1. 1.

    The entire MD trajectory is divided into segments of 3 ps, achieving a balance of spectral resolution and number of effective segments. The segments where the special pair motif is well sustained will be selected to form the dataset for further analysis. The average structure of the motif for each selected segment is determined.

  2. 2.

    For a spectral signature of interest at a specific frequency, one degree of freedom of the most relevant atom will be selected as the reference. The velocity autocorrelation function (VACF) for this reference degree of freedom will be calculated, as well as the velocity cross-correlation functions (VCCFs) between it and all other degrees of freedom. These functions are subsequently converted into the VDOS and cross spectra using fast Fourier transform (FFT).

  3. 3.

    After performing dimensional conversion on the VDOS and cross spectra, and selecting a specific frequency, IFFT is applied to quantify the vibrational amplitudes for all degrees of freedom, along with their phase differences. Within each segment, these amplitudes and phase differences are mapped onto the average structure to generate the vibrational vectors.

  4. 4.

    A set of vibrational coordinates are defined appropriately for all atoms in the special pair moiety to facilitate the averaging of the vibrational vectors across segments. The segment-specific vibrational vectors are transformed from the original Cartesian coordinate system to the defined vibrational coordinate system, averaged across all selected segments, and casted onto the average structure of all segments.

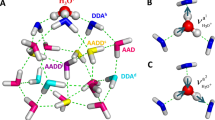
Fig. 1: An integrated approach for assigning vibrational spectrum derived from molecular dynamics (MD) simulations.
figure 1

A “special pair'', consisting of the excess proton and its two flanking water molecules, is employed as the fundamental moiety for interpreting the solvated proton’s vibrational spectrum49. For an arbitrary frequency in the vibrational spectrum, the vibrational vectors of all atoms in the moiety can be derived via the four distinct steps: a Segmentation of the MD trajectory. b Calculation of vibrational density of states (VDOS) and cross spectra using fast Fourier transform (FFT). vi(t) and vj(t) denote the velocity evolutions of the ith and jth degrees of freedom within the moiety. c Derivation of segment-specific vibrational vectors through inverse fast Fourier transform (IFFT). d Averaging of vibrational vectors across segments.

Full size image

The core of this integrated approach lies in utilizing the IFFT to determine, for any given frequency, the vibrational amplitudes and phases associated with all atoms within a specified structural motif of interest. Through a carefully designed strategy that involves averaging the vibrational vectors over different segments, this method offers a feasible framework for assigning vibrational spectra in highly flexible structures, such as liquids. This scheme integrates the merits of Fourier transform-based vibrational spectra simulation techniques, encompassing concurrently anharmonic and dynamical effects13,14, and the merit of static cluster-based vibrational analysis methods in generating frequency-specific vibrational vectors8,9,10,12,17,18,19.

Decomposing the vibrational spectrum of hydrated proton

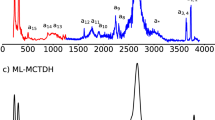
Experimental infrared (IR) spectra of HCl solutions were usually obtained with concentrations above 1 M6,7,23,24,25, inevitably introducing a concentration effect that may obscure the intrinsic behavior of excess protons. To investigate this influence, we conduct an attenuated total reflection Fourier-transform infrared (ATR-FTIR) experiment on a series of HCl solutions with concentrations down to 0.01 M. As shown in Fig. 2a, the 0.1 M of dilute HCl solution can still present explicitly the markedly broadened “proton continuum” previously observed in more concentrated solutions25, a spectral signature being recognized as a key indicator of the high complexity of proton dynamics in water. The concentration effect exerts non-negligible impact on this spectral signature, likely due to the relatively weaker capacity of chloride ions to share the excess proton, compared to water oxygen14. This results in more pronounced positive and negative signals around 3000 cm−1 in the more dilute solution.

Fig. 2: Simulation and decomposition of the vibrational spectra of the hydrated proton in water.
figure 2

a The dark blue trace indicates the experimental infrared (IR) difference spectrum between 0.1 M HCl and water. The red trace indicates the theoretical vibrational density of states difference spectrum between 0.1 M HCl and water. The light blue trace indicates the experimental IR difference spectrum between 4 M HCl and water from ref. 25. The horizontal dashed line is the zero line for the difference spectra. All intensities of the difference spectra have been normalized to the same number of protons with arbitrary units (Arb. Units). b The experimental IR spectra of 0.1 M HCl (red trace) and water (dark blue trace). The shaded areas represent the proton stretching bands for Zundel-like and Eigen-like configurations in refs. 8,13,17 with different patterns. c The average vibrational density of states (VDOS) spectra of the excess proton (red), the flanking water (FW) hydrogens (dark blue), and the bulk water hydrogens (light blue). d The cyan trace is the same as the red one in (c). The yellow trace is the average VDOS spectrum of proton stretch. Peak 1–6 are the Gaussian peaks obtained by fitting the cyan trace. The blue dashed line is the sum of these Gaussian peaks.

Full size image

Due to the limitations imposed by the instrumental signal-to-noise ratio, the difference spectrum of the 0.01 M solution fails to clearly reproduce the proton continuum (refer to Supplementary Fig. 3). Nevertheless, an analysis of the distance distribution between the chlorine ion and the hydrated proton based on the MD simulation trajectory reveals non-random aggregation of this ionic pair even in the 0.1 M solution (Supplementary Fig. 4), as well as its impact on the vibrational spectrum of the proton (Supplementary Fig. 5). The concise discussion on the influence of chloride ions is in the Supplementary Information. Consequently, the subsequent theoretical investigation into the local structures of the excess proton will focus on the MD trajectory of the more dilute 0.01 M HCl solution, ensuring the minimization of the interference from the chloride anion.

For comparative purposes, the theoretical IR difference spectrum between a 0.9 M HCl solution and pure water is computed (refer to Supplementary Information and Supplementary Fig. 6). This theoretical spectrum demonstrates excellent agreement with the experimental IR difference spectrum in terms of lineshape, thereby validating the accuracy of the trajectory-based vibrational spectral analysis methodology. Despite the recent progress in machine learning techniques for predicting the polarization properties of molecules, which has enabled the direct simulation of IR spectra for liquids26, earlier research has demonstrated that the VDOS spectrum, particularly the difference spectrum between HCl solution and pure water, can effectively capture the majority of the characteristic spectral features observed in the experimental proton continuum14. The simulated VDOS difference spectrum for 0.1 M HCl aligns well with the experimental IR spectrum, as illustrated in Fig. 2a. Since the VDOS spectrum is intrinsically linked to the nuclear velocities required for the calculation of vibrational vectors, it serves as a fundamental starting point in the design of a scheme for assigning the vibrational spectrum of the hydrated proton in water.

For a better understanding of the spectral features in IR spectrum, we first separate spectral features of the excess proton and hydrogen atoms in its flanking waters, as well as hydrogen atoms in bulk water. Similarity between the spectra of the flanking water hydrogens and bulk water hydrogens is witnessed, though with obvious red-shift of the OH stretching band broadened down to below 2000 cm−1, as shown in Fig. 2c, which was interpreted as the effect of identity exchange between the excess proton and flanking water hydrogen due to “special pair dance”5,12, as well as the blue shift of the libration and intermolecular vibration bands below 1000 cm−1 17,27. The influence of the excess proton on the spectral feature of its flanking waters is softening the O-H bonds and hindering their libration style of motions, similar to the effects of the external electric field on water28. On the other hand, the VDOS spectrum of the excess proton is distinctively different from the others, presenting clearly the broad continuum across the whole mid-infrared region, the most important feature in the difference spectrum.

By defining proton stretch as the oscillatory motion of the proton between the two oxygen atoms within the flanking water molecules, it becomes straightforward to isolate the partial VDOS spectrum of proton stretch. Subsequently, this partial spectrum is fitted to three Gaussian-type peaks, as illustrated in Fig. 2d. The residual obtained after subtracting the stretching motion from the total proton VDOS spectrum is then fitted with three additional Gaussian-type peaks. Overall, the VDOS spectrum of the excess proton, within the frequency range of 500–4000 cm−1, is comprehensively decomposed into six Gaussian-type peaks, achieving a high coefficient of determination of R2 = 0.990 (see Fig. 2d).

Structure decomposition unveils the “Intermediate”

The robust fit of the partial VDOS of proton stretch into three Gaussian functions underscores the necessity of incorporating additional hydrated proton configuration type beyond the conventionally recognized Zundel and Eigen cations. Earlier MD simulations have disclosed that almost half of the configurations in the trajectory possess atypical features, characterized by a moderate degree of asymmetry, thus precluding their classification into either Zundel-like or Eigen-like configurations4. The nearly barrierless interconversion between Zundel-like and Eigen-like configurations also indicates the increased probability in finding these atypical configurations, as well as their importance in shaping the vibrational signature in the proton continuum.

Various schemes of classifying the excess proton defect have been proposed previously. Among them, spatial coordinates proven to be straightforward for constructing structural descriptors to evaluate the asymmetry of the excess proton’s local environment8,9,12,17,18,19. Alternatively, the number of special pairs10,13, or the smooth overlap atomic positions (SOAPs)29, or even the energetics and hydrogen bonding character relevant to the proton transfer between two flanking waters30, have also been utilized as descriptors to distinguishing between configurations. In this study, we prefer to employ the spatial coordinates of the “special pair”, since previous studies confirmed their relevance to the frequency of proton stretch8,9,13.

The distribution presented in Fig. 3a exhibits a significant broadening along the \({R}_{{{{{\rm{O}}}}}_{2}{{{{\rm{H}}}}}^{*}}\) axis, indicating the substantial fluctuations in the HB length associated with proton rattling. Although the overall structure distribution exhibits a single-peak characteristic, which is consistent with the results from the global free energy surface analysis29, a careful error analysis reveals that at least three two-dimensional (2D) Gaussian functions are indispensable for precisely fitting the distribution with substantial overlap between adjacent functions, achieving an excellent coefficient of determination of R2 = 0.999 in Fig. 3c. Attempts to reduce the number of Gaussian functions lead to a substantial increase in the fitting error, whereas adding more Gaussian functions does not yield notable improvements (see Supplementary Fig. 7). As shown in Fig. 3b, based on the distinct asymmetries of the proton’s position, the decomposed 2D Gaussian distributions can be rationally attributed to Zundel-like, intermediate, and Eigen-like configurations, with weights of 28%, 44%, and 28%, respectively. The populations of the three types are in line with the earlier MD simulation4, only if the atypical configurations are named as the intermediate class. The existence of the intermediate gains supported from geometrical optimizations of the snapshots from the MD trajectories (details are described in ref. 31). As discussed in the Supplementary Information, under dilute conditions below 1 M of concentration, the population ratio of three configurations remains essentially stable (refer also to Supplementary Figs. 8–9, as well as Supplementary Table 2).

Fig. 3: Decomposition of the configurational probability density distribution of the “special pair” moiety of proton in water.
figure 3

a The 2D probability density (PD) distribution in 0.01 M HCl, which is extracted and mapped onto a coordinate space defined by \({R}_{{{{{\rm{O}}}}}_{1}{{{{\rm{H}}}}}^{*}}\) and \({R}_{{{{{\rm{O}}}}}_{2}{{{{\rm{H}}}}}^{*}}\), the distances between the excess proton (H*) and its two adjacent oxygen atoms (O1 and O2) of flanking water molecules (assuming \({R}_{{{{{\rm{O}}}}}_{1}{{{{\rm{H}}}}}^{*}} < {R}_{{{{{\rm{O}}}}}_{2}{{{{\rm{H}}}}}^{*}}\)). b The three 2D Gaussian-type fitting functions are assigned to Zundel-like (blue), Intermediate (yellow) and Eigen-like (green) configurations. The black lines illustrate the contour plot of the sum of the three types. c The absolute error (AE) distribution of the 2D Gaussian-type fitting, defined as the difference between the probability density distribution and the sum of the three 2D Gaussian-type fitting functions. The unit of root mean square error (RMSE) and AE is Å−2.

Full size image

The relatively balanced abundance of each configuration type highlights the importance of considering all three types when discussing the properties of the excess proton. To rationally associate these configurations with the three proton stretching signatures in the vibrational spectrum, we calculate the periods of proton stretch for carefully selected segments of MD trajectories belong to distinct types (refer to the Supplementary Information and Supplementary Fig. 10 for details). The Zundel-like, intermediate, and Eigen-like configurations exhibited average proton stretching periods of 25.3 fs, 18.7 fs, and 13.7 fs, respectively, equivalent to frequencies of 1320 cm−1, 1780 cm−1, and 2430 cm−1. Clear differences in the average proton stretching frequencies were observed, with a progressive increase from Zundel-like to Eigen-like configurations. This trend is consistent with the peaks 1–3 in Fig. 2d, thereby resolving the controversy regarding the structural assignment of proton stretching frequencies as shown in Fig. 2b. While previous studies have suggested the potential presence of intermediate states based on structural classifications9,15, they did not fully substantiate these claims, particularly in terms of definitive vibrational signatures. The vibrational signal at 1770 cm−1 has long been a subject of intense research, but its corresponding proton configuration assignment remains controversial, and it has never been assigned to an intermediate state. Our work successfully identifies the 1770 cm−1 peak as a unique proton stretching vibration corresponding to the intermediate state. This finding contributes to a deeper understanding of linear IR spectra in acid solutions and prompts a re-evaluation of existing interpretations in 2D IR spectroscopy for such systems.

Resolving spectral controversy with vibrational vectors

With the established connection between the vibrational signatures and configurations of the excess proton, the vibrational vectors associated with the frequencies at the centers of peaks 1 to 6 are generated and illustrated in Fig. 4. The vectors in Fig. 4a–c clearly indicate the mixing of the proton stretch with other types of vibrational motions, which is evident from the overlap observed among the fitted Gaussian peaks. Additionally, the vectors shown in Fig. 4d–f highlight the non-stretching motions present in the hydrated proton moiety. All of the assignments of these six spectral signatures to specific vibrational modes are listed in Table 1. As the vibrational vectors were computed using segments of the MD trajectory rather than static structures, the motions of \({{{{\rm{H}}}}}_{5}{{{{\rm{O}}}}}_{2}^{+}\) inherently preserve the dynamical impact of the surrounding water molecules. This underscores one of the advantages of our approach: the chosen cluster size does not affect the vibrational vectors of the concerned motifs, as detailed in the Supplementary Information and Supplementary Fig. 11.

Fig. 4: Schematic illustration of the vibrational vectors of the hydrated proton moiety in water, which are computed for six spectral signatures in the “proton continuum”.
figure 4

From a to c, the vibrational vectors for three proton-stretch signatures located in different frequency regions, which are casted onto their corresponding configuration types. From d to f, the vibrational vectors for libration (d)17, umbrella (e)8,17, and bending (f)13,18, respectively. The latter three vectors are imposed on the average structure of all configurations, since they are insensitive to the configuration changes.

Full size image
Table 1 The assignments of Gaussian vibrational peaks in the average vibrational density of states of the excess proton
Full size table

Mixing of the spectral signatures of proton stretch with other motion styles hindered comprehensive understanding of the spectrum and the arrival of a unanimous consensus regarding the assignment of proton dynamics from molecular spectrum. Being one of the major focuses of dispute, a commonly accepted assessment of the spectral features near 1750 cm−1 has not been fully achieved. Conventionally, both theoretical and experimental studies attributed this spectral signature primarily to the flanking-water bending mode7,11,12,18,25. However, several studies have also indicated the involvement of the proton stretch8,13,17,19,32. The vibrational vectors displayed in Fig. 4b clearly indicate that the signals around 1770 cm−1 are mainly contributed from both proton stretch and flanking water bend. Our analysis reveals that both vibrational modes contribute approximately equally to the observed spectral feature. However, since the proton stretch typically exhibits more intensive IR intensity than the flanking-water bend8, the former mode ought to dominate the IR spectrum at 1770 cm−1. The controversy at  ~1750 cm−1 might arise due to the accuracy limitation of the semiempirical theories, which sometimes resulted in hundreds of wavenumbers of deviations in predicted vibrational peak positions compared to both ab initio MD (AIMD) trajectory and experimental results10,13. This inconsistency, which undermines the reliability of the vibrational mode assignments, has been essentially avoided in our simulations using machine-leaning neural network force fields from first-principles level of calculations. This finding resolves the long-standing controversy regarding the assignment of this spectral feature and provides a more accurate understanding of the vibrational dynamics in aqueous proton systems.

The mixed nature of the vibrational signal at 1750 cm−1, particularly, confirming the distinctive contribution from the proton stretching mode of intermediate configurations, offers a fresh perspective on interpreting state-of-the-art experimental 2D IR spectra for HCl solutions reported by Tokmakoff and colleagues. When assigning the signature solely to the flanking water bending mode of Zundel-like configurations7,11,25, its anisotropy decay should be perfectly fitted with a single exponential similar to water bending33, contrary to the reported biexponential fitting11. By including the proton stretching mode of intermediate configurations, the biexponential fitting can be smoothly interpreted. An additional advantage of introducing this distinct vibrational feature can also be harvested concerning the interpretation of the cross peaks in 2D IR spectra. The cross peak (1200 cm−1, 1750 cm−1) previously attributed to the coupling of proton stretch and flanking water bend in Zundel-like configurations7,9 should also involve the contribution of the chemical exchange effect relevant to Zundel-like and intermediate configurations. The ultrafast interconversion between these configurations, which occurs at a timescale of sub-100 fs5,6,24,34,35, can be observed when using a waiting time of 150 fs in 2D IR experiments, in contrast to the commonly used picoseconds of waiting time for observing most chemical exchange processes. Notably, incorporating the chemical exchange effect does not contradict the established interpretation based on the experimental observations. For instance, the proton stretching modes of Zundel-like and intermediate configurations can also perfectly rationalize the strong parallel polarization preference observed experimentally7.

Impact of local electric field on proton configurations

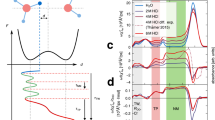
Analysis of the local electric field is helpful to exploring how the surrounding water HB network is involved in shaping the behaviour of a hydrated proton. Figure 5 graphically illustrates the relationship between the local electric field intensity and the collective coordinates, specifically ql and qs, which represent the long (major) and short (minor) axes of 2D Gaussian-type structural distribution functions (see Supplementary Fig. 12 and Supplementary Tables 3–6), respectively. Figure 5a illustrates, for each category of hydrated proton configuration, how the electric field intensity evolves along ql. Notably, while all three categories exhibit an enhanced electric field along ql, the ranges of intensities are distinctly different and essentially non-overlapping. This observation holds even when using the same collective coordinate ql of the Intermediate state for all three configurations, as shown in Supplementary Fig. 14. This finding underscores that the observed variations in the local electric field distributions are not artifacts of the choice of collective variables but rather reflect intrinsic differences in the structural parameters of the three configurations. On the other hand, qs appears to emphasize the uniformity of configurations within a given configuration, when plotting the electric field intensity along qs, essentially horizontal lines are observed for all configurations, as demonstrated in Fig. 5b. The two collective variables incline to focusing on either the distinctiveness among categories of configurations or the tendency of gradual change with each category. Their excellent performance highly validates the structure decomposition scheme via 2D Gaussian-type fitting, and more importantly, reveals the feasibility of utilizing ql as the sole collective coordinate in exploring each category of configurations.

Fig. 5: The distributions of the local electric field computed with conditional ensemble average.
figure 5

a The local electric field distributions along collective coordinate ql, for Zundel-like (0–0.13 V/Å), Intermediate (0.13–0.28 V/Å) and Eigen-like (0.28–0.40 V/Å) configurations, respectively. b The local electric field distributions along collective coordinate qs, for Zundel-like, Intermediate and Eigen-like configurations, respectively. The color bar of the scatter points signifies the structural probability densities (PD), and it is worth noting that the color bar is uniquely defined for each sub-graph. The local electric field surrounding the excess proton is evaluated using Coulomb’s law within the first solvation shell of the \({{{{\rm{H}}}}}_{5}{{{{\rm{O}}}}}_{2}^{+}\) moiety, as long-range contributions have minor impact on the internal electric field37. The atomic charges utilized in this estimation are derived from the SPC/E water model, which are set as  −0.8476e for oxygen and  +0.4238e for hydrogen50. This model has been demonstrated to provide a valid and efficient approximation, with no significant impact on the robustness of the conclusions in our previous work37. Specifically, E1 is defined as the projection of the local electric field onto the O1-H* bond, where a positive value of E1 would stabilize the current configuration by hindering the proton’s transfer towards the opposite atom O2. The introduction of an additional “intermediate” configuration can be necessitated by inspecting the plot of local electric field distribution presented as Supplementary Fig. 13, classifying configurations merely into Zundel-like and Eigen-like cations will result in non-negligible dependence of the field intensity on qs and overlapped electric field between categories of configurations.

Full size image

The current study contributes significantly to the understanding of the mechanisms underlying the remarkable structural diversity of protons in water. Our findings reveal a notable correlation between local electric field intensity and HB network asymmetry surrounding the proton’s two flanking water molecules (refer to Supplementary Information, Supplementary Figs. 15, 16 and Supplementary Tables 7–9). Specifically, from Zundel-like to Eigen-like configurations, there is a progressive enhance in the local electric field intensity, which coincides with an increase in HB network asymmetry. These observations remind us that the emergence of three distinct types of hydrated proton could potentially stem from a finite set of HB network patterns in the immediate environment. Fluctuations in the HB network can induce local electric fields, which in turn stabilize these critical configurations. Conversely, when the proton cation mismatches with its local environment, the surrounding HB networks tend to promote configurational transformations. As detailed in the Supplementary Information, biexponential fitting of the correlation functions reveals lifetimes of the configurations, which are 25 fs, 51 fs, and 36 fs for the Zundel-like, intermediate, and Eigen-like configurations, respectively (see Supplementary Fig. 17). These ultra-short timescales rationalize the experimentally observed sub-100 fs process of structural interconversions5,6,24,34,35.

Conclusions

This study has successfully delved into the dynamical behavior of hydrated protons in water through a theoretical exploration that capitalized on the reliability and efficiency of atomic neural network representations of the force field. This approach has allowed us to perform MD simulations on models encompassing thousands of water molecules, effectively minimizing the confounding effects of concentration and enhancing our comprehension of the protons’ fundamental characteristics. Furthermore, our proposed IFFT scheme has proven to be an expedient tool for extracting vibrational vectors from MD trajectories, enabling the direct characterization of frequency-specific vibrational features within the broad proton continuum. While the interpretation of these features remains a subject of ongoing discussions, our findings have noteworthily contributed to this debate. By integrating vibrational spectrum assignment with structural distribution analysis, we have presented compelling evidence for the existence of distinct intermediate configurations of hydrated protons, alongside the established Zundel-like and Eigen-like configurations. Notably, these intermediate configurations exhibit a unique proton stretching peak at 1770 cm−1, which is approximately equally mixed with the flanking water bending mode. We hypothesize that the local electric field generated by the surrounding HB network in solution plays a pivotal role in stabilizing these intermediate configurations, a phenomenon that is absent in smaller gaseous protonated water clusters. In essence, this study provides a fresh perspective for understanding the dynamical behavior of hydrated protons in water, laying the groundwork for future investigations into the intricate interactions and structures that govern this seemingly simple but profoundly fascinating system.

Although the nuclear quantum effects (NQEs) hold recognized importance in the aqueous proton system, we prefer not to consider it when the currently used generalized gradient approximation (GGA) functional satisfactorily replicates the experimental IR spectrum of HCl solution and the proton’s diffusion coefficient. Notably, the GGA functional appears to offset errors in electron correlation and NQEs14,36. Previous research also warns that combining the GGA functional with NQEs may lead to notable discrepancies compared to experimental observations37,36.

Method

Vibrational spectrum assignment approach

The selection of segments

We began by locating the excess proton in the simulation box for each snapshot in the 1.2 ns MD trajectory. Water molecules were identified by grouping each oxygen atom with its two closest hydrogen atoms, leaving the excess proton as the only remaining unpaired hydrogen atom. To balance spectral resolution and the consistency of the excess proton’s local environment, the entire trajectory was divided into 3 ps segments, given the frequent identity switching between an excess proton and a flanking water hydrogen atom. Applying a criterion that the determined excess proton maintains its identity in more than 60% of the snapshots within a segment, 26 segments were retained for further analysis. In these retained segments, the proton and its two flanking waters were found to form a stable special-pair motif to hold the excess proton, relying on which the vibrational properties of the proton will be analyzed. These segments, totaling 6.5% of the entire trajectory, are outlined in Supplementary Fig. 18 and the Supplementary Information.

The amplitudes and the phase differences for degrees of freedom

To streamline the mathematical derivation, we abstracted atomic motions into harmonic vibrations represented by sinusoidal functions. However, it’s important to note that our approach also contains anharmonic components and other atomic motions.

The dimension conversion factor

For the purpose of maximizing information retention, we picked a reference degree of freedom that exhibits strong relative intensity within the chosen frequency range. The position of this reference degree of freedom, denoted as xref(t), can be described as

$${x}_{{{{\rm{ref}}}}}(t)={x}_{{{{\rm{ref}}}}}(0)+{\sum }_{k}^{{N}_{{{{\rm{ref}}}}}}{A}_{{{{\rm{ref}}}}}^{k}\sin ({\omega }_{{{{\rm{ref}}}}}^{k}t+{\varphi }_{{{{\rm{ref}}}}}^{k}),$$
(1)

where xref(0) is the initial position at time t = 0, Nref represents the total number of vibrational modes encompassed by xref(t), \({A}_{{{{\rm{ref}}}}}^{k}\), \({\omega }_{{{{\rm{ref}}}}}^{k}\) and \({\varphi }_{{{{\rm{ref}}}}}^{k}\) are the amplitude, frequency and phase of the vibrational mode k. The mass-weighted velocity vref(t) was calculated as

$${v}_{{{{\rm{ref}}}}}(t)=\sqrt{{m}_{{{{\rm{ref}}}}}}{\sum }_{k}^{{N}_{{{{\rm{ref}}}}}}{A}_{{{{\rm{ref}}}}}^{k}{\omega }_{{{{\rm{ref}}}}}^{k}\cos ({\omega }_{{{{\rm{ref}}}}}^{k}t+{\varphi }_{{{{\rm{ref}}}}}^{k}).$$
(2)

Therefore, the VACF of the degree of freedom ref can be expressed as

$${{{{\rm{VACF}}}}}_{{{{\rm{ref}}}}}(t) =\langle {v}_{{{{\rm{ref}}}}}(t){v}_{{{{\rm{ref}}}}}(0)\rangle \\ ={\lim }_{\tau \to \infty }\frac{1}{\tau }\int_{0}^{\tau }{v}_{{{{\rm{ref}}}}}({t}_{0}+t){v}_{{{{\rm{ref}}}}}({t}_{0})\,d{t}_{0}\\ ={m}_{{{{\rm{ref}}}}}{\sum }_{k}^{{N}_{{{{\rm{ref}}}}}}\frac{1}{2}{{A}_{{{{\rm{ref}}}}}^{k}}^{2}{{\omega }_{{{{\rm{ref}}}}}^{k}}^{2}\cos ({\omega }_{{{{\rm{ref}}}}}^{k}t).$$
(3)

The VACFref(t) loses the initial phase φref of vref(t). Note that summation replaced all integrations in our practical computations. By performing the FFT on VACFref(t), we obtained the VDOS spectrum Pref(ω),

$${P}_{{{{\rm{ref}}}}}(\omega ) =\int_{-\infty }^{\infty }{{{{\rm{VACF}}}}}_{{{{\rm{ref}}}}}(t){e}^{-i\omega t}\,dt\\ ={m}_{{{{\rm{ref}}}}}{\sum }_{k}^{{N}_{{{{\rm{ref}}}}}}\frac{1}{4}{{A}_{{{{\rm{ref}}}}}^{k}}^{2}{{\omega }_{{{{\rm{ref}}}}}^{k}}^{2}[\delta (\omega -{\omega }_{{{{\rm{ref}}}}}^{k})+\delta (\omega+{\omega }_{{{{\rm{ref}}}}}^{k})].$$
(4)

To rescale the VDOS spectrum to the dimension of mass-weighted velocity, we introduced the dimension conversion factor S(ω), which is defined as

$$S(\omega )=\left\{\begin{array}{ll}\frac{1}{2}\sqrt{{m}_{{{{\rm{ref}}}}}}{A}_{{{{\rm{ref}}}}}^{k}{\omega }_{{{{\rm{ref}}}}}^{k},& \omega=\pm {\omega }_{{{{\rm{ref}}}}}^{k},\\ 0,\hfill&{{{\rm{else}}}}.\hfill\end{array}\right.$$
(5)

The motions of all degrees of freedom for selected frequencies

The position xi(t) of the degree of freedom i at time t can be expressed as

$$\begin{array}{l}{x}_{i}(t)={x}_{i}(0)+{\sum }_{k}^{{N}_{i}}{A}_{i}^{k}\sin ({\omega }_{i}^{k}t+{\varphi }_{i}^{k}),\end{array}$$
(6)

where Ni is the number of vibrational modes. The mass-weighted velocity vi(t) was calculated as

$${v}_{i}(t)=\sqrt{{m}_{i}}{\sum }_{k}^{{N}_{i}}{A}_{i}^{k}{\omega }_{i}^{k}\cos ({\omega }_{i}^{k}t+{\varphi }_{i}^{k}).$$
(7)

We calculated the velocity correlation function (VCF) between vi(t) and vref(t). If i is ref, it is the VACF; otherwise, it is the VCCF.

$${{{{\rm{VCF}}}}}_{i}(t) =\langle {v}_{i}(t){v}_{{{{\rm{ref}}}}}(0)\rangle \\ =\sqrt{{m}_{i}{m}_{{{{\rm{ref}}}}}}{\sum }_{k}^{L}\frac{1}{2}{A}_{i}^{k}{A}_{{{{\rm{ref}}}}}^{k}{{\omega }^{k}}^{2}\cos ({\omega }^{k}t+{\varphi }_{i}^{k}-{\varphi }_{{{{\rm{ref}}}}}^{k}),$$
(8)

where L represents the number of vibrational modes shared by both vi(t) and vref(t). The VCFi(t) preserves the phase difference between these two velocities. By performing the FFT on VCFi(t), we obtained the Pi(ω),

$${P}_{i}(\omega )= \int_{ -\infty }^{\infty }{{{{\rm{VCF}}}}}_{i}(t){e}^{-i\omega t}\,dt\\= \sqrt{{m}_{i}{m}_{{{{\rm{ref}}}}}}{\sum }_{k}^{L}\frac{1}{4}{A}_{i}^{k}{A}_{{{{\rm{ref}}}}}^{k}{{\omega }^{k}}^{2}[{e}^{i({\varphi }_{i}^{k}-{\varphi }_{{{{\rm{ref}}}}}^{k})}\delta (\omega -{\omega }^{k}) \\ +{e}^{-i({\varphi }_{i}^{k}-{\varphi }_{{{{\rm{ref}}}}}^{k})}\delta (\omega+{\omega }^{k})].$$
(9)

For convenience, the VDOS spectra were rescaled to the dimension of mass-weighted velocity. We divided Pi(ω) by the dimension conversion factor S(ω) whenever Pi(ω) is non-zero,

$${P}_{i}^{{{{\rm{Scale}}}}}(\omega )=\sqrt{{m}_{i}}{\sum }_{k}^{L}\frac{1}{2}{A}_{i}^{k}{\omega }^{k}[{e}^{i({\varphi }_{i}^{k}-{\varphi }_{{{{\rm{ref}}}}}^{k})}\delta (\omega -{\omega }^{k})+{e}^{-i({\varphi }_{i}^{k}-{\varphi }_{{{{\rm{ref}}}}}^{k})}\delta (\omega+{\omega }^{k})].$$
(10)

Selecting a specific frequency ωs, we obtained \({P}_{i}^{s}(\omega )\) by retaining only the value of \({P}_{i}^{{{{\rm{Scale}}}}}(\omega )\) at  ± ωs, and zeroing out all other frequencies.

$${P}_{i}^{s}(\omega )=\frac{1}{2}\sqrt{{m}_{i}}{A}_{i}^{s}{\omega }^{s}[{e}^{i({\varphi }_{i}^{s}-{\varphi }_{{{{\rm{ref}}}}}^{s})}\delta (\omega -{\omega }^{s})+{e}^{-i({\varphi }_{i}^{s}-{\varphi }_{{{{\rm{ref}}}}}^{s})}\delta (\omega+{\omega }^{s})].$$
(11)

By performing the IFFT on \({P}_{i}^{s}(\omega )\), we obtained the velocity \({v}_{i}^{s}(t)\) corresponding to the selected frequency ωs,

$${v}_{i}^{s}(t) =\frac{1}{2\pi }\int_{-\infty }^{\infty }{P}_{i}^{s}(\omega ){e}^{i\omega t}\,d\omega \\ =\sqrt{{m}_{i}}{A}_{i}^{s}{\omega }^{s}\cos ({\omega }^{s}t+{\varphi }_{i}^{s}-{\varphi }_{{{{\rm{ref}}}}}^{s}).$$
(12)

From \({v}_{i}^{s}(t)\), we can straightforwardly determine the amplitude \({A}_{i}^{s}\) and the phase difference \({\varphi }_{i}^{s}-{\varphi }_{{{{\rm{ref}}}}}^{s}\) for the degree of freedom i at selected frequency ωs. Subsequently, we can associate the amplitudes and phase differences with their corresponding average structure to generate the vibrational vectors.

The diagonalization of the velocity covariance matrix, as described in ref. 20, is generally effective for systems exhibiting distinct and well-separated vibrational peaks, such as those found in gaseous or certain solid-state substances. Nevertheless, this method becomes less adequate when applied to the investigation of proton vibrations in acids, where the vibrational modes are intricately coupled due to complex proton dynamics. In stark contrast, our approach allows for the mixing of vibrational modes, rendering it particularly suitable for the study of the present system.

By diagonalizing the dipole velocity cross-correlation matrix, it is possible to extract local vibrational vectors for condensed systems, as demonstrated in ref. 21. However, in the case of HCl solutions, frequent proton hopping necessitates the division of MD trajectories into very short segments. This segmentation complicates the extraction of vibrational features for the entire trajectory, as the vibrational modes and corresponding frequency distributions can vary significantly between segments. In contrast, our approach centers on specific frequencies within the vibrational spectrum, allowing us to average the vibrational vectors at the same frequency across multiple segments.

While effective modes analysis based on MD trajectories of small protonated water clusters can provide vibrational vectors for normal modes38, it cannot fully account for the dynamic effect on the vibrational spectrum of hydrated proton in water. It is noteworthy that the utilization of velocity correlation functions, rather than velocity or position time evolution functions as in previous research39, significantly enhances the signal-to-noise ratio in the constructed VDOS spectrum. This advancement ensures a more accurate and reliable analysis of the vibrational properties of the system.

The vibrational coordinates

To obtain the average vibrational vectors across various segments, we have devised the vibrational coordinates for the \({{{{\rm{H}}}}}_{5}{{{{\rm{O}}}}}_{2}^{+}\) moiety. For the hydrogen atoms in the flanking water molecules, we utilized three unit vectors, one aligned with the O-H axis, another situated within the H2O plane and perpendicular to the O-H axis, and a third one perpendicular to the H2O plane. For the oxygen atoms in the flanking water molecules and the proton, our internal coordinates contain three unit vectors as well, one parallel to the O-O axis, one that signifies the mean projection of the two flanking water H-H connections onto the plane orthogonal to the O-O axis, and a third vector perpendicular to the first two. Afterward, we decomposed the vibrational vectors of each segment at the same frequency onto these vibrational coordinates.

The average structures for three types of configurations

For all selected trajectory segments, in cases where \({R}_{{{{{\rm{O}}}}}_{1}{{{{\rm{H}}}}}^{*}} < {R}_{{{{{\rm{O}}}}}_{2}{{{{\rm{H}}}}}^{*}}\), the proton configurations were classified in accordance with the boundary lines shown in Supplementary Fig. 19. Subsequently, the average structure for each configuration type was computed utilizing internal coordinates.

MD simulation details

AIMD simulations were performed utilizing the VASP 5.4.4 package40,41. The valence electron wave functions were expanded in a plane wave basis with an energy cutoff of 400 eV. For the description of core electrons, pseudopotentials were employed using the projector augmented wave (PAW) method42. The exchange and correlation energy were computed using the RPBE functional, formulated within the GGA43,44. To incorporate van der Waals (vdW) interactions, the DFT-D3/zero correction method was utilized45. The Brillouin zone sampling was simplified to a single Γ point.

In the case of 0.9 M HCl, our cubic simulation box (measuring 12.42 Å in length) encompassed 63 water molecules, accompanied by one proton and chloride ion pair, resulting in an approximate density of 1 g/cm3, which is consistent with the experimental density. The convergence criterion for DFT energy and wave function was set to 10−6 eV. By executing three uncorrelated simulations within the canonical ensemble (NVT), maintaining a temperature of 298 K, a pressure of 1 atm, and utilizing a time step of 1 fs, we successfully generated a total of 150 ps trajectories.

To enhance computational efficiency and extend simulation durations with low ion concentration, we constructed the ANNFFs for HCl solutions22. The scalability of ANNFFs is well-established, as they decompose the total energy into the sum of contributions from individual atoms22. This allows an ANNFF trained on smaller systems to predict the potential energy surface for larger configurations simply by adding new components to the total energy, provided the atomic environments are adequately represented in the training dataset. The ANNFF based on RPBE-D3 functional has been successfully employed in modeling water dissociation, providing RDFs and self-diffusion coefficient for liquid water that show good agreement with experimental results37.

For the training process, we utilized the n2p2 package46. Our ANNFFs comprised a series of feedforward neural networks, each featuring two hidden layers with 25 nodes apiece. The local chemical environments of H, O, and Cl atoms were described using a total of 36, 39, and 26 symmetry functions (SFs), respectively, encompassing both radial and angular types, with a cutoff radius of 6 Å. The initial training set contained 1945 configurations randomly chosen from AIMD trajectories. Following this, preliminary ANNFFs were created and employed in NVT MD simulations using the LAMMPS program equipped with the ANNFF library22,47. Structures exhibiting extrapolation warnings during MD were filtered, recalculated using DFT, and subsequently added to the training set. Several iterations of ANNFF training and configuration selection were conducted until the ANNFFs were ready for ns-scale MD simulations with few extrapolation warnings. The final training set contained 3259 configurations. For comparison, the test set encompassed all AIMD configurations. Three parallel ANNFFs were trained and tested, exhibiting promising parallelism and accuracy, as detailed in Supplementary Tables 10 and 11.

By utilizing the first ANNFF listed in Supplementary Table 10, we conducted MD simulations within three cubic simulation boxes of lengths 12.42, 24.84, and 49.67 Å, which contains 63, 511, and 4095 water molecules, respectively, alongside a proton and chloride ion pair48. Additionally, a simulation for pure water was conducted with 512 water molecules using a cubic box with a side length of 24.84 Å. To maintain consistency across all simulations, the cell length for each ANNFF MD simulation was adjusted to align with an experimental density of 1 g/cm3. Following a 0.6 ns equilibration phase at 298 K and 1 atm pressure, with a time step of 0.3 fs, the simulations were extended for an additional 1.2 ns to generate trajectories for subsequent analysis.

For comparison, a system comprising 63 water molecules, a proton, and a chloride ion pair (equivalent to 0.9 M HCl) is presented in the Supplementary Information. Additionally, a system containing 511 water molecules, a proton, and a chloride ion pair (0.1 M HCl), as well as a system with 512 water molecules, were utilized to generate the theoretical difference VDOS spectrum shown in Fig. 2a. The geometrical optimizations were performed on the snapshots from the MD trajectory of 0.1 M HCl. These systems are also included in the Supplementary Information for comparison. All other analyses presented in the manuscript are based on a 0.01 M HCl solution, which consists of 4095 water molecules, a proton, and a chloride ion pair.

Experimental details

Sample preparation

The acid solutions were prepared by diluting concentrated HCl aq. (GR, 36.0–38.0% Sinopharm Chemical Reagent Co., Ltd) with water (Millipore, 18.2 MΩ) to proton concentrations at 0.1 M and 0.01 M.

ATR-FTIR measurements

The IR spectra were recorded on an ATR-FTIR vacuum spectrometer (Bruker VERTEX 80v) equipped with a deuterated triglycine sulfate (DTGS) detector in the range of 650–4000 cm−1. Each spectrum was averaged over 64 scans with a resolution of 4 cm−1. A Platinum ATR unit A 225 with diamond crystal accessory was used. The background spectrum of the bare diamond crystal was recorded and used for the subsequent measurements at room temperature. In all cases a 6 μL of sample solution was placed on the ATR prism. In order to prevent evaporation of the liquid, the sample was sealed with a lid that was pressed tightly against the platform by a Pressure application device.

Data processing

To ensure accurate results, we collected multiple samples of water and HCl solutions and obtained five parallel spectra for each. Afterward, we carefully chose the spectrum sets exhibiting the smallest standard deviation, enabling us to compute the average spectra and the difference spectra between HCl solutions and water.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.