Introduction

The ultimate confinement of guided light takes place in atomically thin films. Metallic monolayers in particular are predicted to provide a new platform in which light couples to spatially confined plasmons—collectively oscillating free electrons. This ability to focus light energy to sub-nanometer length scales makes metallic monolayers one of the prime candidates for enhanced light-matter interaction1, deep sub-diffraction imaging and spectroscopy2,3, and future nanoscale optical computing4,5.

In-plane confinement is characterised by the ratio \({\lambda }_{0}/{\lambda }_{p}\), where \({\lambda }_{0}\) is the light wavelength in free space and \({\lambda }_{p}\) is the plasmon polariton wavelength in the material. This ratio is close to 200 for Dirac plasmons in graphene4. However, at large wave vectors (small \({\lambda }_{p}\)), graphene plasmons enter the electron-hole continuum where the plasmon provides sufficient momentum and energy to facilitate interband or intraband transitions, resulting in severe plasmon damping6. This damping mechanism also applies to other 2D electron gas systems such as Si surface states and monolayer Ag on Si6,7, but is theoretically predicted to be absent in 2H-TaS2.

Metallic Group V transition metal dichalcogenides (TMDs) such as 2H-TaS2, TaSe2, NbS2 and NbSe2 are a particularly promising class of 2D materials for light confinement. These materials have an isolated conduction band, allowing plasmons to disperse up to a much higher wave vector before entering the lossy electron-hole continuum8. Recently, reliable first-principles calculations predicted a flat dispersion relation in 2H-TaS2 monolayers up to a large wave vector \(q=2\pi /{\lambda }_{p}\) of 0.4 Å−1 in the near-infrared frequency range9. The predicted flat dispersion relation indicates ultra-slow light behaviour, resulting in a high confinement ratio and giant field enhancement.

In this work, we use monochromated momentum-resolved electron energy loss spectroscopy (q-EELS) to experimentally demonstrate the existence of highly confined plasmons at room temperature in 2D 2H-TaS2 monolayers and bilayers. We observe flat plasmon dispersions in 2H-TaS2, both in monolayers and bilayers, at least up to 0.15 Å−1 as predicted theoretically9. The corollary of this observation of a flat plasmon dispersion, is that it provides evidence for the existence of ultra-slow plasmon polariton waves in atomically thin metals. In contrast to previous q-EELS studies on bulk metallic TMDs10,11, our work is performed in the true monolayer limit, enabling the direct experimental observation of nonlocal interband screening—proposed as the key mechanism responsible for the peculiar flat plasmon dispersion, and potentially universal across all 2D metallic TMD systems.

By their nature, highly dispersed plasmons have a large momentum-mismatch with light, preventing them to be excited directly with far-field light illumination. To excite and measure these plasmons, several methods can provide the missing momentum. For example, the material can be patterned in an array and measured with Fourier transform infrared spectroscopy (FTIR)12. Alternatively, the plasmons can be excited in the near-field, as in scattering-type scanning near-field optical microscopy (s-SNOM)13,14,15 or with a focused electron beam. However, for FTIR and s-SNOM, the accessible momentum range is limited to 0.01 Å−1, which makes it difficult to observe details of the dispersion, which develops at values well beyond 0.01 Å−1. A fast-moving electron beam, on the other hand, can provide momentum all across the Brillouin zone up to >1 Å−1 16,17, making it useful for quantitative plasmon dispersion measurements. In previous work, the scanning transmission electron microscope (STEM) was used for q-EELS measurements on ~100-nm thick 3D bulk metallic TMD samples of 2H-TaS2, TaSe2, NbS2 and NbSe2, showing a notable negative plasmon dispersion at large wave vectors10,11. This effect was proposed to originate from the detailed structure of the narrow d-band near the Fermi level18,19,20. However, measurements on atomically thin metallic TMDs have not yet been demonstrated so far, preventing experimental evidence for the predicted local field screening, slow light, and its confinement in the monolayer limit.

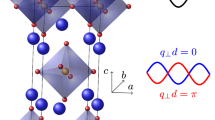
Figure 1a schematically shows the under-focused electron beam projecting the reciprocal lattice of the free-hanging TaS2 at the entrance of the EELS spectrometer, an acquisition method that has been shown to deliver high momentum-resolution in the STEM21,22,23. With this experimental set-up, individual EELS spectra with small collection angles are acquired at different positions in momentum space with typical energy resolutions of 50 meV and momentum-resolutions of 0.0056 \({\mathring{\rm A} }^{-1}\). It provides the conditions to explore whether plasmons indeed avoid the electron-hole continuum and encounter the predicted conditions for low plasmon damping.

Fig. 1: Experimental set-up for momentum-resolved Electron Energy Loss Spectroscopy (q-EELS) on 2H-TaS2 metallic monolayers.
figure 1

a Schematic of the experimental set-up, using a near-parallel, under-focused electron beam (orange) in a Scanning Transmission Electron Microscope (STEM) with very high momentum (q) resolution (0.0056 Å−1) in reciprocal space. 2D plasmons of energy \(\hslash \omega (q)\) are predicted to disperse outside the electron-hole continuum, indicated by the dark region between the interband and intraband Landau damping regions9. b Bright field light microscope image of 2H-TaS2 monolayers after electrochemical exfoliation, and experimental demonstration of superconductivity with measured superconducting transition temperature \({T}_{c}=3\,{K}\), demonstrating the high quality of the used sample material. c Raman spectroscopy of the 2H-TaS2 flakes with varying thicknesses, from monolayer (1 L) to >10 atomic layers (>10 L).

Full size image

High-quality TaS2 flakes were obtained by electrochemical exfoliation24,25, a method that produces large-area, ultrathin flakes with high yield while preserving the crystal structure. X-ray diffraction shown in Supplementary Fig. 1 confirms that the original TaS2 crystal used in this work is in the 2H phase, with high crystallinity. After exfoliation, the solution was drop-cast on SiO2/Si substrates following washing and liquid cascade centrifugation. The optical image in Fig. 1b demonstrates that the as-exfoliated flakes are uniform monolayers with average lateral sizes exceeding 100 μm. Selected area electron diffraction (SAED) measurements, as shown in Fig. 2a and Supplementary Fig. 4 confirm the high crystallinity of the as-exfoliated TaS2 flakes. Atomic resolution images of monolayer and bilayer samples are provided in Supplementary Fig. 2, showing that the atomic structure is conserved in the exfoliated films. The quality of the exfoliated TaS2 monolayers was further examined by superconductivity measurements, which show a transition temperature of 3 K, close to the previously reported 3.4 K for high-quality, mechanically exfoliated TaS2 monolayers26. The two peaks in the measured Raman spectra in Fig. 1c at 301 cm−1 and 396 cm−1 correspond to the \({A}_{1g}\) and \({E}_{2g}^{1}\) phonon modes, also confirming the 2H-phase27,28. The soft mode at 183 cm−1 can be attributed to the two-phonon scattering at room temperature29.

Fig. 2: q-EELS measurements of monolayer and bilayer 2H-TaS2 along the Γ-M direction.
figure 2

a Bilayer spectra, vertically shifted based on the corresponding q-value set in reciprocal space, as indicated by the coloured disks in the inset. 2D plasmon peaks are observed and fitted with a Drude–Lorentz function to extract the q-dependent plasmon energy, forming a dispersion relation. The black dashed line in (a) serves as a visual guide to estimate the group velocity from the slope of the fitted plasmon dispersion relation. The lowest group velocity observed in the measurement is estimated to be\(\, \sim {10}^{-4}c\) at high momentum. b Fitting of the measured dispersion relation of the monolayer (cyan) and bilayer (blue) TaS2 with the model based on Eqs. (2) and (4) with the screening length \({\rho }_{0}\) as described in Supplementary Note 5. The data points are the experimentally extracted plasmon energy and momentum values, and the dashed lines are the fitted dispersion relations. c Interband screening component \({\varepsilon }_{{inter}}\) of the dielectric function calculated with screening lengths \({\rho }_{0,{ML}}=28.4\,{{\text{\AA}}}\) for the monolayer and \({\rho }_{0,{BL}}=56.8\,{{\text{\AA}}}\) for the bilayer (see Supplementary Note 5). The solid cyan and blue lines represent the linear q-dependence expected from the Keldysh model of Eq. (4), serving as a visual guide. The black dashed line shows the interband screening calculated ab initio9. The x-error bars are calculated from the momentum resolution evaluated in Supplementary Note 3b. The y-error bars include uncertainty in the plasmon energy \(\hslash \omega\) due to the peak fitting described in Supplementary Note 4, the width of the ZLP, and from the effect of finite \(\Delta q\) resolution as discussed in Supplementary Note 3 and 5. From this, the y-error bars for \({\varepsilon }_{{inter}}\) are calculated from Supplementary Eq. (S23) using propagation of uncertainty.

Full size image

Results and discussion

Three momentum-dispersed parameters were extracted from our measurements: the plasmon peak position, its intensity, and its width. The peak position is used to quantify the confinement ratio in the slow-light regime as well as the interband screening that is responsible for the flat dispersion relation. From the plasmon peak intensity, we demonstrate the transition from 2D to 3D Coulomb interaction at large wave vectors. Finally, the plasmon peak width measurements show the dominance of phonon-assisted Landau damping for these plasmons at room temperature.

Figure 2a presents a series of momentum-dispersed EELS spectra along the \(\Gamma -M\) direction in reciprocal space, with the individual spectra displaced in the y-direction proportional to their momentum. The green disks in the inset of Fig. 2a represent the collection angles \((\Delta {q}_{\beta })\) of the EELS spectra with the corresponding colour. The EELS spectrum collected in each green disk is the probability density \(\frac{{d}^{2}P}{d\Omega {dE}}({{{\rm{\omega }}}},\,q)\) of the energy loss \(E=\hslash \omega\) and the in-plane momentum transfer \(\hslash {{{\bf{q}}}}\) in a solid angle \(\Omega\). The EELS probability density firstly depends on the Coulomb interaction between the fast electron beam and the plasmons, described by the EELS prefactor \({{I}}_{{kin}}\left(\omega,q\right)\), as derived in Supplementary Note 2. Secondly, it depends on the loss function \({{{\mathscr{L}}}}\left(\omega,q\right)={Im}\left({\varepsilon }_{2D}^{-1}(\omega,q)\right)\) of the sample material, which is described by its dielectric function:

$$\frac{{d}^{2}P}{d\Omega {dE}}\,\left({{{\rm{\omega }}}},\,q\right)={I}_{{kin}}\left(\omega,q\right)\times {Im}\left({\varepsilon }_{2D}^{-1}\left(\omega,q\right)\right)$$
(1)

For the case of a 2D electron gas with vanishing thickness \(d\) \(({qd}\ll 1)\) in the non-relativistic limit with negligible radiation loss \((\omega \ll {cq})\), the EELS prefactor \({I}_{{kin}}\left(q\right)\) scales with \({q}^{-3}\) (Supplementary Eq. 14), agreeing with previous formalisms for the case of graphene30,31.

As suggested by da Jornada et al.9, the optical response of TaS2 monolayers can be modelled as the response of an ideal 2D electron gas embedded in a dielectric environment that accounts for a substrate and for interband screening \({\varepsilon }_{{inter}}(q)\). A similar approach was implemented to model 2H-TaSe2 thin films (>10 nm) by Song et al.12. Using this approach in Supplementary Note 2, we show that the loss function \({Im}\left({\varepsilon }_{2D}^{-1}(\omega,q)\right)\) for free-hanging 2H-TaS2 monolayers and bilayers can be written as a Lorentz–Drude function (Supplementary Eq. 16), characterised by the plasmon angular frequency \({\omega }_{p}\left(q\right)\) and damping rate \(\varGamma \left(q\right)\). For each EELS spectrum, we remove the quasi-elastic background (Supplementary Fig. 6) and fit the plasmon peak with a Lorentz–Drude function. In this way, we obtain for each spectrum a specific set of fitting parameters:

  • The plasmon peak position:

    $${\omega }_{p}\left(q\right)=\sqrt{\frac{{{{\mathcal{D}}}}}{2{{{\rm{\pi }}}}{\varepsilon }_{0}}\frac{q}{{\varepsilon }_{{inter}}\left(q\right)\,}},$$
    (2)

    with the Drude weight of the 2D electron gas \({{{\mathcal{D}}}}={{{\rm{\pi }}}}{e}^{2}{\left[\frac{n}{m}\right]}_{{eff}}(q)\).

  • The peak intensity:

    $${A\left(q\right)=I}_{{kin}}\left(q\right)\times \frac{1}{{\varepsilon }_{{inter}}\left(q\right)},$$
    (3)

  • And the peak width: \(\varGamma \left(q\right)\)

Slow light behaviour and strong confinement

In this section and the next, the measured plasmon frequency, i.e. the peak position, is analysed, to quantify the group velocity and strong confinement of plasmons in TaS2 mono- and bilayers. The scatter plots in Fig. 2b show the measured plasmon frequency \({\omega }_{p}\) as a function of wave vector \(q\) for monolayer TaS2 (in cyan) and bilayer TaS2 (in blue), demonstrating their flat dispersion relations. From the EELS spectra, we also measure an interband transition onset energy of 1.5 eV for both monolayer and bilayer samples (Supplementary Fig. 7). This is direct experimental evidence that 2D plasmons in 2H-TaS2 are well-separated from the electron-hole continuum, up to at least 0.15 Å−1 without entering the electron-hole continuum where plasmons are strongly damped.

From the series of EELS measurements on the bilayer TaS2, we can estimate the plasmon group velocity by taking the gradient of the dispersion relation in Fig. 2b as illustrated in Fig. 2a, resulting in a group velocity \({v}_{g}=d\omega /{dq}\) in the order of \({10}^{-4}c\) at the highest wave vector measured here \(\sim 0.1-0.15\,{{\text{\AA}}}^{-1}\). This slow light behaviour leads to strong field confinement. The confinement factor can be estimated based on the maximum observable wave vector outside the electron-hole continuum. Here, we observe an in-plane confinement ratio of \({\lambda }_{0}/{\lambda }_{p}\, \sim 300\) for \(q=0.15\,{{\text{\AA}}}^{-1}\) at \(\omega \approx 1{eV}\), exceeding the values < 200 previously measured in graphene for Dirac plasmons4 and edge plasmons32,33.

Given the trend we observe towards stronger dispersion at high momentum, it is expected that the confinement ratio in TaS2 will be larger—and consequently, the group velocity lower—for measurements done at even larger wave vectors. The maximum \(q\) value measured here is simply limited by the sensitivity and stability of our experimental set-up, especially due to the low EELS cross-section in the monolayer limit compared to its bulk counter-part. At high \(q\), the signal is also much lower than the unavoidable dark background in our used CCD-based EELS detector. Future measurements with single-electron sensitive EELS detectors17 will be able to explore the whole Brillouin zone to find the onset of the e-h continuum where Landau damping dominates, and to confirm whether the negative dispersion relation that was observed in the bulk11 persists in monolayers and few-layer TaS2.

Nonlocal interband screening

The observed slow light behaviour in TaS₂ arises from nonlocal (i.e. q-dependent) Coulomb screening, a universal feature of 2D materials9,12,20,34,35,36. Unlike bulk 3D materials where the dielectric screening is spatially uniform, the reduced dimensionality in 2D materials causes part of the electric field between charges to extend outside the material, making the screening strongly dependent on the distance (\(r\))—or equivalently—the wave vector (\(q\)). For long-range interactions (\({qd}\ll \,1\)), screening is weak and dominated by the surrounding environment, whereas at short distances (\({qd}\gg \,1\)), it approaches the bulk limit. In 2D metallic TaS₂, this nonlocal screening is attributed to the polarizable background of the valence electrons.

Nonlocal interband screening can be characterized with an effective screening dielectric function \({\varepsilon }_{{inter}}(q)\) that shields the interaction with the free charge carriers in the plasmons9,34,35,37. Equation (2) describes the effect of interband screening \({\varepsilon }_{{inter}}(q)\) on the plasmon dispersion. In the low\(-q\) limit \(({qd}\ll 1)\), \({\varepsilon }_{{inter}}(q)\) can be represented analytically with the Keldysh model38 for an ideal 2D monolayer39:

$${\varepsilon }_{{inter}}\left(q\right)=1+{\rho }_{0}q\,,$$
(4)

where \({\rho }_{0}=d{\varepsilon }_{{bulk}}/2\) is the characteristic screening length. More accurate ab initio calculations (the striped line in Fig. 2c) show the deviation from the Keldysh model of \({\varepsilon }_{{inter}}\left(q\right)\) at large \(q\) due to the finite thickness of the real 2D material40.

Figure 2c extracts the nonlocal screening in monolayers and bilayers of 2H-TaS2 by comparing the measured screened dispersion relation with the \(\sim \sqrt{q}\) dispersion relation of an ideal 2D electron gas. This procedure is described in detail in Supplementary Note 5, with the extracted Drude weight and other fitting parameters listed in Supplementary Table 1, and the robustness of the extracted results shown in Supplementary Fig. 10. The extracted interband screening operates for both monolayer and bilayer TaS₂, and exhibits a clear momentum dependence, consistent with nonlocal dielectric screening in atomically thin metals. For the monolayer, the extracted screening length agrees well with ab initio calculations, validating the accuracy of the experimental model. As expected, the bilayer shows a higher degree of screening, attributed to its increased thickness, consistent with Eq. (4), where the characteristic screening length ρo scales proportionally with layer thickness. At large momentum values, both monolayer and bilayer datasets deviate from the linear dependence predicted by the idealized Keldysh model in Eq. (4). This nonlinearity at high \(q\) highlights a deviation from the ideal 2D electron gas, when the finite thickness of the layers becomes non-negligible and modifies the effective dielectric environment. The implication of finite thickness on plasmon behaviour will be discussed in the following section.

From 2D to 3D Coulomb interaction

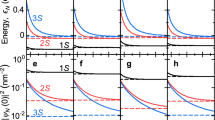
In this section, we analyse the plasmon peak intensity as being the measured EELS probability density. As shown in Eq. (3), this is defined by two terms: the loss function \({{{\mathscr{L}}}}\left(\omega,q\right)\)—defined by the dielectric function of the material, as treated in the previous section—and the EELS prefactor \({I}_{{kin}}(q)\), which describes the interaction of the fast electron beam with the plasmons. In order to reconstruct the optical response of the sample material from measured EELS spectra through a Kramers-Kronig analysis, the EELS prefactor needs to be removed, as described in Supplementary Note 2. Figure 3a, b shows the experimentally extracted loss function after removing the EELS prefactors \({I}_{{kin}}\left(q\right) \sim {q}^{-3}\) derived in Supplementary Eq. (14). The simulated loss functions from the TaS2 monolayer and bilayer are given in Fig. 3c, d, calculated from Supplementary Eq. (16) with the fitted screening length and Drude weight extracted from Fig. 2b and Supplementary Fig. 10.

Fig. 3: Observing the transition from 2D to 3D Coulomb interaction.
figure 3

a Experimental loss function (orange background) of 2H-TaS2 monolayers and b bilayers, extracted from the measured peak intensity and EELS differential loss probability after removing the EELS prefactor \(\sim {q}^{-3}\), assuming purely 2D Coulomb interaction (see Supplementary Note 2b). c Simulated loss function of 2H-TaS2 monolayer and d bilayer using Supplementary Eq. (16) with fitting parameters from Fig. 2b and an estimated damping rate \(\varGamma=0.4\) eV. White dashed lines in panels (a, b) represent the light line. The scatter and line plots in panel (c and d) are the dispersion relation taken from Fig. 2b. e Extracted EELS prefactor \({I}_{{kin}}\) in Eq. (3) for 2H-TaS2 monolayer and f bilayer from the fitted Lorentz–Drude amplitude after removing the interband screening factor \(1/{\varepsilon }_{{inter}}\left({{{\boldsymbol{q}}}}\right)\) in Eq. (3). The y-error bar for EELS prefactor is calculated from Eq. (3) using propagation of uncertainties. Dashed lines show fits to \({I}_{{kin}} \sim {q}^{-3}\) and \({q}^{-3}\), serving as visual guides for the 3D and 2D Coulomb regimes, respectively.

Full size image

The experimental loss function for the monolayer and bilayer 2H-TaS2 is shown as orange background in Fig. 3a, b. It shows an unusual increasing trend at large wave vector \(q\), different from the analytical model presented in Fig. 3c, d. The large mismatch between the experimental and theoretical loss function is due to the underestimation of the EELS prefactor at large\(\,q\), which assumes a purely 2D Coulomb interaction in Supplementary Eqs. (11) and (12). Clearly, an additional effect needs to be accounted for at large \(q\) values. For a more complete description, we extract the EELS prefactor from the fitted Lorentz–Drude peak intensity \(A(q)\) in Eq. (3), by the removing experimentally extracted \({\varepsilon }_{{inter}}(q)\). It now becomes clear that the EELS prefactors follow a \(\sim {q}^{-3}\) relation in the low\(-{q}\) regime and a \(\sim {q}^{-2}\) relation for \(q > 0.05\,{{\text{\AA}}}^{-1}\). Figure 3e, f shows these results, which are robust against different acquisition conditions (see Supplementary Fig. 11), possible normalization artefacts (see Supplementary Fig. 12) and reproducible across different samples (Supplementary Fig. 13).

The extracted EELS prefactors for both monolayer and bilayer TaS₂ (Fig. 3e, f) reveal a clear transition from ideal 2D Coulomb interaction, characterized by a \(\sim {q}^{-3}\) dependence, toward a \(\sim {q}^{-2}\) scaling that is indicative of 3D-like behaviour at larger wave vectors. For the monolayer (Fig. 3e), this deviation becomes noticeable around \({q}\approx 0.03-0.05\,{{\text{\AA}}}^{-1},\) while the bilayer (Fig. 3f) shows a similar crossover at slightly lower values of \({q}\approx \,0.02-0.04\,{{\text{\AA}}}^{-1}.\) This trend is consistent with the expected dependence on material thickness: thicker films lead to an earlier breakdown of the 2D approximation. Notably, this onset coincides with the momentum range where the extracted interband screening \({\varepsilon }_{{inter}}\left(q\right)\) in Fig. 2c also begins to deviate from the linear relation predicted by the Keldysh model. This smooth but consistent departure from ideal 2D electron gas behaviour marks the onset of a dimensional crossover in the Coulomb interaction, where the finite thickness of the flakes begins to confine electric fields within the atomic layers34. Phenomenologically, this can be understood as a transition from a surface plasmon that decays with \({ \sim q}^{-3}\) 41,42 to a bulk plasmon that decays with \({ \sim q}^{-2}\) 41,43,44. Essentially, for 2D electron gases in ultrathin films with vanishing thickness \(d\) (\({qd}\ll 1\)), most of the electric field lines are outside the material, resulting in a surface plasmon-like behaviour. At large \(q\) however, the extent of the electric field in the out-of-plane direction is approximately \({\lambda }_{p}/2\pi \sim 0.6{nm}\), comparable with the layer thickness and the interlayer spacing. In this case, the field is confined almost completely within individual monolayers. As a result, the plasmons behave as bulk plasmons, consistent with the dispersionless property of bulk plasmons. This also means that plasmons in the high\(-q\) regime are more sensitive to local defects and impurities in the 2D material.

It is important to distinguish the plasmons observed in atomically thin TaS₂ from conventional surface plasmons in bulk metals. In bulk systems, surface plasmons are collective oscillations confined to the interface, with dispersion characteristics determined primarily by the dielectric mismatch across the interface. In contrast, the plasmons observed in atomically thin TaS₂ satisfy \({{\mathrm{Re}}}(\varepsilon )\,=\,0\) and exhibit a Lorentz–Drude peak profile, as derived in Supplementary Note 2—features that are conventionally associated with bulk plasmons. Therefore, plasmons in ultrathin metals such as TaS₂ combine characteristics of both surface and bulk plasmons: they are spectrally governed by bulk-like criteria but spatially extended and accessible similar to surface plasmons. These plasmons exhibit unique dispersion features such as a flat band and ultra-slow group velocity not typically observed in conventional bulk metals. As the momentum increases, the field distribution transitions from being external (surface-like) to internal (bulk-like), marking a unique 2D-to-3D crossover in Coulomb interaction.

Highly confined plasmons in suspended metallic monolayers

To further evaluate how plasmons propagate in TaS2, we now quantitatively examine their damping rate from the width of the plasmon peaks. After removing the instrumental broadening from each measured spectrum45 the inherent plasmon peak width \(\varGamma \left(q\right)\) is obtained, presented in Supplementary Fig. 14. As explained in Supplementary Note 3b, the peaks broaden with decreasing wave vector due to the finite \(\Delta q\) resolution. Besides this broadening at low \(q\) predicted in Supplementary Fig. 5, no trend in the peak width is observed in our measurements. \(\varGamma \left(q\right)\) remains 0.3–0.4 eV, irrespective of the wave vector, indicating that there is no observable change in the damping mechanism and that the system does not enter the electron-hole-continuum regime up to the highest measured wave vector of 0.15 Å−1. This conclusion is supported by the measured onset of the interband transition at 1.5 eV, shown in Supplementary Fig. 7. These results underpin the initial hypothesis that the material can support plasmons up to a large wave vector without entering the lossy electron-hole continuum. From our measurements, we therefore conclude that highly-confined plasmons can be established in atomically thin 2H-TaS2 films.

Although the electron-hole continuum is avoided, the 2D plasmons in TaS2 are still very lossy, with quality factors only up to about 3, in stark contrast with the sharp, highly underdamped plasmons calculated by da Jornada et al.9. This suggests that mechanisms beyond intrinsic Landau damping are responsible for the observed losses. Here, we propose that extrinsic Landau damping, driven by atomic defects and especially phonons, plays a crucial role in 2D metals such as TaS2. Landau damping is the energy transfer from the wave (plasmon) to the individual particles (electrons). Sometimes—as in the case of TaS2—this energy transition is forbidden by a mismatch in momentum when the plasmon is outside the electron-hole continuum. This momentum mismatch can be compensated via phonons or atomic defects, allowing energy dissipation through these extrinsic channels.

Extrinsic Landau damping was earlier demonstrated to be temperature-dependent in graphene15,46. Here we argue that this is also the case for TaS2 monolayers and bilayers. First-principles calculations for monolayers47 and optical measurements on bulk TaS248 are used here to calculate the temperature-dependence of the peak widths, shown in Supplementary Fig. 14. The lowest peak widths we experimentally observe are in fact comparable with the calculated electron-phonon relaxation time at room temperature, indeed indicating that phonon-assisted Landau damping is an important damping mechanism. In this regard, the calculated damping rates by Jornada et al.9 are only relevant in the low temperature limit. At room temperature, thermal phonons remain the strongest source of inelastic plasmon scattering, while at lower temperature, thermal phonons are suppressed, making secondary damping pathways more pronounced, such as radiative losses, plasmon scattering on surface inhomogeneities due to oxidation and carbon residues (Supplementary Fig. 15), and scattering on impurities and crystal defects49. We also considered other damping pathways and excluded them. For example, the excitation of electron-hole pairs is inefficient50, and direct plasmon-phonon coupling is weak in this case due to the large mismatch between the plasmon energy around 1 eV and the phonon energy around 0.05 eV, shown in the Raman spectra of Fig. 1c. The dose effect of the electron beam is also excluded, as it does not result in significant changes in the plasmon peak, as shown in Supplementary Fig. 16.

In conclusion, we experimentally confirmed the theoretical predictions that plasmons in monolayer and bilayer 2H-TaS2 disperse to large wave vector values outside the electron-hole continuum. This provides direct experimental evidence of nonlocal screening in 2D metals, demonstrating that the origin of dispersionless plasmons lies in the light field being tightly confined within the atomically thin films. Additionally, our findings confirm the predicted slow light behaviour and extreme light confinement down to the scale of 1–2 nm. Our results compare positively with reported confinement ratios in other ultrathin metallic films, as summarized in Fig. 4.

Fig. 4: Plasmon confinement for various thin films.
figure 4

The dispersion relation of 2D plasmons and polaritons of various thin films are shown, as a function of their confinement ratio. Patterned arrays of 3-nm-thick gold and 40-nm-thick TaSe2 were measured with FTIR12,58; Dirac plasmons and acoustic plasmons in graphene were measured with s-SNOM59,60 and Dirac plasmons in graphene on polar substrates were measured by reflective q-EELS6. The results presented in the present work are indicated by the red star.

Full size image

This work therefore demonstrates that TaS2 and 2D metallic TMDs in general can be potential platforms for flat-band photonics51 and deep sub-wavelength optical spectroscopy applications in the near-infrared regime. The confinement ratio surpasses that of 2D plasmons in graphene and is even on par with phonon-polaritons in the mid-infrared regime17.

Future work at cryogenic temperatures will be able to quantify the reduction in phonon-assisted Landau damping that we predict, as well as the effect of charge density waves on plasmon scattering. Investigations on encapsulated monolayers and multilayers will provide further insight into plasmon coupling and their scattering on structural defects. The experimental and analytical routines we presented here for quantitative q-EELS are applicable to any other (semi-)metallic 2D materials, offering a flexible approach for nano-optical spectroscopy without substrate effects and with high q-resolution.

Methods

Electrochemical exfoliation

A top-down method was used to exfoliate monolayer 2H-TaS2 from a bulk crystal (purchased from HQ graphene). It is particularly more difficult to obtain monolayers of Ta-based TMDs using mechanical cleavage52,53 than from semiconducting TMDs. In this work, we therefore adopt electrochemical exfoliation, to obtain large mono- and few-layer TaS2 flakes with high yield. The liquid also protects the monolayer from oxidation during the exfoliation process, as monolayer and few-layer TaS2 flakes are sensitive to oxidation54. Our electrochemical exfoliation procedure follows the procedure previously described in Zhao et al.25: tetrapropyl ammonium tetrafluoroborate in propylene carbonate was used as the electrolyte, with the bulk TaS2 crystal as the cathode and Pt wire as anode. After exfoliation, the solution was centrifuged at 2500 rpm (419 × g, with g being the free-fall acceleration) to remove the unexfoliated and thick flakes. The supernatant left with ultrathin flakes was collected and further washed at 13,000 rpm (12,040 × g) for three times. If there were still thick flakes, centrifugation at a higher speed would be carried out to get high yield of monolayer and bilayers. The final sediment can be redispersed in various solvents, such as PC, DMF and IPA, with small volume, so that a final dispersion of TaS2 monolayers with high yield and high concentration was obtained.

Crystal structure and electrical transport measurements

Device fabrication for superconductivity and electrical measurements was performed using standard electron beam lithography and e-beam deposition of Ti/Au (5/50 nm) electrodes. The devices were encapsulated with h-BN flakes in an inert glovebox. We carried out four-terminal resistance measurements with an SR830 lock-in amplifier in an Oxford TeslatronPT system operating at a base temperature of 1.5 K.

XRD measurements were performed at room temperature using a Bruker Kappa-APEX2 single crystal diffractometer, equipped with sensitive Apex II CCD detector using a copper X-ray source. The XRD results are shown in Supplementary Fig. 1. Only four peaks are observed in the entire spectrum with sharp lines, indicating the high crystallinity. It agrees well with the pure 2H phase XRD data (PDF 01-080-0685), with the four peaks indexed as (00l) reflections, with l = 2, 4, 6, and 8.

Raman spectroscopy confirms the phase and sample quality of the samples. The spectra were collected at room temperature using a WITec Alpha300 R photon scanning tunnelling microscope (PSTM) equipped with a 532-nm laser. Single spot spectra were collected under a 100× objective and the laser intensity was optimised to get a clear signal from monolayer samples without damaging them. After optimisation, the laser intensity was kept the same for all the measurements.

Monolayers and bilayers were confirmed from optical contrast with reflective bright field light microscopy, and double-confirmed in the STEM through the bulk plasmon peak as shown in Supplementary Fig. 3. The exfoliated flakes are transferred onto holey SiN TEM grids as described in Supplementary Note 1.

Momentum-resolved EELS

STEM-EELS measurements were done using a non-aberration-corrected ThermoFisher Titan TEM with a Schottky electron source operated at 80 kV. A single Wien-type monochromator dispersed the electron beam in energy, and a narrow energy-selecting slit formed a monochrome electron beam with typical full-width at half-maximum values of ~50 meV. Our Titan TEM is a first-generation monochromated system, with a post-column Gatan Tridiem EELS detector. This system does not provide the convenience of performing q-EELS using a modern ω-q slit that would allow fast, parallel acquisition. Instead, our q-EELS experiments were performed in a serial manner using free-lens control to perform precise shifts in momentum-space for each spectrum measurement. Following a method described earlier21,22, we used a convergence semi-angle of 1.38 mrad and physically pushed the sample furthest out of focus (~300 μm) to obtain a continuously magnified diffraction pattern on the Tridiem camera. The irradiated area of the sample was about 500 nm in diameter. The projector lenses magnified the diffraction pattern by 10,000–27,000 times, resulting in an estimated camera length of about 4–8 m (Supplementary Fig. 4). We varied the projector magnification to control the EELS collection angles, as shown by the different sizes of the green disks in Fig. 2a. For each measurement, the projector shift was used to allow different positions in k-space to enter the 1 mm entrance aperture of the EELS detector. Despite the lack of a ω-q slit, it is possible to obtain a high momentum resolution, up to \(q=0.0056\,{{\text{\AA}}}^{-1}\), limited by the \(z\)-height range, sample charging, optical stability and the size of the smallest EELS entrance aperture. The total momentum resolution is presented as the error bars for wave-vector \(q\) in all experimental data points presented above. For each q value, a series of 2000 individual, raw (unprocessed) spectra were collected, each with an exposure time ranging from 50 ms to 200 ms using the StripeSTEM routine55, and applying binned gain averaging56. Separately, 2000 dark background spectra were collected with the same StripeSTEM routine, but now with the electron beam blanked. The average dark background spectrum was subtracted from all raw lowloss spectra, which were subsequently aligned and summed to finally obtain one EELS spectrum with very high signal-to-noise values.

The momentum resolution \(\Delta q\) of our error bars also includes the Heisenberg uncertainty limit \(\Delta {q}_{\beta }\) defined by the collection angle, and the Abbe diffraction limit \(\Delta {q}_{\alpha }\) defined by the convergence angle. This setup provides us with a flexibility to continuously vary the camera length, and therefore \(\Delta {q}_{\beta }\) through defocus \(z\) and the magnification from the projector lenses, as shown in Supplementary Note 3. As our samples are atomically thin and free-hanging, substrate effects and multiple scattering effects are excluded.

Aberration corrected STEM images (Supplementary Fig. 2) were acquired with a JEOL ARM200CF equipped with a cold field emitter and DCOR aberration corrector57, operating at 60 kV. An electron beam convergence semi-angle of 31 mrad was used, and electrons that were forward-scattered between 68 and 280 mrad were measured for atomic-resolution annular dark field imaging.