Introduction

Ferromagnetic materials are essential for modern technologies and industries1,2. Magnetic anisotropy, a fundamental property of ferromagnetic materials, plays a crucial role in tuning their properties for a variety of applications where magnetic hardening and stabilizing are required3,4,5. The conventional strategy for achieving significant magnetic anisotropy relies on two key concepts: the synthesis of magnetic compounds incorporating heavy elements (for instance, the rare earths), and the development of shape anisotropy through nanoscale engineering6,7.

Recent advancements have seen 2D and 3D assemblies of nanoparticles or quantum dots demonstrate collective properties that cannot be found in bulk materials of the same compositions8,9,10,11. Attempts for building up magnetic assemblies have also been made and interesting results on enhanced magnetic hardening are found in the field-induced self-assembled nanoparticles and the patterned soft magnetic nanomagnets12,13. However, the approaches employed thus far encounter limitations in achieving the proximity necessary among the nanomagnets to feasibly develop high anisotropy, while the fundamentals of the collective anisotropy are not well understood.

In recent studies, the high-pressure induced nanocrystal assembly has shown that upon compression, it forms nanowires14,15. In this study, we compressed spherical Fe3O4 nanoparticles of 5 nm in a diamond anvil cell (DAC) under continuously monitored pressure conditions recorded by electron microscopy and in-situ high-pressure synchrotron X-ray scattering. To elucidate the relationship between the developed mesoscale and atomic scale structural modulations and the emergence of novel magnetic properties, we carried out a comprehensive investigation of the magnetic properties by experimental and theoretical studies.

In this work, we report superstructure high magnetic anisotropy resulting from Fe3O4 nanoparticle chains.

Results and discussion

Morphology and crystal structure of the Fe3O4 nanoparticle arrays

Figure 1a shows a representative transmission electron microscopy (TEM) image of the as-synthesized Fe3O4 nanocrystals. The average nanocrystal size is 5 nm with a standard deviation of 10 %. The Fe3O4 nanocrystal multilayers before compression had a closely packed fcc superlattice structure (see also Fig. S1, Supplementary Information). When compressed under an applied isostatic pressure of 18.8 GPa in the sealed DAC, the chain arrays in the form of bundles are formed as shown in Fig. 1b. Each bundle contains many aligned chains that look like nanowires. High-resolution TEM observation found that the wires are nanoparticles assembled in line as shown in Fig. 1c, d. The chains are smooth with lengths of ~800 nm. The formation of the chains may be related to magnetic interactions between the Fe3O4 particles.

Fig. 1: Morphology of Fe3O4 nanoparticles before and after the high-pressure-induced assembly.
figure 1

a Representative TEM images of Fe3O4 nanocrystals synthesized via thermal decomposition process; b Fe3O4 arrays formed after the high-pressure compression. c HR-TEM image of the Fe3O4 nanowires. d HR-STEM image of the Fe3O4 particles in the chains. e SAXS pattern of Fe3O4 nanocrystal arrays at varied pressures, here r is used to display the releasing pressure. The superlattice d111-spacing calculated from first Bragg peak is shown in Fig. S2.

Full size image

The in-situ high-pressure small-angle X-ray scattering (HP-SAXS), shown in Fig. 1e reveals that before the compression, the nanocrystals are arranged in a face-centered cubic (fcc) superlattice with a unit cell parameter afcc = 9.1 nm. Upon continuous increase of pressure, the SAXS peaks gradually shift to higher angles (lower d-spacing), which is an indication of shrinkage of interparticle distances. This shrinkage is more directly noticed in the pressure dependence of the d-spacing plot of the first Bragg peak shown in Fig. S2 (Supplementary Information). It can be seen from this compression curve that the d-spacing continuously decreases and the Fe3O4 nanocrystals continuously approach each other with increasing pressure. The nanocrystals are in contact at a threshold pressure of ~10 GPa, where a minimal d-spacing is reached. When the pressure is released from 9.5 GPa to ambient condition, the SAXS peaks, and the d-spacing returns to the original positions of starting materials, indicating that the change of the unit cell is reversible in the pressure range between 0 and 10 GPa. However, when the pressure is increased above 10 GPa, the contacting nanocrystals began to consolidate, accompanied by a transformation of the mesophase from fcc packing to 2D hexagonal packing as observed in similar size CdSe, PbS, and Au nanocrystals14,15.

To investigate if the applied high-pressure resulted in any structure change at the atomic scale, in-situ wide-angle synchrotron X-ray scattering (WAXS) measurements have been performed. Figure 2 shows the WAXS data collected from the same specimens during compression and pressure release. The results also revealed pressure-induced phase transitions at the atomic scale. Figure 2a–c indicate that the initial spinel cubic Fe3O4 nanocrystals remained cubic with increasing pressure up to ~11 GPa. Above 11 GPa, the phase transformation from cubic to orthorhombic phase occurred. The nanocrystals then remained as orthorhombic with increasing pressure up to about 18.8 GPa. When the pressure is released, the nanocrystals remain in the orthorhombic structure at ambient pressure. The phase transition of Fe3O4 nanocrystals was further confirmed from the calculation of the d-spacing and d-spacing ratio during compression and release (see Fig. 2d, e). It can be seen from this compression curve that the d311- and d400- spacings continuously decreased to ~11 GPa, where minimal d-spacings are reached. When the pressure increased above 11 GPa, the d400- spacing showed a sharply increase as compared to the d311- spacing. More interestingly, if pressure is released from 9.5 GPa to ambient condition, the d400- spacing does not return to the original positions of starting materials, confirming that the change of the unit cell is irreversible. The spacing ratio matches the d103/d004 of the orthorhombic structure of Fe3O4, which further confirmed the atomic scale phase transformation. Experiments and theoretical calculations have illustrated that the pressure-induced phase transitions of Fe3O4 from magnetite (Fd3̅m) to a high-pressure phase h-Fe3O4 (orthorhombic CaTi2O4-type (Bbmm) structure)16,17,18,19. In this work, we observed the pressure-induced phase change in Fe3O4 nanoparticles for the first time The detailed WAXS analysis shown in Fig. 2c reveals the presence of 30% spinel cubic Fe3O4 phase which is likely due to the recovery of the cubic phase of magnetite upon release of pressure (see Fig S3, Supplementary Information), as reported in ref. 18.

Fig. 2: Pressure-induced atomic scale structure change in Fe3O4 nanocrystal during compression and release.
figure 2

a WAXS patterns of Fe3O4 nanocrystal arrays at varied pressures. b WAXS patterns of Fe3O4 as-synthesized nanocrystal, conforming to spinel cubic structure of Fe3O4. c WAXS patterns of Fe3O4 nanoparticle arrays were synthesized with an applied pressure of 18.8 GPa and WAXS data was collected after the pressure release. The WAXS peak matches with the orthorhombic structure of Fe3O4. d The d311- and d400-spacings change with the pressure during compression and release. e d-spacing ratios at different pressures. In the spinel cubic and orthorhombic phases, the d-spacing ratio is d311/d400 and d103/d004, respectively.

Full size image

Magnetic properties of the Fe3O4 nanoparticle arrays

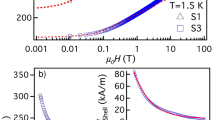
To explore the mesoscale and atomic scale structural transformation effects on magnetic properties of the high-pressure compressed samples (i.e., Fe3O4 nanowire arrays), the zero-field-cooled (ZFC) and field-cooled (FC) magnetization curves and magnetization loops have been measured and compared with that of the as-synthesized nanocrystals with random orientation, the closely packed fcc superlattice before the compression and the compressed bundles of Fe₃O₄ chains, as shown in Fig. 3. In the ZFC curve, as the temperature increased, thermal agitation helps to unblock the randomly frozen particle moments, giving rise to an increase in the magnetization up to the blocking temperature (TB). Above the TB, the further reduction in the timescale of thermal agitation (to below that of the measurement technique) leads to decrease in the magnetization. Figure 3a shows that the samples after the compression have a significantly higher average blocking temperature (TB = 50 K) than the samples before compression (TB ~ 18 K). The enhanced TB in sample after compression is mainly a result of magnetic anisotropy20,21. The deviation from the linear dependence of TB with the packing fraction, especially for NWAs, suggests that the enhanced anisotropy arises from the superstructure (see Fig. S4. Supplementary Information). We calculated the effective magnetic anisotropy constant Keff based on the blocking temperature22,23. Remarkably, the Keff value is found to be a substantial ~2.9 × 105 J/m³. When comparing this to the effective anisotropy value of un-pressed samples (~9.4 × 104 J/m³), it becomes evident that the Keff value for the pressed sample is significantly higher by three times. Although the numbers of Keff are based on estimation without considering the interactions details (see “Method”), the comparison is valid as the TB shift is likely caused by the chain formation. This striking result is supported by the magnetic hysteresis loops shown in Fig.3e, in which only the compressed sample showed coercivity. This is in good consistent with the simulation discussed later.

Fig. 3: Magnetic hardening of Fe3O4 nanowire arrays synthesized by high-pressure compression of Fe3O4 nanocrystal assemblies.
figure 3

a Temperature dependence of low field (50 Oe) ZFC–FC magnetization of as-prepared Fe3O4 nanocrystals (NCs), Fe3O4 self-assembled nanocrystals (SANCs) before compression and Fe3O4 nanowire arrays (NWAs) after compression. b, c The field dependent ZFC magnetization plots of NCs and NWAs, respectively. The red arrow indicated the direction of shift of ZFC maxima (i.e., average TB) with the applied magnetic field. d, e Zoom in of the low field region of room-temperature and 5 K magnetization loops of NCs, SANCs and NWAs, respectively. (See complete magnetization loops in Fig. S5. Supplementary Information) f Temperature dependence of coercivity with Kneller’s law fit for random NWAs.

Full size image

To understand the effects of chain formation on the blocking behavior, we have measured the ZFC magnetization curves with various applied fields for NCs and NWAs (see Fig. 3b, c). The TB of the as-synthesized sample shifts to lower temperatures with an increase of applied magnetic field from 50 Oe to 100 Oe, which is a typical blocking behavior. However, the peaks correspond to the average blocking temperature completely disappeared when field is increased to 500 Oe, indicating that the applied magnetic field overcomes the energy barrier for superparamagnetic relaxations. In contrast, the compressed samples exhibit a strong field dependence of TB, the TB value decreased rapidly with increase of field from 50 to 500 Oe which may be related to proximity effects, mainly the interparticle magnetic dipolar interactions. As the pressure-induced self-assembled particles are present in bundles, they will show strong magnetic interactions as seen in other coalesced magnetic nanoparticle systems. More interestingly, the compressed samples do show blocking behavior at 500 Oe, revealing high Keff value for NWAs.

At 300 K, all the samples showed no hysteresis (Fig. 3d, zero remanence and zero coercivity), indicating that these samples are in the superparamagnetic state with thermally unstable magnetization. If we look at the 5 K magnetization loops, the coercivity (HC) value for the compressed sample is ~400 Oe (Fig. 3e), while that for the un-compressed samples is zero. Figure 3f shows the coercivity onset temperature for the random NWAs sample. The Kneller’s law, \({H}_{c}(T)={H}_{c}(0)[{1-(T/{T}_{B})}^{3/4}]\) is used for the random NWAs assemblies that yield \({H}_{c}\left(0\right)=423{Oe}.\) Since the compressed sample does not exhibit any exchange bias effects when the hysteresis loop is measured after field cooling with an applied field of 50 kOe (Fig. S6, Supplementary Information), the strong magnetic hardening observed upon compression is attributed to the enhanced Keff24,25. To prove the efficacy of high-pressure compression process in developing magnetic hardening in magnetic nanocrystals, we have compared the magnetic properties of the compressed samples with the synthesized Fe3O4 nanorods with average diameter 16 nm and aspect ratio ~10 (see Fig. S7, Supplementary Information). The coercivity value at 5 K for the Fe3O4 nanorods is around 250 Oe, which is considerably lower than that we observed for the compressed samples, indicating that the chain-formation induced magnetic anisotropy is not equivalent to the shape anisotropy.

Micromagnetic modeling of Fe3O4 nanoparticle arrays

Experimental measurements can be validated and better understood by micromagnetic simulations. We create spherical nanoparticles with a diameter of 5 nm similar to those in Fig. 1 using the Salome platform (www.salome-platform.org) and a tetrahedral mesh with a maximum edge length of 0.5 nm. Figure 4 shows the magnetic anisotropy depending on the applied pressure, the nanoparticles show a cubic at pressures less than ~11 GPa (P < 11 GPa) and orthorhombic at pressures up to ~18.8 GPa (P ~ 18.8 GPa) and after the pressure is released from this value. In the following, we compare micromagnetic simulations of several possible particle chain alignments. We are interested in the high-pressure phase of the nanoparticles; therefore, we focus the simulations on the orthorhombic anisotropy particles. For the material properties of Fe3O4, the orthorhombic anisotropy may be approximated to be an easy plane anisotropy, which is defined by its axis normal to the magnetic easy axis of a particle and a negative anisotropy K1.

Fig. 4: Magnetocrystalline anisotropy energy surfaces.
figure 4

Energy surface for the cubic Fe3O4 phase (a) and for the orthorhombic phase (b). The color and shape denote the energy required to rotate the magnetization in the respective direction. Please note the different scale of the two plots.

Full size image

The surface plots of Fig. 4 shows the energy required to rotate the magnetization into the respective direction. Our micromagnetic solver, a hybrid finite element boundary method for magnetostatics26, computes demagnetization curves with the time-dependent Landau–Lifshitz–Gilbert (LLG) equation. As a figure of merit, we are interested in coercivity, given by the external field that drives the magnetization of the model system to zero. We used the intrinsic magnetic properties for low- and high-pressure systems listed in Table 1.

Table 1 Intrinsic magnetic properties for cubic and orthorhombic Fe3O4 nanoparticles
Full size table

For the anisotropy constants of the values reported by Lima et al.27 for the cubic and the orthorhombic phase of Fe3O4. We approximate the magnetocrystalline anisotropy of the high-pressure orthorhombic phase with that of the low-temperature orthorhombic phase27. For the low-pressure cubic phase, we use our own measurements for the spontaneous magnetization and use literature values for the anisotropy constants27 and the exchange constant28. For the magnetization of the high-pressure phase a decrease of the net magnetic moment with pressure has been reported by Ju et al.16. To understand the impact of the magnetization on the magnetization reversal of the high-pressure phase we performed the simulations with high-magnetization (same as that of the cubic phase) and low magnetization (magnetization of the cubic phase reduced by a factor of 0.28). The exchange constant of cubic Fe3O4 was reported by Wu et al.28. We use this value also for the high-pressure orthorhombic phase. Though this is an approximation, the particular value will not influence the reversal process as the Fe3O4 particles have a diameter of only 5 nm. The particles will stay in a quasi-single domain state for a wide range of exchange constants. The time scale for the Landau-Lifshitz-Gilbert (LLG) equation is in the nanosecond or sub-nanosecond range given by the intrinsic precession frequency of the material26. In permanent magnet application and for magnetic hysteresis measurements the relevant time scale is much larger. With respect to the intrinsic time scale, the external field changes slowly and the system moves quasi-statically through the energy landscape. Therefore, we ignore the fast dynamics29 and set the Gilbert damping constant α to 1.

Figure 4. shows the anisotropy energy surfaces for the anisotropy constants given in Table 1. The cubic phase shows an easy axis along the [111] direction. The anisotropy surface for the orthorhombic phase is close to that of a phase with easy-plane anisotropy. However, the b-axis is also a hard axis but its anisotropy constant is about an order of magnitude smaller than that of the a-axis. Figure 5 shows the magnetization reversal curves of the artificially constructed nanoparticle chains with different crystal structures and particle line spacing. Orientation of the particles in chains is assumed to be parallel to the chain axes which gives rise to the upper limits of the coercivity. As an alternative, we selected a set of different parameters from the literature and experiments listed in Table S1 (in Supplementary Information). As a comparison, the simulation results based on Table S1 are shown in Fig. S8.

Fig. 5: The correlation between the particle orientation and the coercivity.
figure 5

a Comparison of magnetization reversal curves for cubic and orthorhombic particles: single particle or chain with 3 or 7 particles stuck together. b Symmetry effects in particle rotations for odd and even number of particles in a chain. c Magnetization reversal curves for hard and easy axis alignment of particle chains. From (a– c), red color maps the magnetization component parallel to the c-axis, and blue color denotes magnetization parallel to the c-axis. d–f Representative HR-STEM images of Fe3O4 nanoparticle arrays obtained via pressure-induced assembly.

Full size image

In our simulations we use a chain of seven particles oriented and arranged along the easy axis. The particle orientation along the easy axis is a hypothesis of the simulations. Therefore, the simulations will give an upper limit for the coercive field that can be achieved in Fe3O4 nanoparticle chains. The external field is applied 1 degree off the easy axis. In order to compute the coercive field, we ramp the external field from µ0Hext = 4 T to µ0Hext = −4 T in 4 µs. The critical value of the external field at which the magnetization component parallel to the external field reaches zero is the coercive field. Fig. S8 compares the coercive field for different configurations. A higher coercivity can be found with orthorhombic anisotropy particles than with cubic anisotropy. With increasing distance between the particles, the coercive field is decreasing. For comparison we also included simulations in which the magnetostatic interactions were switched off. Without magnetostatic interactions the coercive field is smaller for all configurations. The low-magnetization orthorhombic configuration (see Fig. S8c) shows a higher coercive field than the high-magnetization orthorhombic configuration (see Fig. S8b). In the orthorhombic phase the magnetocrystalline energy changes for different directions within a plane perpendicular to the easy axis. As shown in Fig. 4b, it costs more work to rotate the magnetization into the a-axis than into the b-axis. During switching, the magnetization will rotate from the +c through b towards −c. The field required to rotate the magnetization into the b axis is 2Kb/Ms. Multiplying this anisotropy field with the Stoner-Wohlfarth factor for one degree, αΨ = 0.907, gives the coercive field without magnetostatic interactions. The values are 0.121 T for the high magnetization sample and 0.435 T for the low magnetization sample which are close to those of the dashed lines in Fig. S8b–c. Magnetostatic interactions between the particles in the chain increase the coercive field with respect to these values. The magnetic states during magnetization reversal given in Fig. S8c emphasis the importance of magnetostatic interactions. Fig. S8c also shows the magnetization reversal in the particle chain as a function of time for the configuration with a gap of 0.1 nm between the particles. When the external field approaches the coercive field, the magnetization vectors of the two particles at the end start to reverse. The magnetization of these two particles is not stabilized by the magnetostatic interaction field. The reversed magnetization vectors of the particles at the ends create an opposing magnetostatic field at their neighbors which in turn switch their magnetization. This process is continued until the entire chain is reversed. The time difference between the magnetic states is 0.5 ns.

The local arrangement of the Fe3O4 particles in the nanoparticle chains will impact their hysteresis properties. Figure 5d–f shows HR-STEM images of the nanowire structure. Most of the particles coalesce along the vertical direction forming nanowires. For the orientation relationship, Fig. 1c and the associated text depict it briefly. Here, our focus is also on the spatial grouping of the particles. We see that after three to six particles touch each other and form a sub-chain, small gaps can occur (see Fig. 5d). In the transverse direction, the nanowires may touch each other (see Fig. 5e) or are separated by small gaps (see Fig. 5f). The vertical and transverse spacing of the nanoparticles will have a significant impact on the coercive field. In Fig. S9 (Supplementary Information) from top to bottom, we show different magnetic states during demagnetization reversal for 3 chains coupled along the easy axis of the particles. We varied the distance between the particle chains (Fig. S9 from left to right). The very strong interaction indicates that particles connect and switch at the same time vertically or horizontally, can be observed until a gap between the chains of about 4 nm. As soon as particles vertically align, they switch at the same time (green arrows), the coercivity is increased. If upper and lower particles are not coupled, the coercivity is low (red arrows). Micromagnetic simulations showed that dense packing is favorable to achieve high coercivity of Fe3O4 nanoparticles. Certainly, a coupling of particles along an easy axis can improve magnetic performance, which could be seen for single chains as well as for parallel chains.

To compare the results of simulations in Fig. 5 with the results of experiments in Fig.3, we found a good agreement in the coercivity change trend. It is revealed in Fig.5 how strong the particle orientation has effect on the coercivity, especially in the case of orthorhombic particles. Figure 5d–f show practically the particles are not well oriented, which explains why the coercivity values in experiments are lower than the simulations. In addition, the vertical and horizontal spacing has significant effect on the coercivity. These findings are the most important characteristics in the superstructure anisotropy. The micromagnetic simulations show that magnetostatic coupling between the patterned Fe3O4 particles improves the coercivity of particles chains. The closer the particles stronger are the magnetostatic interactions and the higher is the coercive field (see Fig. S8a–c). Owing to the arrangement of the particles into particle chains (see also Fig. S9, Supplementary Information), magnetostatic interactions enhance coercivity. This is a contrast to magnetostatic interactions in systems of randomly placed particles, in which interparticle dipolar interactions reduce the coercive field30,31. However, the simulations were performed for the ideal situation with the particle oriented along the easy axis. Random orientation and coupling of multiple chains may diminish the high coercivity of a single chain of the Fe3O4 particles.

In summary, we have successfully demonstrated a method for preparing ordered arrays of magnetic Fe3O4 nanoparticles via pressure-induced self-assembling under isostatic high-pressure compression in a sealed DAC. It is striking to see a dramatic change in magnetic properties upon compression. The formation of the pressure-induced nanoparticle chain morphology gives rise to greatly enhanced magnetic anisotropy. Although both the cubic Fe3O4 and the orthorhombic Fe3O4 are not uniaxial anisotropy materials with negative in-plane anisotropy, the chain assemblies possess high uniaxial anisotropy with the effective anisotropy constant Keff ~ 2.9 × 105 J/m³, which is several times higher than the assemblies before the compression, leading to magnetic hardening in the compressed nanoparticle chains as measured from the coercivity which is mainly due to the dipolar interactions between the particles in the superstructured chains.

Even though more work is needed to fully understand the mechanisms of collective anisotropy by assembling magnetic nanoparticles, these findings reported open a new window to build up highly anisotropic nanoparticle assemblies for future applications.

Methods

Sample preparation

Monodispersed Fe3O4 nanoparticles were prepared by a solvent-less, energy efficient thermal decomposition approach32. In a typical synthesis of 5 nm nanoparticles, 20 mmol of Iron(III) acetylacetonate (Fe(acac)3) and 100 mmol Oleylamine (OAm) were taken in a european style three-neck round bottom flask. The reaction mixture was dehydrated at 100 °C for 30 min under forming gas ambience, then heated to 150 °C and remained at this temperature for 15 min. The temperature was raised to 240 °C later at a rate of 5 °C/min with further heating for 4 h. After the reaction, the final product was centrifuged and washed with a mixture of hexane and acetone several times to remove uncoordinated OAm molecules.

The crystallization process of Fe₃O₄ nanoparticles occurred within vertically positioned glass test tubes to synthesize the corresponding supercrystals. In a typical growth procedure, a test tube was initially filled with colloidal solutions containing Fe₃O₄ nanoparticles dispersed in toluene. Subsequently, the anti-solvent, isopropyl alcohol (IPA), was gradually introduced from the top, maintaining a precise volumetric ratio of IPA to toluene (4:1). As a result, an interface formed between the two solvents. The total liquid height within the tube was ~56 mm for rapid diffusion and 120 mm for slower diffusion. Throughout the process, the tubes remained undisturbed as counter-diffusion proceeded, evident by the blurring interface. Completion of growth was indicated when the interface vanished, resulting in a homogeneous and colorless mixture. Finally, the Fe₃O₄ supercrystals were collected by removing the liquid, followed by rinsing, and then stored in ethanol.

High pressure compressing

To explore the high pressure–induced self-assembly magnetic nanoparticles, we prepared multilayers of spherical Fe3O4 nanocrystal arrays by solvent evaporation. The dried multilayer samples were loaded into a DAC to allow reversible compression under controlled and continuously monitored pressure conditions. Electron microscopy and in situ high-pressure synchrotron X-ray scattering have been performed to investigate the structure and morphology changes of the nanoparticle assemblies during the pressure application and releasing.

Characterization techniques

TEM was conducted using a JEOL 2010 instrument operating at a 200 kV acceleration voltage. The TEM setup included a Gatan slow scan CCD camera. Additionally, in-situ HP-SAXS and high-pressure wide-angle X-ray scattering (HP-WAXS) measurements were carried out at B1 station within the Cornell High Energy Synchrotron Source. Monochromatic X-ray radiation with a wavelength (λ) of 0.485946 Å was employed33,34. The sample-to-large-area MAR345 detector distance was precisely determined to be 727.19 mm using both CeO2 and silver behenate powder standards. To monitor sample pressure, several small ruby chips were loaded into the DAC chamber, utilizing a standard pressure-dependent ruby fluorescence technique. The blocking behavior of the samples were studied using physical property measurement system (Quantum Design Dyanacool-PPMS). The ZFC, and FC measurements were performed over the temperature range 5–400 K with applied field of 50–500 Oe. The low temperature and room temperature magnetic hysteresis loops were measured with magnetic field of 25 kOe.

Determination of the effective anisotropy constant

The relaxation time of the magnetic moment due to thermal agitation is expressed by the Neel-Arrhenius expression22,23

$$\tau={\tau }_{0}\exp \left(\frac{{K}_{{eff}}V}{{k}_{B}T}\right)\ldots \ldots \ldots \ldots \ldots \ldots$$
(1)

where \({\tau }_{0}\) = 10−9 s. If the experimental measurement time (τm) is longer than the relaxation time (τ), the system remains in superparamagnetic state, while for τ > τm, the system is in blocked state. In typical laboratory measurements, τm ≈ 100 s and τ0 ≈ 10-9 s, the blocking temperature (TB) is expressed as22,23

$${T}_{B}=\frac{{K}_{{eff}}V}{25{k}_{B}}\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots .$$
(2)

Therefore, the TB depends on the magnetic anisotropy and particle volume. In our study, we have used Eq. 2 to calculate effective magnetic anisotropy values for both the samples.

Simulation methods

In order to compute the demagnetization curves, the LLG equation was solved using finite element solver. The magnetostatic interactions were computed with a hybrid finite element boundary method for magnetostatics26. Computational models of the spherical particles and particle chains were created with the Salome platform (www.salome-platform.org, last visited on 2023/04/25). Micromagnetism is a continuum theory. The atomic magnetic moments of a particle are replaced with the magnetization vector M(x) which may change continuously with position x within each particle. For the numerical solution, we use the finite element method. Within each tetrahedral finite element, the magnetization vector is interpolated by a linear function. The particles were discretized with tetrahedral finite elements whereby the maximum edge length of the tetrahedrons was 0.5 nm. The time scale for the LLG equation is in the nanosecond or sub-nanosecond range given by the intrinsic precession frequency of the material12. In permanent magnet application and for magnetic hysteresis measurements the relevant time scale is much larger. With respect to the intrinsic time scale, the external field changes slowly and the system moves quasi-statically through the energy landscape. Therefore, we ignore the fast dynamics29 and set the Gilbert damping constant α to 1.