Introduction

Quantum computers promise to solve classically intractable problems1,2,3,4,5. However, they are unlikely to do so by running quantum programs consisting solely of reversible unitary logic operations (“gates”)2,6,7. Gates are noisy, and their errors accumulate and obscure the answer. All promising avenues to quantum computational advantage rely critically on mid-circuit measurements (MCMs) to reduce entropy during program execution. The best-known (and most trusted) path is fault-tolerant quantum computing using quantum error correction (QEC)8,9,10,11,12, but other approaches like dynamic quantum circuits13 also rely on high-fidelity MCMs. But whereas errors in reversible gates can be measured and quantified using a wide range of well-tested protocols14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29, relatively few methods for quantifying errors in MCMs are available5. Those proposed so far30,31,32,33,34,35,36,37,38,39 have limited scope.

Most previous work on characterizing measurement errors has focused on circuit-terminating measurements that can be described by positive operator-valued measures (POVMs)28,29,40,41,42,43. Investigations of MCMs have emphasized tomographic reconstruction of quantum instruments30,31,32, which enables detailed modeling of one- and two-qubit dynamics but not in situ characterization of errors in large processors. Another approach, certifying that a measurement is near-perfect or possesses certain properties33,34, can rule out specific errors but does not quantify the experimental impact of errors. Recent papers have probed MCM-induced crosstalk35,36, explored Pauli noise learning for MCMs37,38, and assessed single-qubit feedforward operations39, but do not attempt to detect or measure all the errors caused by MCMs in situ in many-qubit circuits.

RB is the most commonly used characterization protocol for measuring gate errors in situ in many-qubit circuits because it mixes all kinds of gate errors together to yield a single, simple error rate14,15,16,17,18,19,20,21,22. But integrating MCMs into this framework is challenging. RB protocols are designed to measure the average fidelity of invertible quantum logic operations (i.e., gates), and most RB protocols execute motion-reversal circuits. A circuit (e.g., a sequence of d Clifford operations) is followed by a circuit that implements its inverse. The combined circuit’s fidelity with the identity operation can be measured easily, and this is the core of standard RB. However, MCMs are inherently irreversible, collapsing the quantum state of the measured qubit(s). Motion-reversal circuits are not possible with MCMs. A different approach is required.

To address this gap, we introduce and demonstrate the first fully scalable protocol for quantifying and measuring the combined rate of all errors in MCM operations on all qubits. Our protocol integrates MCMs into the canonical framework of randomized benchmarking (RB)14,15,16,17,18,19,20,21,22, and models noisy measurement operations as general quantum instruments30,44. MCM operations are placed naturally within random circuits, making it straightforward to measure the rate at which they cause errors in those circuits. We call the protocol quantum instrument randomized benchmarking (QIRB) because it captures general MCM errors described by quantum instruments and yields an overall rate of MCM errors that can be directly compared to RB-derived gate error rates found throughout the experimental quantum computing literature. In contrast to other recent work37,38 that isolates and measures errors in specific circuit layers, QIRB reports the average error rate of all MCM+gate layers, as standard multiqubit RB does for gates.

In this work, we demonstrate QIRB’s validity and practical power by using it to probe, understand, and reduce MCM errors in two very different quantum processors. First, we show how we applied QIRB to study MCMs in a 20-qubit Quantinuum system (H1-1) that was previously used to demonstrate high-performance QEC45. The results (Fig. 1) revealed unexpectedly high rates of MCM-induced crosstalk errors that other methods failed to detect, and allowed us to deduce their location and cause. After we implemented a targeted intervention—micromotion hiding35 in the system’s auxiliary zones—we ran QIRB again, and found the errors had been eliminated. Second, we show how to use QIRB to demonstrate that dynamical decoupling46 reduces MCM-induced errors in 15-qubit layers on IBM Q’s 27-transmon ibmq_algiers system (Fig. 2). These experiments required a protocol that was both scalable (i.e., could characterize MCMs in situ in many-qubit circuits) and generic (i.e., predictably sensitive to all kinds of MCM errors). These same properties enable measuring and predicting the impact of noisy MCMs on fault-tolerant circuits.

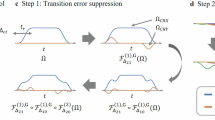
Fig. 1: Quantifying measurement-induced crosstalk in a trapped-ion quantum computer using QIRB.
figure 1

Quantum instrument randomized benchmarking (QIRB) uses the mid-circuit-measurement-containing (MCM-containing) random circuits shown in (a, b) to measure the average error rate (rΩ) of MCM-containing circuit layers. QIRB retains the simplicity and elegance of RB methods for measuring gate errors, as it estimates rΩ as the decay rate of the average circuit success rates (\({\overline{F}}_{d}\)) versus circuit depth, as shown in the examples of (c). We used QIRB to study MCMs in Quantinuum’s H1-1 system, depicted in (g), which arranges 20 171Yb+ ions into auxiliary ("A'') and gate ("G'') zones. Our initial experiments on H1-1 applied micromotion hiding35 only to unmeasured ions in gate zones during MCMs, as ions in auxiliary zones are distant from measured ions. We observed higher error rates in six-qubit QIRB than predicted [compare left with center bars in (d, e)]. We added micromotion hiding for all unmeasured ions, reran QIRB, and observed that the six-qubit error rate was approximately halved [right bars in (d, e)] and was now consistent with the predictions of Quantinuum’s emulator. Results from bright-state depumping experiments (f) independently confirmed the existence of long-range, MCM-induced crosstalk and its mitigation by extra micromotion hiding. These experiments quantify MCM-induced crosstalk errors by measuring the rate at which unmeasured ions, prepared in the \(\left\vert 1\right\rangle\) state, leak out of the computational space as gate-zone ions are measured. All error bars represent bootstrapped 1σ deviations from the sample mean.

Full size image
Fig. 2: Quantifying the impact of dynamical decoupling on measurement-induced errors on ibmq_algiers.
figure 2

a, b Success decay curves from performing 5-qubit (blue), 10-qubit (orange), and 15-qubit (green) QIRB on ibmq_algiers. Experiments were performed with (a) and without (b) dynamical decoupling (DD) on idling qubits during MCMs. c Even with DD, the observed QIRB error rate (rΩ) and the MCM error rate (εMCM) are much larger than predicted by IBM's reported measurement error data, suggesting significant MCM-induced crosstalk errors that are not mitigated by DD. All error bars are 1σ bootstrapped error bars.

Full size image

Results

Quantum instrument randomized benchmarking

QIRB is based on a class of random Clifford circuits that contain MCMs (see Methods for full details). These circuits (Fig. 1a, b) integrate MCMs into the Ω-distributed random circuits used in many modern RB protocols19,20,21,22,23,24. Like other modern RB protocols, QIRB is designed to measure the average error rate of a layer in an Ω-distributed random circuit.

QIRB does so by extending the Pauli-tracking techniques introduced in binary RB22 and first developed for direct fidelity estimation25,47 to circuits with MCMs. Each n-qubit QIRB circuit C containing m MCMs is designed to mimic measuring a random (n  +  m)-qubit Pauli operator sC, with the key innovation being that the processor’s state is ideally stabilized by every MCM. When averaged over all depth-d QIRB circuits, the average expectation value of these Pauli measurements decays exponentially in d (under reasonable assumptions). As shown in the Methods section, the decay rate is an average layer error rate (again under reasonable assumptions).

An n-qubit, depth-d QIRB circuit consists of (i) d circuit layers L1, …, Ld, each sampled from a user-specified distribution Ω, and (ii) additional dressing layers of randomizing single-qubit gates before and after each Ω-distributed layer. Each layer Li specifies the parallel application of MCMs and Clifford gates to the n qubits. QIRB only uses layers that (ideally) implement a computational basis measurement on k≤n qubits. Both reset-free (non-demolition) MCMs intended to leave a measured qubit in the state \(\left\vert k\right\rangle\) conditional on observing k, and reset MCMs intended to re-initialize each measured qubit to \(\left\vert 0\right\rangle\), can be used.

An n-qubit QIRB circuit C containing m MCMs produces m + n readout bits. We use Pauli-tracking techniques to divide the 2m + n possible output strings into two subsets of equal size, called success and fail. Whenever a fail string is observed, it means that at least one error occurred in the circuit’s execution. We quantify the error in a QIRB circuit C with the metric F  =  (Nsuccess  −  Nfail)/N22, where N is the number of repetitions of C, and Nsuccess and Nfail are the number of times a bit string from C’s “success” and “fail” sets (respectively) was observed. We define \({\overline{F}}_{d}\) as the average value of F over all depth-d QIRB circuits. The QIRB error rate (rΩ) is the decay rate of \({\overline{F}}_{d}\) with respect to d.

The QIRB protocol is as follows: For a range of depths d ≥ 0, sample kd Ω-distributed QIRB circuits of depth d. Run each circuit N ≥ 1 times to compute its F. Average F for all of the sampled depth-d circuits to obtain an estimate of \({\overline{F}}_{d}\), and fit it to \({\overline{F}}_{d}=A{(1-{r}_{\Omega })}^{d}\), where A and rΩ are fit parameters. A captures initial state preparation and final measurement error, and rΩ is the estimated QIRB error rate.

Our theoretical analysis of QIRB (see Methods) shows that it satisfies all the expected properties of an RB protocol, and faithfully measures the rate at which MCMs cause errors in random circuits. We show that \({\overline{F}}_{d}\) decays exponentially in circuit depth d (the key property of an RB protocol) for many-qubit QIRB circuits and that the QIRB error rate rΩ is bounded above and below by constant-factor multiples of the average layer infidelity (εΩ): \(\frac{3}{4}{\varepsilon }_{\Omega }\le {r}_{\Omega }\le \frac{3}{2}{\varepsilon }_{\Omega }\), under certain assumptions (see the Methods and Supplementary Note 4 for more details). In most cases, rΩ ≈ εΩ.

Trapped-ion experiments

We used QIRB to detect and quantify unexpected MCM crosstalk in Quantinuum’s H1-1, a 20-qubit trapped-ion quantum computer. H1-1’s qubits are encoded in the atomic hyperfine states of 171Yb+, with \(\left\vert 0\right\rangle\) corresponding to a “dark” state and \(\left\vert 1\right\rangle\) corresponding to a “bright” state that fluoresces when probed by a laser resonant with the \({}^{2}{{{{\rm{S}}}}}_{1/2}\left\vert {{{\rm{F}}}}=1\right\rangle {\leftarrow }^{2}{{{{\rm{P}}}}}_{1/2}\left\vert {{{\rm{F}}}}=0\right\rangle\) transition. Throughout the execution of a circuit, ions are stored in interleaved gate and auxiliary zones (Fig. 1g). When an ion is measured, it (and another possibly unmeasured ion) is moved into a gate zone where the detection laser beam is pulsed on. Stray light from the laser beam or the fluorescing ion can interact with the unmeasured ions to cause MCM-induced crosstalk errors.

Prior to this experiment, it was believed that the large physical separation between each gate zone and auxiliary zone would prevent MCM-induced crosstalk errors on the distant ions in the auxiliary zones, and that only the neighboring ion in a gate zone would be affected by stray light. As a result, Quantinuum’s detailed system emulator accounted for local MCM-induced crosstalk errors (within each gate zone), but no long-range crosstalk. However, our QIRB experiments showed this assumption to be false, revealing significant MCM-induced crosstalk errors in the auxiliary zones.

We ran 2-qubit and 6-qubit QIRB experiments on the first two and six qubits (respectively) of H1-1, and we simulated the exact same circuits on Quantinuum’s emulator. Each QIRB experiment comprised 75 circuits, 15 each at depths d  =  0, 1, 4, 32, and 128. We used Ω-distributed layers consisting of parallel single-qubit Clifford gates, \({\mathsf{cnot}}\) gates, and MCMs. The Ω-distributed layers were sampled to contain a single MCM with probability \({p}_{{\mathsf{MCM}}}=0.35\) and a single \({\mathsf{cnot}}\) with probability \({p}_{{\mathsf{cnot}}}=0.2\). Other experiments with different \({p}_{{\mathsf{cnot}}}\) and \({p}_{{\mathsf{MCM}}}\) showed consistent results (see Supplementary Note 7) and were used to estimate the MCM error rate (see Methods). We ran (and simulated) N  =  100 shots of each circuit to estimate F. All experimentally estimated quantities are reported with 1σ error bars computed via a bootstrap.

The 2-qubit QIRB experiments yielded results (rΩ  =  0.16  ±  0.02 %) consistent with emulator simulations (rΩ  =  0.18  ±  0.02 %). However, the 6-qubit experimental and emulated results showed a significant and unexpected discrepancy (Fig. 1d). The emulator predicted rΩ  =  0.17  ±  0.02 % for 6-qubit QIRB, consistent with the 2-qubit results, while the 6-qubit experiment revealed almost twice as much error (rΩ  =  0.35 ± 0.03 %). Because the QIRB error rate contains contributions from both gate errors and MCM errors, we used the analysis methods of ref. 48 to isolate the MCM error rate (εMCM). We did so by fitting an error model with local depolarizing gate errors and bit-flip measurement errors to the data (see Supplementary Note 5 for more details). The discrepancy between the 6-qubit experimental and emulated εMCM was even larger (Fig. 1e). Consistency between experimental and emulated 2-qubit QIRB results, and between emulated 2-qubit and 6-qubit QIRB results, indicated that the emulator was accurately modeling interactions between neighboring qubits in gate zones. This suggested that the significant discrepancy in the 6-qubit results was due to long-range crosstalk errors, which are not modeled in the emulator.

We hypothesized that these errors were caused by stray light emanating from the detection beam used to measure ions or fluorescence from the measured ions in a circuit layer. To verify our hypothesis, we ran a bright-state depumping experiment35 to independently quantify the strength of MCM-induced crosstalk errors within the auxiliary and gate zones (see Supplementary Note 7). These experiments confirmed our hypothesis (Fig. 1f).

To definitively confirm long-range MCM-induced crosstalk as the cause, we implemented micromotion hiding35 on distant ions during mid-circuit measurements, and then ran 6-qubit QIRB again to measure its efficacy. Micromotion hiding reduces an unmeasured ion’s sensitivity to scattered light by displacing the ion from the RF null, causing micromotion oscillations that Doppler-broaden the resonant detection light. This partially protects the unmeasured ion from stray photons emitted by the detection beam or a fluorescing measured ion during the measurement process. In the initial experiments, micromotion hiding was only applied within each gate zone, not to ions in the auxiliary zones.

When micromotion hiding was applied to ions in the auxiliary zone, the experimental 6-qubit QIRB rΩ dropped from 0.35  ±  0.03 % to 0.18  ±  0.03 % (Fig. 1d). This value is consistent with the 0.17  ±  0.02 % obtained from the emulator. The estimated \({\varepsilon }_{{\mathsf{MCM}}}\) dropped from 0.63  ±  0.09 % to 0.29 ±  0.06 % (Fig. 1e), which is consistent with the 0.23  ±  0.09 % MCM error rate obtained from the emulator. These 6-qubit experimental error rates are also consistent with those observed in 2-qubit experiments and simulations. Finally, we confirmed the physical mechanism of the reduced error rates by repeating the bright-state depumping experiment with the extra micromotion hiding in the auxiliary zones. We observed a substantial drop in the unmeasured ions’ sensitivity to scattered light (see Fig. 1f).

Quantifying MCM crosstalk mitigation on ibmq_algiers

Next, we used QIRB to probe the nature of MCM errors, and measure the positive impact of dynamical decoupling, on an IBM Q processor (ibmq_algiers). For this transmon-based processor, we had neither a high-fidelity emulator nor a detailed theoretical physics model for MCM errors, but its faster clock speed allowed for more detailed experimental exploration. We ran 5-, 10-, and 15-qubit QIRB experiments on ibmq_algiers, with various values of \({p}_{{\mathsf{cnot}}}\) and \({p}_{{\mathsf{MCM}}}\). We focus here on experiments with \({p}_{{\mathsf{cnot}}}=0.3\) and \({p}_{{\mathsf{MCM}}}=0.3\). Other experiment designs are described in the Methods, and experimental results are located in Supplementary Note 6.

To quantify the strength of crosstalk errors, we compared experimental QIRB results – the estimated rΩ and error rates for one-qubit gates, two-qubit gates, and MCMs (ε1Q, ε2Q, and \({\varepsilon }_{{\mathsf{MCM}}}\), respectively)—to predictions made using IBM’s calibration data. IBM’s calibration data is gathered by running two-qubit RB, simultaneous one-qubit RB, and readout assignment error experiments. These protocols are not directly sensitive to MCM crosstalk errors, so discrepancies between observed and predicted quantities can be ascribed to MCM crosstalk errors.

We observed significant gate- and MCM-induced crosstalk errors in ibmq_algiers (Fig. 2a). The 5, 10, and 15-qubit QIRB experiments yielded an experimental rΩ that was 4–5 × larger than simulations using the calibration data (see Fig. 2c). Comparing observed and predicted εMCM indicates that most of this discrepancy is due to measurement-induced crosstalk. The discrepancy between the observed and predicted εMCM increases with n (number of qubits), and for n  =  15, εMCM is 26 × larger than predicted.

MCM-induced errors in transmons can have multiple causes. One mechanism is idling errors on unmeasured qubits. MCMs have a longer duration than one- and two-qubit gates, so unmeasured qubits have more time to decohere and dephase. This can be mitigated by performing dynamical decoupling (DD)46 on the idling qubits, echoing away some of the idling errors. This approach is common and well-motivated, but its efficacy has not been systematically quantified in situ (i.e., in the context of many-qubit circuits).

We ran QIRB circuits into which we introduced XX dynamical decoupling sequences49, and observed a significant reduction in the average layer error rate (Fig. 2c). The observed rΩ decreased by  ~22% at each circuit width, and the estimated \({\varepsilon }_{{\mathsf{MCM}}}\) decreased by as much as 38% (for n  =  15 qubits). This suggests that a large fraction of MCM-induced crosstalk errors are caused by structured T2 idling errors on unmeasured qubits, and confirms that dynamical decoupling on idle qubits can reduce MCM-induced crosstalk significantly. However, the large residual discrepancy between predicted and observed error rates indicates that the majority of MCM-induced crosstalk errors are not mitigable in this way.

Fully characterizing the source of these errors is beyond QIRB; however, we can use the QIRB error rate to test hypotheses about the source of the remaining error. While XX dynamical decoupling sequences echo away structured T2 errors, they do not mitigate T1 decay and unstructured T2 errors. A simple error model based on the IBM calibration data, along with assuming only T1 decay errors on the idling qubits and bit-flip errors on the measured qubits, predicts QIRB error rates of 3.78, 7.17, and 10.2% for the 5-, 10-, and 15-qubit experiments, respectively. This suggests that, while some of the remaining MCM-induced errors are due to additional T1 idling errors, a substantial portion of the error remains uncharacterized.

Discussion

RB is ubiquitous precisely because it is generic. RB protocols mix together all the errors in all of a system’s gates to produce a single exponential decay and a single error rate that can be easily monitored, reported, and compared. But until recently, motion-reversal circuits—concatenating a random circuit with another circuit that inverts it—was the only way to achieve this simplicity. QIRB builds on the recent innovations in binary RB (which sidestepped motion reversal) to extend the simplicity and genericity of RB to MCMs. As our deployment here illustrates, QIRB scales seamlessly to many qubits, and can easily measure error rates below 10−3. It enables in situ characterization of MCMs in processors designed and optimized to implement quantum error correction (QEC), paving the way for full, simultaneous characterization of errors in all the key operations required for fault-tolerant QEC (one-qubit gates, two-qubit gates, and MCMs). We anticipate the techniques introduced here can be used to extend other RB protocols, especially those that measure leakage50,51,52,53, to work with MCMs.

Methods

QIRB circuits

Conceptually, QIRB works by extending the Pauli-tracking approach underlying both binary RB and direct fidelity estimation to circuits with mid-circuit measurements (see Supplementary Note 1). An n-qubit QIRB circuit is designed so that, after each circuit layer, the n qubits are (ideally) always in the  + 1 eigenspace of a particular n-qubit Pauli operator. To ensure this, each qubit that gets measured is immediately rotated to a + 1 eigenstate of a uniformly random single-qubit Pauli. Moreover, before each measurement, single-qubit gates are applied so that the measurement results can be compiled to determine if an error has occurred in the circuit. Thus, a QIRB circuit \(\tilde{C}\) mimics preparing the eigenstate of an (n + m)-qubit Pauli operator and performing an (n  +  m)-qubit Pauli measurement \({s}_{\tilde{C}}\). The success metric for \(\tilde{C}\) is the expectation of its associated Pauli measurement, \(\langle {s}_{\tilde{C}}\rangle\).

The core component of a depth-d QIRB circuit is a sequence of d “dressed” n-qubit circuit layers, each composed of three sublayers, \(\tilde{L}={l}_{3}{l}_{2}{l}_{1}\). The middle layer l2 is an Ω-distributed layer and may contain MCMs. We often refer to l2 as L. Both l1 and l3 are layers of parallel single-qubit gates and/or idles. The single-qubit gates in l1 are chosen to rotate the processor’s state so that it is (ideally) an eigenstate of the n-qubit Pauli operator \({s}^{{{{\rm{pre}}}}}={s}_{{{{\rm{meas}}}}}^{{{{\rm{pre}}}}}\otimes {s}_{{{{\rm{unmeas}}}}}^{{{{\rm{pre}}}}}\), where (i) \({s}_{{{{\rm{unmeas}}}}}^{{{{\rm{pre}}}}}\) has support on the unmeasured qubits, (ii) \({s}_{{{{\rm{meas}}}}}^{{{{\rm{pre}}}}}\) has support on the measured qubits, and (iii) \({s}_{{{{\rm{meas}}}}}^{{{{\rm{pre}}}}}\) is the tensor-product of Pauli-Z or identity operators (i.e., a Z-type Pauli) (see Fig. 3). The gates in l3 are selected so that the k qubits measured in l2 end up in the  +1-tensor-product eigenstate of a uniformly randomly sampled k-qubit Pauli operator (see Fig. 3). When “reset” measurements are used, the l3 layer is constructed to achieve this result assuming the measured qubits are in \({\left\vert 0\right\rangle }^{\otimes k}\); when “reset-free” measurements are used, l3 involves either Xπ gates conditioned on the measurement results or a sign correction in post processing.

Fig. 3: A “dressed” QIRB circuit layer.
figure 3

The bulk of a QIRB circuit consists of a sequence of “dressed” layers \(\{{\tilde{L}}_{i}\}\), each composed of three sublayers: (i) li,1, (ii) li,2, and (iii) li,3. The middle sublayer, li,2 is an Ω-distributed circuit layer, while the other two sublayers are specially crafted. Ideally, the state of the processor before the dressed layer \({\tilde{L}}_{i}\) is stabilized by the Pauli si−1. The first sublayer, li,1 is designed to rotate the state of the processor into an eigenstate of \({s}^{{{{\rm{pre}}}}}\), whose support, \({s}_{{{{\rm{meas}}}}}^{{{{\rm{pre}}}}}\), on the measured qubits in li,2 is a tensor-product of Pauli-Z and I operators. Likewise, li,3 is designed to (ideally) rotate the post-measurement state of the processor into an eigenstate of si, whose support on the measured qubits in li,2 is a uniform randomly chosen m-qubit Pauli operator, \({s}_{{{{\rm{meas}}}}}^{i}\).

Full size image

Formally, the construction of a depth-d QIRB circuit \(\tilde{C}\) is a sequential process that begins by randomly sampling a depth-d Ω-distributed circuit C  =  Ld ⋯ L1. Then, with m being the number of MCMs in C, we sample a uniformly random (n  +  m)-qubit Pauli operator

$$s=s(1)\otimes \cdots \otimes s(n+m)$$
(1)

and a uniform random + 1-tensor-product eigenstate of s

$$\left\vert \psi (s)\right\rangle=\left\vert \psi {(s)}_{1}\right\rangle \otimes \cdots \otimes \left\vert \psi {(s)}_{n+m}\right\rangle,$$
(2)

where \(\left\vert \psi {(s)}_{i}\right\rangle\) is stabilized by s(i). The first layer \({\tilde{L}}_{0}\) in \(\tilde{C}\) is a layer of single-qubit gates that locally prepares the first n-entries in \(\left\vert \psi (s)\right\rangle\). Hence, in the ideal case, the state of the processor following \({\tilde{L}}_{0}\), denoted \({\left\vert \psi (s)\right\rangle }_{0}\) is stabilized by s0: = s(1) ⊗ ⋯ ⊗ s(n).

The d dressed layers \({\{{\tilde{L}}_{i}\}}_{i=1}^{d}\) are constructed in an iterative fashion. In what follows, U(l) denotes the unitary map induced by the circuit layer l on any unmeasured qubits in l, and ki denotes the number of measured qubits in the Li. The first dressed layer \({\tilde{L}}_{1}\) is constructed as follows:

  • Set l1,1 to be a layer of single-qubit gates such that \(U({l}_{1,1}){s}_{0}U{({l}_{1,1})}^{-1}={s}_{0{{{\rm{,meas}}}}}^{{{{\rm{pre}}}}}\otimes {s}_{0{{{\rm{,unmeas}}}}}^{{{{\rm{pre}}}}}\) is a Z-type Pauli on the k1 measured qubits in L1.

  • Set l1,2  = L1, the “core” Ω-distributed circuit layer. Define \({s}_{0}^{{{{\rm{post}}}}}=U({l}_{1,2}){s}_{0,{{{\rm{unmeas}}}}}^{{{{\rm{pre}}}}}U{({l}_{1,2})}^{-1}\otimes {s}_{0,{{{\rm{meas}}}}}^{{{{\rm{post}}}}}\), where \({s}_{0,{{{\rm{meas}}}}}^{{{{\rm{post}}}}}={s}_{0,{{{\rm{meas}}}}}^{{{{\rm{pre}}}}}\).

  • Set l1,3 to be a layer of single-qubit gates such that the measured qubits are re-prepared in a + 1 tensor-product eigenstate of s1,meas  =  s(n  + 1) ⊗ ⋯ ⊗ s(n  +  k1).

In the ideal case, the state of the processor after \({\tilde{L}}_{1}\) should be stabilized by the Pauli,

$${s}_{1}:=U({\tilde{L}}_{1}){s}_{0,{{{\rm{unmeas}}}}}U{({\tilde{L}}_{1})}^{-1}\otimes s(n+1)\otimes \cdots s(n+{k}_{1}).$$
(3)

The remaining dressed layers are constructed similarly using si−1 in place of s0, and the final layer \({\tilde{L}}_{d+1}\) is constructed to transform sd into a Z-type Pauli operator, sd+1. The above description leaves some freedom in the exact choice for each li,1 and li,3 and, in practice, we leverage this freedom to populate li,1 and li,3 with random single-qubit gates on any unmeasured qubits in order to implement randomized compilation for subsystem measurements54 (see Supplementary Note 3).

Overall, \(\tilde{C}\) is constructed to mimic measuring the Pauli operator

$${s}_{\tilde{C}}:={s}_{0{{{\rm{,meas}}}}}^{{{{\rm{pre}}}}}\otimes \cdots \otimes {s}_{d+1},$$
(4)

and we record the expectation of this Pauli operator \(\langle {s}_{\tilde{C}}\rangle\). In practice, this is accomplished by concatenating the results from each MCM and each final computational basis state measurement into a bit string b  =  (b1, …, bn+m), and then returning 1 (“success”) if the corresponding computational basis state \(\left\vert b\right\rangle\) is stabilized by \({s}_{\tilde{C}}\) and  −1 (“failure”) otherwise.

QIRB theory

The QIRB protocol exhibits all of the expected properties of an RB protocol. Which is to say that, under reasonable assumptions about the noise, the average success rate of QIRB circuits (\({\overline{F}}_{d}\)) decays exponentially in circuit depth, at a decay rate that is directly related to the rate at which MCMs and gates cause errors in random circuits. Moreover, this decay rate—or the QIRB error rate (rΩ)—is bounded above and below by constant-factor multiples of the average layer infidelity.

Outside of our description of uniform stochastic instruments, we will assume that n ≫ 1 and that si is uniformly random for each layer i  =  1, …, d in a QIRB circuit. Under standard assumptions on the noise model (e.g., Pauli stochastic errors), this second assumption is approximately true as long as Ω contains layers with sufficiently many entangling gates (it breaks down, e.g., when n  =  1 as non-trivial single-qubit Paulis cannot be rotated into the identity by single-qubit Clifford gates).

Uniform stochastic instruments

To analyze the QIRB protocol, we will model noisy circuit layers as uniform stochastic instruments54. This is a specific ansatz generalizing the Pauli stochastic noise model to quantum instruments, and a processor’s native layers may display errors that are not consistent with it—but any layer L’s error can be transformed into uniform stochastic noise using randomized compiling (RC) for subsystem measurements54. RC for subsystem measurements can be implemented within QIRB (see the section on QIRB circuits); it is not required for the protocol, but is required to guarantee the validity of our theory describing it. As uniform stochastic instruments describe “reset-free” measurements, we introduce a refinement of the general uniform stochastic instrument model to describe “reset” measurements (see Supplementary Note 4).

A uniform stochastic instrument describes errors, in an n-qubit, k-measurement layer, that are the composition of a pre-measurement Pauli X error X⊗a on the measured qubits (specified by the k-bit string \(a\in {{\mathbb{Z}}}_{2}^{k}\)), with a post-measurement error that is the tensor-product of a generic Pauli error P on the unmeasured qubits and a bit-flip error X⊗b on the measured qubits. Here, X⊗a denotes the Pauli operator \({\otimes }_{i=1}^{k}{X}^{{a}_{i}}\).

We denote each possible error by its corresponding tuple (a, P, b) and the probability of (a, P, b) occurring in L by pL(a, P, b). The process (entanglement) fidelity of a uniform stochastic instrument equals the probability of no error occurring55:

$${{{\mathcal{F}}}}(L)=1-{\sum}_{(a,P,b)\ne (0,{\mathbb{I}},0)}{p}_{L}(a,P,b).$$
(5)

The Ω-averaged layer infidelity is defined as

$${\varepsilon }_{\Omega }:=1-{{\mathbb{E}}}_{L\in \Omega }[{{{\mathcal{F}}}}(L)].$$
(6)

In the absence of MCMs, εΩ reduces to the same quantity that is (approximately) measured by most modern RB protocols including direct RB19, mirror RB20, binary RB22 and cross-entropy benchmarking56.

\({\overline{F}}_{d}\) decays exponentially

To show that \({\overline{F}}_{d}\) decays exponentially, we need to calculate the probability Prd(S) of recording + 1 (“success”) and the probability Prd(F) of recording −1 (“failure”) when executing a random depth-d QIRB circuit. Ignoring end-of-circuit measurement error, we can calculate Prd(S) and Prd(F) recursively:

$${\Pr }_{d}(S)={\Pr }_{d-1}(S)(1-{p}^{{{{\rm{trans}}}}})+{\Pr }_{d-1}(F){p}^{{{{\rm{trans}}}}}$$
(7)
$${\Pr }_{d}(F)={\Pr }_{d-1}(F)(1-{p}^{{{{\rm{trans}}}}})+{\Pr }_{d-1}(S){p}^{{{{\rm{trans}}}}},$$
(8)

where ptrans is the probability of errors in a random Ω-distributed layer flipping a stabilizer state of a pre-layer Pauli into an anti-stabilizer state of the post-measurement Pauli. Equivalently, we can compute Prd(S) and Prd(F) by considering a two-state, discrete-time stochastic process with states {S, F} and transition matrix

$$M=\left(\begin{array}{rc}1-{p}^{{{{\rm{trans}}}}}&{p}^{{{{\rm{trans}}}}}\\ {p}^{{{{\rm{trans}}}}}&1-{p}^{{{{\rm{trans}}}}}\end{array}\right).$$
(9)

If A is the probability of preparing in the S (“success”) state and B the probability of preparing in the F (“failure”) state, then

$${\overline{F}}_{d}: \! \!={\Pr }_{d}(S)-{\Pr }_{d}(F)$$
(10)
$$=(A-B){(1-2{p}^{{{{\rm{trans}}}}})}^{d}.$$
(11)

The equality of Eq. (10) and Eq. (11) follows from diagonalizing M and noting that its eigenvalues are 1 and 1 − 2ptrans.

So far, we have ignored end-of-circuit measurement errors. These errors contribute a depth-independent cofactor as they modify the rate at which the S and F states are recorded in a depth-independent fashion. Hence,

$${\overline{F}}_{d}\propto {(1-2{p}^{{{{\rm{trans}}}}})}^{d}.$$
(12)

This result shows that \({\overline{F}}_{d}\) decays exponentially and that rΩ is well-defined, rΩ  =  2ptrans. Moreover, rΩ represents twice the rate at which errors flip stabilizer states to anti-stabilizer states in a circuit layer, a generalization of the interpretation of entanglement fidelity as twice the rate at which errors in a circuit layer anti-commute with a random Pauli. This interpretation allows us to compute rΩ for a given error model, and to relate rΩ to the average layer infidelity of that error model.

Interpreting r Ω

Because rΩ is twice the rate at which errors flip stabilizer states to anti-stabilizer states in a circuit layer, it has the following form:

$${r}_{\Omega }={{\mathbb{E}}}_{L\in \Omega }\left[{\sum}_{a,P,b}{\lambda }_{L,a,P,b}\right],$$
(13)

where λL,a,P,b is twice the rate at which the error (a, P, b) occurring in a layer L causes a state transition. We now argue that λL,a,P,b depends upon: (i) the probability pL(a, P, b) at which (a, P, b) occurs in L; (ii) the probability of X⊗a anti-commuting with a random \({s}_{{{{\rm{meas}}}}}^{{{{\rm{pre}}}}}\); (iii) the probability of X⊗b anti-commuting with a random \({s}_{{{{\rm{meas}}}}}^{{{{\rm{post}}}}}\); and (iv) whether \(P={\mathbb{I}}\). Table 1 summarizes an error (a, P, b)’s contribution to rΩ.

Table 1 Individual error contributions for QIRB
Full size table

An error (a, P, b) causes a state transition when one (but not both) of the following occurs: (I) the pre-measurement error causes the reported state to be anti-stabilized by the pre-measurement Pauli instead of stabilized and (II) we prepare a post-measurement state that is anti-stabilized by the post-measurement Pauli instead of stabilized. Event (I) occurs when X⊗a anti-commutes with \({s}_{{{{\rm{meas}}}}}^{{{{\rm{pre}}}}}\). Event (II) occurs whenever X⊗b anti-commutes with \({s}_{{{{\rm{meas}}}}}^{{{{\rm{post}}}}}\) (exclusive) or P anti-commutes with \({s}_{{{{\rm{unmeas}}}}}^{{{{\rm{pre}}}}}\). Averaging over all possible pre- and post-measurement Paulis, either event (I) or (II) occurs with probability 1/2 when \(P={\mathbb{I}}\). Otherwise, they occur with probability panti(a)  + panti(b) − 2panti(a)panti(b). The values in Table 1 come from multiplying these results by 2pL(a, p, b).

Bounding r Ω

We now prove the following bound on rΩ,

$$\frac{3{\varepsilon }_{\Omega }}{4}\le {r}_{\Omega }\le \frac{3{\varepsilon }_{\Omega }}{2}.$$
(14)

This bound comes from analyzing the term

$${p}_{{{{\rm{anti}}}}}(a)+{p}_{{{{\rm{anti}}}}}(b)-2{p}_{{{{\rm{anti}}}}}(a){p}_{{{{\rm{anti}}}}}(b)$$

in the \(P={\mathbb{I}}\) entry of Table 1 for all possible values of a and b. The possible values of this term form a discrete set on the two-dimensional surface in \({{\mathbb{R}}}^{3}\) defined by the equation x  +  y  − 2xy. The grid points are determined by the Hamming weight of a and b. As shown in Supplementary Note 4, this set has a minimum value of 3/8 when the sum of the Hamming weights of a and b is 2, and a maximum value of 3/4 when the sum of the Hamming weights is 1. This completes the proof.

In practice, this bound is pessimistic. Closer analysis of panti(a)  +  panti(b)  −  2panti(a)panti(b) shows that it rapidly approaches 1/2 as the Hamming weights of a and b increase. Thus, most errors contribute roughly pL(a, P, b)/2 to ptrans and rΩ ≈ εΩ.

Simulations

We used simulations to validate the predictions of our QIRB theory: \({\overline{F}}_{d}\) decays exponentially at a rate rΩ predicted by our theory. To do so, we simulated QIRB on simulated noisy 2, 4, and 6-qubit quantum computers with native single-qubit Cliffords, \({\mathsf{cnot}}\) gates with all-to-all connectivity, and MCMs with post-measurement reset. We modeled gate errors as local depolarizing channels and noisy measurements as perfect computational basis measurements preceded by a bit-flip error channel. We used the same layer sampling rules as in our trapped-ion and IBMQ experiments, with \({p}_{{\mathsf{cnot}}}\) values of 0.2, 0.35, 0.5 and \({p}_{{\mathsf{MCM}}}\) values of 0.01, 0.02, 0.05, 0.10, 0.25, 0.5. See Supplementary Note 5 for additional details on the noise model, experiment designs, and full results.

Figure 4 summarizes the results from our simulations. The data shows close agreement with our theory: the decays are exponential, rΩ is well predicted by our theory, and our extracted error rates agree with those used to generate the data. These results confirm QIRB’s validity in simulation.

Fig. 4: Simulation of QIRB on few-qubit QPUs with a simple error model.
figure 4

a, b RB curves from two two-qubit [(a)] and two [(b)] six-qubit QIRB-r simulations performed using \({p}_{{\mathsf{cnot}}}=.35\) and \({p}_{{\mathsf{MCM}}}=.01\) (blue) or \({p}_{{\mathsf{MCM}}}=.5\) (orange). The points show \({\overline{F}}_{d}\), and the violin plots show the distributions of \(\langle {s}_{\tilde{C}}\rangle\) over circuits of that depth. QIRB has succeeded in all four cases as evidenced by the exponential decay of \({\overline{F}}_{d}\). c A plot comparing rΩ from eight two-, four-, and six-qubit simulations (blue, orange, and green, respectively) with varying \({p}_{{\mathsf{MCM}}}\) and fixed \({p}_{{\mathsf{cnot}}}=.35\) (the points) against our predictions for rΩ (the lines) based on the data-generating model. The error bars are 1σ error bars generated by performing each simulation eight times. These results validate QIRB as the rΩ observed in each simulation matches that predicted by our theory. d Table containing the extracted one-qubit gate, \({\mathsf{cnot}}\), and MCM error rates (resp. \({\varepsilon }_{{{{\rm{1Q}}}}}{{,}}\,{\varepsilon }_{{{{\rm{2Q}}}}}{{,and}}\,{\varepsilon }_{{\mathsf{MCM}}}\)). We see close agreement between the estimated error rates and those used to generate the model. See Supplementary Note 5 for additional details.

Full size image

Trapped-ion experimental details

We conducted QIRB experiments on Quantinuum’s H1-1, utilizing the first 2 and 6 qubits of the device, both with and without micromotion hiding (MMH) in the auxiliary zones. Using the layer rules described in the main text, we constructed QIRB experiment designs using \({p}_{{\mathsf{cnot}}}\) equal to 0.2 and 0.35, and \({p}_{{\mathsf{MCM}}}\) of 0.2 and 0.3. For each experiment, we generated a total of 15 circuits at the depths d  = 0, 1, 4, 32, and 128, resulting in 75 circuits per experiment, with each circuit executed 100 times. We also simulated each experiment on Quantinuum’s emulator. We employed the fitting procedure outlined in Supplementary Note 5 to extract estimated one-qubit gate, two-qubit gate, and MCM error rates from both the experiments and simulations. Additionally, we generated 100 bootstrapped samples to assess the uncertainty of and 30 bootstrapped samples to estimate the uncertainty in the extracted error rates. Results from each experiment are detailed in Supplementary Note 7.

IBM Q demonstration details

We conducted QIRB demonstrations on the first 5, 10, and 15 qubits in ibmq_algiers. The layer rules applied in our ibmq_algiers demonstrations were consistent with those used in our trapped-ion experiments, with the exception that we limited the placement of \({\mathsf{cnot}}\) gates to the edges of ibmq_algiers’ connectivity graph. We used \({p}_{{\mathsf{cnot}}}\) values of 0.2, 0.35, and 0.5 and \({p}_{{\mathsf{MCM}}}\) values of 0.2, 0.3, and 0.4. Results from all of these experiments were used to estimate one-qubit, two-qubit, and MCM error rates using an error rate model (see Supplementary Note 5). The QIRB error rates for each demonstration can be found in Supplementary Table 1, along with bootstrapped standard deviations derived from 30 bootstrapped samples.