Introduction

Geometric phases, originating from the evolution of instantaneous eigenstates of a system’s Hamiltonian in parameter space, are universal features that play a fundamental role in a wide range of phenomena. It is a manifestation of the underlying curvature of the parameter space, which was first observed in a generalized interference experiment with vector fields by Pancharatnam1, later formalized by Berry in the context of adiabatic evolution of quantum mechanical states2. Since its discovery, the geometric phase has led to a foundational ground for a variety of ubiquitous features in several areas of physics, including topological phase transitions in condensed matter systems, Aharonov-Bohm effect, spin-orbit coupling, polarization manipulation, and singular optics3,4,5,6,7,8,9,10,11,12,13,14. Furthermore, with the rapid advancement of nanophotonic technology, the geometric phase has become a routine tool to manipulate and control wavefront in a spin-dependent manner15. In metasurfaces, it specifically accounts for the relative geometric orientation of the meta-atoms and the helicity reversal of evolving polarization states on the Poincaré sphere—popularly known as the Pancharatnam-Berry (P-B) phase16,17,18,19,20,21,22,23,24,25. However, all existing P-B phase methods fail to modulate the input polarized light, which we define herein as the co-polarized channel.

To address this issue, we propose and experimentally demonstrate a novel phase addressing mechanism that works similarly as the P-B phase but for co-polarized channel, by encircling a C-point polarization singularity in the parameter space14. In this approach, we exploit the mapping of the phase dynamics from the eigen parameter space onto the Poincaré sphere, uncovering a hidden phase singularity on the surface of the Poincaré sphere, referred to as the co-polarized singular phase. This previously untapped topologically protected singular phase enables the realization of innovative wavefront control devices. The experimental demonstration of the co-polarized singular phase is achieved through manipulating the chiral response of a lossless multi-layer metasurface that operates in the microwave regime. As opposed to the classical P-B phase, the co-polarized singular phase is fundamentally distinct and can be integrated with other phase addressing mechanisms, such as dynamic phase, to achieve asymmetric phase modulation for two orthogonal input polarizations, broadband wavefront engineering and so forth26, thus enabling advanced wavefront modulation capabilities that go beyond the limitations of conventional techniques.

Results

The polarization properties of paraxial light propagating in a medium, or through any polarization-sensitive device, are described by a two-dimensional incident polarized field, mathematically represented by a ket vector, and a 2 × 2 matrix representing the polarization response of the medium. The change of polarization is therefore mathematically analogous to the evolution of a spin state in a classical two-level quantum system. Each polarization state is uniquely mapped onto the surface of the Poincaré sphere under the Cartesian coordinate of the Stokes vector, where the north and south pole of the sphere correspond to right- and left-hand circular polarization (RHCP and LHCP) respectively, both constituting the orthonormal basis of the polarized light. In this representation, the degree of polarization, that is the amount of light presenting a well-defined polarization state, is given by the distance of the representative polarization point inside the sphere from the center, ranging from zero at the origin for an unpolarized light, to unity (1) at the sphere surface for a completely polarized light. Assuming a Hermitian optical device (lossless) with orthonormal eigenstates |n±〉 and corresponding eigenvalues exp(iϕ±), its polarization-dependent Jones matrix can be expressed as:

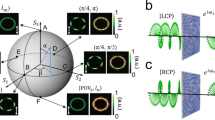
$$\hat{U}(\hat{n},\delta )=\exp \left(i\frac{\delta }{2}\hat{n}\cdot {\hat{{{\boldsymbol{\sigma }}}}}^{*}+i\phi \right)$$
(1)

where \(\hat{n}\) is the Stokes vector of |n+〉 and \(\hat{{{\boldsymbol{\sigma }}}}=\left({\hat{\sigma }}_{x},{\hat{\sigma }}_{y},{\hat{\sigma }}_{z}\right)\) is the vector of Pauli spin matrices (see supplementary text 1). Parameters ϕ and δ correspond to the dynamic phase (also dubbed the propagation phase) and the eigen birefringence, respectively. These quantities are related to the mean and difference between ϕ+ and ϕ−, respectively. Equation 1 indicates that the polarization evolution for any arbitrary input state is solely determined by the evolution operator \(\hat{U}\). Especially, the degeneracy of the Jones matrix (\(\hat{U}\)) occurs when all three components of the eigen Stokes vector become identically zero—corresponding to a completely unpolarized eigenstate. In other words, the degeneracy point lies exactly at the center of the Poincaré sphere, acting as the source of Berry curvature, namely a virtual magnetic monopole with intensity −1/2 gathering magnetic field inward. We should keep in mind that using magnetic parlance for illustration is merely a matter of convention. As shown in Fig. 1A, the magnetic flux enclosed by the loop associated with a polarization evolution along a closed curve represents the well-known P-B phase in optics. For instance, when an RHCP state |R〉 is converted to LHCP state |L〉 by a device with eigenstate |n〉 whose Stokes vector has an azimuth 2ψ, state |R〉 evolves from north pole to south pole along the meridian at 2ψ − π/2 (blue meridian). Compared to a device with an azimuth zero, evolving along the black dashed meridian at −π/2, the solid angle swept counterclockwise from the black meridian to the blue meridian is Ω+ = 4ψ (blue area). Conversely, input |L〉 is converted to |R〉 along the same meridian with an opposite sweeping direction of the solid angle, and thus Ω− = 4π − Ω+. The magnetic flux is equal to half of the area, i.e., γ+ = −γ− = −2ψ, where the sign on the two orthogonal cross-polarized channels is always opposite. Continuously changing the azimuth ψ of the device’s eigenstate up to π, a linearly varying P-B phase accumulation as a function of ψ, ranging from 0 to 2π, can be imparted on the cross-polarized wave.

Fig. 1: Comparison between different phase-addressing mechanisms.
figure 1

A Typical Pancharatnam-Berry phase, associated to cross-polarized phase modulation and originating from the degeneracy of the Jones matrix, corresponds to the magnetic flux of a virtual monopole of intensity −1/2 positioned at the center of the Poincaré sphere. Considering the transmission of a right incident circularly polarized wave \({|}R\rangle \,\) through birefringent materials with eigenstate of azimuth ψ (thick blue arrow), polarization evolves along the meridian from the north to the south pole. Choosing two different meridians, two cross-polarized beams taking two different meridian trajectories would present a phase difference equal to half of the magnetic flux through the blue solid angle Ω swept counterclockwise between the two meridians (blue and dashed blacklines). B The dynamic phase is polarization-independent and only depends on mean phase ϕ = (ϕ+ + ϕ−)/2 of the eigenvalues exp(iϕ±), and therefore applies to any polarization channel equally. C The evolution of polarization state and the emergence of a co-polarized phase singularity on the Poincaré sphere are governed by the system’s eigen parameters \((\delta,\chi )\). The input state \({|}R\rangle\) undergoes precession around the eigenaxis \(\hat{n}\left(\chi \right)\) by an angle \(\delta\), transitioning to an intermediate state \({|}\Psi \rangle\), tracing the red curve. The subsequent projection back to the initial state follows the blue dashed curve, acquiring an additional phase, which is evident from the relative configuration of the initial and final \({|}R\rangle\) states. The accumulated phase, solely depends on the curvature of the traversed path, has a pure geometric origin. Variation in the eigen parameters alters polarization trajectory on the Poincaré sphere and thereby modifying the accumulated geometric phase. When the eigen axis crosses the equator \(\hat{n}\left(\chi=0,\,\psi={constant}\right)\,\) with \(\delta=\pi\), the input \({|}R\rangle \,\) state reverses its helicity (red dashed curve), and the accumulated geometric phase through the projective measurement depends on the shortest geodesic path. A very small variation around \((\delta=\pi,\chi=0{)}\) shifts the position of \({|}\Psi \rangle\), affecting the projection path. This leads to a co-polarized singular phase, which lies exactly at the antipodal point |L〉 denoted with the star mark. This phase singularity emerges in complex amplitude of the co-polarized transmission channel at the Stokes parametric position of \({|}\Psi \rangle\), representing a topological variant of the geometric P-B phase.

Full size image

Meanwhile, the dynamic phase is generic and has been widely applied for phase engineering. Such phase corresponds to the mean phase ϕ of the eigenvalues exp(iϕ±), which is equally applied to both eigen polarization channels. Notably, the dynamic phase can be set to zero by selecting opposite eigenvalues, i.e., ϕ+ = −ϕ−. Since it is trivial and exhibits homogeneously for any polarization state, the dynamic phase is monotonically distributed on the Poincaré sphere as shown in Fig. 1B.

Considering the polarization properties of both the P-B and dynamic phases, it is evident that a non-trivial phase for the co-polarized wave is still missing. The transmission amplitude in a pure co-polarized channel drops to zero at the antipodal point, directly opposite the incident polarization on the Poincaré sphere. This basic observation reveals that a singularity exists only when considering a projection onto the co-polarized transmission channel. A continuous and topologically protected 2π phase shift accumulation is expected when choosing a continuous parametric evolution that traces a polarization trajectory around the singularity.

Consider the input is a RHCP state, denoted as \({|}R\rangle\), and the polarization evolution on the Poincaré sphere is governed by the Jones matrix \(\hat{U}(\hat{n},\delta )\), characterized by its eigen birefringence δ and eigen ellipticity χ. The input state precesses counterclockwise around the eigen axis \(\hat{n}\left(\chi \right)\,\) by an amount of δ, tracing the red curve from \({|}R\rangle\) to \({|}\Psi \rangle \,\) as shown in Fig.1C. The projection of \({|}\Psi \rangle\) back to the initial input state \({|}R\rangle\), is followed by the blue dashed curve representing the shortest geodesic, which can be mathematically performed with the projection operator as \({\hat{P}}_{+}\left|\Psi \right\rangle=\left|R\right\rangle \left\langle R\right|\left|\Psi \right\rangle\). Notably, the initial and projected states are exactly at the same position on the Poincaré sphere, i.e., the north pole. However, the final projected state picked up an additional phase, which can be distinctly seen from the relative configuration of the initial and final polarization state |R〉. This additional phase arises due to the underlying curvature of the trajectory on the Poincaré sphere. Importantly, this phase accumulation is independent of the rate at which the path is traversed; rather, it depends solely on the geometry of the Stokes parameter space. Therefore, the projected phase in the co-polarized channel is purely geometric in origin, which can be referred to as the co-polarized geometric phase. The complex co-polarized transmittance across eigen parametric coordinates R = (δ, χ), can be derived from Eq. 1 as:

$${t}_{{co}}=\cos \frac{\delta }{2}+i\sin \frac{\delta }{2}\sin 2\chi$$
(2)

Now, by tuning the eigen vectors \(\hat{n}\left(\chi \right)\) while keeping the same azimuth, the orientation of the eigen axis shifts along the meridian. Consequently, the RHCP input |R〉 follows different trajectories on the Poincaré sphere, leading to varying accumulated geometric phases in the co-polarized channel projective measurement. Interestingly, when the eigen axis of the material crosses the equator \(\hat{n}\left(\chi=0\right)\), with a retardance of \(\delta=\pi\), the RHCP state reverses its helicity. At this point, the accumulated geometric phase upon projection to the initial \({|}R\rangle \,\) state depends on the shortest geodesic path followed. A small variation of the eigen parameters around δ = π, χ = 0, alters the position of the state \(\left| \Psi \right\rangle\) and thereby modifies the projection path. The shortest geodesic would follow any meridian trajectory at the antipodal point, leading to a co-polarized singular phase at the corresponding antipodal point \(\left| L \right\rangle\) of the input \(\left| R \right\rangle\) state. This singularity is evident when plotting the phase of the complex projection amplitude \({{{\arg }}}(t_{{co}})\) at the Stokes parametric position of \(\left| \Psi \right\rangle\) as shown in Fig. 1C. The proposed co-polarized singular phase represents a distinct variant of the geometric P-B phase, that has a deep topological root in the polarization ellipse dynamics, and its dependence on the system’s eigen parameters.

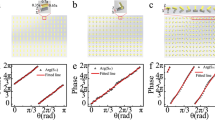
To further analyze the singular behavior of the geometric P-B phase, we plot the polarization ellipse of the intermediate state\({|}\Psi \rangle\) in the 2D eigen-parameter space in Fig. 2A. As it is very evident that at the center \(\delta {{=}}\,\pi,\chi=0\), a C-point polarization singularity appears with a unity transmission amplitude as we are dealing with only lossless Hermitian systems. Moreover, the state \({|}\Psi \rangle\) is decomposed into two orthogonal circular components using the respective projection operators: \({\hat{P}}_{+}=|R\rangle \langle R|\) for RHCP and \({\hat{P}}_{-}={|L}\rangle \langle L|\) for LHCP state. In Fig.2C, D, the co-polarized projection reveals the existence of a phase singularity with a vortex like behavior in the eigen parameter space for complex transmission amplitude \({t}_{{co}}\). However, it is important to note that the projected co-polarized beam should not be confused with vector vortex or orbital angular momentum (OAM) carrying beams, as it always preserves its initial input spatial modes—here a plane wave. This observed co-polarized singular phase provides a foundation for designing the meta-atoms to modulate wavefronts in a spin-preserved manner. The transmission amplitude of the co-polarized component is zero at the singular C-point and reaches maximum unity at the edges of the parameter space as shown in Fig. 2C. Moreover, three closed loops in the eigen parameter space—the solid (outside), dashed (crossing) and dotted curve (enclosing the singular C-point) are considered. The corresponding trajectories of the state \({|}\Psi \rangle\), along with the co-polarized phase distribution, are shown on the surface of the Poincaré sphere (Fig. 2B). When the singular C-point is enclosed in the eigen parameter space, such as along the dotted trajectory, the co-polarized transmission channel undergoes a complete 0 to 2π phase modulation, which validates the proposed concept. In contrast, the cross-polarized channel has a constant phase across the eigen spectrum as shown in Fig. 2F, and a maximum transmission amplitude at the C-point, which gradually decays toward the edges. Considering any arbitrary path enclosing this singularity, that is, assuming a path in material parameter space that enables continuously changing the \((\delta,\chi )\) values to circulate around the singular point \((\delta=\pi,\chi=0)\), a 2π phase accumulation can be obtained. This parametric circulation of the material parameters can potentially be realized, for example, by tailoring the structural properties of a set of meta-atoms.

Fig. 2: C-point polarization singularity and associated co-polarized singular phase in the eigen parameter space(δ, χ).
figure 2

A Distribution of the polarization ellipses of \({|}\Psi \rangle\) in the eigen parameter space. The evolution of the input state creates a C-point polarization singularity at \(\delta=\pi,\chi=0\), containing the antipodal LHCP state at the singular point. Three different closed loops outside (solid circle), crossing (dashed circle), and encircling (dotted circle) the singular C-point are considered. B The corresponding trajectories of \({|}\Psi \rangle\), along with the co-polarized phase distribution are displayed on the Poincaré sphere. The yellow star represents the position on the Poincaré sphere where the singularity appears. C–F The decomposition of the \({|}\Psi \rangle\) into the co-and cross-polarized channels is performed by the respective projection operators, representing amplitude and phase distribution in the eigen-parameter space. Notably, at the C-point, the co-polarized phase becomes singular and circulation of this topologically protected phase enables complete 2π wavefront modulation in a spin-preserved manner.

Full size image

In addition to 2π phase coverage, the amplitude is also crucial since it delimits the transmission efficiency in applications. To explicitly display the topological relationship between the complex amplitude of the path around the singularity, the sphere in Fig. 1C is expanded according to the amplitude and phase at each point, as shown in Fig. 3A. The conical surface denotes the transmission amplitude, and the tip corresponds to the singularity at the south pole of the sphere, indicating as well that the phase projected on the bottom plane gradually varies by 2π around the singularity. Significantly, the path on the top of the conical surface offers a constant transmission coefficient approaching unity, corresponding to the case of optical rotation with χ = ±π/4, i.e., the eigenstate of the meta-atom and incident polarization are consistent (both are CP here), and the co-polarized singular phase imposed to the RHCP preserved transmittance is linear to δ/2. Exploiting circular birefringent meta-atoms, that is, designing subwavelength structures that exhibit polarization rotation by manipulating the phase delay of \({|L}\rangle \,\) and \(|R\rangle\) using optical chirality, we encircle the singularity by eight representative elements. As shown in Fig. 3B, the meta-atom consists of three layers of copper structure, where both the top and bottom layers contain four identical copper patches forming chiral C4z symmetry to protect the eigenstate as CP. The corresponding top and bottom patches are electrically connected by vertical metal vias, carefully assembled to avoid touching the middle ground plane. Due to this structural configuration, the meta-atom can manipulate circular birefringence δ quasi-linearly by the relative rotation angle θ between the top and bottom patches, which follows δ ≈ 2θ and the phase of the two co-polarized channels is ζ+ = −ζ− ≈ θ. Elements No. 1 to 4 and No. 5 to 8 correspond to ζ+ increasing from −π/2 to π/2 and decreasing from π/2 to −π/2 respectively (see supplementary text S4). Figure 3C clearly illustrates the spectrum t++ of meta-atom No. 3 when θ varies from 0° to 90°. The amplitude is maintained over 0.9 within 8.8–15.5 GHz while ζ+ is shifted by π/2. Meanwhile, the corresponding cross-polarized transmission coefficient t−+ approaches zero (Fig. 3D), proving the eigenstate of meta-atom is exactly CP and its circular birefringence can be tuned by θ robustly. Note that the transmission amplitude of t++ does not reach unity due to the reflection losses (see Figure. S7).

Fig. 3: Encircling the singularity with unitary transmittance.
figure 3

A Expansion of the Poincaré sphere according to the complex co-polarized transmittance. A conical surface representing the amplitude, in addition to the heat map of the projected phase at the bottom, indicates a vanishing amplitude and a rapidly changing phase from [0,2π] characteristic of phase singularity. Choosing a path that encircles the singular parameter point with unit transmittance can be realized using the designed circular birefringent meta-atoms indicated by stars. B Schematic of the structure of the circular birefringent meta-atoms and the shapes of the eight elements annotated in (A), designed to tune quasi-linearly (δ ≈ 2θ) the circular birefringence using the elements’ relative rotation angle. The C co- and D cross-polarized transmittance of an elementary meta-atom with relative rotation angle from 0° to 90°, indicating almost zero cross-polarized conversion and zero P-B phase.

Full size image

Metasurface technology exploits the phase shift between the incident and scattered radiation of optical resonators that are placed across the interface. The design approach requires spatially distributing the resonators with different geometries to introduce a discontinuous phase profile in agreement with a user-defined wavefront. Here, we provide proof-of-concept wavefront engineering in co-circular polarization by choosing and distributing the meta-atoms to realize phase gradient metasurfaces with an aperture size of 187 × 187 mm operating at 10 GHz. The first result exploits the anti-symmetric co-polarized phase depending on the input helicity, refracting \(|R\rangle\) and \({|L}\rangle \,\) waves at −30° and +30°, respectively, as schematically shown in Fig. 4A. The gradually varying phases as a function of the spatial x-position is obtained using numerical solutions representing the meta-atoms’ transmission properties, as shown in Fig. 4B, which indeed indicate that both \(|R\rangle\) (red) and \({|L}\rangle \,\) (blue) co-polarized channels are imposing opposite discontinuous phase values. The experimentally measured normalized far-field patterns presented in Fig. 4C show the anti-symmetric refraction angles, which decrease as a function of the frequency within 8–12 GHz. At 10 GHz, the refraction angles of θt+ and θt− are consistent with the ideal anti-symmetric refraction, demonstrating that such an intriguing behavior, identical to the conventional P-B phase, can also occur on the co-polarized channels. As mentioned in various examples in the literature related to the P-B phase, it is possible to further decouple such anti-symmetric response by introducing an additional phase modulation mechanism, such as the dynamic phase. Indeed, by simply tuning the size of the meta-atoms while fixing the relative rotation angle of the structure’s patches, the co-polarized singular phase can be preserved. This combination of phases is used to design an asymmetric refractor (Fig. 4D) presenting decoupled and independent phase gradients, indicated as Φ++ and Φ−− in Fig. 4E, for both \(|R\rangle\) and \({|L}\rangle \,\), respectively. Here, we arbitrarily considered a metasurface design with refraction angle θt+ = −15° and θt− = 45° in the two channels at the operation frequency of 10 GHz. The experimentally measured normalized far-field patterns associated with both channels are depicted in Fig. 4F, showing refraction angles in agreement with the design and exhibiting high transmission efficiency (see supplementary text S5). In addition to the demonstration of anomalous refraction using asymmetric one-dimensional phase gradients, we achieved arbitrary and decoupled co-polarized engineering of complex wavefronts, as often reported using two-dimensional phase profiles, including OAM generation from co-polarized singular geometric phase (see supplementary text S6). Here, the generated OAM does not result from helicity reversal, and consequently, the total angular momentum is not conserved in the co-polarized transmission channel. OAM is achieved by strategically placing the co-polarized phase elements in a vortex-like spatial phase distribution, and as a result, this process can be utilized to exert torque on the spiral phase plate27.

Fig. 4: Results of metasurfaces for wavefronts tailoring.
figure 4

A Schematic of the designed antisymmetric refractor at 10 GHz. B The designed phase profile of the co-polarized channel of RHCP (red) and LHCP (blue) at 10 GHz of refractor, which are opposite because of the conjugate coupling between the responses. The inset is the photograph of the fabricated prototype, which consists of two kinds of structures with different geometric sizes. C The measured normalized far-field patterns of the two co-polarized channels. D Schematic of the designed asymmetric refractor at 10 GHz. E The decoupled phase profile of the two co-channels, and the constituent structures in the inset show multiple geometric sizes since the dynamic phase is introduced. F The measured normalized far-field patterns of the asymmetric refractor.

Full size image

Discussion

We introduce and experimentally validate a novel concept of the co-polarized singular phase for polarization-preserving wavefront engineering, complementing the classical cross-polarized P-B phase. This mechanism exploits a full 2π-phase discontinuity originating from a topologically protected singularity, intrinsically embedded in the eigen-parameter space and manifested on the surface of the Poincaré sphere. Furthermore, the emergence of this hidden geometric phase and the associated polarization singularities can also be interpreted through modal interference of quasi-normal modes, governed purely by reciprocity and symmetry principles28. Unlike conventional approaches, it enables geometric phase modulation in co-polarized transmission channels, while remaining fully compatible with other phase modulation mechanisms. This unique phase addressing strategy significantly expands the design capabilities of flat optics, enabling a new class of spin-conserving optical devices. The ability to modulate phase without altering the polarization state is particularly advantageous in applications requiring helicity preservation, including chiral meta-optics, polarization-multiplexed systems, and chiral matter spectroscopy.

Beyond its immediate impact, this mechanism holds strong potential for integration into the domain of higher-dimensional structured light29,30, where multiple degrees of freedom—such as polarization, spatial modes, OAM, and temporal shaping—are simultaneously exploited31. The topological robustness and compatibility of the co-polarized singular phase make it a compelling tool for tailoring non-separable vector fields, enabling sophisticated control over spin-orbit interactions, vector beam shaping, and light-matter coupling at both classical and quantum levels. Importantly, this approach lays the groundwork for future applications in optical communication (e.g., high-capacity polarization-preserving multiplexing), optical sensing and metrology (via spin-selective phase encoding), and secure information processing (through topologically robust state control). As the demand grows for compact, multifunctional, and scalable photonic platforms, our co-polarized phase mechanism provides a versatile and foundational addition to the metasurface engineering toolkit.

Methods

Detailed methodologies for prototype fabrication and experimental characterization are comprehensively described in Supplementary Information Note 5.