Abstract
Chiral metasurfaces provide invaluable tools for controlling structured light required for biosensing, photochemistry, holography, and quantum photonics. Here we suggest and realize a universal strategy for engineering chiral response of resonant metasurfaces via the interplay of meta-atom geometry and lattice arrangements within all five possible planar Bravais symmetries. By introducing chiral gradient metasurfaces, we illustrate how our approach allows producing a predictable chiral response tunable by simple parameter variations. We highlight that the symmetry-controlled chiral response provides an additional degree of freedom in optical signal processing, and showcase this with simultaneous mid-IR image encoding in two fundamental quantities, transmission and circular dichroism. Our proposed concept represents a universal toolkit for on-demand design and control of chiral metastructures that has potential for numerous applications in life sciences, quantum optics and more.
Similar content being viewed by others
Introduction
Chirality is a fundamental geometric property that describes a special type of asymmetry of an object, where it cannot be superimposed on its mirror image1,2,3,4. Chirality plays a critical role in numerous fields, from chemistry and biology to solid state and quantum physics5,6,7,8.
One of the most effective ways to manipulate and probe chiral systems is through the use of light, which can exhibit chiral properties, with circularly polarized (CP) plane waves being a straightforward example. The selective interaction of light with chiral media manifests as difference in right and left CP light absorption (circular dichroism (CD))6,7,9 or phase delay (circular birefringence)10. Employing chiral light enables the development of highly specific and efficient characterization systems for applications such as drug design, where the interaction between chiral molecules and biological systems can significantly affect efficacy and safety5,11. Beyond structural chirality, light can be used to probe the chiral properties of quantum mechanical systems, including orbital momentum12, spin, chiral wave functions, geometric phases, and topological phenomena13. Additionally, chiral structures can be employed in counterfeit prevention or authentication methods, offering a high level of security through unique non-fungible optical signatures14,15.
Enhancement and manipulation of chiral response, have been long-term goals in photonics, with applications spanning both far-field polarization control and augmenting the chiral light-matter interaction. A natural candidate for both these challenges are metasurfaces that already showed great prospects for light control in diverse applications, such as replacing bulky optical components16,17, biosensing18,19, frequency conversion20,21, optical computing22,23,24, geometric phase manipulation25,26, and more. Likewise, metasurfaces proved to be an excellent tool for engineering chiral light27. In the far-field optics, chiral metasurfaces are the backbone of meta-holograms28 and devices for polarization conversion and polarimetry29,30,31,32,33. At the same time, they can be used for generation of superchiral near-fields34 for enhanced interaction with chiral molecules35,36,37.
A number of strategies to achieve chiral response in metasurfaces have been suggested so far38,39. Among these, one notable approach involves designing chiral meta-atoms that break all the in-plane mirror symmetries irrespective of their periodic arrangement (here, the term ‘in-plane’ refers to the plane defined by a substrate). Breaking only the in-plane mirror symmetries results in differences exclusively between the transmission of right-to-left circular polarization and left-to-right circular polarization (cross-polarized transmissions), without affecting co-polarized transmission40. However, this is not always sufficient, as, for example, in metasurfaces with threefold rotational symmetry and higher, the cross-polarized transmission contrast is zero41. The breaking of out-of-plane mirror symmetry is essential for achieving differences in co-polarized transmission between RCP and LCP light (Here, the term ‘out-of-plane’ refers to normal direction with the respect to a substrate). It is generally achieved either by the 3D geometry of the meta-atoms themselves42,43,44,45,46,47,48 or by the presence of the substrate41,49,50,51,52. Another strategy involves chiral lattices: non-chiral meta-atoms arranged in a monoclinic lattice on a substrate53 or in a twisted bi-layered structures (moiré chiral photonic metasurfaces)54,55,56. Furthermore, chiral response can be achieved if the metasurface is based on bianisotropic material with its anisotropy axis inclined with respect to the metasurface normal57. Lastly, the symmetry can also be broken externally by using non-normal light incidence58,59,60, which induces the so-called extrinsic (or pseudo-) chirality10. A combination of all strategies is also possible, but would result in a system with a huge number of free parameters hard to design, optimize, and often fabricate. At the same time, precise control of the chirality of the nanophotonics structures remains crucial both for generation of structured light and for reliable quantitative chiral detection61,62,63.
In this paper, we suggest a universal strategy for controlling metasurface chiral response by leveraging the interplay of lattice and meta-atom symmetries to produce a predictable chiral behavior tunable by simple parameters. While particular cases of such interaction were discussed before both in theory64,65,66,67 and experiment68, here we develop a generalized framework that addresses all possible symmetry combinations, serving as a universal toolkit for on-demand chiral design.
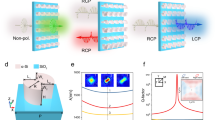
We showcase this approach experimentally using chiral gradient metasurfaces. In these structures, the rotation angle of the meta-atom within the unit cell is continuously varied along the chip, which allows to probe the full range of mutual orientations of lattice and resonator in the chiral signal measured with polarization-resolved mid-infrared spectroscopy (Fig. 1a). We observe robust zeros of the metasurface chirality for resonator rotation angles consistent with the chiral selection rules that we devise (Fig. 1b), as well as variable enhancement of the chirality at intermediate angles stemming from the metasurface resonant modes.
a Artistic view of a chip hosting a chiral gradient metasurface and a metasurface encoding an image in circular dichroism signal in the mid-IR spectral range. The inset shows a tilted angle SEM image of a metasurface encoding a chiral image. b Schematic illustrating the interaction of the metasurface lattice symmetry with the resonator symmetry leading to a locked set of resonator rotation angles β that render the structure non-chiral.
Remarkably, our approach enables seamless integration of resonant behavior in the chiral response with the simplest resonator geometries, which in turn opens the opportunities for data encryption. We demonstrate its application for mid-IR image encoding in two fundamental quantities, unpolarized transmission and transmission CD. Importantly, the symmetry-protected anchor points expand the encoding range to cover a full spectrum of negative to positive values of CD, as schematically shown in Fig. 1a. The choice of different combinations of lattice and resonator symmetries determines the trade-off between the encoding ranges, allowing for precise control over the encoded data, while the design simplicity ensures its high spatial resolution. Furthermore, the amplitude-based encoding approach does not require additional polarization optics for data extraction. This highlights the strength of our general chiral design toolkit and ensures its straightforward adaptability to a wide field of applications.
Results
Lattice vs. resonator symmetries for chirality control
The core idea of our approach is the interplay between the 2D arrangement of the metasurface and the orientation of symmetric meta-atoms with respect to this arrangement. By keeping the meta-atom shapes within simple non-chiral geometries, we can easily integrate resonant behavior into our system and achieve predictable chiral response using achiral configurations as symmetry-protected anchor points. In this section we devise the selection rules which define the chiral response of such metasurfaces for all possible lattice types, Table 1.
Based on the geometrical definition of chirality1,2, a structure is chiral when it has no mirror symmetry planes. Let us consider the conditions for achieving achiral response in our lattice—that is, when at least one mirror symmetry plane appears. For the considered structures, we can discard the out-of-plane mirror symmetry, which is broken by default due to the presence of a substrate10,41,53,69. The chiral response is then solely dependent on the in-plane symmetries of our structure. There are two symmetries we have to take into consideration: symmetry of the meta-atoms and symmetry of the arrangement. Without the loss of generality, we will consider meta-atoms which are n-fold symmetric and thus have n in-plane mirror symmetry lines (such meta-atom on a substrate has Cnv point symmetry group). While a single Cnv object is achiral, this restriction can be lifted for a 2D periodic arrangement of Cnv objects, which opens the opportunity for precise chirality control that is unavailable for chiral meta-atoms.
In two dimensions, there are only five distinct variants of periodic lattices. These five 2D Bravais lattice types70 are hexagonal (6), square (4), centered rectangular (2), primitive rectangular (2), and monoclinic (0), where the number in parentheses indicates number of in-plane mirror symmetry lines, m. The only arrangement that is chiral for any shape of meta-atoms on a substrate is monoclinic lattice, which was described theoretically and verified experimentally very recently53. However, it gives little room for an efficient chirality parametrization.
Two sets of in-plane mirror symmetry lines (m from lattice arrangement and n from meta-atom) give us an easily parameterized system, which is chiral for the particular relative orientations. The relative angle of meta-atom rotation β with respect to the arrangement lattice is the parameter of choice. By figuring out when exactly there is at least one match between symmetry lines from m-set and n-set, we derive the chiral selection rules, Table 1 (see Supplementary Note 1 for the detailed derivation). For specific angles β the metasurface is achiral and hence must provide null for any chiral optical response. The angular period of these symmetry-induced zeros folds down to an elegant and compact formula
where lcm(m, n) is the least common multiple of two integers m and n. These symmetry induced zeros can serve as “anchors points” for any chiral design in general, including metasurfaces with gradient design, which is the showcase of our choice in this work. The later one is the showcase of our choice in this work.
To characterize the chirality of our system, we use
which can take values from −1 to 1. Here, TR and TL denote the total transmission coefficients for the right and left circularly polarized input light, respectively. The value defined by Eq. (2) is related to both anisotropic dissymetry factor71,72 (with a factor of 2 difference) and to CD as defined for lossless metasurfaces41,52,73. Importantly, for 2D achiral metasurface configurations defined by Table 1, CDtot is zero and thus can be used as a measure of chirality in our design. In general, however, one should be careful when operating with total/co-polarized CD in cases when polarization conversion is critical41,44,53,73,74, as there is a possibility of CDtot ≠ 0 for 2D chiral (3D achiral) metasurfaces40. Here, we define co-polarized CD as CDco = (TRR − TLL)/(TRR + TLL) where TRR and TLL are the intensity transmission coefficients with the first and last indexes denoting the output and input polarizations, correspondingly, and discuss the differences in more detail in Supplementary Section S2. For simplicity, hereafter we refer to CDtot as simply “circular dichroism” or CD.
Metasurfaces with gradient chirality
The designs of our mid-IR chiral metasurfaces are based on Ge resonators on CaF2 substrates, which was established as a flexible platform for light control in mid-IR75,76. To achieve strong resonances of the far-field chirality of the structure within the mid-IR range (1000–2000 cm−1), we set the resonator height at 1070 nm. Furthermore, we focus on the two resonator symmetries: C2v (“bar”) and C3v (“spinner”), see the first two rows of Table 1. The lateral dimensions of the bar resonator are 3.542 × 1.566 microns, while the spinner is constructed from three bars of the same size rotated by 120° with respect to each other and sharing a common origin. The period of both square and hexagonal lattices is 4.30 μm (see schematics in Supplementary Fig. 2). These geometries exhibit well-defined and spectrally separated resonances with different Q-factors, which showcases the general applicability of our approach. A more detailed discussion on the structure design is presented in Supplementary Notes 6 and 7.
For the quantification of the chirality, we use the CD introduced in Eq. (2). Figure 2a–d shows the four combinations of the resonator (bar and spinner) and lattice symmetries (square and hexagonal) that we considered in numerical simulations. According to the selection rules (Table 1), these combinations should yield chiral zeroes for β = sπ/4 (C2v/square, Fig. 2a), β = sπ/6 (C2v/hexagonal, Fig. 2b), β = sπ/6 (C3v/hexagonal, Fig. 2c) and β = sπ/12 (C3v/square, Fig. 2d). To verify this, we calculated the maps of CDtot for infinitely periodic metasurfaces for β within 0 to π/2 range excited from the top (air). These maps shown in Fig. 2e–h demonstrate strict lack of chirality (CD = 0) for discrete sets of β (horizontal dashed lines), fully consistent with the selection rules. Notably, these zeros hold irrespective of the resonant modes of the metasurface that manifest as peaks of CD at intermediate β values. The sections of the maps at the wavelengths close to the respective CD maxima shown to the left of each map indicate that CD is strictly anti-symmetric with respect to each of the β “anchors”. Finally, Fig. 2i–l show the unpolarized light transmission spectra of the respective symmetry configurations calculated for β = 0. The resonant modes of the metasurface are manifested as transmission dips. These spectral bands of low transmission also manifest the highest CD, as according to definition in Eq. (2) the maximal values of CD are achieved at the minima of either right-circularly polarized (RCP) or left-circularly polarized (LCP) transmission (shown in Supplementary Fig. 7). This also explains low values of CD outside the resonant bands of the metasurface.
a–d Schematic of the lattice symmetries and unit cell configuration for four type of metasurfaces: (a, b) based on C2v bar resonator and (c, d) based on C3v spinner resonator. e–h Corresponding calculated maps of circular dichroism (CD) depending on the excitation wavelength and rotation angle of the resonator. The maps demonstrate angle-equidistant zeroes governed by the interplay of the symmetries of the resonator and the lattice. Horizontal dashed lines mark the β corresponding to symmetry-protected zeroes of CD. The insets on the left of each map shows the section of CD taken at a wavelength marked with black dashed line in each of the (e–h). i–l Unpolarized light transmission spectra calculated for each type of metasurface for β = 0.
To showcase this general concept experimentally, we utilize chiral gradient metasurfaces. Each of the fabricated metasurfaces addresses a certain combination of the resonator and lattice symmetries. However, instead of fabricating a discrete set of arrays for different angles β, we implemented a slow gradient of the rotation angle of the resonator along one of the chip coordinates. This yielded 600 × 3000 μm2 sized strips of gradient metasurfaces with β varied within 0 to π/2 range along the long axis of the structure as schematically illustrated in Fig. 3a. Such scale results in Δβ ≈ 0.1° between the neighboring columns.
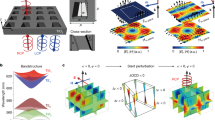
a Schematic illustration of the chiral gradient metasurface with bar resonators arranged in a square lattice. The rotation angle β of the resonator within the unit cell varies smoothly along the chip coordinate. The color of the bars encodes the chiral signal characteristic for the corresponding β. b Optical image of the fabricated chiral gradient metasurface based on Ge resonators on CaF2 substrate. The insets show the SEM images, with six unit cells each, taken at different coordinates along the chiral gradient stripe. Gray dashed line indicates the signal collection area that is scanned along the gradient stripe during the measurement. c Comparison of simulated chiral signal map (left) and the experimentally measured dependence of chiral signal on the coordinate along the chip (right).
An optical image of the fabricated metasurface featuring bar (C2v) resonators in a square lattice is shown in Fig. 3b, with SEM insets highlighting its structural details at multiple points along the chiral gradient. Locking of the local value of β with the chip coordinate of a gradient metasurface enables full characterization of the chiral properties of a given resonator-lattice symmetry pair through the measurements of the evolution of the LCP and RCP transmission spectra along the chip. We perform these measurements using a mid-IR microscope (Bruker Hyperion) in transmission configuration paired with Fourier transform infrared spectrometer as schematically illustrated in Fig. 1a (see “Methods” for further details). The experimental data of CD for C2v/square metasurface are in excellent agreement with our simulations (Fig. 3c) in all its features, including relative amplitude and spectral positions of the chirality peaks and, most importantly, robust zeroes of CD for β = 0, 45° and 90°. We note that while the maximum chiral response is not the main focus of our study, CD for the proposed design reaches values larger than 0.8, which gives a dynamic range of 1.6 within the same structure. Additional narrow spectral features found in the experimental map in Fig. 3c are attributed to the modes excited at non-normal light incidence, which is present in the experiment due to finite numerical aperture of our mid-IR microscopy system (see Supplementary Note 4 for simulations).
Figure 4 and Supplementary Fig. 3 show the IR measurements of the gradient metasurfaces for the remaining lattice-resonator combinations showcased in numerical simulations (Fig. 2b–d), in particular, C2v/hexagonal (Fig. 4a), C3v/hexagonal (Fig. 4b), and C3v/square (Fig. 4c). The results for hexagonal lattice closely reproduce the numerical calculations and the expected chirality-canceling β angles. Notably, the overall low transmission of both C3v samples due to the overlap of multiple resonances within the 1400–1600 cm−1 range leads to an increased noise level of the observed chiral features.
A more complex picture of CD zeros is manifested for C3v/square structure (Fig. 4c). The pronounced mode at ≈ 1570 cm−1 hosts 7 nodes with Δβ = 15° as expected from the simulation (Fig. 2g). However, the two longer wavelength modes at 1320 and 1400 cm−1 demonstrate nodes with Δβ = 60° instead (see also experimentally measured reflectivity maps in Supplementary Fig. 5). We attribute the suppression of the intermediate chirality zeroes to the contribution of oblique incidence in the experiment, leading to the manifestation of extrinsic chirality.
In contrast to the well-defined symmetry-protected anchor angles (Table 1), the behavior of CD at the intermediate angles—particularly, the positions and the amplitudes of maximum values—is less straightforward. The few approaches proposed so far still ultimately rely on numerical optimization procedures.39 For example, it is possible to estimate the transmission CD using the mode CD, a property associated with the optical eigenmodes of the structure44,53,69. Methods based on the eigenmode analysis have demonstrated their effectiveness in the vicinity of resonances, both for single high-Q resonances44,51,53,69,77,78 and for broadband chiral responses achieved through multipolar superposition engineering50. Instead, our approach enforces a predictable behavior of the chiral response controlled by a single parameter, the meta-atom rotation angle. Importantly, the Cnv point symmetry of the meta-atom on a substrate guarantees a symmetric range of CD values (apart from monoclinic arrangement). That is, for an optimized structure design exhibiting maximum chirality (∣CD∣ = 1), the entire CD range [−1, 1] is automatically available by variation of β, while an additional constraint of Cnv symmetry narrows down the parameter space for resonator design optimization. This distinguishes our platform from designs relying on inherently chiral meta-atoms, enabling adiabatic control of chirality in diverse designs through variation of a single parameter. Importantly, it also minimizes the changes to the optical modes of the structure, which are inevitable for approaches that involve modifications of the resonator shape.
One implication of the high dynamic range of CD offered by the symmetry interaction scheme is facilitated chiral information encoding. Contrary to the well-developed chiral holograms28, where the metasurfaces are used to induce the near-field phase profile that is then converted to a far-field image, our encoding principle is based on direct generation of signal amplitude profile as illustrated in Fig. 5a, b. Specifically, we encode information in two fundamental quantities—total transmission and CD, which is possible with any resonator/lattice combination within our general model. Each unit cell of a metasurface acts as a single pixel in an image encoded at a chosen frequency of light ω0, which is fundamentally different from other amplitude encoding approaches relying on interference effects of multiple elements79. The size of the resonator is used to encode data in total transmission signal, which is modulated due to the size-dependent spectral shift of the resonant modes. The resonator rotation angle is used to encode data in CD, as the detuning of β from the symmetry nodes leads to the increase of the chirality. Similar double-parameter encoding approach was recently used in the paper by ref. 80, where the resonator rotation angle was used to encode the vibrational mode coupling strength. Reference grayscale images are then mapped on the available ranges ΔT and ΔCD so that each pixel (single unit cell) of a metasurface is assigned a particular combination of scale and β. Notably, CD is not fully independent of the resonance shift, which leads to mutual mixing of the resonator scale and β parameters in the encoding protocol and limits the total range of encoding depending on the lattice and resonator symmetries. This is illustrated in more detail in Supplementary Fig. 9.
a Mechanism of encoding information in transmission image. Each scale of the resonator corresponds to a different level of transmission signal at a target wavelength ω0. b Mechanism of encoding information in chirality through changing the rotation angle β of the resonator within a unit cell. c Optical image of the metasurface encoding two different images in transmission signal and chiral signal. The inset shows the SEM image of the metasurface area encoding 6 × 6 pixels of the original image. d Reference images. Top: a photo of an Australian cockatoo for encoding in transmission signal. Bottom: photo of Swiss Matterhorn mountain for chiral encoding (adapted from a public domain image (CC0), originally available at Pixabay https://pixabay.com/photos/matterhorn-switzerland-zermatt-1301802/). e Transmission (top row) and chiral signal (bottom row) images recorded from the encoding metasurface with square lattice design. f Respective images recorded from metasurface with hexagonal lattice design.
We used two reference pictures—of an Australian cockatoo and Swiss Matterhorn mountain (Fig. 5d)—to demonstrate chiral mid-IR image encoding in the total transmission and CD signals, respectively. As a showcase, we converted these two images into spatial maps of resonator scale and β for metasurfaces based on C2v/square and C2v/hexagonal combinations, which show the largest tuning range of CD and transmission (see also Supplementary Fig. 7), using the procedure described above. The image of the fabricated C2v/square sample in the visible light (Fig. 5c) reveals the shape of the mountain, as the scattering of light mostly depends on the orientation of the bars, while the change of the size does not lead to noticeable modulation of reflectivity. In the mid-IR, where the resonant modes of the bars reside, the situation changes drastically. Fig. 5e, f show the images of two C2v resonator metasurfaces with square and hexagonal lattices recorded at the excitation frequencies of 1384 and 1402 cm−1, respectively, using a quantum cascade laser-based microscopy system (Daylight Solutions Spero, see “Methods”). The physical size of each metasurface was approximately 4 × 4 mm2, which was tailored to fit into 2 × 2 fields of view of our microscope (this leads to barely noticeable stitching in the middle of the images). Comparison of the images for two lattice symmetries—square (Fig. 5e) and hexagonal (Fig. 5f)—highlights the advantages and drawbacks of using each option. Lower symmetry of square lattice leads to larger maximum amplitude of CDtot for intermediate β (Fig. 2e) that improves the chiral encoding, but at the same time limits the ΔT range, which influences the transmission encoding. Hexagonal lattice, while lacking in the maximum amplitude of chirality (Fig. 2f), provides a better balance of the encoding ranges, leading to good image quality in both signals. Additionally, the small angle range required to switch the sign of chirality for the hexagonal lattice bears the potential for dynamic encoding in active metasurfaces. This highlights the opportunities for more flexible control of chirality provided by custom lattice symmetries that can be tailored depending on particular application. Strikingly, even though the lattice symmetries are locally broken due to variations of the rotation angle β in high-contrast CD data (see also SEM inset in Fig. 5c), the quality of the encoding is well-preserved in both cases.
Discussion
In summary, we have developed a universal approach to design chiral metasurfaces based on symmetry considerations. We have established general selection rules that define the mutual orientations of the lattice and meta-atoms at which chiral response of metasurface vanishes. These zero-chirality “anchors” are protected by the interplay of the meta-atom and lattice symmetries, and they do not depend the presence of resonant optical modes. We have demonstrated this powerful concept experimentally using mid-IR chiral gradient metasurfaces, where the mutual orientation of a resonator and a lattice has been varied over the chip length, displaying the periodic vanishing of chirality according to the selection rules. While our results have been obtained for dielectric metasurfaces, the approach is more broadly applicable for plasmonic metasurfaces as well81,82. Furthermore, predictable behavior of CD enforced by the interplay of symmetries enables a unique opportunity for simultaneous information encoding in two fundamental quantities, transmission and CD. This feature is showcased through mid-IR image encoding, where a metasurface unveils distinct images in these two channels, paving the way for advanced anti-counterfeiting, camouflage, and security applications. Our generalized chiral design toolkit opens new opportunities for control of structured light in the dynamic field of chiral photonics, with possible applications in polarimetry, optical computing, sensing, chemistry, and quantum photonics.
Methods
Metasurface fabrication
Germanium (Ge) metasurfaces were fabricated on calcium difluoride (CaF2) substrates. First, the material stack was prepared by subsequent sputtering of a 5 nm silicon oxide (SiO2) adhesion layer and a 1070 nm Ge layer on top of a 1 mm thick CaF2 chip. The inverted metasurface pattern was written using electron beam lithography (Raith EPBG500+) on a spin-coated single-layer PMMA (PMMA 495k A8) positive tone resist. After the development, the pattern was directly transferred to the Ge film using a fluorine-based dry plasma etching process (Alcatel AMS 200 SE).
Infrared spectroscopy
We obtained the infrared (IR) transmission spectra using a Bruker Vertex 80v FT-spectrometer with an attached IR Microscope (HYPERION 3000) equipped with a liquid nitrogen cooled MCT detector. The metasurfaces were excited from the air side using a ZnSe lens with the focal length of 25 mm mildly focusing circularly polarized IR light on the sample surface. Transmitted light was collected with another 25 mm lens equipped with an additional iris placed at its back focal plane. Closing the iris allowed for limiting the numerical aperture of the system down to approximately 0.06 and thus suppressing the unwanted signal from oblique excitation angles. We measured transmission spectra for both RCP and LCP generated using a broadband quarter-wave plate (model XCN13 from G& H, 5–8 μm). Signal collection area was limited to a thin stripe by a double-blade aperture placed in the conjugate image plane of the IR microscope. This collection area was then scanned along the gradient stripe (as in Fig. 3b) to obtain the wavenumber vs angle maps. The sample chamber was constantly purged with dry air to provide consistently low level of humidity.
Infrared images
The images of metasurface encoding the data in transmission and chiral signals were collected with a quantum cascade laser based imaging microscope (Daylight SPERO-QT-Z) featuring a 480 × 480 pixel microbolometer array. Separate LCP and RCP transmission images were collected by introducing a broadband quarter-wave plate (2.5–7.0 μm from B.Halle) into the collimated incident beam. The measurements were performed with a sample uniformly illuminated with a monochromatic (full width at half maximum < 0.1 cm−1) laser source at the encoding wavelength. LCP and RCP images were normalized to the corresponding transmission image of a bare CaF2 substrate. The images shown in the manuscript were stitched together from four fields of view of the microscope each covering a 2 × 2 mm2 area.
Numerical simulations
We obtained transmission and CD using the Frequency Domain Solver in CST Studio Suite with circularly polarized light excitation. In the simulations, we set the dielectric permittivity of germanium to εGe = 17.45 + i0.1668 with imaginary part added to account for the effective losses due to grained structure of thermally evaporated amorphous Ge. The level of losses was chosen based on fitting the spectral shape and position of the resonances. The dielectric permittivity of calcium fluoride was \({\varepsilon }_{{{{\rm{CaF}}}}_{2}}=1.87\). By design, the resonator with C2v symmetry had 1566 nm width, 3542 nm length, and 1070 nm height, arranged in a lattice with a period of 4.24 μm. The schematics and dimensions of C2v and C3v resonators are illustrated in Supplementary Fig. 2.
Data availability
The data supporting the findings of this study are available within the Article and its Supplementary Information files and in the Zenodo database under accession code https://doi.org/10.5281/zenodo.15524649.
Change history
19 September 2025
A Correction to this paper has been published: https://doi.org/10.1038/s41467-025-64119-1
References
Kelvin, W.T. The Molecular Tactics of a Crystal 27. (Clarendon Press, Oxford, 1894).
Caloz, C. & Sihvola, A. Electromagnetic chirality, Part 1: the microscopic perspective [Electromagnetic Perspectives]. IEEE Antennas Propag. Mag. 62, 58–71 (2020).
Caloz, C. & Sihvola, A. Electromagnetic chirality, Part 2: the macroscopic perspective [Electromagnetic Perspectives]. IEEE Antennas Propag. Mag. 62, 82–98 (2020).
Barron, L. D. From cosmic chirality to protein structure: lord kelvin’s legacy. Chirality 24, 879–893 (2012).
Smith, S. W. Chiral toxicology: it’s the same thing…only different. Toxicol. Sci. 110, 4–30 (2009).
Kobayashi, N. & Muranaka, A. Circular Dichroism and Magnetic Circular Dichroism Spectroscopy for Organic Chemists (Royal Society of Chemistry, 2011).
Fasman, G.D. Circular Dichroism and the Conformational Analysis of Biomolecules (Springer, New York, 2013).
Aiello, C. D. et al. A chirality-based quantum leap. ACS Nano 16, 4989–5035 (2022).
Baase, W. A. & Johnson, W. C. Circular dichroism and DNA secondary structure. Nucleic Acids Res. 6, 797–814 (1979).
Nechayev, S., Barczyk, R., Mick, U. & Banzer, P. Substrate-induced chirality in an individual nanostructure. ACS Photonics 6, 1876–1881 (2019).
Nguyen, L. A., He, H. & Pham-Huy, C. Chiral drugs: an overview. Int. J. Biomed. Sci. 2, 85 (2006).
Bahramy, M.S. et al. Emergent quantum confinement at topological insulator surfaces. Nat. Commun. 3 https://doi.org/10.1038/ncomms2162 (2012).
Lodahl, P. et al. Chiral quantum optics. Nature 541, 473–480 (2017).
Deng, J. et al. Multiplexed anticounterfeiting meta-image displays with single-sized nanostructures. Nano Lett. 20, 1830–1838 (2020).
Singh, S. et al. Stimuli-responsive chiral cellulose nanocrystals based self-assemblies for security measures to prevent counterfeiting: a review. ACS Appl. Mater. Interfaces 16, 41743–41765 (2024).
Khorasaninejad, M. & Capasso, F. Metalenses: versatile multifunctional photonic components. Science 358 https://doi.org/10.1126/science.aam8100 (2017).
Arbabi, A. & Faraon, A. Advances in optical metalenses. Nat. Photonics 17, 16–25 (2023).
Zhang, S. et al. Metasurfaces for biomedical applications: imaging and sensing from a nanophotonics perspective. Nanophotonics 10, 259–293 (2021).
Tittl, A. et al. Imaging-based molecular barcoding with pixelated dielectric metasurfaces. Science 360, 1105–1109 (2018).
Krasnok, A., Tymchenko, M. & Alù, A. Nonlinear metasurfaces: a paradigm shift in nonlinear optics. Mater. Today 21, 8–21 (2018).
Jangid, P. et al. Spectral tuning of high-harmonic generation with resonance-gradient metasurfaces. Adv. Mater. 36, 2307494 (2023).
Zhou, H. et al. Optical computing metasurfaces: applications and advances. Nanophotonics 13, 419–441 (2024).
Hwang, Y. & Davis, T. J. Optical metasurfaces for subwavelength difference operations. Appl. Phys. Lett. 109, 181101 (2016).
Hu, J. et al. Diffractive optical computing in free space. Nat. Commun. 15, 1–21 (2024).
Xie, X. et al. Generalized Pancharatnam-Berry phase in rotationally symmetric meta-atoms. Phys. Rev. Lett. 126, 183902 (2021).
Guo, Y. et al. Classical and generalized geometric phase in electromagnetic metasurfaces. In Photonics Insights, Vol. 1, 03 https://doi.org/10.3788/PI.2022.R03 (SPIE, 2022).
Kim, J. et al. Chiroptical metasurfaces: principles, classification, and applications. Sensors 21, 4381 (2021).
Balthasar Mueller, J. P., Rubin, N. A., Devlin, R. C., Groever, B. & Capasso, F. Metasurface polarization optics: independent phase control of arbitrary orthogonal states of polarization. Phys. Rev. Lett. 118, 113901 (2017).
Zhu, H. L., Cheung, S. W., Chung, K. L. & Yuk, T. I. Linear-to-circular polarization conversion using metasurface. IEEE Trans. Antennas Propag. 61, 4615–4623 (2013).
Teng, S., Zhang, Q., Wang, H., Liu, L. & Lv, H. Conversion between polarization states based on a metasurface. Photonics Res. 7, 246–250 (2019).
Shah, Y. D. et al. An all-dielectric metasurface polarimeter. ACS Photonics 9, 3245–3252 (2022).
Ding, F., Chen, Y. & Bozhevolnyi, S. I. Metasurface-based polarimeters. Appl. Sci. 8, 594 (2018).
Arbabi, E., Kamali, S. M., Arbabi, A. & Faraon, A. Full-stokes imaging polarimetry using dielectric metasurfaces. ACS Photonics 5, 3132–3140 (2018).
Tang, Y. & Cohen, A. E. Enhanced enantioselectivity in excitation of chiral molecules by superchiral light. Science 332, 333–336 (2011).
Mohammadi, E. et al. Nanophotonic platforms for enhanced chiral sensing. ACS Photonics 5, 2669–2675 (2018).
Mohammadi, E. et al. Accessible superchiral near-fields driven by tailored electric and magnetic resonances in all-dielectric nanostructures. ACS Photonics 6, 1939–1946 (2019).
Garcia-Santiago, X. et al. Toward maximally electromagnetically chiral scatterers at optical frequencies. ACS Photonics 9, 1954–1964 (2022).
Khaliq, H.S., Nauman, A., Lee, J., Kim, H. Recent progress on plasmonic and dielectric chiral metasurfaces: fundamentals, design strategies, and implementation. Adv. Optical Mater. 11 https://doi.org/10.1002/adom.202300644 (2023).
Deng, Q.-M. et al. Advances on broadband and resonant chiral metasurfaces. NPJ Nanophoton. 1, 1–22 (2024).
Plum, E., Fedotov, V. A. & Zheludev, N. I. Planar metamaterial with transmission and reflection that depend on the direction of incidence. Appl. Phys. Lett. 94, 131901 (2009).
Koshelev, K., Toftul, I., Hwang, Y. & Kivshar, Y. Scattering matrix for chiral harmonic generation and frequency mixing in nonlinear metasurfaces. J. Opt. 26, 055003 (2024).
Arteaga, O. et al. Relation between 2D/3D chirality and the appearance of chiroptical effects in real nanostructures. Opt. Express 24, 2242–2252 (2016).
Goerlitzer, E. S. A. et al. Chiral surface lattice resonances. Adv. Mater. 32, 2001330 (2020).
Gorkunov, M. V., Antonov, A. A. & Kivshar, Y. S. Metasurfaces with maximum chirality empowered by bound states in the continuum. Phys. Rev. Lett. 125, 093903 (2020).
Tanaka, K. et al. Chiral bilayer all-dielectric metasurfaces. ACS Nano 14, 15926–15935 (2020).
Kosters, D. et al. Core–shell plasmonic nanohelices. ACS Photonics 4, 1858–1863 (2017).
Esposito, M. et al. Nanoscale 3D chiral plasmonic helices with circular dichroism at visible frequencies. ACS Photonics 2, 105–114 (2015).
Kaschke, J. et al. A helical metamaterial for broadband circular polarization conversion. Adv. Opt. Mater. 3, 1411–1417 (2015).
Shi, T. et al. Planar chiral metasurfaces with maximal and tunable chiroptical response driven by bound states in the continuum. Nat. Commun. 13, 1–8 (2022).
Wang, R., Wang, C., Sun, T., Hu, X. & Wang, C. Simultaneous broadband and high circular dichroism with two-dimensional all-dielectric chiral metasurface. Nanophotonics 12, 4043–4053 (2023).
Koshelev, K. et al. Resonant chiral effects in nonlinear dielectric metasurfaces. ACS Photonics 10, 298–306 (2023).
Tonkaev, P. et al. Nonlinear chiral metasurfaces based on structured van der Waals materials. Nano Lett. 24, 10577–10582 (2024).
Toftul, I. et al. Chiral dichroism in resonant metasurfaces with monoclinic lattices. Phys. Rev. Lett. 133, 216901 (2024).
Lyu, B. et al. Manipulating the chirality of moiré metasurface by symmetry breaking. Laser Photonics Rev. 17, 2201004 (2023).
Wu, Z., Liu, Y., Hill, E. H. & Zheng, Y. Chiral metamaterials via Moiré stacking. Nanoscale 10, 18096–18112 (2018).
Han, Z., Wang, F., Sun, J., Wang, X. & Tang, Z. Recent advances in ultrathin chiral metasurfaces by twisted stacking. Adv. Mater. 35, 2206141 (2023).
Asadchy, V. S., Díaz-Rubio, A. & Tretyakov, S. A. Bianisotropic metasurfaces: physics and applications. Nanophotonics 7, 1069–1094 (2018).
Cao, T., Wei, C.-w & Li, Y. Dual-band strong extrinsic 2d chirality in a highly symmetric metal-dielectric-metal achiral metasurface. Opt. Mater. Express 6, 303–311 (2016).
Hwang, Y. et al. Optical chirality from dark-field illumination of planar plasmonic nanostructures. Laser Photonics Rev. 11, 1700216 (2017).
Nicolas, M. et al. True circular dichroism in optically active achiral metasurfaces and its relation to chiral near-fields. ACS Appl. Optical Mater. 1, 1360–1366 (2023).
Graf, F. et al. Achiral, helicity preserving, and resonant structures for enhanced sensing of chiral molecules. ACS Photonics 6, 482–491 (2019).
Gilroy, C. et al. Roles of superchirality and interference in chiral plasmonic biodetection. J. Phys. Chem. C. 123, 15195–15203 (2019).
Both, S. et al. Nanophotonic chiral sensing: how does it actually work? ACS Nano 16, 2822–2832 (2022).
Volkov, S. N. et al. Optical activity in diffraction from a planar array of achiral nanoparticles. Phys. Rev. A 79, 043819 (2009).
Meng, J. et al. Angle-selective chiral absorption induced by diffractive coupling in metasurfaces. Opt. Lett. 47, 5385–5388 (2022).
Movsesyan, A., Besteiro, L. V., Kong, X.-T., Wang, Z. & Govorov, A. O. Engineering strongly chiral plasmonic lattices with achiral unit cells for sensing and photodetection. Adv. Opt. Mater. 10, 2101943 (2022).
Ávalos-Ovando, O. et al. Chiral bioinspired plasmonics: a paradigm shift for optical activity and photochemistry. ACS Photonics 9, 2219–2236 (2022).
Gryb, D. et al. Two-dimensional chiral metasurfaces obtained by geometrically simple meta-atom rotations. Nano Lett. 23, 8891–8897 (2023).
Gorkunov, M. V., Antonov, A. A., Mamonova, A. V., Muljarov, E. A. & Kivshar, Y. Substrate-induced maximum optical chirality of planar dielectric structures. Adv. Opt. Mater. n/a, 2402133 (2024).
Kittel, C. Introduction to Solid State Physics, 8th edn. (Wiley, Hoboken, NJ, 2005).
Wakabayashi, M. et al. Anisotropic dissymmetry factor, g: theoretical investigation on single molecule chiroptical spectroscopy. J. Phys. Chem. A 118, 5046–5057 (2014).
Berova, N., Bari, L. D. & Pescitelli, G. Application of electronic circular dichroism in configurational and conformational analysis of organic compounds. Chem. Soc. Rev. 36, 914–931 (2007).
Shalin, A.S. & Valero, A.C., Miroshnichenko, A. All-Dielectric Nanophotonics (Elsevier, San Diego, 2023).
Kondratov, A. V. et al. Extreme optical chirality of plasmonic nanohole arrays due to chiral Fano resonance. Phys. Rev. B 93, 195418 (2016).
Leitis, A. et al. Angle-multiplexed all-dielectric metasurfaces for broadband molecular fingerprint retrieval. Sci. Adv. 5, 2871 (2019).
Richter, F. U. et al. Gradient high-Q dielectric metasurfaces for broadband sensing and control of vibrational light-matter coupling. Adv. Mater. 36, 2314279 (2024).
Gromyko, D. et al. Unidirectional chiral emission via twisted Bi-layer metasurfaces. Nat. Commun. 15, 1–10 (2024).
Gromyko, D., Loh, J.S., Feng, J., Qiu, C.-W. & Wu, L. Enabling all-to-circular polarization upconversion by nonlinear chiral metasurfaces with rotational symmetry. Phys. Rev. Lett. 134, 023804 (2025).
Fan, Q. et al. Independent amplitude control of arbitrary orthogonal states of polarization via dielectric metasurfaces. Phys. Rev. Lett. 125, 267402 (2020).
Aigner, A., Weber, T., Wester, A., Maier, S. A. & Tittl, A. Continuous spectral and coupling-strength encoding with dual-gradient metasurfaces. Nat. Nanotechnol. 19, 1804–1812 (2024).
Wu, B. et al. Near-infrared chirality of plasmonic metasurfaces with gold rectangular holes. Adv. Compos. Hybrid. Mater. 5, 2527–2535 (2022).
Liang, Y., Tsai, D. P. & Kivshar, Y. From local to nonlocal high-q plasmonic metasurfaces. Phys. Rev. Lett. 133, 053801 (2024).
Acknowledgements
The authors acknowledge the funding from the Swiss State Secretariat for Education, Research and lnnovation (SERI) under contract numbers 22.00081 (I.S., N.G., H.A.) and 22.00018 (F.R. H.A.), in connection to the Horizon Europe projects MIRAQLS (under agreement 101070700) and TWISTEDNANO (under agreement 101046424), respectively. Open access publishing of this article is supported by SERI under contract number 22.00081. Y.K. acknowledges a support from the Australian Research Council (Grant No. DP210101292) and the International Technology Center Indo-Pacific (ITC IPAC) via Army Research Office (contract FA520923C0023). Y.H. and D.G.L. acknowledge a support received from Electro Optic Systems Pty. Limited. Y.H. acknowledges a support from the National Computational Infrastructure (NCI) by the Australian Government via Adapter Allocation Scheme for computing resources. I.T. thanks Kristina Frizyuk for valuable discussions on the selection rules. I.S. and F.R. acknowledge Timothy Mann for help with early experiments. The authors acknowledge the use of nanofabrication facilities at the Center of MicroNano Technology of École Polytechnique Fédérale de Lausanne.
Author information
Authors and Affiliations
Contributions
I.S., N.G., and F.R. fabricated the structures and performed the measurements. I.T., K.K., and Y.H. developed the theoretical model. F.R. and N.G. performed numerical simulations with input from K.K., I.S., F.R., and N.G. processed and analyzed the experimental data. I.S., F.R., and I.T. wrote the manuscript with input from all authors. I.S. designed the figures. D.G.L. participated in discussions. Y.K. and H.A. guided the research.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Sinev, I., Richter, F.U., Toftul, I. et al. Chirality encoding in resonant metasurfaces governed by lattice symmetries. Nat Commun 16, 6091 (2025). https://doi.org/10.1038/s41467-025-61221-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-61221-2