Introduction

Doublet radical emitters are potential candidates for highly efficient optoelectronics as they eliminate inefficiencies connected to spin statistics of conventional closed-shell systems1,2. Their excited state can often be formed by a superposition of a few configurations involving the occupations of different molecular space orbitals (MOs), reflecting the simultaneous excitation of different electron-hole pairs3,4,5,6,7,8,9,10,11. The interference of these configurations can then result in a strong reduction or enhancement of optical transition dipoles and thus absorption and emission intensities related to the molecular electronic transition and is expected to impact the molecular optoelectronic properties. In particular, the electrons and holes emerging in the process of electron-hole pair splitting can originate from different electronic configurations, and hence from different pairs of occupied and unoccupied MOs, both belonging to the same excited state. This may lead to unintuitive dynamics of exciton splitting, governing e.g. the charge transfer in donor-acceptor interfaces in organic solar cells12, whose understanding relies on theoretical modeling13,14,15,16, but is hardly accessible by experimental methods. The widely employed angle-resolved photoelectron spectroscopy17, working on large molecular ensembles can solely provide averaged electron emission spectra that reflect the multiconfigurational character of excited states indirectly. Instead, a direct real-space observation of the orbitals involved in charge transfer upon photoexcitation of a single open-shell emitter made with submolecular resolution would be required.

To reach this goal, the scanning tunneling microscopy (STM) with light can be employed to induce and detect photocurrent with atomic-scale precision18,19,20,21,22. This technique was applied to visualize photon-induced in-gap electron transport in a single closed-shell charge-neutral phthalocyanine18 and pentacene19 to elucidate how the frontier orbitals are involved in the transport-mediated decay of the optically excited states. The experiments confirmed the participation of the highest occupied MO (HOMO) and lowest unoccupied MO (LUMO) in the photocurrent channels as the optically excited states in the studied molecules have the HOMO-LUMO character.

In this work, we use this technique and complement it with tip-enhanced photoluminescence (TEPL) mapping to unravel the multiconfigurational character of a doublet excited state of a singly-negatively-charged 3,4,9,10-Perylenetetracarboxylic dianhydride (PTCDA). Based on the acquired TEPL data, analysis of photocurrent maps, scanning-tunneling spectra and detailed theoretical modeling of the photon-driven process, we establish the essential electronic dynamics and composition of the excited state. We explore the sensitivity of the technique to the components constituting the superposition by controlling recombination channels, employing electrical field and tip position.

Results

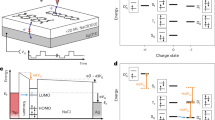
The concept of the simultaneous photocurrent and TEPL measurement with submolecular resolution is shown in Fig. 1a. An STM Ag-tip is scanned over PTCDA molecules deposited on a decoupling layer of 3ML-NaCl on a crystalline Ag(111) surface, and the tunneling current and photon emission rate are recorded, using a standard high-gain preamplifier and a single-photon detector, respectively. The tip apex is illuminated by a laser spot of ~10 micrometer radius. Using the resonant antenna effect of the tip, the laser electric field is directed into the tip-surface gap plasmonic nanocavity and concentrated around the atomic-scale tip apex, where it interacts with the molecular excitations23,24,25. The excitation laser wavelength is above the energy needed to reach the first excited state of the PTCDA anion, the known equilibrium charge state in this scenario4,26,27. Moving the tip along the surface varies the coupling strength of the nanocavity with the molecules as well as the tunneling probability, and leads to tip-position dependent absorption, emission and charge transport.

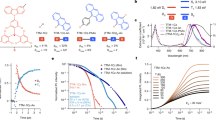
Fig. 1: Photon-induced current and luminescence of a single open-shell molecule in a STM-nanocavity.
figure 1

a Scheme of the experiment: plasmonic tip apex is illuminated by focused laser light and scanned parallel to the surface plane of 3ML-NaCl/Ag(111) above an organic radical dye, PTCDA anion. The laser light is focused by the plasmonic cavity and excites the molecule, inducing photoluminescence and electron tunneling between the molecule and the tip or the substrate. b The recorded net tunneling current map above a group of four identical molecules. A model of PTCDA is shown for orientation (2x magnified). c A map of the photon rate at the photodetector with a 912-938 nm bandpass filter. The measurements were taken with 785 nm excitation wavelength and at zero bias voltage. The map sizes are 14 × 8.5 nm2.

Full size image

Figure 1b, c show the recorded spatially-resolved zero-bias tunneling current and the photon rate at the energy of the fundamental PTCDA anion emission above an area with four identical molecules in two orientations with respect to the lattice of the NaCl. The magnitude and direction of the net current varies strongly with the precise location of the tip above their backbones, changing from negative (red) to positive (gray) at distances comparable to bond lengths and reaching pA values. Since the applied bias voltage is set to zero, the current is solely driven by the absorption of the incident light. Without the laser illumination, no current is observed at zero bias (see Supplementary Fig. 6). The complex character of the contrast is strikingly different from the one observed on the same system without irradiation at positive-ion-resonance (PIR) and negative-ion-resonance (NIR) onsets where it is dominated by the singly occupied and singly unoccupied MOs (SOMO and SUMO)4,27,28. This hints at the involvement of other frontier orbitals in the recombination channels at play29. The TEPL maps for the same area taken at the energy of luminescence of the PTCDA anion first excited state show two-lobe patterns above each molecule, oriented in the direction of the PTCDA longitudinal axes. It should be noted that the detected TEPL emission patterns in fact reflect the combined probabilities of absorption and emission, both dependent on the nanocavity position24,30,31.

An interpretation of the observed characteristic contrast in the photon-induced current maps requires identifying the states of the molecule and relevant charge transport pathways that may significantly contribute to the net current. To that end we develop a model considering the most relevant molecular states and transitions among them, capturing the essential mechanisms involved in the formation of the photocurrents and TEPL under the explored experimental conditions (schematically depicted in Fig. 2a, details in SI). The D0− ↔ D1− and D0− ↔ D2− optical gaps are apparent from the TEPL spectra (Fig. 2b, c), assuming negligible Stokes shifts between the absorption and emission in our scenario. We note that the observed peak which we assign to the D1 → D0 transition is very similar to the previously reported electroluminescence which has been interpreted as a triplet emission28, however, later evidence confirms the present assignment4. The neutral S0 and doubly negative S02− levels and the effect of substrate reorganization (represented by the gray shading above the ground-state levels of the three charge states) are deduced from matching the electron transport resonances measured in dI/dV spectroscopy without illumination (Fig. 2d)4,27. These levels are consistent with recent single-electron charging experiments (see Supplementary Table 1)26,32,33. Time-dependent density-functional theory (TD-DFT) simulations provide the respective electronic configurations for each of the levels that can be represented by the frontier orbital occupations. In this model, the driving mechanism is the absorption of a photon, mediated by the plasmonic cavity, converting the D0− state into the D1− or D2− excited states. The experimental evidence based on the analysis of TEPL patterns discussed further below points toward a mechanism where either a vibronic Franck-Condon D0− → D1−(\({\nu }_{j}\)) or a Herzberg-Teller D0− → D2−(\({\nu }_{j}\)) transition is induced and the excitation is subsequently distributed between the D1− and D2− states by the vibrationally driven internal conversion (see Supplementary Note 1. Theoretical methods for more details). In both cases, the spatial distribution of the absorption is driven by the D0− → D1− zero-phonon transition density.

Fig. 2: The recombination pathways of the PTCDA anion under irradiation.
figure 2

a Scheme of the excitations and transitions (denoted by vertical and horizontal arrows, respectively) between the five considered energy states of the molecule with various charges and electronic configurations, at zero bias. S0 is the neutral ground state, D0-, D1-, D2- are the singly-negative charged ground and first two excited states, respectively. The S02− is the doubly-negative charged ground state. The state D1- is composed of two dominating configurations denoted as A and B, all the other states are well-described as single-configurational states. The gray band above each state represents the effect of a threshold function reflecting the substrate reorganization energy. The legend identifies the orbitals (red and blue color indicate positive and negative isosurfaces) involved in the transitions, which are shown in the insets with the corresponding simulated spatially dependent normalized probability of tunneling (gray color scale). b, c Tip-enhanced photoluminescence (TEPL) spectra and the corresponding maps of the D1- and D2- radiative decays derived from TEPL mapping measurements. The blue and orange shaded areas in the plots mark the integration ranges for the maps. Dimensions of both maps are 5 × 3.3 nm2. d Matching of the resonant onsets E(S0) and E(S02−) in the differential conductance (dI/dV) measured on a PTCDA (location in the inset) without illumination to estimate the S0, S02− and substrate reorganization energies, using the calculated threshold function. The solid line denotes the matched part of the theoretical curve. e The comparison of the experimental and simulated photon-induced tunneling current. Source data are provided as a Source Data file.

Full size image

Theoretical calculations show the multiconfigurational character of the doublet D1− state which is mainly composed of two electronic configurations, denoted A and B in the scheme of Fig. 2a. Consequently, two major indirect decay paths are allowed from the D1− to the D0− ground state, each involving two single-electron resonant-charge-transfer steps (horizontal arrows) via one of the singlet S0 or S02− states. The steps are realized by sequentially giving up an excited electron from the molecule and filling the hole by the resonant charge transfer from the substrate or the tip (the D1− → S0 → D0− path), or vice versa - filling the hole first and then giving up the excess electron (the D1− → S02− → D0− path). In contrast, the D2− state has a single-configurational character and, in the first step, is only allowed to decay by a resonant electron transfer into the S0 state. The path through S02− involving an electron capture is unlikely due to the mismatch of the electron configurations of the D2− and S02- states as the configuration of S02− cannot be obtained by adding a single electron into the configuration of D2−. Within the framework of this simplified picture, in which the neutral or doubly negative triplet states, photon-assisted tunneling, and role of hot electrons are omitted34, we can identify and computationally evaluate two simultaneously acting mechanisms that spatially modulate the observed photon-induced current depending on the tip-position: (i) tunneling probabilities and (ii) plasmon-exciton coupling.

The first one arises from the spatial modulation of the tip-molecule tunneling probability. The photocurrent is nonzero only if the tunneling process results in a net transfer of charge from the tip to the substrate or vice versa, i.e. the tunneling between the tip and the molecule is followed or preceded by a transfer from/to the substrate. The presence of nonzero photocurrent therefore always involves the tip-molecule tunneling step, which is tip-position-dependent and scales with the density of states (DOS) derived from the molecular Dyson orbital related to the respective tip-mediated tunneling event35,36,37. This DOS can be approximated as the square modulus of the MOs, which are either being populated or depopulated, evaluated at a constant height in a close distance to the molecule (the grayscale insets 1–4 of the Fig. 2a, details of the calculations are provided in the SI).

The second mechanism modulates the contrast as a function of the tip position on a few-angstrom scale characteristic for the nanocavity confinement38. The modulation originates from the tip-position-dependent absorption that proportionally determines the excitation rate of D1−, as inferred in the recent work of Zhu et al. 19 but also from the effect of tip-position-dependent emission probability that competes with the non-radiative decay paths and co-determines the D1− equilibrium population. The respective spatial dependencies can be deduced from the patterns of the emission from the D1− and D2− in TEPL maps in Fig. 2b, c. For the D1− (emission energy 1.330 eV), it is the characteristic two-lobe pattern oriented along the longitudinal axis of the molecule, which can be attributed to the sequence of absorption, thermalization and emission, i.e. D0− → D1−(\({\nu }_{i}\))/D2−(\({\nu }_{j}\))→D1− → D0−, where D1−(\({\nu }_{i}\)) and D2−(\({\nu }_{j}\)) are the vibronically excited states. On the other hand, the four-lobe intensity map of the D2− emission (at 1.456 eV) is strikingly different from the expected two-lobe pattern oriented along the short axis of the molecule4. It indicates that the D2− is reached indirectly, through an internal conversion from the vibronically excited state D1−(\({\nu }_{i}\)) or D2−(\({\nu }_{j}\)), by undergoing the D0− → D1−(\({\nu }_{i}\))/D2−(\({\nu }_{j}\))→D2− → D0− process, in which the spatially-dependent probabilities of D0− → D1− and D2− → D0− transitions multiply and generate the four-lobed pattern (a simulation is shown in Supplementary Fig. 8). Consequently, both absorption probabilities as well as the emission follow the tip-position dependent nanocavity coupling with the D0− ↔ D1− transition, which we simulate using the transition charge density from TD-DFT convolved with the function representing the plasmonic quasi-electrostatic potential of the nanocavity4,39.

To simulate the current and TEPL maps, we calculate the rates associated with the position-dependent plasmon-exciton interaction and all considered charge-exchanges between the PTCDA, the tip and the substrate and use them to create a set of rate equations (see the SI). The solution yields the spatially dependent net current flowing between the tip and the molecule that reproduces the observed contrast, as shown by the comparison with the experiment in Fig. 2e. Because the tunneling probabilities are evaluated in a plane close to the molecule, the orbital-like character of the maps has a high spatial resolution40. The current maps calculated using the zero-bias model indicate that the three transitions from the D1− and D2− to S0 and S02− that involve orbitals 1, 3 and 4 play a similarly important role in the experimentally observed contrast. On the other hand, the SOMO- and SUMO-like character associated with the transitions of S0 and S02− to D0−, reflecting the shape of the orbital 2, is less apparent. The decay channels involving D1−,D2− → S0 or D1− → S02− contribute with a characteristic pattern that is a fingerprint of the respective electron configuration forming the excited states. The positive current (mapped to gray color scale in Fig. 2e) is dominantly generated by the injection of an electron into the unoccupied orbital 1 of the configuration B of D1−. The negative portion of the current (red color scale) is mostly generated by two contributions. One involves the extraction of an electron from orbital 3 that is occupied in the configuration of D2− and the second one is associated with the extraction of an electron from the occupied orbital 4 in configuration A of the D1− state (see the orbital occupations in Fig. 2a for reference). The signatures of both orbital 1 (in the positive current) and orbital 4 (in the negative current) in the photon-induced current map therefore prove the presence of both configurations A and B in the state D1−.

We can test the possibility of disentangling different components of the multiconfigurational excited state by selectively promoting the decay path involving either the A- or the B-configuration of D1−. To that end, we tune the bias voltage and anticipate one of the two patterns that identifies the respective pathway in the current maps. To separate the photon-induced component from the total tunneling current (I) we modulate the laser intensity and detect the response in the current - obtaining the dI/dP signal, which is proportional to the photocurrent in our scenario (see Supplementary Fig. 5 for details of the setup).

The detailed maps of the bias-dependent current, dI/dP and the differential conductance dI/dV under irradiation are shown in Fig. 3 (for completeness, TEPL maps at −450 and 650 mV are provided in Supplementary Fig. 10). The bidirectionality of the net electron transport over the PTCDA molecule is gradually lost as the bias is increased to higher positive or negative values. At positive bias above 150 mV the current map strongly resembles the tunneling probability distribution generated for orbital 1, corresponding to the D1− → S02− transition, suggesting that at this bias the contrast is dominated by the process where an electron from the tip is injected into this orbital. Similarly, at the negative polarity below -150 mV, the current map is comparable to the tunneling from orbitals 3 and 4 (D2−,D1− → S0). At both onsets of the resonant tunneling, −450 and 650 mV, the current is apparently dominated by the extraction from SOMO and injection to SUMO, respectively, which is detected also in the dI/dV maps. While the dI/dP map essentially corresponds to the current map recorded within the gap region (~−350–250 mV) it retains its character beyond the onsets of resonant tunneling, where it reaches a saturation. The same trend can be reproduced using the theoretical model that considers the bias, including a voltage drop between the molecule and the substrate. The voltage-induced changes of the photocurrent patterns can be understood as a result of the variation of the transition rates promoting either the D1− → S0 → D0− or the D1−,D2− → S02− → D0− path as a function of the bias voltage, which occurs due to the smooth onset of the thresholds of the tunneling steps S0 → D0− and S02− → D0−. These smooth onsets result from the Franck-Condon blockade due to the reorganization of the substrate atoms upon changing the total charge of the molecule during a tunneling event41 (see also Supplementary Fig. 4 and related Supplementary Discussion for more details). In addition, the theoretical simulations show that the contribution of the transition from the excited state D1− could in principle be distinguished from that of D2− by resonantly exciting the D0− → D1− transition (as shown in supplementary Fig. 7), which would require a tunable laser source.

Fig. 3: Comparison of bias-dependent maps of current, photocurrent, dI/dV and simulations.
figure 3

The current, the photon-induced component of the current proportional to photocurrent (dI/dP) and conductance (dI/dV) maps are taken simultaneously over a PTCDA molecule in a constant-height mode as a function of the applied bias voltage in the range from −450−650 mV. Theoretical simulations are provided for comparison. The area of the images is 2 × 2 nm2. The numbers at the top and bottom right corner of each image represent the minimum and maximum data value, respectively. The +max and -min in the color scale bar refer to the maximum positive and minimum negative intensity of the signal.

Full size image

The set of experimental dI/dV maps in Fig. 3 measured within the transport gap shows an overall weak magnitude compared to the resonant onsets. Yet, the contrast is significantly more intense than the almost negligible signal measured without illumination (Supplementary Fig. 6) and shows very specific patterns. This indicates that the conduction channels are modified in the transport gap as a result of the photon absorption and charge transfer decay of the excited states. The dI/dV curves measured at two positions over the molecule with the tip close to the molecule in Supplementary Fig. 9 reveal relatively broad peaks near to zero bias depending on the measurement location. We observe a single peak in the location corresponding to the outer lobes of the orbital 1 and a doublet of peaks above the inner lobes. The dI/dV maps and curves extracted from the results of the model qualitatively reproduce this behavior, confirming its validity.

In conclusion, by imaging photocurrents generated in a single open-shell PTCDA anion using the light-STM, we have identified signatures of the two dominating configurations composing its multiconfigurational excited state D1−. We found that these two configurations are fingerprinted in the tip-position-dependent photocurrent maps as a contrast associated with positive and negative photocurrents, respectively. This finding is supported by a theoretical model combining ab-initio calculations of molecular properties with rate-equations describing the charge-transfer, plasmon-enhanced photon absorption and emission. Furthermore, we have experimentally demonstrated that it is possible to achieve selective mapping of the photocurrent paths associated with the positive and negative current contributions. Such tuning is enabled by exploiting the smooth variation of the voltage-dependent tunneling rates between the molecule and the tip/substrate even at small bias voltages. Such smooth variation arises due to the substrate reorganization upon changing the molecular charge, combined with the relatively small energy of tunneling onsets associated with the alignment of the many-body states of PTCDA. Our findings prove that an optically driven variety of the well-established STS mapping can be instrumental in deciphering the electronic character of hard-to-access multi-configurational excited states of molecules by directly imaging the constituent electronic configurations.

Methods

Measurements and sample preparation

All presented experiments were done in the constant-height mode with an optical Createc SPM with an internal fixed-focus lens at a temperature below 6 K. The scheme of the lock-in measurements of the current, dI/dV and dI/dP maps is shown in Supplementary Fig. 5. A fiber coupled excitation source (Thorlabs SHG stabilized laser diode) at 785 nm was used with power of 400 μW, modulated by 200 μW at 743 Hz to obtain the dI/dP signal. The bias modulation for the dI/dV measurements was 10 mV at 923 Hz. The optical setup for coupling the external laser was a confocal arrangement with a dichroic mirror, lenses, filters and optical fibers placed outside of the vacuum5,30. For the photon rate and TEPL spectra acquisition we used the PerkinElmer SPCM-AQR-15 single-photon avalanche detector and the Andor Kymera 328i with Newton 920 CCD (BEX2-DD sensor), respectively. The samples were prepared by standard cycles of Ar+ sputtering and annealing, followed by thermal deposition of NaCl from a Ta crucible at 858 K onto the sample held at 390 K. The PTCDA molecules of 98% purity were obtained from Sigma-Aldrich, further purified by vacuum sublimation and deposited on the sample held below 6 K. Plasmonic tips with a spectrum matching the excitation and emission wavelengths were prepared by a series of controlled indentations and voltage pulses on a clean Ag(111) surface.

Rate equations

The theoretical model of the photocurrent generation relies on solving a system of rate equations governing the transitions among the many-body states of the PTCDA molecule as sketched in Fig. 2a. Steady-state solutions of the rate equations are obtained for each lateral position of the tip to generate the photocurrent maps. More explicitly, for each many-body state population \({N}_{i}\), where \(i\) runs over the many-body states S0, D0−, D1−, D2−, S02−, we have a system of rate equations in the steady-state:

$$0=\frac{{{{\rm{d}}}}{N}_{i}}{{{{\rm{d}}}}t}=-{\sum }_{j}\left({\gamma }_{{ji}}^{{{{\rm{T}}}}}+{\gamma }_{{ji}}^{S}+{\kappa }_{{ji}}\right){N}_{i}+{\sum }_{j}\left({\gamma }_{{ij}}^{{{{\rm{T}}}}}+{\gamma }_{{ij}}^{{{{\rm{S}}}}}+{\kappa }_{{ij}}\right){N}_{j}$$
(1)

where the rates \({\gamma }_{{ji}}^{{{{\rm{T}}}}}\) and \({\gamma }_{{ji}}^{{{{\rm{S}}}}}\) are the tip and substrate mediated tunneling rates connecting state \(i\) to state \(j\) of different charge and \({\kappa }_{{ji}}\) are the plasmon-mediated excitation and deexcitation rates connecting the states of the same charge. We do not consider spin degeneracy, for simplicity. The tunneling currents are obtained as

$$I\propto {\sum }_{{ij}}{N}_{i}{\gamma }_{{ji}}^{{{{\rm{T}}}}}\left({Q}_{i}-{Q}_{j}\right)$$
(2)

with \({Q}_{i}\) being the total charge of the molecular state \(i\).

The tip-mediated tunneling rates \({\gamma }_{{ji}}^{{{{\rm{T}}}}}\) used in the model carry both the spatial dependence and the bias-voltage (\(V\)) dependence and have the form:

$${\gamma }_{{ji}}^{{{{\rm{T}}}}}={\gamma }_{0}^{{{{\rm{T}}}}}{{{\rm{DO}}}}{{{{\rm{S}}}}}_{{ji}}\left(x,y\right)\varTheta \left({E}_{i}^{{{{\rm{T}}}}}-{E}_{j}^{{{{\rm{T}}}}}\right)$$
(3)

where

$${{{\rm{DO}}}}{{{{\rm{S}}}}}_{{ji}}(x,y)={|{\psi }_{{ij}}(x,y,z={z}_{{{{\rm{T}}}}})|}^{2}/\max \left({|{\psi }_{{ij}}(x,y,z={z}_{{{{\rm{T}}}}})|}^{2}\right)$$
(4)

with \({\psi }_{{ij}}\left(x,y,z={z}_{{{{\rm{T}}}}}\right)\) being an approximation of the Dyson orbitals of the transition from \(i\) to \(j\), evaluated at a plane \(z={z}_{{{{\rm{T}}}}}\), \(\varTheta \left({E}_{i}^{{{{\rm{T}}}}}-{E}_{j}^{{{{\rm{T}}}}}\right)\) being a threshold function, and \({\gamma }_{0}^{{{{\rm{T}}}}}\) being a scaling constant. We use \({\hslash \gamma }_{0}^{{{{\rm{T}}}}}\) = 1 µeV as it simulates the situation when the tip-molecule tunneling is dominating over the substrate-molecule tunneling40, as expected in the experiment due to the small tip-molecule distance required to detect photocurrents. We calculate \({\psi }_{{ij}}\left(x,y,z={z}_{{{{\rm{T}}}}}\right)\) using the density-functional theory from which we extract the orbitals that correspond to the dominating single-particle change of configuration between many-body states \(i\) and \(j\), as described below. The threshold function takes as inputs the energies \({E}_{i}^{{{{\rm{T}}}}}\) that are related to the many-body state energies \({E}_{i}\) and are evaluated assuming that the electron is exchanged between the molecule and the tip, and the voltage \(V\). \({E}_{i}^{{{{\rm{T}}}}}\) is related to \({E}_{i}\) as follows:

$${E}_{i}^{{{{\rm{T}}}}}={E}_{i}+{\alpha Q}_{i}V$$
(5)

where \(\alpha\) = 0.8 accounts for the fraction of the voltage drop across the molecule-tip gap. The value of \(\alpha\) is justified by the small tip-molecule distance and a good match of the simulation with experimental data, particularly the dI/dV curves. The many-body energies \({E}_{i}\) are summarized in Supplementary Table 1 and are derived from the experimentally obtained data including the photon emission energies and dI/dV spectra. The procedure of obtaining these energies is described below in the next section.

The substrate-mediated rates \({\gamma }_{{ji}}^{{{{\rm{S}}}}}\) are calculated similarly, but are independent of the lateral position of the tip:

$${\gamma }_{{ji}}^{{{{\rm{S}}}}}={\gamma }_{0}^{{{{\rm{S}}}}}\varTheta \left({E}_{i}^{{{{\rm{S}}}}}-{E}_{j}^{{{{\rm{S}}}}}\right)$$
(6)

with \({{\hslash }}{\gamma }_{0}^{{{{\rm{S}}}}}\) = 0.1 µeV. Here the superscript \(S\) indicates that the respective parameters are considered for the substrate side, whose values will generally differ for the ones on the side of the tip as they are dependent on the voltage drop between the molecule and the underlying metal:

$${E}_{i}^{{{{\rm{S}}}}}={E}_{i}-{(1-\alpha )Q}_{i}V$$
(7)

The charge-conserving plasmon-mediated decay D1−\(\to\)D0− and D2−\(\to\)D0− are modeled assuming that they are mediated by the interaction of the transition density \({\rho }_{{ji}}\) corresponding to the respective transition from state \(i\) to \(j\) with the tip plasmon, whose quasi-electrostatic potential \({\phi }_{{{{\rm{pl}}}}}\) is localized around the tip apex. The plasmon-mediated decay rates are then calculated as

$${\kappa }_{{ji}}={\kappa }_{0}+{\kappa }_{{{{\rm{pl}}}}}{|{g}_{{ji}}(x,y)|}^{2}/\max \left({|{g}_{{ji}}(x,y)|}^{2}\right)$$
(8)

with

$${g}_{{ji}}(x,y)=\int {\rho }_{{ji}}(X,Y,Z){\phi }_{{{{\rm{pl}}}}}(X-x,Y-y,Z){{{{\rm{d}}}}}^{3}{{{\bf{R}}}}$$
(9)

where \({{{\bf{R}}}}\) = (\(X\), \(Y\), \(Z\)) are cartesian coordinates and the highest point of the molecule lies in the plane Z = 0. The parameters \({\hslash \kappa }_{0}=0.1{{{\rm{meV}}}}\) and \({\hslash \kappa }_{{{{\rm{pl}}}}}=0.5{{{\rm{meV}}}}\) account for the substrate-mediated tip-position-independent background component of the exciton decay (e.g. due to the electron-hole pair excitations in the substrate) and the tip-position-dependent decay, respectively, and their values are selected and modeled consistently with previous studies42. To model the plasmonic potential \({\phi }_{{pl}}\) we used the simple point-charge model

$${\phi }_{{{{\rm{pl}}}}}\left(X,Y,Z\right)=1/\sqrt{{X}^{2}+{Y}^{2}+{(Z-{z}_{1})}^{2}}-1/\sqrt{{X}^{2}+{Y}^{2}+{(Z+{z}_{2})}^{2}}$$
(10)

Here \({z}_{1}\) = 30 a.u. and \({z}_{2}\) = 40 a.u. are suitable chosen parameters approximating the localization of the plasmonic field.

In the experiment the molecule is excited by an off-resonant laser whose energy is higher than that of the D0−\(\to\)D1− and D0−\(\to\)D2− absorption energies. It is therefore likely that the photons generate a vibrationally excited state of either D1− or D2−. Based on the spatial distribution of the TEPL maps we further conclude that the orientation of the transition dipole of the vibronic transition in question is the same as that of the D0−\(\to\)D1− ZPL. This can happen either via the Franck-Condon mechanism involving the D0−\(\to\)D1−(\({\nu }_{i}\)) transition or via the Herzberg-Teller mechanism involving the D0−\(\to\)D2−(\({\nu }_{i}\)) transition, where the transition dipole moment is borrowed from a different (e.g. D0−\(\to\)D1−) electronic transition43. Since in our model we assume that after the absorption event the excitation is redistributed between D1− and D2, both mechanisms would yield similar results. Hence, we cannot decisively pinpoint which mechanism is involved in our experiment purely based on symmetry of the TEPL maps. Nonetheless, as the energy of the exciting laser is about 250 meV (2000 cm-1) above the energy of the D0−\(\to\)D1− transition and there are no PTCDA vibrational modes5 at that energy, we find the Franck-Condon mechanism less likely. On the other hand, there are vibrational modes around the energy of 992 cm-1 that could mediate Herzberg-Teller transitions and we therefore chose for definiteness that the energy is absorbed via a Herzberg-Teller transition into D2− (with transition dipole borrowed from D0−\(\to\)D1−) and is then redistributed by internal conversion (IC) between D1− and D2−. The plasmon-mediated excitation process D0−\(\to\)D2− is implemented similarly to the decay rates as:

$${\kappa }_{{{{{\rm{D}}}}}_{2}^{-}{{{{\rm{D}}}}}_{0}^{-}}={\eta }_{0}{|{g}_{{{{{\rm{D}}}}}_{1}^{-}{{{{\rm{D}}}}}_{0}^{-}}(x,y)|}^{2}/\max \left({|{g}_{{{{{\rm{D}}}}}_{1}^{-}{{{{\rm{D}}}}}_{0}^{-}}(x,y)|}^{2}\right)$$
(11)

where \(\hslash {\eta }_{0}\) = 3\(\times\)10-7 eV represents a weak pumping due to the external laser. We select the value of \({\eta }_{0}\) such that the ratio of the maxima of photocurrents to the maxima of currents emerging from the standard sequential tunneling obtained in the map corresponds to the experiment. We consider an internal conversion D2−\(\to\)D1− characterised by the rate \(\hslash {\kappa }_{{{{{\rm{D}}}}}_{1}^{-}{{{{\rm{D}}}}}_{2}^{-}}={{\hslash }}{\gamma }_{{{{\rm{IC}}}}}\) = 2 meV that leads to the population of D2− as observed in the experiment.

For convenience, all rates (or constants scaling the tip-position and voltage-dependent rates) used in the model are summarized in Supplementary Table 2.

The threshold function

The threshold function \(\varTheta ({E}_{i}^{{{{\rm{S}}}}({{{\rm{T}}}})}-{E}_{j}^{{{{\rm{S}}}}({{{\rm{T}}}})})\) is obtained from a model accounting for the effect of substrate atom reorganization upon molecular charging. In essence, the substrate ions respond to the change of the perceived electric field generated by the molecule which leads to Franck-Condon effects in charge transfer from and into the molecule. In our earlier work43, we have implemented a mathematical model for the line-shape \(S(v)\) of peaks in tunneling dI/dV spectra. Here we consider \(S(v)\) normalized such that \({\int }_{-{\infty }}^{{\infty }}S(v){{{\rm{d}}}}v=1\). In particular,

$$S(v)\propto {{\mathrm{Re}}}\left\{{\int _{0}^{{\infty }}}{e}^{{\int _{0}^{{\infty }}}J(\varOmega ){e}^{{{{\rm{i}}}}\varOmega t/{{\hslash }}}{{{\rm{d}}}}\varOmega }{e}^{-{{{\rm{i}}}}{vt}/{{\hslash }}}{{{\rm{d}}}}t\right\}$$
(12)

with

$$J(\varOmega )=\frac{{E}_{{{{\rm{R}}}}}}{\left({\varOmega }_{\max }^{2}-{\varOmega }_{\min }^{2}\right)}{{{\rm{rect}}}}\left[\frac{\varOmega -{\varOmega }_{\min }-0.5\left({\varOmega }_{\max }-{\varOmega }_{\min }\right)}{{\varOmega }_{\max }-{\varOmega }_{\min }}\right]$$
(13)

where \({\varOmega }_{\min }\) = 18 meV and \({\varOmega }_{\max }\) = 31 meV are the lower and upper bounds of the optical-phonon frequencies in NaCl and ER = 850 meV is the reorganization energy considered in the present model, consistently with the previous work26. The threshold function \(\varTheta (E)\) is then the cumulative integral of \(S(v)\)

$$\varTheta (E)={\int _{-{\infty }}}^{\!\!\!\!\!\!\!E}S(v){{{\rm{d}}}}v$$
(14)

Importantly, the onset of \(\varTheta (E)\), as compared to a regular step function, is offset since the zero-phonon charging transition is unlikely as the reorganization energy is high. This therefore realistically accounts for the stabilization of charge states by the reorganization of the NaCl layer and is a critical component of our model as it leads to gradual variations of charge-transfer rates with varying voltage \(V\). The functions \(\varTheta (x)\) and \(S(x)\) are shown in Supplementary Fig. 1.

Extracting many-body-state energies from the experiment

The energies of the states considered in the model are summarized in Supplementary Table 1. They have been extracted from the experimental data as follows. The vertical transition energies have been estimated from the optical emission spectra. The energies E(S02−) and E(S0) have been obtained from the experimental dI/dV spectra using the threshold function and assuming \(\alpha\) = 0.8 and \({\gamma }_{0}^{{{{\rm{T}}}}}=0.01{{{\rm{\mu eV}}}}\) as the tip-sample distance is larger when the tunneling spectroscopy is performed than in the case of the photocurrent measurements.

Ab-initio calculations

To approximate the spatial distribution of tunneling currents and plasmon-exciton coupling we perform density-functional theory (DFT) and time-dependent DFT (TD-DFT) calculations. Since the spatial distribution of constant-height photocurrent maps can strongly depend on the details of the molecular geometry, we first optimize the molecular structure including the substrate. To that end we assume a patch of 2 ML NaCl containing 6√2\(\times\)6√2 unit cells as shown in Supplementary Fig. 2. The patch is composed of units of 8 atoms (4 Na and 4 Cl) that form an electrostatic octupole and therefore minimize stray electric fields that could spuriously influence the properties of the molecule. Prior to relaxation we assume dNaCl = 2.805 Å, we then fix the positions of the atoms in the bottom layer and all the border atoms, leaving only the atoms of the top layer that have 5 nearest neighbors to relax. The molecule is placed on top of the layer as depicted in Supplementary Fig. 2 consistently with experimental observations. We optimize the system geometry in the ground state assuming a singly negative doublet configuration using the hybrid B3LYP44 functional and the 6-31 G(d) double-zeta gaussian basis using the Gaussian 16 rev. C.01 software45. An empirical dispersive interaction (GD3BJ46) is considered between the atoms to account for the dispersive molecule-NaCl interaction.

After relaxing the structure, we extract the ground-state geometry of the molecule that is considerably bent compared to its flat geometry obtained in a vacuum. This geometry is used to calculate the excited states using the linear-response TDDFT implemented in Gaussian 16 and the D0−\(\to\)D1− and D0−\(\to\)D1− transition densities are extracted using the Multiwfn tool47 in the form of 3D cube files that are used to calculate the spatial dependence of plasmon-exciton coupling and are shown in Supplementary Fig. 3a. From the TDDFT result we also note the composition of the D0−\(\to\)D1− that dominantly consists of the transitions 2 \(\to\) 4 (26%) and 1\(\to\)2 (74%) (see the orbital notation in Fig. 2a of the main text and Supplementary Fig. 3b). For definiteness, we use the information to estimate the relative weights of the two configurations contributing to the formation of D1−, although we note that a different parametrization of the model could yield similar results even if different contributions of the two configurations were considered (e.g. obtained using a different ab-initio model, perform the calculations in the excited-state molecular geometry, etc.). We note that a more precise TDDFT calculation including the substrate or relaxing the molecular geometry on the substrate in the excited-state geometry and then extracting the transition densities and other quantities is demanding and for TDDFT calculations we therefore resort to only using the ground-state relaxed geometry of the molecule.

Finally, to obtain the spatial dependency of the photocurrents, we approximate the Dyson orbitals of the respective transitions sketched in Fig. 2. These correspond to the orbitals from which (into which) a single electron must be extracted (added) to obtain the configuration of the final state. Since molecular orbitals constructed using gaussian basis sets do not feature a physically meaningful spatial dependence at a plane \(z={z}_{{{{\rm{T}}}}}\) above the molecule, we resort to a different DFT software implementing the Kohn-Sham scheme on a real-space grid, Octopus v. 11.448. We use the geometry obtained from Gaussian 16 and perform a ground-state DFT calculation using the Perdew-Zunger49 parametrization of the local density approximation (LDA) correlation and the Slater density functional for the LDA exchange functional50,51. To achieve Kohn-Sham energies of the orbitals similar to the ionization potentials and electron affinities of the molecule, that can be estimated from Supplementary Table 1 upon correction for the substrate work function (WNaCl/Ag ~ 3.5 eV52), we perform the calculation assuming a total charge of the molecule to be -0.5|e|. We use a tight box shape composed of atom-centered spheres of the radius 15 Å and grid step of 0.1 Å and export the orbitals into cube files. We evaluate the orbitals at a plane \(z={z}_{{{{\rm{T}}}}}\approx 9.4\) a.u. ≈ 5 Å above the highest point of the molecule and use these slices to define the 2D density of states (DOS) \({|{\psi }_{{ij}}\left(x,y,z={z}_{T}\right)|}^{2}\) belonging to the respective transitions. The respective transitions and corresponding orbitals are schematically shown in Fig. 2 and summarized in Supplementary Fig. 3b.