Abstract
Significant success has been achieved in fabricating angstrom-scale artificial solid ionic channels aiming to replicate the biological ion channels (BICs). Besides high selectivity, BICs also exhibit sophisticated ion gating and interplay. However, such behavior and functionality are seldomly recreated in the artificial counterparts due to the insufficient understanding of the molecular origin. Here we report cooperative and inhibitory ion transport in angstrom-scale acetate functionalized MoS2 two-dimensional channels. For cooperative ion transport, the permeability of K+ is doubled in the presence of only 1% Pb2+ (versus K+ by molarity), while the permeability of Pb2+ is independent of K+. Molecular dynamics simulations reveal complex interplay among K+, Pb2+, and the anions in governing the cooperativity, such that Pb2+ ions capture and slow down the anions via long-range interaction, which leads to the synchronization of anions with K+ to transport as ion pairs with reduced interaction with the channel surface. For inhibitory ion transport, divalent Co2+ (or Ba2+) and Pb2+ can replace each other in the confined channel and compete for the limited transport cross section. Our work reveals ion transport phenomena in extreme confinement and highlights the potential of manipulating ion interplay in confinement for achieving advanced functionalities.
Similar content being viewed by others
Introduction
Biological ion channels (BICs), which are abundant in cell membranes, are critical in many cellular processes1. The primary signature shared by BICs is their tailored selectivity filter on the angstrom (Å) scale, which regulates specific ion transport (e.g. K+, Na+ and Ca2+) across the cell membrane2. It has long been envisioned to replicate such marvelous BICs artificially, aiming at realizing high-performance separation of target ions and ion-based functional devices3. In the past two decades, significant progress has been achieved in preparing devices with Å-scale confinement with many different classes of materials including porous materials4,5,6,7,8, 1D nanotubes9,10,11, 2D nanochannels12,13,14,15,16,17,18,19,20, thanks to advances in the precision synthesis and fabrication21. All these materials platforms have deepened our understanding of how water, organic solvents and ions behave in extreme confinement.
If we look at the BICs, it can quickly be realized that besides the high selectivity, rich and exquisite ion interplay phenomena play out in BICs under physiological conditions22. For example, in the small-conductance Ca2+-activated K+ ion channels, i.e. the KCNN4 channel, Ca2+ can promote the permeability of K+ via binding with calmodulin (CaM) to induce a conformational change, which in turn opens the channel pore (Fig. 1a)23,24. It is also well-established that some ions, e.g. Ba2+, can block the K+ ion channel (Fig. 1b) and that the Ba2+ blockage is sensitive to extracellular K+ concentration (the so-called “lock-in effect”)25. Similar blocking effects are also observed in Ca2+ ion channels26,27. All these observations suggest that there is a rich ion interplay in governing the sophisticated functions of BICs. By contrast, the predominant works on artificial channels, whether porous materials6 or 1D nanotubes9,10 or 2D channels13,14,15,16,17,18,19,20, are tested with a single salt to explore ion transport behavior, with few measurements using mixed salts28,29. This implies that the information on ion interplay in artificial channels is far from adequate30,31, which naturally sparks the important question: How do ions interplay in artificial channels? Can ion interplay be harnessed controllably in artificial ionic channels? Motivated by these questions, we explore ion interplay in the artificial channels. We use a MoS2-based 2D channel that is covalently functionalized with acetic acid as the model system to investigate ion interplay. We have discovered two kinds of ion interplay phenomena in this system, i.e. cooperative ion transport and inhibitory ion transport. For cooperative transport, the permeability of K+ is doubled in the presence of only 1% mol Pb2+, while the permeability of Pb2+ is independent of K+. Molecular dynamics (MD) simulation reveals the molecular mechanism underpinning this complex ion behaviors that mobile Pb2+ plays a key role in slowing down the anions via long-range interactions, which influences the pairing between K+ and anions in the two-dimensional channels. The correlated transport between K+ and anions in the channel reduces the K+ interaction with channel surface, and therefore enhances its permeability. For inhibitory ion transport, divalent Co2+ (or Ba2+) cannot pair with monovalent anions due to its slow diffusion and competes strongly with Pb2+ to enter the confined channel and interacts with the functional groups on the channel surface, which result in the reduced flux.
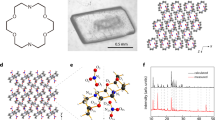
a Schematic of the working mechanism of the Ca2+-activated K+ ion channels, where calmodulin (CaM) can open the channel upon binding Ca2+. b Schematic of the working mechanism of the Ba2+-blocked K+ ion channels. c Experimental procedure for exploring ion interplay in artificial 2D channels. (i) and (ii) represent different metal cations. d Cross-section of STEM image of MoS2-COOH membrane showing the 2D channels in the dry state. e Schematic of the structure of the MoS2-COOH nanosheet, as boxed out in (d). Orange circle indicates a covalently bonded carboxyl group attached to the MoS2 plane, which is illustrated in detail in (f, left). f Schematic showing the Pb2+ induced deprotonation and its bidentate binding mode with the acetate functional group.
Experimental design
To explore the ion interplay in the artificial 2D channels, we designed the experimental procedure shown in Fig. 1c. We have systematically examined the permeabilities of individual ions (Cases 1 and 2 in Fig. 1c) and for mixed ions (Case 3 in Fig. 1c) and compare them accordingly. The model 2D material platform we chose is acetic acid-functionalized MoS2 (MoS2-COOH, Fig. 1d, e, and Supplementary Fig. 1) for the following two reasons: first, the covalently bonded carboxyl groups can lead to controlled hydration of the MoS2-COOH membrane32, which, for comparison, cannot be achieved using the unfunctionalized MoS2 membrane33,34; second, our previous work has shown that carboxyl groups have strong chelating capability with metal ion35, which will be further discussed later. 2D channels are built by stacking MoS2-COOH nanosheets using vacuum filtration. A cross-sectional scanning transmission electron microscopy (STEM) image clearly shows the layered structure of the restacked MoS2-COOH membrane in its dry state (Fig. 1d). Details of functionalization method and membrane preparation are provided in the Supplementary Information.
In the MoS2-COOH system, we particularly focus on Pb2+, because our previous study has revealed: i) it can induce deprotonation of the carboxyl functional group and ii) Pb2+ uniquely adopts a bidentate binding mode with the carboxylate functional group (Fig. 1f) and locks the interlayer spacing, as confirmed by FTIR measurements and DFT calculations35. High-angle annular dark-field (HAADF) STEM image clearly shows the presence of single-site Pb2+ in the MoS2-COOH membrane treated by Pb2+ solution (Supplementary Fig. 2). We focus our study on binary ion interplay between Pb2+ and monovalent ions (K+/Li+) or between Pb2+ and divalent ions (Co2+ and Ba2+). We conducted permeation transport tests using an H-type cell, where one chamber is filled with feed salt solution and the other filled with an equal volume of deionized water, with the membranes mounted in between (Supplementary Fig. 3). The transmembrane permeabilities of Pb2+ and other ions (K+, Li+, Co2+ and Ba2+, with ion parameters listed in Supplementary Table 1) were measured using single ion solutions and corresponding binary mixture solutions sequentially, as mentioned in Fig. 1c. Inductively coupled plasma mass spectrometry (ICP-MS) is used to identify and quantify the metal cations. Other experimental details and the method for calculating permeability are detailed in the Supplementary Information. All the salt solutions were tested with natural pH values after dissolving in deionized water without further tuning (solution pH values ranging from ~3.6 to ~6.6).
Results
Cooperative ion transport
We started by examining the interplay between K+ and Pb2+ (both salts are nitrate-based). The results are summarized in Fig. 2a, with more detailed results in Supplementary Fig. 4 and Supplementary Table 3. Each bar of Fig. 2a refers to the ion flux into the permeate observed in a sequence of experiments in which the membrane is exposed to different feed solutions indicated at the bottom. Thus, the first bar in Fig. 2a refers to K+ only. Then the feed is switched to Pb2+ only with the same membrane for the second bar, and followed by K+ only in the third bar and mixtures of K+ and Pb2+ in the subsequent bars. These results show that the permeability of K+ (third bar) decreases by ~20% after the Pb2+ test when compared to the initial permeation test of K+ (first bar), despite the enlarged channel. We attribute this to the increased cation concentration within the channels and the electrostatic repulsion forces between Pb2+ in the channel and K+ ion in the feed, which creates a barrier preventing K+ from entering the channel. This is supported by the MD calculations vide infra (Supplementary Fig. 18). More interestingly, with a tiny fraction of Pb2+ (1% by mol K+) added into the feed (4th bar), the permeability of K+ is doubled. After that the permeability of K+ continues to rise with the addition of more mobile Pb2+ in the feed, and reaches a peak value ~350% when the Pb2+/K+ ratio is 25% (8th bar, as also shown in Fig. 2b). Further increase of the Pb2+/K+ ratio beyond 25% leads to a slight decrease of K+ permeation. In contrast to this, the permeability of Pb2+ only scales with the feed concentration of Pb2+ (Fig. 2b), regardless of the presence of K+ or not (Supplementary Fig. 5). Similarly enhanced transport is also observed in the Li+/Pb2+ pair tests (Supplementary Fig. 6, nitrate anions) and K+/Pb2+ pair tests with chloride anions instead of nitrate anions (Supplementary Fig. 7) in the MoS2-COOH 2D channel. Our results are also contrasted with previous works reporting suppressed transport of a monovalent cation by a divalent cation in nanotube28 and nanopore tests29. Clearly, all our results unambiguously confirm that there is clear interplay between K+ (or Li+) and Pb2+ when they transport in the 2D MoS2-COOH channels, and the ion interplay is asymmetric. We term this asymmetric ion interplay as a cooperative ion transport effect. Additionally, the cooperative ion transport effect is absent in tests using the polytetrafluoroethylene (PTFE) membrane with large pores of ~200 nm (Supplementary Fig. 8), where the permeabilities of K+ and Pb2+ are totally independent of each other (Fig. 2c and Supplementary Fig. 9) and the measured permeability ratio of K+/Pb2+ across the PTFE membrane is ~1.76, close to their bulk diffusion coefficient ratio of ~2.07. The results indicate independent bulk ion transport properties in the large pore PTFE membrane without any ion interplay. Cooperative ion transport is also absent in the commercial MCE membrane with a smaller pore size ~25 nm (Supplementary Fig. 10), which further highlights the significance of angstrom-scale confinement to ion interplay.
a Summary of the sequential permeation test results of K+, Pb2+, and K+/Pb2+ mixtures across one MoS2-COOH membrane. b, c The fluxes of K+ and Pb2+ versus concentration of Pb2+ in the feed for the series of tests across the MoS2-COOH membrane and PTFE membrane, respectively. In the panel, both the ion fluxes and osmotic pressure are normalized to values corresponding to the initial K+ test. Data: mean ± standard error. d Systematic XRD measurements for the MoS2-COOH membrane. The effective height of the Pb2+-locked channel is ~11.4 Å−6.2 Å=5.2 Å, where 6.2 Å corresponds to the intrinsic thickness of monolayer MoS2. The annotation “solution 1 to solution 2” in the legend of (d) indicates that the MoS2-COOH membrane was first saturated in solution 1 and then switched to solution 2 for uptake, and finally the MoS2-COOH membrane was taken out of solution 2 for XRD measurements. The pink triangle indicates the PTFE peak. a.u. is arbitrary unit. The salts used are nitrate-based.
To the best of our knowledge, this is the first such observation of cooperative ion transport effect in artificial channels in the nanofluidics studies. To understand the mechanism underlying this cooperative ion transport, we first calculated the osmotic pressure change, given that the ion permeation tests are driven by osmotic pressure. Clearly, as plotted in Fig. 2a, the enhanced permeation of K+ cannot be solely attributed to the change in osmotic pressure, because the enhancement is well above the change of osmotic pressure, particularly in the low Pb2+/K+ regime, e.g. 1% mol Pb2+ addition. We also notice that the cooperative ion transport observed bears striking resemblance to the Ca2+-activated K+ BICs, where enhanced K+ transport is attributed to the pore opening due to conformational change induced by CaM upon binding Ca2+. Inspired by the pore opening mechanism, we systematically examined the interlayer spacings of MoS2-COOH channels in a series of tests for K+/Pb2+. However, the results show that after the single Pb2+ test (2nd bar in Fig. 2a), the 2D MoS2-COOH confinement is fixed (or locked) by Pb2+ with an effective channel height ~5.2 Å (Fig. 2d). The locking effect of Pb2+ is not surprising, given the dominant uptake of Pb2+ as compared with K+ in the MoS2-COOH membrane (Supplementary Fig. 11). Apparently, this cooperative ion transport cannot be attributed to a change in confinement size either and points to an origin different from the Ca2+-activated K+ channels.
MD simulations and mechanism
To elucidate the mechanism underlying our observations, we conducted all-atom MD simulations of ion and fluid transport through a single, straight nanochannel. This simplified model was designed to include the essential features needed for transport behavior, although it may overlook effects such as inter-channel coupling and directional variations in ion or fluid flow. The density of grafted acetate functional groups was set to match the experimental value and randomly distributed without manual bias. We carefully selected key simulation parameters, including interlayer spacing and applied pressure, to ensure consistency with the experimental setup. We conducted a sequence of permeation tests in the same order as the experiments, and the simulated layer spacings were also consistent with the experiments. Specifically, each bar in Fig. 3b represents the ion flux into the permeate as observed in a series of calculation tests, with the specific ion numbers for the feed solutions indicated at the bottom of the figure. The first bar represents the flux with a feed solution containing only K+ ions and no Pb2+ ions in the membrane. The second bar represents the flux after switching the feed solution to contain only Pb2+ ions, using the same membrane. The third bar represents the flux with a feed solution containing only K+ ions. From the third bar onward, the membrane contains Pb2+ ions to neutralize the deprotonated -COO- in the channel. The subsequent bars represent the feed solution with a mixture of K+ and Pb2+ ions. The parameters are outlined in the Supplementary Information (Supplementary Tables 4 and 5) and additional details regarding the permeation tests in the MD simulations can be found in the Supplementary Information and Supplementary Table 6. We simulated ion transport from the feed into the membrane by applying high pressure to the piston wall (Fig. 3a), with the applied pressure changes (Fig. 3b) consistent with the osmotic pressure changes shown in Fig. 2a. Ion fluxes for a series of permeation tests are presented in Fig. 3b and Supplementary Fig. 15. The fluxes of K+ and Pb2+ in our simulations exhibit a trend in good agreement with the experimental results. Particularly with one Pb2+ added into the feed (Test 4), the flux of K+ is enhanced by ~ two-fold compared to that in Test 3 without mobile Pb2+ in the feed. Note that limited by the simulation scale, the observed Pb2+ flux here includes Pb2+ from the membrane, and therefore is much larger than what is observed in experiments. Nevertheless, our model provides a reliable qualitative explanation for the increase in Pb2+ flux.
a Simulation modeling of ion transport through 2D MoS2-COOH channels, which includes six extra MoS2 sheets as the supporting membrane (Mo in yellow and S in gray), water (transparent ice blue), ions (in cyan, green, and magenta) and two MoS2 sheets as piston wall. Note that Pb2+ here are divided into mobile Pb2+ in the feed and Pb2+ in the membrane (shown in semi-transparent magenta beads for clarity), because additional Pb2+ is needed to neutralize the deprotonated -COO- in the channel. b MD simulation results analogous to the experimental results in Fig. 2a for the fluxes of Pb2+ and K+ across the MoS2-COOH channel with K+/Pb2+ concentration ratios indicated for each test. In the panel, both the ion fluxes and applied pressure are normalized to values corresponding to the initial K+ test. Note that the flux of Pb2+ (purple bar) observed in Test 3 originates from the Pb2+ present in the membrane. c The diffusion coefficients of K+, mobile Pb2+ and Cl– throughout the simulations. The dotted framework indicates synchronized interaction between K+ and Cl–. d Diffusion coefficients for Cl– beyond and within a 10 Å radius of mobile Pb2+ before entering the membrane for the simulation in Test 4. e The probability of all kinds of K+ passing through the channel (steel blue bar) and that of K+ that are knocked by Cl– to form a K+/Cl− ion pair passing through the channel (coral bar). Inset shows a snapshot of the K+/Cl- ion pair (within 3.5 Å) inside the channel for Test 4. Data is presented as mean ± standard error, based on three independent MD simulations. f Schematic showing the permeation of K+ and Cl– with poor ion pair formation in the Pb2+-locked MoS2-COOH channel in the absence of mobile Pb2+ in the feed. g Schematic showing the permeation of K+ and Cl– with enhanced ion pair formation in the Pb2+-locked MoS2-COOH channel with mobile Pb2+ slowing down Cl– via long-range interaction. h Schematic showing ion migration under electric field. Synchronized interaction between K+ and Cl–, i.e. ion pair formation between+ and Cl– is absent in the channel due to their opposite migration direction. i Measured I-V curves in the Pb2+-locked MoS2-COOH channel.
To explain the flux changes, we first calculated the diffusion coefficients of K+/Pb2+/Cl– (Fig. 3c). The diffusion coefficients of Pb2+ in both the feed (Fig. 3c) and the membrane (Supplementary Fig. 16) increase with mobile Pb2+ concentration in Test 4 and thereafter, which is consistent with experiment (Fig. 2b). Therefore, we attribute the increased flux of Pb2+ to the effect of applied pressure (equivalent of osmotic pressure). Evidently, the diffusion coefficients of K+/Cl– in Test 1 are markedly higher than those in Test 3. This is attributed to the fact that the membrane locked by Pb2+ in Test 3 has deprotonated -COO− groups, which attract K+ and thus reduce its flux. The flux of K+ increases from Test 3 to Test 7 and starts to decrease thereafter, similar to the experimental results. The increase in applied pressure can also explain the increase of K+ flux from Test 5 to Test 7. After Test 7, as Pb2+ diffuses more rapidly, it escapes trapped sites, allowing more vacant -COO− groups to capture K+, resulting in decreased K+ flux (Supplementary Fig. 17). However, the applied pressure change cannot explain the difference between Test 3 and Test 4, as they have the same pressure with only 1 Pb2+/2 Cl– ion difference, whereas the K+ fluxes differ by a factor of two.
To distinguish whether the two-fold increase of K+ permeability in Test 4 is caused by Pb2+ or Cl–, we replaced 1PbCl2 with 2KCl in the feed (Test 9, Supplementary Table 6). The result shows that increasing the concentration of KCl does increase the flux of K+, but only by 30–40% (Supplementary Fig. 18), well below the two-fold increase observed in Test 4. Therefore, the two-fold increase in K+ flux observed in Test 4 is mostly caused by the additional Pb2+. As shown in Fig. 3c, due to the very low diffusion coefficient of mobile Pb2+, its entry into the membrane is much slower than that of other ions. Consequently, we hypothesize that the main place where mobile Pb2+ plays a role is in the feed. To verify this, we further calculated the radial distribution function (RDF) of each Cl– (relative to Pb2+) before entering the membrane (Supplementary Fig. 19a–c), as well as the diffusion coefficients of these Cl– (Supplementary Fig. 19d–f). We find that ~15–20% of Cl– ions are close to Pb2+ ions (within 10 Å), and the diffusion coefficient of these Cl- in the feed is only ~1/3 that of Cl– ions not within 10 Å (Fig. 3d). Meanwhile, the diffusion coefficients of water molecules near mobile Pb2+ are reduced by 30–50% compared to those far away from Pb2+ (Supplementary Fig. 20). This result is consistent with previous research on Pb2+ and other divalent ions36,37,38, with the key difference being that the previous study focused on the interactions between Pb2+ ions and water molecules in the first or second solvation shell, whereas our investigation suggests that interactions beyond the second solvation shell (out to 10 Å from Pb2+) are important as well. Moreover, we find that K+ in the MoS2-COOH channel is easily trapped by acetate, while the presence of Cl– facilitates the movement of K+. K+ tends to either form K+/Cl– ion pairs with Cl– in the membrane (Fig. 3e, Supplementary Fig. 21 and Supplementary Movie 1) or K+ follows the trajectory of Cl– moving out of the channel (Supplementary Fig. 22). Notably, in Test 3 and 4, where the cooperative effect is most pronounced (Fig. 3b, c), water diffusion is quite similar, indicating that ion-pairing is the dominant factor (Supplementary Fig. 23).
Combining the systematic analysis above, the cooperative transport is attributed to the complex interactions among Pb2+, Cl–, and K+. In the absence of mobile Pb2+ in the feed (Test 3 and Test 9), the larger diffusion coefficient of Cl– compared to K+ (Fig. 3c and Supplementary Fig. 24) reduces the frequency of K+ and Cl– collisions, resulting in less ion pair formation (Fig. 3e, f). The probability of ion pair formation in Test 3 is only ~55% of that in Test 4 (Fig. 3e). Additionally, a potential of mean force calculation shows that Pb2+ and Cl– that are within 10 Å have relatively strong long-range interactions (Supplementary Fig. 25). Therefore, in the presence of mobile Pb2+ in the feed, even Cl– beyond the second solvation shell of Pb2+ (5–10 Å) can be captured to be slowed down (Fig. 3d), which leads to its synchronization of Cl− with K+ to form ion pairs (Fig. 3g). Consequently, ion-pair formation opens up pathways for K+ diffusion, significantly increasing the flux of K+.
To verify the proposed mechanism, we measured the electric field driven transport of K+ and Cl– using KCl solution (with and without mobile Pb2+) in the PTFE membrane and the Pb2+-locked MoS2-COOH membrane. In the electric field driven transport tests, the movement of K+ and Cl– are in opposite directions in the channel (Fig. 3h and Supplementary Fig. 26a, more details in the Supplementary Information), as opposed to their movement in the same direction in the osmotic pressure driven permeation test (Fig. 3f, g). In other words, the synchronization-induced enhanced pairing between K+ and Cl– in the channel is absent under the electric field. The results show that 1% mol Pb2+ addition almost makes no change to the conductance (i.e. ion flux) and 10% mol Pb2+ addition only enhances the conductance only by ~8.7% (Fig. 3i). The enhancement in the Pb2+-locked MoS2-COOH membrane is similar to that observed in the PTFE membrane in the electrical test (Supplementary Fig. 26b, c), but much lower than the large enhancement of K+ permeability in the presence of corresponding Pb2+ ratios in the permeation tests (~2–4 fold, Supplementary Fig. 7 and Fig. 2b). Also, conductances in the Pb2+-locked MoS2-COOH membrane are observed to be higher than those in the PTFE membrane, which is attributed to the surface charge governed transport in nanofluidics39. These contrasting results therefore corroborate the ion pairing mechanism as we propose above. Finally, we observed that the enhanced K+ transport by Pb2+ addition is much weakened in the 1 M KNO3 tests, which we attributed to the shortened Debye length due to higher concentration, leading to significant changes in ion interactions in the feed and ion pairing behaviors within the 2D channel (Supplementary Fig. 27). The results echo the significance of and phenomena originating from the ion pairing in confinement20,40.
Inhibitory ion transport
Besides monovalent ions, we also studied the interplay between Pb2+ and divalent cations. Divalent ions have slower diffusion coefficients, it is important to examine whether monovalent anions can be slowed down by Pb2+ via long-range interaction to the level that it can form ion pairs to enable cooperative ion transport for divalent cations. Given the importance of dehydration to ion transport under confinement17,19, Co2+ and Ba2+ are chosen because Ba2+ has one of the smallest hydration enthalpy (−1332 kJ/mol) among divalent ions, while Co2+ has one of the largest (−2036 kJ/mol, ref. 41 and Supplementary Table 1). Moreover, our previous work has revealed that both Co2+ and Ba2+ adopt a monodentate binding mode with the acetate functional group (Supplementary Fig. 28)35. We observed a different ion interplay between Pb2+ and Co2+ (or Ba2+). The permeability of either Co2+ or Ba2+ decreases with increasing Pb2+ concentration in the feed, while the permeability of Pb2+ increases with increasing Pb2+ concentration in the feed, but in a seemingly nonlinear way (Fig. 4a, b, Supplementary Figs. 29 and 30, Supplementary Tables 7 and 8). The relatively higher Ba2+ flux as compared with Co2+ can be attributed to the fact that Ba2+ has a smaller hydration enthalpy than Co2+, which means a smaller dehydration barrier for Ba2+ than Co2+ in the Pb2+-locked MoS2-COOH channels. Given that this is the opposite to the cooperative ion transport observed between K+ and Pb2+, we term the ion interplay between Co2+ (or Ba2+) and Pb2+ as inhibitory ion transport. Similar to the cooperative ion transport case, inhibitory ion transport is absent in the large pore PTFE test (Supplementary Fig. 31).
a Measured fluxes of Ba2+ and Pb2+ versus the concentration of Pb2+ in the feed in the series of Ba2+/Pb2+ pair permeation tests across one Pb2+-locked MoS2-COOH membrane. b Measured fluxes of Co2+ and Pb2+ versus the concentration of Pb2+ in the feed in the series of Co2+/Pb2+ pair permeation tests across one Pb2+-locked MoS2-COOH membrane. In (a) and (b), both the ion fluxes are normalized to values corresponding to the initial Ba2+ test and Co2+ test, respectively. Data: mean ± standard error. The dashed lines are used for visual guides. c Calculated diffusion coefficients of Co+, mobile Pb2+ and Cl– throughout the MD simulations. d Probability of ions passing through the channel. Solid lines and dashed lines represent Co2+/Pb2+ and K+/Pb2+ tests, respectively. Data is presented as mean ± standard error, based on three independent MD simulations. e Schematic of the passage for single divalent ion transport. f Schematic of competition for the passage for binary divalent ion transport.
To figure out the mechanism of the inhibitory ion transport, we conducted MD simulations of the Co2+/Pb2+ pair tests. Settings for the permeation tests in the MD simulations are detailed in Supplementary Table 9. In the simulations, we observe a reduced trend of Co2+ flux (Supplementary Fig. 32) with increasing Pb2+ concentration in the feed, consistent with the experimental results. We also investigated the ion flux into the membrane (Supplementary Fig. 33) and observed that the overall ion fluxes in the Co2+/Pb2+ test are lower than that in the K+/Pb2+ test. Specifically, due to the higher dehydration enthalpy of Co2+, its flux into the membrane is significantly lower than that of K+. Additionally, the diffusion coefficient of Co2+ is much lower as compared with Cl– (Fig. 4c), suggesting a lower chance of forming ion-pairs between Co2+ and Cl–. More Pb2+ ions pass through the channel in the Co2+/Pb2+ test while more K+ ions pass through the channel in the K+/Pb2+ test (Fig. 4d). This suggests that Co2+ can replace Pb2+ within the membrane due to its strong binding affinity with the membrane.
As the concentration of mobile Pb2+ increases, the flux of Co2+ is impeded. This can be interpreted as that in Å-scale confinement, bypassing ions that block the channel is unlikely, therefore Co2+ and Pb2+ cannot permeate independently and have to compete for the limited transport cross section (i.e., area of the channel available for transport) in the 2D channels (Fig. 4e, f). Therefore the increase of Pb2+ flux will decrease the flux of Co2+ and vice versa.
To conclude, we have provided conclusive experimental evidence of complex ion interplay under angstrom-scale 2D confinement. Several issues were found to contribute to this interplay, including the locking of layer separation by Pb2+ ions, the strong binding of Pb2+ to acetate such that once the membrane has been exposed to Pb2+, the layer spacing doesn’t change to accommodate the other ion. This leads to an osmotic pressure that increases with increasing Pb2+ concentration, which leads to increasing K+ diffusion given that the acetate sites are less likely to be bound to Pb2+. In addition, we found that cooperative transport is mediated by the anion, which more effectively forms K+-anion ion pairs in the presence of Pb2+ due to slowing of Cl– diffusion in the presence of Pb2+. These effects lead to cooperative ion transport, which has not been reported in nanofluidic devices. Due to the Å-scale spacing in the 2D MoS2-COOH channel, but inhibitory ion transport is observed, when the diffusion coefficient of cations is too slow to catch up with the anions, such as for divalent metal cations (Co2+ and Ba2+).
In further work, our methods can be extended to study ion interplay in channels with varied confinement size compared to MoS2, with more sophisticated confinement chemistry and with more complex ion combinations than binary combinations. For example, in the 2D confinement, one direction is to study ion interplay in a channel with dynamic change in size, e.g. Pb2+/Al3+ pair in MoS2-COOH channel (Supplementary Fig. 34). Altogether, all these efforts not only unveil mass transport rules in extreme confinement, but also point to the great potential of manipulating ion transport and achieving responsive ion transport based on chemical environment. Our work also offers a perspective to advance the design of iontronics, e.g. the emerging neuromorphic computing devices20,42,43,44.
Methods
Chemicals
KNO3(≥99%, Sigma-Aldrich), Co(NO3)2.6H2O (98%, Sigma-Aldrich), Pb(NO3)2 (>99%, Sigma-Aldrich), LiNO3 (99 + %, Acros Organics), Ba(NO3)2 (99.999%, Alfa Aesar), KCl (99.0–100.5%, Alfa Aesar), PbCl2 (≥99%, Oakwood Products Inc), MoS2 powders (Sigma-Aldrich) iodoacetic acid (ICH2COOH, Sigma-Aldrich) were used as received without further treatments. All the reactions were done at room temperature.
Preparation of MoS2-COOH dispersion solution
First the single- or few-layer MoS2 nanosheet aqueous dispersion solution was prepared through the intercalation of MoS2 powders (Sigma-Aldrich) in n-butyl lithium/hexane solution (1.6 M) (Caution!), as widely reported previously. Then the acetic acid functionalization of the MoS2 nanosheet was achieved through its nucleophilic reaction with iodoacetic acid (ICH2COOH), as we reported in ref. 32 of the main text. Our previous measurement shows that the functionalization degree is ~25% -COOH per MoS2.
Note that before membrane preparation, to remove possible ions contaminations, the prepared MoS2-COOH solution were washed with dilute trace-metal HCl (~2–5 mM), followed by filtration and redispersion of MoS2-COOH in water under sonication (~10–15 min). The “HCl washing-filtration-redispersion” cycle was repeated at least three times. Then, the redispersed MoS2-COOH solution was dialyzed in dialysis tubings (Sigma-Aldrich, Part No. D9527-100FT) to remove extra HCl. Finally, repeated centrifugations (~4000 rpm/10 min) were used to get the aqueous dispersion solutions of single- or few layer MoS2-COOH nanosheets (concentration 0.1–0.2 mg/ml), which were stored under 4 °C for use.
Preparation of the MoS2-COOH membrane
The MoS2-COOH membrane was prepared via the vacuum assisted filtration method. The substrate used is hydrophilic polytetrafluoroethlene (PTFE) (Supplementary Fig. 8, pore size: 0.2 μm, purchased from Sigma-Aldrich, Part No. JGWP04700). Upon filtration, the MoS2-COOH/PTFE complex membrane was transferred to clean Petri dishes for natural air drying. Note that to avoid membrane shrinkage or deformation in the drying process, several drops of DI water were put beneath the complex membrane before membrane transfer to remove air bubbles between PTFE and dishes. After the air-drying process, the prepared complex membranes were used for ion transport tests, membrane uptake tests and other characterizations.
The sequential permeation tests across one MoS2-COOH membrane
We used a pair of H-cells to conduct the series of permeation tests of binary mixture solutions across the membranes, including the porous PTFE membrane and MoS2-COOH/PTFE complex membrane. The membranes were mounted in between the H-cells by commercial Silicon paste (Supplementary Fig. 3). The H-cells are ready for permeation tests upon solidification of the Silicon paste. All the permeation tests were done at room temperature.
In a typical permeation test, 20 ml solution (either single salt solution or binary mixture) and 20 ml deionized water were simultaneously poured into the feed side and the permeate side of H-cells, respectively. Note that the MoS2-COOH faces the feed side in the MoS2-COOH/PTFE complex membrane tests. Both chambers were strongly stirred to mitigate concentration polarization. Inductively coupled plasma mass spectrometry (ICP-MS) is used to identify and quantify the metal cations. The concentration changes of every metal cation in the permeate side were monitored through periodic samplings (20–60 μl per sampling subject to change according to permeation time), which were diluted by 3% HNO3 (trace-metal grade) to 3–5 ml for standard ICP-MS measurements. Both chambers were tightly sealed with parafilm to avoid undesired evaporation throughout the process, except when sampling. We observed no obvious level differences developed between feed and permeate in the short test time (~2 h).
The sequential permeation tests for one binary cation pairs were conducted across one MoS2-COOH/PTFE membrane by switching the feed solutions, while different cation pairs tests used new and independent MoS2-COOH/PTFE membranes. We fixed one series of tests to one membrane to preclude the effect of the membrane variation when interpretating the results, while different membranes tests are used to cross-check the results. After every switching, both the permeate and the feed chambers were thoroughly washed with DI water several times to remove ions leftover from the prior test (until the washing solutions of both chambers had a conductivity close to DI water, <1 µS/cm). Note that we repeated some tests like single K+ permeation tests and other K+/Pb2+ mixed solution permeation tests with the same ratio to confirm that the tested MoS2-COOH membrane was intact throughout the series of tests. Three independent membranes were repeated for the results shown in the main text. Also note that the membranes were always kept in the wet state throughout the series of tests.
Calculation of the permeabilities/flux ratio/effective diffusion coefficient
As our previous studies show, ion concentration changes in the permeate side in the early stage show a linear increase versus time (Supplementary Figs. 4b, c, 6b, c, 7b–d, 9, 26b, c, 28b, c, 29b, c and 30a, b). We can get the permeabilities of the ions, Pi (mol/s), by calculating the slopes of linear profiles to make quantitative analysis.
Given that every series tests of binary ions were done with one membrane, the relative flux ratio is the ratio of the permeabilities. More details about the calculations of the effective diffusion coefficient are provided in the SI.
Electrical test
The setup for the electrical test is shown in Supplementary Fig. 25. Briefly, the MoS2-COOH/PTFE complex membrane was mounted between two O rings (orifice ~1 mm) separating the two chambers. PbCl2 solution (10 mM, ~200 μl) was first added into both chambers to convert the MoS2-COOH membrane into Pb2+-treated MoS2-COOH membrane.
The I-V curves were recorded on a Bio-Logic VMP3 workstation using standard Ag/AgCl electrodes. The calculated conductance is the slope from the linear fitting of the measured I-V curves. CV tests with voltages ranging from 0 V to 0.1 V with a scan rate of 5 mV/s. Note that before every test, both chambers were thoroughly washed with DI water to remove salt leftover from prior test or treatment.
The membrane uptake test
The MoS2-COOH membranes (typical mass loading 0.2–0.3 mg) were put into 2.5 ml solution of either single salt solutions (K+, Co2+, Ba2+, Pb2+) or binary mixture solutions overnight. Then the membranes were taken out and thoroughly washed with flowing DI water (typically for ~2 min) to remove the ions solution remaining on the surface. Then the washed membranes were dissolved in 3 ml HNO3 (3%) under sonication overnight. Finally, the leaching HNO3 solution was filtered and diluted for ICP-MS measurement.
XRD measurement
The diffraction patterns in Bragg-Brentano geometry were obtained using a Rigaku benchtop Xray diffractometer equipped with HyPix-400 MF 2D hybrid pixel array detector (HPAD) and a Cu Kα X-ray source (1.5406 Å) operating at 40 kV and 15 mA. The interlayer spacing of the 2D channel is calculated according to the (002) peak position in the XRD spectra of MoS2-COOH membranes.
Scanning transmission electron microscopy (STEM) measurement
For the cross-section view imaging, the MoS2-COOH membrane was embedded into Poly/Bed 812 resin and cut into ~90-nm thick slides using a ultramicrotome (Ultracut E, Reichert-Jung). Scanning transmission electron microscopy experiments were carried out using aberration corrected JEOL ARM 200CF with cold field emission gun (200 kV).
STEM imaging and EDS mapping in Supplementary Fig. 2 were conducted on aberration corrected Themis Z (S)TEM (Thermo Fisher Scientific) operated at 80 kV. Energy-dispersive X-ray spectroscopy (EDS) mapping was performed using a continuous scan with a dwell time of 2 μs and a beam current of 20 pA. The total acquisition time was about 30 min.
All-atom MD simulations
Computational method
We performed all-atom Molecular dynamics (MD) simulations to study the cooperative transport of mixed (Pb2+/K+) ions in the MoS2-COOH membranes. Our model (Fig. 3a) consists of a bilayer MoS2 sheet acting as a piston wall to exert external pressure, an ion-filled feed region, a multi-layered MoS2 membrane serving as an ion channel, and a pure water permeate region45,46. The multi-layered MoS2 membrane can be visualized as extracting two layers of MoS2 from bulk crystals (2H-MoS2) and being modified with corresponding acetate functional groups, while leaving a 11.4 Å interlayer spacing (Mo-Mo distance) that is consistent with the experiment (Pb2+ locked membrane). We built a rectangular box with dimensions 170 Å × 57.2 Å × 54.0 Å, and we chose the OPC3 water model, and visualized the model using Visual Molecular Dynamics (VMD)47. We used the parameters taken from Heinz48 for the MoS2 membrane. We applied the general AMBER force field (GAFF)49 for the -COOH functional groups. We selected the 12-6-4 LJ-type nonbonded model50 for the monovalent/divalent ions with the following potential function:
Herein, M and W represent the metal ion and an atom inside a water molecule, respectively. \({r}_{{MW}}\) is the distance between M and W. e is the charge of a proton. \({Q}_{M}\) and \({Q}_{W}\) are charges of M and W, respectively. \({R}_{\min,{MW}}\) is the distance between M and W when their LJ potential reaches its minimum, and \({\varepsilon }_{{MW}}\) is the corresponding well depth at this minimum. The C4 term was added to account for the ion-induced dipole interactions between the metal ion and water molecule. These parameters were optimized to reproduce the experimental hydration free energy (HFE), ion-oxygen distance (IOD), and coordination number (CN) values simultaneously. For more detailed optimization procedure, please refer to our previous work51. The parameters of the ions we used in this work are shown in Supplementary Table 4, the target/calculate values of the HFE, IOD, and CN in the first solvation shell for Pb2+ are listed in Supplementary Table 5. Note that due to the lack of parameters in the 12-6-4 model of nitrate anion, we used Cl–in our simulation instead of the nitrate anion used in the experiment. We chose Cl– for two reasons: first, its diffusion coefficient is similar to that of nitrate anion52; second, it is a commonly used anion in MD simulations11. In addition, calculation of the radial distribution function (RDF) of Pb2+ and Cl– in the bulk solution shows that PbCl does not form ion clusters in the simulation (see Supplementary Fig. 12).
Molecular dynamics (MD) simulations were performed using the OpenMM package53 and the settings of the K+/Pb2+ permeation test were consistent with the experimental settings (Supplementary Table 6). We kept the MoS2-COOH functional group in the Test 1 fully protonated, but starting from Test 2, we deprotonated half of the MoS2-COOH groups, as suggested by the infrared (IR) vibrational spectroscopy results that Pb2+ can deprotonate the -COOH function group (ref. 35 of main text). Experiments have shown that the MoS2-COOH membrane soaked with Pb2+ will be locked by Pb2+(fixed interlayer distance), so we put 18 Pb2+ in the membrane of the Test 3-Test 9 system to neutralize and lock the negatively charged membranes, where the initial position of Pb2+ in the membrane was taken from the equilibrium state of Test 2 after applying a force of 400 kcal/mol/nm (see snapshots in Supplementary Fig. 13). We also conducted similar permeation test for the Co2+/Pb2+ system (Supplementary Table 9).
All the systems were subjected to a 10,000-step energy minimization followed by a 5 ns NVT ensemble at 300 K using Langevin dynamics to equilibrate the system. The piston wall and membrane were positionally restrained, whereas ions were restrained to pass through the channel by applying a flat-well potential. We then removed the constraints on the ions and performed the non-equilibrium production simulations in the NVT ensemble where different external pressures (Supplementary Tables 6 and 9) were applied on the piston wall to simulate ions with different ratios permeating through the MoS2-COOH membrane45,54. The temperature was kept at 300 K using a Langevin thermostat with a friction coefficient of 1 ps−1. The particle mesh Ewald method55 was employed to calculate electrostatic interactions with a short-range cutoff of 1.0 nm. Periodic boundary conditions were employed, and with a simulation time step of 2 fs. To speed up the MD simulations and collect sufficient statistics in the simulations at the ns scale, we employed external pressures higher than the experimentally measured osmotic pressure (∼0.5 MPa). Atomic coordinates were saved every 20 ps.
To validate the accuracy of the ion parameters we used in this work, we applied steered molecular dynamics (SMD) simulations to calculate the potential of mean force (PMF) of a single Pb2+or Co2+ or K+ ion passing through the MoS2-COOH membrane. We first constructed a 4 layer MoS2-COOH membrane with dimensions 55.0 Å × 57.2 Å × 30.0 Å, while leaving interlayer spacings that are consistent with experiment. We then placed the membrane in a rectangular box of size 100.0 Å × 57.2 Å × 30.0 Å and solvated with 2904 OPC3 water molecules. We kept the MoS2-COOH functional group in the K+ system fully protonated while half deprotonated in the Pb2+ and the Co2+ system. 18 Pb2+ and 18 Co2+ ions were added to neutralize the Pb2+ system and the Co2+ system, respectively. For each simulation, we added 1 cation and a corresponding number of Cl− ions to neutralize the system, where we placed the cation 10 Å outside the membrane (Supplementary Fig. 14a). Following the equilibration procedure mentioned above, we performed an SMD simulation for 40 ns where the cation position was increased gradually from an initial −10 Å to a final 30 Å. We used harmonic restraints with a force constant 50 kcal/mol to gradually move the cation from outside of the membrane (distance = –10 Å) to the inside of the membrane. We then used the steered MD trajectories as initial coordinates for our umbrella sampling windows. We used the distance as our reaction coordinate, and we divided the trajectories into 40 umbrella windows with 0.1 nm intervals (−10 Å–30 Å). We then applied a harmonic potential with force constant 20 kcal/mol to constrain each window to the specific distance along the reaction coordinate. Each umbrella window was simulated for 10 ns, where the first 4 ns was discarded as equilibration. We then calculated the potential of mean force using the weighted histogram analysis method (WHAM)56, as shown in Supplementary Fig. 14b.
Here the diffusion coefficient D we calculated is obtained by fitting the MSD with respect to the lag-time to a linear model: \({D}_{d}=\frac{1}{2d}{{{\mathrm{lim}}}}_{t\to \infty }\frac{d}{{dt}}{MSD}({r}_{d})\), where d is the dimensionality of the MSD (d = 3). MSD was computed from the following expression, known as the Einstein formula:
where N is the number of equivalent particles the MSD is calculated over, r are their coordinates and d the desired dimensionality of the MSD.
Data availability
Source data are provided with this paper.
Code availability
Relevant data supporting the key findings of this study are available within the article, Supplementary Information. Parameters used to generate molecular dynamics (MD) simulation data are provided in the Supplementary Information. The codes used in the MD simulations are available from the corresponding author upon reasonable request.
References
Dolphin, A. C., Insel, P. A., Blaschke, T. F. & Meyer, U. A. Introduction to the Theme “Ion Channels and Neuropharmacology: From the Past to the Future”. Annu. Rev. Pharmacol. Toxicol. 60, 1–6 (2020).
Gouaux, E. & MacKinnon, R. Principles of selective ion transport in channels and pumps. Science 310, 1461–1465 (2005).
Epsztein, R., DuChanois, R. M., Ritt, C. L., Noy, A. & Elimelech, M. Towards single-species selectivity of membranes with subnanometre pores. Nat. Nanotechnol. 15, 426–436 (2020).
Cohen-Tanugi, D. & Grossman, J. C. Water desalination across nanoporous graphene. Nano Lett. 12, 3602–3608 (2012).
Feng, J. et al. Observation of ionic Coulomb blockade in nanopores. Nat. Mater. 15, 850–855 (2016).
Jain, T. et al. Heterogeneous sub-continuum ionic transport in statistically isolated graphene nanopores. Nat. Nanotechnol. 10, 1053–1057 (2015).
Shen, J. et al. Fast water transport and molecular sieving through ultrathin ordered conjugated-polymer-framework membranes. Nat. Mater. 21, 1183–1190 (2022).
Li, Q. et al. Artificial sodium channels for enhanced osmotic energy harvesting. J. Am. Chem. Soc. 145, 28038–28048 (2023).
Tunuguntla, R. H. et al. Enhanced water permeability and tunable ion selectivity in subnanometer carbon nanotube porins. Science 357, 792–796 (2017).
Siria, A. et al. Giant osmotic energy conversion measured in a single transmembrane boron nitride nanotube. Nature 494, 455–458 (2013).
Li, Z. et al. Breakdown of the Nernst–Einstein relation in carbon nanotube porins. Nat. Nanotechnol. https://doi.org/10.1038/s41565-022-01276-0 (2022).
Radha, B. et al. Molecular transport through capillaries made with atomic-scale precision. Nature 538, 222–225 (2016).
Mouterde, T. et al. Molecular streaming and its voltage control in ångström-scale channels. Nature 567, 87–90 (2019).
Xue, Y. et al. Atomic-scale ion transistor with ultrahigh diffusivity. Science 372, 501–503 (2021).
Goutham, S. et al. Beyond steric selectivity of ions using ångström-scale capillaries. Nat. Nanotechnol. https://doi.org/10.1038/s41565-023-01337-y (2023).
Gopinadhan, K. et al. Complete steric exclusion of ions and proton transport through confined monolayer water. Science 363, 145–148 (2019).
Esfandiar, A. et al. Size effect in ion transport through angstrom-scale slits. Science 358, 511–513 (2017).
Joshi, R. K. et al. Precise and ultrafast molecular sieving through graphene oxide membranes. Science 343, 752–754 (2014).
Abraham, J. et al. Tunable sieving of ions using graphene oxide membranes. Nat. Nanotechnol. 12, 546–550 (2017).
Robin, P. et al. Long-term memory and synapse-like dynamics in two-dimensional nanofluidic channels. Science 379, 161–167 (2023).
Shen, J., Liu, G., Han, Y. & Jin, W. Artificial channels for confined mass transport at the sub-nanometre scale. Nat. Rev. Mater. 6, 294–312 (2021).
Elinder, F. & Århem, P. Metal ion effects on ion channel gating. Q. Rev. Biophys. 36, 373–427 (2003).
Lee, C.-H. & MacKinnon, R. Activation mechanism of a human SK-calmodulin channel complex elucidated by cryo-EM structures. Science 360, 508–513 (2018).
Xia, X.-M. et al. Mechanism of calcium gating in small-conductance calcium-activated potassium channels. Nature 395, 503–507 (1998).
Rohaim, A. et al. Open and closed structures of a barium-blocked potassium channel. J. Mol. Biol. 432, 4783–4798 (2020).
Sakipov, S., Sobolevsky, A. I. & Kurnikova, M. G. Ion permeation mechanism in epithelial calcium channel TRVP6. Sci. Rep. 8, 5715 (2018).
Hess, P. & Tsien, R. W. Mechanism of ion permeation through calcium channels. Nature 309, 453–456 (1984).
Tunuguntla, R. H., Allen, F. I., Kim, K., Belliveau, A. & Noy, A. Ultrafast proton transport in sub-1-nm diameter carbon nanotube porins. Nat. Nanotechnol. 11, 639–644 (2016).
Lin, K., Lin, C.-Y., Polster, J. W., Chen, Y. & Siwy, Z. S. Charge inversion and calcium gating in mixtures of ions in nanopores. J. Am. Chem. Soc. 142, 2925–2934 (2020).
Faucher, S. et al. Critical knowledge gaps in mass transport through single-digit nanopores: a review and perspective. J. Phys. Chem. C. 123, 21309–21326 (2019).
Kavokine, N., Netz, R. R. & Bocquet, L. Fluids at the nanoscale: from continuum to subcontinuum transport. Annu. Rev. Fluid Mech. 53, 377–410 (2021).
Hoenig, E. et al. Controlling the structure of MoS 2 membranes via covalent functionalization with molecular spacers. Nano Lett. 20, 7844–7851 (2020).
Wang, Z. et al. Understanding the aqueous stability and filtration capability of MoS2 membranes. Nano Lett. 17, 7289–7298 (2017).
Ries, L. et al. Enhanced sieving from exfoliated MoS2 membranes via covalent functionalization. Nat. Mater. 18, 1112–1117 (2019).
Wang, M. et al. Anomalously enhanced ion transport and uptake in functionalized angstrom-scale two-dimensional channels. Proc. Natl Acad. Sci. 121, e2313616121 (2024).
De Araujo, A. S., Sonoda, M. T., Piro, O. E. & Castellano, E. E. Development of new Cd 2+ and Pb 2+ Lennard-Jones parameters for liquid simulations. J. Phys. Chem. B 111, 2219–2224 (2007).
Thaunay, F., Ohanessian, G. & Clavaguéra, C. Dynamics of ions in a water drop using the AMOEBA polarizable force field. Chem. Phys. Lett. 671, 131–137 (2017).
Obst, S. & Bradaczek, H. Molecular dynamics study of the structure and dynamics of the hydration shell of alkaline and alkaline-Earth metal cations. J. Phys. Chem. 100, 15677–15687 (1996).
Stein, D., Kruithof, M. & Dekker, C. Surface-charge-governed ion transport in nanofluidic channels. Phys. Rev. Lett. 93, 035901 (2004).
Kavokine, N., Marbach, S., Siria, A. & Bocquet, L. Ionic Coulomb blockade as a fractional Wien effect. Nat. Nanotechnol. 14, 573–578 (2019).
Marcus, Y. The thermodynamics of solvation of ions. Part 2.—The enthalpy of hydration at 298.15 K. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 83, 339 (1987).
Noy, A. & Darling, S. B. Nanofluidic computing makes a splash. Science 379, 143–144 (2023).
Emmerich, T. et al. Nanofluidic logic with mechano–ionic memristive switches. Nat. Electron. 7, 271–278 (2024).
Xiong, T. et al. Neuromorphic functions with a polyelectrolyte-confined fluidic memristor. Science 379, 156–161 (2023).
Wang, M. et al. Lanthanide transport in angstrom-scale MoS 2 -based two-dimensional channels. Sci. Adv. 10, eadh1330 (2024).
Xiong, Q., Liu, C. & Schatz, G. C. Effects of interlayer spacing and applied pressure on the lanthanide transport in MoS2 -based two-dimensional channels. Int. J. Smart Nano Mater. 15, 579–592 (2024).
Humphrey, W., Dalke, A. & Schulten, K. V. M. D. Visual molecular dynamics. J. Mol. Graph. 14, 33–38 (1996).
Liu, J. et al. Interpretable molecular models for molybdenum disulfide and insight into selective peptide recognition. Chem. Sci. 11, 8708–8722 (2020).
Wang, J., Wolf, R. M., Caldwell, J. W., Kollman, P. A. & Case, D. A. Development and testing of a general amber force field. J. Comput. Chem. 25, 1157–1174 (2004).
Li, P., Roberts, B. P., Chakravorty, D. K. & Merz, K. M. Rational design of particle mesh Ewald compatible Lennard-Jones parameters for +2 metal cations in explicit solvent. J. Chem. Theory Comput. 9, 2733–2748 (2013).
Li, Z., Song, L. F., Li, P. & Merz, K. M. Systematic parametrization of divalent metal ions for the OPC3, OPC, TIP3P-FB, and TIP4P-FB water models. J. Chem. Theory Comput. 16, 4429–4442 (2020).
Hill, D. Diffusion coefficients of nitrate, chloride, sulphate and water in cracked and uncracked Chalk. J. Soil Sci. 35, 27–33 (1984).
Eastman, P. et al. OpenMM 7: rapid development of high performance algorithms for molecular dynamics. PLOS Comput. Biol. 13, e1005659 (2017).
Heiranian, M., Farimani, A. B. & Aluru, N. R. Water desalination with a single-layer MoS2 nanopore. Nat. Commun. 6, 8616 (2015).
Darden, T., York, D. & Pedersen, L. Particle mesh Ewald: An N ⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 98, 10089–10092 (1993).
Kumar, S., Rosenberg, J. M., Bouzida, D., Swendsen, R. H. & Kollman, P. A. THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 13, 1011–1021 (1992).
Acknowledgements
We thank helpful discussions with One-Sun Lee. This work is supported by Advanced Materials for Energy-Water-Systems (AMEWS) Center, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences. Cross-sectional STEM experiments used instruments in the Electron Microscopy Core of UIC’s Research Resources Center. Other STEM experiments were carried out in part in the Materials Research Laboratory Central Research Facilities, University of Illinois.
Author information
Authors and Affiliations
Contributions
M.W. and C.L. conceived the project. M.W. designed the experiments, performed the bulk of the permeation/electrical/uptake/XRD tests and analyzed the data. Q.X. designed the MD model, performed the MD simulations and analyzed the data. X.Y. conducted SEM and AFM analysis and collected most of the data in the revision stage. G.Y. contributed to ICPMS tests. Y.H. performed cross-sectional STEM imaging. Z.Lyu and Q.C. performed STEM imaging and EDS mapping. E.H. and K.X. contributed to electrical tests. L.S. contributed to ICPMS tests. Z.Li and K.M.M. Jr contributed to the parameterization of the MD model. N.H.C.L contributed to IR measurements and analysis. M.W., Q. X., G.C.S. and C.L. wrote the manuscript with inputs from all the authors. G.C.S. and C.L. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Kalon Gopinadhan, Young-Shin Jun and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Wang, M., Xiong, Q., Yue, X. et al. Cooperative and inhibitory ion transport in functionalized angstrom-scale two-dimensional channels. Nat Commun 16, 5854 (2025). https://doi.org/10.1038/s41467-025-61307-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-61307-x