Synchronous detection of cosmic rays and correlated errors in superconducting qubit arrays

Abstract

Quantum information processing at scale will require sufficiently stable and long-lived qubits, likely enabled by error-correction codes. Several recent superconducting-qubit experiments, however, reported observing intermittent spatiotemporally correlated errors that would be problematic for conventional codes, with ionizing radiation being a likely cause. Here, we directly measured the cosmic-ray contribution to spatiotemporally correlated qubit errors. We accomplished this by synchronously monitoring cosmic-ray detectors and qubit energy-relaxation dynamics of 10 transmon qubits distributed across a 5 × 5 × 0.35  mm³ silicon chip. Cosmic rays caused correlated errors at a rate of $1/\left(592\begin{array}{c}+48\\ -41\end{array}\,{\rm{s}}\right)$, accounting for 17.1 ± 1.3% of all such events. Our qubits responded to essentially all of the cosmic rays and their secondary particles incident on the chip, consistent with the independently measured arrival flux. Moreover, we observed that the landscape of the superconducting gap in proximity to the Josephson junctions dramatically impacts the qubit response to cosmic rays. Given the practical difficulties associated with shielding cosmic rays, our results indicate the importance of radiation hardening—for example, superconducting gap engineering—to the realization of robust quantum error correction.

Introduction

Ionizing radiation from cosmogenic and terrestrial sources is ever-present in the laboratory environment. The former includes cosmic rays and their secondary particles (muons, neutrons, etc.), which shower the Earth with a continuous flux of high-energy ionizing radiation¹. Terrestrial examples include gamma-ray emission from trace quantities of potassium-40 and progeny nuclei of the uranium and thorium decay chains², all arising from isotopes found in common laboratory materials, from the concrete in the walls to metal fixtures and printed circuit boards^3,4. While terrestrial sources of radiation can generally be abated by dense shielding (typically lead) and the careful selection of low-radioactivity materials^3,4,5, cosmogenic radiation penetrates matter with such incredibly high momentum (≳1 GeV/c) that it is only significantly attenuated by the overburden present in underground facilities. The difficulty of shielding cosmic rays thus presents a challenge for solid-state quantum processors.

Ionizing radiation affects the electrical response and quantum coherence of superconducting circuits^6,7,8. Radiation ionizes atoms within a circuit substrate, creating energetic electron-hole pairs that relax via a cascade involving electron-hole recombination, secondary charge carriers, and phonons. A portion of the energy imparted to the substrate is thereby transported to the superconducting circuit elements⁹, where it generates non-equilibrium quasiparticles that alter the circuit performance^10,11.

Several groups worldwide have recently studied the impact of ionizing radiation and quasiparticles on the performance of superconducting circuits in the context of quantum information processing. For example, in the presence of manufactured radioactive sources, excess levels of ionizing radiation increased the average energy-decay rate of superconducting transmon qubits⁸, increased the number of quasiparticle bursts in granular aluminum resonators¹², and increased the rate of quasiparticle-induced phase slips in fluxonium qubits¹³. The use of lead shielding was shown to reduce qubit decay rates⁸ and deep underground operation reduced the rate of both quasiparticle bursts¹² and phase slips¹³, which were attributed to the reduction of terrestrial and cosmogenic radiation. Spatiotemporally correlated anomalies in multi-qubit arrays, such as correlated charge-offsets, were also attributed to ionizing radiation^14,15,16. In addition, the rate and energy of chip-scale failure events¹⁷ that inhibited the faithful decoding of quantum error detection protocols^18,19 motivates the hypothesis that radiation induces correlated errors, with critical implications for future large-scale applications.

While this body of work is consistent with ionizing radiation being a cause of spatiotemporally correlated errors, to our knowledge, it has not been shown explicitly that environmental ionizing radiation—whether of terrestrial or cosmogenic origin—is a source of chip-scale qubit errors. Moreover, the relative contributions of terrestrial and cosmogenic radiation to superconducting qubit errors have been inferred through simulation^8,14, but not yet directly measured.

In this work, we explicitly identified and quantified spatiotemporally correlated qubit relaxation events caused by cosmic rays and their secondary particles. We positioned several scintillating radiation detectors in proximity to a chip with 10 transmon qubits, such that a portion of the cosmogenic radiation flux traverses both (Fig. 1). We then synchronously monitored multi-qubit relaxation and cosmic-ray detection over a period of 266.5 h, searching for coincident events. We determined the rate $1/(59{2}_{-41}^{+48}\,{\rm{s}})$ of spatiotemporally correlated events caused by cosmic rays, and furthermore showed that cosmic rays account for 17.1 ± 1.3% of all such correlated qubit relaxation events, while the remaining portion of events are most likely caused by a source of terrestrial origin²⁰. Finally, we observe that the qubit recovery time following an event is modified by the spatial orientation of the superconducting gap profile around the Josephson junctions relative to the embedding circuitry²¹. Our results demonstrate that cosmic rays cause a significant fraction of quasiparticle bursts and indicate that gap engineering²² may alleviate their impact and obviate the need for deep-underground facilities in order to shield superconducting quantum processors from cosmic rays.

Fig. 1: Synchronous detection of cosmic rays and qubit relaxation.

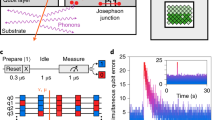
The experiment included a qubit array and scintillating radiation detectors (below the cryostat) for continuous monitoring of qubit relaxation and cosmic rays. We identified individual cosmogenic particles (purple arrow) impacting the qubit array by coincidence-timing of spatiotemporally correlated qubit relaxation and detector pulses.

Results

The qubit device under test (denoted by Q) was an array of 10 fixed-frequency transmon qubits (Fig. 2a)²³. Each transmon qubit comprises a Josephson junction shunted by a capacitor to a ground plane patterned on a silicon substrate (5 × 5 × 0.35 mm³). Occupation of each qubit’s ground and excited states was determined by single-shot interrogation of the qubit-state-dependent response of separate readout resonators²⁴.

Identification of spatiotemporally correlated relaxation events required sampling transient (~1 ms) changes of each qubit’s inverse energy-relaxation rate 1/Γ₁ = T₁ when it decreased below 1 μs¹⁷. Instances of qubit relaxation were measured for each qubit using repeated cycles of a pulse sequence for control and state readout (Fig. 2b). During each of the repeated cycles, the sequence included state preparation (π-pulse), a fixed 1–μs delay, readout, and a 10.2–μs wait-time before the following cycle. An instance of qubit relaxation occurred whenever a qubit was prepared in the excited state after the control pulse and, following the 1–μs delay, it was then found in the ground state. Instances of relaxation were likely if a qubit’s inverse decay-rate change was comparable to the 1–μs delay duration (1/Γ₁ = T₁≲ 1 μs). Relaxation rate fluctuations could be monitored with sufficient sampling within a duration of  ~ 1 ms since the pulse sequence was repeated every Δt_cycle = 15.3 μs. As each cycle was performed consecutively, the single-shot readout signal not only indicated qubit decay but also the preparation state for the following measurement cycle (see “Methods”, Qubit measurement pulse sequence). Each cycle in which the qubit was found in the excited state prior to the π-pulse was discarded.

Fig. 2: Energy-relaxation dynamics from a cosmic ray and the measurement pulse sequence.

a A false-colored micrograph of the qubit array with 10 aluminum transmon qubits (orange), each capacitively coupled to a readout resonator (blue). Microwave signals for qubit control and readout were routed through a common feedline (red). The energy-relaxation response of individual qubits to a cosmic-ray impact (identified in Fig. 1) have chip-scale spatial correlations for multiple milliseconds. b Qubit relaxation events are identified from repeated measurement cycles of a pulse sequence for qubit control and readout.

After monitoring qubit relaxation for continuous periods of 10⁶ measurement cycles (≈ 15 s), we searched for spatiotemporally correlated events. We identified events by evaluating a cross-correlation time-series between instances of qubit relaxation (summed over all qubits for each cycle) and an expected temporal evolution of qubit relaxation rates during an event (Supplementary Note 1, Identification of Spatiotemporally Correlated Qubit Relaxation Events). The expected temporal correlation of total qubit relaxation was defined as a one-sided exponential with a 5 ms recovery time constant. The onset of each event was recognized as a transient peak in this cross-correlation above a threshold value. The example event shown in Fig. 1 resembles the expected temporal evolution, and the corresponding relaxation rate dynamics of each qubit (Fig. 2a) exhibit a sudden increase and exponential-like recovery.

The qubit array and detectors were measured for 266.5 h total between 2023-06-07 and 2023-06-29, amounting to 62.82 billion measurement cycles. After data collection, we identified the timestamps of spatiotemporally correlated qubit relaxation event arrival times {t_k} for a total of 9460 events. Our observed rate of events, r_Q = 1/(101 ± 1 s), is similar to other published results^14,16,17, considering the expected contribution of ionizing radiation impacts due to substrate size of qubit arrays and given the general variability of radiation levels among laboratory environments^3,4.

We identified signatures of cosmic rays in the qubit data using synchronized measurements of cosmic rays from six scintillating detectors (collectively denoted by s) positioned under the experiment cryostat (Fig. 1). Each detector is a rectangular prism of scintillating polymer optically coupled to a photomultiplier tube (PMT) (see “Methods”, Scintillating detectors). The PMTs produce a 10–ns pulse of current that is commensurate with the energy deposited in the scintillator from ionizing radiation impacts. We used a multi-channel analog-to-digital converter to record detector pulse arrival times and amplitudes. We ensured selective detection of cosmic rays by only accepting pulse amplitudes within a calibrated range (Supplementary Note 10, Detector Calibration).

All six detectors were monitored concurrently during qubit measurements. Processing of detector data involved the assignment of each pulse arrival to its contemporaneous qubit measurement cycle. We observed 14,403,488 measurement cycles during which at least one detector pulse occurred. This corresponds to an occurrence rate of r_S = 1/(66.616 ± 0.017 ms), which is consistent with our modeled rate of cosmic-ray energy depositions in these scintillating detectors.

We identified the contribution of cosmic rays to qubit relaxation events by analyzing temporal correlations between the detector and qubit datasets. From the qubit relaxation event arrival times {t_k} and all instances of detector pulses, we calculated each inter-arrival delay {Δt_k} between a given qubit relaxation event paired with the nearest-in-time detector pulse from any of the detectors. A coincidence occurs if an inter-arrival delay is within a coincidence window ∣Δt_k∣ ≤ δt_QS/2. We define the window duration δt_QS = 3Δt_cycle to maximize the acceptance of coincidences while minimizing accidental coincidences (false-positives) (Supplementary Note 3, Qubit-detector Coincidences). The example event in Figs. 1 and 2a, shows a detector pulse during the same measurement cycle that marks the onset of the qubit event. Each coincidence of a qubit relaxation event with a detector pulse indicates an event of cosmogenic origin.

We justify the high likelihood of this claim using the distribution of inter-arrival delays. Figure 3 displays the same inter-arrival distribution using two different histogram bin intervals: Fig. 3a depicts the coincidence signal using a smaller (3 cycles) bin width, and Fig. 3b has a larger bin width (200 cycles) to emphasize the background component of the inter-arrival distribution. Figure 3a shows 222 observed qubit-detector coincidences contained in the central bin spanning the coincidence window [ − δt_QS/2, + δt_QS/2]. The measured coincidence rate r_QS =$1/(72\pm 5\,\min )$ has contributions from both individual cosmic rays and accidental coincidences:

$$\underbrace{{r}_{{\rm{QS}}}}_{{\rm{measured}}}=\underbrace{{r}_{{\rm{QS}}}^{\mu }}_{{\rm{cosmic-ray}}}+\underbrace{{r}_{{\rm{QS}}}^{{\rm{acc}}.}}_{{\rm{accidental}}},$$

(1)

where ${r}_{{\rm{QS}}}^{\mu }$ is the cosmic-ray coincidence rate caused by individual muons (denoted by μ) and ${r}_{{\rm{QS}}}^{{\rm{acc}}.}$ is the rate of accidental coincidences. Accidental coincidences occur from the random confluence of multiple independent sources (Fig. 3b, inset). We created a background model for the rate of accidental coincidences and all other inter-arrival delays outside the coincidence window. The expected background distribution was calculated from measured quantities alone (qubit event rate r_Q, the detector pulse rate r_S, and the measured rate of coincidences r_QS) with the consideration that each background inter-arrival delay is not from an individual cosmogenic muon (Supplementary Note 5, Inter-arrival Distribution Background Model). The background distribution has a characteristic two-sided exponential shape from the spurious correlation between two independent Poisson processes, which is visually noticeable when the inter-arrival distribution is binned with 200Δt_cycle intervals (Fig. 3b). We find excellent agreement between the observed inter-arrival distribution and the background model among all inter-arrival delays outside the coincidence window. The background model prediction within the coincidence window gives an accidental coincidence rate ${r}_{{\rm{QS}}}^{{\rm{acc}}.}=1/(41.9\pm 0.9\,{\rm{h}})$, implying that 6.36 ± 0.07 of the 222 coincidence events are accidentals (Fig. 3a). We find the rate of coincidences from individual cosmic rays (Eq. 1) is ${r}_{{\rm{QS}}}^{\mu }=1/(7{4}_{-5}^{+6}\,\min )$, which accounts for 2.3 ± 0.2% of all identified qubit events. Since accidental coincidences are relatively rare (${r}_{{\rm{QS}}}^{{\rm{acc}}.}\ll {r}_{{\rm{QS}}}$), we have high confidence that any given coincidence is from a shared source among the qubit array and detectors, namely a cosmogenic particle.

Fig. 3: Distribution of inter-arrival delays.

a A histogram of the inter-arrival distribution (3Δt_cycle-bin-width) shows the observed counts (black), expected background distribution (red), and expected cosmic-ray coincidence counts (blue) (Supplementary Note 3, Qubit-detector Coincidences). The illustration of a cosmic-ray coincidence event (inset) shows a cosmogenic muon traversing the qubit array and detectors. b The 200Δt_cycle-bin-width histogram of the inter-arrival distribution highlights the agreement between the expected and observed background counts (except in the central bin that also contains cosmic-ray coincidence events). Example background events (inset) include a muon or gamma ray impacting the qubit array and an unrelated cosmogenic muon traversing the detectors.

Cosmic rays are only one source of spatiotemporally correlated qubit relaxation events:

$${r}_{{\rm{Q}}}={r}_{{\rm{Q}}}^{\mu }+{r}_{{\rm{Q}}}^{{\rm{other}}},$$

(2)

where ${r}_{{\rm{Q}}}^{\mu }$ is the rate of events caused by cosmic rays, and ${r}_{{\rm{Q}}}^{{\rm{other}}}$ is the rate of events caused by other sources, such as terrestrial radiation. Note the difference between ${r}_{{\rm{Q}}}^{\mu }$ and ${r}_{{\rm{QS}}}^{\mu }$; the former requires an energy deposition to the qubit array, while the latter requires coincident energy depositions to both the qubit array and a detector.

Most cosmic rays incident on the qubit array were not registered as coincidences, because the detectors do not surround or otherwise provide a full coverage of the qubit array. Nevertheless, the cosmic-ray coincidences ${r}_{{\rm{QS}}}^{\mu }$ are a known portion of C_QS of all qubit relaxation events from cosmic rays ${r}_{{\rm{Q}}}^{\mu }$, and we can estimate the rate ${r}_{{\rm{Q}}}^{\mu }$ from the relationship,

$${r}_{{\rm{QS}}}^{\mu }={C}_{{\rm{QS}}}\cdot {r}_{{\rm{Q}}}^{\mu },$$

(3)

where C_QS = 13.3 ± 0.4% is the coverage provided by the detectors. The coverage was calculated as, C_QS = ϵσ_QS/σ_Q, where σ_Q = 0.131 cm² is the cross-section for a cosmic ray to impact the qubit array, σ_QS = 0.0189 cm² is the cross-section for a cosmic ray to impact the qubit array and also deposit energy in the detectors within the energy range for pulse acceptance, and ϵ = 92% is the efficiency of qubit-detector coincidence identification due to the efficiency of the scintillating detectors and the timing accuracy of qubit-event identification (Supplementary Note 3, Qubit Detector Coincidences).

Cross-sections were based on the numerical sampling of cosmic-ray interactions with the detectors and qubit array using GEANT4²⁵. The calculation of each cross-section accounts for the interdependence among the cosmic-ray flux distribution, the geometric arrangement of each detector, and the deposited energy in the detectors. The hemisphere in Fig. 4a shows the angular position of cosmic-ray muons that were numerically sampled to calculate the interaction cross-sections for impacts to the qubit array (pink, Q) and impacts to both the qubit array and any of the detectors (green, QS). The coverage of the qubit array that is collectively provided by detectors is represented by the relative number of points for Q and QS in the hemisphere (Fig. 4a). We have also calculated cross-sections for coincidence combinations among the six detectors themselves and found they accurately predict their observed energy spectra and coincidence rates (see “Methods”, Model of the cosmic-ray flux and exposure rate of detectors and Supplementary Note 10, Detector Calibration).

Fig. 4: The rate of spatiotemporally correlated qubit relaxation events from cosmic rays.

a Simulation of cosmic rays in GEANT4 informed the cross-section of energy depositions to the qubit array substrate and detectors. The left and right panels show the originating azimuthal and zenith angles for cosmic-ray muons that deposit energy into the qubit array (Q, pink) and into both the qubit array and any of the detectors (QS, green). The relative number of QS and Q samples informs the coverage---the portion of all cosmic-ray impacts on the qubit array that are also cosmic-ray coincidence events. b The rate of cosmic-ray coincidences depends on the coverage provided by the detectors. The rate of spatiotemporally correlated qubit relaxation events from cosmic rays, ${r}_{{\rm{Q}}}^{\mu }$ (pink), shown as a proportionality factor, was calculated from the observed coincidence counts QS (green) and the coverage (Eq. 3). We overlay selected coincidence combinations (black), which are each consistent with the total coincidence rate. c The rates of cosmic-ray coincidences ${r}_{{\rm{QS}}}^{\mu }$, cosmic-ray events ${r}_{{\rm{Q}}}^{\mu }$, and all events r_Q are represented by overlapping areas. The overall rate of qubit events (yellow) has contributions from cosmic rays and other sources. The cosmic-ray coincidences (green) are a known portion (C_QS = 13.3 ± 0.4%) of all cosmic-ray-induced events (pink), which account for 17.1 ± 1.3% of the overall event rate.

The rate of spatiotemporally correlated qubit relaxation events caused by cosmic rays, ${r}_{{\rm{Q}}}^{\mu }=1/(59{2}_{-41}^{+48}\,{\rm{s}})$, is calculated from Equation (3) (also see Table 1 for all model parameters). This rate is shown as the slope of the confidence band in Fig. 4b, which also plots the number of cosmic-ray coincidences for selected combinations of detectors and the qubit array. The data point qs (green) includes all observed coincidences in the experiment. We highlight the accuracy and predictive power of the cross-section model by decomposing the observed coincidences into sub-categories (black) among the detectors (qa, qb, etc.), and find these are each consistent with the overall coincidence rate. In addition, there is close agreement between the cosmic-ray event rate ${r}_{{\rm{Q}}}^{\mu }$ and an expected rate of cosmic-ray impacts ${\sigma }_{{\rm{Q}}}\Phi=1/(57{4}_{-33}^{+38}\,{\rm{s}})$, based on the measured cosmic-ray flux in the laboratory, Φ = 0.0133(8) s⁻¹cm⁻² (see Supplementary Note 9, Estimation of Detector Efficiencies and Muon Flux). We conclude that likely all cosmic-ray impacts resulted in a detectable event of spatiotemporally correlated qubit relaxation for this device.

Table 1 Experiment and cosmic-ray rate model parameters

We found cosmic rays account for 17.1 ± 1.3% of all the spatiotemporally correlated events detected. The remaining events are likely from ionizing radiation impacts from gamma rays sourced in the laboratory and the experimental apparatus. Phonon and quasiparticle burst events may also result from the absorption of non-ionizing radiation, such as luminescence, Cherenkov radiation, and transition radiation, which is generally induced by ionizing radiation^{26,27,28,29,30}. Potential non-radiation contributions to the spatiotemporally correlated event rate may include stress-relaxation³¹ and mechanical impulses, e.g., from the pulse-tube cryocooler³².

We analyzed the dynamics of qubit relaxation rates during spatiotemporally correlated events in terms of temporal and spatial correlations. For each event, we estimated the change in qubit decay rates and characterized their recovery dynamics. We analyzed the single-shot readout signal of each qubit individually by binning the single-shot measurement results in time. The decay probability within each time bin is

$$p=\frac{{n}_{{\rm{decay}}}}{{n}_{{\rm{prep}}}},$$

(4)

where n_prep is the number of preparations and n_decay is the number of relaxation instances within a bin of 40 measurement cycles. The decay probability relates to a decay rate as

$$p=1-A{e}^{-\Gamma \Delta t},$$

(5)

where Γ is the decay rate, Δt = 3 μs is the effective delay time between qubit state preparation and measurement (Δt > 1 μs due to relaxation during qubit readout), and A is a constant related to preparation and measurement fidelity. We used 1,880 pre-trigger measurement cycles (≈ 29 ms prior to the event onset) to evaluate, ${p}_{{\rm{pre}}}$, a baseline probability of relaxation (Eq. 4). We also evaluated the decay probability using shorter duration time bins (40 cycles  ≈ 0.7 ms) to capture the dynamics of decay-rate fluctuations and recovery. Figure 5a displays the decay probability of Q2 during an example event. We show the pre-trigger baseline probability ${p}_{{\rm{pre}}}$ (gray) and the 40-cycle bins, labeled p_t, both before and after the event onset. We calculated (Eq. 5) the decay-rate change ΔΓ_t relative to the pre-trigger baseline, as shown in Fig. 5b for for the pre- and post-trigger time bins.

Fig. 5: Severity of spatiotemporally correlated relaxation events.

a The probability of relaxation is calculated for each qubit within each event. As an example, we show the decay probability of Q2 for an example event. The probabilities p_t are evaluated for each bin of 40 measurement cycles (black). The baseline decay probability ${p}_{{\rm{pre}}}$ was evaluated from a single pre-trigger bin of 1880 single-shots (gray). b The decay-rate change during this event displays a rapid onset and  ≈ 6 ms timescale recovery. The initial decay-rate change, ΔΓ_init was evaluated to determine the participation of each qubit within each event. c The average decay-rate change over all events shows two distinct timescales of recovery among the qubits. Traces are incrementally offset by 1 μs⁻¹. d The number of qubits participating in each event was based on thresholding the initial decay rate (ΔΓ_init ≥ 1/(5 μs)). The error bars indicate counting statistics for the total in each bin. Stacked histograms show the relative contribution from cosmic rays (purple) and other sources (gray), as calculated from coincidence measurements. Uncertainty in the constructed distributions is based on the counting statistics of coincidence events.

Temporal correlations within an event were summarized in terms of a time constant τ_i (of each qubit i) for the decay rate recovery to baseline. Each qubit exhibits a recovery time constant that is consistent from event to event. The average recovery dynamics for each qubit (Fig. 5c) clearly have two distinct timescales among the qubits: five qubits have a slow (τ ≈ 6 ms) recovery while the other five qubits have a fast (τ ≈ 0.7 ms) recovery. The recovery timescales are directly related to the orientation of the Josephson junction electrodes relative to the aluminum ground plane of the qubit array (see “Methods”, Details of the qubit array).

The origin of these differences is explained by the influence of the superconducting gap profile near the Josephson junction on quasiparticle dynamics²¹, as we have demonstrated by varying the orientation of each Josephson junction throughout the qubit array (see “Methods”, Influence of gap engineering on qubit relaxation rate recovery). Since the junctions were fabricated using a Dolan bridge double-angle evaporation process, there is an inherent difference of the superconducting gap energy for the two junction electrodes. The salient feature of this asymmetry is that the thin junction electrode (higher superconducting energy gap compared to other films) can inhibit quasiparticle transport toward the Josephson junction^{21,22,33,34,35,36}. We hypothesize that the gap engineering of the junction electrodes, combined with the presence of stronger quasiparticle trapping in the ground plane compared to the transmon islands, results in a faster recovery of the quasiparticle density after a burst for half of the qubits in the experiment.

We characterized the scale of spatial correlations in terms of the number of qubits participating in each event. Here, we analyzed the latter 147.1 h of data for which all 10 qubits were measured (Supplementary Note 2, Summary of Data Runs). We defined a qubit to participate in an event if its initial decay-rate change (example indicated in Fig. 5b) exceeded a threshold ΔΓ_init ≥ 1/(5 μs), which was chosen to limit false-positive assignment. The likelihood that a given qubit participated in any given event ranges from 47% – 67% (and is not directly related to Josephson junction placement). The participating qubits of each event were generally clustered in a group of adjacent qubits. Figure 5d shows the distribution of the number of qubits participating in each event (black points) from both cosmic-ray and non-cosmic-ray sources. The distribution is bimodal, with a tendency for 4-qubit and 10-qubit events to occur. Events that have more than eight qubits participating may result from a saturation effect due to limited qubit-count and variability of qubit sensitivity; a portion of events categorized in the 9-qubit and 10-qubit bins might have otherwise affected a larger qubit array with more than 10 qubits. This is reasonable if one considers that the spatial extent of an event can be a proxy for the amount of energy deposited in the qubit array substrate from ionizing radiation sources, which is expected to have a distribution with an exponentially-decreasing tail as energy increases.

We have established high confidence that a given qubit-detector coincidence event was of cosmogenic origin, and effectively all cosmic-ray impacts resulted in a detected spatiotemporally correlated event. Accordingly, the qubit relaxation dynamics from coincidence events are representative of all cosmic-ray-induced spatiotemporally correlated events. Figure 5d shows stacked histograms for cosmic-ray (purple) and non-cosmic-ray (gray) contributions to the qubit participation in events. The cosmic-ray distribution of Fig. 5d was constructed by scaling the measured coincidence counts per bin by the inverse coverage (1/13.3%) of the detectors. We found that cosmic-ray events have all qubits participate most frequently. In comparison, for non-cosmic-ray sources, it was most likely that 4 of the qubits (localized to the impact site) would respond to the impact event. These results suggest that cosmic rays tend to cause correlated errors of greater spatial extent compared to events from non-cosmic-ray sources. This is consistent with the expected deposited energy in the qubit array from background gamma rays and cosmic rays: cosmic rays deposit  ≈ 300 keV on average, while ambient gamma rays deposit less³⁷.

Discussion

We have shown that cosmic rays cause superconducting qubit errors. This was achieved by adopting coincidence-timing techniques that correlate cosmic-ray detection events with changes of the energy-decay rates in a 10-transmon qubit array. The measured rates of cosmic-ray-induced errors are consistent with interaction cross-sections calculated from a GEANT4 model and the independently measured muon flux in the laboratory. To within statistical certainty, all cosmic rays incident on the qubit array resulted in detectable spatiotemporally correlated error events. Cosmic rays contribute to a significant fraction (17.1 ± 1.3%) of all spatiotemporally correlated error events that occur, although the majority of such events are of non-cosmogenic origins, such as gamma-ray sources near the qubit array or within the laboratory environment. Furthermore, cosmic-ray events were most likely to affect all 10 qubits in the array, whereas non-cosmogenic sources peaked at four qubits.

Low-background radiation environments may be helpful for understanding overall device susceptibility to ionizing radiation and could be one means to achieve robust operation of real-time quantum error correction. However, while underground facilities may protect quantum devices^38,39 and advance scientific knowledge, it would be advantageous from a practical standpoint to develop design and fabrication techniques that mitigate the impact of ionizing radiation on solid-state quantum devices operated above ground. For example, radiation-hardened superconducting qubits may obviate the need for operation in low-background underground facilities.

Radiation-hardened superconducting qubits could be realized by several methods, including phonon trapping^15,40,41,42, quasiparticle trapping^43,44,45, or inhibiting quasiparticle tunneling^33,34,35,36. In our experiment, we varied the spatial structure of the superconducting gap near the Josephson junctions⁴⁶ to alter the observed quasiparticle recovery timescale. Further engineering of the superconducting gap at the Josephson junction electrodes and beyond may be able to sufficiently suppress the excess quasiparticle tunneling that arises from ionizing radiation events⁴⁷.

More studies are needed to understand possible tertiary effects of ionizing radiation on superconducting qubits, such as restructuring the density of states of two-level systems, which in turn cause qubit relaxation¹⁶ and may be responsible for relaxation time T₁ fluctuations^48,49,50,51. Through this effect, radiation impacts are a source of spatially correlated quasi-static noise that could be problematic for the stable performance of quantum error correction. Radiation hardening may help mitigate such tertiary effects as well.

Furthermore, error correction protocols can be tailored to detect and accommodate spatiotemporally correlated errors. Recently proposed schemes adapt error correction codes around specific error-prone qubits^52,53 and mid-circuit anomalies^54,55, or they spatially separate physical-qubit chiplets⁵⁶. A complementary approach is to embed radiation sensors within qubit arrays^57,58 to flag that an error may have occurred. Each of these protocols benefits from physical hardware platforms that remain resilient in the presence of ionizing radiation.

Methods

Experiment setup

Qubit measurement setup

This reported experiment was performed in the same laboratory space (latitude 42.36 °N) and cryostat as the experiments of Vepsäläinen et al.⁸. The mixing chamber (MXC) of the Leiden Cryogenics CF-CS81-1500 dilution refrigerator was held at approximately 10 mK throughout data collection. The qubit array package was mounted to a gold-plated copper paddle attached to the MXC. For shielding of electromagnetic radiation, the qubit package and the MXC paddle were surrounded by a nested enclosure of superconducting aluminum, tin-plated copper, and high-permeability magnetic shielding (Cryoperm-10).

The wiring setup for qubit measurement is shown in Fig. 6. The readout signal from the qubit array was first amplified by a Josephson traveling-wave parametric amplifier (JTWPA)⁵⁹, pumped by an Agilent RF source signal joined into the measurement chain with a directional coupler. The readout signal was further amplified with a high-electron-mobility transistor (HEMT) amplifier at the 4K stage, followed by an amplifier (MITEQ) at room temperature. After frequency downconversion, the readout signal was further amplified using a Stanford Research SR445A before analog-to-digital conversion using quadrature channels on the Quantum Machines OPX +.

Fig. 6: Schematic of the qubit measurement setup.

The diagram includes components and connectivity for qubit control and readout. Quantum Machines OPX + hardware was used for all AWG signals and the analog-to-digital conversion of qubit single-shot readout signals.

All arbitrary waveform generator (AWG) signals for qubit control and readout pulses were sourced by the Quantum Machines OPX+ hardware and upconverted as single-sideband tones with the internal IQ mixer of the Rohde and Schwarz SGS100A SGMA RF sources. A reference tone from the “Readout” RF source was used as the local oscillator for downconversion of the multiplexed readout signals. All control electronics were synchronized by a common 10 MHz rubidium clock source (Stanford Research Systems FS725).

Details of the qubit array

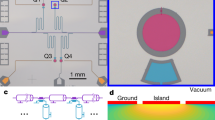
The qubit array (Fig. 7) has 10 fixed-frequency (single-junction) transmon qubits. The transmon circuits have a single-ended capacitance to an aluminum ground plane patterned on the 〈001〉 plane of a double-sided polished silicon substrate. The intrinsic silicon substrate has dimensions 0.35 mm × 5 mm × 5 mm along the x, y, and z axes, respectively. The coplanar waveguide (CPW) geometry of the feedline and readout resonators have a nominal 10 μm width and 6 μm gap. The qubit array has 10 charge lines (CPW width/gap: 5 μm/3 μm) for microwave driving of each qubit, although these were not used for the experiment reported here. Air-bridge crossovers span across the CPWs of the feedline, readout resonators, and charge lines⁶⁰. The aluminum crossovers have a nominal thickness of 700 nm.

Fig. 7: Optical micrographs of the qubit array.

a The qubit array mounted in its package by 107 wirebonds and surrounded by the package PCB (TMM10). Labels for each transmon qubit are in Fig. 2a. b Micrograph detail of qubits Q5 and Q9 shows the placement (red outline) of the Josephson junction relative to the transmon capacitor and ground plane. Corresponding profiles of the superconducting film thicknesses near a junction is shown in Fig. 8.

The quarter-wavelength fundamental mode of each CPW readout resonator is inductively coupled to the microwave feedline while the opposite end of the resonator is capacitively coupled to its respective transmon capacitor. Each transmon capacitor is cross-shaped, with the cross arms each having 30 μm-width and 480 μm-length (Fig. 7b). Each capacitor is separated from the ground plane by a 30 μm gap around the cross. The transmon qubit capacitors are each separated by 0.85 mm on center within each row of the qubit array and 2.54 mm between rows. The bottom row of transmons are offset to the right (Fig. 7a, along the y-axis) by 0.225 mm relative to the top row. All thin film aluminum, except for the Josephson junction electrodes and air-bridge crossovers, were deposited with a thickness of 250 nm. After an ion milling procedure, the aluminum Josephson junction electrodes were deposited with thicknesses of 30 nm and 150 nm to create a Dolan-style junction geometry (Fig. 8). These thin film thicknesses were measured by atomic force microscopy on the junction electrodes of Q1 and Q3.

Fig. 8: Diagram of the Dolan bridge Josephson junction thin films.

The Josephson junction was formed by double-angle deposition of aluminum thin films (30 nm followed by 150 nm). The deposited thin films connect to the 250 nm aluminum (gray) transmon island and ground plane, which are respectively the left- and right-hand (right- and left-hand) gray regions of the diagram for JJ-placement-A (JJ-placement-B). The labels L1-4 represent four separate regions of the layered thin films. L1 is a 150 nm film connected to the 250 nm film on the left-hand side and is one of the qubit junction electrodes (as it connects to L4 through the junction barrier). L3 is another 150 nm region, which contacts L4 and the 250 nm film on the right-hand side. L4 is a 30 nm film that forms the other junction electrode, on the right-hand side of the junction barrier.

This particular qubit array was designed such that each qubit’s Josephson junction is either on the right side (JJ-placement-A) or left side (JJ-placement-B) of the transmon capacitor island (Fig. 7b and Table 2). The junction placement was intentionally disordered among the qubits in the array to clarify the direct correspondence between each qubit relaxation rate recovery time scale and junction placement, rather than other, possibly spatially-dependent, differences among the qubits. Since the junctions were fabricated using a Dolan bridge double-angle evaporation process, there is an inherent asymmetry of the two junction electrodes (Fig. 8). Qubits with JJ-placement-A (JJ-placement-B) have the thicker (thinner) junction electrode L1 oriented towards the transmon island (ground plane).

Table 2 Qubit array parameters

The qubit array was placed in a gold-plated copper package. The outer dimensions of the package are 13.0 mm × 52.2 mm × 52.2 mm along the axes x, y, z, respectively. No glue, epoxy, or varnish was used to deliberately thermalize the qubit array to the package^12,31. Rather, the bottom corners of the qubit array substrate rest upon the gold-plated copper base of the package and was secured in place by wirebonds (Al-Si alloy wirebonds)⁶¹. The electrical traces and ground plane of the qubit array are wirebonded to the electrical traces and ground plane of a printed circuit board (PCB), as shown in Fig. 7⁶². The PCB dielectric is Rogers TMM10 material. We note that the PCB dielectric could be a contributing source of ionizing radiation by containing trace quantities of potassium-40 and progeny nuclei of the uranium and thorium decay chains^3,4.

The critical current density of each Josephson junction (J_c = 0.55 μA/μm²) is estimated based on room-temperature conductance measurements of witness junctions from the same wafer. The anharmonicity of each transmon is 160 ± 5 MHz, where the uncertainty reflects variation among qubits in a representative qubit array with the same capacitor and readout coupling geometry.

Qubit decay rates were measured periodically after each collection of 100 entries ($\approx 45\,\min$ real time) using an inversion-recovery pulse sequence as is traditionally performed to characterize a superconducting qubit’s 1/T₁ energy-decay rate⁶³. In Table 2, we report the median decay rate for each qubit as measured through Run-09 to Run-13, and additional measurements thereafter. The upper and lower uncertainties represent deviation from the median for the 84.1^st and 15.9^th percentile values. These percentiles correspond to  ± 1 standard deviations for a Gaussian distribution. The delay duration between preparation and measurement in each pulse sequence was varied from 8 ns to 117.608 μs in 50 equal steps. The full range of delay times were repeated for 500 single-shots per delay duration, with 600 μs between each single-shot readout and the following preparation pulse. An exponential decay rate was extracted from a least-squares fit to the averaged single-shot voltages.

Influence of gap engineering on qubit relaxation rate recovery

Quasiparticles generated from burst events can cause qubit relaxation when they tunnel across the Josephson junction of the qubit. The direct correspondence between the qubit recovery timescale after a spatiotemporally correlated event and junction placement (Table 2) can be explained by a combination of quasiparticle trapping effects among the gap-engineered junction thin films (Fig. 8) and the 250 nm aluminum (transmon capacitor island and ground plane).

We hypothesize that the recovery timescale is determined by the rate of quasiparticle tunneling into only one of the two junction electrodes (L1 but not L4). Since the thicker 150 nm electrode L1 has a smaller superconducting gap, we consider that it should have a higher quasiparticle density relative to the 30 nm electrode L4²¹. Because of this, we expect quasiparticle-induced qubit relaxation to be dominated by the quasiparticle dynamics on a single side of each Josephson junction.

It is known that the thickness of thin-film aluminum influences the superconducting gap in that film, with thinner films having a slightly larger gap^64,65,66. Based on superconducting transition temperature T_c measurements of films from the same fabrication process, we estimate the superconducting gap energy differences between the 150 nm (L1, L3) and 30 nm (L2, L4) films are δΔ ≈ h(2.8 GHz), where h is the Planck constant. (Notably, this energy difference is not larger than that of the qubit transitions h(4.3 − 5.2 GHz), and therefore does not block quasiparticle-induced qubit relaxation at the Josephson junction barrier^22,66.)

Since the timescale of quasiparticle downconversion to energies near the superconducting gap-edge is sufficiently short (≲100 μs)⁹, we consider a thermal energy distribution for the quasiparticles. The effect of the superconducting gap energy difference of the two shadow-evaporated junction films is that quasiparticles are less likely to reside in the 30 nm film, with a relative factor of $\sim {e}^{-\delta \Delta /{k}_{{\rm{B}}}T}$, where k_BT is the effective energy of the quasiparticles^21,47. Quasiparticle-induced qubit relaxation should generally occur from quasiparticles in the 150 nm film L1 that tunnel across the Josephson junction into L4. Consequently, the various recovery timescales among the qubits may arise from differences of quasiparticle dynamics in the 250 nm film that is connected to each L1 electrode.

We estimate the gap difference between the 150 nm films (L1 and L3) and the 250 nm aluminum is  ≈ h(1 GHz). This energy difference may set the longest recovery timescale due to the suppression of quasiparticle tunneling into the 150 nm film L1 from the adjacent 250 nm film with a rate that scales inversely with the Arrhenius factor $\sim {e}^{-h(1{\rm{GHz}})/{k}_{{\rm{B}}}T}$.

At timescales shorter than this and longer than  ≈ 1 ms, which is an estimated timescale of diffusion throughout the ground plane⁴⁴, we suspect there is a significant asymmetry of the quasiparticle density between the ground plane and transmon island. The direct correspondence between recovery timescale and whether L1 connects to either the transmon capacitor island (JJ-placement-A) or the ground plane (JJ-placement-B) suggests that these films have different quasiparticle dynamics. Although both the ground plane and the transmon islands are 250 nm aluminum films, it is plausible that the quasiparticle density is much lower in the ground plane due to the presence of vortices and lower-gap aluminum air-bridge crossovers acting as quasiparticle traps.

The two distinct recovery timescales that we observed from JJ-placement-A and JJ-placement-B could result from the combination of (a) whether the junction’s 150 nm electrode (L1) connects to either the transmon island or ground plane, and (b) the asymmetry of the quasiparticle density in the transmon island compared to the ground plane. For qubits with JJ-placement-B, the 150 nm film L1 connects to the ground plane, which is quickly depleted of quasiparticles due to diffusion and trapping effects, resulting in a recovery of the qubit relaxation rate within a timescale of  ≈ 0.7 ms. In contrast, qubits with JJ-placement-A have their 150 nm electrode film L1 connected to the transmon island, which supplies quasiparticles to the junction electrode L1 for  ≈ 6 ms, which we interpret to be the timescale at which quasiparticles in all films diminishes.

In conclusion, the fast recovery qubits display a timescale consistent with quasiparticle diffusion and trapping in the ground plane. The timescale of slow recovery qubits is likely determined by quasiparticle dynamics in the transmon island, which modeling in quantitative detail is beyond the scope of this work. We consider that the significant difference of recovery timescales can be attributed to the combination of gap-engineered Josephson junction electrodes and whether the electrode L1 is connected to the transmon island (quasiparticle rich) or ground plane (quasiparticle poor).

Scintillating detectors

Each detector is a rectangular prism of scintillating polymer wrapped with reflective film and optically coupled to a photomultiplier tube (PMT) that produces pulses of current that are commensurate with the energy deposited in the scintillator from ionizing radiation impacts. The materials and components of each scintillator are provided in Supplementary Table II. The scintillating materials (EJ-200 and BC-412) were chosen for their long light attenuation lengths (>2 m), which is relevant to ensure the PMT efficiently collects light produced anywhere within the scintillator volume. The detectors are labeled alphabetically and are grouped in three pairs of similar construction (A & B, C & D, E & F).

The use of scintillating detectors for measurements of cosmic rays required the discrimination, filtering, and digitization of pulse signals produced by the scintillators and PMTs. Since the PMT produces rapid (≈ 10 ns) pulses of current, we used a charge pre-amplifier as a low-pass integrator of the PMT current. The pre-amplifier effectively accumulates charge on a capacitor, which is then measured as a voltage pulse with the analog-to-digital converter. The amplitude of each voltage pulse is thus proportional to the number of photons collected by the PMT from the scintillator, which itself is proportional to the total deposited energy in the scintillator from an impact of ionizing radiation. We operated each PMT using a negative high-voltage (HV) bias, chosen for sufficiently high detection efficiency of cosmic rays while minimizing dark counts.

Each pre-amplified detector signal was fed into a commercial FPGA-based analog-to-digital converter (Caen DT5725S), which has a 250 MS/s sampling rate and a 14-bit amplitude resolution. The on-board FPGA was programmed to discriminate, filter, and digitize each pulse timestamp and amplitude. The recorded pulse amplitude and arrival time were stored offline for further filtering and analysis. Supplementary Table III lists the electronic equipment used for detector operation and data collection.

Positions of the detectors and qubit array

The orientation and aspect ratio of the detectors and qubit array substrate influenced the rate and distribution of energy depositions from cosmogenic particles. In addition, the positioning of detectors determined the rate of coincidence events among the detectors themselves and the coincidences with the qubit array. We chose a geometric configuration of the detectors that enabled an accurate calibration of our cosmic-ray model (detector response and cosmic-ray flux) and a sufficient rate of qubit-detector coincidences.

The qubit array was mounted vertically in the cryostat such that the normal vector of the thin film (x-axis) points to the horizon (Fig. 2a). We note that a rotation of the chip from a vertical to horizontal orientation would approximately double the cosmic-ray impact rate³⁹. A vertical orientation exposes the qubit array to cosmic rays that can traverse long distances  ~5 mm through the substrate, thus depositing higher energy on average compared to a horizontal orientation.

We placed the scintillating detectors outside the experiment cryostat and underneath the qubit array as shown in Figs. 1, 4a, and Supplementary Fig. 5. An accurate representation of the experiment’s geometric configuration was required for modeling interaction cross-sections from cosmic rays using GEANT4 (see Supplementary Note 8, GEANT4 Simulation). The measured positions of the detectors, relative to the qubit array, are included in Supplementary Table II. The detectors were placed and aligned according to reference coordinates marked on the floor of the laboratory. We defined the coordinate system relative to the volumetric center of the qubit array substrate when the cryostat cans were removed prior to cooldown. Distance measurements were performed using a laser range finder, meter stick, and calipers. The alignment of each detector was aided by a laser level and plumb bob. The uncertainty of the detector positions relative to each other is  ≈ 2 mm, and the uncertainty of the qubit array position (relative to all detectors) is  ≈ 5 mm. This geometric uncertainty does not significantly affect our estimation of interaction cross-sections. For the chosen detector arrangement, we found the calculated interaction cross-sections are insensitive to deviations of position that are small compared to the detector dimensions.

The detectors were arranged directly below the qubit array, nearly centered on the z-axis, to maximize the qubit-detector coincidence rate. The qubit array was mostly exposed to cosmic rays that originated from near-zenith and azimuthal angles along the x-axis, symmetrically entering from the front-side and back-side of the substrate chip. Accordingly, we aligned the longest dimension of each detector with the x-axis to maximize coincidences from these azimuthal angles.

We created two vertical stacks of three scintillators each. Each detector stack provided a sufficient rate of two-fold and three-fold detector-detector coincidences, which enabled the calibration of the detector energy response (see Supplementary Note 10, Detector Calibration). We placed the two stacks adjacent to each other (along the y-axis). Lead bricks were arranged around the stacks to reduce the flux of gamma radiation incident on the detectors.

Qubit measurement pulse sequence

Qubit measurements for all data runs were performed by repeated cycles of a pulse sequence for qubit control and single-shot readout. Each measurement cycle has a duration period of Δt_cycle = 15.3 μs. The pulse sequence (Fig. 2b) performed during each cycle consists of a control pulse for each qubit (π-pulse, 100 ns), a 1–μs delay, a single-shot readout (4 μs) for each qubit, and a wait-time (Δt_wait = 10.2 μs) before the following measurement cycle. The wait-time following readout was chosen for sufficient resonator ring-down and to have a data collection time (≈ 15 s) per entry that was comparable to the downtime (≈ 12 s) between data entries (see Supplementary Note 2, Summary of Data Runs).

We used frequency-multiplexed microwave pulses for qubit control and resonator readout. The readout pulse amplitudes and frequencies were individually set to maximize the single-shot fidelity of separation between qubit pointer states while minimizing readout-induced excitations of the transmon circuit outside the qubit manifold^67,68.

An instance of qubit relaxation occurred whenever a qubit was prepared in the excited state after the control pulse and, following the 1–μs delay, it was then found in the ground state. While readout informed of qubit decay, it also informed the preparation state for the next measurement cycle. All instances of measured qubit decay occurred from post-selected measurement cycles, which were conditioned on a ground-state result from the readout of the previous measurement cycle. This procedure results in a stochastic and non-uniform sampling rate of qubit relaxation instances and results in measurement cycles in which we do not evaluate if a qubit has decayed or not. However, the sampling bias is favorable for event detection since the heightened rate of qubit relaxation during an event results in a higher rate of state preparation and thus a higher sampling rate of for qubit relaxation. If a qubit was found in the ground state, the qubit remained in the ground state with high probability after the single-shot measurement and throughout the Δt_wait wait-time before the next measurement cycle. Since the qubit remained in the ground state during the wait time, the control pulse transitioned the qubit to the excited state (assuming perfect π-pulse fidelity).

We checked that qubit excitation was unlikely by measuring excitation rates using an adapted version of the presented pulse sequence; every other cycle presented in Fig. 2b was replaced with a sequence lacking a π-pulse, which allowed for excitation measurements interleaved with spatiotemporally correlated relaxation event detection. We found that qubit excitation rarely occurred (Γ_↑≪ 1/Δt_wait) both in steady-state and during spatiotemporally correlated relaxation events.

The pulse sequence allowed for the detection of qubit relaxation not only during the 1–μs delay, but also during the single-shot readout process. We estimated an effective delay duration of Δt = 3 μs by comparing the traditional 1/T₁ energy-decay measurements (Table 2) to the steady-state decay probability measured by this pulse sequence (Fig. 2b).

Excited-state readout results are not highly informative of the qubit state after the Δt_wait wait-time due to the effect of qubit energy-relaxation (Γ_↓~1/Δt_wait), where Γ_↓ is the rate of energy-relaxation of the qubit. A measurement result that occurs in a cycle after an excited-state readout of the previous cycle does not inform if qubit relaxation occurred, and the result is used only to condition the next measurement cycle.

Synchronization of qubit and detector measurements

This experiment correlated qubit relaxation errors and cosmic ray detection, which relied on the synchronization of qubit and detector data sets. Throughout data collection, we recorded all detector pulses that occurred while qubits were measured. We synchronized detector and qubit measurement data by referencing each detector pulse arrival to a specific single-shot qubit measurement.

We synchronized the detector and qubit data by producing a square reference pulse from the qubit measurement hardware and recording its occurrence with an additional channel of the analog-to-digital (ADC) converter for the detectors. Within each entry of 10⁶ qubit measurement cycles, a reference pulse was generated by the Quantum Machines OPX + after the first 100 qubit measurement cycles and every 100 cycles thereafter. After data collection, we found all timestamps of the reference pulses in the detector data, as recorded by the ADC with 4 ns resolution. A group of 10,000 consecutive reference pulses marked the 10⁶ measurement cycles of each data entry. Accordingly, we assigned each reference-pulse timestamp to its respective measurement cycle index within an entry. For each entry, we performed a linear interpolation between reference-pulse timestamps versus cycle index, which served to relate every scintillator pulse timestamp to its contemporary measurement cycle index within the entry.

The assignment of each detector pulse to a measurement cycle coarse-grained their 4-ns-resolution arrival times to Δt_cycle = 15.3 μs time bins. The coarse-graining procedure was unlikely to separate the pulses of detector-detector cosmic-ray coincidences into consecutive cycles (which would result in false negatives) because detector-detector coincidences occur within a short duration (≈ 100 ns, observed in the 4 ns resolution detector data) compared to the 15.3–μs measurement cycle window.

Model of the cosmic-ray flux and exposure rate of detectors

Our model of cosmic rays describes the occurrence rate of cosmogenic particles that are incident to the scintillating detectors and the qubit array. The application of this model not only provides a comprehensive account of the cosmic-ray effect on our detectors, but also establishes a predictive tool for the rate of cosmic-ray impacts to the qubit array.

Cosmogenic particles, such as muons, neutrons, protons, electrons, and neutrinos, are created in the upper atmosphere from primary cosmic rays (90% protons, 9% alpha particles, 1% heavier nuclei)¹. Our detection scheme is sensitive to simultaneous energy depositions in the scintillators and qubit array substrate, which are, overwhelmingly, caused by cosmogenic muons traversing the laboratory space (compared to protons, neutrons, pions, and other particles created by primary cosmic rays)¹. In this work, we consider energy depositions from cosmogenic muons and the additional particles they create while traversing the laboratory space, such as knock-on electrons and gamma rays.

Flux distribution and sampling of cosmic-ray muons

The cosmogenic muon flux distribution has a cosine-squared dependence on zenith angle θ and is independent of azimuthal angle φ. We consider a differential flux distribution based on the energy distribution described by the Gaisser formula at zenith^69,70,

$${J}_{\mu }(\theta,\varphi,{E}_{\mu })= \frac{d\Phi }{d{E}_{\mu }d{\Omega }}=\frac{d{I}_{\mu }(\theta )}{d{E}_{\mu }}\\= {C}_{\mu }{\left(\frac{{E}_{\mu }}{1\,{\rm{GeV}}}\right)}^{-2.7}\left[\frac{1}{1+\frac{1.1{E}_{\mu }}{115\,{\rm{GeV}}}}+\frac{0.054}{1+\frac{1.1{E}_{\mu }}{850\,{\rm{GeV}}}}\right]{\cos }^{2}\theta,$$

(6)

where Φ is the total muon flux, E_μ is the muon energy (10 GeV to 1 TeV), Ω denotes solid angle, I_μ is the muon flux integrated over energy, and C_μ is a free scale factor that is absorbed into the overall muon flux Φ upon model calibration (see Supplementary Note 10, Detector Calibration).

Although the Gaisser formula is most applicable for muon energies $\gtrsim (100\,{\rm{GeV}}/\cos \theta )$ and small zenith angles, this angular distribution model and sampled energy range is reasonable for our use case: the calculation of deposited energy to the detectors and qubit device. High-energy muons are minimum ionizing, meaning the energy they deposit in a detector or the qubit array substrate depends on the distance traveled through it, which generally depends on the muon’s zenith angle but is independent of the muon’s energy¹. Since the cross-sections are rather insensitive to the muon energy that is sampled, we sampled an energy range that provides a faithful approximation of the actual muon angular distribution.

We additionally compared the zenith-dependent flux of our model (Eq. 6) to another distribution⁷⁰ that accounts for the Earth’s curvature and the muon energy-dependence on zenith angle. We found negligible differences relevant to energy deposition rates to detectors and the qubit array substrate between these models, especially for the zenith angles relevant for coincidence cross-sections in our experiment.

We performed Monte Carlo simulations of cosmic rays in our laboratory using the GEANT4 toolkit (see Supplementary Note 8, GEANT4 Simulation). We sampled individual cosmic-ray muons from the flux distribution of Equation (6) to estimate the exposure of the detectors to cosmic-ray muons. (The qubit array is also considered a detector in this regard.) This sampling technique ultimately provided cross-sections for the rate of energy depositions into each detector, the qubit array, and their coincidences within a specific energy range.

We used the following sampling procedure to calculate the interaction cross-sections. We define a hemisphere with a radius (15 m) that surrounds the scintillating detectors and qubit array (Supplementary Fig. 4) along with other objects in the laboratory environment. The procedure for sampling each muon is

• 1. Randomly sample a position on the hemisphere by choosing zenith and azimuthal angles from $({\cos }^{2}\theta \sin \theta )$ and uniform φ ∈ [0, 2π) distribution, respectively.

• 2. Define a square of side length ℓ that is centered on, and tangent to, the sampled position. (The side-length ℓ is a fixed length for all samples. Ensure that ℓ > 2d where d is the farthest distance of the detector objects from the hemisphere origin that is relevant for particle interactions.)

• 3. Randomly sample a point within the extent of the tangent square.

• 4. Randomly choose a muon energy according to the muon flux distribution (Eq. 6).

• 5. "Throw” the muon from the sampled point in the direction normal to the tangent square toward the detectors.

• 6. Propagate the muon trajectory and its interactions within the laboratory.

• 7. Record the total energy deposited in each detector.

Energy-deposition occurrence rate and interaction cross-sections

Interaction cross-sections σ relate an occurrence rate r of energy depositions and the total cosmogenic muon flux Φ as

$$r=\epsilon \sigma \Phi,$$

(7)

where ϵ represents the efficiency of the detector(s). For a detector, or combination of detectors, the cross-section σ is calculated from the sampled energy depositions (see Flux distribution and sampling of cosmic-ray muons),

$$\sigma=\frac{\#\,{\rm{of}}\,{\rm{energy}}\,{\rm{depositions}}\,{\rm{to}}\,{\rm{the}}\,{\rm{detector(s)}}}{\#\,{\rm{of}}\,{\rm{muons}}\,{\rm{sampled}}/{\ell }^{2}}.$$

(8)

Each cross-section has a geometric quality, as it depends on the dimensions of the detector(s) and, in the case of coincidence combinations, the relative placement of detectors.

Coincidence events result from particle energy depositions to multiple detectors from one initially sampled muon. Similar to Eq. 7, the occurrence rate for multi-detector coincidences is

$$r=\left(\prod _{k\in \alpha }{\epsilon }_{k}\right)\sigma \Phi,$$

(9)

where the efficiency factor is the product of the efficiencies for each detector k within the combination α. The cross-section for a multi-detector coincidence is calculated according to Equation (8) by counting the number of sampled muons that each resulted in an energy deposition to every detector within the coincidence combination. For example, the cross-section for a coincidence of detector A and detector B is,

$${\sigma }_{{\rm{AB}}}=\frac{\#\,{\rm{of}}\,{\rm{energy}}\,{\rm{depositions}}\,{\rm{to}}\,{\rm{both}}\,{\rm{A}}\,{\rm{and}}\,{\rm{B}}}{\#\,{\rm{of}}\,{\rm{muons}}\,{\rm{sampled}}/{\ell }^{2}},$$

(10)

where the numerator counts the number of sampled muons that resulted in a coincidence of both detectors A and B. For the experimental analysis, we calculated all cross-sections for a specific range of energy depositions for each detector, matching the acceptance criteria for pulse detection (Supplementary Table VII).

We refer to the cross-section σ as an inclusive cross-section (as defined in Eqs. 8 and 10) since it corresponds to a detector combination that is mutually inclusive with other detector combinations that could also occur from the same muons. We define exclusive cross-sections σ^*, that correspond to the set of coincidence observations that are mutually exclusive and completely exhaustive among all detectors included in the simulation. An exclusive observation for a given combination requires there are no energy depositions to the other detectors. For example, the exclusive cross-section for the coincidence of detectors A and B requires that the energy depositions to A and B occur when there are no energy depositions to other detectors ({C, D, E, F, Q}):

$${\sigma }_{{\rm{AB}}}^{*}=\frac{\#\,{\rm{of}}\,{\rm{energy}}\,{\rm{depositions}}\,{\rm{to}}\,{\rm{A}}\,{\rm{and}}\,{\rm{B}}\,{\rm{only}}}{\#\,{\rm{of}}\,{\rm{muons}}\,{\rm{sampled}}/{\ell }^{2}}.$$

(11)

While an inclusive combination α only relies on the detectors within that combination, an exclusive combination α depends on every detector in the analysis. The set of exclusive cross-sections have the property ${\sum }_{\alpha }{\sigma }_{\alpha }^{*}={\ell }^{2}$, where α sums over all combinations of the detectors (including the null cross-section for no energy deposition to any detector).

The exclusive and inclusive cross-sections are related by linear combinations. For example, the inclusive cross-section for the combination α is the sum of the exclusive cross-section ${\sigma }_{\alpha }^{*}$ and all other exclusive combinations that include α with other detectors:

$${\sigma }_{\alpha }={\sigma }_{\alpha }^{*}+\sum _{{\alpha }^{{\prime} }}{\sigma }_{{\alpha }^{{\prime} }}^{*},$$

(12)

where the sum is over all combinations ${\alpha }^{{\prime} }$ such that $\alpha \in {\alpha }^{{\prime} }$ (meaning that ${\alpha }^{{\prime} }$ contains all the detectors in α).

In the context of modeling experiment observations, our estimated value of a cross-section can have an error. Inclusive cross-section errors are positively correlated, e.g., δσ_A ∝ δσ_AB, which states that an over-estimate of the AB coincidence cross-section connotes an over-estimate of the A cross-section. In contrast, exclusive cross-sections can have positive or negative correlations, e.g., $-\delta {\sigma }_{{\rm{A}}}^{*}\propto \delta {\sigma }_{{\rm{AB}}}^{*}$, which states that an over-estimate of the exclusive AB coincidences contributes to an under-estimate of the A exclusive cross-sections. In general, the systematic error of any particular exclusive cross-section affects the error of all other exclusive cross-sections, resulting in both over- and under-estimated rates for any particular exclusive combinations we may observe.

We consider coincidence observations that are generally insensitive to the error of any particular cross-section by summing over exclusive cross-section combinations. Specifically, we refer to the rate of (two or more)-fold coincidences of detector d and any other detector S:

$${r}_{d-{\rm{S}}}={\epsilon }_{d}\sum _{\alpha }\left(1-\prod _{\begin{array}{c}k\!\!\in \!\alpha \\ k\ne d\end{array}}{\overline{\epsilon }}_{k}\right){\sigma }_{\alpha }^{*}\Phi,$$

(13)

where the sum is over all combinations α that contain detector d with other detectors, each product is over detectors k ∈ α (except d), and ${\overline{\epsilon }}_{k}=1-{\epsilon }_{k}$ are detector inefficiencies. The products within Equation (13) account for the rate that at least one detector of the combination α (except d) produces a pulse, provided there are coincident energy depositions to the detectors in the exclusive combination α. We define the coverage of detector d provided by all other detectors,

$${C}_{d-{\rm{S}}}=\frac{{r}_{d-{\rm{S}}}}{{r}_{d}}=\frac{1}{{\sigma }_{d}}\sum _{\alpha }\left(1-\prod _{\begin{array}{c}k\!\!\in \!\alpha \\ k\ne d\end{array}}{\overline{\epsilon }}_{k}\right){\sigma }_{\alpha }^{\ast },$$

(14)

which again includes the sum over all combinations α such that d ∈ α and each product is taken over detectors k ∈ α (except d). We remark that the coverage C_d−S is independent of both the muon flux and the efficiency of detector d.

Application of the rate model to qubit-detector coincidences

Calculation of coverage

We used cross-sections and detector efficiencies to estimate the coverage that the detectors provide to the qubit array. We then calculated the rate of cosmic-ray-induced spatiotemporally correlated qubit relaxation events from the coverage and the measured qubit-detector coincidence rate.

The calculated cross-section for all cosmic-ray energy depositions to the qubit array is σ_Q = 0.131 cm². A portion of cosmic rays also deposit energy in a detector: The total cross-section for QS coincidences is the sum of exclusive cross-sections for all combinations that include the qubit array:

$${\sigma }_{{\rm{QS}}}=\sum _{\alpha }{\sigma }_{\alpha }^{*}=0.0189\,{{\rm{cm}}}^{2}$$

(15)

where α sums over all combinations in the set {A, B, C, D, E, F, Q} that include Q and a detector. The expected occurrence rate of QS coincidences r_QS depends on the efficiency of the detectors within each combination (Eq. 13),

$${r}_{{\rm{QS}}}^{\mu}={\epsilon}_{{\delta t}_{{\rm{QS}}}}{\epsilon}_{{\rm{Q}}}\overbrace{\sum_{\alpha}\left(1-\prod _{\begin{array}{c}k\!\!\in \!\alpha \\ k\ne {\rm{Q}}\end{array}}{\overline{\epsilon }}_{k}\right){\sigma}_{\alpha }^{*}}^{{\sigma }_{{\rm{QS}},\epsilon}}\Phi$$

(16)

where k iterates over all detectors in the combination α (except Q), ${\overline{\epsilon }}_{k}=1-{\epsilon }_{k}$ is the detector inefficiency, and ϵ_Q is an unknown cosmic-ray detection efficiency for the qubit array, and we have also included ${\epsilon }_{{\delta t}_{{\rm{QS}}}}=94\%$ as a known detection efficiency factor specific to coincidence identification within the coincidence window (see Supplementary Note 3, Qubit-detector Coincidences).

We refer to σ_QS,ϵ as an effective cross-section that accounts for the collective efficiency of the detectors: ϵ_S = σ_QS,ϵ/σ_QS = 98.7 %. The coverage of the qubit array provided by the detectors is (Eq. 14),

$${C}_{{\rm{QS}}}=\frac{{r}_{{\rm{QS}}}^{\mu }}{{r}_{{\rm{Q}}}^{\mu }}={\epsilon }_{{\delta t}_{{\rm{QS}}}}{\epsilon }_{{\rm{S}}}\frac{{\sigma }_{{\rm{QS}}}}{{\sigma }_{{\rm{Q}}}}=13.3 \pm 0.4 \%,$$

(17)

where the uncertainty is estimated from detector coverage measurements (see Supplementary Note 9, Estimation of Detector Efficiencies and Muon Flux). The overall efficiency for these coincidences is $\epsilon={\epsilon }_{{\delta t}_{{\rm{QS}}}}{\epsilon }_{{\rm{S}}}=92\%$. The coverage of other qubit-detector coincidence combinations (shown in Fig. 4) were calculated similarly, e.g., ${C}_{{\rm{QA}}}={r}_{{\rm{QA}}}^{\mu }/{r}_{{\rm{Q}}}^{\mu }$.

The coverage C_QS was used to calculate the occurrence rate of spatiotemporally correlated qubit relaxation events ${r}_{{\rm{Q}}}^{\mu }$ from cosmic rays:

$${r}_{{\rm{Q}}}^{\mu }=\frac{1}{{C}_{{\rm{QS}}}}{r}_{{\rm{QS}}}^{\mu }=\frac{1}{{C}_{{\rm{QS}}}}({r}_{{\rm{QS}}}-{r}_{{\rm{QS}}}^{{\rm{acc}}.})=\frac{1}{59{2}_{-41}^{+48}\,{\rm{s}}}$$

(18)

where ${r}_{{\rm{QS}}}^{\mu }$ is the rate of qubit-detector coincidences from cosmic rays, r_QS is the rate of all observed qubit-detector coincidences, ${r}_{{\rm{QS}}}^{{\rm{acc}}.}$ is the rate of accidental qubit-detector coincidences, and the uncertainty was propagated from the uncertainty of the coverage (Eq. 17) and statistical uncertainty of r_QS.