Introduction

Electric control of spins is an appealing field of research in materials science1,2,3,4,5,6. Its realization is expected to bring significant advantages in quantum information technology7, as it enables faster, less energy-consuming, and more space-confined spin manipulation compared to the use of magnetic fields. Since the electric field does not couple directly to spins, spin-electric (SE) effects based on the spin-orbit coupling (SOC) are harnessed to manipulate the spin of quantum dots8, diluted spins in inorganic lattices9, and magnetic molecules10.

A SE effect that acts directly on the exchange interactions is also very appealing because it would allow the local electric control of the interaction between spin qubits, as proposed by Kane for a scalable quantum computer11. Such an effect is poorly investigated; thus, its origin and possible strategies to maximize it remain elusive. Theoretical investigations have concentrated on a simple but captivating platform: triangles of antiferromagnetically coupled half-integer spins12,13,14,15,16,17,18. The result of the isotropic exchange, \({H}_{{ex}}={\sum }_{i=1}^{3} \, {J}_{i,i+1}{s}_{i}\cdot {s}_{i+1}\), is the occurrence of two degenerate spin doublets if the triangle is equilateral. The attention has been concentrated on systems where SOC mediates an antisymmetric exchange interaction, also known as Dzyaloshinkii-Moriya (DM) interaction, \({H}_{{DM}}={\sum }_{i=1}^{3}{G}_{i,i+1}{s}_{i}\times {s}_{i+1}\). This term removes the zero-field degeneracy of the two Kramers doublets and imparts them opposite vector chirality. The resulting energy gap and the anisotropic response to the magnetic field, typical manifestations of DM interactions, are strongly affected by a lowering of the symmetry of the triangle. With the assumption that the isotropic exchange interaction is affected by the electric field, its application in the plane of the triangle lowers the symmetry and modifies the effects of DM interactions. Oscillating electric fields at the appropriate frequency can induce transitions between states of opposite chirality and the same spin projection, but also induce spin transitions for specific orientations of the magnetic field12,19.

Experimental observations of these phenomena have been recently reported for a Fe3 triangle19 and predicted for a Cu3 triangle20. In both cases, the DM interaction is sizeable, with the ratio between the DM interaction and the isotropic coupling being (10–20)%21,22. For such systems, it is difficult to distinguish the possible options for the microscopic origin of the spin-electric effect. It remains to be proven that a SE effect exists and is detectable even in the absence of DM interaction, as in the case of spin qubits, which are generally characterized by a negligible orbital contribution to maximize spin coherence.

As far as the detection of SE effects is concerned, continuous wave (CW) and pulsed electron paramagnetic resonance (EPR) spectroscopies under static electric fields have been used for decades23. Recent experiments with electric field pulses during Hahn-echo sequences confirmed the presence of SE effects in polynuclear 3d metal complexes, such as a Cr7Mn antiferromagnetic ring24 and frustrated Cu324 and Fe325,26,27 triangles. CW EPR under modulation of a moderate electric field (EFM-EPR) is an alternative technique that combines the high sensitivity of phase-sensitive detection with the possibility of investigating both diluted and concentrated samples in the single crystal form28,29,30,31. The technique has been employed by some of us to study SE effects in a manganese(II)-radical molecular helix30, revealing a significant modulation of the spin correlation length along the chain originated by the electric field effect on the isotropic exchange interaction.

In this work we employ an antiferromagnetic (AF) frustrated spin triangle of copper(II) s = 1/2 ions, selecting a molecular geometry that minimizes DM interaction, to demonstrate that a SOC-independent electric field control of the isotropic exchange can be detected at the molecular level. Non-centrosymmetric crystals of the AF copper(II) triangle32 [Cu3(saltag)(py)6]ClO4 (H5saltag = tris(2-hydroxybenzylidene)triaminoguanidine and py = pyridine), hereafter referred to as Cu3, previously investigated under electric field pulses in frozen solutions24, are investigated by EFM-EPR spectroscopy to quantify the SE effect and characterize its anisotropy. Simulations of the EFM-EPR spectra and a comprehensive ab initio analysis of the electric field effects on different terms of the spin Hamiltonian (SH) reveal a modulation of the isotropic exchange interaction when an electric field is applied in the plane of the triangle. No evidence of SOC-related DM interactions is detected, demonstrating that electric field control of magnetic exchange is achievable in this case as well. Interestingly, the major contribution to the SE coupling originates from the atoms of the bridging ligands, opening the perspective of tailoring it through rational chemical design.

Results

Cu3 crystallizes in the P31c non-centrosymmetric polar space group32. Each copper(II) ion is coordinated by four nitrogen and one oxygen donor. It adopts a distorted trigonal bipyramidal (tbp) geometry, with the axis of the tbp lying in the plane of the triangle. The three-fold symmetry axis at the center of the triangle relates the three copper(II) ions. The unit cell contains two crystallographically independent copper triangles (labeled A and B in Fig. 1a) and two mirror symmetry-related molecules (A' and B’) (Fig. 1b). We note that A’ and B (or A and B’) are almost centrosymmetric images of each other (see Supplementary Fig. 1), making their subtle differences32 crucial for detecting the SE effect by EFM-EPR. Nevertheless, A’ and B exhibit different packing along the polar c axis due to co-crystallized solvent molecules and the disordered perchlorate anions (see Supplementary Note 1).

Fig. 1: Structure, g-tensor orientation and experimental setup.
figure 1

a Crystallographically independent molecules (A, green and B, orange) in the asymmetric unit of Cu3 viewed along the crystallographic c axis (hydrogen and carbon atoms of the aromatic rings in the pyridine and Schiff-base ligands are omitted for clarity). The A’/B families are related by pseudo-inversion symmetry with a small tilt angle of 1.2° between the triangular planes. b Unit cell content of Cu3. Triangles A and A’ as well as B and B’ are related by the glide reflection planes (100), (010) and (1-10), resulting in the absence of crystallographic chirality. For all triangles, the g reference frame of the copper ions has been reported (gx = red, gy = blue, gz = violet)32. Color code: Cu: green for triangles A and A’ and orange for triangles B and B’, O: red, N: blue, C: grey, H and pyridine rings are omitted for clarity. Green and orange lines between the copper ions emphasize the triangular structure of the molecules. c Schematic representation of the sample holder for the EFM-EPR measurements and related reference frame. Images of the crystal in three experimental configurations are shown in Supplementary Fig. 2.

Full size image

EFM-EPR spectra

EFM-EPR experiments on a single crystal of Cu3 were performed by replacing the magnetic field modulation (Bm) of CW-EPR with a 30 kHz oscillating electric field (Em = 69 kV m−1). The long-wavelength Em was introduced in the comparatively small X-band cavity by means of a modified version of the standard sample-holder, consisting of a home-made propagating structure without cutoff given by two thin parallel conducting wires separated by ca. 1 mm30 (a scheme of the EFM-EPR sample holder is reported in Fig. 1c and Supplementary Fig. 2). Thanks to the phase-sensitive detection, a derivative signal is revealed in the EFM-EPR spectrum if the electric field affects the resonance field, i.e., if a linear SE effect is active. Consequently, contrary to standard EPR, the absorption resonance line is modulated by Em. Moreover, the first harmonic signal cancels when responses for positive and negative Em equalize, e.g., for random distribution of orientations, along specific symmetry directions, or when the effect is only proportional to an even power of the electric field. It is also worth noting that, although linear electric field effects can be observed in centrosymmetric crystals or frozen solutions using different techniques9,10,24, provided the active site lacks an inversion center, a first-order detection by EFM-EPR requires non-centrosymmetric crystals23,29,30,31.

The EPR and EFM-EPR spectra were acquired at 30 K for different mutual orientations between the crystal axes, the magnetic field B0, and the electric field Em. The experimental configurations in the ab plane are described in terms of the angles φM and φE, indicating the direction of the fields B0 and Em with respect to the a axis, respectively (see Fig. 1c). Experimental details are reported in Methods.

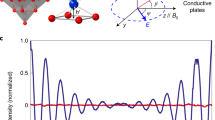
The top panel of Fig. 2a shows the standard EPR spectrum with B0 in the ab plane at φM = 0° (see Fig. 1c), which is centered at 3279 G (linewidth 160 G). The related EFM-EPR spectrum acquired with Em parallel to the a axis (φE = 0°, Fig. 2a) has the same phase and center. Reversing the direction of Em flips the phase (Fig. 2b), and the intensity scales linearly with Em (Supplementary Fig. 3), confirming a linear SE effect. The EPR spectrum is invariant with respect to the direction of B0 in the ab plane (Supplementary Fig. 4). On the contrary, when Em is applied at ±30° from the a or b axes, i.e., perpendicular to a glide plane, the EFM-EPR intensity drops to noise level (see Fig. 2c, Supplementary Fig. 5), matching the signal cancellation expected for A/A’ and B/B’ mirror-related pairs.

Fig. 2: EFM-EPR spectra.
figure 2

EPR spectra (top panels) and corresponding EFM-EPR spectra (bottom panels) acquired on a single crystal of Cu3 at 30 K in different experimental configurations (a schematic representation of the crystal in the sample holder for EFM-EPR viewed from the top and orientation of A’/B triangles are reported at the bottom of the figure. For the conventional EPR spectra the Em is not present, and replaced by Bm || B0): (a) The a crystallographic axis, B0, and Em all are oriented toward the same direction (φM = 0°, φE = 0°); (b) The a axis is parallel to B0 and antiparallel to Em (φM = 0°, φE = 180°); (c) A –150° rotation of the crystal about the c axis and B0 parallel to –Em (φM = 150°, φE = –30°); (d) The c axis, B0, and Em all are oriented toward the same direction. The EFM-EPR spectra intensities are rescaled by the number of acquisitions n (n = 15, 16, 59, and 8, respectively), necessary to achieve a reasonable signal-to-noise ratio. Gray dash lines indicate the  EPR resonance field. In the top panels, red lines represent the simulations with the SH model given in Eq. (1) with parameters reported in Table 1. In the bottom panels, red lines represent the simulations performed using the SH model from Eq. (1) with the δg and δJ from ab initio and DFT calculations (see Table 2). Source data are provided with this paper.

Full size image

Finally, a broader line (320 G) is observed at ~3060 G when B0 aligns with the c axis (Fig. 2d). When Em is also applied along c a stronger EFM-EPR signal is observed than when Em is in the plane of the triangles. The phase changes when Em is reversed (Supplementary Fig. 6a), and the signal exhibits an absorption-like shape, differing from the ab plane response. When Em is along the c axis and B0 perpendicular to it, the signal shifts to high field, but the EFM-EPR line shape remains unchanged (Supplementary Fig. 6b).

Spin Hamiltonian model

To simulate the EPR spectra, the spin Hamiltonian (SH) used for each C3 symmetric triangle of the unit cell includes the Zeeman term and isotropic exchange term:

$$\hat{H}={\sum }_{i=1}^{3}{{{{\rm{\mu }}}}_{{{\rm{B}}}}{{\bf{B}}}}_{{{\boldsymbol{0}}}} \, {\cdot \, g}_{i}\cdot {{{\bf{S}}}}_{{{\bf{i}}}}+{\sum }_{{ij}=1{i}\ne j}^{3} \, J{{{\bf{S}}}}_{{{\bf{i}}}}\cdot {{{\bf{S}}}}_{{{\bf{j}}}}$$
(1)

Ab initio calculations previously performed23 revealed a rhombic g tensor for each copper(II) center, with slight differences between the two crystallographically independent triangles. The rhombicity of g in the spin Hamiltonian framework is related to a residual spin-orbit interaction. The smallest g value (gx) aligns with the Cu–O bond corresponding to the axis of the tbp polyhedron oriented approximately in the ab plane (see Fig. 1), while the largest value (gz) is along the c axis, collinear for all three ions. DFT calculations revealed strong, nearly identical isotropic antiferromagnetic coupling between the copper(II) ions for the two triangles, consistent with magnetic data32. The DM interaction was not considered as magnetic measurements suggested that |Gz/J | < 0.00332. Additionally, the EPR spectra do not show the typical g < 2 when the magnetic field is applied in the plane, which was instead detected in Fe325 and other Cu3 systems with different bridging ligands21,22. This assumption was validated by theoretical calculations of the energy splitting in zero field of the two ground-state Kramers doublets, ca. 0.004 cm−1 (see Computational studies). The vanishing DM interaction results from the negligible overlap of the singly occupied orbital in the ground configuration of a spin site and the SOC-admixed excited state of the neighboring spin site21,33. This confirms that we are exploring a different regime in Cu3 compared to previous studies on AF triangles.

To reproduce the single-crystal EPR spectra (Fig. 2, top panels), we summed the contributions of the four molecules in the unit cell (Fig. 1b). The g values were fitted while keeping the g-principal axes and J values fixed to the computational values. The simulation parameters used are reported in Table 1, and Supplementary Note 2 contains a detailed model description. The unresolved hyperfine coupling with copper nuclear spins was neglected for the x and y components and treated as a magnetic field strain for the z direction (see Table 1). The fitting procedure for the orientational dependence of the EPR spectra is reported in Supplementary Note 3.

Table 1 Spin Hamiltonian parameters
Full size table

Simulation of the spin-electric effect: phenomenological model

The orientational dependence of the EFM-EPR spectra was phenomenologically rationalized by considering the electric field perturbation of the g-tensor and exchange coupling J in the SH described by Eq. (1). The modulated spectra were simulated as the difference between absorption spectra at +Em and –Em using a MATLAB script with EasySpin34 (see Methods). This approximation is valid if the shift of the resonance field is much smaller than the linewidth, as clarified by Mims23.

Considering the SE effect as a perturbation of the g-tensor, we introduced a variation Δgα (α = x, y, z) for each copper(II) center:

$${g}_{\alpha,E}={g}_{\alpha }+(\hat{{{\boldsymbol{\alpha }}}}\cdot {\hat{{{\bf{E}}}}}_{{{\bf{m}}}})\Delta {g}_{\alpha }$$
(2)

where \({\hat{{{\bf{E}}}}}_{{{\rm{m}}}}\) is the unit vector of Em. The scalar product in Eq. (2) marks a simplification, as an electric field directed along the \(\hat{{{\boldsymbol{\alpha }}}}\) principal direction may also influence other components of the g-tensor.

According to theoretical predictions14, the effect of Em on J is proportional to the scalar product between Em and the electric dipole moment \({{{\bf{p}}}}_{{{\bf{ij}}}}\) (ij = 12, 13, 23; as depicted in Fig. 3a), which is associated with spins flipping from parallel to antiparallel configuration (see Computational studies), and can be expressed as follows:

$${J}_{{ij},E}=J+({\hat{{{\bf{E}}}}}_{{{\bf{m}}}}\cdot {\hat{{{\bf{p}}}}}_{{{\rm{ij}}}})\Delta J$$
(3)

where the unit vectors of \({\hat{{{\bf{E}}}}}_{{{\bf{m}}}}\) and \({\hat{{{\bf{p}}}}}_{{{\rm{ij}}}}\) are considered, and ΔJ is the phenomenological parameter accounting for SE coupling.

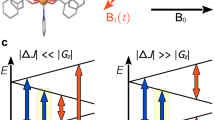
Fig. 3: Schematic representation of the spin-electric effect inside a spin-frustrated triangle.
figure 3

a Effect of an electric field E applied in the plane of the triangle on the exchange coupling constant of each Cu–Cu pair, with the simplifying assumption of the relevant dipole moment being perpendicular to the Cu–Cu direction and pointing towards the center of the triangle, i.e., assuming a D3h symmetry for the system, which does not alter the ground-state characteristics in terms of chirality compared to the real C3 molecular symmetry of Cu3. b Energy levels of the spin triangle showing the two ground-state Kramers doublets15,. If only isotropic exchange is active, the two doublets are degenerate and the eigenvalue of the spin chirality operator is zero. In the absence of DM, the degeneracy can be lifted by applying an in-plane electric field E or by simultaneously applying an additional magnetic field B, as illustrated. c, EFM-EPR spectra for a single triangle (A) with Em and B0 in the plane of the triangle and perpendicular to one Cu–Cu vector, simulated by using the SH parameters reported in Table 1, and different SE mechanisms. The blue line is computed assuming that the electric field induces Δgx/gx = Δgy/gy = 10−6 for each Cu ion according to Eq. (2), while the red line is obtained assuming a variation ΔJ/J = 10−5 for each Cu pair according to Eq. (3). The dashed black line shows the center of the EPR spectrum of the triangle.

Full size image

When Em is applied in the triangle plane, the J couplings increase or decrease, depending on the direction and sign of Em, lifting the degeneracy of the two ground doublets (Fig. 3b). If Em is applied along the three-fold symmetry axis, g tensors can be influenced, but any out-of-plane component of \({\hat{p}}_{{ij}}\) pij affects all three J couplings identically, retaining the degeneracy of the two doublets. Simulated spectra for one triangle with applied Em as shown in Fig. 3a are depicted in Fig. 3c considering either a ∆g or ∆J variation. The computed angular dependence of the complete EFM-EPR signal is reported in Supplementary Fig. 7 and shows the expected 120° symmetry and the phase inversion at 60°.

This scenario remains substantially unaltered when the three-fold symmetry is removed, and two different J are assumed. Notably, the EFM-EPR detection of the variation of J induced by the electric field in the triangle requires an initial rhombicity of the g-tensor (see Supplementary Fig. 8). In extension to previous predictions12, SOC in the case of EFM-EPR is necessary to make the individual spins distinguishable due to the different orientation of the g-tensors and to induce a resonance shift with the electric field E, but it does not play any role in the SE coupling. The phenomenological model qualitatively describes the SE effect for an individual triangle; if all triangles were symmetry-related, a quantitative estimation of a linear SE effect would be possible by comparing the rescaled EFM-EPR and EPR intensities30. However, the EFM-EPR signals of the two families in the unit cell must be considered (Supplementary Figs. 9, 10 and Supplementary Note 4). The result is that for Cu3 crystals, the EFM-EPR signal is much weaker than the contributions of the individual triangles due to cancellation by superposition and is highly sensitive to subtle SH parameter differences between the two sets of pseudo-inversion symmetry-related triangles, preventing direct SE parameter quantification. To resolve this issue and separate the contributions to the SE effect, we performed ab initio computational studies.

Computational studies

An electric field affects a spin system through both electronic and ionic components, originating from electron density deformation and atomic displacement, respectively35,36. Computational studies for the exchange-coupled triangular complex Cu3 allow us to disentangle these contributions and quantify their impact on the g-tensor δg(Em) and coupling constants δJ(Em).

The prerequisite for SE coupling is the presence of electric dipole moments in the spin-frustrated ground state of the Cu3 molecule, which were investigated using the broken-symmetry (BS)-DFT ansatz. After calculating the high-spin (HS) state (| ↑↑↑⟩), a spin-flip procedure was applied to break the wavefunction symmetry. The charge rearrangement in the BS state and the resulting in-plane dipole moment \({{{\bf{p}}}}_{{{\bf{xy}}}}\) (\(|{p}_{{xy}}|=\sqrt{{p}_{x}^{2}+{p}_{y}^{2}}\) = 2.61 × 10−31/2.55 × 10−31 C m for A’/B) are shown in Fig. 4. As each BS state represents only one possible spin configuration, whereas each doublet of the spin-frustrated ground state consists of an equally weighted linear combination of all three configurations (| ↓↑↑⟩, | ↑↓↑⟩, and | ↑↑↓⟩), there is no permanent dipole in the ab plane. However, the application of an external electric field unbalances the energy and weight of the three BS configurations, resulting in the EFM-EPR signal. In a chemical picture, the SE effect originates from the presence of an in-plane C3-symmetric radial charge disparity in the electronic ground state of the spin-frustrated triangular molecule. In contrast, the C3 symmetry allows a permanent dipole moment \({{{\bf{p}}}}_{{{\bf{z}}}}\) along c in the BS state (\(\left|{p}_{z}\right|\) for A’/B: 1.07 × 10−30/1.25 × 10−30 C m), with a similar value for the HS state, which is about five times larger than the in-plane moment \({{{\bf{p}}}}_{{{\bf{xy}}}}\).

Fig. 4: Ab initio calculated charge distribution.
figure 4

Contour plots representing the computed change in charge density within the trinuclear copper plane for the molecular species A’ (left) and B (right) in Cu3 after flipping the spin of Cu1 (\(|\downarrow \uparrow \uparrow \rangle\)), starting from the C3 symmetric ferromagnetic state (\(|\uparrow \uparrow \uparrow \rangle\)). Grey lines represent chelate rings in the molecular structures. The in-plane dipole moment \({{{\bf{p}}}}_{{{\bf{xy}}}}\) is shown as a black arrow. The insets define the angle φ0 between the x-axis and \({{{\bf{p}}}}_{{{\bf{xy}}}}\), where x corresponds to the Cu2-Cu3 direction. The dipole moment \({{{\bf{p}}}}_{{{\bf{xy}}}}^{{{\bf{Cu}}}}\) (cyan vector) of the three copper centers was obtained by a charge separation procedure utilizing natural atomic orbitals (see Supplementary Note 5). The dipole moment \({{{\bf{p}}}}_{{{\bf{xy}}}}^{{{\bf{L}}}}\) (orange vector) corresponding to the ligand system was determined by the difference \({{{\bf{p}}}}_{{{\bf{xy}}}}^{{{\bf{L}}}}={{{\bf{p}}}}_{{{\bf{xy}}}}-{{{\bf{p}}}}_{{{\bf{xy}}}}^{{{\bf{Cu}}}}\).

Full size image

In Fig. 4, it is apparent that after flipping the spin of Cu1 (| ↑↑↑⟩ → | ↓↑↑⟩), the orientation of the dipole moment \({{{\bf{p}}}}_{{{\bf{xy}}}}\) does not fully coincide with the position vector of the flipped spin center, as schematized in Fig. 3. This is related to the lower C3 symmetry and can be rationalized by the electron density of the bridging diazine moiety, which is asymmetric with respect to Cu–Cu vectors (Supplementary Fig. 11). Separation of \({{{\bf{p}}}}_{{{\bf{xy}}}}\) into a metal (\({{{\bf{p}}}}_{{{\bf{xy}}}}^{{{\bf{Cu}}}}\)) and ligand part (\({{{\bf{p}}}}_{{{\bf{xy}}}}^{{{\bf{L}}}}\)), are depicted in Fig. 4 and their calculation is discussed in Supplementary Note 5. As expected, the more pronounced changes in electron density upon spin-flipping are localized on the copper sites. However, having both negative and positive signs, they weakly impact the induced dipole moment. On the contrary, the atoms on the bridging ligands exhibit clear electron depletion on the saltag arms bound to the flipped spin, thus providing the leading contribution to \({{{\bf{p}}}}_{{{\bf{xy}}}}.\) This suggests that ligand modifications influencing the radial charge disparity could eventually allow tuning the SE effect. Indeed, the computed \({{{\bf{p}}}}_{{{\bf{xy}}}}\) are around two orders of magnitude larger than the one computed for a Cu3 polyoxometalate structure14.

The electric field dependence δJij(Em) of the individual magnetic Cu–Cu pair interactions required for the EFM-EPR simulation were computed using electric-field-dependent broken-symmetry (EFD-BS) DFT (Supplementary Note 6). Under experimental conditions (69 kV m−1, the largest |δJ| was calculated to be 6.0 × 10−4 cm−1 (A’) and 5.9 × 10−4 cm−1 (B) (Table 2 and Supplementary Note 6), yielding relative magnitudes of |δJ/J | = 2.14 × 10−6 and 2.15 × 10−6 for the two triangles, respectively. The quadratic Stark effect, depending on the polarizability, was found negligible for the applied experimental field (Supplementary Note 6).

Table 2 Calculated SE coupling parameters
Full size table

While DFT methods are known to provide accurate estimates of magnetic exchange interactions at an affordable computation cost, more demanding ab initio CASSCF/RASSI-SO calculations in the presence of electric fields were necessary to compute the SE effect on the local g-tensor of the individual copper ions, denoted as δg(Em) (Supplementary Note 7). The influence of the electric-field components \({E}_{k}\) (k = {X, Y, Z}), expressed in the orthogonal crystal reference frame (ab’c), on the single-ion g-tensor can be quantified by the SE coupling-tensor components \({T}_{k}=\frac{\partial g}{\partial {E}_{k}}\) within the frame of the local magnetic axes (α = {x, y, z}). Due to the low local symmetry, all \({T}_{k}\) are non-zero, indicating a strong anisotropy (Supplementary Note 7). Notably, \({T}_{k}({{\bf{A}}}^{{{\prime }}}){\approx -T}_{k}({{\bf{B}}})\) are consistent with the pseudo-inversion center. The largest in-plane absolute tensor component is \({{|T}}_{{Xy}}|\) = 1.8 × 10−12 m V−1 (A’) and 1.6 × 10−12 m V−1 (B), leading to a |δg| of approximately 1.2 × 10−7 (A’) and 1.1 × 10−7 (B) under the experimentally applied electric field. The relative effect |δg/g| is ~ 6 × 10−8, significantly smaller than |δJ/J | . \(|{{{\bf{p}}}}_{{{\bf{xy}}}}^{{{\bf{Cu}}}}| < |{{{\bf{p}}}}_{{{\boldsymbol{xy}}}}^{{{\boldsymbol{L}}}}|\).

The permanent pz dipole allows for atomic displacement under an electric field35,36. To investigate the extent of the phenomenon and its effect on SH parameters, DFT geometry optimizations under applied electric fields along the c axis and subsequent ab initio CASSCF/RASSI-SO calculations were performed (Supplementary Note 8). The resulting effect, represented by δgdisp(Em), is shown in Table 2. Clearly, along c the atomic displacement dominates over the effect on the electronic cloud, being one order of magnitude larger (largest |δgdisp| at 69 kV/m: 6.0 × 10−6 (A’), 5.2 × 10−6 (B)). Furthermore, this effect strongly depends on the modeling of the disorder in the perchlorate anions near the trinuclear cationic complexes.

Simulation of the EFM-EPR spectra

The ab initio calculated field-dependent quantities δg(Em), δgdisp(Em), and δJ(Em) were used to simulate the EFM-EPR spectra (Supplementary Note 9).

Concerning the effect on the g-tensor, Eq. (2) was modified (∆gα → δgα(Em)) according to the calculated Tij matrix elements (Supplementary Note 7) as in Eq. (4), which also includes the deformation effect along the z axis, represented by \({{\bf{T}}}^{{\bf{disp}}}\). Note that all three gα values are affected by a general orientation of the electric field.

$${g}_{\alpha }\left({{{\bf{E}}}}_{{{\bf{m}}}}\right)={g}_{\alpha }+\,\delta {g}_{\alpha }\left({{{\bf{E}}}}_{{{\bf{m}}}}\right) \; {{\rm{with}}}\,\delta g\left({{{\bf{E}}}}_{{{\bf{m}}}}\right)=({\bf{T}}+{{{\bf{T}}}^{{\bf{disp}}}})\cdot {{{\bf{E}}}}_{{{\bf{m}}}}$$
(4)

The effect on the exchange constant of each Cu–Cu pair was adapted from Eq. (3) (∆Jij → δJij(Em)) to incorporate EFD-BS-DFT results, leading to Eq. (5).

$${J}_{{ij}}\left({{{\bf{E}}}}_{{{\bf{m}}}}\right)=J+\delta {J}_{{ij}}({{{\bf{E}}}}_{{{\bf{m}}}})$$
(5)

The modulation of exchange constants by the electric field (δJ12, δJ13, and δJ23) for each copper triangle is given in Supplementary Note 6, considering the dipole moment orientations.

Using the ab initio calculated parameters, the intensity of the single-crystal EFM-EPR spectra in the ab plane is correctly simulated, while the shape, as well as the center of the spectrum, are only approximately reproduced (Fig. 2a–c). Despite that, it is evident that for in-plane EFM-EPR spectra the effect induced by δJ(Em) dominates over the one induced by δg(Em) (Supplementary Figs. 12 and 13), as |δJ/J| is about 35 times larger than |δg/g | . Moreover, the comparison of the simulated EFM-EPR signals between individual triangles and the crystal unit cell shows that, in the ab plane, only ca. 25% of the signal of the individual triangles is left due to the partial cancellation resulting from pseudo-inversion symmetry between the two families of molecules (Supplementary Fig. 14).

When electric and magnetic fields are oriented along the polar c axis, atomic displacements by the electric field due to the permanent dipole moment \({{{\bf{p}}}}_{{{\bf{z}}}}\) become dominant. The best agreement with experimental data was found with one perchlorate species per trinuclear complex (Supplementary Note 8). The distinct shape of the EFM-EPR signal compared to that in the ab plane is attributed to the vanishing \(|\delta {g}_{z}^{{disp}}|\), resulting in no shift of the individual signals. Simultaneously, the larger in-plane \(|\delta {g}_{x,y}^{{disp}}|\) values alter transition probabilities and EPR intensity, resulting in the absorption-like EFM-EPR signal, in contrast to the first derivative shape of the weaker purely electronic δg(Em) contribution (Supplementary Fig. 15). Including both δg(Em) and δgdisp(Em) effects, the simulated spectrum reproduces the experimental shape but with lower intensity (Supplementary Fig. 16). This discrepancy could arise from approximations in the theoretical calculation and/or unresolved hyperfine interactions with the copper nuclear spin. Generally, hyperfine interactions in metal ions correlate with g values and are expected to be affected by electric fields37,38 (Supplementary Note 9). A tentative simulation addressing the implications of electric field effects on unresolved copper hyperfine interactions is reported in Supplementary Fig. 16.

Discussion

Frustrated AF spin triangles are a fascinating workbench to explore the electric field control of spin systems. Studies on Cu3 in frozen solution indicated SE coupling via pulsed EPR due to its good spin coherence24. However, single-crystal investigations are superior for detecting anisotropy of interactions, which is fundamental to discriminating its microscopic origin. For Cu3, where a diamagnetic isostructural crystalline host for echo-detected experiments is lacking, CW EFM-EPR spectroscopy is key to accessing SE phenomena.

Detailed analysis of EFM-EPR spectra, supported by ab initio computational studies, allowed rationalizing the large anisotropy of the SE effect, revealing that perpendicular to the triangular plane atomic displacement - driven by a permanent electric dipole moment - dominates the SE effect on the g-tensors, being two orders of magnitude larger than the influence on the electronic cloud. In contrast, when the Em field is applied within the triangular plane, where a permanent electric dipole moment is absent, only the latter effect is permitted. The resulting SOC-independent modulation of the isotropic exchange interaction (ΔJ ~ 10−3 cm−1, or 10−8 cm−1/(Vm−1)) leads to satisfactory simulation of the experimental EFM-EPR spectra and is the leading term in the SE coupling, overcoming the effect on the g-tensors mediated by the residual SOC.

The modulation in J, originating from the in-plane dipole moment of the spin-frustrated ground state, is dominated by ligand contributions, highlighting the major influence of the electric field on the electronic cloud of the ligand. Interestingly, the electric field effect on J appears to be significantly larger than that computed for a polyoxometalate Cu3 system14 but about two orders of magnitude smaller than that observed in a Mn-radical helix30, where the bridging ligand carries an unpaired electron in a largely delocalized molecular orbital. Our findings pave the way for a rational design of bridging ligands, unlocking enhanced control over spin-spin exchange interaction with electric fields. This novel SE mechanism of exchange control, independent of spin-orbit contributions and atomic displacement, could be a key factor in implementing scalable architectures for quantum information based on molecular spin qubits.

Methods

Sample preparation

Single crystals of [Cu3(saltag)(py)6]ClO4 with the shape of hexagonal rods and dimensions of approximately 1 mm × 1 mm × 2 mm were obtained by a modified procedure from bulk material synthesized following the procedure reported by some of us32.

EPR and EFM-EPR measurements

X-band EPR measurements were performed using a 9 GHz Elexys E500 instrument (Bruker) equipped with a microwave frequency counter. An Oxford Instruments ESR900 continuous He flow cryostat was used to achieve low temperatures. An ER4122SHQE EPR resonator (Bruker) was used for the measurements.

The single-crystal EPR study of Cu3 was realized at 20 K (see Supplementary Note 3). The EFM-EPR and the corresponding EPR spectra of Fig. 2 were acquired at 30 K, where optimal temperature stability in the presence of the heat load of the EFM-EPR setup is guaranteed. EPR spectra were acquired with a magnetic field modulation amplitude of 5 G, frequency of 100 kHz and a microwave power of 53 μW. The magnetic field sweeps of 1670 G in the ab plane and 1400 G along c were sampled with 2048 points, a time constant of 40.96 ms, and a conversion time of 20.48 ms, resulting in an acquisition time of 42 s for each spectrum. Details on the fitting procedure of the single-crystal EPR spectra and data evaluation can be found in Supplementary Note 3. EFM-EPR measurements were realized with the same setup as used for the EPR measurements, except for the modified version of the sample holder (see Fig. 1c, already described in ref. 30). A 30 kHz oscillating electric field of the order of 69 kV m−1 was used. The applied voltage was taken from the external modulation output of the EPR console, the signal passed through a home-made electronic circuit for a 180° phase control, and subsequently amplified using a high-voltage amplifier (Trek, model 50/750). Therefore, a voltage of about 76 V was fed into the wires, the distance of which was around 1.1 mm. To avoid discharge, the EPR tube hosting the electrodes and the sample was filled with He gas and sealed. The EFM-EPR spectra were acquired with 1000 times higher microwave power with respect to the EPR spectra. The magnetic field sweep of 1400 G was sampled with 512 points, a time constant of 327.68 ms, and a conversion time of 1310.72 ms, resulting in an acquisition time of 671 s. Moreover, multiple acquisitions were needed to increase the signal-to-noise ratio of EFM-EPR spectra. The number of acquisitions varied in the range 10 − 60, depending on the intensity and shape of the EFM-EPR signal. Given the low intensity of the detected EFM-EPR spectra, the system was left to thermally equilibrate for two hours to warrant the necessary thermal stability before the measurements. The reported signals (Fig. 2, bottom panels) are the sum of all the acquisitions normalized to the number of acquisitions.

Different experimental configurations were realized by inverting the sign of Em, and by rotating the sample holder about its vertical axis to vary the relative orientation between Em and the static magnetic field B0, and by mounting the crystal in different orientations. Moreover, the anisotropy of the SE effect in the crystallographic ab plane was investigated by rotating the crystal about its c axis every 30°.

Computational details

Structures for the computational models A’ and B were taken from the original publication of Cu332. All DFT calculations have been performed with the Turbomole v7.2 package of programs39, utilizing def2-TZVPP basis sets40. To obtain high precision results, a fine DFT grid (grid 7) combined with a high SCF convergence threshold of 10−10 Hartree was used for all DFT calculations. The procedure for separating the dipole moment contributions based on a natural population analysis and corresponding natural atomic orbitals41 is described in Supplementary Note 5. Computational results from the initial publication of Cu332, namely the high-spin (HS) and broken-symmetry (BS) state calculations for A’ and B, respectively, were used as a base for the theoretical studies in this work to obtain the electric-field dependence δJij(Em) in the individual coupling constants (see Supplementary Note 6 for further details). Ab initio calculations (CASSCF/RASSI-SO) were performed with the OpenMolcas v18.09 package of programs42 based on different computational model structures (for more details see Supplementary Note 7). State-averaged CASSCF calculations were performed for the 2D multiplet (5 states) with an active space consisting of 9 electrons in 5 orbitals which represented the 3d9 valence shell of a copper(II) ion. For all ab initio calculations, the ANO-RCC basis sets43,44 (copper and donor atoms: ANO-RCC-VTZP; remaining atoms: ANO-RCC-VDZ) were employed in combination with a scalar-relativistic second-order Douglas-Kroll-Hess Hamiltonian and the Cholesky decomposition of the two-electron integrals with a threshold of 10−8. Subsequently, SO-RASSI calculations were carried out to take spin-orbit coupling into account. Magnetic parameters like single-ion g factors were obtained from the CASSCF/RASSI-SO wavefunction using the SINGLE_ANISO program from OpenMolcas. For A’ and B electric-field-dependent DFT (EFD-DFT) geometry optimizations were performed along the polar crystallographic c axis. These EFD-DFT-optimized structures have been subsequently used in CASSCF/RASSI-SO calculations to study the ionic effect (δgdisp) in Cu3 (see Supplementary Note 8 for further details).

Simulations

The simulations of the EPR and EFM-EPR spectra were realized with EasySpin v6.0.034, a computational package for spectral simulation and analysis in EPR. As a first step, to simulate solid state CW EPR spectra, the SH of the system is supplied to the program, together with the orientations of the tensors with respect to the molecular frame, which is related to the laboratory frame. Each investigated orientation is then specified with respect to the laboratory frame. The magnetic field is also fixed in the laboratory frame, as well as the B1 field of microwave radiation. The program calculates the field-dependent energies of the spin states by finding the eigenvalues of the SH corresponding to the specified orientation, and subsequently the resonance positions and transition probabilities. Finally, from these values the absorption spectrum is reconstructed. Eventually, through appropriate convolution functions, the final spectrum is shown as the desired harmonic.

The EFM-EPR spectra were simulated as the difference between the absorption (A) spectrum corresponding to +Em and that corresponding to −Em. Indeed, the effect of the electric field modulation in combination with phase-sensitive detection in first harmonic is like a magnetic field modulation in that the first derivative of the absorption signal vs. Em is sensed. In this frame, since the variations induced by the applied electric field are small, A(+Em) − A(−Em) is proportional to the first derivative of A with respect to Em23,45, thus justifying the simulation approach followed for the EFM-EPR. Hyperfine coupling was not explicitly included in the simulations unless otherwise stated, and its effect on the broadening of the lines along z was accounted for using a Hstrain parameter. For further details, see Supplementary Notes 3 and 9.