Direct entorhinal control of CA1 temporal coding

Guardamagna, Matteo; Chadney, Oscar; Stella, Federico; Zhang, Qiangwei; Kentros, Clifford; Battaglia, Francesco P.

doi:10.1038/s41467-025-61453-2

Download PDF

Article
Open access
Published: 11 July 2025

Direct entorhinal control of CA1 temporal coding

Nature Communications volume 16, Article number: 6430 (2025) Cite this article

2895 Accesses
2 Citations
15 Altmetric
Metrics details

Subjects

Abstract

Theta sequences of hippocampal activity supports planning and prediction, and in CA1 they are shaped by CA3 and entorhinal (layer III) inputs. We targeted entorhinal inputs with highly specific optogenetic inhibition, leaving the remaining circuit intact. While CA1 spatial coding properties were largely unaffected, the slope and range of theta phase precession were impaired. Surprisingly, theta sequences were strengthened. These results suggest that sequence organization is not a simple consequence of precession and depends on circuit-level dynamics across the trisynaptic circuit, while direct entorhinal inputs may act as a supervisory signal driving learning and representational updates.

Distinct roles of dentate gyrus and medial entorhinal cortex inputs for phase precession and temporal correlations in the hippocampal CA3 area

Article Open access 02 January 2025

Lateralization of CA1 assemblies in the absence of CA3 input

Article Open access 20 October 2021

Entorhinal cortex directs learning-related changes in CA1 representations

Article Open access 02 November 2022

Introduction

Temporal coding at multiple scales, from milliseconds to seconds, is used by the brain to convey information and process parallel computations. Within the hippocampus, “theta sequences” of spikes from cells with consecutive place fields, rapidly sweeping through a theta oscillation cycle (≈100 ms), are a prominent expression of temporal coding^1,2,3. Theta sequences have been linked to memory of events taking place at different times, prediction of future occurrences, and action planning⁴, functions that require the comparison of previously stored traces with the current stream of information about the external world⁵. The hippocampal sub-field CA1 is an interesting candidate for this operation as it sits at the confluence of two excitatory inputs: a tri-synaptic pathway through the CA3 sub-field (from Entorhinal Cortex Layer II, EC LII)⁶ and a direct extra-hippocampal pathway from the Entorhinal Cortex Layer III (EC LIII)⁶, which are thought to carry, respectively, memorized and novel information^7,8. Classic theoretical models view phase precession, the correlation between the animal's position and the firing phase of place cells within the entire theta cycle⁹, as the generating mechanism of theta sequences¹⁰. This does not take into account the influence of dual input to CA1, which may act by itself as a considerable source of variability. It also neglects multiple results indicating (i) a partial dissociation of phase precession and theta sequences during novel spatial experiences¹¹ and development¹², and (ii) how phase precession and sequences tend to appear most strongly under different network states, which in turn have been associated with prevalence of the EC LIII or CA3 inputs, respectively^13,14,15. While dynamical interactions between these inputs have been studied in detail^{7,13,14,15,16}, including via the use of activity perturbations^{17,18,19,20,21}, dissecting their relative role is made difficult by the fact that EC LII also innervates CA3 through the tri-synaptic circuit. Thus, standard, unspecific manipulations of EC end up affecting both input streams^4,17,18,20. Here, we address this issue with a combination of ensemble physiology, layer-resolved oscillation recordings, and highly-specific manipulation of EC LIII projections to CA1.

Results

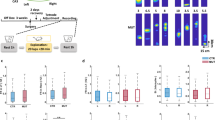
We used the enhancer-driven gene expression (EDGE) approach²² to create a transgenic mouse cross expressing an inhibitory opsin, JAWS²³, specifically in EC LIII pyramidal cells (Fig. 1a–h). We quantified expression levels by counting the number of JAWS-GFP RNA-positive nuclei within all brain areas and we estimated that the majority (78%) were in EC LIII (Fig. 1c). The expression of JAWS-GFP was also largely overlapping with Purkinje cell protein 4 (PCP4)-positive neurons (Figs. 1d–h and S1a–d), which can be used as a marker for EC LIII principal neurons that project to CA1²⁴. Since EC LIII projects directly to the distal dendrites of CA1 pyramidal cells⁶, applying light to a region of CA1 inhibits the local direct input without affecting the circuit as a whole, or arguably even EC LIII cell bodies themselves. We recorded both large CA1 pyramidal cell populations and layer resolved oscillations with the Hybrid Drive, combining 13 independently movable tetrodes, one linear silicon probe and one optic fiber in a single device^15,25 (Fig. 1i). Individual tetrodes were located in dorsal CA1 and the optic fiber was positioned above (≈100 μm) the pyramidal layer and enabled optical manipulation of the direct EC LIII projection in stratum lacunosum moleculare (s.l.m.) (Figs. 1j–m and S1e). All animals (N = 6 animals, n = 11 sessions) were trained in a familiar environment, to run back and forth on a linear track collecting food rewards at both ends. The light of the laser was delivered continuously (max 30 s, 640 nm, 20 mW input power, 16 mW output power—See Methods) every other lap, for both running directions consecutively (Fig. 1n).

**Fig. 1: A transgenic cross for optogenetic manipulation of entorhinal cortex layer III and layer resolved ensemble electrophysiology in CA1.**

We first examined the effect of EC LIII distal input suppression on the firing rate property of CA1 spatially-selective neurons (Fig. 2a). Among pyramidal neurons, we only selected those with significant spatial modulation (see Methods section “Place cell identification”). Place fields were divided into two groups: “locking” (N = 103) and “precessing” (N = 199), to better characterize their multiphase relationship to the theta rhythm (See Methods section “Place cell classification”¹⁵). Peak firing rates remained unchanged (Fig. 2b), but we observed a small decrease in mean firing rate (Fig. 2c) in the precessing sub-population, an effect also observed in cells excluded from the place cell analysis (Fig. S1f). Place field size also decreased during our manipulation only in the precessing sub-population (Fig. 2d). Results remained consistent across multiple velocity intervals (Fig. S2a–c).

**Fig. 2: Spatial coding in CA1 does not rely on entorhinal cortex layer III direct input.**

Importantly, place field representations remained largely stable between the laser ON and OFF conditions: place field centers shifted by a similar amount in within-condition controls (Fig. 2e, f), and no differences were found when comparing place field properties within each condition (Fig. S3). The asymmetry of the place field was also not affected by our manipulation (Fig. 2g). Additionally, control littermates, mice that did not express the inhibitory opsin but received the same light stimulation protocol, exhibited unchanged rate coding and field size properties (Fig. S6a–c). These results point to the fact that the EC LIII direct input is not essential for the consistent expression of a stable place field representation of a familiar environment (Figs. 2g and S4), and only a subset of place fields are affected by its inhibition.

We then asked how the inhibition of EC LIII inputs affects temporal coding processes within the CA1 network. This is likely to be state-dependent, as the intensity of CA3 and EC inputs has been found to fluctuate in time. In fact, the magnitude of slow gamma (SG; 20–45 Hz) and medium gamma (MG; 60–90 Hz) oscillations correlates with the relative instantaneous strength of, respectively, CA3 and EC inputs to CA1^{7,15,16,26,27,28}. We found that CA1 single cell temporal coding is perturbed by inhibition of EC LIII inputs (Fig. 3a-d): during periods of EC LIII inputs inhibition, we observed a shift/suppression of spikes in the earliest phases of the theta cycle (Figs. 3a, b and S5), which led to a decrease in slope and phase range of the precession (Fig. 3c, d). It has been previously shown^13,15 that theta phase precession is more strongly observed during elevated MG periods. Here we show that EC LIII inputs inhibition strongly reduces phase precession even during periods of spontaneously elevated MG network-states (Fig. 3c, d). Spike densities of phase locking fields in the position-by-theta phase plane remain unaffected by our manipulation (Fig. 3c). On a cell-by-cell basis, EC LIII inhibition removes any dependence of the phase-position slope on theta index¹⁵ (Fig. 3d), reducing the variability in the phase plane between precessing and locking cells. Importantly, the effects were independent of the running speed of the animals (Fig. S5b). Together, these observations show how the EC LIII afferents are crucial for the typical expression of theta phase precession in CA1, i.e., in the full phase range. Conversely, our manipulation did not cause any alteration in temporal coding properties of place fields in control littermates (Fig. S6d, e).

**Fig. 3: Entorhinal cortex layer III input inhibition weakens theta phase precession but enhances theta sequences.**

Since its discovery, phase precession and the resulting temporal distribution of place field spikes have been proposed as the “engine” underlying the formation of theta sequences¹⁰. This would predict that EC LIII inputs inhibition, which weakens phase precession, should also reduce the expression of theta sequences. We first tested this prediction by quantifying the correlation between field spacing and average theta phase separation of place cell pairs, an index of how consistently neurons fire in a stable sequence¹. In contrast to the prediction above, the spatio-temporal correlations actually improved during periods of EC LIII inhibition (Fig. 3e), regardless of whether SG or MG dominated the local field potential. Elevated SG-network states retained the highest spatio-temporal ordering in both conditions. Importantly, the effects were consistent across velocity intervals (Fig. S5c).

We confirmed and expanded these results by applying a Bayesian decoder (Fig. 3f, g), looking at the coding of current animal position and sequence expression across CA1 populations. These two measures can be considered to be complementary to each other: as sequential coding spans a relatively broad range of spatial location during each theta cycle, it can be expected to conflict with a precise encoding of the animal’s instantaneous location over the entire period of a theta oscillation. Consistent with the pairwise result, we found an improvement in sequential coding during periods of inhibition of EC LIII input (Fig. 3g, right panel). In parallel, the accuracy of decoded position decreased, especially during MG network states (Fig. 3g, left panel).

Additionally, we explored the effect of the manipulation as a function of theta phase (1st half vs. 2nd half of the theta cycle²⁹). At the single cell level, inhibition of EC LIII input selectively inhibits the high slope region of the precession curve in the first half of the theta cycle, during MG states (Figs. 4a and S7a). At the population level, sequential decoding improved in the second half of the theta cycle (Fig. 4b) while positional decoding decreased in the first half of the theta cycle during our manipulation (Fig. S7b, top panel). This apparently surprising result is, in fact, consistent with the partial dissociation between the expression of precession and sequences previously reported in interventional studies^19,21,30. We have previously shown that precessing and locking populations form two groups of neurons that express theta sequences in a largely independent fashion¹⁵. Here, overall correlations increased during EC LIII inhibition, with cells from both groups expressing the highest ordering during SG states (Fig. S7c). The phase precessing population improved their spatio-temporal correlations with the phase locking one during MG states (Fig. S7c, right panel), while phase locking cells improved their correlations both with the other group and among themselves (i.e., with phase precessing population; Fig. S7c, left panel). Notably, when EC LIII inhibition is applied, within- and across-group correlations became largely indistinguishable (Fig. S7c, d). Thus, by releasing a subset of place fields from the influence of the EC LIII input, sequences are expressed more coherently across the network, eliminating the differentiation between groups observed under normal input conditions. Additionally, animals had the tendency to run at slightly higher velocities during optogenetic manipulation (Fig. S8a, b). Because this could affect the results on the temporal organization of theta sequences, we excluded sessions with higher average running speed (Fig. 2e, g) and found no difference in the results, with periods of EC LIII inhibition retaining the highest degree of temporal order (Fig. S8d).

**Fig. 4: Phase-related features of spatial coding in CA1.**

Finally, we explored the effects of the manipulation on global oscillatory rhythms. We did not find any major change in the power profiles of theta (6–10 Hz) and MG (60–90 Hz) oscillations across CA1 layers (Fig. S9). Similarly, theta-gamma phase-frequency coupling was largely left intact by our manipulation (Fig. S10). These results suggest that our spatially restricted manipulation did not impair the global coordinated synaptic activity in CA1, beyond the pool of neurons from which we recorded action potentials.

Discussion

Theta sequences are a fundamental organizing principle of hippocampal activity³¹, which has been suggested to support planning and predictive coding³². Indeed, disrupting hippocampal sequences leads to impairment in planning behavior⁴. The mechanisms of sequence generation are still unclear, but phase precession has been considered as the ’engine’ of sequence generation and a unitary organizing principle for hippocampal neural activity, even generating a temporal phase code for animal position^10,33 more precise than the information contained in the firing rate. A number of potential network mechanisms have been proposed (for a review³⁴), each with implications for hippocampal computations. Based on this ingrained theoretical stance, phase precession is considered a proxy for memory encoding in studies across species, including humans^35,36.

While phase precession relies on intrinsic neuronal properties³⁷, here we also show that CA1 phase precession is selectively influenced by the temporal distribution of incoming inputs, from CA3 and EC LIII (Fig. 4c^16,38). More precisely, EC LIII exerts tight control over the CA1 spiking activity in the earliest phases of the ongoing theta cycle and in the second part of the place field (Fig. S4b,^15,39). Phase precession is best observed when spikes in both earlier and later theta phase, for which presumably the CA3 input is sufficient, are present. In fact, the remnant negative slope in the phase-position plane during EC LIII inhibition (Fig. 4d) is likely due to the presence of sequential assemblies in the later phase of the theta cycle⁴⁰, where the influence of CA3 on CA1 is strongest. Thus, our data suggests that rather than a unitary generating mechanism for sequences, CA1 theta phase precession may be better understood studying the temporal distribution of incoming inputs (in this case CA3 and EC LIII^{13,16,19,30,38}) (Fig. 4d), with less immediate computational implications⁴¹.

Correlational evidence already casts doubts on a tight link between phase precession and sequential coding^11,12, but here we present the even more striking finding that EC LIII inhibition improves the organization of theta sequences. The most parsimonious interpretation of this result is that sequence generation is not a simple consequence of phase precession in individual cells^11,12,21,30, but requires other global coordination mechanisms within the hippocampus proper^11,19, or across the tri-synaptic pathway (originating from EC LII)⁴². For example, CA3 is endowed with the optimal recurrent connectivity to hold a reservoir of short-time spatial sequences, or internally-generated preexisting neuronal dynamics^40,43, which may be passed on to CA1. Indeed, spikes in the first part of the place field, more robustly supported by CA3 input, appear to have a predictive coding character^13,32,44. These spiking sequences may represent the basic units of many computations. In contrast, the EC LIII input seems to be extraneous to such precise temporal organization, so that its presence disrupts sequence decoding. A hypothesis compatible with our data is that EC LIII, carrying external information, drives plasticity in CA1, which may be used for prediction validation⁴⁵ and online retrospective updates^3,29. This plasticity, however, cannot depend on precise spike timing, but it may rely on mechanisms at a longer time scale, as it has been proposed, bridging the ≈100 ms gap between theta phases⁴⁶. What is then, one may ask, the role of spreading CA3 and EC inputs at different phases of the theta cycle? It is possible that it is just the by-product of the feedback dynamics among the structures that produce theta oscillations (in the hippocampus and elsewhere)^5,47. On the other hand, we may speculate that such an arrangement in the temporal segregation of inputs may provide a time window (the later theta phase), in each theta cycle, where sequences can be expressed “undisturbed”, favoring their readout in downstream structures. As it has been hypothesized, the theta cycle may be separated into a phase for “encoding” and a phase for “retrieval”, prediction, and other computations^32,44. Our data suggest a clear role for direct EC LIII inputs in the encoding phase²¹, suggesting a specific network architecture²⁸.

Methods

Subjects

Ten male mice were used in this study. Nine mice were implanted with a Hybrid Drive²⁵ and one with a 4-tetrode drive for representative examples of CA1 pyramidal unit inhibition with repeated stimulations (Figs. 1m and S1e). All animals received the implant between 16 and 31 weeks of age. After surgical implantation, mice were individually housed on a 12-h light-dark cycle and tested during the dark period. Water and food were available ad libitum. All experiments were performed in accordance with the Norwegian Animal Welfare Act and the European Convention for the Protection of Vertebrate Animals used for Experimental and Other Scientific Purposes. Protocols were approved by the Norwegian Food and Safety Authority (FOTS ID 17898).

Transgenic mouse lines

We crossed two transgenic mouse lines in this study. The ECLIII-tTA driver line expressing the tetracycline transactivator (tTA) within a subpopulation of cells confined to the Entorhinal Cortex Layer III (EC LIII) was made using the Enhancer Driven Gene Expression method with enhancer LEC13-8A, mapped to the Dok5 gene²². This ECLIII-tTA driver line was crossed to a tTA-dependent JAWS-tetO line generated as follows: transgene JAWS-GFP-ER2 (Addgene plasmid #65016) was cloned with restriction enzymes BamHI and NotI into an injection plasmid containing TRE tight 2 promoter (Clontech, now Takara Bio International). The injection plasmid was linearized by enzyme digestion to keep the relevant elements but remove the bacterial elements of the plasmids. Linearized DNA was run on a 1% agarose gel and isolated using a Zymoclean Gel DNA Recovery Kit (Zymo Research, D4001). The resulting final injection construct thus consisted of a TREtight2 promoter followed by JAWS-GFP-ER2 sequences, WPRE element, and SV40 polyA (TRE-Tight-2-tetO-JAWS-GFP-ER-WPRE-SV40). Fertilized oocytes from strain B6D2F1 × B6D2F1 were injected with the purified DNA. Both injection constructs were generated by the Kentros group at the Kavli Institute for Systems Neuroscience and sent for pronuclear injections at the Transgenic Mouse Facility at the University of Oregon, Eugene, OR, USA.

Implant device and surgical procedures

The fabrication of the Hybrid Drive was done as previously described²⁵. This version of the Hybrid Drive is equipped with a linear silicon probe (16 channels, Atlas Neuro, Belgium), 13 tetrodes, and an optic fiber was incorporated in the design to carry out in vivo optogenetic manipulations. The optic fiber was placed at the center of the array and glued in place at a depth of 1 mm from brain surface, sitting above the pyramidal layer ≈100 μm, to maximize the light coverage in the s.l.m. with minimal disruption of the cell layer. Mice were anaesthetized with isoflurane (5% induction and 1–2% maintenance). Prior to implantation, mice were given a subcutaneous injection of analgesics (Metacam, 5 mg/kg and Temgesic, 0.1 mg/kg), plus a local anesthesia (Marcain, 1 mg/kg). Anaesthetized mice were secured in a stereotaxic frame. The skull was exposed, cleaned, and dried. Three stainless steel M0.8 screws were used to secure the drive (1 ground screw in the frontal plate, 1 screw in the parietal plate opposite to the drive, 1 screw in the occipital plate). Using a 0.9 mm Burr drill, a craniotomy was made over the right cortex (top-left corner at AP: −1.20 mm; ML: 0.6 mm relative to bregma; bottom-right corner at AP: −2.30 mm; ML: 2.10 mm relative to bregma). The dura was removed, and the array of the drive was slowly lowered into the brain with the silicon probe shaft and the optic fiber already adjusted at the final depth. To prevent cement from entering the guide tube array and the exposed brain, the craniotomy was filled with sterile Vaseline before lowering the array. The drive was cemented onto the skull using dental adhesive (Superbond C&B, Sun Medical, Japan), and tetrodes were individually lowered into the brain (5 turns - ≈900 μm). Mice were left to recover from surgery for at least seven days before experiments began.

Neural and behavioral data collection

Animals were transported to the recording room from post-surgery day 3, and electrophysiological signals were studied during a rest session in the home cage. Each day, tetrodes were lowered individually in 45/60 μm steps (1/2 of a screw turn), until clear physiological markers for the CA1 pyramidal layer were discernible (sharp wave ripple complexes during sleep or theta during locomotion). The target location was usually reached in 10 days. Electrophysiological signals from the silicon probe contacts helped to refine the final position of the tetrodes.

Electrophysiological data were recorded with an Open Ephys acquisition board⁴⁸. Signals were referenced to ground, filtered between 1 and 7500 Hz, multiplexed, and digitized at 30 kHz on the headstages (RHD2132, Intan Technologies, USA). Digital signals were transmitted over two custom 12-wire cables (CZ 1187, Cooner Wire, USA) that were counter-balanced with a pulley-system. Waveform extraction and automatic clustering were performed using Dataman (https://github.com/wonkoderverstaendige/dataman). Clustered units were manually curated using the MClust toolbox. During all experiments, video data were recorded using a video camera (The Imaging Source, DMK 37BUX273) mounted above the linear track.

Behavioral paradigm

Each behavioral session was preceded and followed by a 60-minute rest session in the animal’s home cage (“Pre sleep” and “Post-sleep”) to ensure units’ stability. Mice were placed at one end of a 1-m long track and trained to run to the other end, collecting a food reward (a piece of Weetos chocolate cereal). Following the animal’s consumption of the reward, a new one was placed at the opposite end. A lap was defined as an end-to-end run in which the animal’s body started at the first 10 cm of the track and finished at the other end without returning to its starting place. When the animals consistently carried out the task with a high number of laps, after ~10 days of consecutive training, the session with the optogenetic manipulation was carried out. Recordings typically lasted between 20 and 30 min. Animals were familiar with the recording room and the proximal and distal cues around the linear track. Mice were not food nor water-deprived.

Optogenetics

For optical silencing of EC LIII projections to s.l.m. of the hippocampal CA1 subregion, an optic fiber (core diameter: 100 μm, numerical aperture: 0.37, Doric Lenses) with a cone termination was incorporated in the Hybrid Drive and unilaterally implanted in the right hemisphere at a depth of 1 mm (N = 6). Optogenetic stimulation was performed by the delivery of continuous red light (640 nm, 20 mW input power, 16 mW output power) by a diode laser (Coherent Obis LX 1185054) for maximum 30 s. Laser power was carefully curated to obtain sufficient irradiance in s.l.m. while avoiding excessive, detrimental effects. The onset and offset of light delivery were triggered as the animal finished eating the reward from one end and upon arrival at the other end of the linear track, respectively. Each lap with light stimulation was followed by a non-stimulated lap, providing an internal control for the effect of light stimulation. Optogenetic silencing sessions were performed once the mice had proficiently performed on the linear track. The control group (N = 3) consisted of littermates that did not express the inhibitory opsin JAWS but received the same light stimulation and behavioral protocol. One control animal was excluded from the gamma network-state analysis due to damage to the silicon probe and the impossibility to recover layer-specific gamma-derived network states.

Histology

Following the end of experiments, tetrodes were left untouched. Animals were euthanized using an overdose of pentobarbital and perfused transcardially with RNase-free 4 % paraformaldehyde in PBS. The brains were extracted and stored in RNase-free 4 % paraformaldehyde for 24 h before being transferred into RNase-free 30 % sucrose for 2 days. For each animal (N = 6), the left hemisphere was used to monitor transgene labeling and the right hemisphere was used to verify the location of tetrodes, silicon probe, and optic fiber. Both hemispheres were sectioned sagitally in 30 μm thick slices using a Cryostat (Fisher Scientific, Cryostar NX70). Sections were divided into 6 series and stored in a −80 °C freezer. For the identification of recording sites and the position of the optic fiber, the tissue was stained with Cresyl violet. The slides were coverslipped, and brightfield images were taken using a scanner (Zeiss Axio Scan Z1, Germany) at a magnitude of 5×. Tracts were assigned to the Allen Mouse Brain Atlas and visualized in 3D using MeshView (https://www.nesys.uio.no/MeshView/). To validate transgene expression, the tissue was stained using both fluorescent in situ hybridization and immunohistochemistry. The sections were hybridized overnight at 62 °C with a FITC-riboprobe for GFP (2.5:1200; Roche, Cat. 11685619910). Next, the sections were washed with a tris-buffered saline with tween (TBST) solution and incubated in a blocking solution (600 μl MABT, 200 μl sheep serum, 200 μl 10% blocking reagent; Roche, Cat. 285 No. 11096176001) at room temperature for 4 h. The blocking solution was replaced with anti-FITC-POD (1:1000), and the sections were left to incubate overnight at room temperature. The following day, the tissue was washed with a TBST solution before the fluorescein signal was developed using Tyr-FL (1:50, PerKinElmer kit) for 45 min at room temperature, then washed in a TBST solution. The sections were then stained for PCP4 and NeuN with antibodies. The tissue was washed with 1X phosphate-buffered saline (PBS) (2 × 10 min), placed in a permeabilisation buffer (1X PBS + 0.3% Triton-X100, 10 min) and preincubated in a blocking buffer (1x PBS + 0.3% Triton X-100 + 3% bovine serum, BSA, 1 h). The sections were then incubated at room temperature for 48 h with primary antibodies: Rabbit anti-PCP4 (1:300, Sigma, HPA005792) and Guinea Pig anti-NeuN (1:1000, Millipore, ABN90P) diluted in a solution of 1x PBS + 0.3% Triton X-100 + 3% BSA. Following primary antibody processing, sections were washed with 1X PBS + 0.3% Triton X-100 + 3% BSA (3 × 10 min), then incubated at room temperature overnight with secondary antibodies: Goat anti-Rabbit Alexa Fluor 546 (1:400, Life technologies, A11010) and Goat anti-Guinea pig Alexa Fluor 647 (1:400, Life technologies, A21450) diluted in a solution of 1X PBS + 0.1 % Triton + 1 % BSA. The slides were coverslipped and images were taken using a scanner (Zeiss Axio Scan.Z1, Germany) at a magnitude of 5x.

Automated cell counting

Cell counting was performed on one series of brain slices per animal. The EBRAINS semi-automated workflow QUINT (refs. ^49,50,51; https://ebrains.eu/service/quint/) was used for brain-wide cell quantification. The brain slices were registered to the Allen Mouse Brain Atlas (http://www.brain-map.org/) using the QuickNII software. Anatomical boundaries from the atlas were fine-tuned to fit the data using non-linear adjustments in VisuAlign (https://www.nitrc.org/projects/visualign/). Cells were extracted by using machine-learning image segmentation toolkit ilastik (interactive machine learning for (bio)image analysis, https://www.ilastik.org/, (ref. ⁵²). Finally, Nutil Quantifier was used to quantify and assign anatomical locations to labeled cells obtained by segmentation of brain images.

Place cell identification

We first selected putative excitatory pyramidal cells using their auto-correlograms, firing rates, and waveform information. Specifically, pyramidal cells were classified as such if they had an average firing rate (across the whole recording session) < 8 Hz and the average first moment of the autocorrelogram (i.e., the mean value) occurring before 8 ms. Only cells classified as pyramidal cells were used for further place cell analysis. One-dimensional ratemaps were obtained by binning the linear track using 1 cm bins and by applying a Gaussian filter with a 3 cm standard deviation. Place cells were defined applying a combination of different criteria: all analysis were performed on speed-filtered activity, after removing periods in which the animal's speed was smaller than 3 cm/s. Only cells with an average activity above 0.3 Hz were taken into account. Then, for each of these cells, the Skaggs information per second

$$I={\sum}_{x}\xi (x)log\frac{\xi (x)}{ < \xi { > \ }_{x}}$$

(1)

was compared to the distribution of information values resulting from randomly shuffling cell spike times. A cell passed the selection if its Skaggs information was significantly higher than the ones of the surrogate distribution. Lastly, only place cells with peak firing rates higher than 1 Hz were kept for further analysis. Only the main place field, where the peak firing rate occurs, was considered for further analyses.

Place cell classification

Spikes were filtered both in speed (>3 cm/s) and in position, by taking only those emitted within the boundaries of the cell place field. For each place field, a “Theta Score”¹⁵ was calculated as follows: Theta Score = Precession Score − Locking Score. For the Precession Score, we used a circular-linear correlation to measure the degree of dependency between the spike phase and the position within the field. For the Locking Score, we computed the length of the Reyleigh vector associated to the distribution of spike phases with respect to the instantaneous theta phase. Each measure produced a score between 0 and 1, with 1 denoting a perfect phase-position relation or perfect phase locking. Negative Theta Score values indicate that spike probabilities are mostly modulated by specific phases of theta (“phase locking”), while positive Theta Scores suggest a stronger phase precession pattern (“phase precessing”); but most of the population could be described as a mixture of the two modalities¹⁵. Place fields with Theta score < 0 were included in the phase locking group, and place field with Theta score > 0 in the phase precessing group.

Place cell properties

All place cell properties were calculated using a Generalized Linear Model (for more details, see: Generalized-Linear Model (GLM) section). We inferred the activation probability of each cell in the linear environment given (i) the position on the track; (ii) the instantaneous theta phase, and (iii) the instantaneous power in a specific gamma range and layer. In all our analysis, we considered a partition of the environment in bins of 2.5 cm. Having obtained spiking probability maps from the GLM, place fields were defined as continuous regions in the rate map with rate higher than 20 % of the cell's maximum activity. Spatial mean firing rate was calculated integrating these probabilities over theta phase, gamma power, and spatial bins. Spatial firing rate of each cell was calculated within each condition and separately for laser OFF and laser ON. As place field center, we took the bin within the place field with highest firing rate. The effect of speed on the firing probabilities was addressed in a similar manner by including the instantaneous velocity of the animal as a further covariate in the GLM. Rate coding analysis was restricted to the place field without substantial change in peak firing rate between conditions (<15 cm, based on average peak firing rate shift).

Neural data analysis on oscillations

Before applying other analysis, continuous (LFP) signals were down-sampled to 1 kHz. Power spectral density (PSD) estimates were calculated across the frequency range 0–100 Hz using the pwelch function in MATLAB, for each condition (laser OFF vs. laser ON) separately. Peri-stimulation periods (±300 ms) were excluded from the analysis. LFP across the probe’s 16 contacts was also used to compute the corresponding Current Source Density (CSD) signal. This transformation is based on computing the discrete Laplacian along the probe axis (that is, along the direction running through CA1 layers). The resulting CSD signal is limited to 14 channels (16 minus the 2 extremes). CSD signals were used to compute the layer-specific power profiles and the phase-amplitude coupling strength between a reference theta oscillation and faster oscillations, in a [25–150] Hz range. We first applied a wavelet transform to obtain the analytical signal over time, and then we tracked the evolution of the phase-amplitude couplings across different layers and frequencies, as previously described¹⁵. For each of the identified main gamma frequency ranges (slow [20–45] Hz and medium [60–90] Hz), we extracted layer-specific coupling strength and phase range of frequencies. The theta oscillation reference was generally taken from the s.l.m., where theta modulation of the LFP is strongest. Additionally, the CSD signal was used to estimate the layer-resolved gamma coefficient as follows: the instantaneous balance between the power in the slow gamma (P_Slow(t)) and medium gamma (P_Med(t)) frequency range. Both the slow gamma power and medium gamma power during running periods were separately z-scored, and a power-ratio score, spanning the [−1, 1] interval, was computed as:

$$\gamma=\frac{{P}_{Slow}^{z}(t)-{P}_{Med}^{z}(t)}{{P}_{Slow}^{z}(t)-{P}_{Med}^{z}(t)}$$

(2)

so that a value of −1 would correspond to total medium gamma domination and +1 to total slow gamma domination.

Generalized-Linear Model (GLM)

The GLM analysis was carried out (separately for periods with and without laser manipulation) as previously described in ref. ¹⁵. We employed a maximum entropy model inference approach to estimate the firing probability distribution for each neuron. The statistical framework utilized was the maximum entropy model known as kinetic Ising model. To distinguish active movement from rest, we applied a speed threshold of 5 cm/s to isolate running periods. Neuronal activity was segmented into 10 ms intervals, with a binary variable S_i(t) assigned to each neuron per time bin. This variable S_i(t) took values of +1 or −1, reflecting whether neuron i produced a spike in time bin t. Since the length of time bins was relatively short, this was a reasonable approximation, as the case of multiple spikes per bin was uncommon. The state of each neuron at time t was modeled as dependent on the population’s state at the prior time step t − 1, yielding a maximum entropy distribution for neuron i at time t as follows:

$$P({S}_{i}(t))=\frac{exp[{S}_{i}(t)H(t-1)]}{2cosh[H(t-1)]}$$

(3)

Here, H(t) serves as a time-varying covariate akin to an external field in statistical mechanics. Equation 1 outlines a Generalized Linear Model (GLM), where each bin typically contains zero or one spike, and the interaction kernel spans one prior time step. To determine the most probable values of H(t) given the observed data and Equation 3, we optimized the log-likelihood function:

$${{{\mathcal{L}}}}[S,H]={\sum}_{i,t}{S}_{i}(t){H}_{i}(t-1)-log[2cosh[{H}_{i}(t-1)]]$$

(4)

with respect to H(t). This log-likelihood quantifies how effectively the model captures the observed data’s statistical properties, using the natural logarithm in our calculations. As H(t) accounts for firing rate fluctuations tied to the mouse’s spatial navigation, its accurate modeling is essential. We posited that spatial input emerges from a sum of one-dimensional Gaussian basis functions, centered at evenly spaced intervals L along the linear track. Distinct running directions were treated as separate contexts and analyzed independently. Thus, the spatial field for neuron i at time t is expressed as:

$${H}_{i}^{Spat}(t)={\sum}_{k}{\alpha }_{ik}exp\left[-{(x-{x}_{k})}^{2}/{l}^{2}\right]+{h}_{i}$$

(5)

where h_i denotes a neuron-specific, constant baseline, and x_k and l represent the interval centers and Gaussian widths, respectively. We extended this spatial model by integrating contributions from theta oscillation phases and a slow-to-medium gamma power ratio. This involved constructing a three-dimensional space from: (i) track position, (ii) theta phase (within [0, 2π]), and (iii) the relative strength of the instantaneous power in the slow and medium gamma range, computed as a normalized difference: $\gamma=\frac{{P}_{Slow}^{z}(t)-{P}_{Med}^{z}(t)}{{P}_{Slow}^{z}(t)-{P}_{Med}^{z}(t)}$ (ranging from [−1, 1]), where the z apex indicates previous z-scoring of both power time-series. This 3D space was tiled with a regular square lattice of L × T × G three-dimensional Gaussians, with 0 off-diagonal terms and variance l, t, and g in the three directions. The external field of cell i can thus be expressed as:

$${H}_{i}(t)={\sum}_{kqp}{\alpha }_{ikqp}exp\left[-{(x-{x}_{k})}^{2}/{l}^{2}-{(\phi -{\phi }_{q})}^{2}/{t}^{2}-{(\gamma -{\gamma }_{p})}^{2}/{g}^{2}\right]+{h}_{i}$$

(6)

incorporating dependencies on theta phase ϕ and gamma balance γ. To accurately depict neuronal activity in this space-phase framework, we inferred the coefficients α_ikqp of the Gaussian basis functions. We first optimized the values of L and T (the number of Gaussian basis functions in the lattice) and l, t (their widths), while keeping G and g fixed (G = 6 and g = 0.4). We maximized the likelihood over a range of values of L (from 15 to 25), T (from 4 to 10), l (from 5 to 30 cm), and t (from 0 to π/2) and chose the values of the parameters that gave the highest Akaike-adjusted likelihood value. The Akaike information criterion (AIC) is a measure to compensate for overfitting by models with more parameters, where the preferred model is that with the minimum AIC value, defined as:

$$AIC=2ln({{{\mathcal{L}}}}[S,H,{(L,T,l,t)}_{ML}])+2n$$

(7)

where ${{{\mathcal{L}}}}$ is the likelihood at maximum likelihood estimates of α’s and h_i, and n is the parameter count (unaffected by scale factors r and p, but increasing with L and T). This optimization spanned all sessions, yielding optimal values (L = 20, T = 6, l = 8 cm, t = π/3) applied universally. Firing rate maps for any position, phase, and gamma combination are then:

$${H}_{i}(t)={\sum}_{kqp}{\alpha }_{ikqp}exp\left[-{(x-{x}_{k})}^{2}/{l}^{2}-{(\phi -{\phi }_{q})}^{2}/{t}^{2}+-{(\gamma -{\gamma }_{q})}^{2}/{g}^{2}\right]+{h}_{i}$$

(8)

with x, ϕ, and γ as specified values. The environment was divided into 2.5 cm bins for analysis. Speed effects on firing probabilities were similarly modeled by adding instantaneous velocity as a covariate in the Gaussian decomposition, extending the GLM to a 4D space (position × phase × gamma × speed) with weights α_ikqpz. Speed-dimension parameters were set at V = 4 Gaussians with a 6 cm/s standard deviation, without further optimization.

Phase precession analysis

Single-cell phase precession slope was computed as following: for each cell, we collected spikes by filtering by running speed and by the relative strength of slow and medium gamma oscillations. In particular, we took 6 quantiles of increasing slow-to-medium gamma power. Using the selected spikes, we then computed a phase-position spiking probability density. As position, we used the relative position within the main place field of each cell. We then fitted a linear slope by minimizing the dispersion of the probability density around the fit. Given a linear fit of the form Y(x) = ax + b, where a and b are the slope and intercept of the fit, respectively and x and Y are the relative position within the place field and the theta phase, respectively, the dispersion was computed as: L(a, b) = ∑_{x∈[0, 1]}∑_{dy∈[−π, +π]}P_spikes(x, y)∗ΔY² where ΔY represents the difference between a theta phase and the phase Y of the linear fit: ΔY = y − Y(x). By cycling through values of a and b we then looked for the best combination (a*, b*) minimizing the cost function L(a, b). We then took a* as an estimate of the phase precession slope of the cell for a particular slow-to-medium gamma power ratio. We constrained the values of possible parameters using a ∈ [−10, 10].

Pairwise spike timing correlations

We performed pairwise correlation analysis as previously described in ref. ¹⁵. Firstly, the analysis was done separately for periods with and without laser manipulation. For each cell, only the first spike in each theta cycle and only spikes emitted within the main place field (where the peak firing rate occurs) were considered. For each of these spikes, the simultaneous slow/medium gamma power ratio was calculated and then used as a label to further subdivide the spikes. Then, all the cell pairs in the population of simultaneously recorded place cells were considered. Each pair (A, B) was defined by (i) the spatial distance between the place fields of cell A and B, computed as the distance between the centers of mass (using the distance between the fields peaks did not change the results) and (ii) the average phase interval between the spikes selected for the two cells. The latter was computed by taking spikes of cell A as reference and within each theta cycle (for which a spike from both cells was available) taking the dθ_A−>B(k) (where k stands for the kth theta cycle), that is, the signed difference between the phase of the spike of cell A and that of cell B spike. The center of mass of the dθ_A−>B distribution was then computed and used as a measure of the average phase offset between that cell pair. The spatial distance and phase distance were then organized in a two-dimensional space, and the average phase offset was calculated for a range of spatial distances, provided that there were at least ten pairs of cells available in that range. The analysis was repeated using cell pairs from different subgroups, and selecting spikes released under a particular gamma balance.

Bayesian decoding

Bayesian decoding analysis was carried out as previously described in ref. ¹⁵. First, we separated periods with and without laser manipulation and analysed them independently from each other. We selected periods of active locomotion and segmented time using the peaks of theta oscillation (extracted from the s.l.m.). A sliding window of 30 ms length, with an offset of 10 ms, was used to further divide each theta period. For each of these sub-windows, we built a population vector $\overrightarrow{\eta }(t)$, where t indicates the time within the theta cycle. Using Bayes’ formula, we computed $P(x| \overrightarrow{\eta }(t))$: the likelihood of position on the track x given the population activity. The set of probabilities $\left.P(\overrightarrow{\eta }(t))| x\right)$ was obtained from marginalizing the result of the GLM over the phase of spiking. The resulting probability density P(x, t) was normalized so that ∑_xP(x, t) = 1 for each time window t that contained 3 spikes or more. Time windows with 3 or less spikes were excluded from further analysis. Similarly, theta cycles with less than n ’active’ time windows were removed from the following analysis (n was set to 5 when considering the entire cell population and decreased to 3 when decoding from subgroups of cells). For each theta cycle, we computed two scores using the normalized probability density. The amount of ’local’ information in the activity was first quantified by summing the probability concentrated around the current position of the animal ϒ_Local = ∑_tP(x*, t). x* denotes the set of spatial bins in a range of 5 cm of the animal's position at time t. Running a set of linear regression over a modified version of the P*(x, t) matrix, where the ‘local’ decoding probability density had been subtracted out of the original P(x, t) (so that we could factor out the effect of positional decoding from the reconstructed trajectory), allowed us to detect the presence of ’non-local’ sequence-like activity over a significant spatial interval around the animal position. The best fit was identified among these regressions, overlapping with the largest amount of probability density. That is, ϒ_NonLocal = max_β∑_kP*(x_β(k), t_β(k)) where β indicates a set of linear parametrizations of x and t: x = β₁ + t × β₂. Importantly, β₂ was taken to be always > 0 so to exclude fits very close to the ϒ_Local defined above. The same procedure was applied using different sets of cells to compute the probability density, so to obtain an estimation of the spatial information carried by specific cell groups (the entire population and either phase precessing or phase locking cells). Theta cycles were further classified according to the simultaneously expressed gamma power ratio. To compare the nature of activity across different cell populations, the decoding scores obtained from each cell group were first normalized to max_Θϒ = 1 (where the max is taken over all available theta cycles); then, for each theta cycle in which enough spikes were emitted by cells from both independent cell groups, we computed the difference between the two obtained decoding scores ϒ₁ and ϒ₂ (either Local or Non-Local) as the distance of the point (ϒ₁, ϒ₂) from the equal-score diagonal ϒ₁ = ϒ₂.

Statistics

No statistical methods were used to predetermine sample sizes, but our sample sizes are similar to those reported in previous publications¹⁹. We used a transgenic mouse to promote stable and homogenous expression of the opsin across animals. Following genotyping, double-positive animals (expressing the inhibitory opsin JAWS) were assigned to the experimental group, and single-positive littermates (that did not express the inhibitory opsin JAWS) were assigned to the control group. Data collection and analysis were not performed blind to the conditions of the experiments. Data analyses were performed using custom MATLAB scripts (The MathWorks). Paired and unpaired tests were performed using standard built-in MATLAB functions. 2-D Kolmogorov–Smirnov test was performed using custom code based on the Peacock algorithm. For circular statistics, the CircStat Matlab toolbox was used⁵³. All tests were two-tailed, except where stated otherwise. Data is presented as mean ± SEM, except where stated otherwise.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Data availability

All data is publicly available as of the date of publication at https://doi.org/10.5281/zenodo.15270624. Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request. Source data are provided with this paper.

Code availability

Code is available as of the date of publication at https://zenodo.org/badge/latestdoi/450059041. Additional routines are available at https://github.com/NeuroNetMem/LinearTrack_Code. Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

References

Dragoi, G. & Buzsáki, G. Temporal encoding of place sequences by hippocampal cell assemblies. Neuron 50, 145–157 (2006).
Article CAS PubMed Google Scholar
Foster, D. J. & Wilson, M. A. Hippocampal theta sequences. Hippocampus 17, 1093–1099 (2007).
Article PubMed Google Scholar
Gupta, A. S., van der Meer, M. A. A., Touretzky, D. S. & Redish, A. D. Segmentation of spatial experience by hippocampal theta sequences. Nat. Neurosci. 15, 1032–1039 (2012).
Article CAS PubMed PubMed Central Google Scholar
Liu, C., Todorova, R., Tang, W., Oliva, A. & Fernandez-Ruiz, A. Associative and predictive hippocampal codes support memory-guided behaviors. Science 382, eadi8237 (2023).
Article CAS PubMed PubMed Central Google Scholar
Buzsáki, G. & Moser, E. I. Memory, navigation and theta rhythm in the hippocampal-entorhinal system. Nat. Neurosci. 16, 130–138 (2013).
Article PubMed PubMed Central Google Scholar
Witter, M. P., Wouterlood, F. G., Naber, P. A. & Van Haeften, T. Anatomical organization of the parahippocampal-hippocampal network. Ann. N. Y. Acad. Sci. 911, 1–24 (2000).
Article ADS CAS PubMed Google Scholar
Colgin, L. L. et al. Frequency of gamma oscillations routes flow of information in the hippocampus. Nature 462, 353–357 (2009).
Article ADS CAS PubMed Google Scholar
Cabral, H. O. et al. Oscillatory dynamics and place field maps reflect hippocampal ensemble processing of sequence and place memory under NMDA receptor control. Neuron 81, 402–415 (2014).
Article CAS PubMed Google Scholar
O’Keefe, J. & Recce, M. L. Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus 3, 317–330 (1993).
Article PubMed Google Scholar
Skaggs, W. E., McNaughton, B. L., Wilson, M. A. & Barnes, C. A. Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. Hippocampus 6, 149–172 (1996).
Article CAS PubMed Google Scholar
Feng, T., Silva, D. & Foster, D. J. Dissociation between the experience-dependent development of hippocampal theta sequences and single-trial phase precession. J. Neurosci. 35, 4890–4902 (2015).
Article CAS PubMed PubMed Central Google Scholar
Muessig, L., Lasek, M., Varsavsky, I., Cacucci, F. & Wills, T. J. Coordinated emergence of hippocampal replay and theta sequences during post-natal development. Curr. Biol. 29, 834–840.e4 (2019).
Article PubMed PubMed Central Google Scholar
Bieri, K. W., Bobbitt, K. N. & Colgin, L. L. Slow and fast gamma rhythms coordinate different spatial coding modes in hippocampal place cells. Neuron 82, 670–681 (2014).
Article CAS PubMed PubMed Central Google Scholar
Zheng, C., Bieri, K. W., Hsiao, Y.-T. & Colgin, L. L. Spatial sequence coding differs during slow and fast gamma rhythms in the hippocampus. Neuron 89, 398–408 (2016).
Article CAS PubMed PubMed Central Google Scholar
Guardamagna, M., Stella, F. & Battaglia, F. P. Heterogeneity of network and coding states in mouse CA1 place cells. Cell Rep. 42, 112022 (2023).
Article CAS PubMed Google Scholar
Fernández-Ruiz, A. et al. Entorhinal-CA3 dual-input control of spike timing in the hippocampus by theta-gamma coupling. Neuron 93, 1213–1226.e5 (2017).
Article PubMed PubMed Central Google Scholar
Brun, V. H. et al. Place cells and place recognition maintained by direct entorhinal-hippocampal circuitry. Science 296, 2243–2246 (2002).
Article ADS CAS PubMed Google Scholar
Schlesiger, M. I. et al. The medial entorhinal cortex is necessary for temporal organization of hippocampal neuronal activity. Nat. Neurosci. 18, 1123–1132 (2015).
Article CAS PubMed PubMed Central Google Scholar
Davoudi, H. & Foster, D. J. Acute silencing of hippocampal CA3 reveals a dominant role in place field responses. Nat. Neurosci. 22, 337–342 (2019).
Article CAS PubMed PubMed Central Google Scholar
Zutshi, I., Valero, M., Fernández-Ruiz, A. & Buzsáki, G. Extrinsic control and intrinsic computation in the hippocampal CA1 circuit. Neuron 110, 658–673.e5 (2022).
Article PubMed Google Scholar
Venditto, S. J. C., Le, B. & Newman, E. L. Place cell assemblies remain intact, despite reduced phase precession, after cholinergic disruption. Hippocampus 29, 1075–1090 (2019).
Article CAS PubMed PubMed Central Google Scholar
Blankvoort, S., Witter, M. P., Noonan, J., Cotney, J. & Kentros, C. Marked diversity of unique cortical enhancers enables neuron-specific tools by enhancer-driven gene expression. Curr. Biol. 28, 2103–2114.e5 (2018).
Article PubMed PubMed Central Google Scholar
Chuong, A. S. et al. Noninvasive optical inhibition with a red-shifted microbial rhodopsin. Nat. Neurosci. 17, 1123–1129 (2014).
Article CAS PubMed PubMed Central Google Scholar
Tang, Q. et al. Anatomical organization and spatiotemporal firing patterns of layer 3 neurons in the rat medial entorhinal cortex. J. Neurosci. 35, 12346–12354 (2015).
Article CAS PubMed PubMed Central Google Scholar
Guardamagna, M. et al. The hybrid drive: a chronic implant device combining tetrode arrays with silicon probes for layer-resolved ensemble electrophysiology in freely moving mice. J. Neural Eng. 19, 036030 (2022).
Article ADS Google Scholar
Schomburg, E. W. et al. Theta phase segregation of input-specific gamma patterns in entorhinal-hippocampal networks. Neuron 84, 470–485 (2014).
Article CAS PubMed PubMed Central Google Scholar
Lasztóczi, B. & Klausberger, T. Layer-specific GABAergic control of distinct gamma oscillations in the CA1 hippocampus. Neuron 81, 1126–1139 (2014).
Article PubMed Google Scholar
Lopes-dos Santos, V. et al. Parsing hippocampal theta oscillations by nested spectral components during spatial exploration and memory-guided behavior. Neuron 100, 940–952.e7 (2018).
Article ADS PubMed PubMed Central Google Scholar
Wang, M., Foster, D. J. & Pfeiffer, B. E. Alternating sequences of future and past behavior encoded within hippocampal theta oscillations. Science 370, 247–250 (2020).
Article ADS CAS PubMed PubMed Central Google Scholar
Middleton, S. J. & McHugh, T. J. Silencing CA3 disrupts temporal coding in the CA1 ensemble. Nat. Neurosci. 19, 945–951 (2016).
Article CAS PubMed Google Scholar
Buzsáki, G. & Tingley, D. Space and time: the hippocampus as a sequence generator. Trends Cogn. Sci. 22, 853–869 (2018).
Article PubMed PubMed Central Google Scholar
Lisman, J. & Redish, A. Prediction, sequences and the hippocampus. Philos. Trans. R. Soc. B Biol. Sci. 364, 1193–1201 (2009).
Article Google Scholar
Huxter, J., Burgess, N. & O’Keefe, J. Independent rate and temporal coding in hippocampal pyramidal cells. Nature 425, 828–832 (2003).
Article ADS CAS PubMed PubMed Central Google Scholar
Drieu, C. & Zugaro, M. Hippocampal sequences during exploration: mechanisms and functions. Front. Cell. Neurosci. 13, 232 (2019).
Article PubMed PubMed Central Google Scholar
Qasim, S. E., Fried, I. & Jacobs, J. Phase precession in the human hippocampus and entorhinal cortex. Cell 184, 3242–3255.e10 (2021).
Article PubMed PubMed Central Google Scholar
Zheng, J. et al. Theta phase precession supports memory formation and retrieval of naturalistic experience in humans. Nat. Hum. Behav. 8, 2423–2436 (2024).
Article PubMed PubMed Central Google Scholar
Sloin, H. E. et al. Local activation of CA1 pyramidal cells induces theta-phase precession. Science 383, 551–558 (2024).
Article ADS CAS PubMed Google Scholar
Chance, F. S. Hippocampal phase precession from dual input components. J. Neurosci. 32, 16693–16703 (2012).
Article CAS PubMed PubMed Central Google Scholar
Lasztóczi, B. & Klausberger, T. Hippocampal place cells couple to three different gamma oscillations during place field traversal. Neuron 91, 34–40 (2016).
Article PubMed Google Scholar
Tsodyks, M. V., Skaggs, W. E., Sejnowski, T. J. & McNaughton, B. L. Population dynamics and theta rhythm phase precession of hippocampal place cell firing: a spiking neuron model. Hippocampus 6, 271–280 (1996).
Article CAS PubMed Google Scholar
Jaramillo, J. & Kempter, R. Phase precession: a neural code underlying episodic memory? Curr. Opin. Neurobiol. 43, 130–138 (2017).
Article CAS PubMed Google Scholar
Vollan, A. Z., Gardner, R. J., Moser, M.-B. & Moser, E. I. Left-right-alternating theta sweeps in entorhinal-hippocampal maps of space. Nature 639, 995–1005 (2025).
Article CAS PubMed PubMed Central Google Scholar
Valero, M., Zutshi, I., Yoon, E. & Buzsáki, G. Probing subthreshold dynamics of hippocampal neurons by pulsed optogenetics. Science 375, 570–574 (2022).
Article ADS CAS PubMed PubMed Central Google Scholar
Hasselmo, M. E. & Stern, C. E. Theta rhythm and the encoding and retrieval of space and time. NeuroImage 85, 656–666 (2014).
Article PubMed Google Scholar
Grienberger, C. & Magee, J. C. Entorhinal cortex directs learning-related changes in CA1 representations. Nature 611, 554–562 (2022).
Article ADS CAS PubMed PubMed Central Google Scholar
Bittner, K. C. et al. Conjunctive input processing drives feature selectivity in hippocampal CA1 neurons. Nat. Neurosci. 18, 1133–1142 (2015).
Article CAS PubMed PubMed Central Google Scholar
Mizuseki, K., Sirota, A., Pastalkova, E. & Buzsáki, G. Theta oscillations provide temporal windows for local circuit computation in the entorhinal-hippocampal loop. Neuron 64, 267–280 (2009).
Article CAS PubMed PubMed Central Google Scholar
Siegle, J. H. et al. Open ephys: an open-source, plugin-based platform for multichannel electrophysiology. J. Neural Eng. 14, 045003 (2017).
Article ADS PubMed Google Scholar
Yates, S. C. et al. QUINT: workflow for quantification and spatial analysis of features in histological images from rodent brain. Front. Neuroinform. 13, 75 (2019).
Article PubMed PubMed Central Google Scholar
Groeneboom, N. E., Yates, S. C., Puchades, M. A. & Bjaalie, J. G. Nutil: a pre- and post-processing toolbox for histological rodent brain section images. Front. Neuroinform. 14, 37 (2020).
Article PubMed PubMed Central Google Scholar
Puchades, M. A., Csucs, G., Ledergerber, D., Leergaard, T. B. & Bjaalie, J. G. Spatial registration of serial microscopic brain images to three-dimensional reference atlases with the QuickNII tool. PLoS ONE 14, e0216796 (2019).
Article CAS PubMed PubMed Central Google Scholar
Berg, S. et al. Ilastik: interactive machine learning for (bio)image analysis. Nat. Methods 16, 1226–1232 (2019).
Article CAS PubMed Google Scholar
Berens, P. CircStat: a MATLAB toolbox for circular statistics. J. Stat. Softw. 31, 1–21 (2009).
Article Google Scholar
Yamaguchi, Y., Aota, Y., McNaughton, B. L. & Lipa, P. Bimodality of theta phase precession in hippocampal place cells in freely running rats. J. Neurophysiol. 87, 2629–2642 (2002).
Article PubMed Google Scholar

Download references

Acknowledgements

We thank Morgane Audrain for help with the 3D illustration of the Hybrid Drive, Jordan Carpenter, Abraham Z. Vollan, the Kentros and Battaglia labs for comments on the manuscript, and helpful discussions at different stages of the project. This work was supported by the European Union’s Horizon 2020 research and innovation program (MGate, grant agreement no. 765549; M.G., O.C., C.K. and F.P.B.), the European Research Council (ERC) Advanced Grant “REPLAY-DMN” (grant agreement no. 833964; F.P.B.), and European Union’s Horizon 2020 Research and Innovation Program Grant “BrownianReactivation” (grant agreement no. 840704; F.S.), FRIPRO ToppForsk grant Enhanced Transgenics (90096000) of the Research Council of Norway (O.C., Q.Z. and C.K), the Kavli Foundation (O.C., Q.Z. and C.K), the Centre of Excellence scheme of the Research Council of Norway-Centre for Biology of Memory and Centre for Neural Computation (O.C., Q.Z. and C.K), The Egil and Pauline Braathen and Fred Kavli Centre for Cortical Microcircuits (O.C., Q.Z. and C.K), and the National Infrastructure scheme of the Research Council of Norway-NORBRAIN (O.C., Q.Z. and C.K).

Author information

These authors contributed equally: Matteo Guardamagna, Oscar Chadney, Federico Stella.
These authors jointly supervised this work: Clifford Kentros and Francesco P. Battaglia.

Authors and Affiliations

Kavli Institute for Systems Neuroscience and Centre for Neural Computation, Norwegian University of Science and Technology, Trondheim, Norway
Matteo Guardamagna, Oscar Chadney, Qiangwei Zhang & Clifford Kentros
Donders Institute for Brain, Cognition and Behaviour, Radboud University, Nijmegen, the Netherlands
Matteo Guardamagna, Federico Stella & Francesco P. Battaglia
Institute of Neuroscience, University of Oregon, Eugene, OR, USA
Clifford Kentros

Authors

Matteo Guardamagna
View author publications
Search author on:PubMed Google Scholar
Oscar Chadney
View author publications
Search author on:PubMed Google Scholar
Federico Stella
View author publications
Search author on:PubMed Google Scholar
Qiangwei Zhang
View author publications
Search author on:PubMed Google Scholar
Clifford Kentros
View author publications
Search author on:PubMed Google Scholar
Francesco P. Battaglia
View author publications
Search author on:PubMed Google Scholar

Contributions

Conceptualization: M.G., O.C., F.S., C.K., and F.P.B.; Investigation and Data Curation: M.G.and O.C.; Methodology and Software: M.G., O.C., Q.Z., F.S., C.K., and F.P.B.; Resources: C.K. and F.P.B.; Formal Analysis and Visualization: F.S. with the help of M.G. and O.C.; Writing—Original Draft: M.G., O.C., and F.P.B.; Writing—Review and Editing: M.G., O.C., F.S., C.K., and F.P.B.; Supervision and Funding Acquisition: F.S., C.K., and F.P.B.

Corresponding author

Correspondence to Francesco P. Battaglia.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Reporting Summary

Transparent Peer Review file

Source data

Source Data

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Guardamagna, M., Chadney, O., Stella, F. et al. Direct entorhinal control of CA1 temporal coding. Nat Commun 16, 6430 (2025). https://doi.org/10.1038/s41467-025-61453-2

Download citation

Received: 04 August 2024
Accepted: 20 June 2025
Published: 11 July 2025
DOI: https://doi.org/10.1038/s41467-025-61453-2

Subjects

Abstract

Similar content being viewed by others

Distinct roles of dentate gyrus and medial entorhinal cortex inputs for phase precession and temporal correlations in the hippocampal CA3 area

Lateralization of CA1 assemblies in the absence of CA3 input

Entorhinal cortex directs learning-related changes in CA1 representations

Introduction

Results

Discussion

Methods

Subjects

Transgenic mouse lines

Implant device and surgical procedures

Neural and behavioral data collection

Behavioral paradigm

Optogenetics

Histology

Automated cell counting

Place cell identification

Place cell classification

Place cell properties

Neural data analysis on oscillations

Generalized-Linear Model (GLM)

Phase precession analysis

Pairwise spike timing correlations

Bayesian decoding

Statistics

Reporting summary

Data availability

Code availability

References

Acknowledgements

Author information

Authors and Affiliations

Contributions

Corresponding author

Ethics declarations

Competing interests

Peer review

Peer review information

Additional information

Supplementary information

Supplementary Information

Reporting Summary

Transparent Peer Review file

Source data

Source Data

Rights and permissions

About this article

Cite this article

Share this article

Search

Quick links