Introduction

Mercury, the innermost planet of our solar system, is encompassed by a collisionless exosphere. This exosphere consists of various species originating from the solar wind, (micro-)meteoroid impacts, and interactions with the planetary surface. Based on ground-based and spacecraft observations of the Mariner 10 spacecraft in 1974/751 and, four decades later, by the MErcury Surface, Space ENvironment, GEophysics and RangingMESSENGER; 2 spacecraft, the exosphere is known to contain H, He, Na, K, Ca, Mg, Al, Fe, and Mn3. Early estimates from the Mariner 10 occultation experiment already suggested that Mercury’s total exospheric surface pressure is expected to be higher than that calculated from the known exospheric species4, indicating that Mercury likely contains several unknown exospheric species as well5. After the discoveries of the lithophile elements sodium (Na) and potassium (K) in Mercury’s exosphere6,7, it has been speculated that a low abundance of lithium (Li) may be present in the exosphere, where some fraction originates from infalling micrometeoritic material and the rest results from lithospheric surface materials8. In Earth’s atmosphere, the major source of Na, K, and Li is meteoritic evaporation9.

While on Earth, small meteoroids that contribute these elements to the atmosphere typically do not reach the surface, the lack of a dense atmosphere on Mercury allows these meteoroids to consistently impact the surface. Consequently, the surface of Mercury is continuously bombarded by (micro-)meteoroids and, less frequently, by centimeter- to meter-sized meteoroids10. In 2013, MESSENGER observed a rare event where a significant enhancement at high altitudes of the exosphere occurred due to the impact vaporization of sodium caused by the impact of meter-sized meteoroid11. This impacting material adds meteoritic elements to the upper regolith, causing it to mix and vitrify in a manner akin to processes observed on the Moon. Apollo drill cores of the Lunar surface material show for example non-monotonic variations in the composition of the upper meter of the regolith12,13. At the meteor impact site, the regolith’s upper surface layers underwent a transformation that creates a melt phase, solid ejecta, and a vapor phase where surface material and meteoritic material are released into the lunar exosphere. Also at Mercury, meteoroids are one of the sources for the exosphere formation14. While a portion of the meteoritic elements escapes as neutrals or ions, a fraction is retained on the surface5.

So far, however, the presence of Li has not been confirmed at Mercury. Neither in-situ particle measurements onboard Mariner10 and MESSENGER, nor remote observations with telescopes could prove the presence of Li. Because of the non-detection with the 1.5-m telescope at the Catalina Observatory, Arizona, the upper limit of the Li surface column density was expected to be less than 8.4 × 107 cm−215, which is in the same order of magnitude estimated from the non-detection with the European Southern Observatory-New Technology Telescope observations at La Silla, Chile16.

Previous studies on comets17, Mars18, and Venus19, alongside the recent discoveries on Mercury20, have shown the existence of exospheric elements at all of these bodies based on the detection of so-called pick-up ion cyclotron waves (ICWs) in the in-situ magnetic field measurements. Pick-up ion cyclotron waves (ICWs) are transverse electromagnetic waves that propagate nearly parallel to the ambient magnetic field. Their polarization, either left- or right-hand elliptical, is determined by the pick-up geometry of freshly ionized neutrals. Left-handed waves are primarily generated when the magnetic field is oriented perpendicular to the plasma flow, whereas right-handed waves dominate when the magnetic field aligns parallel to the flow. At Mercury’s orbit within the solar wind, right-handed polarized ICWs are preferentially excited due to the relatively small angle (approximately 30°) between the interplanetary magnetic field and the solar wind’s flow direction20,21. These waves travel sunward with a phase velocity roughly equal to the Alfvén speed,

$${V}_{{{\rm{A}}}}={B}_{0}/\sqrt{{\mu }_{0}\rho },$$
(1)

with B0 the background magnetic field strength, μ0 the permeability of free space and ρ the mass density of the charged particles in the plasma. The propagation speed of these waves is lower than the solar wind velocity, causing them to be advected in the anti-sunward direction across the spacecraft. In the spacecraft’s frame of reference, the waves exhibit left-hand polarization and are consistently detected at the local ion gyrofrequency. This is due to the negligible velocity of newly introduced exospheric ions relative to the spacecraft. As a result, any potential misidentification with plasma waves generated at the bow shock by back-streaming solar wind protons is eliminated, since the latter are observed at significantly different frequencies due to their substantial velocity relative to the spacecraft19,22.

In this work, we report the observation of pick-up ICWs generated by the solar wind pick-up of freshly ionized Li atoms. We analyze MESSENGER’s magnetic field data in the solar wind to identify ICWs and use the observed wave power to infer the local density of Li required to produce these waves. Applying a Chamberlain exospheric model23, we provide insights into the origin of these Li particles, which are released from Mercury’s surface through evaporation of sporadic meteoroid impacts. Upon photoionization, these neutral Li atoms gyrate around the interplanetary magnetic field and are subsequently picked up by the solar wind. The velocity difference between the newly formed Li ions and the solar wind plasma creates an instability, leading to the excitation of the pick-up ICWs24. A schematic illustration of this pick-up ICW generation mechanism is presented in Fig. 1.

Fig. 1: Illustration of the generation mechanism of pick-up ion cyclotron waves in Mercury’s space environment.
figure 1

Lithium (Li) released through (micro-)meteoroid evaporation at the surface can ascend beyond Mercury’s planetary magnetic field (depicted by blue lines) and the bow shock (light blue arc), reaching the solar wind region where it becomes photoionized by the Sun’s extreme ultraviolet radiation, characterized by the light frequency, ν times Planck’s constant, h. The freshly ionized Li+ starts to gyrate in the presence of the interplanetary magnetic field (IMF) and gets picked up by the background solar wind. The solar wind plasma becomes unstable, which excites the ion cyclotron waves (ICWs) that are subsequently detected by the MESSENGER spacecraft. The display elements are not to scale. Credit: The MESSENGER spacecraft and Mercury images are provided by NASA/Johns Hopkins APL/Carnegie Institution of Washington.

Full size image

Results

Detection of lithium pick-up cyclotron waves

To identify ion cyclotron waves (ICW) that specifically originate from the pick-up of newly-born Li+ ions, we adopt the selection criteria that have successfully been used for the identification of ICWs generated from freshly ionized hydrogen around Mercury20.

Because the abundance of 6Li is negligible compared to 7Li25 we adapt the procedure to the heavier ion. To ensure that the observed waves are freshly generated from local ion pick-up26, we preselect intervals where the MESSENGER spacecraft was located in the solar wind on the dayside with respect to the terminator.

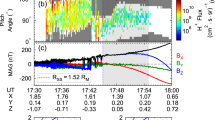
In Fig. 2, an example of an identified Li+ ion cyclotron wave is shown. Figure 2a shows the magnetic field observation in mean-field aligned (MFA) coordinates, where B∣∣ denotes the parallel component and B⊥,1 and B⊥,2 the perpendicular components with respect to the background magnetic field. The two perpendicular components (red and blue) exhibit a strong degree of coherence, and their fluctuations are stronger than the parallel magnetic field variations (orange). This is also evident from the power spectral density in Fig. 2b, where the perpendicular power density, determined by the two perpendicular components (black) dominates over the parallel power density (orange), indicating that the observed wave is rather transverse than compressional around the Li+ cyclotron frequency \({f}_{{{\rm{c}}},{{{\rm{Li}}}}^{+}}\) of approximately 0.05 Hz (marked as a dashed black line). The gray shaded area depicts the frequency range ΔF, used to evaluate the characteristics of the ICWs. Figure 2c shows the hodogram of the time interval. The observed wave is planar in the transverse direction to the background magnetic field and nearly circular in the (B⊥,1, B⊥,2)-plane. The orange star and cyan diamond mark the start and end times of the time interval, clearly showing the left-handed rotation of the wave about the background magnetic field.

Fig. 2: Example of an identified Li ion cyclotron wave (ICW).
figure 2

a Magnetic field observations in mean-field-aligned (MFA) coordinates. B∣∣ denotes the parallel magnetic field component (orange), while B⊥,1 (blue) and B⊥,2 (red) represent the perpendicular magnetic field components. b Power spectrum of the parallel (orange) and the two perpendicular (black) magnetic field components. The dashed black line denotes the local lithium cyclotron frequency \({f}_{{{\rm{c}}},{{{\rm{Li}}}}^{+}}\) and the gray shaded area depicts the frequency range ΔF, used to evaluate the characteristics of the ICWs. c Hodogram of the magnetic field components in MFA coordinates. The green star and cyan diamond in the (B⊥,1, B⊥,2)-plane mark the start and end times of the time interval. Source data are provided as a Source Data file.

Full size image

Estimation of the local lithium density

From the observed wave power of the ICWs we can derive the required neutral Li densities with a method similar to the one successfully used for atomic hydrogen at Mercury27. The total free energy, Efree, which is required to excite the cyclotron waves, is approximately given by17:

$${E}_{{{\rm{free}}}}=\frac{1}{4}{m}_{{{\rm{Li}}}}{n}_{{{{\rm{Li}}}}^{+}}{V}_{{{\rm{A}}}}{V}_{{{\rm{inj}}}}\left[{(1+\cos (\alpha ))}^{2}+{(1-\cos (\alpha ))}^{2}\right].$$
(2)

Here, mLi = 6.941 u = 1.16 × 10−23 g and \({n}_{{{{\rm{Li}}}}^{+}}\) are the mass and density of the pick-up Li+ ions. VA is the local Alfvén velocity, Vinj is the injection velocity of the Li+ ions into the solar wind and α = ∠(Vinj, B0) is the angle between the injection velocity and the background magnetic field vector. Inverting Eq. (2) for \({n}_{{{{\rm{Li}}}}^{+}}\) yields the pick-up ion density, under the assumption that the entire free energy of the newly-born pick-up ions is transferred to the wave growth. Computer simulations, however, show that only a fraction of the energy is transferred to the wave so that

$${E}_{{{\rm{free}}}}=\Phi \cdot {E}_{{{\rm{ICW}}}},$$
(3)

where Φ describes the efficiency of the energy transfer (Φ ≤ 1) and

$${E}_{{{\rm{ICW}}}}={\int}_{\Delta F}{P}_{\perp }{{\rm{d}}}f,$$
(4)

is the observed wave energy determined by the power spectral density of the perpendicular magnetic field components around the local Li+ gyrofrequency (see e.g., Fig. 2). For heavy ions, an efficiency factor of Φ of approximately 0.3 is realistic28. Since the pick-up ion density is balanced by the ion production rate, which can be estimated by multiplying the neutral Li density nLi by the photoionization rate, khν, it is possible to derive the neutral Li density from the estimated ion densities \({n}_{{{{\rm{Li}}}}^{+}}\) from Eq. (2) with:

$${n}_{{{\rm{Li}}}}=\frac{{n}_{{{{\rm{Li}}}}^{+}}\cdot {\Omega }_{{{{\rm{Li}}}}^{+}}}{100\cdot {k}_{h\nu }}.$$
(5)

We use the characteristic time (\({\Omega }_{{{\rm{c}}},{{{\rm{Li}}}}^{+}}\cdot t\)) of 100 gyroperiods until the ICWs are fully developed and a quasi-steady state is reached. The (conservative) assumption of 100 gyroperiods is motivated by computer simulations that have shown that the full energy transfer from the ions to the waves takes approximately 60–100 ion gyrations29. Since the photoionization rate significantly varies with the solar activity and the radial distance of Mercury to the Sun, we also adapt khν for each ICW event accordingly.

By surveying four years of MESSENGER data, we identified 12 ICW events near the local Li+ gyrofrequency. The results of our detection and analysis are shown in Table 1 and Fig. 3.

Table 1 Summary of the observation times, locations, and estimated Li densities for the 12 identified ICW events
Full size table
Fig. 3: Radial observation location of the 12 events alongside their Li density.
figure 3

Black dots are the neutral Li number density derived from the ICW observation, using Eqs. (2) and (5). The error bars are the 95% quantiles determined from a Monte Carlo error analysis on the determined Li densities. The transparent red (blue) lines illustrate Chamberlain models fitted to the upper (lower) error bar value for each event individually, with the opaque lines indicating the median of these fits. The dashed gray line depicts the Chamberlain profile for an average surface temperature of 450 K and the upper limit of the surface density based on the non-detection by remote instruments. Source data are provided as a Source Data file.

Full size image

Figure 3 depicts the radial observation distance, measured from both, the planetary center in Mercury radii (RM = 2440 km) (top axis), and the planetary surface (bottom axis), pertaining to the 12 independent events alongside their estimated neutral Li number densities. The black error bars are the 95% quantiles determined from a Monte Carlo error analysis of Eqs. (2) and (5).

Potential origin of lithium at Mercury

Basically, Mercury’s exosphere is predominantly sustained through four main mechanisms: thermal desorption, photon-stimulated desorption, ion sputtering, and impact vaporization30. Thermal desorption and photon-stimulated desorption release atoms due to heating and photon bombardment of the surface, respectively, which produce atoms with insufficient energies to reach high altitudes. Ion sputtering and impact vaporization involve ion impacts from the solar wind particles and high-energy impacts of (micro-) meteoroids, respectively, and can produce high energetic particles that can reach high altitudes.

To further analyze which mechanism was responsible for the detection of Li, we apply a Chamberlain exospheric model23, which is commonly used to model Mercury’s exospheric populations5,31,32. In this model, the only controlling factors considered are the gravitational attraction and the near-surface density and temperature of the exospheric particle population32.

The dashed gray line in Fig. 3 depicts the Chamberlain profile for an average dayside surface temperature of T0 = 450 K and the upper limit of the expected surface density based on the non-detection by remote instruments which is n0 = 5.8 cm−315. Given that the surface density must be less than this threshold (as otherwise, remote instruments would have detected Li), thermal desorption of Li from the surface cannot account for the extended observation location of the events. Just like thermal desorption, photon-stimulated desorption generates atoms with energy levels too low to reach high altitudes. Therefore, it is not considered a significant contributor.

Ion sputtering leads to high escape rates, driven by solar wind and/or energetic magnetospheric ions30. Magnetic reconnection, which occurs under antiparallel orientations of the interplanetary magnetic field (IMF) and planetary magnetic field, enhances sputtering by directing solar wind particles and/or energizing magnetospheric ions. These particles travel along reconnected field lines to the planetary surface, potentially sputtering upward-moving surface particles33. Prolonged antiparallel IMF alignment reduces the dayside magnetic field’s shielding, allowing increased solar wind ion precipitation and further sputtering34. These effects are particularly significant during strong solar wind events, where precipitation rates significantly increase35. A brief examination of interplanetary coronal mass ejection (ICME) MESSENGER observations at Mercury36, whether sputtering due to ICME collisions with the planet could have been responsible during the time of the observed Li enhancements, shows that only one event occurred during an ICME (March 5, 2012) and two events (May 27, 2012; May 1, 2013) occurred several hours before and after an ICME. Typically, the ballistic time scales before the sputtered particles are lost to the surface or carried away by the solar wind extend to a couple of hours following a significant impulsive ion precipitation event35,37. Given the significant presence of ICMEs during the four-year observation period of the MESSENGER mission, it is reasonable to anticipate that Li events would be consistently observed across a wide range of the spacecraft’s orbit. However, the observed Li events are only detected within a few minutes and very rarely, suggesting that they are unlikely to be associated with magnetic reconnection, since the orientation of the interplanetary magnetic field is highly variable21, and thus magnetic reconnection occurs frequently. Thus, observed Li events are unlikely to be connected to ICMEs and/or antiparallel IMF conditions directly and sputtering is considered unlikely to be the source of the detected Li.

Consequently, impact vaporization, caused by high-energy impacts, appears to be the most likely explanation for the observed events. In fact, the sporadic occurrence of the events and their short observation periods correspond well to the ballistic time scales of tens of minutes after meteoroid impact vaporization38.

Following studies of the chemistry of impact-produced vapor clouds, Li is delivered to the exosphere mainly in the form of Li atoms during meteoroid impacts39. In this case, the kinetic temperature of Li atoms is close to 2500–5000 K, which has also been inferred from hypervelocity impact experiments40. To estimate the Li surface density required to produce the derived Li densities in the exosphere, we applied a Chamberlain model, assuming an average meteoritic impact-related cloud temperature of 3750 K for each event individually. Specifically, we performed a least-squares fit of the Chamberlain model to the upper and lower error margins of the inferred Li densities for each event. The resulting profiles are illustrated in Fig. 3 with transparent red (blue) lines for the upper (lower) error margin. The median of the Chamberlain profiles (red and blue lines in Fig. 3) subsequently determines the expected average surface density range, which is n0 = 0.03–0.2 cm−3. Notably, all 12 events fall within this range, even though they are independent, indicating that the observed Li number densities can be accurately reproduced under meteoroid impact-related cloud temperatures.

Table 1 provides a summary of the observation time (UTC) and observation locations of the 12 ICW events. The events are observed to be evenly distributed throughout the Mercury year, as evidenced by the uniformly distributed true anomaly angles (TAA) of Mercury around the Sun. Furthermore, the geographic observation locations of the events do not exhibit a clear trend, as the local time (LT) and corresponding longitude (Lon) of the S/C during the event observation are uniformly distributed across the dayside of Mercury. The fact that the majority of events are detected in the southern hemisphere, indicated by the negative latitude (Lat), is attributable to the S/C orbital path, as MESSENGER exhibits a highly elliptical orbit, with its periherm located at the geographic north (shorter dwelling time in this region of its orbit) and its apoherm situated far into the geographic south (longer dwelling time in this region of its orbit). To obtain the Li surface density (n0) during the detected events, a least squares fit of a Chamberlain profile was applied to the inferred Li densities (nLi) for the case of a near-surface temperature of T0 = 3750 K. The black dots represent individual observations recorded at various times during the MESSENGER mission and, as such, do not constitute a measured radial profile. However, within the context of this analysis, it is reasonable to treat them as a radial profile. Utilizing the derived surface number densities and giving that the average vapor cloud temperature, Tvc, near the surface is about 3750 K, the vertical Li column density (N) can be determined through

$$N={n}_{0}\cdot H,$$
(6)

where H represents the characteristic scale height

$$H=({{{\rm{k}}}}_{{{\rm{B}}}}\cdot {T}_{{{\rm{vc}}}})/({m}_{{{\rm{Li}}}}\cdot {g}_{{{\rm{pl}}}}),$$
(7)

with kB denoting the Boltzmann constant and gpl = 3.78 m/s2 the gravitational acceleration on Mercury.

Discussion

Considering that the average temperature of the Li cloud near the surface Tvc of about 3750 K, the average speed of the Li particles can be estimated with

$${v}_{{{\rm{Li}}}}={(2{k}_{{{\rm{B}}}}{T}_{{{\rm{vc}}}}/{m}_{{{\rm{Li}}}})}^{1/2},$$
(8)

which is approximately 3 × 105 cm s−1. Based on this velocity and the upper and lower Li surface density limits provided in Table 1, we can determine the average Li mass flux with

$${f}_{{{\rm{Li}}}}={n}_{{{\rm{Li}}}}\cdot {v}_{{{\rm{Li}}}}\cdot {m}_{{{\rm{Li}}}},$$
(9)

which yields approximately 1.7 × 10−19 − 5.3 × 10−19 g cm−2 s−1.

Previous research indicates that high-speed meteoroid impacts, with velocities between 100 and 120 km/s, are considered the primary contributors to Mercury’s surface impact vaporization rate41. Additionally, studies on meteoroid impactors on regolith targets have determined that the target-to-impactor mass ratios, Y, in impact-produced vapor clouds are approximately 100 for impacts at 90 km/s and approximately 180 for impacts at 120 km/s42. Therefore, it can be inferred that the mass ratio between the target and the impactor in the impact-produced vapor clouds on Mercury is approximately 150, assuming an average meteoroid impact velocity of 110 km/s.

The relative abundances of moderately volatile elements in meteorites can be compared. According to previous findings, Li and Na vary in carbonaceous chondrites only by about 30–40%43,44. This indicates that the composition of the meteorites might have been very similar. Indeed almost 85% of meteorite-falls on Earth are related to ordinary chondrites of types H (High total iron contents), L (Low total iron contents), and LL (Low total iron and low metal contents), with H and L types comprising about 70% of all impacts. Carbonaceous and enstatite chondrites together add about 6%, while achondrites and iron meteorites add about 5% and 2% of all falls, respectively. However, beside EL (Enstatit-chondrite with Low metal contents) chondrites, all chondrite types show similar Li/Na values between about 2.6 − 3.8 × 10−444. The Li/Na ratio, measured from meteoroid ablation in Earth’s mesopause, is about 3.3 × 10−49, which is consistent with this range.

The average atomic percentage of Na in ordinary chondrites is approximately 0.68%, whereas the total Na content in Mercury’s exosphere is around 2.1%45. This suggests that the Na concentration on Mercury is about 3–4.3 times higher than that of chondrites. Taking into account that Mercury’s surface composition is likely similar to that of enstatite or metal-rich chondrite meteorites46, it can be inferred that Na has accumulated on the planet’s uppermost layer over billions of years due to (micro-)meteoroid impacts. Since all alkali metals have a similar behavior, also Li is expected to enrich on Mercury. Assuming that the enrichment of Li on Mercury is comparable to that of the Na enrichment, the Li content on Mercury, \({\chi }_{{{\rm{pl}}}}^{{{\rm{Li}}}}\), can be estimated from the average values of ordinary chondrites and is approximately 3 × 10−4 ⋅ 2.1 Li at%, which corresponds to approximately 0.0006 at% or about 6 ppm41. Based on these values, the minimum and maximum total meteoroid mass flux, ftot,

$${f}_{{{\rm{tot}}}}={f}_{{{\rm{Li}}}}/(Y\times {\chi }_{{{\rm{pl}}}}^{{{\rm{Li}}}}),$$
(10)

during the detected events can be estimated and ranges between 1.9 and 5.9 × 10−16 g cm−2 s−1. Considering that the Li content of the impacting meteorites \({\chi }_{{{\rm{imp}}}}^{{{\rm{Li}}}}\) is approximately 1.86 ppm41, it’s likely that the Li found in Mercury’s exosphere primarily originates from the planet’s surface.

Based on the minimum and maximum vertical column density, N, which ranges between 5.8 × 106 and 1.8 × 107 cm−2 (see Table 1), it is possible to give a rough estimate of the masses and sizes of the impacting meteoroids. Assuming that the Li column density is the same over the bombarded hemisphere of Mercury (i.e., the area of half of the planet: 3.74 × 1017 cm2), the minimal and maximal number of Li atoms in the exosphere ranges between 2.2 and 6.7 × 1024. By multiplying the minimal and maximal number of Li atoms by the atomic mass of Li (6.941 g/mol) and dividing by Avogadro’s number 6.022 × 1023 mol−1, the resulting minimal and maximal masses of the impact-produced Li in the exosphere are approximately 25 g and 77 g, respectively. Based on these impact-produced Li masses and considering that the Li content in Mercury’s exosphere is approximately 6 ppm, the total mass of the impact-produced vapor clouds is estimated to range between approximately 4.2 × 106 g and 1.8 × 107  g. Now, given that the target-to-impactor mass ratio, Y, in the impact-produced clouds is approximately 150, the mass of the impacting meteoroids, mimp, is then expected to range between about 2.8 × 104 g and 1.2 × 105 g. Provided that the average mass density of the impacting meteoroids, ρimp, is approximately 3 g cm−3, the minimal and maximal radii, r, of the impacting meteoroids,

$$r={(3\cdot {m}_{{{\rm{imp}}}}/(4\cdot \pi \cdot {\rho }_{{{\rm{imp}}}}))}^{1/3},$$
(11)

range between approximately 13 cm and 21 cm, respectively. These values align closely with previous studies, which reported on impactors of similar size causing three short-term Na and Mg content enhancements in Mercury’s exosphere47.

In accordance with studies on the chemistry of the impact-produced vapor clouds, Li is expected to be delivered to the exosphere mainly during meteoroid impacts39 with temperatures close to 3000–5000 K, whereas Li originating from the photolysis of impact-produced LiO and LiOH molecules are typically much hotter48 but with smaller fractions. In addition to infalling (micro-)meteoritic and larger meteoritic material, lithophile elements such as Na, K, and Li can also be present in Mercury’s regolith15, where they can be released into the exosphere via photo-stimulated desorption, sputtering or thermal diffusion. Mercury’s exosphere has a total Na column density of about 1.5 × 1011 cm−25, which yields an average Li/Na ratio of about 5 × 10−5 during the studied impact events. Such values are smaller than the purely chondritic values mentioned above, suggesting that there must be significantly more Na in the exosphere than was delivered by the studied meteor events. This indicates that a significant fraction of Na in the exosphere comes from the regolith and not just from the event-related meteoritic material because Na is detected all the time, whereas Li is not.

The findings support the hypothesis that (micro-)meteoroids and larger meteoroids, which have continuously and sporadically impacted the surface of Mercury for billions of years, serve as a significant external source of volatile elements such as Na, K, and Li. This suggests that Mercury’s surface has been modified and overlain by impact material, contributing substantially to Mercury’s unexpectedly volatile-rich surface.

We expect that future measurements by the ESA/JAXA BepiColombo mission, in particular by the SERENA package49,50 on board the Mercury Planetary Orbiter spacecraft51, will help characterize the contribution of (micro-)meteoroid evaporation to the origin of Li and several other (yet-to-be-detected) heavy elements in the exosphere of Mercury. The discovery of Li at Mercury demonstrates the power of plasma physics methods in diagnosing the exospheric composition of planets using only magnetic field measurements. Hence, this method stands as a valuable complement to in-situ particle measurements, particularly when their availability is limited.

Methods

Pick-up ion cyclotron wave identification

In order to identify ICWs specifically produced by the pick up of freshly ionized lithium, we employ the same identification approach that was recently published for pick-up proton cyclotron waves20,27. Magnetic field observations at 20 Hz, collected by the MESSENGER spacecraft2,52 between March 2011 and April 2015, are analyzed using a sliding interval of approximately 200 s, with the following procedures applied:

  1. 1.

    During each time interval, the magnetic field data are converted into a mean-field-aligned (MFA) coordinate system. The parallel component, \({\hat{{{\bf{b}}}}}_{| | }={{{\bf{B}}}}_{0}/| {{{\bf{B}}}}_{0}|\), is derived from the average magnetic field over the interval, B0 = [Bx,0, By,0, Bz,0]. The perpendicular components are computed as \({\hat{{{\bf{b}}}}}_{\perp 2}={\hat{{{\bf{b}}}}}_{| | }\times [0,0,1]\) and \({\hat{{{\bf{b}}}}}_{\perp 1}={\hat{{{\bf{b}}}}}_{\perp 2}\times {\hat{{{\bf{b}}}}}_{| | }\).

  2. 2.

    Each time interval of approximately 200 s (4096 data points) is divided into three sub-intervals of approximately 100 s (2048 data points), with a 50% overlap. For each sub-interval, the power spectral density matrix is computed53. Within the power spectral density matrix, the diagonal elements represent the in-phase power density of the parallel component (P∣∣) and the perpendicular component (\({P}_{\perp }=\frac{1}{2}\cdot ({P}_{\perp 1}+{P}_{\perp 2})\)). The off-diagonal elements correspond to the out-of-phase cross powers, where the complex part provides information on the ellipticity and handedness of the wave54,55,56,57.

  3. 3.

    For the frequency range of interest, i.e., around the ion cyclotron frequency, the degree of polarization (DOP) is computed for each sub-interval to assess the coherence of the wave. A value of 100% signifies a pure state wave, while values below 70% indicate noise57.

The arithmetic averages of the calculated power densities and ellipticities from the three sub-intervals are subsequently computed. A key criterion for ion cyclotron waves generated by local ion pick-up is that the observed wave frequency in both the spacecraft frame and plasma frame remains consistent and closely aligns with the local ion gyrofrequency19. To ensure reliable identification, the lithium gyrofrequency \({f}_{{{\rm{c}}},{{{\rm{Li}}}}^{+}}=q{B}_{0}/(2\pi \,{m}_{{{\rm{Li}}}})\) and its associated error range \(\Delta {f}_{{{\rm{c}}},{{{\rm{Li}}}}^{+}}=q{\sigma }_{B}/(2\pi \,{m}_{{{\rm{Li}}}})\) are calculated for each approximately 200 s time interval. Here, 7Li mass mLi, charge q, along with the average and standard deviation of the magnetic field magnitude, B0 and σB, are utilized. Subsequently, the same selection criteria that have been successfully applied in previous studies for the identification of pick-up ICWs around Venus and Mercury are employed19,20:

  • The power density of each component is integrated over the frequency range \(\Delta F=[0.8\cdot ( \, \, {f}_{{{\rm{c}}},{{{\rm{Li}}}}^{+}}-\Delta {f}_{{{\rm{c}}},{{{\rm{Li}}}}^{+}}),{f}_{{{\rm{c}}},{{{\rm{Li}}}}^{+}}+\Delta {f}_{{{\rm{c}}},{{{\rm{Li}}}}^{+}}]\) to account for power maxima occurring slightly below the computed gyrofrequency. Subsequently, the ratio of the (numerical) integrated perpendicular fluctuations (E⊥ = ∫ΔF P⊥df ) to parallel fluctuations (E∣∣ = ∫ΔF P∣∣df ) is calculated, which must satisfy the condition E⊥ /E∣∣ > 5 to ensure that the observed waves are transverse.

  • Within the frequency range ΔF, the ellipticity must satisfy the condition ϵ < −0.5 to confirm left-handed polarization of the observed wave in the spacecraft frame.

  • To ensure substantial coherence of the observed wave and a high signal-to-noise ratio, the degree of polarization (DOP) for each sub-interval within ΔF must exceed 0.7.

  • The maximum of the perpendicular fluctuating field (P⊥) lies within ΔF, ensuring that the observed wave’s dominant mode corresponds to the ion cyclotron mode.

  • Only time intervals during which MESSENGER was situated within the solar wind58,59, and at least \(10\,\min\) away from the bow shock, are preselected to ensure that solely upstream waves are considered19.

These five selection criteria ensure that only upstream waves exhibiting the defining characteristics of pick-up ion cyclotron waves are included. Over four (Earth) years of MESSENGER observations, 28 time intervals meet the selection criteria.

Estimation of injection velocity

Given the limitations of MESSENGER’s plasma measurements, a solar wind propagation model60 provided by the AMDA database61 is employed. This model, which has been successfully applied to Mercury20,27, offers approximate estimates of the solar wind’s plasma density (nSW) and velocity (VSW) during the ICW observation period. The injection velocity (Vinj) is defined as the aberrated solar wind velocity (VSW), adjusted by Mercury’s orbital motion (VMercury). Mercury’s orbital motion is determined using the Navigation and Ancillary Information Facility62,NAIF through the WebGeocalc toolkit, employing ECLIPJ2000 coordinates with Mercury set as the target, the Sun as the observer, and the event observation time as the input. Consequently, the injection velocity is expressed as Vinj = −VSW + VMercury.

The injection velocity vector is additionally utilized to calculate the solar zenith angle (SZA). The SZA is subsequently employed to identify events occurring on the dayside of the terminator (SZA < 90°), ensuring that the observed waves are freshly generated through local ion pick-up26,27. Of the 28 preselected time intervals, 20 correspond to observations made on the dayside of the terminator (see Table 2).

Table 2 Observation time of the 28 time intervals that fulfill the ICW selection criteria
Full size table

Due to the limiting factor of the selection window size (approximately 200 s) the number of events is overestimated, since unique ICW events may continue up to approximately 900 s. From the 20 time intervals, 12 events are identified as independent ICW events.

Figure 4a shows the observation location of the 12 events in Mercury–Solar–Orbital (MSO) coordinates,  +XMSO points toward the sun,  +YMSO lies in the orbital plane, perpendicular to XMSO and opposite to the direction of planetary orbital motion, and  +ZMSO is normal to the orbital plane and positive northward. To verify that the identified ICWs are locally generated through the initial ionization of neutral lithium (Li), the observation locations are transformed into an local electromagnetic (MBE) coordinate system to investigate potential asymmetries relative to the convection electric field. Figure 4b illustrates the positions of the 12 ICWs within the local MBE coordinate system. In this system, the XMBE axis is oriented positively towards the Sun and directed opposite to the aberrated solar wind velocity vector (\({{{\bf{V}}}}_{{{\rm{SW}}}}^{{\prime} }\)), which corresponds to the injection velocity of Li+ ions into the solar wind plasma (\({{{\bf{V}}}}_{{{\rm{inj}}}}=-{{{\bf{V}}}}_{{{\rm{SW}}}}^{{\prime} }\)). The YMBE axis is aligned positively with the background magnetic field component (B0), while the ZMBE axis is oriented positively in the direction of the convection electric field (E = Vinj × B0).

Fig. 4: Position of the observed Li+ ICW events.
figure 4

a Observation location in Mercury Solar Orbital (MSO) and b Mercury electromagnetic (MBE) coordinates. In this coordinate system,  +XMBE aligns with the Sun along the Li+ ion injection velocity, Vinj,  +YMBE aligns with the background magnetic field B0, and  +ZMBE aligns with the convection electric field E = Vinj × B0. The color-scale in panel b indicates the velocity ratio between the Alfvén speed, VA, and the injection velocity, Vinj. Source data are provided as a Source Data file.

Full size image

Figure 4b provides several indications that the observed ICWs are generated locally: (1) The majority of ICWs are detected at large positive XMBE, far from the planet, implying that they would have had to propagate against the solar wind flow at velocities exceeding the solar wind speed. This scenario is incompatible with the observations, as ICWs generally propagate at speeds comparable to or lower than the local Alfvén velocity (VA), and the Alfvén velocity associated with the detected ICWs is significantly smaller than the aberrated solar wind speed, which defines the injection velocity of the ions into the solar wind (VA /Vinj < 0.6). (2) ICWs are distributed symmetrically across the  ± ZMBE hemispheres. Since there is no known mechanism capable of transporting ions across the magnetic field against the electric field into the region of negative motional electric field, the ICWs must have been generated locally19. Based on this analysis, we conclude that the 12 ICWs are indeed locally generated, validating the underlying assumptions required for reliable on-site density estimation.

Photoionization rate

The photoionization rate significantly varies with the solar activity and the heliocentric distance of Mercury to the Sun. Since the photoionization rate is important to obtain a reliable Li density estimation, we modify the ionization rate, khν, in Eq. (5) as follows: As the first step to provide an estimate of solar activity, the FISM-P irradiance, derived from the Flare Irradiance Spectral Model63, FISM-P for Mercury, is normalized to the range [0, 1]. Here, 0 corresponds to 0.028 Wm−2s−1 nm−1 and 1 corresponds to 0.1 Wm−2s−1 nm−1, representing the minimum and maximum spectral irradiance indices at 121.5 nm during solar cycle 24. In the second step, the normalized FISM-P irradiance index is used to interpolate the corresponding photoionization rate at Earth’s orbit, ranging between a minimum of 1.97 × 10−4 s−1 (quiet Sun = 0) and a maximum of 2.07 × 10−4 s−1 (active Sun = 1)64. In the final step, this ionization rate is rescaled from Earth’s orbit (1 AU) to Mercury’s heliocentric distance during the ICW observation period, which varies between 0.31 AU and 0.47 AU, by applying the inverse square law.

Monte Carlo error analysis

To capture the effect of uncertainty of the parameters (VA, Vinj, α, Φ, and the characteristic time \({\Omega }_{{{\rm{c}}},{{{\rm{Li}}}}^{+}}\cdot t\)) used in Eqs. (2) and (5) on the derived Li densities, we applied a Monte Carlo error propagation with 50,000 samples.

We use the error information about the solar wind propagation model60 and assume that the solar wind velocity and density, obtained from the solar wind propagation model, are normal-distributed about the values predicted by the model with a variance of 50 km/s in each velocity component and a variance of 5 cm−3 for the solar wind density. In addition we varied the efficiency parameter Φ according to a beta-distribution, \({{\mathcal{B}}}e(\Phi ;3,6)\), that has an expectation value of  〈Φ〉 = 0.3, as shown by simulations29. We also normally distributed the characteristic time for the ICW development (\({\Omega }_{{{\rm{c}}},{{{\rm{Li}}}}^{+}}\cdot t\)) around 100 gyroperiods with a variance of 40 gyroperiods (conservative estimate), as found in simulations29.