Introduction

Semiconductor spin qubit arrays hold significant promise for the future of quantum computing, primarily due to their easier scalability thanks to existing semiconductor industry processes1,2,3,4,5. By facilitating the integration of a larger number of qubits6,7,8,9,10, semiconductor spin qubit arrays should enable complex computations and enhance problem-solving capabilities. In this context, developing semiconducor spin qubits using industrially compatible process flows should lead to reliable devices produced at high yields with low variability11,12, cointegration with cryoelectronics is also possible13. Furthermore, the redundancy potential of large arrays is compatible with the implementation of quantum error correction techniques14, which are a critical component if we are to achieve fault-tolerant quantum computation.

However, the control and readout of large, dense arrays still presents a number of challenges. Firstly, precise tuning of charge configurations faces various technical hurdles, such as handling capacitive coupling between neighboring quantum dots6,7,15,16 or dealing with a diverging number of accessible charge configurations in arrays open to reservoirs17,18,19. Secondly, readout of qubit states must be consistent if we are to extract useful information from the quantum system. The charge detectors currently used for readout from arrays often have a large footprint and limited depth of sensitivity6,7,8,16,20,21,22,23. Consequently, they are incompatible with the control of dense arrays. To address these challenges, innovative strategies must be developed to distribute and control single charges in an array and to develop new measurement schemes.

In this paper, we describe a novel approach which consists in operating a small array as an isolated unit cell with embedded charge and spin readout. In this regime, the number of accessible charge configurations is relatively small compared to arrays open to reservoirs. This reduced complexity greatly facilitates electrostatic tuning24,25,26,27,28. We exploit gate-based reflectometry to probe electron distribution in the array. This method is potentially scalable as it does not require a dedicated charge detector in the quantum device3,29. Moreover, operating in the dispersive regime allows for a clear identification of spin states using quantum capacitance spectroscopy30, and single shot readout31,32,33: a singlet state gives finite quantum capacitance at the charge transition, changing the resonator’s response; and a triplet state leaves the response unchanged32,34,35,36,37. The results presented here provide guidelines for scaling-up by replicating the unit cell to build larger bilinear or 2D qubit arrays, and pave the way for the design of spin-based quantum architectures.

Results

Load, isolate and read a double quantum dot

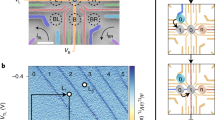
Our device (Fig. 1a) was fabricated in an industrial-research foundry using 300-mm CMOS processes on a silicon-on-insulator substrate. It features a 40 nm-wide 10 nm-thick silicon channel, separated from the substrate by a 145-nm buried oxide layer. Titanium nitride and poly-silicon gates are isolated from the nanowire by a 6-nm layer of thermally grown silicon dioxide. A combination of deep-ultraviolet and electron-beam lithography is used to pattern a single-layer gate structure, as described in refs. 22,38.

Fig. 1: Device description and double quantum dot stability diagram.
figure 1

a SEM micrograph of the 4 split-gate devices. The source (S) and drain (D) ends of the channel are doped, forming electron reservoirs. On the right, an electronic diagram of the experiment is shown. T1 and T2 are connected to tank circuits comprising L1 and L2 and the capacitance to ground. b First, a large voltage (1 V) is applied to ILT to accumulate electrons in the underlying QD. c Then, a finite voltage Vload is applied to T1 to transfer a given number of electrons to the underlying QD. d Finally, ILT is pulsed back to 0 V. At this point, the electrons are trapped in the central array and they can be probed by reflectometry by sweeping the detuning ϵX between T1 and B1. e Derivative of the resonator response at f1 as a function of double dot detuning after completion of the loading procedure. Vload corresponds to the gate voltage applied to T1 during the loading sequence. Horizontal lines indicate charge tunneling between the two dots. The number of lines for a given Vload corresponds to the number of electrons in the isolated structure.

Full size image

The 8 gates of the device, arranged in a 2 × 4 pattern, are labeled as follows: external gates labeled isolation gates (ILB, IRB, IRT and ILT), and central gates, which form the quantum dot array, labeled either top (T1, T2) or bottom (B1, B2) (Fig. 1b). All gates are 40 nm wide and spaced 40 nm apart in both longitudinal and transversal directions. These dimensions were selected to have nominal transverse tunnel couplings in the range of a few GHz, since the dispersive regime requires tunnel coupling to be relatively large compared to RF drive frequency and amplitude39,40. Silicon nitride spacers (35 nm thick) were deposited between the gates before doping the source and drain reservoirs to implant ions. The whole device is encapsulated, and the gates are connected to aluminum bond pads through standard Cu-damascene back-end-of-line processing.

The device is electrically operated as follows: the gates are DC-biased, and T1, T2, B1, and B2 are also connected to a bias tee with cutoff frequency fc = 30 kHz. In addition, T1 and T2 are connected to two tank circuits (Fig. 1a), each comprising an Nb spiral inductor. Inductance was set to L1 = 69 nH for gate T1 and L2 = 120 nH for gate T2. When combined with the parasitic capacitance, CP, of the device, the final LC resonance frequencies were f1 = 1.2 GHz and f2 = 0.8 GHz. At zero magnetic field, CP = 0.25 pF is extracted from the resonance frequencies, with quality factors of around 50 and 20, respectively. The amplitude variation of the reflected radio frequency signal close to the resonance (noted ΔΓ in Fig. 1a) is measured using analog demodulation. At the base temperature of the dilution fridge, applying a positive voltage to the gates leads to the accumulation of quantum dots at the Si-SiO2 interface, allowing the formation of a 2 × 2 quantum dot array when the isolation gates ILB, IRB, IRT, and ILT are used as barriers with respect to the reservoirs.

To isolate charges in the 2 × 2 central array, we first completely deplete the device by applying negative voltages to all gates. Next, we open ILT to accumulate a reservoir underneath (Fig. 1b) and bias T1, the loading dot, at a finite voltage noted Vload (Fig. 1c). By rapidly negatively pulsing ILT, we isolate electrons in dot T1 (Fig. 1d). We then perform quantum capacitance measurements at f1 in the isolated double quantum dot (DQD) T1-B1 and plot them against the voltage applied to T1 during the loading sequence (Fig. 1e). In this representation, the horizontal lines correspond to interdot charge transitions (ICT) in the isolated DQD T1-B1. The number of lines for a given loading voltage corresponds to the number of electrons in the isolated structure. This is further verified by combining traditional charge detection and quantum capacitance measurements. A very good correlation was obtained for the additions of the first electrons (see Supplementary Fig. 1). In subsequent experiments, the number of electrons loaded is in the structure is defined by choosing the proper Vload applied during the loading sequence. Depending on the voltage detuning between the isolation and plunger gates, the electrons loaded can be trapped in the structure for minutes to weeks. Hereafter, we biased our isolation gates to ensure that electrons remained trapped for at least three hours.

An isolated triple quantum dot

Having demonstrated electron loading and control in a DQD, we extended tuning to a triple quantum dot (TQD). A right angle triangular TQD unit cell (see Fig. 2a) could be used to pave a 2D qubit lattice along two orthogonal directions. We start the TQD characterization by loading N electrons into the storage dot T1. Leaving gate T2 at VT2 = 0.6 V, we mapped the stability diagram for gates T1 and B1 with resonator 1, producing Fig. 2b, c for N = 2 and N = 3, respectively. These figures show two sets of lines: one set with slope close to unity and one set with a slightly negative slope. The first set corresponds to ICTs between T1 and B1 and the second set to ICTs between T1 and T2, as confirmed by the electrostatic simulations (inset on Fig. 2b, c). The vertical lines visible in the simulations, corresponding to ICTs between T2 and B1, cannot be resolved in the experimental stability diagram due to their small tunnel coupling, as reflectometry is only sensitive for relatively large tunnel coupling (above 100 Mhz in the present experiment).

Fig. 2: The isolated triple quantum dot.
figure 2

a SEM micrograph of the central array, showing the isolated TQD and the two detuning axes involved. b, c Stability diagrams for the TQD loaded with 2 and 3 electrons, respectively. The insets show electrostatic simulations of the stability diagrams. d, e Stability diagrams using virtual gates for the 2-electron TQD probed at f1 and f2, respectively, in frequency multiplexing. f Sum of the two signals extracted from (d) (red) and (e) (blue). Each bare signal is thresholded giving a colorized pixel for points with signal above the threshold. The dashed black lines correspond to transitions in the diagonal DQD (not visible in the signal).

Full size image

A TQD configuration of particular relevance for quantum information processing is the \(\left(\begin{array}{cc}1&1\\ 1&\end{array}\right)\) charge occupation state10, which is achieved in the middle of the stability diagram for 3 electrons (Fig. 2c). This charge state can be readily induced starting with the DQD which gives the best signal (T1-B1) and tuning it to the (2,1) state before reducing T1 to transfer one electron to T2. Applying this procedure produces unambiguous, clearly visible transitions. Moreover, the \(\left(\begin{array}{cc}1&1\\ 1&\end{array}\right)\) charge occupation state is further confirmed by spin and valley measurements at different ICTs closing this charge state (see Supplementary Fig. 2).

For arrays with capacitive cross couplings, virtual gates are required to achieve accurate tuning6,7,8,15,16. In our array, we extracted a lever arm ratio matrix from the stability diagram and simulations41. Assuming constant electrostatic interactions we constructed the virtual gates matrix (see Supplementary Note 2). Figure 2d presents a 2-electron TQD stability diagram for the two detuning axes (T1-T2 and T1-B1) along the two arms of the TQD following application of virtual gates. The ICTs are now mostly aligned with the horizontal (ϵx) and vertical (ϵy) detuning axis directions, confirming the good approximation of our lever arm ratios and of the constant interaction model.

Frequency multiplexing can provide additional information about which QD is involved in the different ICTs. This information is required to explore a larger number of quantum dots in interaction. As an illustration, we start here with the simple TQD case but will expand to a 2 × 2 array in the next section. Figure 2d, e shows the same stability diagram probed at the same time but at two different frequencies. At f1, we see the transitions involving T1, while at f2 we see those involving T2. Therefore, when we add these two signals after thresholding (see Fig. 2f) we can confirm that the horizontal transitions (blue and red) correspond to an electron tunneling between T1 and T2, whereas the vertical transitions (red only) involve T1 and B1.

The combination of virtual gate and frequency multiplexing greatly facilitates interpretation of the stability diagram, and will be further applied to the 2 × 2 array.

Multiplexed readout of the 2 × 2 array

Having demonstrated control and multiplexed readout of the TQD, we now move to the tuning of the 2 × 2 quantum dot array in the single-electron-occupancy regime, see Fig. 3a. After extracting the virtual gate matrix (see Supplementary Note 2), linear combinations of virtual gates are used to build vertical (ϵy between the lines) and horizontal (ϵx between the columns) detuning of the 2 × 2 array (see Fig. 3b). It is worth noting that those detunings have a different definition from the ones in the TQD case : ϵy, TQD = VT’1 − VB’1 while ϵy, QQD = VT’1 − VB’1 + VT’2 − VB’2 and similarly for ϵx. As a result, and like with the TQD configuration, an ICT can be labeled as a transition between rows if it produces a horizontal line, or between columns if it produces a vertical line, or diagonal when tunneling occurs along the diagonals. The isolated regime can be used to tune the array by applying a simple strategy. First we load the desired number of electrons in the structure and we check at large ϵX, that 4 ICTs are visible, corresponding to transitions within the T1-B1 DQD (Fig. 3c). We easily identify the \(\left(\begin{array}{cc}4&0\\ 0&0\end{array}\right)\) charge state at ϵX = 200 mV and ϵy = −200 mV. Figure 3d presents the multiplexed signal after thresholding. At ϵy = −100 mV, we see two vertical ICTs in both resonators responses as we reduce ϵX toward zero (at ϵX = 65 mV and ϵX = 20 mV). They correspond to transitions between T1 and T2. leading to \(\left(\begin{array}{cc}2&2\\ 0&0\end{array}\right)\) charge state from which we move toward zero ϵY. We see now two horizontal ICTs around ϵY = 50 mV, one in each resonators responses centered around. They correspond to a transition from T1 to B1 (red) and from T2 to B2. After these two transitions we end up in the \(\left(\begin{array}{cc}1&1\\ 1&1\end{array}\right)\) charge state. Therefore, following this path leads to unambiguous determination of charge occupancy.

Fig. 3: Isolated 2 × 2, 4-electron array.
figure 3

a SEM micrograph of the central 2 × 2 array. b Illustration of vertical (top) and horizontal (bottom) detunings using virtual gates \({{{{{\rm{T}}}}}}_{1}^{{\prime} }\), \({{{{{\rm{T}}}}}}_{2}^{{\prime} }\), \({{{{{\rm{B}}}}}}_{1}^{{\prime} }\) and \({{{{{\rm{B}}}}}}_{2}^{{\prime} }\). c Stability diagram at large positive horizontal detuning where 4 electrons are distributed in the left column. d Stability diagram of the 2 × 2 array in the large tunnel coupling regime using vertical and horizontal detuning. The signal is the combination of resonator 1 and 2. Each bare signal is digitized using a threshold with a color pixel for points with signal above the threshold (red for resonator 1 and blue for resonator 2) and a white pixel for points below. To find the \(\left(\begin{array}{cc}1&1\\ 1&1\end{array}\right)\) charge configuration we start with all electrons in T1 (large positive ϵX and large negative ϵY). We play then with ϵX to transfer two charges in T2 and reach \(\left(\begin{array}{cc}2&2\\ 0&0\end{array}\right)\). ϵY is then swept toward zero detuning to transfer one electron from each top quantum dot to each bottom quantum dot.

Full size image

Confirmation of single-occupancy by magnetospectroscopy

To confirm further that we have reached the single-occupancy in each dot we probe spin signature at ICTs. We use magnetospectroscopy which consists in probing the spin-dependent quantum capacitance at the ICTs around zero detuning, see Fig. 4a, as a function of magnetic field. It is important to note that this has been achieved in a smaller tunnel coupling regime compared to Fig. 3d in order to see a spin signature at low magnetic field42. We perform magnetospectroscopy at the \(\left(\begin{array}{cc}1&1\\ 1&1\end{array}\right)\) to \(\left(\begin{array}{cc}1&0\\ 1&2\end{array}\right)\) and the \(\left(\begin{array}{cc}1&0\\ 1&2\end{array}\right)\) to \(\left(\begin{array}{cc}0&0\\ 2&2\end{array}\right)\) transitions, using resonator 2 and 1, respectively. Assuming each column starts in the (1,1) configuration, these two electrons can either form a singlet or a triplet state, the difference in population between these two states depends on the magnetic field and on the temperature during detuning. Moreover, as the detuning is swept across the singlet triplet anti-crossing (see Fig. 4b), a triplet ground state can become an excited state and vice versa. Knowing that only the singlet state gives a finite quantum capacitance response at the ICT, tracking the reflected signal with magnetic field provides information on the spin states present. Figure 4c, d shows a funnel-like quantum capacitance variation as a function of the magnetic field, which is consistent with a singlet-triplet-minus (ST-) response: at zero field, the ground singlet state produces a finite quantum capacitance signal at the ICT, while as the magnetic field increases, the zero quantum capacitance triplet state becomes the ground state. The fluctuations in the background are due to thermal population of the singlet states. These data can be modeled with a two-spin system, where tunnel couplings of 40 μeV and 200 μeV are extracted, respectively, for the left and right columns. These spin signatures confirm that there is an even number of electrons involved. When combined with the multiplexed stability diagram data, they validate that the two transitions are appropriately labeled and that probing quantum capacitance is a viable method to probe spins in the array.

Fig. 4: Spin signature in each column.
figure 4

a Stability diagram using combined signal from the two multiplexed frequencies around zero detuning in the intermediate coupling regime. The two stars label the position where magnetospectroscopy are performed in next (c) and (d). b Energy diagram of the two ground spin states for the left column during the \(\left(\begin{array}{cc}0&0\\ 2&2\end{array}\right)\) to \(\left(\begin{array}{cc}1&0\\ 1&2\end{array}\right)\) transition. In this context, only the singlet state tunneling between (1,1) and (0,2) gives a finite quantum capacitance at the interdot charge transition. c, d Quantum capacitance magneto-spectroscopy at the ICTs \(\left(\begin{array}{cc}0&1\\ 2&1\end{array}\right)\)-\(\left(\begin{array}{cc}1&1\\ 1&1\end{array}\right)\) and \(\left(\begin{array}{cc}1&0\\ 1&2\end{array}\right)\)-\(\left(\begin{array}{cc}1&1\\ 1&1\end{array}\right)\). These are also labeled with a red and blue stars star in (a). Both show a spin-funnel feature characteristic of a transition involving two spins in each column of the array. The dashed line is a parabolic fit showing the position of the ST+ crossing with the applied field also circled in (b).

Full size image

Dispersive single-shot spin readout in the array

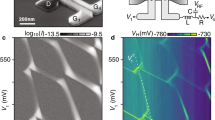
We have demonstrated that dispersive readout is a powerful tool to read interdot charge transitions and tune small arrays. However, if we want to omit external charge sensors in the final device, we must demonstrate that the method can read spin states in a single-shot manner within the array. To demonstrate this, we focus on the transition from \(\left(\begin{array}{cc}2&1\\ 0&1\end{array}\right)\) to \(\left(\begin{array}{cc}1&1\\ 1&1\end{array}\right)\) (Fig. 4a) which will be referred to as (1,1) to (2,0) hereafter. Due to Pauli spin blockade, we can exploit the difference in quantum capacitance between a singlet state that can tunnel between (1,1) and (2,0) and a triplet state that stays blocked in (1,1): the singlet response is finite whereas the triplet response is null. Figure 5a presents multiple detuning sweeps across the ICT from (1,1) to (2,0). At zero field in (1,1), singlet and triplet states are almost degenerate, therefore at finite temperature and within a few ms, these states adopt a Boltzmann distribution. This leads to similar probabilities of finding zero signal and finite signal as we approach the ICT, represented as pixels at two signal levels. As we approach the (2,0) charge state, the singlet state becomes a well separated ground state. Consequently, the top side of the ICT is mostly associated with signal corresponding to the singlet state (see Fig. 4a). To be more quantitative, we extracted the single-shot measurement of the singlet-triplet states. To do so, we started with a mixture of singlet and triplet states, and measured on the ICT where we integrated signals for 100 μs. The result of 30,000 repetitions is binned in the histogram presented in Fig. 5 (b). A charge readout fidelity in the 98% range is determined by fitting the distribution with two Gaussian functions. However, the triplet relaxation time at the measurement point is around 1.5 ms, which reduces spin readout fidelity to 95%. To illustrate the quality of the dispersive spin readout in the array, we replicated the same spin-funnel measurement as we did in Fig. 4c, d but using single-shot readout. More precisely, the experiment consists in initializing a singlet state in (2,0) followed by a detuning pulse toward (1,1). At the detuning amplitude where the Zeeman energy Ez matches the exchange energy (see Fig. 4b), J, the S and T− states mix due to spin orbit interaction, leading to a singlet return probability of 0.543. By mapping the anticrossing position as a function of magnetic field, we reconstruct the variation of exchange interaction with detuning. From this, we extract a tunnel coupling in the order of 30 μeV with a residual exchange interaction J0 deep in (1,1) of 150 MHz. It is worth noting that single shot readout is also possible at other ICTs when T1 is involved in the transition. Unfortunately, the resonator on T2 offers a lower signal-to-noise ratio which precludes single shot measurements in the right column. This limitation can be overcome using resonator with higher quality factor and with a resonance frequency closer to the tunneling rate. Moreover, processing compact inductors in the back-end-of-line should offer a more efficient and integrated readout for arrays.

Fig. 5: Dispersive single-shot spin readout.
figure 5

a Pauli spin blockade signature at the the \(\left(\begin{array}{cc}2&1\\ 0&1\end{array}\right)\)-\(\left(\begin{array}{cc}1&1\\ 1&1\end{array}\right)\) ICT. The detuning is swept across the ICT at zero magnetic field 100 times. On the ICT, the signal strength is maximized when the electron spins on the right column form a singlet state and null when they form a triplet. b Histogram of single-shot measurements performed on the ICT for an equal population of singlet and triplet states with an integration time of 50 μs. The charge readout fidelity of 98% drops to 95% when spin relaxation is accounted for. c Single-shot spin “funnel" experiment at the \(\left(\begin{array}{cc}0&1\\ 2&1\end{array}\right)\)-\(\left(\begin{array}{cc}1&1\\ 1&1\end{array}\right)\) ICT. The right column spins are first initialized in a singlet state followed by a pulse in \(\left(\begin{array}{cc}1&1\\ 1&1\end{array}\right)\) and finally coming back to the ICT for measurement. At finite magnetic field, when the detuning pulse amplitude matches the position of the singlet-triplet minus (S-T−) anticrossing, the singlet state mixes with the triplet state to produce a 0.5 probability of measuring a singlet. The position of this anticrossing is mapped as a function of magnetic field.

Full size image

Discussion

We have demonstrated the operation of a quantum dot array in the isolated regime, where charge occupancy states are characterized by gate-based reflectometry, eliminating the need for a dedicated charge sensor. The low static disorder of the device enables the formation of clean double, triple, and quadruple quantum dots through virtual gating. In triple and quadruple dot configurations, single-occupancy is confirmed by probing spin physics at interdot charge transitions, using dispersive single-shot spin readout where possible and magnetospectroscopy otherwise. This approach offers straightforward electrostatic tuning and represents a scalable pathway for controlling larger quantum dot arrays.

As the size of the array grows, new challenges are expected. A central consideration arises from the dispersive nature of the readout : the signal strength is strongly dependent on tunnel coupling. Precise control of this coupling—whether through dedicated gates or by leveraging geometric control in low disorder devices—is essential. It is worth noting that such control is also necessary for implementing two-qubit gates, making this a shared requirement rather than a limitation specific to gate-based readout.

The increase in the number of qubits also raises the question of the integration and footprint of the tank circuits. Currently, the inductors have an area of around 103 μm2, but using superconducting materials with high kinetic inductance at low temperatures could reduce this footprint by two orders of magnitude44. With such compact dimensions, inductors could be monolithically integrated into the back-end-of-line of industrial semiconductor fabrication processes45.

This method is also promising for extension to other spin qubit platforms, such as SiGe heterostructures. A potential limitation in such systems is their typically smaller lever arm (<0.1 eV/V), compared to the 0.15 eV/V achieved in the present devices. However, strategies such as bringing the two-dimensional electron/hole gas closer to the top interface, or increasing the size of plunger gates, could enhance the lever arm and achieve signal-to-noise ratios comparable to those demonstrated here.

In conclusion, while challenges related to tunnel coupling control, circuit integration, and platform-specific adaptations remain, this method enables the removal of bulky charge sensors from the quantum active area while keeping excellent spin detection properties. Combined with recent advances in resonator technology and qubit design, gate-based reflectometry in the isolated regime presents a clear and scalable path toward large-scale spin qubit arrays.

Methods

Experiments were performed on the CMOS device shown in Fig. 1a using a dilution refrigerator with a base temperature of 30 mK. Gate-based reflectometry was achieved through analog modulation/demodulation followed by digitization using an NI ADC board. The per-point acquisition time is 100 μs. Gate voltages were applied using digital-to-analog converters controlled by an sbRIO-9208 FPGA board and rapid pulses controlled by an RFSoC with a Xilinx ZCU111 FPGA.