INTRODUCTION

Fathoming nonequilibrium universal properties near a quantum critical point (QCP) is one of the central issues in modern physics1,2. Although the general organizing principle for the nonequilibrum critical dynamics is still elusive, a unified framework for understanding the generation of topological defects after the linear quench was proposed by Kibble in cosmological physics and then generalized by Zurek in condensed matter systems3,4. This celebrated Kibble-Zurek mechanism (KZM) has aroused intensive investigations from both theoretical and experimental aspects, exerting far-reaching significance in both classical and quantum phase transitions3,4,5,6,7,8,9,10,11,12,13,14,15,16. More interestingly, it was found that scaling behaviors can also manifest themselves in the driven process17,18,19,20,21. As a generalization of the KZM, a finite-time scaling (FTS) theory was proposed to systematically understand the full scaling properties22,23. These full scaling forms have been verified in various systems from numerical to experimental works11,12,20,22,23,24,25,26,27,28,29. Moreover, the KZM and the FTS recently show their fabulous power in state preparations and probing critical properties in fast-developing programmable quantum devices11,12,28,29,30.

At the core of the original KZM lies the adiabatic-impulse scenario1,2,31. According to it, a crucial prerequisite for the implementation of the KZM is the existence of a gapped initial stage, wherein the system evolves adiabatically along the equilibrium state. The border of this initial stage with the intrinsically nonequilibrium impulse region gives rise to a frozen time1,2,3,4, which dominates the critical dynamics near the critical point, yielding the FTS forms22,23. Moreover, intriguing dynamic scaling behavior dominated by the QCP was also found for driven dynamics from gapless initial phase to cross the QCP in one dimensional spin systems32,33. However, the universal criterion for the validity of KZM and FTS with a gapless initial state has yet to be established.

The QCP occurring in strongly interacting Dirac systems, dubbed as Dirac QCP, represents a typical class of QCP which has joint critical fluctuations from both order parameter and gapless fermions. Studies of Dirac QCP stem from the research in modern high-energy physics, such as chiral symmetry in QCD and mass generation via spontaneous symmetry breaking34,35,36,37. From the perspectives of statistical mechanics and condensed matter physics, the Dirac QCP also attracts enormous attentions, particularly after the experimental realization of two-dimensional Dirac fermions in graphene and various topological insulators or semimetals38,39,40. The presence of Dirac fermions is theoretically revealed to tremendously enrich quantum critical properties, rendering novel universality classes of quantum phase transition without classical counterpart41,42,43,44,45,46,47,48,49,50,51,52.

Interesting aspects of Dirac QCP in equilibrium can suggest interesting phenomena out of equilibrium. Dynamic scaling behaviors were studied in QCPs that feature non-interacting Dirac fermions53,54,55. However, nonequilibrium dynamics in strongly interacting Dirac QCP is still largely unexplored. Particularly, for driven dynamics along the gapless Dirac semimetal (DSM) phase to cross the QCP, whether the original KZM is still applicable remains unknown. Consequently, investigating the nonequilibrium driven dynamics in Dirac QCP has overarching meaning in fundamental theory, as well as immediate applications in the context of detecting and exploring fermionic QCP in experimental platforms38,39,40.

However, directly tackling the real-time dynamics in two or higher spatial dimension is largely hindered by the lack of reliable theoretical or numerical methods. Specifically, quantum Monte Carlo (QMC) fails as a result of the notorious sign problem56,57, while the tensor-network method still needs tremendous improvements despite remarkable progress in recent years58. Fortunately, scaling analysis demonstrates that both real- and imaginary-time driven dynamics share the same scaling form59 as elucidated in Supplementary Note 1. This inference has been verified in various systems27,28,59, bridging the gap between the QMC imaginary-time simulations without sign problem and the real-time dynamics as discussed in Supplementary Note 2.

In this work, we investigate the driven critical dynamics of two representative strongly interacting Dirac QCPs, belonging to chiral Heisenberg and chiral Ising universality classes, respectively, via the determinant QMC method56. By linearly varying the interaction strength along the imaginary-time direction to cross the QCP from both the DSM and Mott insulator phases, we uncover that the driven process near the Dirac QCP satisfies the scaling form of FTS despite the violation of the adiabatic-impulse scenario of the KZM due to the existence of the gapless initial state. Furthermore, we develop a universal criterion for the validity of the KZM and FTS with the gapless initial state. In addition, our numerical simulation achieves the critical exponents of the Dirac QCP, whose values obtained in previous studies on equilibrium properties are still under debate. Through the generalization of quantum driven critical dynamics to strongly interacting Dirac QCP, our study not only leads to an extension of the fundamental theory of KZM and FTS, but also contributes a feasible approach to investigate the fermionic quantum critical phenomena in realistic platform such as quantum materials and devices.

RESULTS

Dynamics in chiral Heisenberg criticality

A typical model hosting Dirac QCP belonging to chiral Heisenberg universality class is the Hubbard model on the half-filled honeycomb lattice with the Hamiltonian42,46,47,48,49

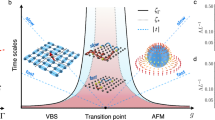
$$H=-t {\sum}_{\langle ij\rangle,\sigma }{c}_{i\sigma }^{{{\dagger}} }{c}_{j\sigma }+U {\sum}_{i}\left({n}_{i\uparrow }-\frac{1}{2}\right)\left({n}_{i\downarrow }-\frac{1}{2}\right),$$
(1)

in which \({c}_{i\sigma }^{{{\dagger}} }\) (cjσ) represents the creation (annihilation) operator of electrons with spin σ, \({n}_{i\sigma }\equiv {c}_{i\sigma }^{{{\dagger}} }{c}_{i\sigma }\) is the electron number operator, t is the hopping amplitude between nearest neighbor sites and set as the energy unit in the following, and U is the strength of the on-site repulsive interaction. The model is absent from sign problem in QMC simulation as discussed in Supplementary Note 2. As shown in Fig. 1, a critical point Uc ≈ 3.85 separates two phases49. When U > Uc, the system is in the antiferromagnetic (AFM) Mott insulator phase in which fermions acquire a mass originating from spontaneous symmetry breaking characterized by the finite AFM order parameter \({m}^{2}={\sum }_{i,j}{\eta }_{i}{\eta }_{j}\langle {S}_{i}^{z}{S}_{j}^{z}\rangle /{L}^{2d}\) with \({S}_{i}^{z}\equiv (1/2){{{{\bf{c}}}}}_{i}^{{{\dagger}} }{\sigma }^{z}{{{{\bf{c}}}}}_{i}\), c ≡ (c↑, c↓), and ηi = ± 1 for i ∈ A(B) sublattice42,48,49. Here, L is the linear size of the system and d = 2 is the spatial dimension. In this phase, the transverse spin excitation is massless due to the presence of the Goldstone modes. In contrast, when U < Uc, the system is in the DSM phase with four-component massless Dirac fermion (Nf = 2). At Uc, both Dirac fermions and AFM order parameter bosons are gapless, yielding the Gross-Neveu QCP belonging to chiral Heisenberg universality class42,46,47,48,49.

Fig. 1: Time scales for driven critical dynamics.
figure 1

The quantum critical point at Uc separates the Dirac semimetal (DSM) phase featured by the fermionic Dirac cone (violet cone) and massive bosonic modes (golden paraboloid) from the antiferromagnetic (AFM) phase featured by the massive fermionic excitation (violet hyperbolic paraboloid) and massless bosonic modes (golden Mexican hat). The gradient yellow background around Uc indicates the critical region. The correlation time scales ζ for both boson (yellow solid curve) and fermion (violet solid curve) are finite in one phase but divergent (symbolized by “∞”) in the other phase. The dashed line denotes the time distance ∣U − Uc∣/R to the critical point for different driving rates. Accordingly, the prerequisite of the original KZM that a gapped initial state should exist to protect an initial adiabatic stage, in which the transition time is larger than the correlation time, breaks down.

Full size image

Here we begin to explore whether the FTS forms are still applicable in the driven dynamics of this Dirac QCP with composite critical fluctuations from gapless initial states. First we study the driven dynamics by varying U with imaginary time τ as U = U0 + Rτ from the DSM initial state with U0 = 0, as illustrated in Fig. 1. We denote the distance to the critical point as g (here g = U − Uc). The smallest lattice size is chosen as L = 18 to eliminate the scaling violation induced by small sizes. When g = 0, from Fig. 2a, we find that for large R, m2 ∝ L−2R−0.26(1) with the exponent on R close to (2β − dν)/νr = − 0.26(2), in which β = 0.76(2) and ν = 1.02(1) are the exponents for order parameter and correlation length, respectively49, and r  = z + 1/ν is the scaling dimension of R. Here the dynamic exponent z equals one in the Gross-Neveu Dirac QCP owing to the Lorentz symmetry of the effective model47. Additionally, the exponent on R is almost independent of L. In contrast, when R is small, Fig. 2a shows that m2 tends to saturate and the usual finite-size scaling m2 ∝ L−2β/ν is restored. To reconcile these rescaling relations, the scaling form must satisfy

$${m}^{2}(R,L,g)={L}^{-d}{R}^{(2\beta -d\nu )/\nu r}{{{\mathcal{F}}}}(R{L}^{r},g{L}^{1/\nu }),$$
(2)

in which \({{{\mathcal{F}}}}\) is a non-singular scaling function and therein dimensionless quantity gL1/ν is also included to take account of the off-critical-point effects. Eq. (2) is consistent with the FTS in conventional bosonic QCP24,25.

Fig. 2: Driven dynamics from the DSM phase of model (1).
figure 2

a, b are log-log plots of m2 versus R for different L driven to Uc = 3.85 before and after rescaling. Inset in (a) shows m2 ∝ L−2 for R = 0.3 (dash-dotted line). For large R, power fitting for L = 24 (black solid line) shows m2 ∝ R−0.26(1) with the exponent close to (2β − dν)/νr  = − 0.26(2) (dash line) from ref. 49. c, d are curves of m2 versus g for fixed RLr = 5.41 and different L before and after rescaling. The arrow indicates the driving direction. The errorbars represent one standard deviation.

Full size image

To confirm Eq. (2), we find that Eq. (2) yields the scaling form \({m}^{2}(R,L)={L}^{-2\beta /\nu }{{{{\mathcal{F}}}}}_{1}(R{L}^{r})\) at g = 0. Here, we rescale m2 and R as m2L2β/ν and RLr with the exponents β = 0.76(2), ν = 1.02(1)49, and z = 147 set as input, and reveal that the rescaled curves collapse well into a single curve, as shown in Fig. 2b, confirming Eq. (2) at g = 0.

In addition, to unravel the scaling properties in the driven process near Uc, we calculate the dependence of m2 on g for an arbitrary fixed RLr = 5.41 and present the results in Fig. 2c. After rescaling m2 and g by L2β/ν and L1/ν, the curves with various L collapse into each other, as displayed in Fig. 2d, confirming that the universal scaling behavior of physical observable in the driven process is described by Eq. (2).

The reason for the appearance of the scaling relation m2 ∝ L−dR(2β−dν)/νr is that for large R, driven induced length scale ξR ~ R−1/r is smaller than L. Thus, the definition of m2 indicates that m2 ∝ L−d owing to the central limit theorem. Meanwhile, the rest part of the dimension of m2 should be borne by R, giving rise to the leading term of Eq. (2). In this case, \({{{\mathcal{F}}}}(R{L}^{r},0)\) tends to a constant. In contrast, for small R, ξR  > L, such that the conventional finite-size scaling at equilibrium m2 ∝ L−2β/ν is recovered, and \({{{\mathcal{F}}}}(R{L}^{r},0)\) obeys \({{{\mathcal{F}}}}(R{L}^{r},0) \sim {(R{L}^{r})}^{d/r-2\beta /\nu r}\).

Next, we turn to explore the driven dynamics starting from the Mott insulator initial state and U is changed as U = U0 − Rτ with U0 = 11.85. This Mott insulator state has the AFM order with transverse gapless modes. For large R, Fig. 3a shows that m2 ∝ R0.73(2) with the exponent close to 2β/νr = 0.75(2)49 and is nearly independent of L. Combining this scaling relation with the usual finite-size scaling m2 ∝ L−2β/ν which is restored for small R, the scaling form should obey

$${m}^{2}(R,L,g)={R}^{2\beta /\nu r}{{{\mathcal{G}}}}(R{L}^{r},g{L}^{1/\nu }),$$
(3)

where \({{{{{\mathcal{G}}}}}}\) is the scaling function and g is also included therein. Eq. (3) is also accordant with the conventional FTS with ordered initial state22,23,24.

Fig. 3: Driven dynamics from the AFM phase of model (1).
figure 3

a, b are log-log plots of m2 versus R for different L driven to Uc = 3.85 before and after rescaling. For large R, power fitting (black solid line) shows m2 ∝ R0.73(2) with the exponent close to 2β/νr  =  0.75(2) (dash line) from ref. 49. c, d are curves of m2 versus g for fixed RLr  =  41.5 and different L before and after rescaling. The arrow indicates the driving direction. The errorbars represent one standard deviation.

Full size image

We rescale curves of m2 versus R for various L at g = 0 according to the scaling function \({m}^{2}(R,L)={L}^{-2\beta /\nu }{{{{\mathcal{G}}}}}_{1}(R{L}^{r})\) and find that the rescaled curves collapse well, which confirms Eq. (3) at g = 0. Note that in Fig. 3b slight deviation appears in the large R region, which may stem from the influence of high-energy modes caused by fast driving. Furthermore, Fig. 3c shows the curves of m2 versus g for an arbitrary fixed RLr. The rescaled results (gL1/ν, m2L2β/ν) for various L collapse into a single smooth curve, as displayed in Fig. 3d, confirming that the driven process from AFM initial state is described by Eq. (3).

The appearance of m2 ∝ R2β/νr reflects the fact that when ξR < L the initial ordered magnetization domain is maintained. In this case, \({{{\mathcal{G}}}}(R{L}^{r},0)\) in Eq. (3) tends to a constant and \({{{{\mathcal{G}}}}}_{1}(R{L}^{r}) \sim {(R{L}^{r})}^{2\beta /\nu r}\). In contrast, for small R with ξR  > L, the usual finite-size scaling m2 ∝ L−2β/ν is recovered, indicating that \({{{\mathcal{G}}}}(R{L}^{r},0) \sim {(R{L}^{r})}^{-2\beta /\nu r}\) and \({{{{\mathcal{G}}}}}_{1}(R{L}^{r})\) tends to a constant.

Dynamics in chiral Ising criticality

To further verify the FTS in Dirac systems, we also explore the driven dynamics of Dirac QCP belonging to chiral Ising universality class, which is realized in the interacting spinless fermion model on the half-filled honeycomb lattice with the Hamiltonian50,51,60:

$$H=-t {\sum}_{\langle ij\rangle }{c}_{i}^{{{\dagger}} }{c}_{j}+V {\sum}_{\langle ij\rangle }\left({n}_{i}-\frac{1}{2}\right)\left({n}_{j}-\frac{1}{2}\right),$$
(4)

where V measures the nearest-neighbor interaction. The model is amendable to sign-problem-free QMC simulation as discussed in Supplementary Note 261,62,63. It was shown that the ground state undergoes a continuous quantum phase transition at Vc ≈ 1.355 from the DSM phase to the charge-density-wave (CDW) insulator phase, characterized by the order parameter m2 ≡ ∑i,jηiηj〈(ni − 1/2)(nj − 1/2)〉/L2d with ηi = ± 1 for i  ∈  A(B) sublattice50,51,60. At V  = Vc, both fermion and boson degrees of freedom are gapless, similar to model (1). However, a difference is that in the CDW phase, the bosonic fluctuation is fully gapped owing to the discrete symmetry breaking.

For the driven dynamics under changing V as V = V0 + Rτ from the DSM initial state with V0 = 0, Figure 4a shows that at g = 0, for large R, m2 ∝ L−2R−0.336(4) with the exponent on R close to (2β − dν)/νr = − 0.31(4) in which β = 0.47(4), ν = 0.74(4)60, and z = 164; whereas m2 ∝ L−2β/ν for small R, similar to the results in model (1). In addition, we find the rescaled curves of m2 versus R and g collapse well, as shown in Fig. 4b, d, confirming that Eq. (2) gives a universal description on the driven critical dynamics from the DSM initial state.

Fig. 4: Driven dynamics from the DSM phase of model (4).
figure 4

a, b are log-log plots of m2 versus R for different L driven to Vc  = 1.355 before and after rescaling. Inset in (a) shows m2 ∝ L−2 for R  = 0.3 (dash-dotted line). For large R, power fitting for L = 24 (black solid line) shows m2 ∝ R−0.336(4) with the exponent close to (2β − dν)/νr = − 0.31(4) (dash line) from ref. 60. c, d are curves of m2 versus g for fixed RLr  = 63.34 and different L before and after rescaling. The arrow indicates the driving direction. The errorbars represent one standard deviation.

Full size image

For the driven dynamics under changing V as V  = V0 − Rτ from the CDW initial state with V0 = 2.5, Fig. 5a shows that at g =  0, for large R, m2 ∝ R0.496(6) with the exponent close to 2β/νr = 0.54(4)60, whereas m2 ∝ L−2β/ν for small R, similar to the case of chiral Heisenberg universality class. Moreover, Eq. (3) is verified by the data collapse of the curves (RLr, m2L−2β/ν) at fixed g = 0 and (gL1/ν, m2L−2β/ν) for an arbitrary RLr, as shown in Fig. 5b, d. Consequently, Eq. (3) provides a universal description on the driven dynamics from ordered initial states, regardless of whether or not initial gapless bosonic modes exist.

Fig. 5: Driven dynamics from the CDW phase of model (4).
figure 5

a, b are log-log plots of m2 versus R for different L driven to Vc = 1.355 before and after rescaling. For large R, power fitting (black solid line) shows m2 ∝ R0.496(6) with the exponent close to 2β/νr = 0.54(4) from ref. 60 (dash line). c, d are curves of m2 versus g for fixed RLr  = 87.97 and different L before and after rescaling. The arrow indicates the driving direction. The errorbars represent one standard deviation.

Full size image

General scaling theory

The above numerical results remarkably demonstrate that the FTS forms are applicable despite the existence of gapless initial states which can violate the adiabatic-impulse scenario of the original KZM. Thus, it is imperative to develop a universal scaling scenario.

In driven dynamics starting from a ground state far from the critical point, the driving rate R uniquely quantifies the extent of departure from the equilibrium state. Within the original KZM, the existence of an initial adiabatic stage stabilized by a finite gap can remarkably suppress excitations triggered by external driving1,2,31. This leads to the fact that the excitations are predominantly generated near the QCP. Consequently, the dimension of the driving rate R, namely r, is exclusively determined by the critical exponents of the QCP, forming the basis for the original KZM and FTS.

In contrast, at first sight, for the driven dynamics evolving along a gapless initial stage and then crossing the QCP, the excitations can also be copiously produced in the initial gapless phase and subsequently brought into the critical region to influence the nonequilibrium properties near the QCP. Accordingly, we can formulate a scale transformation under which a macroscopic quantity Q should transform as

$$Q(R,g,L,{Q}_{0};R^{\prime} )={b}^{-\kappa }Q(R{b}^{r},g{b}^{1/\nu },L{b}^{-1},{Q}_{0}{b}^{{\kappa }_{0}};R^{\prime} {b}^{r^{\prime} }),$$
(5)

in which b (b > 1) is the rescaling factor, κ is the scaling dimension of Q, and \(R^{\prime}\) along with its exponent \(r^{\prime}\) characterizes the contribution from the excitations generated in the gapless initial stage. Note that although the value of \(R^{\prime}\) is equal to that of R, in general, they can have different scaling dimensions. Specifically, \(r^{\prime}\) is dictated by the exponent of the gapless phase; whereas r is determined by the exponent of the QCP. In addition, in Eq. (5), Q0 and κ0 represent the initial value of Q and its scaling dimension, respectively. From Eq. (5), one finds that when \(r^{\prime} < r\), the nonequilibrium dynamics across the QCP is governed R with dimension r and the usual KZM and FTS can be restored.

Moreover, in practice, the condition can be further refined. Since the gapless phase can be viewed as a continuous set of critical points belonging to the same universality class, its stability requires that the tuning parameter Λ [for example, U or V in the DSM phase in models (1) and (4), respectively] must be either irrelevant or at most marginally irrelevant. More precisely, under a scale transformation with a coarse graining factor b (b > 1), Λ changes as Λ → Λbλ with λ≤ 0. Applying this scaling to a change in the tuning parameter, \(\Delta \Lambda=R{\prime} \Delta t\), we obtain \(\Delta \Lambda {b}^{\lambda }=R^{\prime} {b}^{r^{\prime} }\Delta t{b}^{-z^{\prime} }\). This leads to the relation \(r^{\prime}=\lambda+z^{\prime}\), where \(z^{\prime}\) is the dynamic exponent of the gapless phase (which may differ from z characterizing QCP). Hence, \(r^{\prime} \le z^{\prime}\) because λ ≤ 0, with equality holding for the marginally irrelevant case.

Consequently, we arrive at the precondition under which the usual KZM and FTS can be recovered for the gapless initial state,

$$z^{\prime} < r,\,\,r=z+\frac{1}{\nu }.$$
(6)

Should Eq. (6) be met, the preponderant nonequilibrium universal behaviors will originate from the critical region of QCP because \(r^{\prime} < r\), and R with exponent r will govern the dynamic scaling behaviors, while the variable \(R^{\prime}\) can be neglected in Eq. (5). To illustrate this, we consider the scaling of m2. By setting the coarse-graining factor to b = R−1/r in Eq. (5), we can transform Eq. (5) into,

$${m}^{2}(R,g,L,{m}_{0}^{2})={m}_{0}^{2}{R}^{2\beta /\nu r-{x}_{0}/r}{{{\mathcal{K}}}}(g{R}^{-1/\nu r},L{R}^{1/r}),$$
(7)

The scaling function \({{{\mathcal{K}}}}(g{R}^{-1/\nu r},L{R}^{1/r})\) can be equivalently rewritten as \({{{{\mathcal{K}}}}}_{1}(g{L}^{r},L{R}^{1/r})\). For the ordered initial state, \({m}_{0}^{2}\) approaches a saturation value, and x0 = 0. In this case, Eq. (7) reduces to Eq. (3), thus recovering the expected scaling. In contrast, for the DSM initial state, since \({m}_{0}^{2}\propto {L}^{-d}\), x0 = d and Eq. (7) recovers Eq. (2).

Now we apply the general discussion elaborated above to the models we are currently dealing with.

  • For driven dynamics from the DSM phase, as illustrated in Fig. 1, the DSM phase is characterized by low-energy physics dominated by the fermion fluctuations exhibiting linear dispersion, \({E}_{k}={v}_{f}| k{| }^{z^{\prime} }\), where \(z^{\prime}=1\) and vf represents the fermion velocity. Given that in the DSM phase \(z^{\prime}=1\), Eq. (6) is apparently fulfilled. Consequently, the nonequilibrium dynamics across the QCP should be described by the standard FTS form.

  • For driven dynamics from the AFM phase, in the AFM phase, the Dirac fermions feature a gap related to the amplitude of the AFM order parameter, and the low-energy excitations are predominantly attributed to bosonic spin waves, which correspond to the gapless Goldstone modes due to the broken spin rotation symmetry. The AFM spin wave has the linear dispersion as \({E}_{k}={v}_{b}| k{| }^{{z}^{\prime}}\), where \(z^{\prime}=1\) and vb denotes the spin wave velocity. Again, Eq. (6) is satisfied and the standard FTS form should be recovered.

Physically, in both DSM and AFM phases, different interaction strengths just yield different low-energy excitation velocity, but do not change the linear form of low-energy dispersion65. Therefore, the interaction strength are marginally irrelevant and the dimension of \(R^{\prime}\) reduces to \(z^{\prime}=1\). In contrast, in the critical region of the QCP, with the onset of ordering of the bosonic order parameter fields, both the bosonic and fermionic degrees of freedom evolve into the low-energy excitations. Apart from the remarkable proliferation of low-energy modes, the mutual interactions among them trigger intrinsic changes in the scaling dimensions of both Dirac fermion and order parameter, rather than merely adjusting vf and vb. In this case, U in model (1) [or V in model (4)] becomes relevant and (U − Uc) in model (1) [or (V − Vc) in model (4)] has the dimension of 1/ν. Consequently, R with dimension r is more relevant than \(R^{\prime}\).

DISCUSSION

In summary, we investigate the driven dynamics of QCP in two representative interacting Dirac-fermion systems, belonging to chiral Heisenberg and chiral Ising universality classes, respectively, through sign-problem-free QMC simulation. Driving the system from both DSM and Mott insulator phases as the initial states, we discover varieties of interesting nonequilibrium scaling behaviors. Furthermore, we confirm that these scaling behaviors can be unified by the full scaling form of the FTS theory.

From the theoretical perspectives, through this work we not only successfully generalize the KZM and FTS to critical systems with joint fluctuations of gapless fermions and bosons, but also propose a general criterion for the validity of the KZM and FTS with a gapless initial state. The general criterion, Eq. (6), can extend well beyond the scope of Dirac QCP. For instance, it was found that the density of excitations nex in the driven dynamics of the one dimensional spin chain with dispersion \({E}_{k}\propto \sqrt{{c}^{2}{k}^{2}+{k}^{4}}\) shows the scaling relation nex ∝ R1/3 under changing c linearly to cross its QCP at c = 032. In this case, the low-energy mode of the gapless phase has the linear dispersion with \(z^{\prime}=1\) and c is marginally irrelevant with zero scaling dimension. In contrast, near the QCP, the quadratic dispersion begins to dominate such that z = 2, and c becomes relevant with the scaling dimension of 1/ν = 1, which can be obtained by comparing the dimensions of c and k. Apparently, the criterion of Eq. (6) is fulfilled and nex satisfy the KZM of the QCP, i.e., n ∝ Rd/r with d = 1 and r = 3. In addition, Eq. (6) can also apply to the dynamic scaling in other QCPs18,33, as discussed further in Supplementary Note 3.

From the application perspectives, we demonstrate that the nonequilibrium scaling form is capable of determining the critical exponents in Dirac QCP, providing an effective method to deciphering quantum critical properties in terms of driven dynamics. A large discrepancy in the critical exponents of the chiral Heisenberg universality class still exists despite extensive studies42,49. By directly fitting the curves of m2 versus R in large R region with the power function for both DSM and AFM initial states, as shown in Fig. 2a and Figure 3a, respectively, we obtain (2β/νr − d/r) = −0.26(1) and 2β/νr = 0.73(2). By setting z = 1, we obtain critical exponents ν = 0.98(4) and β = 0.72(4), which are consistent with ν = 1.02(1) and β = 0.76(2) from ref. 49 within error-bars. The detailed derivation and other ways to estimate critical exponents via FTS are shown in Supplementary Notes 4 and 5, and the corresponding results are shown in Supplementary Tables 1 and 2. It is important to note that equilibrium methods often require larger system sizes and careful finite-size scaling corrections to achieve comparable accuracy49. In contrast, in the framework of driven dynamics, the driven rate R constitutes a new tuning parameter. At large R, the impact of finite-size corrections is diminished, allowing for reliable critical exponent determination with relatively small system sizes. Moreover, the availability of diverse driving protocols with distinct FTS forms provides a compelling means to confirm the robustness and accuracy of these critical exponent determinations, as discussed further in Supplementary Note 5.

From experimental perspectives, driven dynamics is observed in cold-atom systems11,20. Due to recent developments in cold-atom-based quantum simulators of fermions66,67,68, it is promising to detect driven dynamics in Dirac QCP and verify the generalized KZM and FTS as discussed in our study in these platforms. In real experiments, thermal fluctuations will inevitably enter. Thus, the scaling form should include TR−z/r as an additional variable in the full scaling form26,69. Nonetheless, as T−1/z plays similar roles as the system size in QCP, the scaling behaviors for large R are expected to be almost independent of T, in analogy to the finite-size cases. Physically, for large R, excitations induced by driving dominate over those induced by thermal fluctuations and therefore contribute the main dynamic scaling behaviors. Accordingly, it is foreseeable that the methodological approach developed here can be used to probe the critical properties in real experiments.

METHODS

Quantum Monte Carlo simulation of driven dynamics in imaginary-time direction

We have explored the driven dynamics of the Hubbard model (1) and the t-V model (4). Here, we elucidate the implementation of QMC to simulate the imaginary-time driven dynamics.

For models (1) and (4), we linearly vary the interaction strength U(V) with imaginary time variable τ at the rate R as

$$U(\tau )={U}_{0}\pm R\tau,$$
(8)
$$V(\tau )={V}_{0}\pm R\tau,$$
(9)

where the  + ( − ) represents driving from disordered (ordered) initial state at U0(V0). In our numerical simulation, for disordered initial state, we set U0 = 0, V0 = 0, while for ordered initial state we set U0 = 11.85, V0 = 2.5 far from the critical point.

The wave function \(\left\vert \psi (\tau )\right\rangle\) obeys the imaginary-time Schrödinger equation59

$$-\frac{\partial }{\partial \tau }\left\vert \psi (\tau )\right\rangle=H(\tau )\left\vert \psi (\tau )\right\rangle .$$
(10)

The formal solution of Eq. (10) is given by \(\left\vert \psi (\tau )\right\rangle=U(\tau,0)\left\vert \psi (0)\right\rangle\) in which time evolution operator

$$U(\tau,0)={{{\rm{T}}}}\,\exp \left[-\int_{0}^{\tau }d{\tau }^{{\prime} }H({\tau }^{{\prime} })\right],$$
(11)

with T being the time-ordering operator in imaginary-time direction. For the left vector \(\left\langle \psi (\tau )\right\vert=\left\langle \psi (0)\right\vert {U}^{{{\dagger}} }(\tau,0)\) with \({U}^{{{\dagger}} }(\tau,0)=\overline{{{{\rm{T}}}}}\,\exp \left[-\int_{0}^{\tau }d{\tau }^{{\prime} }H({\tau }^{{\prime} })\right],\) the Hermite conjugate simply changes the time-ordering operator T to an anti-time-ordering operator \(\overline{{{{\rm{T}}}}}\). Since the model (1) and (4) is sign-problem-free and imaginary-time evolution does not induce additional sign problem, the imaginary-time dynamics of the models can be simulated by the determinant quantum Monte Carlo (DQMC) method.

To facilitate DQMC simulations of models (1) and (4), we begin by expressing the Hamiltonian in the form

$$H(\tau )={H}_{t}+{H}_{I}(\tau ),$$
(12)

where Ht represents the kinetic energy and HI(τ) the interaction term, in which the interaction strength varies with τ. The initial state \(\left\vert \psi (0)\right\rangle\) is the ground state of H(0). In the DQMC simulation56, the ground state of a given Hamiltonian is accessed by performing imaginary-time evolution on a trial wave function:

$$\left\vert \psi (0)\right\rangle={{\lim}}_{{\tau }_{0}\to \infty }{e}^{-{\tau }_{0}H(0)}\left\vert {\psi }_{T}\right\rangle,$$
(13)

where \(\left\vert {\psi }_{T}\right\rangle\) is a Slater-determinant wave function generated as the ground state of the Ht. Consequently, for disordered DSM initial state \(\left\vert \psi (0)\right\rangle=\left\vert {\psi }_{T}\right\rangle\), we set projection time τ0 = 0. For the AFM or CDW ordered initial state, a sufficiently long τ0 is necessary to project the ∣ψT onto the ground state of H(0). In our simulations, we implement τ0 = 120 for the model (1), and τ0 = 20 for the model (4). We have numerically verified the convergence of our results with respect to increasing τ0.

Following the standard DQMC methodology56, we employ the Trotter decomposition to discretize imaginary time. Subsequently, we apply the Hubbard-Stratonovich (HS) transformation to decouple the fermion-fermion interaction, transforming it into a fermion bilinear form coupled to auxiliary fields. First, we perform Trotter decomposition on the process of imaginary-time evolution to generate initial state in (13):

$$\left\vert \psi (0)\right\rangle={{\lim}}_{\Delta \tau \to 0}{\prod }_{n=1}^{{N}_{{\tau }_{0}}}{e}^{-\Delta \tau {H}_{t}}{e}^{-\Delta \tau {H}_{I}(0)}\left\vert {\psi }_{T}\right\rangle,$$
(14)

where Δτ is the imaginary-time Trotter time defined by \(\Delta \tau={\tau }_{0}/{N}_{{\tau }_{0}}\).

Similarly, the Trotter decomposition in driven dynamics is expressed as

$${{{\rm{T}}}}\,\exp \left[-\int_{0}^{\tau }d{\tau }^{{\prime} }H({\tau }^{{\prime} })\right]={{\lim}}_{\Delta \tau \to 0}{\prod }_{n=1}^{{N}_{\tau }}\left[{{{{\rm{e}}}}}^{-\Delta \tau {H}_{t}}{{{{\rm{e}}}}}^{-\Delta \tau {H}_{I}({\tau }_{n})}\right],$$
(15)

where the Trotter time is defined as Δτ  = τ/Nτ, with with Nτ the number of time slices and τn = nΔτ. Combining these two parts, the wave function \(\left\vert \psi (\tau )\right\rangle\) is expressed as:

$$\left\vert \psi (\tau )\right\rangle=U(\tau,0){P}_{G}\left\vert {\psi }_{T}\right\rangle,$$
(16)

where \(U(\tau,0)={{\lim}}_{\Delta \tau \to 0}{\prod }_{n=1}^{{N}_{\tau }}\left[{{{{\rm{e}}}}}^{-\Delta \tau {H}_{t}}{{{{\rm{e}}}}}^{-\Delta \tau {H}_{I}({\tau }_{n})}\right]\) and \({P}_{G}={{\lim}}_{\Delta \tau \to 0}{\prod }_{n=1}^{{N}_{{\tau }_{0}}}\left[{e}^{-\Delta \tau {H}_{t}}{e}^{-\Delta \tau {H}_{I}(0)}\right]\). In our practical implementation, we choose Δτ = 0.05 in both (14) and (15). We have numerically confirmed that Δτ = 0.05 is sufficiently small to guarantee that the time-step error introduced by the Trotter decomposition is negligible, with the details shown in the Supplementary Note 6.

Next, we apply the HS transformation to decouple the interacting part HI(τ) in models (1) and (4). For the Hubbard interaction in (1):

$${{{{\rm{e}}}}}^{-\frac{\Delta \tau U({\tau }_{n})}{2}{\left({n}_{i\uparrow }+{n}_{i\downarrow }-1\right)}^{2}}=\mathop{\sum}_{{l}_{i,{\tau }_{n}}=\pm 1,\pm 2}\gamma ({l}_{i,{\tau }_{n}}){{{{\rm{e}}}}}^{{{{\rm{i}}}}\sqrt{\frac{\Delta \tau U({\tau }_{n})}{2}}\eta ({l}_{i,{\tau }_{n}})\left({n}_{i\uparrow }+{n}_{i\downarrow }-1\right)},$$
(17)

and for the density interaction in (4):

$${{{{\rm{e}}}}}^{-\frac{\Delta \tau V({\tau }_{n})}{2}{\left({c}_{i}^{{{\dagger}} }{c}_{j}+{c}_{j}^{{{\dagger}} }{c}_{i}\right)}^{2}}=\mathop{\sum}_{{l}_{i,{\tau }_{n}}=\pm 1,\pm 2}\gamma ({l}_{i,{\tau }_{n}}){{{{\rm{e}}}}}^{{{{\rm{i}}}}\sqrt{\frac{\Delta \tau V({\tau }_{n})}{2}}\eta ({l}_{i,{\tau }_{n}})\left({c}_{i}^{{{\dagger}} }{c}_{j}+{c}_{j}^{{{\dagger}} }{c}_{i}\right)},$$
(18)

where the four-component space-time auxiliary fields γ and η take the following values:

$$\gamma (\pm 1)=1+\sqrt{6}/3,\gamma (\!\pm\! 2)=1-\sqrt{6}/3,$$
(19)
$$\eta (\pm 1)=\pm \sqrt{2\left(3-\sqrt{6}\right)},\eta (\!\pm\! 2)=\pm \sqrt{2\left(3+\sqrt{6}\right)}.$$
(20)

Subsequent to the procedures outlined above, both the imaginary-time evolution operator U(τ, 0) and the generator of the initial state PG can be expressed as products of exponentials of fermion bilinear operators. This representation significantly simplifies calculations, enabling the straightforward determination of wavefunction overlaps under imaginary-time evolution 〈ψ(τ)∣ψ(τ)〉 and the expectation values of observables \(\langle O(\tau )|=\rangle \frac{\left\langle \psi (\tau )\right\vert O\left\vert \psi (\tau )\right\rangle }{\langle \psi (\tau )| \psi (\tau )\rangle }\) in the framework of conventional DQMC56.

For updating the auxiliary fields, we employ a local update scheme, sequentially updating the field at each site and time slice. In non-equilibrium simulations, one Markov chain consists of Nsweep iterations. Each iteration involves updating all sites across all time slices, resulting in a total of \({N}_{{{{\rm{sweep}}}}}({N}_{\tau }+{N}_{{\tau }_{0}}){N}_{{{{\rm{site}}}}}\) Monte Carlo updates per chain, where Nsweep typically ranges from 102 to 103. Here, Nsite represents the number of lattice sites. To ensure thermalization, we perform an initial equilibration of 5 sweeps before taking measurements. Finally, for each data point, we typically run two independent Markov chains to improve statistical sampling.