Introduction

Symmetry breaking is a fundamental concept, underpinning interesting phenomena such as collective excitations, phase transitions, and odd viscosity and elasticity1,2,3,4,5. Spatial or temporal symmetry breaking in open, non-equilibrium systems leads to so called non-reciprocal forces between the constituents6,7. Non-reciprocal forces have been observed in mechanical systems with asymmetric (pair-wise) mutual interactions8,9, symmetric assemblies of particles with different chemical properties10,11, charged particles in flowing ion solutions12, complex plasmas13,14,15, in acoustically bound many-particle systems16, in optically bound nanoparticle heterodimers5,17,18,19,20,21,22,23,24,25,26,27 and in quantum, non-hermitian systems of optically coupled nanoparticles28,29.

Despite these successes that are based on 2-body interactions, our understanding of symmetry breaking-associated N-body forces remains a challenge. For example, other than the Axilrod-Teller three-body Van der Waals force30,31,32, little is known of what symmetries must be broken to produce N-body forces. This limited knowledge makes it difficult to predict or quantify how symmetry breaking at the microscopic level affects macroscopic behavior, especially in nonrelativistic, non-equilibrium systems where long-range interactions (like electromagnetism) dominate. Moreover, theoretical modeling often struggles to fully capture and elucidate N-body forces in complex systems, as the complexity of the interactions grows exponentially with the number of particles involved. Therefore, statistical approaches have been serving as the primary theoretical treatment of these systems33.

Although some studies have explored non-reciprocal effects in various systems of asymmetric interactions34,35,36, current theoretical frameworks fall short in demonstrating the dynamics resulting from N-body interactions among particles with homogeneous properties. This is largely because existing symmetry-breaking models are rooted in the inhomogeneity of interacting particles, such as distinct polarizabilities25,26,37,38 and surface boundary conditions36. Addressing these limitations is essential for advancing our understanding of collective behaviors across diverse fields.

In this paper, we consider optical matter (OM) systems5,17,18,19,20,21,22,23,24,25,26,27 of three or more identical Ag nanoparticles in a laser trap with optical forces arising from N-body electrodynamic interactions among them. We show that breaking the spatial symmetries of 3 or more nanoparticles gives rise to non-reciprocal force that, in turn, determines the collective behavior of the system. The electrodynamic interactions and N-body forces are calculated using rigorous Generalized Multiparticle Mie Theory (GMMT) simulations and Maxwell stress tensor analysis. We demonstrate that these interactions manifest in an analytical description of 3-body terms in the point-dipole model of particle-field interactions. The N-body non-reciprocal forces only arise for three or more particles maintained in a bent configuration (see Fig. 1d) where the OM system has broken mirror (reflection) symmetry. The requisite symmetry breaking is realized in experiment by trapping many Ag nanoparticles using an optical ring trap to sustain the bent configuration39. Having assured the absence of transverse phase gradients in the ring that would drive the nanoparticles25,37,38, the observed collective azimuthal motion of the ring of optically bound nanoparticles is due to these N-body non-reciprocal forces. The phenomenon we describe is fundamentally distinct from previous studies of self-rotation of particles due to spin-orbit conversion in light-matter interactions40,41,42,43,44,45,46,47,48,49,50,51. The magnitude of the N-body force is shown to increase with the number of particles in the ring, and is sensitive to the inter-particle separations.

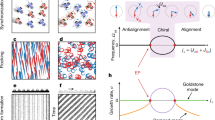
Fig. 1: Symmetry breaking and non-reciprocal force.
figure 1

a, b Induced dipoles in the linear and bent trimer for y-polarized light (vertical in the panel); the trimer in (b) is bent at 19° and has a net force in the y direction. c, d Induced dipoles in the linear and bent trimer for rhc-polarized light; the bent trimer in (d) has a net force in the x direction. e, f Electromagnetic field intensity contours around the linear and bent trimer for rhc-polarized light. Parity symmetry is broken in the bent configuration. g The net force as a function of the trimer’s bending angle for rhc-polarized light. The net force has a linear dependence for a small bending angle, shown by the red dashed line described by the empirically derived formula shown, where α is the particle’s polarizability and Rcurv is the radius of curvature defined by the bend angle, and f(d) is a function of the separation, d, between the particles. h The bent trimer has interparticle forces that would restore it to the linear trimer configuration; red arrows show the initial forces on the bent dimer and the empty circles show the final position of the particles.

Full size image

This paper extends the concept of non-reciprocal forces24,25,26,27 to three or more identical particles, where symmetry-breaking leads to the emergence of N-body forces that determine the dynamics of the OM system. These results advance our understanding of the properties of a well-posed N-body system and demonstrate the need to consider symmetry breaking as a source for non-reciprocal N-body forces in all active matter systems.

Results

Simulation and theory

Figure 1a, b shows the induced polarization for linear and bent Ag nanoparticle trimers, respectively, for an incident plane-wave polarized along the y (vertical) axis. Figure 1c, d shows the same for an incident plane wave that is right-handed circularly (RHC) polarized. In the case of a linear trimer (or linear multimer52) (Fig. 1a), the induced polarization between the particles has mirror symmetry along both the x and y directions. As a result, there is no net force other than single particle rotation. However, Fig. 1b shows (for linearly polarized light) that a bent trimer of electrodynamically interacting nanoparticles breaks (spatial) mirror symmetry along the y (vertical) direction and also the mirror symmetry of the induced polarization of the particles in the y direction. As a result of this broken symmetry, the trimer experiences a net force in the y direction. Note that this force is an N-body in nature (i.e., is not due to a sum of 2-body forces that are all symmetrical for identical particles). However, the more novel result is for the case of circularly polarized light.

By contrast, in the case of right-handed circularly (RHC) polarized light, as shown in Fig. 1c, d, the induced dipoles (i.e., induced-polarizations) are elliptical with the same handedness as the incident light. The elliptical (non-circular) shape of the induced polarization results from the phase delay associated with light scattered between the particles. The induced dipoles would be circular (i.e., have equal magnitudes in all orientations) in the case of non-interacting particles illuminated by circularly polarized light, and there would be no net force other than single particle rotation. The induced dipoles, shown by the ellipses in Fig. 1c for a linear trimer, have parity (inversion) symmetry, and consequently no net force; i.e., Fnet = 0. This symmetry is broken in the x direction in the bent trimer. Figure 1d shows the phases and tilts of the induced polarizations, resulting in Fnet ≠ 0 and a net transfer of linear momentum to the bent trimer. Figure 1e, f shows that broken mirror and/or inversion symmetry is manifest in the EM field intensity scattered amongst the particles (see Supplementary Note 2 for more details). These broken symmetries also extend to the total scattered EM field (not shown) giving rise to net torques and forces on the (rigid) 3-body OM system. While Fig. 1e maintains inversion symmetry, and its mirror symmetry is broken, Fig. 1f shows that both symmetries are broken for the bent trimer.

Figure 1g shows the dependence of the net force (i.e., the sum of forces on all of the constituent particles) of the optical matter system on bending angle of the trimer for rhc-polarized plane-wave. The only stationary conditions for the trimer are θ = 0° (linear) and θ = 60° (equilateral triangle), where the net force goes to zero due to the symmetry of the interactions. However, in the latter cases there is still a net torque (that is non-conservative in nature) that would cause rigid-body rotation of the trimer50. The net N-body force exhibits a linear dependence on bending angle for small bending angles, which is given by the following formula (also shown in Fig. 1g):

$${F}_{x}\propto | \alpha {| }^{3}{R}_{curv}^{-1} \, f(d)+{{{\mathcal{O}}}}\left(| \alpha {| }^{4},{R}_{curv}^{-2}\right)$$
(1)

where α is the particle’s polarizability, Rcurv is the radius of curvature defined by the bend angle, and f(d) is a function of the separation, d, between the particles.

In a plane-wave, the bent trimer is not a stable structure due to forces and torques that would restore the trimer to the linear configuration if the particles were allowed to move. Figure 1h shows these forces on individual Ag nanoparticles obtained by numerically solving Newton’s equations with the electrodynamic forces (determined by Maxwell stress tensor analysis) and damping. We term this iterative process at each time step an electrodynamics-Langevin dynamics (EDLD) simulation51. The damping is to balance the continuous creation of forces by way of the CW optical trapping beam even for T = 300 K deterministic simulations.

In a system of electromagnetically interacting particles illuminated by a plane wave, the time-averaged net inter-particle force along the xξ direction is given by:

$$\langle F\rangle \propto \frac{| \alpha {| }^{2}}{2}{\sum}_{i}\left[{\sum}_{j\ne i}{\partial }_{{x}_{\xi }}\left({\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ij}\right)+{\sum}_{j\ne i}{\sum}_{k\ne i,j}\left({\alpha }^{ * }{\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ij}^{ * }{\partial }_{{x}_{\xi }}\left({\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ik}\right)+\alpha {\partial }_{{x}_{\xi }}\left({\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ij}\right){\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ik}\right)\right]+{{{\mathcal{O}}}}({\alpha }^{4}).$$
(2)

Here \({\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ij}\) is the dyadic Green’s function and α is the polarizability of the particle. The summations in Eq. (2) are over all the particles. The first term in Eq. (2) represents a strictly two-body force that cancels out when the interacting nanoparticles are identical. This cancellation occurs due to its dependences: the polarizability, α, of each particle interacting with the incident field, the gradient of the field scattered from the other constituents in the OM structure, and implicitly the induced-polarization of each nanoparticle induced by the incident and scattered fields. The dependences ensure that the pairwise (2-body) forces between two identical nanoparticles are equal in magnitude and opposite in direction as manifest in the symmetry of the dyadic Green’s function. Specifically, \({\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ij}={\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ji}\) and \(| \alpha {| }^{2}{\partial }_{{x}_{\xi }}\left({\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ij}\right)=-| \alpha {| }^{2}{\partial }_{{x}_{\xi }}\left({\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ji}\right)\).

In contrast, the second and third terms in Eq. (2), which are proportional to α3, represent 3-body forces. Unlike 2-body forces, 3-body forces can arise even among identical nanoparticles. For instance, the term \({\alpha }^{ * }{\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ij}^{ * }{\partial }_{{x}_{\xi }}\left({\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ik}\right)\) corresponds to the field scattered from particle k to the location of particle i (\({\partial }_{{x}_{\xi }}{\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ik}\)) with the polarization of particle i induced by light scattered from particle j (\({\alpha }^{ * }{\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ij}\)). Simply switching indices in the second and third terms does not result in mutually canceling forces except in specific cases like a linear trimer as shown in Fig. 1a, c, where the mirror and inversion symmetry of the configuration leads to cancellation.

In order to make and maintain the bent configuration of the trimer stable, we utilize an optical ring trap24,37,39 of radius R (see Supplementary Note 7 for details). The particles in this ring trap are attracted to regions of high intensity due to optical intensity gradient forces, Fρ, that are radially perpendicular to the annular EM beam. The ring trap has no orbital angular momentum, so there is no externally applied force tangential to the ring, i.e., Fϕ = 0. Therefore, the steady-state structure of the nanoparticles is an optically bound bent trimer. Apart from random thermal fluctuations (diffusion), any net motion along the azimuthal direction, ϕ, must be due to electrodynamic interparticle interactions.

Moreover, the ring configuration (optical ring trap) enables the addition of multiple particles in a curved arrangement where the increasing number of optically-induced polarizations in the nanoparticles enhances the system’s scattering through electromagnetic coupling among the constituent particles. Therefore, the non-reciprocal (N-body) forces increase for progressively larger continuous (contiguous) OM structures (see Supplementary Notes 3 and 5).

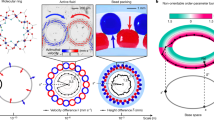
Figure 2a shows the induced dipoles of 28 nanoparticles in a filled optical ring trap (R = 2.5 μm), obtained from GMMT simulations. Since the incident light is right-hand circularly polarized, the broken symmetry of the interactions induces a right-handed (counter-clockwise) tilt of the dipoles around the ring. Furthermore, the N-body interactions in the ring cause a N-body induced-polarization around the ring that behaves as a unidirectionally propagating wave in the clockwise direction resulting in a broken spatial symmetry7,8. The scattering of light due to this induced polarization causes a persistent directional flux of electromagnetic field (and power) around the ring and in the scattered field. By conservation of angular momentum, the ring experiences mechanical force in the opposite (counter-clockwise) direction, resulting in driven transport of the particles in the counter-clockwise (i.e., rhc) direction.

Fig. 2: N-body interactions and rotational velocity in simulation and experiment.
figure 2

a Electromagnetic field intensity (increasing from black to white) of the optical ring trap with 28 trapped nanoparticles. The ellipses show the sample-dependent magnitude of the induced dipole in each nanoparticle. The tilt of the ellipses results from the symmetry breaking-induced N-body interaction. b Total azimuthal forces increase as a function of the magnitude of the single particle polarizability (relative to the static polarizability, α053). The inset shows the coefficients of a power-series expansion of the interparticle interaction for both a trimer and the 28 nanoparticle Ag filled ring. c Total azimuthal force as particles are added to the ring; insets (red dots) show the particles for the trimer, half-filled ring, and filled ring. d Velocity distributions obtained from a GMMT-Langevin Dynamics (LD) simulation at T = 300 K. e, f Image of experiments with filled rings of 44 150 nm dia. Ag nanoparticles. Color-coded trajectory of a single Ag NP's motion is superimposed with a single trajectory for (e) rhc and (f) lhc-polarized light. The trajectories are from time intervals (e) 2.625–3.25 s and (f) 5.66–6.285 s of a single experimental video (see Supplementary Movies 1 and 2). Each distinct color represents 100 ms of the trajectory (except purple, which is 25 ms). Note that imaging (video) data are collected at 200 frames (images) per second. g Mean angular displacement of the ring versus time in experiments (solid dark points) with rhc, lhc, and linearly polarized light. Gray shaded regions about the mean values represent one standard deviation of collective angular displacements. See Supplementary Movies 1–3.

Full size image

In order to determine that the net force on trimers and larger nanoparticle structures in a ring is due to N-body interactions, we simulated the magnitude of the net force as a function of the magnitude of the particle polarizability, α. Figure 2b shows the dependence of the azimuthal force, Fϕ, as the single nanoparticle polarizability is varied in the cases of the trimer and 28 nanoparticle filled ring. For clarity, the polarizability strength is expressed as values relative to the static polarizability, α053. The inset shows a power series decomposition of each curve. In each case, the first two terms, proportional to ∣α∣ and ∣α∣2, vanish and only n ≥ 3 higher-order terms remain. In fact, the filled ring has significant 4th and 5th-order contributions to the net force. The small 4th-order term for the trimer results from the small quadrupolar terms used to model the induced-polarization in GMMT simulations.

Figure 2c shows that the azimuthal force on the particles in a ring increases until the ring is filled. Note that the azimuthal force vanishes for N<3 particles since there is no symmetry breaking that can give rise to a directional N-body force. When the ring is filled (N = 28 nanoparticles), Fϕ is nearly 40 times stronger than it is for the trimer despite only having 9 times as many particles. This non-linear increase of Fϕ with the number of particles in the ring is also indicative of N-body interactions. The increase of force with the number of particles means a larger average velocity for more populated rings. Further details on the proportionality of Fϕ with respect to the increasing number of particles (accommodated by the expanding radius of the ring trap) is provided in Supplementary Note 3.

Figure 2d shows the results of EDLD simulations. The calculated distributions of azimuthal velocity of three different configurations: a bent trimer, a ring that is half-filled with particles and a ring that is fully filled with particles (see red dotted configurations in Fig. 2c). In the case of a trimer, the net force is small (see Fig. 2c). As a result, the mean of the velocity distribution is slightly greater than 0 and the thermal noise causes fluctuations of the velocity that are negative as well as positive. By contrast, the fully filled ring has a mean angular force, Fϕ, that is 40 times larger resulting in driven transport with a 40 × larger average velocity. By “fully filled rings” we mean the configuration of nanoparticle in the ring trap with the maximum number of electrodynamically interacting nanoparticles possible for a fixed ring radius, as demonstrated in Fig. 2a, b. In addition to the dependence of the N-body forces on the strong electromagnetic interactions as the particle number increases, the ellipticity of the polarization of incident light also influences the performance of the N-body effect. This is discussed in Supplementary Note 6.

Experimental

Figure 2e, f shows experimental results for an optical ring trap of radius 4.1 μm filled with 44 Ag nanoparticles of 150 nm diameter in right-handed and left-handed circularly polarized light, respectively. The superimposed single particle trajectories (color: red-to-blue with increasing time) indicate that the direction of motion has the same handedness as that of the incident circularly polarized light. Figure 2g shows the mean angular displacement of the particle trajectories as a function of time. The figure shows that the direction of angular velocity is reversed when switching from right-handed to left-handed circularly polarized light. The figure also shows that there is no net angular displacement in the case of linear polarization. The fluctuations in the trajectories are due to thermal Brownian noise from the environment; i.e., the water solution. See Supplementary Notes 8–16 for more details on the transport behavior of the particles in the ring.

The velocities of the particles in the ring are sensitive to small changes in inter-particle separations. Figure 3a–c exemplifies three distinct states of particle spacing in the ring in a single experimental video: (a) the ring contains 43 particles that arrange with equal spacing; (b) 43 particles that arrange with smaller spacing so that the ring contains a gap (empty spot/no particle); and (c) the ring is fully filled with 44 particles after an additional particle joins. Figure 3d shows the velocity distributions of the entire ring for the three states; Fig. 3a–c are the images of these three configurational states. The mean velocities of the three states (43; 43-gap; 44) are 0.0049, 0.019, and 0.023 mm/s, respectively. The velocity distributions for the second and the third states are similar to each other and distinct from the first state; the velocity increases fourfold from the first (43 NP) state to the second (43-gap) and third (44 NP) states. The distribution of inter-particle separations in the ring are shown in Fig. 3e. The second and third states have similar inter-particle separations and have similar velocity probability distributions. To be clear, while the first and second states have the same number of particles, they have different inter-particle separations and different rotational velocities. Therefore, in addition to the number of particles, the inter-particle separations (in the ring) can enhance or diminish the observed N-body rotational force depending on inter-particle separations.

Fig. 3: Collective rotational velocities and inter-particle spacing in experiment and simulation.
figure 3

a–c Experimental images of the three configurational states of the ring: (a) 43 particles with equal inter-particle spacing in a ring; (b) 43 particles with smaller inter-particle spacing in a ring with a gap; and (c) 44 particles in a filled ring. Radius of the ring is 4.1 μm. d Experimental velocity distributions for states (i)–(iii). The mean velocities (vertical dashed lines) from Gaussian fits (solid curve) to the data (circles) are 0.0049, 0.019, and 0.023 mm/s, respectively. e Corresponding inter-particle separations. The mean separations are 597.8, 588.0, and 587.5 nm, respectively. The thickness of the vertical solid lines represents their corresponding 95% confidence intervals. f Velocity distributions from GMMT-LD simulations for a ring with radius R = 4.05 μm and temperature T = 300 K for the same configurations of particles in experiment. The mean velocities (vertical dashed lines) are 0.018 mm/s (trimer), 0.937, 1.347, and 1.451 mm/s, for states (i)–(iii), respectively. g Corresponding inter-particle separation distribution. The mean separations are 577.1 nm (trimer), 595.3, 586.3, and 586.6 nm, for states (i)–(iii), respectively. See Supplementary Movies 4–6.

Full size image

Figure 3f, g shows the distributions of rotational velocity and inter-particle separation for the same configurations (i.e., states) of particles obtained from GMMT-LD (i.e., EDLD) simulations (T = 300 K). The distribution of velocities and inter-particle separations for the three states in the GMMT-LD simulations qualitatively agree with the experimental results in Fig. 3d, e. The quantitative differences between the velocities in experiment and simulations arise from smaller power density in experiment (≈108 W/m2 in experiment and 1010 W/m2 in simulation) and frictional drag with the nearby charged glass surface in experiments (see Supplementary Notes 10, 13, and 14 for the effect of frictional drag on the motion of the particles in experiment). The trimer has small mean rotational velocity in simulation, similar to what is shown in Fig. 2c, d, because the N-body forces are small for a trimer.

Finally, the inter-particle separations in the trimer shown by Fig. 3g are close to that of optical binding interactions expected from a point-dipole model description of optically bound dimers20. However, as the number of particles in the ring increases the N-body forces become larger. Furthermore, the associated electrodynamic interactions cause the inter-particle separations to decrease. The contraction occurs for geometric reasons; Eq. (2) shows that the N-body interactions have contributions along chords between non-nearest neighbors between nearest and more distant neighbors.

Discussion

Spin-orbit coupling and conversion of spin angular momentum (e.g., from circularly polarized light) into Laguerre-Gauss beams and orbital angular momentum has been widely established40,41,42,43,44,45,46,47,48. Momentum conversion processes are also manifest in optically-bound nanoparticle-based optical matter structures since the particle positions are separated by approximately the wavelength of light. Therefore, inter-particle interactions are very sensitive to interference effects and inter-particle electrodynamic coupling24,25,54. Field-retardation is a necessary condition as is the rotational symmetry of the structure to obtain negative torque49,50,55 and even to create optical matter machines51.

In contrast, the present work is of symmetry breaking-induced forces arising from N-body electrodynamic interactions in optical matter systems. The N-body symmetry breaking and “non-reciprocal” force generation mechanism for a system of optically bound nanoparticles gives rise to driven transport. When 3 or more particles are organized into a 1-dimensional array with a non-zero curvature (i.e., a bending angle) in an optical trap, the curvature (bending) of the optical matter configuration results in a broken symmetry in the electromagnetic field scattered between the particles and from the OM array. Since the bent trimer is not a stable structure at finite temperature, we utilized an optical ring trap to experimentally sustain the bent structure to manifest the N-body force on the particles in the ring. The motion of the ring depends on the number of constituent particles and their inter-particle separation. The higher order power law of the polarizability-dependence of the N-body force (F ~ ∣α∣n, n ≥ 3) highlights the N-body nature of the force.

We believe that this work is the first explicit realization of non-conservative27 collective transport of nanoparticle-based in optical matter systems due to symmetry breaking-induced N-body electrodynamic interactions. N-body interactions are the foundation of numerous interesting classical and quantum phenomena. Therefore, the results presented here should be viewed as a starting point for further experimental and theoretical studies of N-body optical matter systems. These N-body non-reciprocal interactions (and photonic forces) induced by symmetry breaking are general and should arise in other “coherently illuminated dry” active matter systems.

Finally, having demonstrated that the non-reciprocal forces generated are due to spatial symmetry breaking in the scattered field of light due to the curvature (bending) of nanoparticle arrangement in the optical ring trap. The resulting collective electric field circulating around the ring also induces a DC magnetic field pointing in the direction opposite to the propagation direction of RHC polarized beam. This provides an additional interesting prospect for breaking time reversal symmetry and therefore realizing non-reciprocity in the stricter sense56,57.

Methods

Simulation methods

Point-dipole three-body non-reciprocal force equation

In the point-dipole approximation, the time-averaged force on a particle with induced-polarization \(\overline{{{{\boldsymbol{p}}}}}\) in the xξ direction is refs. 20,58

$$\left\langle {F}_{{x}_{\xi }}\right\rangle=\frac{1}{2}Re\left[{\overline{{{{\boldsymbol{p}}}}}}^{ * }{\partial }_{{x}_{\xi }}\left({{{\boldsymbol{E}}}}\right)\right]$$
(3)

where E is the electric field, \({\partial }_{{x}_{\xi }}\) denotes a partial derivative in the xξ direction, and an asterisk denotes the conjugate transpose. For a particle with an isotropic (scalar) polarizability α the induced-polarization is directly proportional to the electric field at the location of the particle (i.e., \(\overline{{{{\boldsymbol{p}}}}}=\alpha {{{\boldsymbol{E}}}}\)). Under these conditions, the induced-polarization of a particle labelled by its subscript i in the presence of an arbitrary collection of other particles in the transverse plane can be written as

$${\overline{{{{\boldsymbol{p}}}}}}_{i}=\alpha \left(1+\alpha {\sum}_{j\ne i}{\overline{\overline{{{{\boldsymbol{G}}}}}}}_{{r}_{i}{r}_{j}}+{(\alpha )}^{2}{\sum}_{j\ne i}{\sum}_{k\ne j}{\overline{\overline{{{{\boldsymbol{G}}}}}}}_{{r}_{i}{r}_{j}}{\overline{\overline{{{{\boldsymbol{G}}}}}}}_{{r}_{j}{r}_{k}}+...\right)$$
(4)

where \({\overline{\overline{{{{\boldsymbol{G}}}}}}}_{{r}_{i}{r}_{j}}\) is the dyadic Green’s function20 that propagates an electric field due to a polarization at position rj to the position ri. Similarly, the field gradient in the xξ direction at the position ri for an incident plane wave can be written as

$${\partial }_{{x}_{\xi }}\left({{{{\boldsymbol{E}}}}}_{{r}_{i}}\right)=\alpha \left({\sum}_{j\ne i}{\partial }_{{x}_{\xi }}\left({\overline{\overline{{{{\boldsymbol{G}}}}}}}_{{r}_{i}{r}_{j}}\right)+\alpha {\sum}_{j\ne i}{\sum}_{k\ne j}{\partial }_{{x}_{\xi }}\left({\overline{\overline{{{{\boldsymbol{G}}}}}}}_{{r}_{i}{r}_{j}}\right){\overline{\overline{{{{\boldsymbol{G}}}}}}}_{{r}_{j}{r}_{k}}+...\right).$$
(5)

Substituting Eqs. (4) and (5) into Eq. (3) and summing over three particles denoted by the labels L (left), C (center), and R (right) gives

$$\langle {F}_{{x}_{\xi }^{L}}\rangle+\langle {F}_{{x}_{\xi }^{C}}\rangle+\langle {F}_{{x}_{\xi }^{R}}\rangle=Re\left[{{{{\boldsymbol{E}}}}}_{0}^{ * }\,{\overline{\overline{{{{\boldsymbol{H}}}}}}}_{{x}_{\xi }}\,{{{{\boldsymbol{E}}}}}_{0}\right]$$
(6)

where E0 is the incident electric field and

$${\overline{\overline{{{{\boldsymbol{H}}}}}}}_{{x}_{\xi }}=\frac{| \alpha {| }^{2}}{2}\left({\sum}_{i}{\sum}_{j\ne i}{\partial }_{{x}_{\xi }}\left({\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ij}\right)+{\sum}_{i}{\sum}_{j\ne i}{\sum}_{k\ne i,j}{\alpha }^{ * }{\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ij}^{ * }{\partial }_{{x}_{\xi }}\left({\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ik}\right)+\alpha {\partial }_{{x}_{\xi }}\left({\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ij}\right){\overline{\overline{{{{\boldsymbol{G}}}}}}}_{ik}\right)+{{{\mathcal{O}}}}({\alpha }^{4}).$$
(7)

The net inter-particle force on the three-particle system in the xξ direction for an elliptically polarized incident field [1, iβ, 0] is thus

$$\langle {F}_{{x}_{\xi }^{L}}\rangle+\langle {F}_{{x}_{\xi }^{C}}\rangle+\langle {F}_{{x}_{\xi }^{R}}\rangle=Re\left[\left({H}_{xx}+{\beta }^{2}{H}_{yy}\right)+i\beta \left({H}_{xy}-{H}_{yx}\right)\right].$$
(8)

Generalized multiparticle mie theory

Electrodynamic simulations were performed with Generalized Multiparticle Mie Theory (GMMT) using the MiePy (https://github.com/johnaparker/miepy) software we developed. As stated in a previous paper59, in GMMT, incident and scattered fields are represented by electric- and magnetic-associated vector spherical harmonic (VSH) wavefunctions, \({N}_{mn}^{(1),(3)}\) and \({M}_{mn}^{(1),(3)}\)60,

$${E \, }_{inc}^{j}({{{\bf{r}}}})=-{\sum}_{n=1}^{{N}_{max}}{\sum}_{m=-n}^{n}i{E}_{mn}\left[{p \, }_{mn}^{j}{N}_{mn}^{(1)}({{{\bf{r}}}})+{q \, }_{mn}^{j}{M}_{mn}^{(1)}({{{\bf{r}}}})\right]$$
(9)
$${E \, }_{scat}^{j}({{{\bf{r}}}})={\sum}_{n=1}^{{N}_{max}}{\sum}_{m=-n}^{n}i{E}_{mn}\left[{a \, }_{mn}^{j}{N}_{mn}^{(3)}({{{\bf{r}}}})+{b \, }_{mn}^{j}{M}_{mn}^{(3)}({{{\bf{r}}}})\right]$$
(10)

where \({N}_{mn}^{( \, J)}\) and \({M}_{mn}^{( \, J)}\) are the corresponding VSH wavefunctions for the electric and magnetic modes, respectively. J = 1 represents incident fields and J = 3 represents scattered fields, n and m are the multipolar (dipole, quadrupolar, etc) and azimuthal (from −n to n) orders of the VSH wavefunctions, and Nmax is the maximum multipole order the fields need to be expanded to, Emn is a normalization factor, and pmn and qmn are the electric and magnetic beam shape coefficients, respectively, amn and bmn are the electric and magnetic scattering Mie coefficients, respectively.

For a system of electrodynamically interacting nanoparticles, the scattered field is calculated as:

$${E}_{scat}({{{\bf{r}}}})={\sum}_{j}{E \, }_{scat}^{j}(r-{r}_{j})$$
(11)

where r is the position where the field is being evaluated and rj is the position of particle j.

Maxwell stress tensor

As stated in our previous paper59, the total optical force that the nanoparticles experience in the elctromagnetic field of light is evaluated by integrating a Maxwell Stress Tensor (MST), \({{{\boldsymbol{T}}}}^{\leftrightarrow}\), over a closed surface Ω encompassing the investigated particle61:

$$\langle {{{{\boldsymbol{F}}}}}^{{{{\rm{MST}}}}}\rangle=\int_{\Omega }\langle {{{\boldsymbol{T}}}}^{\leftrightarrow}\rangle .{{{\boldsymbol{n}}}} \, da$$
(12)

where

$$\langle {{{\boldsymbol{T}}}}^{\leftrightarrow}\rangle=\frac{1}{2}Re\left[{\epsilon }_{m}{{{\boldsymbol{E}}}}\otimes {{{{\boldsymbol{E}}}}}^{ * }+{\mu }_{m}{{{\boldsymbol{H}}}}\otimes {{{{\boldsymbol{H}}}}}^{ * }-\frac{1}{2}({\epsilon }_{m}{E}^{2}+{\mu }_{m}{H}^{2}){{{\boldsymbol{I}}}}^{\leftrightarrow}\right]$$
(13)

where 〈. . . 〉 indicates a time average, n is the unit vector perpendicular to an infinitesimal surface element da, ⊗ is the vector outer product, \({{{\boldsymbol{I}}}}^{\leftrightarrow}\) is the unit tensor, ϵm and μm are the permittivity and permeability of the surrounding medium, and the asterisk superscript represents the conjugate fields.

For the Langevin dynamics simulations, forces on particles were computed using analytical expressions for GMMT and integrating the Maxwell stress tensor51. These electrodynamic forces were used in an over-damped Langevin equation of motion that also includes Stokes frictional damping and a random force (noise) term that depends on temperature51,62,63.

Simulations of optical ring traps

The optical ring trap in experiment can be simulated using phase-shaping holography37,39. For a ring trap with radius R and winding number l, the field in the conjugate focal plane is given by:

$$\psi ({{{\boldsymbol{\rho }}}})=\int\frac{{d}^{2}r}{f\lambda }a(\phi )\delta (r-R){e}^{il\phi }\exp \left(i\frac{\pi }{\lambda f}{{{\boldsymbol{r}}}}.{{{\boldsymbol{\rho }}}}\right)$$
(14)

where ρ is the cylindrical radial coordinate, r is the radial coordinate in 3 dimensions, ϕ is the azimuthal coordinate in the x-y plane, λ = 770 nm is the wavelength of the incident light (i.e., trapping beam), f is the focal length of the system, and a(ϕ) = 1 is the azimuthal amplitude function of the ring trap. Equation (11) can be further simplified and expressed as:

$$\psi ( \, {{{\boldsymbol{\rho }}}})={\psi }_{0} \, {J}_{l}(C\rho ){e}^{il\phi }$$
(15)

where ψ0 is the normalization factor, Jl is the l-th order Bessel function of the first kind and C is determined by the radius of the optical ring trap, the wavelength of the coherent laser light and the focal length of the optical system. We generate this optical field in simulation (and experiment) by using a phase-only spatial light modulator (SLM). The phase function associated with the ring trap is given by:

$$\varphi ( \, {{{\boldsymbol{\rho }}}})=\{l\phi+\pi H(-{J}_{l}(C\rho ))\}{{{\rm{mod}}}} \, 2\pi .$$
(16)

where H(x) is the Heaviside function. The first term (lϕ) controls the azimuthal phase profile and the second term controls the radial amplitude profile of a ring with a fixed radius R that does not vary with l 37. In our simulations, Eq. (13) was used with l = 0 to generate a ring trap with no azimuthal phase gradient. Simulations (and experiments) employed 150 nm dia. Ag NPs were trapped with an optical ring (illumination with 770 nm light) of radius R = 2.5 μm (Fig. 2) and R = 4.05 μm (Fig. 3), which was implemented using phase-shaping holography. See Supplementary Note 4 for additional details concerning electrodynamics-Langevin dynamics (EDLD) simulations.

Experimental setup

Optical trap setup

Optical trapping experiments were conducted with a single-beam optical tweezers set-up in an inverted microscope. The experimental setup has been described previously37,64. A CW Ti-Sapphire laser (Spectra Physics Millenia Vs) is used to generate a linearly polarized Gaussian beam (λ = 770 nm), which is incident on a phase-only spatial light modulator (SLM) (Meadowlark Optics). A half wave plate is placed before the SLM to convert the linear polarization state of the beam to p-polarized (perpendicular to the optical table), which is optimal for the SLM. The SLM modifies the incident Gaussian beam according to the desired phase function for a ring trap, which is relayed through a 1 to 0.75 telescope, into an inverted microscope (Nikon Eclipse Ti). A half-wave plate and polarizing beam splitter are placed after the SLM to convert the polarization of the beam back to s-polarized (parallel to the optical table). The beam gets reflected by a dichroic mirror and passes through a quarter wave plate, which converts the polarization of light from linear to circular. The quarter wave plate was mounted on a piezoelectric rotation stage that could rotate at a maximum speed of 430° per second to enable fast switching between polarization states. The beam is then incident at the back aperture of a 60× water immersion microscope objective (Nikon 60× Plan Apo IR, NA = 1.27). With an additional 1.5× magnifier inside the microscope, the total magnification for imaging is approximately 90×. The total power measured before the microscope is 300 mW. Nanoparticles (NPs) were illuminated with a high NA dark field condenser (Nikon, NA = 1.2–1.43, oil immersion), and the light scattered and collected by the microscope objective was imaged onto a sCMOS array detector (Andor Neo).

A 3D closed-loop piezoelectric translation stage (Mad City Labs) was used to control the 2D position of the sample and allows fine tuning of the imaging plane. Ring traps of radii 4.1 μm and 6.2 μm were used in the experiments. The zeroth-order reflection from the SLM causes the ring trap in experiment to have a Gaussian spot in the center of the ring. Even though particles occasionally get trapped in the center, they do not have an effect on the particles situated in the ring as they are far away. The focus of the optical trapping beam was adjusted independently from the imaging focus by applying a phase function of the Zernike polynomial \({Z}_{2}^{0}\) (Defocus) on the SLM. The optical defocus resulted in tight confinement (in the radial direction) of nanoparticles. In addition, optical aberrations of the trap were also corrected by applying the Zernike polynomials \({Z}_{2}^{2}\) (Vertical astigmatism), \({Z}_{2}^{-2}\) (Oblique astigmatism) and \({Z}_{3}^{-3}\) (Vertical trefoil). See Supplementary Note 11 for additional details of the experimental setup and experiments.

Nanoparticles

A solution of PVP (polyvinylpyrrolidone)-coated or citrate-coated Ag nanoparticles (150 nm diameter, NanoComposix 0.02 mg/mL) was diluted with 18 MΩ deionized water at a ratio of 1:300 and was placed inside a sample cell that consists of a 120 μm thick adhesive spacer (Grace Bio-Labs) sandwiched between two glass cover-slips. The glass surface of the top cover slip is electrostatically charged (negative potential) and repels the similarly charged PVP-coated Ag nanoparticles. This downward repulsive force balances the upward radiation pressure creating 2D confinement of the nanoparticles.

Particle imaging and tracking

Darkfield microscopy images and videos of the incoherent (illumination) light scattered from the Ag nanoparticles were recorded at a frame rate of 200 fps with an exposure time of 1 ms. Each frame was 200 × 200 pixels. The effective pixel size on the sCMOS camera was measured to be 74.86 nm using the piezo stage. The particles were localized in each frame (image) and linked (tracked) into single NP trajectories using the Mosaic plugin of ImageJ65. A kernel radius of 3 pixels was employed for particle detection, and a maximum frame-to-frame displacement of 10 pixels was chosen for linking particle positions to form trajectories.

Experimental analysis

Multi-timescale considerations

The characteristics of motion of a dynamic system can vary depending upon the different time scales used to characterize it. We quantitatively characterize the transport behavior of the ring of nanoparticles in experiments on various time scales. These lag times are the time windows (in frames) between which angular displacements or velocities are calculated. This is important to do because different behaviors (characteristic phenomena) are dominant on different time scales. The Brownian motion of individual nanoparticles in the ring trap is more dominant at small lag times (i.e., on shorter time-scales), whereas the driven transport behavior of the ring of nanoparticles is more dominant at large lag times. See Supplementary Notes 8 and 10 for more experimental details.

Collective coordinate

Since experiments were performed at room temperature in aqueous solution, the nanoparticles in the ring trap experience Brownian diffusive forces and fluctuations as a result of thermal energy. The fluctuations of individual nanoparticles in the ring obscure precise analysis of the driven transport of the ring of nanoparticles. To overcome this challenge we devised an angular coordinate, termed the collective coordinate, that is obtained by cumulatively averaging the angular displacements of individual nanoparticles from one frame to another in darkfield microscopy videos:

$${\theta }_{collective}^{i}={\theta }_{collective}^{i-1}+\frac{1}{N}{\sum}_{n}({\theta }_{n}(i)-{\theta }_{n}(i-1))$$
(17)

where i is the frame number, n is a given trajectory present between frames (i − 1) and i and N is the total number of trajectories present between frames (i − 1) and i.

The averaging of individual nanoparticle displacements reduces the noise associated with random thermal fluctuations of the individual nanoparticles that dominates the short timescale motion of the individual nanoparticles. See Supplementary Notes 8 and 10 for more experimental details.

Mean-squared displacement analysis

Mean-Squared Displacement (MSD) analysis of the transport behavior provides further corroboration that the rotational motion of the nanoparticles in a ring trap is a collective phenomenon with the driven motion arising from symmetry-breaking from N-body interactions between the nanoparticles in the ring. The MSD is calculated as:

$$MSD=\left\langle {| {\theta }_{collective}^{t}-{\theta }_{collective}^{t-\tau }| }^{2}\right\rangle=2dD{\tau }^{\alpha }$$
(18)

where θcollective is the collective angular coordinate of the ring, d is the number of dimensions (here d = 2), D is the diffusion coefficient, t is the time in frames (seconds), τ is the lag time for which the MSD is calculated. α is the transport exponent or the slope of the log(MSD) vs. log(lag time), which indicates the behavior of the transport. α = 2 indicates driven (ballistic) motion with constant velocity, α = 1 indicates random diffusive motion, and α < 1 indicates sub-diffusive (e.g., confined) motion. See Supplementary Note 10 for more details about the transport behavior.