Abstract
Understanding the binding dynamics of liquid molecules is of fundamental importance in physical and life sciences. However, nanoscale fast dynamics pose great challenges for experimental characterization. Conventionally, the binding dynamics have been assumed to be memoryless. Here, we integrate large scale computer simulation, scaling theory, and real-time single particle tracking microscopy with high spatiotemporal precision to unveil a universal memory effect in the binding dynamics of liquid molecules. This binding memory can be quantified by a binding time autocorrelation function, whose power-law decay depends on binding affinity, the topological and materials properties of the surrounding environment and the heterogeneity of the binding landscape. Context-dependent biomolecular binding memory is likely exploited by biological systems to regulate biochemical reactions and biophysical processes. Deciphering this binding memory offers a novel strategy to probe complex biological systems and advanced soft materials.
Similar content being viewed by others
Introduction
The dynamics of molecular binding in liquid environments is of critical importance across a variety of fields, from chemical physics to biophysics and nanotechnology. For instance, the initial viral infection involves binding to the cell membrane, and transcription factors (TFs) must reside at cis-regulatory elements to activate gene expression. On the other hand, engineering molecular and nanoparticle binding is key to optimizing material properties with applications in catalysis1,2, self-assembly3,4, stimuli-responsiveness5,6, and drug delivery7. Despite its fundamental importance, our understanding of the binding dynamics is still limited due to the experimental difficulty in capturing the fast molecular binding events.
Since a single binding event may not always trigger downstream activities, it is necessary to consider the impact of rebinding dynamics. In many soft matter systems, particularly biological ones, functionality often depends on a sequence of weak binding and rebinding events rather than a single, strong interaction. For instance, a recent study revealed that frequent on-and-off binding of TFs at cis-regulatory elements is associated with prolonged transcriptional bursts, suggesting that rebinding is functionally important in gene regulation8. Other studies reported that rebinding has profound influences on enzymatic reactions9, ligand recognization10,11 and drug binding affinity12. Nevertheless, aside from these observations, it remains largely unknown how frequently rebinding happens and how it shapes the time dependence of molecular binding probability.
It is widely believed that the binding probability decreases exponentially over time, with the rate of decay characterized by a dissociation rate constant koff13,14. The underlying assumption is that molecular binding dynamics is stochastic and memoryless. This assumption is deeply rooted and a cornerstone in almost every model that concerns molecular binding dynamics. For example, continuum affinities models have been developed to explain non-exponential binding dynamics based on the superposition of multiple single-exponential functions15,16,17,18,19. In other cases, an “apparent” koff is introduced to account for observed binding lifetime that is much longer than theoretical prediction20,21,22. These empirical models provide only limited molecular insights, as they cannot distinguish between single strong binding and multiple weak binding/rebinding events. To fully reconcile the discrepancies between theory and experiment, a new paradigm is needed wherein the effect of rebinding is properly incorporated.
Here, we propose that the intricate interplay between the binding kinetics and the molecular dynamics can lead to a binding memory effect. Combining simulation, theory and experiment, we show that binding memory is ubiquitous in liquid and may play important roles in functional soft matter systems. In a homogeneous binding environment, we develop a general theoretical framework to understand this memory effect and elucidate its dependence on key physical parameters. In contrast, heterogeneous systems exhibit emergent memory effects arising from the complex coupling between binding and transport—behaviors that lie beyond the reach of traditional diffusion-centric theories. Finally, we show how binding dynamics can be used to probe the properties of soft matter, and we discuss the broader biological implications of molecular binding memory, including its potential role in regulating cellular processes.
Results
The concept of molecular binding memory
Unlike particles in solid that have fixed neighbors, liquid molecules regularly update their neighboring lists as they engage in transient interactions driven by noncovalent forces, such as electrostatic attraction, hydrogen bonding, van der Waals forces, pi-pi interactions, and the hydrophobic effect. Given the weak and highly dynamic nature of these forces, the notion that liquid molecules could retain any form of binding memory may initially seem counterintuitive—especially considering the long-standing view that nanoscale particles experience memoryless random forces, as described in Einstein’s classical theory of Brownian motion. However, it was not until more than half a century later that scientists realized microscopic hydrodynamics could induce a memory effect in the motion of Brownian particles. The overlooked hydrodynamic memory was first discovered in the seminar computer simulation by Alder and Wainwright23, and later captured by optical tweezer experiments24,25.
If Brownian motion has memory, what about the binding of molecules and nanoparticles? Can the concept of memory be extended to molecular interactions? To explore this, we first need a mathematical definition of binding memory that can be analyzed theoretically and measured experimentally. A natural choice is the time autocorrelation function, also known as the memory kernel. For example, hydrodynamic memory is quantified by the velocity-time autocorrelation function of the Brownian particle. Here, we introduce the binding time autocorrelation function (BAF) to study the molecular binding memory, which can be expressed as:
where \(n\left(t\right)\) represents the number of molecular pairs at time \(t\), and \(n\left(t+\Delta t\right)\) counts the number of the same pairs remain bound or rebind following a lag time \(\Delta t\). Here, \(T\) is the total observation time. The summation averages overall all possible initial times t, which makes BAF \(t\)-independent. The denominator normalizes the function, making it independent of absolute binding numbers.
Unlike the lifetime distribution function (LDF) that concerns only the duration of a single binding event, the BAF accounts for the contribution of rebinding events to the overall binding probability (Fig. 1). A memoryless BAF would reduce to the LDF (see Supplementary Fig. 1), which typically follows an exponential decay. However, molecules with binding memory will exhibit BAFs that decay slower than an exponential function. Besides BAF, binding memory can also be characterized by other quantities, as we will discuss later.
Source data are provided as a Source Data file. a Schematic definition of the lifetime distribution function and binding time autocorrelation function. Bound state is marked in red and unbound in gray. b Hydrogen bonding BAFs of water and ethanol in systems of different dimensions (1D to 3D from the bottom to the top). All systems exhibit long-time tails that can be fitted to a universal power law of \({t}^{-D/2}\), where D represents the dimensionality of the system. The fitted scaling exponents and their corresponding standard errors are shown in the figure. All fittings were performed over a consistent time window ranging from 500 to 14,000 ps, covering systems from 1D to 3D.
All-atom molecular dynamics simulations unveil binding memory effect
Computer simulation has been proven a powerful tool to investigate molecular autocorrelation functions23,26,27. However, accurately calculating the BAF is computationally expensive, as it requires continuous tracking of the binding dynamics among a vast ensemble of molecules. Moreover, the periodic boundary condition (PBC) of the simulation box can lead to artifacts of BAF at long-time scale (Supplementary Fig. 2). We address these problems and accelerate the data processing by about three orders of magnitude via optimizing the molecular neighboring analysis (see the Methods for more details). By using this technique and performing large-scale simulations (particle number up to 3.75 million) over more than 1000 times, we obtain high-quality statistics of the BAFs across multiple timescales.
We first conduct all-atom molecular dynamics (MD) simulations of associated liquid rich in hydrogen bonds, such as water and alcohol. The BAFs of hydrogen bonding in systems of different dimensions are analyzed and shown in Fig. 1b. In these log-log plots, all the BAFs are clearly non-exponential with long-time tails following power law functions. The scaling exponents of the power law functions unequivocally align with \(-D/2\), where \(D\) is the dimension of the system. The dimension-dependent power law scaling is universal, as it does not depend on the type of the associated liquid or the specific definition of its hydrogen bonding (Fig. 1 and Supplementary Fig. 3).
It is intriguing that ethanol manifests a stronger binding memory than water, despite having weaker hydrogen bonds. This result highlights the fact that the collective behavior of liquid molecules may have a greater impact on the binding memory than their individual binding affinities. Water, with its extensive hydrogen bonding network and high molecular mobility, allows for rapid rearrangement and exchange of neighbors, leading to a short memory of previous binding partners. While our all-atom simulations are limited to small solvent molecules, the significant increase of binding memory from water to ethanol suggests that the memory effect could be much more pronounced for large solute molecules.
Langevin dynamics simulations identify factors that control binding memory
The observed universality of the BAF scaling could be attributed to the conservation laws, such as mass conservation (governing diffusion) and momentum conservation (governing hydrodynamics), both of which are implemented in all-atom MD. Using Langevin dynamics (LD) simulations without hydrodynamics, we further show that diffusion alone can preserve the dimension-dependent scaling law of BAF (Supplementary Fig. 4). The high efficiency of the LD simulation allows us to systematically study the dependence of BAF on a wealth of factors including viscosity (Fig. 2a), binding strength and range (Fig. 2b and Supplementary Fig. 5), crowding (Fig. 2c), molecular weight (Supplementary Fig. 6), as well as residence cutoff distance (Fig. 2d). All these factors affect the amplitude of the BAF rather than the scaling exponent.
Source data are provided as a Source Data file. a The effect of liquid viscosity on molecular BAFs in a three-dimensional system, modeled by changing friction coefficients in Langevin dynamics simulations. Large viscosity enhances molecular binding memory. b Crowded liquid systems tend to have a strong binding memory effect. c Strengthening binding energy increases binding memory. Note that molecular binding affinity affects the amplitude rather than the scaling exponent of the BAF. d The amplitude of the BAF power law depends on the choice of binding criterion, i.e., the residence cutoff distance. The error bars in panels (a–d) represent variations across fifty independent simulation runs. Due to small statistical errors in some conditions, the error bars are not clearly visible. The power-law exponents and fitting errors for all BAF curves in (a–d) are listed in Supplementary Table 1. All BAF curves are fitted over the time range of 50000 to 500000 timesteps. The power-law amplitudes in bar charts (a–d) are obtained by linear fitting of the BAFs in double-logarithmic plots and taking the intercepts at log(t) = 0, or t = 1 in timesteps. e Rebinding heavily contributes to the effective binding time, demonstrated by comparing liquid systems of different viscosities. The binding dynamics profiles at the single-molecule level are sorted by the accumulated binding time within 500,000 simulation steps. The starting points are always in the binding state, which is marked in red.
The above computer simulations suggest that the scaling exponent and amplitude of the BAF encode different characteristics of the liquid environment, with the former being sensitive to the dimensionality and the latter sensitive to the material properties of the liquid as well as the binding affinity. While the binding affinity largely determines the LDF (Supplementary Fig. 1c), with stronger affinity leading to slower decay, it is only one of the many factors that shape the BAF. The fact that the binding affinity does not affect the scaling exponent of the BAF has an important implication, i.e., mixing different binding affinities does not break the power law. In realistic systems, binding interactions are often heterogeneous. To better reflect these conditions, we constructed a polymer solution containing multiple types of polymers with varying interaction strengths. In this heterogeneous system, the LDF remains exponentially decaying, while the BAF continues to exhibit a long-tailed power-law decay (Supplementary Fig. 7), underscoring the robustness of the BAF’s scaling behavior. In addition, we examined the effect of varying residence cutoff distance, which mimics changes in imaging resolution. Our results show that while this modification significantly affects the LDF (Supplementary Fig. 1d), the BAF scaling remains unaffected, further highlighting the distinction between these two functions and reinforcing the robustness of the BAF as a descriptor of binding memory.
The universal scaling of BAF, invariant of binding energy and imaging resolution, is in striking contrast with the exponential LDF, stressing the importance of rebinding events that have been often neglected in biophysical models. By sorting and analyzing individual binding profiles, we show that rebinding heavily contributes to the effective binding time (Fig. 2e). Ignoring rebinding can lead to significant underestimation of the effective binding time, especially in low-dimensional systems such as cell membranes.
Scaling theory explains the power law of binding probability decay
We then carry out a theoretical analysis to gain deeper understanding of the scaling of the BAF. While the exact BAF is difficult to predict analytically, its scaling exponent can be determined using scaling theory28, a powerful tool widely used in polymer physics. Our simulation results indicate that the asymptotic behavior of the BAF is dictated by diffusion, and the effect of binding kinetics can thus be absorbed into a time-independent term at a long-time scale that only contributes to the amplitude of the power law. This separation allows us to study the scaling exponent in the extreme case of vanishing binding energy. In this case, the trajectory of a liquid molecule can be mapped onto the conformation of a polymer. Therefore, analysis of the BAF is converted to solving the contact probability function \({P}_{c}\left(l\right)\) that describes the likelihood of contact between two loci of the trajectory “polymer” as a function of the contour length between them. Here, the contour length \(l\) is equivalent to the time \(t\) in the BAF context.
The scaling property is associated with the concept of fractal29, i.e., self-similarity across scales. Not to loss generality, we assume that the trajectory “polymer” is of dimension \(\theta\) (the dimension of the walk), embedded in a \(D\)-dimensional space. The contact probability function \({P}_{c}\left(l\right)\) follows a power law
where \(s\) is also the scaling exponent of BAF that we are interested in. Two loci can be said to be in contact if they are within a contact cutoff distance \(b\), or \(b/\varepsilon\) in the measure of the scale unit \(\varepsilon\). Changing the contact criterion will rescale the amplitude of the contact probability function
where \(A\) is a constant that does not depend on the contact distance. On the other hand, the contour length of a fractal is scale-dependent and can be written as
with \({l}_{0}\) being scale-invariant. Substituting Eq. 3 and Eq. 4 into Eq. 2, we have
Since \({P}_{c}({l}_{0},b)\) is scale-invariant, \(\theta s-D\) must vanish, leading to
For normal diffusion, we have \(\theta=2\). In a more general situation that considers anomalous diffusion, we have \(\theta=2/\alpha\), where \(\alpha\) is the diffusive exponent. Therefore, Eq. 6 can be rewritten as
The above theoretical analysis explains the dimension-dependent scaling behaviors observed in our computer simulations (Fig. 1), where both \(D\) and \(\theta\) are integers.
Applicability and limitations of the scaling theory
In principle, both numerator and determinator in Eq. 6 can be non-integer, i.e., fractal dimensions. Fractal space30,31,32 and anomalous diffusions33,34,35 are often encountered in biological liquid systems. To test the applicability of our theory in complex systems, we have constructed two different liquid environments featuring a Hilbert curve (Fig. 3a) and diffusion-limited aggregation (DLA)36,37 (Fig. 3b), respectively. In the former case, the Hilbert curve is a wall of fixed particles that cannot be penetrated by the mobile molecules whose binding memory is of our interest. In the latter case, the mobile molecules are confined within the DLA. Both fractal structures are embedded in a 2D space. The mobile molecules are adhesive to each other, undergoing dynamic binding and dissociation. We calculate the fractal dimension \(D\) of the environments based on mass scaling (Supplementary Fig. 10) and analyze the diffusion of the mobile particles to obtain \(\theta\) or \(\alpha\) (Fig. 3a, b). The mean squared displacement (MSD) in both cases are clearly non-Fickian and subdiffusive. We then use Eq. 6 to predict the scaling exponent of the BAF. The simulated results, i.e., the ground truth, are shown in Fig. 3c. As shown in the inset of Fig. 3c, our theoretical predictions are in good agreement with our simulation results. This agreement is remarkable as it proves that our theory of BAF scaling is not limited to simple topologies or normal diffusion processes, but also applicable to describe the intricate binding dynamics in sophisticated scenarios. Given the complexity of biological systems, the scaling exponents of biomolecular BAFs are expected to cover a continuous spectrum, rather than a few discrete values. Once the scaling exponent is obtained, it can be used to infer the fractal dimension of the environment based on our theory. Such inference offers practical advantages because it is non-invasive and more convenient than directly characterizing the whole environment.
Source data are provided as a Source Data file. a A liquid system of dynamic binding particles walled by a Hilbert curve. The particles are shown in red. Zooming in on the system does not change the fractal structure. b A different fractal system constructed by two-dimensional diffusion-limited aggregation. Mean squared displacements (MSDs) of particles in both systems are shown in the rightmost subpanels. c Data points represent averages over 60 independent simulations for BAF characterization in the 2D DLA system and 80 for the 2D Hilbert system. Error bars indicate the standard deviation across these simulations. Power-law fitting of the averaged BAFs was conducted over the time window from \(7\times {10}^{5}\) to \(1\times {10}^{7}\). The resulting scaling exponents, together with the corresponding fitting errors, are displayed in the figure, showing that the two fractal binding environments give rise to BAFs with different scaling exponents. Inset: Agreement between simulation and theory on the scaling of BAFs in fractal systems. d Probability density functions (PDFs) of molecular displacements in the Hilbert geometry at two different time points collapse onto a Gaussian form, \(\frac{1}{\sqrt{4\pi {D}_{\alpha }{t}^{\alpha }}}\exp \left(-\frac{{x}^{2}}{4{D}_{\alpha }{t}^{\alpha }}\right)\), with consistent parameters \({D}_{\alpha }=0.048\), \(\alpha=0.69\), confirming \({t}^{\alpha }\)-scaling.
While our scaling theory performs well in the above fractal systems, it may not fully capture binding dynamics in more complicated scenarios. To further clarify the regime where our BAF scaling theory applies, we analyzed the displacement probability density function (PDF) in the case of Hilbert curve confinement. We found that the PDF exhibits self-similarity under time rescaling and remains Gaussian when plotted against tα. This self-similarity is necessary for the applicability of our scaling theory, even though the underlying transport process need not be strictly Fickian or Gaussian.
Thus far, our analysis has focused on homogeneous environments. We now extend our investigation to heterogeneous settings, which are more representative of biological systems. To explore how environmental heterogeneity affects molecular binding memory, we used the Hilbert curve confinement model and introduced trapping sites along the boundaries. As shown in Fig. 4c, although the MSD scaling remains unchanged compared to the homogeneous case, the presence of heterogeneous boundaries leads to a non-Gaussian, non-convex PDF (Fig. 4e), which is difficult to capture with existing theoretical models. This PDF evolves over time in a non-self-similar fashion, breaking a key condition for the validity of our scaling theory and resulting in noticeable deviations in the BAF from theoretical predictions (Fig. 4d). Compared to the case with homogeneous, repulsive boundaries, the introduction of boundary heterogeneity reduces the strength of binding memory, highlighting the sensitivity of memory effects to environmental heterogeneity.
Source data are provided as a Source Data file. a Simulation of binding dynamics in a two-dimensional fractal environment constructed using a Hilbert space-filling curve, with specific binding sites highlighted in green. b Representative molecular trajectory showing trapping behavior due to interactions with specific binding sites in the fractal environment. c MSD characterization of molecular motion. d BAF analysis for molecules in this newly modified fractal environment. e Non-Gaussian probability density of molecular displacements. f Simulation snapshots of the binding dynamics between protein polymer and binding site distributed along a chromatin fiber. g A representative trajectory of the protein polymer showing significant heterogeneity, including hopping behavior, which is zoomed in the inset. h MSD of the protein polymers. i BAF analysis, revealing a scaling exponent of approximately -2.5 (indicated by a red dashed line), deviating from the theoretical prediction of -1.5. j PDFs of molecular displacements at two time intervals. k Simulation of polymer-polymer interactions in a heterogeneous binding environment, induced by two coexisting phases. l Trajectory of a polymer molecule transitioning between condensed (red) and dilute (green) regions. m MSD of polymer molecules exhibiting normal diffusion. n BAF analysis of polymer–polymer associations in the phase-separated system. o Displacement probability density showing non-Gaussian characteristics. Data points in BAF and MSD characterizations represent averages over 200, 150 and 500 independent simulation runs, respectively, for three different heterogeneous adsorption systems. Error bars indicate the standard deviation across independent trajectories. Power-law fitting were performed for each BAF curve over the following time ranges: (d) 2500000 to 100000000 steps; (i) 3500000-17000000 steps; (n) 30000–4300000 steps. Scaling exponents and errors are shown in the respective panels.
This sensitivity is especially relevant in biological contexts, where heterogeneity is often inherent to molecular landscapes. For example, TFs can become transiently trapped at various binding sites dispersed along chromatin fibers. As shown in Fig. 4g, such a heterogeneous landscape leads to a hopping mechanism, resulting in a novel BAF scaling of t−2.5, which deviates markedly from the classical t−1.5 scaling associated with pure diffusion. MSD and PDF analyses show that transport in this regime remains Fickian but becomes non-Gaussian, with the PDF again exhibiting a non-convex structure that reflects the strong coupling between binding dynamics and spatial disorder. Notably, when the number of TF binding sites is moderate (Supplementary Fig. 11), reflecting intermediate heterogeneity, we observe a transition in the PDF from non-Gaussian to Gaussian behavior. Concurrently, the BAF scaling evolves from approximately − 2.5 to − 1.5, highlighting the sensitivity of binding dynamics to the degree of heterogeneity.
A further layer of heterogeneity in biological systems arises from membraneless compartmentalization. These compartments possess soft, permeable boundaries that allow for molecular exchange. To evaluate how such soft confinement influences binding memory, we performed additional simulations incorporating penetrable boundary conditions. As shown in Fig. 4n, soft confinement leads to a faster decay in BAF compared to hard-walled systems38, indicating weaker binding memory. Interestingly, despite MSD indicating Fickian diffusion, the PDFs at intermediate times are non-Gaussian, again leading to anomalous BAF scaling that diverges from theoretical expectations.
Together, these simulation examples illustrate how different forms of environmental heterogeneity profoundly impact molecular binding memory. In biological systems, where these factors often coexist, their interplay introduces further complexity. Our systematic analysis highlights that binding memory is an intrinsically multifaceted phenomenon that challenges conventional, diffusion-centric theoretical frameworks39. A comprehensive understanding requires going beyond traditional models to account for the intricate coupling between transport, binding, and environmental heterogeneity.
Biological implications of molecular binding memory
Molecular binding memory—arising from multiple transient and weak interactions—can significantly prolong the effective binding duration through cumulative effects. This dynamic mode of interaction creates a multi-step verification mechanism, enhancing binding specificity. In contrast, a single strong binding event may result in rigidity and reduced adaptability, increasing susceptibility to erroneous recognition. Importantly, binding memory is sensitive to the local microenvironment, offering an additional layer of tunability beyond intrinsic binding affinity—an advantage particularly valuable in complex biological systems.
Biological environments are rich in molecular diversity, where specific binding partners are often spatially sparse. This sparsity, combined with high viscosity, molecular crowding, and slow diffusion, provides ideal conditions for the emergence of binding memory. Notably, many proteins contain intrinsically disordered regions (IDRs), which increase hydrodynamic radii and further reduce diffusion rates, thereby amplifying binding memory according to the Stokes-Einstein relationship.
Binding memory is likely at play at the intra-molecular level within IDRs. From a polymer physics point of view, many IDRs can be modeled as associative polymers composed of stickers and spacers40,41,42. The reversible binding of stickers allows dynamic changes of IDR conformations over time. Different sticker-spacer sequences could lead to distinct binding memory effects within the IDRs. To gain insights into this problem, we designed and studied three sticker patterns with significant differences: uniform, random, and patched, all with the same number of stickers (Fig. 5a and Supplementary Fig. 13). It is important to note that that the specific biological sequence is not the primary focus of this study. Instead, we aim to explore sequence-dependent binding memory, with an emphasis on sequence diversity. This is the rationale behind selecting such varied sequence features. The sticker-spacer model provides a minimal yet effective framework to capture the underlying physical principles relevant to this aspect. For each sequence, we analyzed the fluctuation of the total sticker binding number as a function of time. As shown in Fig. 5a, the time autocorrelation functions of this binding fluctuation exhibit power laws whose scaling exponents depend on the specific sticker pattern. Interestingly, the two well-mixed patterns-uniform and random-can be easily distinguished by their scaling exponents, with the former showing a slower decay. Clustering stickers into patches further slows down the dynamics. These results suggest the presence of a memory effect during the conformational changes of IDRs, encoded by the sequence-specific arrangement of stickers.
Source data are provided as a Source Data file. a Fluctuation autocorrelation function of the number of binding pairs formed between stickers in a sticker-spacer polymer model with three different sequence types. While all sequences feature power-law behavior, they exhibit significantly different scaling exponents. The sequence patterns and corresponding typical conformations are shown on the right. b BAF of molecules adsorbed on the surface of a liquid droplet, in comparison with binding dynamics in bulk. Molecules at the droplet interface exhibit a stronger binding memory effect. Typical simulation snapshots of the two different systems are shown on the right. c BAF of CTCF, modeled as a ring polymer undergoing sliding adsorption on chromatin. A simulation snapshot, shown below, illustrating this process, with the CTCF molecule depicted as a red ring polymer and specific binding sites marked as blue dots on the gray chromatin polymer. d BAF characterization of interactions between two lipid components in mixed DPPC/DPPS and DOPC/DHPC lipid bilayers. Side and top views of the simulated mixed lipid bilayer (DOPC/DHPC) are presented below, while a corresponding snapshot of the DPPC/DPPS bilayer is provided in Supplementary Fig. 14. Data points in panels (a–d) represent averages over 40, 200, 200, and 1 independent simulation runs, respectively. Error bars indicate the standard deviation across independent trajectories. Power-law fitting were performed for each BAF curve over the following time ranges: (a) 7500-200000 steps; (b) 4000 to 35000 steps (droplet interface), 3000–100000 steps (bulk case); (c) 60000–1000000 steps; (d) 100–2000 ns. Scaling exponents and fitted errors are shown in the respective panels.
Many biochemical reactions and assembly of protein complexes occur on biological interfaces, such as membranes43,44 or surfaces of membraneless compartments45,46,47. Compared to the three-dimensional (3D) bulk environment, such interfaces have reduced dimensionalities, sometimes even lower than two dimensions. Such low dimensionality, combined with the slow interfacial diffusion, could yield a strong binding memory effect at biological interfaces. As a proof of concept, we constructed a liquid droplet in our simulation and analyzed the binding memory of molecules trapped to the droplet surface. Our calculation shows that the BAF of interfacial molecules decays much slower than that of the bulk molecules, exhibiting a power law whose scaling exponent is 0.598 (Fig. 5b). Note that the binding memory is stronger than that on a flat interface, indicative of the existence of a curvature effect. The BAF decay flats out at longer timescales due to the limited surface area of the droplet. These findings suggest that the surfaces of biological condensates could play a role in regulating molecular binding, memory and downstream biological processes. The sensitivity of binding memory to phase separation also enables the development of sensors for biological condensates using advanced imaging techniques.
Chromatin presents another compelling example where binding memory may play a role. Its polymeric nature imposes constraints on molecular mobility, and proteins such as transcription factors (TFs) or chromatin architectural proteins often engage in one-dimensional (1D) sliding along DNA. Prior studies, including ours, have shown that 1D sliding by proteins like cohesin can affect chromatin organization48,49,50. It has also long been proposed that combining 1D sliding with 3D diffusion facilitates more efficient target search by TFs51,52. Here, we extend this concept by demonstrating through simulation that 1D sliding not only improves target search efficiency but also enhances molecular binding memory. As shown in Fig. 5c, the presence of 1D sliding leads to a distinct BAF scaling of t-0.5, indicative of a strong and persistent memory effect. Notably, this scaling is consistent with experimental observations of CTCF—a DNA-binding protein known to act as a barrier to cohesin—whose binding dynamics also follow a t-0.5 decay. These findings suggest that a 1D sliding mechanism could contribute to molecular binding memory on chromatin, with potential implications for transcriptional regulation and genome organization.
Finally, we turn to biological membranes, another critical class of molecular systems where binding memory may be functionally significant. Lipid bilayers, which form the structural foundation of cellular membranes, are composed of dynamic assemblies of phospholipids, cholesterol, and membrane proteins. These components interact through weak, reversible forces such as van der Waals and hydrophobic interactions, precisely the type of transient associations conducive to binding memory. Importantly, many membrane-associated processes, including protein insertion, anchoring, and signal transduction, rely on these reversible interactions to maintain a balance between stability and adaptability. However, the highly dynamic and cooperative nature of lipid-lipid and lipid–protein interactions makes experimental detection and theoretical modeling of binding memory particularly challenging. To address this, we performed simulations using mixed lipid bilayers composed of DOPC/DHPC and DPPC/DPPS as representative model systems (Fig. 5d). Our analysis reveals that binding memory is indeed encoded in lipid–lipid interactions, with BAF scaling behavior characteristic of a two-dimensional confined system, consistent with the planar geometry of the bilayer. These findings further support the notion that reduced dimensionality and interfacial dynamics together amplify binding memory effects across diverse biological interfaces.
High-resolution single-particle tracking experiments revealed strong binding memory on artificial and live-cell membranes
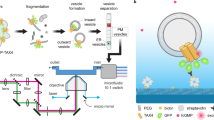
Extensive simulations and theoretical modeling strongly support the existence of binding memory at the single-molecule level and highlight the potential of the BAF as a powerful tool for experimentally probing the local microenvironment. As proof of concept, we integrate high spatiotemporal precision single-particle tracking (SPT) experiments to track single-molecule adsorption dynamics and detect binding memory in different complex environments. Recently, we developed a real-time 3D single particle tracking system with one microsecond temporal resolution and nanometer spatial resolution, termed Single Metal-nanoparticle Active Real-time Tracking with Enhanced Resolution (3D-SMARTER) microscopy53 (Fig. 6a). This advanced tracking capability enables precise extraction of biomolecular dynamics both in vitro and in live-cell environments, and is particularly well-suited for characterizing BAF.
Source data are provided as a Source Data file. a Schematic illustration of the 3D-SMARTER setup and the working procedure. b Trajectory of gp120-AgNP diffusing on a supported lipid bilayer. c, d 2D and 3D density maps of the residence time for the gp120-AgNP. e LDF of gp120-AgNP with a single-exponential fit. f BAF of gp120-AgNP exhibits a power law at a long-time scale. The inset displays the mean squared displacement analysis, indicating a subdiffusive exponent, \(\alpha=0.8460\pm 0.0002\). Based on Eq. 7, the fractal dimension of the lipid bilayer is inferred to be 1.97. Power-law fits, applied over a 0.5–8.5 s time window, quantify the scaling behavior of BAF and MSD, with exponents and fitting errors annotated in the figure. The corresponding exponents and fitting errors are indicated within the figures. g Trajectory of TATp-AgNP on a live-cell membrane. h, i 2D and 3D density maps of the residence time for TATp-AgNP. j LDF of TATp-AgNP on the live-cell membrane, with a double-exponential fit. k Power-law BAF and the MSD analysis inset, with the fractal dimension estimated to be 1.22 based on the theoretical model. Power-law fitting parameters and associated errors, extracted over the 0.25–6 s interval, are indicated in the figure.
Here, we focused on the adsorption dynamics of proteins on lipid membranes, as protein motion on the membrane is relatively slow, leading to a slower BAF decay compared to 3D systems, thus enhancing the BAF signal. This makes the system a more suitable candidate for testing binding memory. We began by simulating the adsorption dynamics of nanoparticles on a smooth 2D solid-liquid interface (Supplementary Fig. 15), representing ideal 2D adsorption dynamics under normal diffusion. Our results clearly demonstrate that BAF follows a power-law decay, and the scaling exponent reveals the 2D binding characteristics. Next, we employed 3D-SMARTER to track the dynamics of gp120-modified silver nanoparticles (gp120-AgNPs) on a supported lipid bilayer (SLB). The gp120 protein, a glycoprotein on the surface of the Human Immunodeficiency Virus (HIV) envelope, plays a critical role in viral infection by binding to the CD4 receptor on T cells, initiating viral entry. By using the depolarized scattering signal of AgNP, we tracked the probe motion, with the 2D trajectory shown in Fig. 6b. Furthermore, the density maps of residence time are extracted in both 2D and 3D with 1 μs resolution (Fig. 6c, d). The high spatiotemporal resolution of 3D-SMARTER allows us to easily distinguish BAF and LDF of the molecule, as shown in Fig. 6e, f. Our technique shows that the LDF decays fast and can be fitted to a single-exponential function, whereas the BAF decays much more slowly, exhibiting a power law at long timescales with a scaling exponent of \(-0.833\pm 0.029\), as determined from the fitting of BAF data over the time range of 0.5 s to 8.5 s. The dramatic difference between BAF and LDF revealed by our experiment suggests a high frequency of rebinding events and highlights the significance of binding memory in real biological systems. In addition, the nanoparticle exhibited sub-diffusive behavior, characterized by an anomalous diffusion exponent of \(\alpha=0.8460\pm 0.0002\). Leveraging the scaling properties of both BAF and MSD, our theoretical model (Eq. 7) enabled the prediction of the fractal dimension of the membrane environment. As our model requires minimal binding heterogeneity, we first verified that the displacement PDF was Gaussian (Supplementary Fig. 16a), confirming homogeneity. This validated the use of our theory and allowed us to estimate a fractal dimension of D = 1.97 (Fig. 6f), closely approximating 2 and consistent with the topologically simple nature of the SLB.
We then applied 3D-SMARTER to track the residence dynamics of TAT-peptides functionalized silver nanoparticles (TATp-AgNPs) on a live-cell membrane in vivo (Fig. 6g–i). Unlike the synthetic lipid bilayer, the live-cell membrane is far more complex in its spatial organization, which could lead to nontrivial topological effects. In this system, the LDF is no longer a single-exponential function (Supplementary Fig. 17), but can be better fitted by a bi-exponential function (Fig. 5j), implying the presence of both specific and non-specific interactions with the membrane. The BAF still features a power-law decay, but with a lower scaling exponent of \(-0.515\pm 0.016\) (obtained from fitting the BAF data over the 0.25 s to 6 s time window) (Fig. 6k), indicative of a stronger binding memory on live-cell membranes. The displacement PDF of molecular displacements in live-cell membranes closely approximates a Gaussian distribution (Supplementary Fig. 16b). Based on our theoretical model, we predicted a fractal dimension of \(D=1.22\) for the live-cell membrane, much lower than 2, suggesting a complex topology experienced by the probe. A number of factors could contribute to this topological effect, including heterogeneous distribution of membrane proteins, surface roughness, and even phase separation of the membrane.
The above experimental measurements confirmed the presence of power-law BAF in biological systems. Together with our simulation results, these findings demonstrate that binding memory is not limited to classical Newtonian liquids (e.g., water and ethanol) but also emerges in complex liquids such as fluidic biological membranes and viscoelastic biomolecular condensates. Although some systems involve solid–liquid interfaces or membranes supported on substrates, our primary focus remains on the binding behavior of molecules within the fluid phase, where interactions are transient and reversible.
It is important to recognize that fluids such as biological membranes can exhibit solid-like behavior at short timescales, due to local ordering or mechanical rigidity. However, at longer timescales, these systems develop some degree of fluidity, with transient interactions faciliting components exchange with neighboriung molecules. In this regime, binding memory becomes particularly relevant, as it captures the persistent influence of past interactions within a dynamically evolving environment.
Notably, the contrast in binding behavior between synthetic and live-cell membranes highlights the sensitivity of BAF to environmental complexity and organization. These observations suggest that biological systems may strategically exploit reduced dimensionality and structural heterogeneity to enhance binding memory, potentially as a mechanism for fine-tuning molecular recognition, signaling fidelity, and regulatory precision.
Molecular binding memory beyond single molecule
So far, we have been focused on molecular binding memory at the single-molecule level, characterized by the BAF. Experimental validation of binding memory has also been achieved, but single-molecule measurements require very high precision, particularly in systems with fast diffusion and rapid BAF decay. In such cases, measuring BAF becomes more challenging, highlighting the need for new perspectives to observe binding memory. Now we explore the collective memory effect of molecular binding, which may first manifest itself in the fluctuations of equilibrium systems. For an ensemble of molecules, the total number of bound molecules, \(N\), fluctuates around its average value, \(\bar{N}\), over time (Fig. 7a). The time autocorrelation of this molecular binding fluctuation, \({C}_{f}\left(\Delta t\right)=\left\langle \left(N\left(t\right)-\bar{N}\right)\left(N\left(0\right)-\bar{N}\right)\right\rangle /\left\langle {\left(N\left(t\right)-\bar{N}\right)}^{2}\right\rangle\), is characterized by computer simulation and a power law is uncovered (Fig. 7b). This result demonstrates that molecular binding fluctuation is not simply random (white noise) but a non-Markovian process with memory effect.
Source data are provided as a Source Data file. a Temporal fluctuations in the total number of bound molecules within the system, analyzed across three independent simulation systems. b Autocorrelation function analysis of binding fluctuations, \({C}_{f}\). c Time evolution of the total binding pairs between initially selected molecules in 2D and 3D systems, both showing power-law tails. d Response of the binding pairs to a sudden weakening of binding affinity in a nonequilibrium simulation, exhibiting a power-law behavior during the transition. In the inset, the high-affinity state of the molecules is shown in red and the low-affinity state in black. The data points correspond to averages over 500 independent simulations for \({C}_{f}\), 25 for binding pair counting, and 100 for the response analysis. Error bars are obtained as standard deviations from these averages. Power-law fits and corresponding fitting errors for panels (b), (c), and (d) are included in the figure, with fitting range spanning \(2\times {10}^{4}\)−\(1.5\times {10}^{5}\) steps for (b), \(7\times {10}^{7}\)−\(3\times {10}^{8}\) (2D) and \(5\times {10}^{7}\)−\(1.2\times {10}^{8}\) (3D) for (c), and 300–6000 steps for (d).
For a population of molecules, the averaged number of intra-population pairing pairs \(\left\langle {N}_{{{{\rm{p}}}}{{{\rm{air}}}}}\left(t\right)\right\rangle\) decays as a function of time. Ignoring binding memory, this quantity is expected to decay exponentially. Nevertheless, our computer simulations show that, like single-molecule BAF, the population-level pairing number exhibits dimension-dependent power laws (Fig. 7c). Therefore, molecular binding memory is not limited to single molecules or time correlation.
Furthermore, binding memory could manifest in systems out of equilibrium. To study this, we conducted a non-equilibrium simulation in which the binding strength is weakened by an external stimulus. Such perturbation leads to a reduction of molecular pairing to a lower level. By tracking the time-dependence of this process in computer simulation, we reveal that the change of molecular pairing number as a function of time follows a power law (Fig. 7d), indicative of a memory effect during the change of system state. The different manifestations of binding memory in macroscopic systems establish a framework for future experimental validation and exploration in broader molecular contexts.
Discussion
In summary, by integrating large-scale computer simulation, scaling theory, and high-resolution SPT experiment, we have systematically investigated the molecular binding dynamics and unambiguously demonstrated the existence of binding memory in liquid systems. The binding probability does not decay exponentially over time but follows a power law on a long-time scale. The scaling exponent and the amplitude of the power law are found to be sensitive to the topological and material properties of the system, respectively. In homogeneous binding environments, we established a universal scaling law linking the scaling of binding probability to the environmental dimension and the diffusion exponent of the molecule, which enables us to characterize complex liquid environments based on SPT technique. However, in heterogeneous binding landscapes, this scaling law can break down due to the emergence of more intricate binding dynamics. Such deviations from universality highlight the need for theoretical frameworks beyond diffusion-centric models to fully understand binding memory in complex systems. The molecular binding memory have important biological implications as demonstrated by our coarse-grained simulations of IDRs, phase separating systems, 1D sliding dyanmics of TFs and biological membranes. Unlike chemically fixed binding strength, binding memory is highly tunable and responsive to environmental changes. Such flexibility could have been leveraged by biological systems to regulate critical processes. Consideration of the binding memory effect will be important in future biophysical studies and soft materials design.
Methods
Computer simulation and analyses of binding dynamics
We use all-atom molecular dynamics simulations conducted in GROMACS54 to study the binding memory of water and ethanol. For one-dimensional confinement, molecules are restricted within a single-walled carbon nanotube of 2.1 nm in diameter, with PBC applied to the axial direction. In the case of two-dimensional confinement, we use two parallel graphene sheets separated by 2.0 nm, applying PBC to the directions parallel to the graphene surfaces. The bulk system is simulated in a cubic box of 16 nm with PBC in all directions.
To further investigate the binding memory in more complex systems, including polymer solutions, phase-separated systems, and biological membranes, both Langevin dynamics (LD) simulations are performed using LAMMPS55, alongside Martini force field-based coarse-grained molecular simulations using GROMACS. The non-bonded isotropic interactions between all monomers are modeled with the standard 12-6 Lennard-Jones potential. Bonded interactions are described by harmonic springs that connect consecutive beads. The specific details of the simulations for each system can be found in the Supplementary Information (SI).
In the post-processing of binding autocorrelation functions (BAF), a common method is to calculate the contact matrix \({M}_{t}\) of size \(N\times N\), where N is the total number of molecules in the system. This matrix records whether two molecules are bonded (1) or not (0). However, for systems with a large number of molecules, this method leads to significant memory overhead. The calculation of BAF involves comparing the \({M}_{t}\) at frames i and i + T for each lage time T to determine the overlap of bonded pairs. This requires scanning all \({N}^{2}\) elements for F-T frame pair and must be repeated for \({T}_{\max }\) different lag times. As a result, the overall computational complexity reaches \({{{\rm{O}}}}\left(F{{T}_{\max }N}^{2}\right)\).
However, in liquid systems, binding interactions are transient, and the contact neighbors are sparse, making the contact map inherently sparse as well. The conventional method becomes inefficient because of the excessive storage of zero entries, leading to both memory waste and unnecessary computations. To optimize this, we propose a hashmap-based approach that records only bonded pairs, eliminating the need to store non-interacting pairs. Specifically, each bonded pair is stored as a unique key in the form “i_j”, mapping to a value that indicates the presence of a bond. This approach significantly improves the search efficiency of the binding list, alleviating the storage burden. During BAF calculations, we traverse only the bonded pairs instead of all \({N}^{2}\) pairs, lowering the computational complexity to \({{{\rm{O}}}}\left(F{T}_{\max }K\log N\right)\), where K is the average number of bonded pairs.
A comparison of the computational efficiency between the two methods for systems of different sizes is shown in Supplementary Fig. 18. It is evident that our approach significantly accelerates the BAF calculation, enabling the efficient processing of bond formation data from large-scale simulations and multiple independent runs, thus yielding more reliable BAF statistics. All data processing steps, including the construction of contact information and analysis of the binding autocorrelation function and lifetime distribution function, were carried out using our in-house Fortran and C + + scripts (https://github.com/sqin5/binding-memory).
Set up of 3D-SMARTER
In 3D-SMARTER, a pair of electro-optic deflectors (Model 310 A, Conoptics Inc) and a tunable acoustic gradient lens (TAGLENS-T1, Mitutoyo) are used to generate an addressable laser scanning pattern in 3D space after the objective lens. A single-photon avalanche photodiode (APD, SPCM-AQRH-15, Excelitas Technologies) is used to collect the photon signals and record the photon arrival time. The target particle position in the illumination volume can be calculated in real time on a field-programmable gate array board (PCIe-7858, National Instruments Corp) with the photon arrival time information. When the target particle is off the center of the illumination volume, a feedback control signal will be sent to the piezoelectric stage (Nano-PDQ275, Nano-OPQ65, Mad City Lab) to move the target particle to the center position. The one microsecond temporal resolution 3D trajectory can be reconstructed with offline recursive Bayesian analysis with the photon arrival time information and laser focus position information. The detailed 1 \(\mu s\) resolution trajectory reconstruction method can be found in Supplementary Note 1 of reference 53. These reconstructions were performed using MATLAB. Following the reconstruction of high-resolution trajectories, LDF and BAF analyses were conducted using the same Fortran and C + + scripts previously used in the simulation.
3D-tracking gp120-AgNPs on supported lipid bilayer (SLB) with CD4 protein
Gp120 protein (HY-P70907, MedChemExpress) was mixed with SH-PEG-NHS (80030802E, Tanshtech) at a ratio of 1:20 and incubated overnight at 4 °C. After purified with a desalting column (89882, Thermo Fisher Scientific), AgNPs (100 nm, AGCB100-1M) were then added to the solution, incubated at room temperature for 2 h to obtain the gp120-AgNPs conjugate. Lipid vesicles were prepared by the way of liquid nitrogen freeze-thaw cycles. In brief, the DOPC and DHPC mixture with a molar ratio of 2.5 and 2.5% DGS-NTA (Ni) were repeatedly freeze-thawed in liquid nitrogen and 60 °C water bath for 5–7 times to obtain vesicles for use. For the preparation of SLB, the glass slide was first sonicated with 50% ethanol and ultrapure water for 15 min each, followed by drying under a gentle stream of nitrogen gas. Subsequently, the slides were subjected to air plasma treatment (PT-5SMT, SANHOPTT) at 200 W for 10 min under controlled vacuum. The 30-fold diluted vesicles were immediately added and incubated at 60 °C for 20 min to form SLB, followed by a wash with Hepes buffer. CD4 protein solution was added to SLB and incubated at room temperature for 1 h. After washing with Hepes buffer, gp120-AgNPs were added to it for real-time tracking using 3D-SMARTER.
3D-tracking of TATp-AgNPs on live-cell membrane
Streptavidin (S4762, Sigma-Aldrich) was first labeled with NHS-PEG-3K-Thiol (PG2-NSTH-3k, Nanocs lnc.) at a molar ratio of 1:6. The reaction mixture was subsequently purified by using a NAP-5 G25 desalting column (17085301, GE Healthcare illustra). The purified streptavidin-PEG-Thiol conjugate was then mixed with 100 nm AgNPs (AGCB100-1M, NanoComposix) to functionalize the nanoparticles. Subsequently, biotin-TAT peptides (AS-612099, Anaspec Inc.) were added to the streptavidin-AgNP complex, and the solution was purified by centrifugation (1600 × g, 20 min). For the 3D tracking experiments, HeLa cells (Cell Bank of the Chinese Academy of Sciences, Shanghai, China) were first cultured on coverslips overnight at 37 °C, with 5% CO2 in DMEM (high glucose) supplemented with 10% FBS (F0193, Sigma). Before imaging, the cells were washed three times with DMEM cell culture medium and transferred to FluoroBrite™ DMEM (A1896701, Gibco). TATp-AgNPs were then added to the solution for real-time tracking of their movement on the cell membrane.
Data availability
All other data supporting the findings of this study are available in the Supplementary Information file. Source data for figures are provided with this paper. Source data are provided in this paper.
Code availability
The analysis codes for the binding states of all molecules in the system, which include generating intermolecular contact maps, evaluating the binding autocorrelation function, and computing the lifetime distribution function, are available on Zenodo (https://doi.org/10.5281/zenodo.15675915).
References
Narlikar, G. J., Gopalakrishnan, V., McConnell, T. S., Usman, N. & Herschlag, D. Use of binding energy by an RNA enzyme for catalysis by positioning and substrate destabilization. Proc. Natl. Acad. Sci. USA 92, 3668–3672 (1995).
Schwans, J. P., Kraut, D. A. & Herschlag, D. Determining the catalytic role of remote substrate binding interactions in ketosteroid isomerase. Proc. Natl. Acad. Sci. USA 106, 14271–14275 (2009).
Cawood, E. E. et al. Modulation of amyloidogenic protein self-assembly using tethered small molecules. J. Am. Chem. Soc. 142, 20845–20854 (2020).
Wei, X., Chen, C., Popov, A. V., Bathe, M. & Hernandez, R. Binding site programmable self-assembly of 3D hierarchical DNA origami nanostructures. J. Phys. Chem. A 128, 4999–5008 (2024).
Li, Y., Yang, G., Gerstweiler, L., Thang, S. H. & Zhao, C. Design of stimuli-responsive peptides and proteins. Adv. Funct. Mater. 33, 2210387 (2023).
Effiong, U. M., Khairandish, H., Ramirez-Velez, I., Wang, Y. & Belardi, B. Turn-on protein switches for controlling actin binding in cells. Nat. Commun. 15, 5840 (2024).
Zhang, Z. et al. Brain-targeted drug delivery by manipulating protein Corona functions. Nat. Commun. 10, 3561 (2019).
Pomp, W., Meeussen, J. V. W. & Lenstra, T. L. Transcription factor exchange enables prolonged transcriptional bursts. Mol. Cell 84, 1036–1048 (2024).
Aoki, K., Yamada, M., Kunida, K., Yasuda, S. & Matsuda, M. Processive phosphorylation of ERK MAP kinase in mammalian cells. Proc. Natl. Acad. Sci. USA 108, 12675–12680 (2011).
Arranz-Plaza, E., Tracy, A. S., Siriwardena, A., Pierce, J. M. & Boons, G.-J. High-avidity, low-affinity multivalent interactions and the block to polyspermy in Xenopus l Aevis. J. Am. Chem. Soc. 124, 13035–13046 (2002).
Oh, D. et al. Fast rebinding increases Dwell time of src homology 2 (SH2)-containing proteins near the Plasma membrane. Proc. Natl. Acad. Sci. USA109, 14024–14029 (2012).
Vauquelin, G. & Charlton, S. J. Long-lasting target binding and rebinding as mechanisms to prolong in vivo drug Action. Br. J. Pharmacol. 161, 488–508 (2010).
Taylor, E. W. Kinetic studies on the association and dissociation of myosin subfragment 1 and actin. J. Biol. Chem. 266, 294–302 (1991).
Kiel, C. et al. Improved binding of Raf to Ras·GDP is correlated with biological activity. J. Biol. Chem. 284, 31893–31902 (2009).
Skaug, M. J., Mabry, J. & Schwartz, D. K. Intermittent molecular hopping at the solid-liquid interface. Phys. Rev. Lett. 110, 256101 (2013).
Skaug, M. J., Mabry, J. N. & Schwartz, D. K. Single-molecule tracking of polymer surface diffusion. J. Am. Chem. Soc. 136, 1327–1332 (2014).
Mazzocca, M., Colombo, E., Callegari, A. & Mazza, D. Transcription factor binding kinetics and transcriptional bursting: What do we really know?. Curr. Opin. Struct. Biol. 71, 239–248 (2021).
Garcia, D. A. et al. Power-law behavior of transcription factor dynamics at the single-molecule level implies a continuum affinity model. Nucleic Acids Res. 49, 6605–6620 (2021).
Rogers, W. B., Sinno, T. & Crocker, J. C. Kinetics and non-exponential binding of DNA-coated colloids. Soft Matter 9, 6412 (2013).
Biancaniello, P. L., Kim, A. J. & Crocker, J. C. Long-time stretched exponential kinetics inxsingle DNA duplex dissociation. Biophys. J. 94, 891–896 (2008).
Chen, J. et al. Single-molecule dynamics of enhanceosome assembly in embryonic stem cells. Cell 156, 1274–1285 (2014).
Asadollahi, K. et al. Unravelling the mechanism of neurotensin recognition by neurotensin receptor 1. Nat. Commun. 14, 8155 (2023).
Alder, B. J. & Wainwright, T. E. Decay of the velocity autocorrelation function. Phys. Rev. A 1, 18–21 (1970).
Li, T., Kheifets, S., Medellin, D. & Raizen, M. G. Measurement of the instantaneous velocity of a Brownian particle. Science 328, 1673–1675 (2010).
Kheifets, S., Simha, A., Melin, K., Li, T. & Raizen, M. G. Observation of Brownian motion in liquids at short times: Instantaneous velocity and memory loss. Science 343, 1493–1496 (2014).
Luzar, A. & Chandler, D. Hydrogen-bond kinetics in liquid water. Nature 379, 55–57 (1996).
Huang, K. & Szlufarska, I. Effect of interfaces on the nearby Brownian motion. Nat. Commun. 6, 8558 (2015).
Gennes, P. G. de. Scaling Concepts in Polymer Physics. (Cornell University Press: Ithaca, N.Y, 1979).
Mandelbrot, B. B. The Fractal Geometry of Nature. (W.H. Freeman: San Francisco, 1982).
Récamier, V. et al. Single cell correlation fractal dimension of chromatin: A framework to interpret 3D single molecule super-resolution. Nucleus 5, 75–84 (2014).
Bancaud, A. et al. Molecular crowding affects diffusion and binding of nuclear proteins in heterochromatin and reveals the fractal organization of chromatin. EMBO J. 28, 3785–3798 (2009).
Mazzocca, M., Fillot, T., Loffreda, A., Gnani, D. & Mazza, D. The needle and the haystack: Single molecule tracking to probe the tanscription factor search in eukaryotes. Biochem. Soc. Trans. 49, 1121–1132 (2021).
Kaur, G. et al. Probing transcription factor diffusion dynamics in the living mammalian embryo with photoactivatable fluorescence correlation spectroscopy. Nat. Commun. 4, 1637 (2013).
Hansen, A. S., Amitai, A., Cattoglio, C., Tjian, R. & Darzacq, X. Guided nuclear exploration increases CTCF target search efficiency. Nat. Chem. Biol. 16, 257–266 (2020).
Höfling, F. & Franosch, T. Anomalous transport in the crowded world of biological cells. Rep. Prog. Phys. 76, 046602 (2013).
Liu, D., Zhou, W., Song, X. & Qiu, Z. Fractal simulation of flocculation processes using a diffusion-limited aggregation model. Fractal Fract. 1, 12 (2017).
Tenti, J. M., Hernández Guiance, S. N. & Irurzun, I. M. Fractal dimension of diffusion-limited aggregation clusters grown on spherical surfaces. Phys. Rev. E 103, 012138 (2021).
Meyer, B., Bénichou, O., Kafri, Y. & Voituriez, R. Geometry-induced bursting dynamics in gene expression. Biophysical J. 102, 2186–2191 (2012).
ben-Avraham, D. & Havlin, S. Diffusion and Reactions in Fractals and Disordered Systems. (Cambridge University Press, 2000).
Choi, J.-M., Holehouse, A. S. & Pappu, R. V. Physical principles underlying the complex biology of intracellular phase transitions. Annu. Rev. Biophys. 49, 107–133 (2020).
Martin, E. W. et al. Valence and patterning of aromatic residues determine the phase behavior of prion-like domains. Science 367, 694–699 (2020).
Farag, M. et al. Condensates formed by prion-like low-complexity domains have small-world network structures and interfaces defined by expanded conformations. Nat. Commun. 13, 7722 (2022).
Leonard, T. A., Loose, M. & Martens, S. The membrane surface as a platform that organizes cellular and biochemical processes. Dev. Cell 58, 1315–1332 (2023).
Bondar, A.-N. & Lemieux, M. J. Reactions at biomembrane interfaces. Chem. Rev. 119, 6162–6183 (2019).
Fallah-Araghi, A. et al. Enhanced chemical synthesis at soft interfaces: A universal reaction-adsorption mechanism in microcompartments. Phys. Rev. Lett. 112, 028301 (2014).
Chao, Y. & Shum, H. C. Emerging aqueous two-phase systems: From fundamentals of interfaces to biomedical applications. Chem. Soc. Rev. 49, 114–142 (2020).
Dai, Y. et al. Interface of biomolecular condensates modulates redox reactions. Chem 9, 1594–1609 (2023).
Fudenberg, G. et al. Formation of chromosomal domains by loop extrusion. Cell Rep. 15, 2038–2049 (2016).
Mach, P. et al. Cohesin and CTCF control the dynamics of chromosome folding. Nat. Genet. 54, 1907–1918 (2022).
Zhao, H. et al. Extensive mutual influences of SMC complexes shape 3D genome folding. Nature 640, 543–553 (2025).
Marklund, E. G. et al. Transcription-factor binding and sliding on DNA studied using micro- and macroscopic models. Proc. Natl. Acad. Sci. USA. 110, 19796–19801 (2013).
Van Den Broek, B., Lomholt, M. A., Kalisch, S.-M. J., Metzler, R. & Wuite, G. J. L. How DNA coiling enhances target localization by proteins. Proc. Natl. Acad. Sci. USA 105, 15738–15742 (2008).
Hou, S., Zhang, C., Niver, A. & Welsher, K. Mapping nanoscale forces and potentials in live cells with microsecond 3D single-particle tracking. Preprint at https://doi.org/10.1101/2022.06.27.497788 (2022).
Van Der Spoel, D. et al. GROMACS: Fast, Flexible, and Free. J. Comput. Chem. 26, 1701–1718 (2005).
Thompson, A. P. et al. LAMMPS - a Flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 271, 108171 (2022).
Acknowledgements
This work was funded by grants from the Major Program of Shenzhen Bay Laboratory (grant no. S241101001 to K.H.), the Shenzhen Medical Research Fund (grant no. B2301003 to S.H.), National Natural Science Foundation of China (grant no. 22203055 to K.H., grant no. 22204106 to S.H., grant no. 22403068 to S.Q.), the Shenzhen Bay Laboratory Open Fund Project (grant no. SZBL2021080601013 to K.H.) and the Guangdong Pearl River Talent Program (grant no. 2021QN02Y495 to K.H., grant no. 2021QN02Z631 to S.H). We acknowledge computational support from the Shenzhen Bay Laboratory High Performance Computing and Informatics Core.
Author information
Authors and Affiliations
Contributions
K.H. and S.H. conceived, guided and supervised the project; S.Q. and Z.Y. designed and performed computer simulations; H.L. and X.W. designed and performed SPT experiments; S.Q. analyzed experimental data; K.H., S.Q., and B.M. formulated the theoretical framework of the manuscript. K.H. and S.Q. wrote the manuscript. All authors discussed the results and reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Steffen Wolf, and the other anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Qin, S., Yang, Z., Liu, H. et al. Binding memory of liquid molecules. Nat Commun 16, 6555 (2025). https://doi.org/10.1038/s41467-025-61630-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-61630-3