Abstract
Halides are promising solid electrolytes due to their high ionic conductivity and high oxidation potential. Here we report a superionic chloride material, NaTaCl6, which exhibits a high ionic conductivity of 3.3 mS cm−1 at 27 °C, being two-orders of magnitude higher than that of NaNbCl6 (0.01 mS cm−1). The considerably higher conductivity exhibited by NaTaCl6 vs. NaNbCl6 arises from the more facile rotational/reorientational dynamics of the [TaCl6] polyanions in comparison to the [NbCl6] anions. [TaCl6] polyanion rotation is readily activated while [NbCl6] polyanion reorientation is hindered at room temperature but can be turned on as the temperature increases or under prolonged mechanical milling. The higher degree of structural disorder exhibited by NaTaCl6 compared to NaNbCl6—likely attributed to its greater mechanical and phonon softness—is found to contribute to the more pronounced [TaCl6] anion rotation. Anion rotation is coupled with, and facilitates, macroscopic Na+-ion diffusion. As a result, enhanced rotational dynamics are directly correlated with the higher Na+-ion conductivity observed in NaTaCl6. The high ionic conductivity, combined with its electrochemical stability against positive electrode materials, enables good rate capability and long-term cycling performance in solid-state cells. These findings provide insights into ion transport mechanism in the newly emerging halide solid electrolytes.
Similar content being viewed by others
Introduction
All solid-state batteries (ASSBs) have received considerable attention as they offer great potential to satisfy the ever-rising demand for high energy density and safe energy storage system over the conventional lithium-ion batteries (LIBs)1,2. However, concerns over the rising lithium costs and limited availability have arisen due to the continued increasing demand for LIBs as a power source for portable electronic devices, vehicles and grids3. Owing to the high abundance and hence low cost of sodium resource, sodium based rechargeable batteries represent as a promising alternative technology, particularly for large-scale energy storage applications4,5. The major challenges facing solid-state sodium batteries are the exploration of highly conductive and electrochemical stable solid electrolytes, as well as the regulation of ion transport across the electrode/solid electrolyte interface1,6.
Solid electrolytes (SEs) that simultaneously possess high ionic conductivity, wide electrochemical window, together with good compatibility with electrode layers are paramount to realize high energy density ASSBs7,8. Among SEs investigated, sulfides show the highest ionic conductivity and high ductility which enables intimate contacts with electrode materials by simple cold-pressing techniques6,9. Na3MS4 (M = P/Sb)10,11,12, Na11Sn2PS1213,14, and their derivatives15,16 are typical examples from this category of SEs. However, they are generally suffering from very limited electrochemical window (1.9-2.6 V)17,18 and hence poor compatibility with both positive and negative electrodes. On the contrary, oxide electrolytes oftentimes exhibit sufficient electrochemical window (oxidation resistive up to 4.5 V) and moderate ionic conductivity (1-5.0 mS cm−1)19,20,21. Unfortunately, oxide superionic conductors (e.g., NaSICONs19,20,21,22,23 and β-alumina24) generally require harsh synthesis conditions (high temperature synthesis) in order to obtain high relative density and hence low grain boundary resistance 25,26.
A newly emerging class of electrolytes, halides, began to attract attention since a seminal report on Li3YX6 (X = Cl, Br) by Asano et al. in 201827. The monovalent nature of halides gives rise to weak Coulombic interactions with the Li+-ions and hence endows potentially high ionic conductivity. Chlorides are particularly promising, as they show higher oxidative stability compared to their bromides and iodides counterparts. Subsequent studies on halide electrolytes with the general formula Li3MCl6 and Li2MCl4, and their derivatives, such as Li3MCl6 (M = In, Sc)28,29,30, Li3−xM1−xZrxCl6 (M = Y, Er, In, Yb)31,32,33, Li3−xM1−xHfxCl6 (M = Yb, Y, In)34,35,36, Li2Sc2/3Cl437, Li2InxSc2/3−xCl438, have demonstrated both high conductivity and good compatibility with high-voltage positive electrode materials. While their sodium counterparts have the similar potentials, sodium chlorides remain relatively underexplored that very few candidates with high conductivity have been reported. To date, the most visited crystalline structures, i.e., NaAlCl439, Na2ZrCl640, and Na3MCl641,42,43 and their Zr-substituted derivatives, Na3−xM1−xZrxCl6 (M = Er, Y, In)44,45,46, exhibited relatively low ionic conductivities (10−6 ~ 10−5 S cm−1). A recent study by some authors of us demonstrated the feasibility of substituting chlorine with oxygen in NaAlCl4, resulting in a viscoelastic inorganic glass that displays a significantly enhanced ionic conductivity of ~1 mS cm−1 at room temperature47. This promising result has motivated us to explore other sodium halides that possess high ionic conductivity.
The lack of decent understanding of the ion conduction mechanism in sodium halides is one of the primary reasons for the scarcity of highly conductive sodium chloride candidates. It has been well established that factors such as anion packing arrangement48, cation or anion sublattice disorder13,49,50,51,52,53,54, and anion polarizability55,56, have significant impact on the ion diffusion process in solids. Our previous work on the thiophosphate series Na11Sn2PnX12 (Pn = Sb, P; X = S, Se) highlights the crucial yet often overlooked role of the paddle-wheel effect, demonstrating how the rotational dynamics of the polyanion sublattice can significantly facilitate cation conduction57. A subsequent comparative study on Li3PS4 and Si-doped Li3PS458 revealed that anion group substitution is an effective strategy to lower the onset temperature of anion rotation, thereby activating the paddle-wheel mechanism and enhancing cation diffusivity at room temperature. This finding motivates the investigation of ion transport in sodium halides, considering their comparable structural softness and lattice flexibility. Indeed, recent investigations of Na3−xY1−xZrxCl645 have suggested a correlation between anion rotational dynamics and improved ionic conductivity. However, a definitive mechanistic link between anion motion and cation transport in these systems remains to be fully established.
Herein, we report a nanocrystalline sodium chloride electrolyte, NaTaCl6, in which fast ion transport is driven by the paddle-wheel effect. This material exhibits a high ionic conductivity of 3.3 mS cm⁻1 at room temperature (RT, referred to 27 °C throughout this study) and a low activation energy of 0.31 eV. Its isostructural Nb analogy, NaNbCl6, demonstrates a much higher crystallinity and correspondingly lower ionic conductivity of 0.01 mS cm−1 at RT under the same milling procedure. The minor difference in the static crystalline lattice between the two materials, as revealed by bond valance approach and Bader charge analysis, suggests that these static structural features alone do not account for the nearly 300-fold discrepancy in conductivity. Further combination of ab initio molecular dynamics (AIMD) simulations and joint-time correlation analysis manifest that the much higher conductivity of NaTaCl6 is attributed to the more facile rotational dynamics of [TaCl6] octahedra compared to the [NbCl6] anions. The anion rotational tendency is revealed to be associated with the degree of polyanion orientational disorder. The higher degree of amorphization and hence greater structural disorder observed in NaTaCl6 relative to NaNbCl6 upon the same milling procedure—likely stemming from its lower mechanical strength and enhanced phonon softness—contributes to the more pronounced rotation of [TaCl6] anions. In accord, the facile rotation of the [TaCl6] polyanion is triggered at room temperature, as suggested by deep potential molecular dynamics (DPMD) simulations. This anion rotation is strongly coupled with, and actively promotes, macroscopic Na⁺-ion diffusion by opening up the bottleneck for Na+-ion diffusion and improving Na+-ion migration entropy. Moreover, anion rotational dynamics have also been demonstrated to exist in other highly conductive halides and oxyhalide, such as LiMCl6 and NaMOCl4 (M = Ta, Nb), and played an important role in enabling high cation conductivities in these materials. Owing to the superionic conductivity and the high oxidative stability of NaTaCl6, ASSBs utilizing uncoated NaCu0.12Ni0.22Fe0.33Mn0.33O2 positive electrode exhibit good electrochemical performance at both RT and moderate temperature (50 °C). Our findings emphasize the crucial role that polyanion rotational dynamics plays in enabling fast cation diffusion, offering a promising strategy for the design of high-performance halide electrolytes with superior ionic conductivity.
Results and discussion
Discovery of high cationic conductivity in NaTaCl6, but not in NaNbCl6
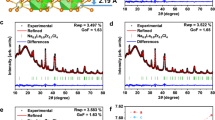
NaTaCl6 and NaNbCl6 were previously synthesized by Henning et al. with the utilization of a solvent-based approach59. Single crystal X-ray diffraction (XRD) revealed that both Ta and Nb analogs crystallize in the monoclinic P21/c space group; however, their ionic conductivities were not reported at that time. In the present study, we synthesized NaTaCl6 and NaNbCl6 via mechanical milling with varying durations. Figure 1a shows the XRD patterns for NaTaCl6 and NaNbCl6 with a ball milling reaction time of 15 h The diffraction patterns confirm the formation of phase-pure NaTaCl6 and NaNbCl6. Notably, NaTaCl6 exhibits significantly lower crystallinity under identical milling conditions, as evidenced by its less intense and more broadened reflections compared to NaNbCl6 (Fig. 1b). As the ball milling time increases, the peak intensities decrease for both materials (Supplementary Fig. 1). In accord with the single crystal study mentioned above, our Rietveld refinement of both the neutron powder diffraction (NPD) and XRD patterns revealed that both Ta and Nb counterparts crystallize in the P21/c structure, with negligible differences in the lattice parameters due to the identical ionic radii of Ta5+ and Nb5+. Supplementary Tables 1–4 in the Supplementary Information summarize the refined lattice parameters, atomic coordinates, occupancy and Uiso values. Notably, the large Uiso values for Cl atoms in NaTaCl6, as revealed by both XRD and NPD refinements, indirectly suggest considerable mobility of Cl atoms.
a Powder X-ray diffraction patterns of NaTaCl6 and NaNbCl6. b The enlarged XRD patterns with the 2θ range from 15.5° to 19.5° (top) and 30.4° to 33.1° (bottom). c The crystal structure of Na(Ta,Nb)Cl6 shown along the [001] direction. The [TaCl6]/[NbCl6] octahedra are shown in blue, and [NaCl6] prisms are shown in pink. d, e The Nyquist plots of impedance spectroscopy measurements at 27 °C for (d) NaTaCl6 and (e) NaNbCl6, along with the equivalent circuit models used for data fitting. The circuit for NaTaCl6 consists of a resistor (R) in series with a constant phase element (CPE), while that for NaNbCl6 includes a CPE in parallel with a resistor, in series with another CPE. f The Na+-ion conductivities of NaTaCl6 and NaNbCl6 at different temperatures (253−333 K). The dotted lines are the linear fit to the data, giving rise to activation energies of 0.31 eV for NaTaCl6, and 0.38 eV for NaNbCl6, respectively. Source data for figure are provided as a Source Data file.
A view of the structure of Na(Ta,Nb)Cl6 is shown in Fig. 1c. The lattice framework is two-dimensional and comprised of two Na(Ta,Nb)Cl6 sheets oriented in the (001) direction; [NaCl6] prisms and [TaCl6]/[NbCl6] octahedra are arrayed in layers perpendicular to the c-axis. Each [NaCl6] prism is connected to four [NaCl6] prisms and four [TaCl6]/[NbCl6] octahedra by edge sharing or vertex sharing manner. Each [TaCl6]/[NbCl6] octahedron links to four [NaCl6] prisms; two via edge sharing and the other two by vertex sharing. The sodium ions (fully occupied at one Na site, labeled as Na1) and voids are arrayed on separate layers running parallel to (001), both of which take part in the cation diffusion process. The large void space is crucial for forming three-dimensional channels that facilitate cations diffusion through the structure. This will be discussed further below. NaTaCl6 show almost identical Na-Cl (2.73–3.00 Å) and M-Cl bond distances (2.26–2.47 Å) compared to NaNbCl6 (2.76–2.94 Å for Na-Cl bond and 2.23–2.47 Å for M-Cl bond).
The ion transport properties of the two materials were investigated by impedance spectroscopy measurements. The effect of the ball milling duration on the ionic conductivity is shown in Supplementary Fig. 2. For NaTaCl6, a short mechanochemical reaction time of 15 h results in an amorphous product with high conductivity of 3.3 mS cm−1 at 300 K, as shown in Nyquist plot in Fig. 1d. In contrast, under identical milling conditions, the Nb analog exhibits a significantly lower conductivity of 0.01 mS cm⁻1, two orders of magnitude lower (Fig. 1e). The fitting parameters associated with the Nyquist plots in Fig. 1d, e, obtained using the equivalent circuit models, are summarized in Supplementary Tables 5–6. Extending the milling time increases the conductivity, accompanied by a decrease in the crystallinity (Supplementary Figs. 1–2). For NaNbCl6, the conductivity can only be improved to 0.1 mS cm−1 after a long milling duration of 120 h. Samples milled for 15 h were used for the comparison study below unless otherwise specified. The electronic conductivities determined from the direct current polarization method are 1.8 × 10−11 S cm–1 for NaTaCl6 and 2.4 × 10−11 S cm−1 for NaNbCl6, respectively (Supplementary Fig. 3), indicating the electronic insulating nature of both materials. Temperature-dependent conductivity measurements suggest that the conductivities follow Arrhenius-like behavior over the narrow temperature range (253 K−333 K) studied (Fig. 1f), allowing for the determination of the activation energies (Ea) for Na+-ion diffusion. The activation energy obtained from the fit is 0.31 eV for NaTaCl6, which is lower than that of NaNbCl6 (0.38 eV). These values are in good agreement with those reported in recent parallel studies60,61,62. Further in-depth impedance analysis, employing the methodology developed by Almond and West el al.63, reveals that the significant difference in ionic conductivity between NaTaCl6 and NaNbCl6 arises from both a disparity in activation energies and a notable difference in the pre-exponential factors. The latter is attributed to the distinct Na+-ion migration entropies in the two materials (Supplementary Figs. 4–7 and Supplementary Tables 7–8; See Supplementary Note 1 for detailed analysis), with the underlying reasons discussed in a later section. Post-annealing of the samples at 200 °C for 5 h leads to more intense and sharper Bragg reflections (Supplementary Fig. 8), and correspondingly dramatic decline in the ionic conductivity by 2–3 orders of magnitude for both NaTaCl6 and NaNbCl6 (4.7 × 10−6 S cm−1 for annealed NaTaCl6 and 7.8 × 10−7 S cm−1 for annealed NaNbCl6, respectively) (Supplementary Fig. 9). The underlying reason for these observations, likely associated with variations in the local disorder arising from different synthesis routes, will be discussed later.
Scanning electron microscopy (SEM) images provide a detailed view of the morphological evolution of two electrolyte materials during high-energy mechanochemical reactions, as shown in Supplementary Fig. 10. The NaTaCl6 sample milled for 7 h exhibits small grains in a few hundred nanometers with discernible boundaries, indicating its crystallinity nature (Supplementary Fig. 10a). As the milling time increases, the conductivity rises, and the secondary particles grow larger, adopting a more uniform distribution (Supplementary Fig. 10a–c). This transformation is attributed to the fusion of grain boundaries, which leads to the merging of the primary particles. Notably, at the longest milling time, the secondary particles grow to ~15 um in size with a uniform distribution and no visible grain boundaries (Supplementary Fig. 10c-d), indicative of amorphous nature. This transition aligns with the decrease in the crystallinity of the samples. These findings are in well agreement with Sun’s work60. The same trend was observed for the NaNbCl6 samples. However, quite differently, the particle size of NaNbCl6 began to grow only after a long ball milling time of 120 h (Supplementary Fig. 10e–h). This suggests that NaTaCl6 is more readily amorphized, with particle merging occurring more quickly.
The Na+-ion diffusion properties in the two materials were evaluated by Bond valence site energy (BVSE) method and AIMD simulations. BVSE has been verified to be reliable in terms of predicting accessible pathways and approximately evaluating the relative site energies for mobile ions in the structure. Shown in Fig. 2a is the possible Na+-ion pathways obtained from BV analysis. In addition to the fully occupied Na1 site, Na+-ions can also be highly populated at two intermediate sites (labeled as i1 and i2 site, respectively, see Fig. 2a) during the diffusion process. Our BVSE analysis reveals that i1 intermediate site is also a low energy site, being merely ~0.1 eV higher than Na1 site. The i2 intermediate site locates in the vacant layer, and is 0.2 eV higher in energy than Na1 site. Na+-ions in the Na layer can jump to another Na1 site (in the same Na layer) through the unoccupied i1 site, or hop into the empty i2 site that locates in the vacant layer, giving rise to three dimensional (3D) diffusion pathways: (1) path I: Na1-i1-Na1-i1-Na1 (in the Na plane); (2) path II: Na1-i1-i2- (in a zigzag chain along the c axis); and (3) path III: i2-i1-i2-i1-i2-i1 (in the vacant layer).
a Calculated Na+-ion isosurface (pink) in NaTaCl6 by BVSE method, displayed in a 2a × 2b × 1c supercell. Blue polyhedra represent [TaCl6] units. The green and yellow dash lines indicate the Na1-i1 and i1-i2 migration pathways, respectively. b, c Na+-ions migration barriers calculated using BVSE method for (b) NaTaCl6 and (c) NaNbCl6. The energy of the Na1 site is set as the reference (zero). The green and yellow segments correspond to the migration barriers along the Na1–i1 and i1–i2 paths, as illustrated in (a). d, e Na+-ion probability density depicted as pink isosurfaces, extracted from AIMD simulations conducted at 600 K for 200 ps in (d) NaTaCl6 and (e) NaNbCl6, demonstrating 3D Na+-ion diffusion pathways involving the Na1 site and two intermediate sites. Blue and green polyhedra represent [TaCl6] and [NbCl6] units, respectively. Red dashed circles highlight regions with notable differences in isosurface connectivity. f The lnD vs. 1000/T relation for NaTaCl6 and NaNbCl6 derived from AIMD simulations. Blue and yellow shaded areas correspond to high- and low-temperature regimes, respectively, indicating similar diffusivities at elevated temperatures and a pronounced divergence in Na⁺-ion mobility at lower temperatures. Error bars denote the relative standard deviation calculated from the mean squared displacement (MSD) based on statistical analysis. Source data for figure are provided as a Source Data file.
The associated migration energy barriers derived from BVSE suggest that both compounds show high barriers, with little difference between the Ta and Nb analogs (0.72 eV NaTaCl6 vs. 0.76 eV for NaNbCl6, see Fig. 2b, c). This is unexpected, as NaTaCl6 has been experimentally shown to exhibit ~300 times higher ionic conductivity than NaNbCl6. While BVSE is useful for a preliminary evaluation of potential diffusion pathways, it often overestimates the migration energy due to the static nature of the structural model used in the analysis. The crystal structure is treated as a rigid body, without accounting for the relaxation of surrounding atoms during cation migration64,65. In fact, the impact of anion sublattice relaxation should not be underestimated, as it creates an instantly fluctuating environment that reduces the energy barriers experienced by cations during diffusion. This effect in NaMCl6 (M = Ta, Nb) will be further demonstrated through AIMD simulations, which have proven to be a successful approach in studying cation-anion interactions in our prior work 57,58,66.
Previous pair distribution function (PDF) analysis has revealed that local lattice structure of NaTaCl6 remains intact under harsh milling conditions, as evidenced by the similar Ta-Ta scattering peaks in both highly crystallized and less crystallized samples60. Therefore, it is reasonable for us to use the crystalline structures obtained from Rietveld refinement as the initial input for constructing the models used in our AIMD simulations. To obtain satisfactory statistics, AIMD simulations were carried out at elevated temperatures ranging from 500 to 1050 K for 200 ps. The Na+-ion probability density isosurface at 600 K clearly reveals the 3D diffusion pathways and significant Na+-ion mobility in NaTaCl6 (Fig. 2d). In accordance with the BVSE analysis, the Na+-ion migration flow is established by the Na1-i1-Na1-i1-Na1 path in the Na plane, the Na1-i1-i2- zigzag chain along the c axis and the i2-i1-i2-i1-i2-i1 path in the vacant layer. With the participation of Na1 site and the two intermediate sites, a well-connected conduction channel forms, leading to the almost 3D isotropic conduction for Na+-ions. In contrast, NaNbCl6 displays a less conjunctive pathway at 600 K (Fig. 2e). However, as the simulation temperature increases to 675 K, the connection is significantly enhanced, with negligible difference to that of NaTaCl6 (Supplementary Fig. 11). The Na+-ion diffusion coefficients (D) calculated using a scheme established by Mo67 also confirm this trend, namely, NaTaCl6 exhibits much higher diffusivity than NaNbCl6 below 600 K, but the difference diminishes at above 675 K (Fig. 2f). The notably different ionic conducting properties of NaTaCl6 and NaNbCl6–despite their similar ionic radii and comparable crystal structures—prompted further investigation into other factors, such as the cation-anion interactions, to better understand this unexpected behavior. This motivation underlies the subsequent analysis presented below.
Lower onset temperature for the [TaCl6] polyanions rotation versus [NbCl6] polyanions
To gain a better understanding of the significantly different Na+-ion conducting propensities exhibited by the two analogs, we performed a detailed analysis of AIMD simulations conducted at 600 K. The 3D spatial distribution of the [TaCl6] and [NbCl6] polyanions was determined by extracting the trajectories of the selected anions in the reference frame of the crystal lattice, as shown in Fig. 3a, b, respectively. Intriguingly, aside from their original crystallographic positions, Cl ligands bonded to the [TaCl6] polyanions were found to be highly populated at intermediate sites, while no such extra density was observed for [NbCl6] polyanions. The corresponding 2D density distributions of these polyanions were obtained by projecting the Ta-Cl or Nb-Cl bonds according to the spherical coordinates defined in Fig. 3a, b. As shown in Fig. 3c, d, [TaCl6] polyanions exhibit a more dispersed distribution, whereas the [NbCl6] polyanions remain mostly localized at their static positions. These findings indicate that intensive rotation/reorientation occur for the [TaCl6] polyanions, but not for the [NbCl6] polyanions at this temperature.
a, b Shown for (a) NaTaCl6 and (b) NaNbCl6 are schematic representations of M-Cl bond orientations and probability distributions of [MCl6] octahedra. The central blue and green spheres in the left panel are Ta and Nb atoms, respectively, while the bonded light gray spheres denote Cl atoms. The angle between the M-Cl bond and the z axis is defined as θ, and φ is the angle between the x axis and the projection of the M-Cl vector in the xy plane. The probability density isosurfaces depict the spatial distributions of Ta/Nb (blue/green) and Cl (light yellow) atoms within a [MCl6] octahedron. c, d Shown for (c) NaTaCl6 and (d) NaNbCl6 are the 2D probability distributions of Cl atoms coordinated to Ta and Nb, respectively. The color bar on the right indicates the probability density values. e, f Shown in (e) NaTaCl6 and (f) NaNbCl6 are the Helmholtz free energy surfaces as a function of angle θ and φ. The Helmholtz free energy A was computed as A(θ, φ) = –kBTln[ρ(θ, φ)], where kB is the Boltzmann constant, T is temperature, ρ(θ, φ) is the probability density distribution of the Cl ligands of [TaCl6]/[NbCl6] anions from the AIMD simulations. Source data for figure are provided as a Source Data file.
To quantitatively assess the rotation/reorientation tendency of the two polyanion groups, we computed the Helmholtz free energy surface, a function of coordinates (angles θ and φ) that reflects the average properties relevant to the thermodynamic states. Specifically, the positions and heights of the local minima and transition states represent the rotation paths and barriers, respectively, allowing us to estimate the rotation barriers. The Helmholtz free energy surfaces shown in Fig. 3e, f explicitly reveal that the Cl ligands bonded to Ta atoms exhibit much shallower and flatter energy landscape than those bonded to the Nb atoms. The very low barriers (0.03–0.12 eV) for the rotational dynamics of Cl ligands in NaTaCl6 enable facile rotation to nearby minima, while the rotation of [NbCl6] anions is hindered by higher barriers (0.07-0.27 eV) due to deeper potential wells. This barrier further decreases as the temperature rises, allowing the [NbCl6] groups to rotate as easily as the [TaCl6] groups above 675 K, as discussed below.
To gain a full picture of the rotational/reorientational dynamics of the [TaCl6]/[NbCl6] polyanions, we monitored the spatial correlations of the Ta-Cl/Nb-Cl vector relative to the crystallographic axes over the entire 200 ps duration of our AIMD simulations. The Ta-Cl and Nb-Cl bonds were maintained throughout the simulations at all temperatures, suggesting the stability of the structure (Fig. 4a, b and Supplementary Fig. 12). The angle θ, defined in Fig. 3a, b, was tracked as an indicator of the polyanion reorientation dynamics. Shown in Fig. 4c–f are the evolution of angle θ for the Ta-Cl/Nb-Cl bonds in the given [TaCl6] and [NbCl6] anion groups. Notably, [TaCl6] polyanion moieties undergo very facile and continuous rotation, with the all the six Cl ligands participating, as suggested by the dramatic variation in θ over the simulation time. In contrast, [NbCl6] groups exhibit only mild reorientation. These reorientations are not random, but occur in a cog-like manner along the C4 axis, with the involvement of only four Cl ligands. Two sudden cog-like jumps were separated by a long break of 18−70 ps, due to the deep potential wells observed in the Helmholtz free energy surface for the Cl ligands of the [NbCl6] moieties (Fig. 3e, f). Closer scrutinization reveals that all the sixteen [TaCl6] moieties in the supercell rotate repeatedly in a random manner, with a full rotation finished within only 10−25 ps, while all the [NbCl6] polyanions exhibit very limited reorientations during the 200 ps timescale (Supplementary Figs. 13–19). The dynamic behavior of [TaCl6]/[NbCl6] polyanions at other temperatures is summarized in Supplementary Figs. 20–25. The angular evolution of the Ta/Nb-Cl bonds demonstrates that rotational dynamics of [TaCl6] polyanions are more favorable than those of [NbCl6] polyanions at low temperature. Within the limited timescale of our simulations, rotation of [TaCl6] polyanions are observed at all the temperatures we visited, suggesting that their rotational dynamics are easily triggered due to the shallow potential wells of the free energy surface of the Cl ligands. [NbCl6] polyanions primarily show cog-like reorientations below 600 K, but begin to show evidence of remarkable rotation at 675 K. The rotation tendency between the two polyanion species becomes negligible as the temperature further increases. This is also reflected by the almost identical depth of the potential wells for the Cl ligands in two moieties at these higher temperatures, as shown in Supplementary Figs. 26–31. We note that the dramatic jump in Na+-ion conductivity in NaNbCl6 coincides with the onset of significant [NbCl6] polyanion rotation, suggesting a potential contribution of polyanion rotational dynamics to the enhanced cationic diffusion.
a, b The bond length of (a) Ta2 and (b) Nb2 and their six Cl ligands during the AIMD simulations. c, d The evolution of angle θ of the six Ta-Cl bonds in the given [TaCl6] anion groups, as illustrated in (c) for Ta2 and (d) for Ta9. e, f The evolution of angle θ of the six Nb-Cl bonds in the given [NbCl6] anion groups, as illustrated in (e) for Nb2 and (f) for Nb9. Source data for figure are provided as a Source Data file.
Effects of anion rotation: coupled to and facilitates cation diffusion
In order to build a definitive connection between anion rotational dynamics and Na+-ion diffusion, a secondary analysis of the AIMD results was prompted. A detailed investigation of the motions of both species were conducted by examining the AIMD snapshots. Shown in Fig. 5a is a snapshot with the embedded trajectories of Cl ligands of [TaCl6] polyanions over a randomly selected 1 ps duration. Notably, the majority of the [TaCl6] polyanions undergo facile rotation during this short timespan. Concurrently, evident diffusion events of nearby Na+-ions occur in synchronization with the rotation of the Cl anions (depicted by the pink and blue arrows, respectively), providing direct evidence for the paddle-wheel mechanism. A parallel analysis of NaNbCl6 over the same duration revealed a distinctly different scenario, i.e., Na atoms mostly linger around their equilibrium sites while the adjacent [NbCl6] polyanion vibrates (Fig. 5b). To further probe how these distinct polyanion dynamics affect Na+-ion transport, a more detailed analysis was performed. The motion of both the cation and anion species (one Cl atom and one Na atom in its vicinity) was tracked by monitoring their coordinates. Very intense rotation of the [TaCl6] polyanion was observed, with a rotation of 27° along the c axis over this 1 ps duration (Fig. 5c). During this process, a neighboring Na+-ion migrated 1.70 Å along the c axis, and 2.64 Å in the ab plane, resulting in a diffusion length of 3.14 Å (Fig. 5d). This jump distance indicates a successful hop, as the distance between Na site and interstitial site in NaTaCl6 is 2.97 ∼ 3.29 Å. These results suggest that the displacement of the Na+-ions is strongly correlated with the rotation of the [TaCl6] polyanions in time and in space, or in other word, the two motions occur cooperatively. For comparison, the coordinates of Na and Cl atoms in NaNbCl6 were also analyzed in the same timescale, with the results displayed in Supplementary Fig. 32. Evidently, the Cl atom vibrates around its equilibrium site with no rotation (indicated by only minor variation in the θ angle), while the Na+-ion lingers around its lattice sites that little diffusion was observed (signified by the minimal changes in the x, y, and z coordinates).
a, b Atomic trajectories from AIMD simulation at 600 K between 13 and 14 ps for (a) NaTaCl6 and (b) NaNbCl6. The trajectories of the six Cl ligands of [TaCl6]/[NbCl6] polyanions are shown in small spheres with different colors (yellow, red, purple, blue, green and brown) in the left panels, while the trajectories of nearby Na atoms are denoted by large pink spheres in the right panels. Coupled motion between the cations and anions are indicated by the arrows: green arrows illustrate the rotational motion of the Cl atoms, and pink arrows indicate the diffusion of Na+-ions (right panels). c The projection of the Ta12-Cl76 bond to the z axis between 13 and 14 ps in NaTaCl6. d The coordinates of Na6 atom during 13-14 ps in NaTaCl6. e The area of the trigonal bottleneck for Na+-ions transport in both NaTaCl6 and NaNbCl6. A widening of the bottleneck size is evidenced when the shared Cl atom rotates in NaTaCl6. f, g The 2D probability density distribution \({\rho }_{{\gamma },r}^{2{\mbox{D}}}\) from AIMD simulations of the Ta(Nb)-Cl-Na angles (γ) and the distance (r) between Cl ligands and Na for (f) NaTaCl6 and (g) NaNbCl6. The color scales at the top right indicate the corresponding probability density values. Pronounced correlation is observed for NaTaCl6, but not for NaNbCl6. h Residence time correlation function for Na+-ions nearest to the polyanion, <hh(t)>, for NaTaCl6 and NaNbCl6. The <PlPl(t)> orientational correlation function is also shown, along with <hPlh(t)Pl(t)> joint time correlation function restricted to Na+-cations nearest to the polyanion. Source data for figure are provided as a Source Data file.
To further probe how anion rotation affects cation diffusion at the microscopic scale, we monitored the variation in bottleneck size for Na+-ion transport and calculated the Na+-ion migration barrier as a function of bottleneck area. In order to diffuse from one lattice site to another, Na+-ions must pass through a triangular bottleneck formed by three Cl atoms shared between [TaCl6]/[NaCl6] polyhedra (see the inset in Fig. 5e). The bottleneck size was enlarged by ~40% as the [TaCl6] rotated, while no dramatic variation was observed in NaNbCl6, where [NbCl6] polyanion rotation was deactivated (Fig. 5e). To quantitively study the influence of the bottleneck size on the Na+-ion diffusion barrier, we performed climbing image nudged elastic band (CI-NEB) calculations using the method developed by Ceder’s group48. We note that this method may slightly overestimate the migration barrier, as it does not account for the vibrations of Cl atoms that definitely would exist in a real system. As shown in Supplementary Fig. 33, the activation energy for Na+-ion migration significantly decreases as the bottleneck area expands, demonstrating that [TaCl6] rotation creates low-barrier pathways for neighboring Na+-ions diffusion. When [TaCl6] rotation is suspended, the bottleneck shrinks that Na+-ions perceive a more rigid and deep potential wells and hence get trapped easily due to much higher escape barriers. It’s also worth noting that when [NbCl6] moiety undergoes cog-like rotation, it also temporarily widens the triangular bottleneck and enhances Na+-ions migration (Supplementary Fig. 34a–d). This suggests that the rotational/reorientational dynamics of polyanions facilitate cationic translational diffusion by transiently opening the triangular bottleneck that cations need to squeeze through, thereby effectively lowering the Na+-ion migration barrier. In addition, polyanion rotation induces pronounced fluctuations in the local configurational environment, leading to a substantial increase in the migration entropy associated with Na+-ion transport. This enhanced migration entropy, in turn, elevates the Na+-ion attempt frequency and consequently improves Na+-ion conductivity, as described by Equation S3 and S4 in the Supplementary Note 1 of the Supplementary Information.
So far, we already observed coupled polyanion rotation and cation diffusion from the AIMD trajectories of Cl and Na atoms. To further establish the correlation between the two motions, we examined the spatial and temporal distribution of polyanion reorientation and Na+-ion migration over a 4 ps segment of the simulations. The 2D probability distribution (\({\rho }_{{\gamma },r}^{2{\mbox{D}}}\)) of the Ta/Nb-Cl-Na angle (γ) and the distance (r) between Cl ligand and Na atom in the first shell was computed. For NaTaCl6, \({\rho }_{{\gamma },r}^{2{\mbox{D}}}\) is dispersed over three maxima (Fig. 5f), suggesting a strong coupling between the angular and radial coordinates of the Na+-ions relative to the [TaCl6] polyanions. This is indicative of strong correlation between Na+-ions diffusion and [TaCl6] polyanions rotation. In contrast, \({\rho }_{{\gamma },r}^{2{\mbox{D}}}\) distribution for NaNbCl6 is confined to a single spot, signifying negligible correlation between Na+-ions diffusion and the [NbCl6] polyanion libration (Fig. 5g), as [NbCl6] rotation is deactivated within the selected time frame. We also examined the effect of the cog-like rotation on cationic diffusion in NaNbCl6 by analyzing a 4 ps time frame (86-90 ps) when [NbCl6] groups exhibit sudden rotational jumps. During this period, two maxima appear in the 2D probability distribution plot, suggesting a correlation between the cog-like rotational motion of the anions and the cation diffusion (Supplementary Fig. 35).
To verify this mechanism and quantitatively evaluate the correlation between polyanion rotation and Na+-ions translational diffusion, time correlation function analysis was performed. The dynamics of Na+-ions escape from local minima were measured using a residence time correlation function, <hh(t)>. By fitting the <hh(t)> function with an exponential model, characteristic times of 15.2 ps for NaTaCl6 and 23.4 ps for NaNbCl6 were obtained (Fig. 5h). This signifies that Na+-ions reside within the [TaCl6] polyanion cage for a shorter duration compared to the [NbCl6] polyanion, indicating that the [TaCl6] cage enables faster Na+-ions diffusion. The decay of the polyanion reorientation was depicted by the <PlPl(t)> correlation function (more details regarding \({P}_{l}\) are provided in Methods). Due to the faster re-orientational motion of the [TaCl6] polyanions, this function decays faster than the [NbCl6] anion groups. To further reveal how polyanion rotation impact cation diffusion, we employed a joint time correlation function (<hPlh(t)Pl(t)>), which we previously developed to study anion dynamics in thiophosphates57,58. This function quantitatively reflects the orientational dynamics of the nearest Na+-ions to the polyhedral anion. All the sixteen [TaCl6] or [NbCl6] polyanions within a time duration of 40 ps were taken into our statistics. The joint time correlation function decays faster for [TaCl6] polyanions, with a charateristic time of 9.6 ps, compared to 16.3 ps for [NbCl6] polyanions (Fig. 5h). The faster decay of the <hPlh(t)Pl(t)> correlation function, compared to both <hh(t)> and <PlPl(t)>, highlights the strong coupling between the translational mobility of the Na+-ion and the rotational mobility of the polyanion framework. Power spectrum also confirmed the coupling between the two motions, as demonstrated in a parallel work by Yang et al.68. At elevated temperatures (675 K and above), all three correlation functions show almost identical characteristic times for [TaCl6] and [NbCl6] polyanions, owing to the onset of free rotation of [NbCl6] polyanions (Supplementary Figs. 26–39). This explains the very close Na+-ion conductivities shown by the two compounds at elevated temperatures. The decreased characteristic time of <PlPl(t)> with increasing temperature reflects the progressively more pronounced polyanion rotation, which, in turn, enhances the contribution of paddle-wheel mechanism to Na+-ion diffusion. This temperature-dependent enhancement in polyanion rotational dynamics leads to a non-linear relationship in lnD vs. 1/T over the broad temperature range probed by the simulations. The extent to which these rotational dynamics lower the activation energy depends on the ease of polyanion rotation, as evidenced by the calculated Na+-ion migration barriers at each temperature using a computational code developed by M. Wagemaker’s group69. The results, summarized in Supplementary Table 9, show that the activation energy for Na+-ion migration decreases with increasing temperature for both compounds. However, over narrower temperature ranges, such as that used for variable temperature impedance measurements near room temperature (253–333 K), polyanion rotational dynamics exhibit minimal variation. Consequently, the change in the Ea values is negligible that Na+-ion diffusion appears to follow Arrhenius behavior. More discussion is referred to Supplementary Note 2 in the Supplementary Information.
To further probe the contribution of anion rotation to cation diffusion on a more generic and macroscopic scale, we calculated the average Na+-ion hop frequency (denoted as vhop), which measures the overall cation diffusional ability, and the conditional Na+-ion hop frequency (denoted as vhop|rot), which reflects the frequency of Na+-ion hops occurring in space (within 3.2 Å) and time (2 ps) upon a [MCl6] (M = Ta, Nb) polyanion rotation event. All simulation data over 200 ps timescale were used for the analysis. As shown in Supplementary Fig. 40, vhop|rot is significantly higher than vhop, indicating that Na+-ions diffusion is notably facilitated when [MCl6] polyanions rotate in both NaTaCl6 and NaNbCl6.
Polyanion rotation invoked by polyhedra orientational disorder at room temperature
While AIMD simulations enable the investigation of anion rotational/reorientational dynamics and their correlation to cation diffusion, this approach is limited to short timescales, making statistical convergence challenging, particularly at lower temperatures. To address this limitation, we performed deep potential molecular dynamic (DPMD) simulations as a complementary method to assess anion rotational behavior at room temperature for longer timescales. The DeepMD-kit package was utilized to train interatomic potential models for NaMCl6 (M = Ta, Nb), with AIMD data serving as the input dataset. The accuracy of these well-trained interatomic potential models was validated by comparing the predicted total potential energies and forces on each atom with those obtained from DFT calculations. The comparison of the predicted energies and forces at different temperatures versus the values obtained from DFT calculation is summarized in Fig. 6a, b, Supplementary Fig. 41a, and Supplementary Fig. 41b. The reliability of our interatomic potential models is confirmed by the very low root mean square errors (RMSE) of both the energy differences (0.0013 eV/atom and 0.0016 eV/atom for NaTaCl6 and NaNbCl6, respectively) and force differences (0.025 eV/Å and 0.029 eV/Å for NaTaCl6 and NaNbCl6, respectively). Subsequently, ordered and disordered structural models comprising 512 atoms were constructed to simulate samples subjected to annealing and intensive ball milling (Fig. 6c and Supplementary Fig. 41c). The disordered model was obtained via a generally used melt-quench method. DPMD simulations were then performed at 300 K for a long period of 10 ns to ensure good statistics. This timescale allows us to probe anion dynamics and Na+-ion conductivity at room temperature that practical batteries operate.
a, b Comparison of (a) energies and (b) forces predicted using deep potential model and DFT calculations for NaTaCl6. c [TaCl6] polyhedral frameworks of ordered NaTaCl6 and disordered NaTaCl6. d, e The evolution of angle θ of the six Ta-Cl bonds of the given [TaCl6] anion group in (d) ordered NaTaCl6 and (e) disordered NaTaCl6. f Calculated MSDs of Na+-ions from the representative ordered and disordered models of NaTaCl6 over a duration of 10 ns at 300 K. Source data for figure are provided as a Source Data file.
The anion dynamics in both ordered and disordered NaTaCl6 were investigated by tracking the angular evolution of the Ta-Cl bonds (Fig. 6d, e). In ordered NaTaCl6, the Cl atoms are restricted to librate around their equilibrium positions, as suggested by the very minor changes in angle θ (Fig. 6d). In sharp contrast, the [TaCl6] polyanions in disordered NaTaCl6 exhibit noticeable rotation at room temperature, as evidenced by the significant variation in θ (Fig. 6e). A similar behavior is observed in NaNbCl6, namely, the [NbCl6] polyanions are frozen in ordered NaNbCl6 but show substantial rotation in the disordered model (Supplementary Fig. 41d, e). The Na+-ion diffusivities calculated from the MSDs show that ordered NaTaCl6 exhibits slow Na+-ion diffusion, with the diffusivity falling beyond measurable limits. In contrast, disordered NaTaCl6 demonstrates a high diffusivity of 8.6 × 10−12 m2/s and a high ionic conductivity of 2.5 mS cm−1 at 300 K (Fig. 6f). Notably, the disordered model closely matches the measured ionic conductivity of the ball-milled NaTaCl6 sample (2.5 mS cm−1 vs. 3.3 S cm−1), indicating that the onset of [TaCl6] anion rotational dynamics at room temperature is representative of the real system. Upon annealing, the ionic conductivity dropped by three orders of magnitude, coinciding with the increase in the crystallinity. This suggests that the decline in conductivity is associated with the reduced local disorder when annealed.
DPMD simulations revealed similar behavior in NaNbCl6. Specifically, disordered NaNbCl6 exhibited high diffusivity (4.6 × 10−12 m2/s) and ionic conductivity (1.3 mS cm−1), while ordered NaNbCl6 demonstrated negligible Na+-ion diffusion at RT within the timescale studied (Supplementary Fig. 41f). In contrast to NaTaCl6, the measured conductivity of ball milled NaNbCl6 can’t be well reproduced using the disordered model (0.01 mS cm−1 for as-prepared NaNbCl6 vs. 1.3 mS cm−1 for the disordered model). This discrepancy is likely due to the predominantly frozen anion dynamics in NaNbCl6, which was synthesized via ball milling and lacks sufficient disorder, as reflected by the sharper, more intense XRD peaks compared to NaTaCl6 (Fig. 1a, b). The observed increase in ionic conductivity with extended milling time can be attributed to the increasing disorder induced by the high-energy mechanical milling process. As the ball milling time increased from 15 h−120 h, the ionic conductivity demonstrated an increase tendency, similar to that observed for NaTaCl6 (Supplementary Fig. 2). This increase in disorder enhances polyanion rotation, which in turn facilitates Na⁺-ion migration. While further extension of the milling time for NaNbCl6 could potentially lead to even higher conductivity, such an investigation is beyond the scope of the current study due to the time constraints associated with prolonged milling.
It’s noteworthy that disordered models derived from the melt-quench method exhibit not only polyanion orientational disorder, but also Na/vacancy distribution disorder (cation sublattice disorder). To disentangle the effects of Na/vacancy disorder and polyhedra orientational disorder, we conducted additional DPMD simulations (Supplementary Figs. 42–43). As shown Supplementary Fig. 44, the Na+-ion diffusion was minimal when only Na/vacancy disorder was present, whether in NaTaCl6 or NaNbCl6, despite being moderately enhanced compared to fully ordered models, as the polyanion rotational dynamics were suppressed. In contrast, models incorporating only polyanion orientational disorder demonstrated clearly activated anion dynamics and significantly enhanced Na+-ion transport properties, with the corresponding ionic conductivities reached 1.9 and 1.1 mS cm−1 for the Ta and Nb-based systems, respectively (Supplementary Fig. 45). These values are very close to those observed in models with both Na/vacancy disorder and polyhedra orientational disorder, which exhibited ionic conductivities of 2.5 mS cm−1 for NaTaCl6 and 1.3 mS cm−1 for NaNbCl6. These comparative studies highlight that polyanion orientational disorder is the key factor triggering anion dynamics and activating the paddle-wheel mechanism, which contributes to the high room temperature conductivity in disordered NaMCl6 (M = Ta, Nb).
To understand why NaTaCl6 and NaNbCl6 exhibit different degrees of disorder under identical milling conditions, we examined their ionic radii, bond lengths, and atomic bonding environments. Both Ta5+ and Nb5+ have identical ionic radii (64 pm) in [MCl6]− polyhedra, suggesting that ionic radius does not explain the higher degree of disorder in NaTaCl6. Furthermore, XRD and NPD Rietveld refinements revealed no significant differences in Na-Cl and M-Cl bond lengths between the two materials (Supplementary Table 10). Bader charge analysis also revealed nearly identical charge distributions on Na, Ta/Nb and Cl (Supplementary Fig. 46), indicating similar atomic bonding environments in both materials. These results suggest that the nearly identical ionic radii, bond lengths and atomic bonding environments in the two compounds do not significantly contribute to the considerably higher degree of disorder observed in NaTaCl6 vs. NaNbCl6.
Inspired by a recent study by Nazar’s group70, which demonstrated that fluoride electrolytes with lower shear and bulk moduli are more prone to amorphization upon mechanical milling—thereby exhibiting enhanced ionic conductivity—we performed DFT-based elastic constant calculations using the same approach to evaluate the mechanical properties of NaTaCl6 and NaNbCl6. Our results show that NaTaCl6 exhibits significantly lower mechanical strength, as indicated by its lower bulk modulus, Young’s modulus, shear modulus, and Vickers hardness (Supplementary Fig. 47). This suggests that the NaTaCl6 crystal lattice is more easily deformed under external stress, allowing it to develop a highly disordered structure after just 15 h of mechanical milling. On the other hand, the higher mechanical strength of NaNbCl6 implies that a longer milling duration or a higher energy milling is necessary to induce similar degree of structural disorder.
Phonon spectrum calculations were further performed to understand the differences in the materials from the perspective of lattice dynamics. The resulting phonon density of states (DOS) is presented in Supplementary Fig. 48a, b. It’s evident that the total phonon DOS for NaTaCl6 exhibits a more pronounced distribution in the low-frequency region (<1 THz) compared to that of NaNbCl6 (Supplementary Fig. 48b). Such low-frequency modes have been identified as a characteristic feature of structural disorder, arising from the pronounced rotational/reorientational dynamics of the disordered polyanions, as previously observed in HT-LiBH4, β-Li3PS4, and Li3.25[Si0.25P0.75]S458,71. Phonon band center was further computed to quantify the phonon softness. NaTaCl6 demonstrates both a lower total phonon band center and a lower Cl-projected phonon band center compared to NaNbCl6 (total: 19.1 meV vs. 20.4 meV; Cl-projected: 20.7 meV vs. 21.2 meV, respectively). According to the Einstein model, the amplitude of thermal atomic displacement is inversely proportional to the square of the phonon frequency. Therefore, the higher population of low-frequency phonon modes, along with a lower phonon band center present by NaTaCl6, indicates inherently higher ion mobility, particularly associated with the anion framework, compared to NaNbCl6. This is consistent with the significantly flatter anion Helmholtz free energy surfaces exhibited by NaTaCl6 at temperatures below 675 K (Fig. 3e, f and Supplementary Figs. 26–27). Furthermore, thermal properties derived from phonon calculations are presented in Supplementary Fig. 49. It is clear that NaTaCl6 exhibits a higher vibration entropy and consequently a lower Gibbs free energy over the broad temperature range we studied. It has been known that flexible anion frameworks generally dictate higher vibration entropy72, in fully consistent with our phonon calculations comparing NaTaCl6 vs. NaNbCl6. The higher vibration entropy indicates that ions in NaTaCl6 possess greater freedom of motions, facilitating larger-amplitude vibrations across various vibrational modes, as highlighted in a previous study73. This enhanced lattice dynamics, together with the structural disorder observed in the low frequency region in PDOS, suggest that local structural disorder—particularly polyanion orientational disorder—can be more readily thermally activated in NaTaCl6 (as confirmed by AIMD simulations at elevated temperatures) or induced upon harsh mechanical milling. These findings provide a lattice-dynamics-based rationale for the higher susceptibility of NaTaCl6 to polyanion orientational disorder. Further analysis suggests that the atomic mass difference and lattice volume difference should be the main reason that leads to a shift of phonon modes toward the low-frequency region, thereby enhancing vibration entropy in NaTaCl6 vs. NaNbCl6. Detailed analysis is provided in Supplementary Note 3 in the Supplementary Information.
Polyanion reorientation/rotational dynamics in other Ta/Nb-based halides and oxyhalides
We also examine whether anion reorientation/rotation is broadly present in the most highly conductive halides and oxyhalides, e.g., Ta or Nb-based (oxy)halides74,75,76,77. AIMD simulations were performed on four typical examples, i.e., LiMCl6 and NaMOCl4 (M = Ta, Nb) at 600 K. The flexibility of these anion framework was evaluated and its connection to the cation translational diffusion was scrutinized.
Unlike NaMCl6 (M = Ta, Nb), both LiTaCl6 and LiNbCl6 exhibit an amorphous nature with remarkably high ionic conductivities exceeding 10 mS cm−1 at room temperature74,75. No crystal structure for these compounds has been reported to date. Shown in Supplementary Figs. 50–51 are the evolution of angle θ of representative Ta-Cl/Nb-Cl bonds in amorphous LiTaCl6 and LiNbCl6, respectively. Notably, both [TaClx] and [NbClx] (x = 5, 6) polyanions exhibit significant rotational dynamics, with no substantial difference observed between the two anions species. The faster decay of <hPlh(t)Pl(t)> joint time correlation function compared to <hh(t)> and <PlPl(t)> function highlights the critical role of anion rotation in prompting Li+-ions migration in LiMCl6 (M = Ta, Nb) (Supplementary Fig. 52). This provides evidence for the existence of paddle-wheel mechanism in both compounds and that this anion rotational dynamics facilitate Li+-ion diffusion in both systems.
NaMOCl4 (M = Ta, Nb) also exhibits amorphous nature and very high ionic conductivity76,77. Our AIMD simulations revealed that both Cl and O within the [MOCl4] polyhedron exhibit pronounced polyanion rotational motion, with rotation being even more pronounced than the [TaCl6] polyhedra in NaTaCl6 (Supplementary Figs. 53–54). Correlation function analysis further reveals comparable characteristic decay times of <hh(t)> and <PlPl(t)> functions for NaTaOCl4 and NaNbOCl4, indicating that there is no significant difference in either cationic conductivity or polyanion rotational/reorientational dynamics between the two materials (Supplementary Fig. 55). Furthermore, the notably shorter characteristic decay time of <hPlh(t)Pl(t)>, compared to those of <hh(t)> and <PlPl(t)>, suggests that cation diffusion is correlated to the [TaOCl4]/[NbOCl4] polyanion rotation, highlighting the pivotal role of paddle-wheel effect in superionic sodium oxyhalides.
Our investigations indicate that anion rotational/reorientational dynamics are prevalent in amorphous Ta/Nb-based halides and oxyhalides, playing a crucial role in enabling the very high cationic conductivities via the paddle-wheel mechanism. NaMCl6 (M = Ta, Nb) exhibit distinctive anion rotational dynamics, primarily due to the high mechanical strength of NaNbCl6, which makes it less susceptible to amorphization through ball milling. In contrast, LiNbCl6 and NaNbOCl4 are readily amorphized under similar conditions. These findings suggest that the polyhedra orientational disorder is a key factor governing anion rotational/reorientational dynamics in these materials. Compounds with lower mechanical strength are more prone to amorphization, resulting in higher flexibility of the anion framework, which in turn facilitates cation diffusion.
Electrochemical performance of NaTaCl6 in all-solid-state batteries
The electrochemical stability of NaMCl6 (M = Ta, Nb) was evaluated by DFT calculations and linear sweep voltammetry (LSV) measurements. Thermodynamic intrinsic electrochemical windows were calculated using an established scheme on the basis of the Materials Project (MP) database17. The equilibrium voltage profile and the corresponding phase equilibria as a function of applied potential referenced to Na/Na+ are illustrated in Supplementary Fig. 56a, b. Both compounds show wide electrochemical stability windows (2.14-3.90 V vs. Na/Na+ for NaTaCl6 and 2.45-3.81 V vs. Na/Na+ for NaNbCl6, respectively). Linear sweep voltammetry further revealed an anodic limit of 4.14 V and 4.08 V, and a cathodic limit of 2.50, 2.97 V for NaTaCl6 and NaNbCl6, respectively (Supplementary Fig. 56c, d). These two materials represent thermodynamic intrinsic windows considerably wider than sulfides. In comparison to NaNbCl6, the slightly higher oxidation potential and lower reduction potential shown by NaTaCl6 suggests that it is more appropriate for use with high-voltage positive electrode materials. Similar to other halides, both NaTaCl6 and NaNbCl6 is unstable when in direct contact with metallic Na or Na-Sn alloy, due to the generally poor reduction stability of chlorides. Given this instability, an anodic buffer layer is typically required to ensure the proper functioning of these solid electrolytes. Critical Current Density (CCD) experiments using a Na2Sn | NPSC | NaTaCl6 | NPSC | Na2Sn symmetric cell (with Na2.9375PS3.9375Cl0.0625, labeled as NPSC, as the buffer layer) demonstrated a CCD of 2.5 mA cm−2 at both room temperature and 50°C (Supplementary Fig. 57a, b). Prolonged deposition/stripping tests at a current density of 0.2 mA cm−2 at RT and 0.5 mA cm−2 at 50°C, with plating capacities of 0.2 mAh cm−2 and 0.5 mAh cm−2, respectively, showed only minor increases in polarization after 1000 h and 600 h of cycling (Supplementary Fig. 57c, d). The slight increase in polarization is mainly attributed to the rising interfacial resistance caused by instability between NPSC buffer layer and the Na2Sn negative electrode, which is consistent with previous study on sulfide electrolytes78.
ASSBs utilizing NaTaCl6 as the separator, uncoated NaCu0.12Ni0.22Fe0.33Mn0.33O2 (labeled as CNFM here and after) as the positive electrode, and Na2Sn alloy as the negative electrode, were assembled to evaluate the electrochemical performance of NaTaCl6. A thin layer of NPSC was positioned between the NaTaCl6 SE layer and the Na2Sn negative electrode to prevent the reduction of chloride SE (see Fig. 7a for the schematic plot of the cell configuration and Supplementary Fig. 58 in the Supplementary Information for the cell setup). The morphology and particle size of the CFNM active materials were characterized by SEM, which revealed a uniform size distribution with particles ~10 μm in diameter (Supplementary Fig. 59). The ductile nature of chloride electrolyte enables composite positive electrode with dense and smooth surface, as confirmed by SEM (Supplementary Fig. 60). Electrode density measurement revealed a relative density of 90.1%, corresponding to a porosity of 9.9% (Supplementary Table 11). X-ray computed tomography (XCT) analysis demonstrated a porosity of ca. 8.7% for composite positive electrode (Supplementary Fig. 61), which is in consistent with the density measurements.
a Schematic illustration of the solid-state batteries, comprising NaCu0.12Ni0.22Fe0.33Mn0.33O2 (CFNM) positive electrode, NaTaCl6 (NTC) solid electrolyte, Na2.9375PS3.9375Cl0.0625 (NPSC) interfacial buffer layer, and Na2Sn (Na-Sn) alloy negative electrode. b, c The rate performance of Na-Sn | NPSC | NTC | CFNM solid-state battery cycled under 14, 28, 42, 70, 112, and 140 mA g−1 at 27 °C: (b) rate capability, and (c) the corresponding 2nd charge/discharge profiles at each rate. d The rate performance of an identical cell cycled under 14, 28, 70, 140, 280 and 420 mA g−1 at 50°C. e The voltage profiles of the solid-state cell upon cycling at 27 °C and 70 mA g−1. f, g Long-term cycling stability of the same solid-state battery at (f) 27°C, and (g) 50 °C. The cell was charged/discharged at 28 mA g−1 during the first two cycles and subsequently under 70 mA g−1 at 27°C or under 140 mA g−1 at 50 °C for the rest of the test. Source data for figure are provided as a Source Data file.
The charge/discharge capacities at different current rates were evaluated by cycling the solid-state cells between 2.3 and 3.8 V vs. Na2Sn (2.6 to 4.1 V vs. Na/Na+). Figure 7b–g displays the electrochemical performance of the CNFM positive electrode with an areal loading of 6.6 mg cm⁻2. At room temperature, the cell delivers an initial charge and discharge capacity of 130.8 mAh g−1 and 125.1 mAh g−1 under a current of 14 mA g−1, respectively, yielding a high initial Coulombic efficiency (CE) of 95.6% (Fig. 7b). Shown in Fig. 7c are the second charge-discharge profiles at each rate. When cycled at room temperature, a reversible capacity of 123.6, 119.1, 115.6, 110.2, 103.4, 98.7 mAh g−1 was achieved at specific currents of 14, 28, 42, 70, 112, and 140 mA g−1, respectively. The capacity is almost fully recovered upon returning to the current of 70 mA g−1. The identical cell operated at 50°C exhibits much-improved reversible capacity, particularly at high current densities (110.4 mAh g−1 at 140 mA g−1, 98.2 mAh g−1 at 280 mA g−1, and 86.4 mAh g−1 at 420 mA g−1) (Fig. 7d). The long-term cycle life of the cell was examined by galvanostatic cycling at room temperature and 50°C. Over 300 cycles at 70 mA g−1 under room temperature, the cell exhibits negligible fading and maintains a discharge capacity of 99.0 mAh g−1, and a high capacity retention of ~90.0% was achieved (Fig. 7e, f). The same cell operated at 140 mA g−1 and 50°C delivers a high discharge capacity of 114.7 mAh g−1 and sustains ~90.3% capacity over 600 cycles (Fig. 7g). The electrochemical performance of two additional independent cells, presented in Supplementary Figs. 62–63, further confirms the consistency and reproducibility our solid-state cell performance. Furthermore, ASSBs with higher mass loading (12.4 mg cm−2) also demonstrated good rate performance and cycling stability at both room temperature and 50°C, as shown in Supplementary Figs. 64–65. The electrochemical performance achieved with NaTaCl6 ranks among the most promising reported to date for ASSBs employing sodium halide electrolytes (Supplementary Table 12)39,40,45,79,80. This favorable performance is attributed to the superionic conductivity and good oxidation stability of NaTaCl6, as well as high compactness of the composite positive electrode (see SEM images in Supplementary Fig. 60, XCT analysis in Supplementary Fig. 61, and Supplementary Table 11 for details).
In summary, we synthesized a family of sodium chlorides, Na(Ta,Nb)Cl6, that simultaneously display high ionic conductivity (up to 3.3 mS cm−1 at 27 °C), good chemical stability and compatibility with high-voltage positive electrode materials. This group of materials serves as a representative prototype for investigating the impact of polyanion reorientational/rotational behavior on the cationic conductivity. AIMD simulations revealed that [TaCl6] polyanions show much higher tendency to rotate than [NbCl6] polyanions, as evidenced by the lower onset temperature for [TaCl6] rotation. [NbCl6] polyanions demonstrate cog-like reorientation at moderate temperatures, but exhibit as facile rotation as [TaCl6] anions upon the temperature increases. Elastic constants and phonon spectrum calculations suggest that the higher degree of structural disorder upon milling exhibited by NaTaCl6 vs. NaNbCl6 is likely attributed to its enhanced mechanical and phonon softness. Comparative DPMD simulations further reveals that the structural disorder—particularly polyhedra orientational disorder—plays a critical role in driving anion rotational/reorientational dynamics, which in turn actives paddle-wheel mechanism to facilitate Na+-ion diffusion. Specifically, polyanion rotation temporarily widens the bottleneck for Na+-ions migration and induces substantial fluctuations in the local configurational environment, thereby lowering the energy barrier and enhancing migration entropy for cation diffusion. As a result of the more readily activated polyanion rotation of [TaCl6] groups, NaTaCl6 exhibits ionic conductivity two orders of magnitude higher than NaNbCl6 at room temperature under the same milling conditions. Other amorphous Ta/Nb-based halides and oxyhalides also exhibit anion reorientation or rotation, which have likewise been shown to contribute to super high ionic conductivities in these systems. These findings offer insights into the pivotal role of polyanion rotational motions in facilitating cationic transport. All-solid-state batteries utilizing NaTaCl6 exhibit good electrochemical performance in terms of rate capability and cycling stability. After >300 cycles at room temperature and 600 cycles at 50°C, the cell maintains a capacity retention exceeding >90.0%.
Our research reveals how anion dynamics can significantly influence microscopic cationic diffusion in halides, and highlights the necessity to looking beyond simple structural characteristics of the lattice framework. Aside from static framework structure, the softness and the rotational dynamics of the polyanion framework also plays critical role in enabling fast cation. The rotational behaviors of other halide polyanions, such as [YCl6], [ZrCl6] anion groups and others, should also be examined, and will be the subject of our subsequent study. Further research should focus on identifying the factors that determine the rotational tendency of halides polyanions, as well as exploring strategies to lower the onset temperature for anion rotation in order to manipulate paddle-wheel mechanism at room temperature.
Methods
Materials synthesis
Na(Ta,Nb)Cl6 was synthesized by mechanochemical method. Stoichiometric quantities of NaCl (Sigma-Aldrich, 99.0%), and TaCl5 (Aladdin, 99.8%) or NbCl5 (Aladdin, 99.9%) were milled at 500 rpm for 7−120 h in a ZrO2 vial with ball/material ratio 20:1 using a planetary ball mill (Retsch PM100). The annealed samples were obtained by heating the ball-milled products at 200°C for 5 h. The prepared samples were used for further analysis. All the powders were handled under Ar atmosphere (O2 < 0.1 ppm, H2O < 0.1 ppm).
Na2.9375PS3.9375Cl0.0625 was synthesized following previous reports81. Stoichiometric amounts of NaCl (Sigma-Aldrich, 99.0%), Na2S (Alfa Aesar, >90%), and P2S5 (Macklin, 99.9%) were mixed using an agate mortar and pestle. The resulting mixture was sealed under vacuum in a quartz tube, heated to 800°C for 4 h, and subsequently quenched in ice water. The obtained product was ground, pressed into pellets under a uniaxial pressure of ~300 MPa, sealed in an evacuated quartz tube, and subsequently heat-treated at 420°C for 2 h to obtain the final product. All procedures prior to vacuum sealing were conducted in an argon-filled glovebox (MBRAUN LABstar; O2 < 0.1 ppm, H2O < 0.1 ppm).
NaCu0.12Ni0.22Fe0.33Mn0.33O2 was synthesized by dispersing stoichiometric amounts of Na2CO3 (Aladdin, 99.5%), NiO (Aladdin, 99.9%), CuO (Aladdin, 99.9%), Fe2O3 (Aladdin, 99%), and Mn3O4 (Aladdin, 97%) into ethanol solvent to form a homogeneous slurry. The slurry was subjected to ball milling at 400 rpm for 5 h. After milling, the slurry was dried, and the resulting powder was pelletized. The pellets were subsequently transferred to a furnace and heat-treated at 850°C in air for 16 h.
The Na2Sn negative electrode was synthesized using a conventional solid-state method. Stoichiometric amounts of sodium metal cube (Aladdin, 99.7%) and Sn powder (Aladdin, 99.9%) were weighted and transferred into a carbon-coated quartz tube. The native oxide layer on the surface of the sodium cube was carefully removed using a surgical blade immediately before use. The quartz tube was then heated at 250°C for over 10 h to obtain Na2Sn powder. All synthesis procedures were carried out within an argon-filled glovebox (MBRAUN LABstar; O2 < 0.1 ppm, H2O < 0.1 ppm).
X-ray powder diffraction
Powder XRD patterns were collected at 40 kV and 40 mA using a bruker D8 advance diffractometer with Cu Kα radiation (λ = 1.5406 Å). The prepared samples were protected from exposure to air by polyimide (Kapton) film and epoxy resin.
Neutron powder diffraction
Neutron powder diffraction data were collected at room temperature using the high-resolution powder diffractometer ECHIDNA at ANSTO in Australia82 and China Spallation Neutron Source (CSNS) in China. The air-sensitive samples were sealed in vanadium sample holders in Ar-filled glovebox (O2 < 0.1 ppm, H2O < 0.1 ppm).
Conductivity measurement
The AC impedance spectra were collected to measure the ionic conductivities in the temperature range over −20 - 60°C, with an equilibration time of 2 h at each temperature. The measurements were performed on a VMP300 (Biologic) impedance analyzer in potentiostatic mode, employing a potential perturbation of 10 mV. The spectra were recorded within the frequency range of 7 MHz to 0.1 Hz, with six data points collected per decade of frequency. Approximately 150 mg of the powder was put into the 10 mm-diameter cylinder peek die and sandwiched by two stainless rods as current collectors. The cells were pressed with a uniaxial pressure of 300 MPa for 1 min. The press cells were fixed in frames utilizing a torque of 10 N m for the subsequent measurements. The electronic conductivity was determined by direct current (DC) polarization measurement of the cold-pressed powder under 300 MPa with an applied potential of 100 mV, 200 mV, 300 mV, 400 mV, and 500 mV using the same cell configuration.
Electrochemical characterization
The electrochemical stabilities of NaTaCl6 and NaNbCl6 were evaluated by linear sweep voltammetry (LSV) measurement. 70 mg SE (NaTaCl6 or NaNbCl6) was pressed in a PEEK mold with a uniaxial pressure of 300 MPa. Subsequently, 20 mg of composite positive electrode material, prepared by hand-grinding the solid electrolyte with carbon (VGCF) in a weight ratio of 70:30 using a mortar and pestle for 1 h, was evenly spread on one side of SE pellet, and pressed under a uniaxial pressure of 300 MPa. Afterwards, 70 mg Na2.9375PS3.9375Cl0.0625 (labeled as NPSC) was dispersed on the other side of the SE pellet, and pressed with the same pressure. Na2Sn alloy was pressed onto the other side of the NPSC layer, and the cell was sandwiched between two stainless-steel rods and sealed in a home-made cell. The LSV measurement was conducted on the as-fabricated Na2Sn | NPSC | Na(Ta, Nb)Cl6 | Na(Ta, Nb)Cl6 + VGCF cells using VMP300 (Biologic) with a scan range from open-circuit voltage to 5 V or 0 V (vs. Na/Na+) at a scan rate of 0.1 mV s−1.
The Na-Sn | NPSC | NaTaCl6 | NaCu0.12Ni0.22Fe0.33Mn0.33O2 (CNFM) all-solid-state cells were assembled in an Ar-filled glovebox. The composite positive electrode mixtures were prepared by grinding CNFM active material, NaTaCl6 electrolyte and VGCF at a weight ratio of 65: 30: 5 using a mortar and pestle for 1 h at ambient temperature. ASSBs were assembled by the following procedures: First, ~40 mg NPSC electrolyte was pressed in a PEEK mold with a diameter of 10 mm (corresponding to an area of ~0.785 cm2) under 3 tons; ~80 mg NaTaCl6 electrolyte powder was then uniformly spread onto one side of the NPSC electrolyte layer and pressed under 3 tons, followed by pressing the composite electrode powder on the other side of the NaTaCl6 layer at 3 tons. For regular loading and high loading ASSBs, the mass of the composite positive electrode is 8 mg and 15 mg, respectively. Finally, 30 mg Na2Sn alloy was pressed onto the other side of the NPSC layer under 0.5 tons, and the cell was positioned between two stainless-steel rods and sealed.
All the above procedures and the electrochemical measurements were carried out in an argon-filled glovebox oxygen and moisture levels maintained below 0.1 ppm. Galvanostatic cycling test was conducted at controlled temperatures of either 27 ± 1°C or 50 ± 1°C using a fanless thermostatic chamber placed inside the glovebox. The cells were cycled galvanostatically between 2.6–4.1 V vs. Na⁺/Na (or 2.3–3.8 V vs. Na₂Sn) at various current densities, using a LANHE battery testing system (CT2001A, LAND Electronic Co. Ltd). The single electrochemical data was collected from at least three independent cells to ensure reproducibility. The specific capacity can be determined from the galvanostatic charge/discharge curve by integrating the current over the discharge time, as given by the equation:
where I is the current and m is the mass of the active material.
Morphology characterization and porosity analysis
Scanning electron microscopy (SEM) images and elemental mapping were obtained using a GeminiSEM 360 field-emission SEM equipped with energy dispersive spectroscopy (EDS). The SEM was operated at an accelerating voltage of 15 kV. All samples were prepared in an argon-filled Ar-filled glovebox and transferred to the SEM chamber using an inert gas-sealed transfer vessel. X-ray transmission computed tomography (XCT) were performed using Xradia 515 Versa (Carl Zeiss AG) with an X-ray source operated at 60 kV. Samples for XCT analysis were sealed in airtight containers within the glovebox to maintain an inert environment throughout the measurement process. The visualization and segmentation of XCT images were carried out using Dragonfly Pro software.
Density functional theory (DFT) calculations
Density functional theory (DFT) calculations were carried out using the Vienna Ab initio Simulation Package (VASP)83 within the projector augmented-wave approach84. The Generalized gradient approximation (GGA) exchange-correlation with the Perdew-Burke-Ernzerhof (PBE)85 function was employed for static calculations. A plane-wave cutoff energy of 520 eV was used. The convergence criterion for the electronic self-consistency loop was set to 10−5 eV and the atomic positions was fully relaxed until the force on each atom was below 0.01 eV/Å. Γ-centered k-point meshes with the density of at least 1000 k-points per reciprocal atom was used for the Brillouin integrations in all calculations.
The electrochemical stability windows of NaTaCl6 and NaNbCl6 were evaluated by constructing grand potential phase diagrams of all relevant phases with compositions of NaTaCl6 and NaNbCl6 in equilibrium with the chemical potential of Na.
where μNa,0 is the chemical potential of the Na metal, e is the elementary charge, and φ is the applied potential referenced to a Na metal negative electrode. The Pymatgen code86 was used to generate the grand phase diagram and determine the electrochemical stability window.
Ab initio Molecular Dynamics (AIMD) simulations
In order to observe the diffusive behavior for the Na+-ions, AIMD simulations for NaMCl6 (M = Ta, Nb) were studied in the canonical (NVT) ensemble at seven elevated temperatures (500 K, 550 K, 600 K, 675 K, 750 K, 900 K, 1050 K). The volume of the supercells (2a2b1c) and the initial positions of atoms were obtained from the fully relaxed cells (Supplementary Data 1 and 2). During the simulations, the cell volume and the shape of the cells were fixed. The samples were heated up to the targeted temperatures by velocity scaling over 5 ps, and then equilibrated at the desired temperatures. Data from the initial 5 ps was excluded from the analysis. During the heating process, polyhedral anion reorientational disorder and Na/vacancy disorder can develop, if present, thereby justifying the use of an ordered crystalline structure as a valid and reasonable initial input for AIMD simulations. The AIMD simulations were performed for 200 ps at each temperature using a Nosé thermostat (Supplementary Data 3–16)87. A time step of 2 fs was employed to integrate the equation of motion. To keep the computational cost at a reasonable level, integration in reciprocal space was merely computed at the Γ-point.
The structural models for LiMCl6 (M = Ta, Nb) were constructed following a previously established protocol88. Specifically, four lithium atoms were removed from the structure of Li2MCl6 (M = Ta, Nb) derived from the Open Quantum Materials Database (OQMD). The resulting structures were then melted by heating to 1500 K and maintained for 50 ps. Following this, the structures were quenched to 300 K at a rate of 15 K/ps and equilibrated at 300 K for 20 ps to obtain the amorphous models (Supplementary Data 17 and 18). The above modeling processes were conducted using the NPT ensemble. For NaTaOCl4 and NaNbOCl4, the models were built by partially substituting Cl with O and introducing appropriate anion vacancy in NaMCl6 (M = Ta, Nb) (Supplementary Data 19 and 20). The subsequent AIMD simulations were performed at 600 K using the same parameters as those used for NaTaCl6 and NaNbCl6 (Supplementary Data 21 and 24).
Activation energy analysis for Na+-ion migration
To extract the activation energy from molecular dynamics simulations, we employed a parsing code developed by Wagemaker’s group that is based on the relation:
where kB is the Boltzmann constant, T is the absolute temperature, ωe is the attempt frequency and ωp is the hopping frequency of Na+-ion.
To obtain ωe, the trajectory of each Na+-ion was first converted into a displacement vector ri(t) relative to its initial position. The instantaneous velocity of each Na+-ion, vi(t), was calculated using a finite-difference scheme:
where Δt is the timestep of AIMD simulations. A discrete Fourier transform was then applied to the velocity trajectory of each Na+-ion to obtain its individual vibrational frequency spectrum. The average frequency of each spectrum was extracted, and the overall vibrational frequency of the system was obtained by averaging these values over all Na+-ions. In their procedure, the attempt frequency was determined by considering every vibration of a diffusing atom as a hopping attempt, with the average vibration frequency defined as the attempt frequency ωe.
The hopping frequency was determined by dividing the AIMD trajectory at each temperature into ten equal-length segments. For each segment, the number of successful Na+-ion jumps between different crystallographic sites was counted and normalized by the segment time and number of Na+-ions to obtain the jump rate. The average value over all segments was taken as ωp. Subsequently, Ea was computed for each segment using Eq. (3). The mean value and standard deviation of Ea over all segments were reported as the final activation energy and its associated error, respectively.
Deep potential model training
The training dataset was generated by randomly extracting 70,000 atomic configurations from AIMD simulations at 500 K, 550 K, 600 K, 675 K, 750 K, 900 K, and 1050 K for NaTaCl6 and NaNbCl6, respectively. The deep neural network method implemented in DeepMD-kit package was used to train the Deep Potential (DP) model with the obtained training dataset as input89. With the utilization of an embedding neural network size of (25, 50, 100) and a cutoff radius of 8.0 Å, the atom-centered descriptors were built. The descriptor values were then mapped to atomic energies and forces by using a fitting neural network that composed of three hidden layers with 240 neurons per layer. The fitting network was trained beforehand by minimizing the loss function L = peLe + pfLf, where Le and Lf were the loss in energy and force, respectively, and pe and pf were the corresponding prefectors varying from 0.02 to 1 and 1000 to 1, respectively. In the minimization of the loss function, the exponential learning rate decayed from 1 × 10−3 to 1 × 10−8 every decay_steps of 5000. A total number of 1,000,000 iterations of training batches were used to generate the final DP models.
Deep Potential Molecular Dynamic (DPMD) simulations
LAMMPS package was employed to conduct DPMD simulations using the well-trained DP interatomic potential energy model90. A 4×4×1 supercell contained 512 atoms was constructed for the simulation. Similar to the AIMD simulations, all DPMD simulations were performed in the NVT ensemble using a Nosé thermostat. The temperature damping parameter and the time step were set to 0.2 ps and 2 fs, respectively.
Two representative input structures of both NaTaCl6 and NaNbCl6 were created using the following procedures, respectively. For the first, the supercell was heated up to 300 K by velocity scaling over 50 ps, and then kept for a duration of 100 ps to obtain the final structure (Supplementary Data 25 and 26). For the second, the supercell was ramped to 1000 K over 50 ps and then kept for 100 ps, after which the cell was quenched to 300 K and then equilibrated for 100 ps to generate the final structure (Supplementary Data 27 and 28). To isolate the effect of polyanion orientational disorder and Na/vacancy disorder on Na+-ion diffusion, disordered models with only polyanion orientational disorder and Na/vacancy disorder were constructed by relocating Na+-ions and polyanions to Wyckoff sites, respectively (Supplementary Data 29–32). Using the above structures as the initial input, DPMD simulations were carried out at 300 K for a period of 10 ns to achieve good statistics (Supplementary Data 33–40).
The diffusion coefficient is determined by linear fitting of the mean square displacement (MSD) of Na+-ions using the following equations:
where d is the dimension of the lattice on which the diffusion takes place, t0 is the initial time, t is the elapsed time, \({\vec{r}}_{i}\left(t\right)\) is the displacement of the i-th Na+-ion at time t and t0 is the initial time. D is obtained by linear fitting to the dependence of averaged mean square displacement over 2dt.
Elastic constant calculation
The energy-strain method was used to calculate elastic constants91,92,93. The distorted models were constructed by applying moderate strain onto the fully relaxed structure with the utilization of the VASPKIT code94. DFT calculations were then performed on these distorted models by only allowing for the ionic degrees of freedom. The convergence threshold of energy for electronic self-consistency and maximum force on each atom were set to be 10−8 eV and 0.01 eV/Å, respectively. Finally, the elastic constants were determined from the second-order derivative of the total energies versus strain in harmonic approximation:
where Cij is the elastic stiffness tensor, ε is the external loading strain, E(V, {εi}) and E(V0, 0) are the total energies of the distorted and undistorted structures, with the volume of V and V0, respectively.
Phonon spectrum calculation
To evaluate the phonon softness and vibration entropy of NaTaCl6 and NaNbCl6, first-principle phonon calculations were performed. The convergence criteria for the electronic self-consistency and atomic forces were set to 10−8 eV and 0.001 eV/Å, respectively. The force constant matrix was computed using density functional perturbation theory, and phonon spectra as well as vibration entropy were obtained using the Phonopy package95. The phonon band center, which characterized the average phonon frequency weighted by the phonon density of states, was calculated according to the following expression:
Bond Valence Site Energy (BVSE) method
BVSE calculations were performed using the SoftBV software for a dense grid with a resolution of 0.1 Å covering the crystal structure using the Morse type interaction potential64. The structural models obtained from Rietveld refinement based on the powder X-ray diffraction data were used as inputs. The obtained Na site energy landscape were plotted with the static structure from refinement embedded.
Helmholtz free energy surface
To quantify the rotational tendency of chloride ligands within [TaCl6]/[NbCl6] polyanions, we first computed the 2D probability density distribution \({\rho }_{\theta,\varphi }^{2{\mbox{D}}}\) from AIMD trajectories. The angle θ is defined as the angle between the selected Ta/Nb-Cl bond and the z axis, while φ corresponds to the angle between the x axis and the projection of the same bond vector onto the xy plane. The associated Helmholtz free energy surface was computed according to the following expression:
where kB is the Boltzmann constant, and T is the temperature.
Analysis of time correlation function
To access the dynamics of Na+-ions escaping from local minima, we calculated the residence time correlation function, <hh(t)>, defined as <h([Rcut − R(t = 0)] h[Rcut − R(t))]>. Here, h denotes the Heaviside function, and R(t) is the distance between a Na+-ion and its nearest [TaCl6]/[NbCl6] polyhedron at time t. The cutoff distance Rcut was set to 6.3 Å, corresponding to the radius of the first coordination shell. Another correlation function, <PlPl(t)>, where Pl denotes the Legendre polynomial of degree l, was computed to probe the temporal decay of the orientation between Ta/Nb-Na and Ta/Nb-Cl bond vectors. In this study, l = 1 was employed to capture the first-order orientational correlations, with the argument of polynomial defined as the cosine of the angle between the two vectors. Joint-time correlation function, <hPlh(t)Pl(t)>, which combines the Na+-ion translational dynamics with the polyanion reorientational dynamics, was also computed to investigate the coupling between cation residence and polyhedral orientation fluctuations.
Frequency analysis of hop events
AIMD simulations data was divided into 1 ps time intervals. For each segment, the maximum angular changes of all M-Cl vectors relative to their initial directions were computed. Rotation events were identified if the angular change is > 60°. Sodium ions that located within a 4.0 Å radius of the rotating anions were classified as neighboring ions. The frequency of successful Na+-ion hops was calculated after each rotation event. A hop is considered successful if the displacement of a Na+-ion exceeds a cutoff value of 3.2 Å during a time duration of 2 ps. The frequency of hop events was obtained by averaging the number of successful hops over the time and the total number of Na+-ions.
Evaluation of bottleneck size on Na+-ion migration barrier
Climbing image nudged elastic band (CI-NEB) method96 was employed on NaTaCl6 to quantitively study the influence of the bottleneck size on Na+-ion diffusion barrier. One Na+-ion was removed to create a Na vacancy, and a uniform background charge was set to maintain the charge neutrality. The bottleneck size was varied by scaling up the cell volume. During CI-NEB calculations, Cl ligands were fixed to keep the triangular bottleneck size unchanged. The convergence criterion of the self-consistent iterations was set to 10−7 eV for the total energy difference and 0.02 eV Å−1 for the forces.
Data availability
The data generated in this study are provided in the Supplementary Information/Source Data file. Source data are provided with this paper.
Change history
14 August 2025
A Correction to this paper has been published: https://doi.org/10.1038/s41467-025-62939-9
References
Manthiram, A., Yu, X. & Wang, S. Lithium battery chemistries enabled by solid-state electrolytes. Nat. Rev. Mater. 2, 16103 (2017).
Janek, J. & Zeier, W. G. A solid future for battery development. Nat. Energy 1, 16141 (2016).
Kundu, D., Talaie, E., Duffort, V. & Nazar, L. F. The emerging chemistry of sodium ion batteries for electrochemical energy storage. Angew. Chem. Int. Ed. 54, 3431–3448 (2015).
Liu, T. et al. Exploring competitive features of stationary sodium ion batteries for electrochemical energy storage. Energy Environ. Sci. 12, 1512–1533 (2019).
Delmas, C. Sodium and sodium-ion batteries: 50 years of research. Adv. Energy Mater. 8, 1703137 (2018).
Zhang, Z. et al. New horizons for inorganic solid state ion conductors. Energy Environ. Sci. 11, 1945–1976 (2018).
Bachman, J. C. et al. Inorganic solid-state electrolytes for lithium batteries: mechanisms and properties governing ion conduction. Chem. Rev. 116, 140–162 (2016).
Famprikis, T., Canepa, P., Dawson, J. A., Islam, M. S. & Masquelier, C. Fundamentals of inorganic solid-state electrolytes for batteries. Nat. Mater. 18, 1278–1291 (2019).
Randau, S. et al. Benchmarking the performance of all-solid-state lithium batteries. Nat. Energy 5, 259–270 (2020).
Hayashi, A., Noi, K., Sakuda, A. & Tatsumisago, M. Superionic glass-ceramic electrolytes for room-temperature rechargeable sodium batteries. Nat. Commun. 3, 856 (2012).
Hayashi, A., Noi, K., Tanibata, N., Nagao, M. & Tatsumisago, M. High sodium ion conductivity of glass–ceramic electrolytes with cubic Na3PS4. J. Power Sources 258, 420–423 (2014).
Banerjee, A. et al. Na3SbS4: a solution processable sodium superionic conductor for all-solid-state sodium-ion batteries. Angew. Chem. 128, 9786–9790 (2016).
Zhang, Z. et al. Na11Sn2PS12: a new solid state sodium superionic conductor. Energy Environ. Sci. 11, 87–93 (2018).
Duchardt, M., Ruschewitz, U., Adams, S., Dehnen, S. & Roling, B. Vacancy-controlled Na+ superion conduction in Na11Sn2PS12. Angew. Chem. Int. Ed. 57, 1351–1355 (2018).
Ramos, E. P. et al. Correlating ion mobility and single crystal structure in sodium-ion chalcogenide-based solid state fast ion conductors: Na11Sn2PnS12 (Pn = Sb, P). Chem. Mater. 30, 7413–7417 (2018).
Yu, Z. et al. Synthesis and understanding of Na11Sn2PSe12 with enhanced ionic conductivity for all-solid-state Na-ion battery. Energy Stor. Mater. 17, 70–77 (2019).
Zhu, Y., He, X. & Mo, Y. Origin of outstanding stability in the lithium solid electrolyte materials: insights from thermodynamic analyses based on first-principles calculations. ACS Appl. Mater. Interfaces 7, 23685–23693 (2015).
Zhu, Y., He, X. & Mo, Y. First principles study on electrochemical and chemical stability of solid electrolyte–electrode interfaces in all-solid-state Li-ion batteries. J. Mater. Chem. A 4, 3253–3266 (2016).
Zhang, Z. et al. A self-forming composite electrolyte for solid-state sodium battery with ultralong cycle life. Adv. Energy Mater. 7, 1601196 (2017).
Zhang, Z. et al. Correlated migration invokes higher Na+-ion conductivity in NaSICON-type solid electrolytes. Adv. Energy Mater. 9, 1902373 (2019).
Ma, Q. et al. Scandium-substituted Na3Zr2(SiO4)2(PO4) prepared by a solution-assisted solid-state reaction method as sodium-ion conductors. Chem. Mater. 28, 4821–4828 (2016).
Lu, Y. et al. A high-performance monolithic solid-state sodium battery with Ca2+ doped Na3Zr2Si2PO12 electrolyte. Adv. Energy Mater. 9, 1901205 (2019).
Chen, D., Luo, F., Zhou, W. & Zhu, D. Influence of Nb5+, Ti4+, Y3+ and Zn2+ doped Na3Zr2Si2PO12 solid electrolyte on its conductivity. J. Alloy. Compd. 757, 348–355 (2018).
Beevers, C. & Ross, ΜA. The crystal structure of “Beta Alumina” Na2O·11Al2O3. Z. Kristallogr. Cryst. Mater. 97, 59–66 (1937).
Hong, H.-P. Crystal structures and crystal chemistry in the system Na1+xZr2SixP3-xO12. Mater. Res. Bull. 11, 173–182 (1976).
Goodenough, J., Hong, H.-P. & Kafalas, J. Fast Na+-ion transport in skeleton structures. Mater. Res. Bull. 11, 203–220 (1976).
Asano, T. et al. Solid halide electrolytes with high lithium-ion conductivity for application in 4 V class bulk-type all-solid-state batteries. Adv. Mater. 30, 1803075 (2018).
Li, X. et al. Air-stable Li3InCl6 electrolyte with high voltage compatibility for all-solid-state batteries. Energy Environ. Sci. 12, 2665–2671 (2019).
Li, X. et al. Water-mediated synthesis of a superionic halide solid electrolyte. Angew. Chem. 131, 16579–16584 (2019).
Liang, J. et al. Site-occupation-tuned superionic LixScCl3+x halide solid electrolytes for all-solid-state batteries. J. Am. Chem. Soc. 142, 7012–7022 (2020).
Park, K.-H. et al. High-voltage superionic halide solid electrolytes for all-solid-state Li-ion batteries. ACS Energy Lett. 5, 533–539 (2020).
Helm, B. et al. Exploring aliovalent substitutions in the lithium halide superionic conductor Li3-xIn1-xZrxCl6 (0 ≤ x ≤ 0.5). Chem. Mater. 33, 4773–4782 (2021).
Kim, S. Y. et al. Lithium ytterbium-based halide solid electrolytes for high voltage all-solid-state batteries. ACS Mater. Lett. 3, 930–938 (2021).
Park, J. et al. Heat treatment protocol for modulating ionic conductivity via structural evolution of Li3-xYb1-xMxCl6 (M = Hf4+, Zr4+) new halide superionic conductors for all-solid-state batteries. Chem. Eng. J. 425, 130630 (2021).
Wang, H. et al. Electrochemically stable Li3-xIn1-xHfxCl6 halide solid electrolytes for all-solid-state batteries. ACS Appl. Mater. Interfaces 15, 5504–5511 (2023).
Tuo, K., Sun, C., López, C., Fernández-Díaz, M. T. & Alonso, J. A. New superionic halide solid electrolytes enabled by aliovalent substitution in Li3-xY1-xHfxCl6 for all-solid-state lithium metal based batteries. J. Mater. Chem. A 11, 15651–15662 (2023).
Zhou, L. et al. A new halospinel superionic conductor for high-voltage all solid state lithium batteries. Energy Environ. Sci. 13, 2056–2063 (2020).
Zhou, L. et al. High areal capacity, long cycle life 4 V ceramic all-solid-state Li-ion batteries enabled by chloride solid electrolytes. Nat. Energy 7, 83–93 (2022).
Park, J. et al. NaAlCl4: new halide solid electrolyte for 3 V stable cost-effective all-solid-state Na-ion batteries. ACS Energy Lett. 7, 3293–3301 (2022).
Kwak, H. et al. Na2ZrCl6 enabling highly stable 3 V all-solid-state Na-ion batteries. Energy Stor. Mater. 37, 47–54 (2021).
Meyer, G., Peter Ax, S., Schleid, T. & Irmler, M. J. The chlorides Na3MCl6 (M = Eu, Lu, Y, Sc): synthesis, crystal structures, and thermal behaviour. Z. Anorg. Allg. Chem. 554, 25–33 (1987).
Liao, W. & Dronskowski, R. Trisodium yttrium (III) hexachloride. Acta Cryst. Sec. E Struct. Rep. Online 60, i72–i73 (2004).
Yamada, K., Kumano, K. & Okuda, T. Conduction path of the sodium ion in Na3InCl6 studied by X-ray diffraction and 23Na and 115In. Nmr. Solid State Ion. 176, 823–829 (2005).
Schlem, R., Banik, A., Eckardt, M., Zobel, M. & Zeier, W. G. Na3-xEr1-xZrxCl6—A halide-based fast sodium-ion conductor with vacancy-driven ionic transport. ACS Appl. Energy Mater. 3, 10164–10173 (2020).
Wu, E. A. et al. A stable cathode-solid electrolyte composite for high-voltage, long-cycle-life solid-state sodium-ion batteries. Nat. Commun. 12, 1256 (2021).
Zhao, T. et al. Synthesis-controlled cation solubility in solid sodium ion conductors Na2+xZr1-xInxCl6. ACS Appl. Energy Mater. 6, 4334–4341 (2023).
Dai, T. et al. Inorganic glass electrolytes with polymer-like viscoelasticity. Nat. Energy 8, 1221–1228 (2023).
Wang, Y. et al. Design principles for solid-state lithium superionic conductors. Nat. Mater. 14, 1026–1031 (2015).
Schlem, R. et al. Mechanochemical synthesis: a tool to tune cation site disorder and ionic transport properties of Li3MCl6 (M = Y, Er) superionic conductors. Adv. Energy Mater. 10, 1903719 (2020).
Li, Y. et al. A lithium superionic conductor for millimeter-thick battery electrode. Science 381, 50–53 (2023).
Yu, S. et al. Design of a trigonal halide superionic conductor by regulating cation order-disorder. Science 382, 573–579 (2023).
Wang, S., Liu, Y. & Mo, Y. Frustration in super-ionic conductors unraveled by the density of atomistic states. Angew. Chem. Int. Ed. 62, e202215544 (2023).
Zhong, P., Gupta, S., Deng, B., Jun, K. & Ceder, G. Effect of cation disorder on lithium transport in halide superionic conductors. ACS Energy Lett. 9, 2775–2781 (2024).
Geng, J., Yan, Z. & Zhu, Y. Elucidating anisotropic ionic diffusion mechanism in Li3YCl6 with molecular dynamics simulations. ACS Appl. Energy Mater. 7, 7019–7024 (2024).
Kraft, M. A. et al. Influence of lattice polarizability on the ionic conductivity in the lithium superionic argyrodites Li6PS5X (X = Cl, Br, I). J. Am. Chem. Soc. 139, 10909–10918 (2017).
Schlem, R. et al. Lattice dynamical approach for finding the lithium superionic conductor Li3ErI6. ACS Appl. Energy Mater. 3, 3684–3691 (2020).
Zhang, Z., Roy, P.-N., Li, H., Avdeev, M. & Nazar, L. F. Coupled cation–anion dynamics enhances cation mobility in room-temperature superionic solid-state electrolytes. J. Am. Chem. Soc. 141, 19360–19372 (2019).
Zhang, Z. et al. Targeting superionic conductivity by turning on anion rotation at room temperature in fast ion conductors. Matter 2, 1667–1684 (2020).
Henke, H. Zur kristallchemischen einordnung von NaSbCl6, NaNbCl6 und NaTaCl6. Z. Kristallogr. Crys. Mater. 198, 1–16 (1992).
Hu, Y. et al. Superionic amorphous NaTaCl6 halide electrolyte for highly reversible all-solid-state Na-ion batteries. Matter 7, 1018–1034 (2024).
Motohashi, K., Tsukasaki, H., Sakuda, A., Mori, S. & Hayashi, A. NaTaCl6: Chloride as the end-member of sodium-ion conductors. ACS Mater. Lett. 6, 1178–1183 (2024).
Huang, Z., Yoshida, S., Akamatsu, H., Hayashi, K. & Ohno, S. NaMCl6 (M = Nb and Ta): a new class of sodium-conducting halide-based solid electrolytes. ACS Mater. Lett. 6, 1732–1738 (2024).
Almond, D. & West, A. Anomalous conductivity prefactors in fast ion conductors. Nature 306, 456–457 (1983).
Chen, H., Wong, L. L. & Adams, S. SoftBV–a software tool for screening the materials genome of inorganic fast ion conductors. Acta Crystallogr. B Struct. Sci. Cryst. Eng. Mater. 75, 18–33 (2019).
Chen, H. & Adams, S. Bond softness sensitive bond-valence parameters for crystal structure plausibility tests. IUCrJ 4, 614–625 (2017).
Zhang, Z. & Nazar, L. F. Exploiting the paddle-wheel mechanism for the design of fast ion conductors. Nat. Rev. Mater. 7, 389–405 (2022).
He, X., Zhu, Y., Epstein, A. & Mo, Y. Statistical variances of diffusional properties from ab initio molecular dynamics simulations. Npj Comput. Mater. 4, 18 (2018).
Yang, Y., Guan, C., Ouyang, R. & Zhu, H. Harvest the polyanion rotation in sodium superionic conductors?. Chem. Mater. 36, 3776–3785 (2024).
de Klerk, N. J., van der Maas, E. & Wagemaker, M. Analysis of diffusion in solid-state electrolytes through MD simulations, improvement of the Li-ion conductivity in β-Li3PS4 as an example. ACS Appl. Energy Mater. 1, 3230–3242 (2018).
Qian, L. et al. Unlocking lithium ion conduction in lithium metal fluorides. Matter 7, 3587–3607 (2024).
Buchter, F. et al. Dynamical properties and temperature induced molecular disordering of LiBH4 and LiBD4. Phys. Rev. B 78, 094302 (2008).
Butler, K. T., Walsh, A., Cheetham, A. K. & Kieslich, G. Organised chaos: entropy in hybrid inorganic–organic systems and other materials. Chem. Sci. 7, 6316–6324 (2016).
Fultz, B. Vibrational thermodynamics of materials. Prog. Mater. Sci. 55, 247–352 (2010).
Ishiguro, Y., Ueno, K., Nishimura, S., Iida, G. & Igarashib, Y. TaCl5-glassified ultrafast lithium ion-conductive halide electrolytes for high-performance all-solid-state lithium batteries. Chem. Lett. 52, 237–241 (2023).
Ishiguro, Y., Iida, G., Ueno, K., Nishimura, S. & Igarashib, Y. All-Solid-State Lithium Batteries In Cold Environments Of -20°C Enabled By Amorphous Halide-based Electrolytes LiNbCl5X and LiTaCl5X. https://www.researchsquare.com/article/rs-3072105/v1 (2023).
Zhao, T. et al. Sodium metal oxyhalides NaMOCl4 (M = Nb, Ta) with high ionic conductivities. ACS Mater. Lett. 6, 3683–3689 (2024).
Zhou, L., Bazak, J. D., Li, C. & Nazar, L. F. 4 V Na solid state batteries enabled by a scalable sodium metal oxyhalide solid electrolyte. ACS Energy Lett. 9, 4093–4101 (2024).
Xu, D. et al. Insights on Na3PS4 solid-state electrolyte dry films: interfacial stability and dry room compatibility. ACS Energy Lett. 9, 2293–2302 (2024).
Fu, J. et al. Halide heterogeneous structure boosting ionic diffusion and high-voltage stability of sodium superionic conductors. Adv. Mater. 36, 2308012 (2024).
Lin, X. et al. A dual anion chemistry-based superionic glass enabling long-cycling all-solid-state sodium-ion batteries. Angew. Chem. 136, e202314181 (2024).
Chu, I.-H. et al. Room-temperature all-solid-state rechargeable sodium-ion batteries with a Cl-doped Na3PS4 superionic conductor. Sci. Rep. 6, 33733 (2016).
Avdeev, M. & Hester, J. R. ECHIDNA: a decade of high-resolution neutron powder diffraction at OPAL. J. Appl. Crystallogr. 51, 1597–1604 (2018).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Perdew, J. P., Ernzerhof, M. & Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 105, 9982–9985 (1996).
Ong, S. P. et al. Python materials genomics (pymatgen): a robust, open-source python library for materials analysis. Comput. Mater. Sci. 68, 314–319 (2013).
Hoover, W. G. Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A 31, 1695 (1985).
Lei, M., Li, B., Liu, H. & Jiang, D. e. Dynamic monkey bar mechanism of superionic Li-ion transport in LiTaCl6. Angew. Chem. Int. Ed. 63, e202315628 (2024).
Zeng, J. et al. DeePMD-kit v2: a software package for deep potential models. J. Chem. Phys. 159, 054801 (2023).
Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19 (1995).
Nielsen, O. & Martin, R. M. First-principles calculation of stress. Phys. Rev. Lett. 50, 697 (1983).
Nielsen, O. & Martin, R. M. Stresses in semiconductors: Ab initio calculations on Si, Ge, and GaAs. Phys. Rev. B 32, 3792 (1985).
Le Page, Y. & Saxe, P. Symmetry-general least-squares extraction of elastic coefficients from ab initio total energy calculations. Phys. Rev. B 63, 174103 (2001).
Wang, V., Xu, N., Liu, J.-C., Tang, G. & Geng, W.-T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 267, 108033 (2021).
Togo, A. First-principles phonon calculations with phonopy and phono3py. J. Phys. Soc. Jpn. 92, 012001 (2023).
Henkelman, G., Uberuaga, B. P. & Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113, 9901–9904 (2000).
Acknowledgements
This work was supported by the Shenzhen Science and Technology Program (RCYX20221008092929074, Z.Z.), the Shenzhen Fundamental Research Program (JCYJ20220530150200001, Z.Z.), the National Natural Science Foundation of China (U22A20439, 52472272, 22109185, Z.Z.; 52394174, Y.-S.H.), and the Guangdong S&T Program (2023B0909060004, Z.Z.). Computations were performed on the National Supercomputing Center at Sun Yat-sen University in Guangzhou. We thank ZEISS for their support in SEM image acquisition and XCT data collection.
Author information
Authors and Affiliations
Contributions
R.L., Z.Z. and Y.H. conceived the project. R.L. and K.X. synthesized the electrolytes, conducted the impedance measurements, Rietveld refinement, assembled the batteries, and performed all the electrochemical characterization. S.W., Z.L., and X.G. carried out the XRD measurements, D.C polarization measurements. X.T. conducted the SEM measurements. M.A. carried out the powder neutron diffraction experiments. R.L. performed BV analysis, CI-NEB calculations, AIMD and DPMD simulations, and first-principles calculations. R.L., K.X., and Z.Z. analyzed the data and wrote the manuscript. Z.Z. and Y.H. supervised the project. All authors contributed to the review and editing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Jun-Woo Park and the other,anonymous, reviewer(s) for their contribution to the peer review of this work. [A peer review file is available].
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Li, R., Xu, K., Wen, S. et al. A sodium superionic chloride electrolyte driven by paddle wheel mechanism for solid state batteries. Nat Commun 16, 6633 (2025). https://doi.org/10.1038/s41467-025-61738-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-61738-6