Introduction

The increase in therapeutic options for patients with metastatic non-small cell lung cancer (NSCLC) has created the need for criteria to help providers select the therapy that carries the highest likelihood of benefit for an individual patient1. While single-feature biomarkers have been identified for numerous targeted therapies, due to the tight correlation between therapeutic efficacy and the presence of certain genomic mutations, such biomarkers have been elusive for immune checkpoint inhibitors (ICIs), which provide long-term disease control to only a minority of all-comers2. The absence of biomarkers has been further complicated by the development of combination strategies, leading to the approval of multiple first-line combinations of ICI plus chemotherapy (ICI-Chemo)3,4,5 in addition to ICI monotherapies (ICI-Mono)6,7, without prospective, randomized data to define which patients benefit most from ICI-Chemo vs ICI-Mono8. While more research is needed to define the biology underlying ICI sensitivity, one possible reason for the absence of robust biomarkers is the biologic complexity of the tumor-immune axis and potentially non-linear relationships between treatment response and tumor intrinsic and immune features. This biological complexity suggests the need for more sophisticated models that can incorporate and weight multiple variables.

Machine learning9 and statistical-based10 modeling represent powerful tools to improve outcome prediction in oncology by modeling the heterogeneity in treatment effects11,12. Several methods for identifying heterogenous treatment effects have been proposed, including interaction trees13,14, differential effect searches15, virtual twins16, sequential bootstrapping and aggregating of threshold from trees17, as well as information-theoretic approaches18. Together, they demonstrate the applicability of machine learning frameworks to the task of prioritizing and evaluating potential treatment options based on patient-specific data, which can complement the larger research enterprise needed to advance clinical care that includes basic science, drug development, and clinical trials.

In this study, we demonstrate the application of machine learning to develop a predictive framework to refine patient selection, focusing on the clinically relevant question of selecting between ICI-Mono vs ICI-Chemo for mNSCLC patients. While these efforts do not supplant the need for prospective clinical trials or mechanistic preclinical work, our objective was to complement these efforts by providing a statistical and machine learning framework that could help prioritize and evaluate potential treatment options based on existing patient-specific data. Given the dearth of clinical trial data comparing these regimens head-to-head on this topic, we use large multi-institutional datasets (from MD Anderson Cancer Center (MDACC), Mayo Clinic (Mayo), Dana Farber Cancer Institute (DFCI), and Stand Up To Cancer Consortium (SU2C)), and focus on clinicogenomic variables that were present in all cohorts. We use weighting subgroup identification approaches to assess the impact of adding chemotherapy on early progression in mNSCLC patients receiving ICI therapy, as well as explore the association of baseline clinicogenomic features with ICI outcomes. Collectively, this work demonstrates the application of machine-learning models to inform and guide treatment selection, while also generating preliminary criteria that may help guide selection between ICI regimens for further validation and expansion.

Results

Clinical and molecular characteristics of study participants

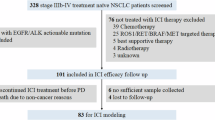
We identified a total of 2300 mNSCLC patients who received ICI containing treatment regimens with available clinicogenomics data: MDACC (n= 750), Mayo (n=80), DFCI (n= 1077), and SU2C (n= 393). Patients were propensity-matched in order to reduce retrospective biases, resulting in 996 matched samples; from these, 678 samples from MDACC, Mayo, and SU2C were utilized as the discovery cohort to develop and assess the predictive models, while 318 DFCI cases were used as the external validation cohort. For the matched patients, 674 patients were treated with first-line ICIs, and 322 were treated in the second-line or subsequent setting. PD-L1 proportion was high (≥50%), intermediate (1–49%), low (0 or <1%) in 328, 344, and 324 patients, respectively. Detailed demographic and clinical information of the matched patients are shown in Table 1. In terms of genomic features, TP53 was the most frequently altered gene, altered in 55% of patients, followed by KRAS (35%), and CDKN2A (15%). The remaining genomic alterations are provided in Supplementary Fig. 1. Example of covariate distribution before and after matching are presented in Supplementary Fig. 2.

Table 1 Demographics and clinical characteristics of patients in discovery and external validation cohort
Full size table

Constructing the modeling framework

The key steps to construct the modeling system are presented in Fig. 1. Following data processing, matching, and separation into discovery and validation cohorts, we applied five distinct scoring functions (Supplementary Note 3) to first build sub-scoring models. Each sub-scoring model was trained and tuned independently in a rigorous manner, including repeated cross validation, feature selection, feature ranking, and refitting. Thereafter, the sub-scoring models were fused to generate an ensemble model through different fusion techniques to mitigate the uncertainty inevitable to one type of model (Supplementary Note 4).

Fig. 1: Overview of the A-STEP system from data collection to clinical translation.
figure 1

Schematic diagram illustrating the A-STEP workflow, including data collection, preprocessing, modeling, and translation to clinical practice. Institutions involved include MD Anderson Cancer Center (MDACC), Stand Up To Cancer Consortium (SU2C), and Dana-Farber Cancer Institute (DFCI).

Full size image

Figure 2 demonstrates the feature importance analysis for five different models during cross validation, in which FBXW7 and APC mutations, along with tobacco use, PD-L1 expression, and pathology, were the most frequently selected parameters when predicting treatment efficacy in individual models. Table 2 shows the averaged treatment effects between ICI-Mono and ICI-Chemo for individual models stratified by recommended treatment arms during cross-validation. We observed that the linear model (sub-model A) had the best performance with risk reductions in both treatment arms during training and testing. However, it did not hold in the external validation cohort, where the risk of early progression increased in the model-recommended ICI-Mono arm (+13.6%, Table 3). The pair-wise correlations between stratification by different sub-models are presented in Supplementary Fig. 3.

Fig. 2: Feature selection consistency across five scoring functions using repeated cross-validation.
figure 2

Repeated 5-fold cross-validation (n = 30) was performed for five scoring functions: (a) linear model with Poisson loss, (b) generalized additive model (GAM) with squared loss, (c) GAM with Poisson loss, (d) GAM with logistic loss, and (e) gradient additive model with logistic loss. Features were ranked based on their frequency of selection across 150 runs and were considered informative if selected in at least 50% of the runs. These informative features were then refitted on the discovery cohort and evaluated on the external validation cohort. Source data are provided as a Source Data file.

Full size image
Table 2 Cross-validated averaged treatment effects reported as weighted risk reduction (WRR) in all sub-scoring models
Full size table
Table 3 Refitted treatment effects reported as weighted risk reduction (WRR) in all sub-scoring and integrated models
Full size table

Among three different ways to ensemble the individual scoring model, the attention-based method (termed A-STEP: Attention-based Scoring for Treatment Effect Prediction) achieved the best performance with weighted risk reduction ranging from −13% to −23% in the discovery cohort, and −16% to −19% in the external validation cohort (Table 3). By contrast, the individual sub-models, excluding sub-model B, or the other two ensemble models, were not able to achieve a significant level of performance, particularly during external validation.

Clinical values of A-STEP recommendations

We then investigated whether the A-STEP model remained predictive in terms of progression-free survival (PFS) for various treatment arms, taking into account early disease progression. When analyzed through the lens of received treatment plans, patients who were treated according to the A-STEP model recommendation associated with better outcome in both the ICI-Mono (hazard ratio [HR, anti-recommendation subgroup as reference] = 0.76, p = 0.048, Fig. 3a) and the ICI-Chemo (HR = 0.63, p < 0.001, Fig. 3b) discovery cohorts. Similar findings were observed in the ICI-Mono (HR = 0.60, p = 0.016, Fig. 3c) and ICI-Chemo (HR = 0.58, p = 0.0076, Fig. 3d) validation cohorts. Patients who received additional chemotherapy, concordant with the model suggestion, experienced 4–5 months longer median survival (Fig. 3b, d). Subsequently, we also performed subgroup analyses per model-recommended treatment plans as depicted in Fig. 3e-h, and observed similar findings. Of note, the attention-based ensemble model outperformed the individual sub-models; details of survival stratification by the sub-models are elaborated in Supplementary Figs. 4–7, and Supplementary Table 1.

Fig. 3: Impact of A-STEP Recommendations on 2-Year Progression-Free Survival.
figure 3

Comparison of 2-year progression-free survival (PFS) stratified by (I) actual treatment plans (received, REC) and (II) treatment plans recommended by A-STEP (RECOM). Subfigures (a–d) and (e–h) represent the discovery and external validation cohorts, respectively. P-values were calculated using the two-sided log-rank test. Hazard ratios (HRs) and 95% confidence intervals (CIs) are shown, with the anti-recommendation group used as the reference. Source data are provided as a Source Data file.

Full size image

The personalized benefit score of adding chemotherapy in A-STEP was estimated by fusing 5 distinct scoring functions through attention-based mechanisms. We observed that the A-STEP model recommended that 357 of 678 patients (53%) in the discovery cohort should switch treatments (244 in the ICI-Mono arm, and 113 in the ICI-Chemo arm) as well as 160 of 318 patients (50%) in the external validation cohort (118 in the ICI-Mono arm, and 42 in the ICI-Chemo arm). The predictive modeling reported that at least 750 patients were expected to benefit from adding chemotherapy to their immunotherapy regimen, comprising 470 (69%) and 235 (74%) in the discovery and external validation sets, respectively.

To understand the relationship of differential treatment effects between the model-based stratification (i.e., the recommended treatment vs. received treatment), we used interaction plots with p-interaction as the quantification metrics. Interaction plots represent the average treatment effect within each subgroup broken down by treatment status. An interaction occurs when the lines are non-parallel to each other (more unparallel indicates a greater strength of interaction). This, coupled with the ANOVA test, can help to evaluate the statistical significance of the model’s predictive capacity. We observed that the A-STEP model presented a substantial level of treatment effect with p-interactions <0.0001 and 0.0094 for the discovery and external validation cohorts, respectively (Fig. 4a–b) and Supplementary Table 2. None of the sub-scoring models managed to outperform A-STEP as demonstrated in Supplementary Figs. 8–9. We also benchmarked the proposed model against conventional methods to evaluate a predictive biomarker (such as one-at-a-time covariate interaction analysis), with CCND1 and FBXW7 identified and tested as univariate predictive biomarkers (Supplementary Figs. 10–11, Supplementary Note 5). Analogous benchmarking to risk-based analysis was also done (Supplementary Fig. 12, Supplementary Note 5). In addition, we tested smoking status as a potential predictive biomarker to stratify patient treatment, which failed to consistently stratify patients’ PFS for different treatment arms (Supplementary Fig. 13). Taken together, these revealed the limitations in traditional statistical approaches to invoke predictive capability, as opposed to our proposed method.

Fig. 4: Treatment–biomarker interaction plots in discovery and validation cohorts.
figure 4

Interaction plots for (a) the discovery cohort and (b) the external validation cohort. Source data are provided as a Source Data file.

Full size image

Impact of individual clinicogenomic parameters

We further assessed how individual clinicogenomic features contributed to A-STEP recommendations by computing the SHAP values, a well-known cooperative game theory approach to disentangle the interplay between features towards model decision-making. Figure 5 elucidates the top 20 features as selected during the cross-validation process, including 6 clinical risk factors ranked in order of importance. Tobacco exposure was the most important treatment moderator from a clinical risk perspective, ranked third after APC and NTRK mutations in deciding that a patient would not benefit from additional chemotherapy. On the other hand, mutations in FBXW7, and MYC were the top ranked features that associated with benefit from combining immunotherapy and chemotherapy. This observation aligns with the interpretations of individual sub-models (Supplementary Fig. 14), wherein FBXW7 and ALK mutations consistently favored combined therapy, while the APC mutation constantly favored ICI monotherapy. Of note, we observed that none of the top 20 features on their own was significantly associated with treatment selection as shown in univariate analysis (Supplementary Fig. 15), which further proves the concept of modeling complex interactions of treatment effect moderators.

Fig. 5: SHAP-based interpretation of the A-STEP model.
figure 5

SHAP interpretation of the A-STEP model showing the top 20 features ranked by their importance, reflecting both the direction and magnitude of their effects on model predictions. Source data are provided as a Source Data file.

Full size image

Discussion

There are few reliable data to guide decision-making and patient selection for ICI monotherapy or combined ICI/chemotherapy; therefore, innovative methodologic approaches to refine patient selection for either approach in order to enhance outcomes and avoid undertreatment (or overtreatment) are crucial. This study of large real-world data used machine learning to create a predictive model that accurately provided insights regarding the individualized benefit of adding chemotherapy to immunotherapy. We observed a synergy between different weighting subgroup algorithms, and their integration into an ensembled model achieved robust stratification, especially during external validation.

Traditional approaches to subgroup identification include unweighted regression algorithms, which treat all variables with equal significance and can potentially overlook the nuanced contributions of critical variables. In contrast, in this study, we demonstrate the utility of a weighted approach for subgroup identification, which can more flexibly account for the varying importance of different predictive variables19,20. By using attention-based ensemble learning to integrate and harmonize different models, a robust, clinically relevant model can be generated that could more accurately identify patient subgroups who would benefit from intensified interventional regimens, ultimately contributing to more effective treatment.

Additionally, this study demonstrates the applicability of this approach to a clinically relevant question. While previous prediction studies have focused on identifying the mNSCLC patients who benefit from immunotherapy8,21,22,23, this does not necessarily pertain to the clinical decision providers must now make, which is how to select between different ICI-containing regimens. In contrasts, the current investigation focused on predicting the expected individualized benefit of two major treatment interventions24, demonstrating the potential of this approach to guide clinically-relevant treatment decisions. Building off our prior work that demonstrated the most significant benefit from adding chemotherapy to ICI arose in preventing early progression at 3 months8 we focused on testing predictive modeling by contrasting the disease progression patterns at 3 months of patients treated with ICI-Mono vs ICI-Chemo. Interestingly, when stratifying the model for PFS, its predictive power remained robust for different treatment arms. This suggests that the model’s effectiveness for early on-treatment disease progression could project to forecasting long-term survival outcomes, but dedicated analyses remain necessary.

One notable strength of this study is the large sample size of 2300 NSCLC patients treated at several major cancer centers, which encompass diverse patient populations, clinical practice patterns, and geographic regions; these “real-world” data help in creating models that are more representative of the broader population. The diversity reduces the risk of overfitting to a specific site’s characteristics, and the large sample size provides sufficient statistical power to detect potential signals. Furthermore, we applied propensity score matching before subgroup analyses, a well-accepted technique to reduce selection bias and enhance the validity of treatment effect estimates within subgroups. More importantly, this method improves the precision and reliability of subgroup analyses, ensuring that any observed differences in outcomes are more likely due to the treatment rather than underlying differences in baseline characteristics.

Our study delves into the realm of predictive biomarkers, shedding light on their role in early progression and treatment outcomes. Our analyses highlighted features previously associated with differential benefit, including tobacco exposure, while helping define a weighting algorithm to integrate multiple diverse features. We note that the genomic variants identified, including FBXW7 and ALK are of uncertain functional significance. FBXW7 alterations have been previously impacted in ICI sensitivity25 whereas ALK mutations in NSCLC may associate with outcome through their association with a higher tumor mutational burden. While further investigations into the biological mechanisms of differential sensitivity are necessary, particularly utilizing datasets with deeper biological information including whole exome sequencing and transcriptomics, these results highlight that meaningful treatment selection inference is feasible from clinicogenomic features readily available across treatment contexts. Subsequent research efforts can help validate these findings, refine clinical markers, and guide more precise therapeutic choices for maximal benefit while minimizing adverse effects.

Despite the unique strengths of this investigation, there are some limitations. First, any retrospective analysis can contain unmeasured biases and confounding, and consequently, the models and findings require further assessment using large prospective cohorts. Second, we focused on routinely collected clinicogenomic variables, mainly because the use of less common information limits applicability to centers where this information is not routinely collected. Owing to variability in available clinical and genomic data across different datasets, this study utilized a limited number of overlapping features. More multimodal data, such as NGS profiling and radiomics, can also be integrated into modeling in the future with likely enhanced model performance. Likewise, in terms of clinical decision-making, it is essential to consider not only the efficacy of treatments, but also the potential toxicities and a myriad of other factors that can influence patient outcomes. Herein, we used 3-month progression as a surrogate for modeling treatment response. Future studies are needed to consider long-term outcomes as well as immune-related adverse effects. Third, the performance of a machine learning model can fluctuate across different datasets, often due to population shifts or limitations in its generalizability. This was particularly evident when we introduced an external validation dataset during the revision process. To address this limitation, we employed ensemble learning, which combines different models to reduce variance and uncertainty. Future efforts could focus on advancing uncertainty quantification through advanced techniques such as Monte Carlo simulations. Fourth, we set FDR threshold at 0.1 (10%) to reflect the exploratory nature of this study, but we also implemented a strict Bonferroni correction to assess statistical significance level. Finally, while the development of multiple therapeutic options is inherently a challenge of basic science, drug discovery, and clinical trials, our approach aims to complement these advances by utilizing statistical and machine learning models to identify the most promising treatment strategies for individual patients with the treatments already available. We recognize the critical role of these foundational efforts and aim to build upon them to enhance the precision and effectiveness of clinical decision-making.

In conclusion, the A-STEP machine learning framework can inform more precise selection of individualized systemic therapy for mNSCLC, which we demonstrate by defining those patients who benefit from adding chemotherapy to ICIs. This research offers an approach to integrating multimodal data to inform complex clinical decisions, while laying the groundwork for further biological investigations to define the mechanisms of treatment response.

Methods

Study design and participants

This study was granted ethical approval by the institutional review board of The University of Texas MD Anderson Cancer Center (MDACC), Mayo Clinic, and Dana-Farber Cancer Institute (DFCI). All procedures were conducted in accordance with ethical standards of the 1964 Declaration of Helsinki. Informed consent was waived due to the retrospective nature of this study.

The objective of this retrospective study was to use machine learning to build a treatment recommendation system that enabled individualized treatment plans for systemic therapy (i.e., immunotherapy with or without chemotherapy). Patients from MDACC, Mayo, and SU2C were utilized for model discovery and tuning of hyperparameters, which was subsequently subjected to external validation using patients from the DFCI cohort. These cohorts are briefly described below.

MDACC cohort—We queried GEMINI, at the University of Texas MD Anderson Cancer Center, funded by the Lung Cancer Moon Shot program, to find patients treated with ICIs between 2020 to 2022. Patients were included if they met the following criteria: (1) pathologically confirmed NSCLC, including adenocarcinoma, squamous cell carcinoma, and others; (2) stage IV disease at the time of commencing ICIs; and (3) received at least 2 cycles of ICI alone with or without chemotherapy.

Mayo cohort—The same inclusion criteria were applied to a cohort of patients treated with ICIs at Mayo Clinic. This cohort constituted patients who were seen at Mayo Clinic in Florida between 2019 and 20208.

DFCI cohort—The same inclusion criteria were applied an external cohort of patients treated with ICIs at Dana-Farber. This cohort constituted consecutive patients who were seen at Dana-Farber Cancer Institute, consented to correlative research protocols 02-180, 20-000 and 17-000 and received at least one dose of PD-(L)1 blockade with or without chemotherapy between 2013 to 2023. Details of this data are published elsewhere26,27.

SU2C cohort–This was a public consortium of 393 patients with advanced NSCLC across nine cancer centers treated with PD-1/PD-L1 agents. This cohort was predominantly adenocarcinoma patients, and details of this data are published elsewhere28.

Genomic profiling

We collected somatic sequencing results from genomic profiling or external vendors from pathology reports and clinical notes. Samples with in-house somatic sequencing data were included for extended genomic analyses. Mutational profiling was conducted on formalin-fixed paraffin-embedded tumor tissue or blood samples as previously described29,30. For the MD Anderson data, tissue molecular profiling used NGS-based analysis to detect mutations in 134 or 146 genes. Sequencing or circulating tumor DNA (ctDNA) was performed using the MD Anderson liquid biopsy panel (70 genes) or the Guardant360 panel (74 genes). For computational power, samples from any time point were included, and a mutational event was considered present if it was detected in tissue and/or in the blood. The sample closest to the date of ICI initiation was selected for patients with multiple samples across different time points. For consistency in analysis across sequencing panels, we limited the genomics set to the 70 genes contained in the ctDNA panel. All reported non-synonymous mutational events were included; copy number alterations with log2 copy ratio<1 (deletion) or >5 (amplification) were included in the analysis. Tumor mutational burden was excluded due to smaller sequencing panel size. Further details are described elsewhere8. Similar genomic event filtering was used in the Mayo, SU2C, and DFCI datasets. In the end, 28 overlapping genes across different cohorts were kept for downstream modeling analysis.

Individualizing treatment plans

Figure 1 summarized the overall pipeline to characterize heterogeneity in treatment response and enhance customized treatment strategies regarding the addition of chemotherapy to baseline immunotherapy (or lack thereof). We integrated 28 genomic features with clinical risk factors including gender, age, tobacco exposure, pathology, PD-L1 expression, and line of therapy as the foundation of the framework. The computational system encompassed several key steps. First, the pooled data were pre-processed and quality checked. Details of genomic profiling were done per prior reports8,26,27,28. To address retrospective biases and confounding, propensity score matching was performed to identify paired samples with similar characteristics (Supplementary Note 1). Subsequently, an optimal subset was identified through recursive feature elimination for model construction. The individualized benefit of adding chemotherapy was estimated through repeated cross-validation (n = 30) using five different weighting methods (Supplementary Note 3). When the stand-alone scoring’s predictive performance did not achieved the desired performance during validation, we have introduced different strategies to integrate them (H-STEP, S-STEP, and A-STEP, Supplementary Note 4) to mitigate the potential biases of any single model by leveraging the diversity of different approaches to capture wider patterns in the data. Similarly, the integrated system subjected to performance validation in both the discovery and external validation cohort to ensure reliability and generalizability. Finally, we investigated the model’s decision-making through the lens of clinical translation and model interpretation.

Step 1: Modeling treatment effect

In this work, we made standard assumptions shown to be sufficient for causal dependencies on the interventions (details in Supplementary Note 2). Without loss of generality and according to Rubin’s potential outcome framework31, the expected outcome \(E\) can be expressed given the desired outcome \(\left(O\right),\) treatment \((T)\), and initial covariates \(C\) as \(E\left[O | T,C\right]={{\varnothing }}\left(C\right)+T\times \triangle \left(C\right)/2\), where ∅(C) is a function that represents the main prognostic effect and can be calculated as \(E\left[O | T=1,C\right]+E\left[O | T=0,C\right]\) and \(\triangle \left(C\right)\) indicates the treatment effect which can be expressed as \(E\left[O | T=1,C\right]-E\left[O | T=0,C\right]\). To construct a model for \(E\left(O | T,C\right)\) involves formulating functions for both \({{\varnothing }}\left(C\right)\) and \(\triangle \left(C\right)\) based on the covariates. Variables used in constructing \({{\varnothing }}\left(C\right)\) are referred to as prognostic variables, while those used in constructing \(\triangle \left(C\right)\) are called treatment moderators24,32. Conventional methods for creating optimal ITRs involve \({{\varnothing }}\left(C\right)\) and \(\triangle \left(C\right)\) simultaneously predicting outcomes and estimate ITEs using these model-based estimates. However, this approach requires accurate specification of both \({{\varnothing }}\left(C\right)\) and \(\triangle \left(C\right)\), even though only the latter is ultimately used to guide treatment selection. As a result, \({{\varnothing }}\left(C\right)\) becomes a nuisance parameter, and its specification may impact the estimation of the treatment function \(\triangle \left(C\right)\), which is particularly problematic because there are often many prognostic variables but only a few treatment moderators that influence treatment recommendations10,33. Nevertheless, if our aim is to rank ITEs or develop ITRs, only the treatment function \(\triangle \left(C\right)\)’s ranks or signs would be relevant. Therefore, it is desirable to have a robust estimate of ITEs that does not require the estimation of \({{\varnothing }}\left(C\right)\)9,10.

The endpoint in this study was progression at 3 months (denoted as \({O}^{(1)}\)) or no progression at 3 months (denoted as O(0)). The two treatments for comparison were ICI-Chemo, denoted as T=1, or ICI-Mono, denoted as T=0. Additionally, we assumed that only a single treatment outcome, either (O(1) or O(0), can be observed per patient. We also assumed that T is not dependent on (O(1)\(,\)O(0))31,34. To assign treatment, we assumed that the probability of receiving treatment, given certain covariates \(C\), is represented by the propensity score π(\(C\)), calculated as \(\pi \left({C}_{i}\right)=\Pr \left(T=1 | C\right)\). In randomized trials, this score is typically known and not influenced by \(C\), but it requires estimation in observational studies. The data we observe is represented by \(n\) independent and identically distributed copies of \(\left(O,T,C\right),\) denoted as \(\{({O}_{i},{T}_{i},\,{C}_{i}),\,i=1,\,.\,.\,.,\,n\}\).

Step 2: Individual benefit score estimation through weighting method

The objective was to utilize the weighting subgroup identification method9,10 to develop a personalized benefit scoring system \(f(C)\) based on the covariates \(C\), in which customized treatment would be suggested for individual patients using \(f(C)\). To clarify, we defined a benefit score as any function \(f(C)\) that met two criteria: (i) it reflects the extent to which patients benefit from a certain treatment and (ii) it has a meaningful and known cut-point value \(c\), such that for a given level of covariates \(C\), \(f\left(C\right) < c\) indicates that ICI-Chemo is more effective than ICI-Mono, and \(f\left(C\right)\ge c\) indicates the opposite. Clearly, \(\triangle \left(C\right)\) can serve as a benefit score, as it represents the expected benefit a patient will derive from ICI-Chemo in terms of their outcome. Thus, estimating \(\triangle \left(C\right)\) or its sign can enable optimal recommendation of different treatments for different patient subgroups. By definition, \(\triangle \left(C\right)\) can also be used to rank patients based on the magnitude of treatment effect9,10.

Another measure of interest is ITR, a function that maps patient covariates to the treatment decision, \(d\left(C\right):C\to T\). Optimal ITRs aim to maximize the average outcomes across the population by making treatment decisions for patients in a way that maximizes the value function \(V\left(d\right)={E}^{d}\left(O\right)=\int {Od}{P}^{d}\) where \({P}^{d}\) is the distribution of \(\left(O,T,C\right)\), given \(T=d\left(C\right).\) As a result, \(\triangle \left(C\right)\) can be used to develop optimal ITRs. Specifically, the sign of \(\left\{f\left(C\right)\right\}\) is considered for optimal ITRs9,10. A convex loss function \(M\left(y;v\right)\) can be used to estimate benefit scores, for example the squared error loss, \(M\left({y;v}\right)={(y-v)}^{2}\). Chen et al.10 originally proposed that \(M\left({y;v}\right)\) should meet two conditions. First, \({M}_{v}\left({y;v}\right)=\,\partial M\left({y;v}\right)/\partial v\) is increasing in \(v\) for every fixed \(y\). Second, \({M}_{v}\left({y;}0\right)\) is monotone in \(y\). These conditions are adequate for Fisher consistent subgroup identification, but they are not mandatory9. Our formulation of different weighting methods to estimate benefit scores and subsequently identify subgroup effects is presented in Supplementary Note 3.

Step 3: Integrating the individual sub-scoring systems

Using the benefit scores from five distinct scoring systems, we further built an ensemble model using three fusion mechanisms. The impetus was to capture common and potential complimentary signals presented across different stand-alone systems while reducing the individual system’s bias and variance by aggregating across multiple model predictions. The assembling steps are detailed in Supplementary Note 4.

Step 4: Model training and validation

We adopted a repeated 5-fold cross-validation strategy (n = 30) to develop and fine tune sub-scoring models’ hyperparameters including the feature importance based on discovery cohort. Features were ranked based on their frequency of being selected from 150 runs and were considered informative if selected at least 50% of the time. We then locked the optimized hyperparameters and refitted the individual models on the whole discovery set, which were further tested on an external validation cohort. All models were developed using open-source Python version 3.9.8 and R version 3.6.1. All models were trained on the NVIDIA DGX A100 station.

Clinical validation

To assess the predictive capability of sub-models and integrated models in estimating the benefit of adding chemotherapy to immunotherapy for a patient, an individualized recommendation was made by contrasting two treatment arms, in terms of treatment effect conditional on the subgroup. The personalized benefit score was utilized to recommend whether chemotherapy was beneficial for a patient. Using this recommendation, patients were stratified into two subgroups, (i) those who were treated according to the model recommendation, or “Follow-recommendation’’, and (2) those who were treated against the recommendation, or “Anti-recommendation”. Subsequently, we investigated clinical significance by conducting a comprehensive analysis by comparing the “Follow” versus “Anti” subgroups in terms of effect measures particularly the weighted risk reduction (WRR), Kaplan–Meier plots, log-rank tests, and hazard ratios (HRs). In brief, WRR represents the percentage of patients potentially saved from early disease progression by adhering to model’s recommendations (details in Supplementary Table 3).

Model interpretation

Finally, we interpretated the association between individual features with a model’s recommendations (ICI-Chemo vs ICI-Mono) using SHAP (SHapley Additive exPlanations) analysis35 to quantify the impact of each feature on both direction and magnitude of the treatment effects.

Statistical analysis

The primary endpoint was defined as early disease progression at 3 months. Disease progression was determined by the recorded assessment of the attending physician based on imaging reports of tumor growth or new disease sites, pathologic conformation, and/or through clinical assessment. We also collected PFS data, where patients who were alive without progression were censored at their last image assessment. The interaction p-value between the recommended and treatment groups was calculated via ANOVA. Kaplan-Meier analysis and log-rank tests were used to evaluate statistical significance of patient stratification. The Wilcoxon signed-rank test or χ² test were used to test the differences in distribution of continuous or categorical variables, respectively, as stratified in different groups. To adjust for multiple statistical testing, the Benjamini-Hochberg method was used to control the false discovery rate (FDR). All statistical tests were two-sided, with a p value less than 0.05 or FDR less than 0.1 considered to be statistically significant. All statistical analyses were done with R version 3.6.1.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.