Introduction

Over the past decades, there has been an increasing enthusiasm for the development of bioinspired tactile sensors for robotic manipulation1,2, aimed at endowing the robots with human-like perception and manipulation capabilities for a wide range of applications such as manufacturing3, industrial automation4, exploration5,6, surgeries7 and healthcare8,9,10. Particularly, tactile sensing plays a significant role in robotic manipulation, mimicking the intricate and coordinated movements of the human hand11,12. A primary objective for artificial tactile sensing systems is to achieve the versatile sensory and adaptive manipulation capabilities inherent in humans, which is accomplished by the coordination of distributed mechanoreceptors (MR) in the human hand, the nervous system in the human body, and the brain13,14 (Fig. 1a). Similarly, this nuance may be realized with Artificial Intelligence (AI) based cyber-physical systems through the convergence of advanced materials, bionic sensors, and efficient algorithms15,16,17,18,19,20 (Fig. 1b). Although tremendous efforts have been dedicated to demonstrate such neuromorphic concept, the state-of-the-art artificial tactile sensing system is still in its infancy to be seamlessly integrated with the robotic framework21.

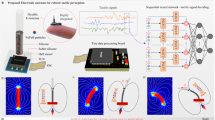
Fig. 1: Comparison of human and the bionic tactile sensing (BTS) integrated robotic sensory and actuation systems.
figure 1

a For humans, different types of mechanoreceptors in the skin detect tactile stimuli, transmit these signals to the brain for processing, followed by muscle actuation. b For robots, the proposed BTS system detects inputs, processes data using computer algorithms, and actuates motors to perform actions. c Schematic diagrams show the hypothetical scenario of touch experiments of a human finger with different steps. d Schematic diagrams show the analogous experimental setup and the steps for the touch experiment of BTS system based on dynamic DC generation mechanism with a modeled finger. e shows the afferent response signals generated in different mechanoreceptors, in which Rapidly Adapting (RA) type of mechanoreceptors (MR) being responsible for the identification of objects slipping from the human hand and the Slow Adapting (SA) MRs being responsible for the perception of object grasp. The signal further reaches the brain for processing and then to muscle for actuation. f The variation of force (F), capacitance (C), and open-circuit voltage (VOC) response at different steps in (d). BTS is capable of detecting slip due to the dynamic sliding between the PEDOT:PSS coated fabric and the titanium (Ti). Electronic excitation of electron-hole pairs is induced at the dynamic Schottky interface (Inset). Further, the signals are transmitted to the processor and to the servo for actuation.

Full size image

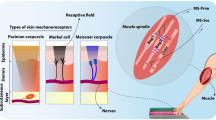
Figure 1 highlights the functioning and response mechanisms of both human and robotic tactile systems22. In the human nervous system, the MR cells of different kinds enable the sensing of object information, which is subsequently sent to brain for processing. In particularly, the MRs dedicated for tactile sensing can be categorized into rapid-adapting (RA) and slow-adapting (SA) types23. RA MRs, such as Meissner/Pacinian corpuscle respond quickly to instantaneous changes in the mechanical stimuli such as grasping, releasing, or slippage of an object from hand. In contrast, the SA MRs, such as Merkel cell (MC), adapt slowly to sustained stimuli such as pressure and stretch14,24,25. As a result, the firing rate of RA and SA MRs in a finger on a surface exhibit different characteristics at the time domain during a touch-slip-lift process (Fig. 1c, e): the SA has a sustained signal throughout the touch-slip-lift process from the time of touch till the loss of contact, whereas the RA MRs only generate signal at the beginning of touch, during slip, and at loss of contact. Notably, the coordination of RA and SA MRs distributed on human hands enables our capabilities for multi-directional and multi-modal (i.e., static and dynamic) tactile sensing. However, the state-of-the-art artificial tactile sensors still lack such coordinated agility and sensitivity26.

To date, multiple approaches have been explored for artificial tactile sensing27,28. Vision-based tactile sensors capture the spatial resolution images of the contact surface, which are processed by computer vision algorithms to track the movement of objects29. Multi-directional sensing is facilitated by vision-based approaches with pixeled data, enabling object detection and tracking across multiple axes. This method is particularly beneficial in dynamic environments, where it can adapt to changes quickly30. However, their implementation relies on the absence of physical obstacles, distinguishable environment/object pattern layers, reflective layers, high-performance cameras, as well as complex computing algorithms to interpret data31,32. Optical fiber-based tactile sensors are another type of vision-based approach, which can be intimately attached to the surface. Such systems use photo-detector array to collect time-dependent differential signal between the incident and reflected light to translate spatial contact information to spatially resolved datasets. However, the optical fiber-based sensors are limited by the surface material selection (e.g., transparent materials with optimal refractive index), miniaturization of the light source/detector, and environmental interference33,34. The response time of commercial vision-based devices (e.g., GelSight, USA) with form factors in few centimeters range is limited by the frequency of image sampling rate at up to 30 Hz, which corresponds to 33.33 ms along with a large form factor35. Non-vision-based tactile sensors consist of powered and self-powered approaches. Traditionally powered sensors (e.g., piezoresistive36, capacitive37, and magnetic38 methods) are similar to the SA MRs in humans, as their properties (voltage, capacitance, etc.) vary proportionally with the changing force on normal direction. Multidirectional sensing like shear force sensing can only be achieved by sophisticated engineering of the sensor structure2,39,40,41. Moreover, the requirement of a power supply adds wiring complexity to the sensor fabrication.

Self-powered solutions such as piezoelectric42,43,44, triboelectric45,46,47 and magnetoelastic48,49 methods are promising solutions for non-vision-based tactile sensing, which resemble the inherent natural characteristics of RA MRs showing electrical output in response to the change in forces or stimulation. In particular, the tribovoltaic effect is emerging as a strategy, which produces sustained direct-current (DC) power output at the dynamic metal-semiconductor Schottky contact or P-N junction, with 3–4 orders higher current density compared to the transient alternating-current (AC) output in conventional piezoelectricity or triboelectricity50. This phenomenon was first discovered nanoscopically in two-dimensional (2D) semiconductor51 and silicon (Si)52, and proved macroscopically in various semiconductor53 systems such as silicon (Si)52,54,55, oxides (TiO2, VO2)56,57,58, wide-bandgap semiconductor (e.g., gallium nitride, GaN)59,60, and perovskite61. Recently, a similar concept has been proved in organic Schottky contact systems, where DC output can be generated in aluminum (Al)-conducting polymers sliding contact, e.g., poly(3,4-ethylenedioxythiophene):polystyrene sulfonate (PEDOT:PSS)50,62,63 and polypyrrole (PPy)64,65. The advantages of tribovoltaic DC effect for tactile sensing are multifaceted. First, the DC electrical output coincides with the sliding velocity in the time domain with high current density. Second, the control algorithms needed to process the DC output data for robotic manipulation are readily available. Third, the response time, as will be shown in the later section, is similar to that of the human sensory system. Last but not least, the self-powered feature reduces the additional energy requirement for tactile sensing. In this work, we demonstrate a bio-inspired solution for robotic tactile sensing and manipulation via the development of a textile-based tribovoltaic DC generator and its integration with robotic fingers.

Results

Tribovoltaic dynamic DC generation as a bionic friction sensing mechanism

To demonstrate this concept, a modeled contact mimicking an artificial finger is designed with a piece of PEDOT:PSS coated stretchable E-textile fabric attached to a polydimethylsiloxane (PDMS) soft hemisphere (diameter d = 15 mm). In the meantime, a capacitive force sensor made of polyester (PET) thin film with Indium-Tin oxide (ITO) electrodes is placed on the linear actuator stage beneath the titanium (Ti) sheet (inset of Fig. 1f) (See Fig. S1 in Supplementary Information for characterization of the capacitive sensor). The synthesis and characterization of the E-textile will be discussed in a later section. The hemisphere is then brought into contact with a Ti foil fixed on a linear actuator stage with wired electrode. Figure 1c, d respectively show different steps of a representative frictional contact process with human finger and our modeled system, where step #1–7 respectively correspond to: step #1- engaging (no contact), step #2- compressing up to a force (F) of 5.0 N, step #3- standing still (no motion), step #4- linear reciprocal sliding with a force variation of <0.25 N, step#5- standing still (no motion), step#6- lifting (releasing the applied force, but the probe still in contact), step #7- lifting (out of contact). In step #1, the artificial finger is attached to a mechanical tester and moved down with a constant speed of 0.16 mm/s before contact. In step #2, it can be observed that as soon as the artificial finger contacts the Ti sheet and continuously exerts increasing F in the normal direction, the output of the capacitive sensor shows a similar trend to the force applied. In the meantime, the bionic tactile sensor (BTS) signal (i.e., open-circuit voltage, VOC) remains negligible, indicating trivial slip between the E-textile fabric and the Ti when an increasing static force is applied in the normal direction. In step #3, the artificial finger stands still without any normal or longitudinal movements under a constant F of 5.0 N. When the linear actuator drives the Ti sheet at a speed of 53.63 mm/s for 10 s in step #4, a minor disturbance in the F with a small variation of <0.25 N is observed, corresponding to a <5% fluctuation of F. During this step, the artificial finger slides back and forth on the Ti sheet. It can be seen that the BTS shows a significant signal of ~50 mV (Fig. 1f), whereas the capacitive sensor shows negligible variation in the signal. Furthermore, steps #5, #6, and #7 are analogous to #3, #2, and #1, respectively, except the force is removed.

In the tribovoltaic effect, mechanical energy is converted into electrical energy through mechano-electronic excitation at dynamic Schottky interfaces55,66,67. As the metal-conducting polymer interface undergoes continuous frictional contact, the interfacial electric field drives the separation and migration of the excited electrons and holes, resulting in the generation of a DC output62,68,69. The results (Fig. 1f) prove that the tribovoltaic DC generation is substantially more sensitive to the dynamic sliding along the shear force direction compared to the normal force variation under static contact. From a bionic perspective, the characteristics of BTS signal resemble the RA MRs, which can operate in conjunction with the capacitive sensors as a SA MRs counterpart to feed input for robotic control algorithm similar to the process in the human sensory system (Fig. 1e).

Dynamic DC generator-integrated E-textile array as one-piece BTS unit

In order to implement the concept for robotic manipulation, it is necessary to integrate the dynamic Schottky generators into a one-piece form factor. Noting that E-textile materials have advantages to be woven, sewn, or manufactured into desirable structures, we developed a material system for dynamic DC generation featuring high electrical conductivity, stretchability, and manufacturability. To fabricate this structure, we developed a highly conductive PEDOT:PSS ink for coating onto a stretchable fabric substrate made of 20% spandex and 80% PET.

Figure 2a shows the fabrication process (see “Methods” for more details)50. After three repeated coatings and thermal treatment, the PEDOT:PSS-coated fabric was cut into small, desired pieces for device integration (Fig. 2b). Figure 2c shows the image of a fully packed BTS sensor. In the BTS sensor prototype, a Ti foil was used with a PEDOT:PSS-coated fabric placed on the top. To ensure the degree of movement between the Ti foil and the PEDOT:PSS coated fabric, as well as the constraint on the edge, a thin layer of double-sided adhesive was applied along the edges of the foil. A thin ITO-coated PET sheet was placed underneath as a capacitive normal force sensor. To further improve humidity stability and anti-wearing properties, the sensor was packaged in between two waterproof vinyl adhesive sheets. In this work, Ti has been chosen over Al for constructing the dynamic Schottky contact. Compared to Al, Ti is more cathodic and less vulnerable to electrochemical corrosion70, which is evident from the DC output characteristics with water added to the metal-conducting polymer interface (See Figs. S2–S4 in Supplementary Information). We have also tested other fabric substrates (e.g., hydrophilic cotton, elastane, non-woven fabrics, nylon, PET, superhydrophobic fiber, tufting fabrics) for PEDOT:PSS coating (See Fig. S5 in Supplementary Information). The results indicate that both the wettability and the mechanical properties of the fabrics are key to the success of conducting polymer coating.

Fig. 2: Fabrication and characterization of PEDOT:PSS-coated E-textile as a fundamental element of BTS for dynamic DC generator-based self-powered sensing.
figure 2

a Schematic illustration of the process for fabricating PEDOT:PSS-coated fabric on a spandex substrate. b Optical images showing the spandex fabric before and after 3 coatings. c Layer-by-layer structure of the BTS sensor prototype. d SEM images of fabric surface morphology with increasing number of PEDOT:PSS coating showing the microstructural changes. e SEM images with higher magnification, highlighting the coating quality on the fibers. f Elemental EDS mapping of sulfur distribution on clean spandex fabric substrate without PEDOT:PSS coating and g after 3 coatings, showing uniformed distribution of the PEDOT:PSS ink on the fabric. h SEM image showing the individual strand of fiber from the uncoated fabric. i SEM image showing the fabric thread with successful wrapping of the PEDOT:PSS ink coating around the fiber and interconnects of the same ink between two adjacent strands. j Tensile test data displaying the change in resistance (R) under mechanical deformation showing less than 13% of ∆R/R0 under the strain (ε) over 90%. k Experimental setup for tensile testing of fabric using a mechanical tester. l Current-voltage (I-V) characteristics of the coated fabric under different normal forces in static conditions. m Statistical analysis of the open-circuit voltage (VOC) output in a Ti/ PEDOT:PSS coated fabric dynamic DC generator system in one-million cyclic testing. The error bars represent the standard deviation (SD) of the sample data collected periodically throughout the million cycles. n A schematic diagram of the experimental setup for evaluating the power output performance during sliding motions.

Full size image

To confirm the effectiveness of coating, scanning electron microscopy (SEM) characterization was carried out. Figure 2d, e shows the morphology of fabric surface before and after 1–3 coatings at different magnifications, revealing a two-phase evolution of the PEDOT:PSS coating. Firstly, it is evident from the SEM results that a continuous PEDOT:PSS coating is developed and wrapped around each fiber in the fabric after one coating cycle. After the second and third coatings, additional thin film of PEDOT:PSS is developed on top of the previously coated fibers, which may act as a conducting pathway and further enhance the overall electrical conductivity. Elemental mapping by energy dispersive spectroscopy (EDS) confirms a homogeneous distribution of sulfur across the textile surface, which is a characteristic element of PEDOT:PSS. (Fig. 2f, g) The SEM images (Fig. 2h, i) at a higher magnification further confirm the resulting coating of the PEDOT:PSS on the fibers, revealing good penetration and adherence of the ink to the fabric. To test the stretchability and electrical conductivity of the as-prepared E-textile, a tensile test was performed with a mechanical tester, while the electrical resistance (R) of the fabric was measured simultaneously. The results demonstrate that the increase in resistance (ΔR) was less than 13% with an overall R in the range of 0.019 kΩ/cm under a tensile strain (ε) of 90% (Fig. 2j). The stability of the electrical conductivity stems from the homogenous and uniform coating of the ink, and penetration of the ink into the fabric.

To investigate the interfacial electronic structure of the contact, the current-voltage (I-V) curve characterization was carried out. The I-V data (Fig. 2l) shows that the contact between the Ti and PEDOT:PSS-coated fabric exhibits non-linear characteristics at different applied loads. At relatively lower forces, rectified I-V curves are observed. When F is increased, the I-V curves become more symmetrical while still showing non-linear features. The results indicate the existence of an energy barrier between the PEDOT:PSS and the Ti, which is in line with the work function (Φ) difference between Ti (ΦTi = 4.33 eV71,72) and PEDOT:PSS (ΦPEDOT:PSS = 5.0 eV50). It is noted that the Schottky-like I-V characteristics of the dynamic contact is a key feature for the tribovoltaic dynamic DC generation50,73 (inset of Fig. 2l).

To test the long-term stability of the BTS, a 1,000,000-cycle sliding test was performed for ~98,350 s (Fig. 2m). A 2.5 N load was applied using a force gauge and the linear actuator was set to a speed of 100 mm/s with a sliding distance of 5 mm. Due to the limitation of the data storage of electrometers, the complete data was collected in 18 consecutive sessions. (See Fig. S6 in Supplementary Information for details). The VOC first exhibits fluctuation and then becomes stabilized to ~40 mV after ~400,000 cycles. This may be due to the PEDOT:PSS-Ti system reaching its equilibrium in contact conditions (force, temperature, contact configuration, etc.) at contact asperities. In addition, we carried out cyclic compressing tests (1000 cycles with maximum contact force of 1 N and compression velocity of 3.33 mm/s) to investigate the robustness of our E-textile. The DC output before and after the test remains similar, though a small extent of coating fracture has been observed from SEM images (See Fig. S7 in Supplementary Information).

Demonstration of robotic manipulation with BTS integrated robotic gripper

The application of the BTS system for robotics was demonstrated for manipulation tasks. We attached BTS sensor to a robotic gripper to demonstrate the robotic control based on DC generation. The block diagram (Fig. 3a) outlines a feedback control system used to maintain a secure grip on an object, preventing slipping despite external disturbances such as gravity or pulling forces. For robotic control experiments, a customized circuit has been made to filter and amplify the voltage generated by the BTS as output signal (Vout) from the sensor output, which is used in par with the analog to digital converter (ADC) (See Fig. S8 in Supplementary Information).

Fig. 3: Slip detection and mitigation with BTS-integrated robotic gripper system.
figure 3

a Schematic of the algorithm used for the BTS system to detect and mitigate slip. b Schematic of the gripper’s operation without feedback, illustrating continuous object movement: (1) Object positioned between robotic fingers; (2) Fingers engage the object, applying a grasping force (Fgrip); (3) Mechanical tester pulls the object upwards with a force (Fpull) of 1.5 N; (4) Object continues to move as the maximum Fpull of 4.5 N is not reached; (5) Gripper fails to stop the object due to lack of feedback, resulting in a final displacement (D) of 30 mm. c Data plots for the gripper’s operation cycle stages, showing synchronized final displacement of the object (D), moving velocity of the object (v), BTS sensor feedback (Vout), change of grip force (ΔFgrip), and change of the pulling force (ΔFpull) exerted by the mechanical tester. d Photos of the gripper manipulating the object without feedback, showing continuous movement and final D of 30 mm. e Schematic of gripper operation with feedback activated, reducing displacement to D = 4.1 mm: (1) Object positioned between fingers; (2) Fingers engage the object; (3) Displacement occurs, but feedback is activated; (4) Gripper exerts higher force as feedback is initiated by the Vout, stopping object movement upon reaching maximum force; (5) Final displacement of 4.1 mm. f Data plots for the 4.1 mm displacement cycle, showing force, displacement, and system response. g Photos of the gripper demonstrating 4.1 mm displacement. h Schematic of the gripper’s initial position and response to added weights without feedback for rotational control: (1) Initial position; (2) Grasping; (3) Weights added, initiating object rotation; (4) Rotation without feedback. i Data plots showing system response without feedback. j Photo of the gripper rotating the object without feedback, resulting in a larger angle (θ = 70°). k Schematic of initial position and response with feedback for rotational control: (1) Initial position; (2) Grasping; (3) Weights added to initiate rotation; (4) Rotation with feedback. l Data plots with feedback activated, demonstrating precise control. (m) Photos showing gripper rotation with feedback, achieving a smaller angle (θ = 7°).

Full size image

Here, two sets of experiments have been designed: sensing and mitigation of slip under: (i) linear pulling of the object with a mechanical tester (Figs. 3b–g) and (ii) gravitational rotation of the object from robotic gripper (Fig.3h–m). The system is operated by calculating an error based on the difference between the desired no-slip condition and any detected slip, which is identified by the BTS (Fig. 3b). To distinguish the signal generated by the BTS and the noise, the threshold set for the Vout was 30 mV. The BTS provides real-time feedback, allowing the control algorithm to compute the necessary adjustments in grip force. The motor controller then executes these adjustments by modulating the servo motors to apply the appropriate grip force (Fgrip), thereby counteracting the slip and stabilizing the object. This closed-loop process ensures continuous adaptation to disturbances, maintaining the grip and preventing the object from slipping.

For the linear pulling experiment, the mechanical tester was set to move upward with a constant speed (v) of 7.25 mm/s. A threshold of pulling force (Fpull) = 4.5 N was set as a force limit, considering the dynamixel servo used to control the grasp having a load constraint of 5 N. It was observed that the safety feature of the mechanical tester activated around 75% of the force threshold, causing the speed to automatically decrease (step #4 in Fig. 3c). This safety feature is a failsafe mechanism set by the manufacturers. Here, the experiments were performed under two scenarios: in the first case, no feedback was activated when the object was pulled away using the mechanical tester. In this scenario, no increase was observed in grasp force even when a signal was generated from the sensor output (Fig. 3c). The steps for experiments are: step #1-initial position of the finger and the object, step #2- the finger is engaged so that the object does not slip/fall under its own weight, step #3- the mechanical tester is initiated and the object moves up with Fpull, step #4- the Fpull reaches ~1.5 N and a displacement (D) of 15 mm, and the object continues to move up as the signal generated is not used to increase the grasp force, step#5- the final D of ~30 mm is seen without any increase of Fgrip (∆Fgrip = 0 N). When the feedback was turned off, the gripper did not increase the Fgrip by adjusting the servo angle (Fig. 3b). Corresponding optical images demonstrate the displacement (D) during each phase, highlighting the magnitude of movement of the object in response to gripper’s applied forces (Fig. 3d). The total D was observed to be ~30 mm since there was no feedback control. In the second scenario, with the feedback from the BTS activated, precise movements were successfully executed by the gripper as shown in the schematic and corresponding photographs (Fig. 3e–g). The steps for experiments are: step #1- initial position of the finger and the object, step#2-the finger is engaged, step #3- the mechanical tester is initiated, and the object moves up with Fpull, step #4- the Fpull reaches ~4.0 N and a D of 4.1 mm mm, and the object stops as the grasp force of ∆Fgrip = 4.0 N is reached with the movement between the object and the finger, generating DC signal by the BTS system, step #5- the final D of 4.1 mm mm is seen. Data plots confirmed the gripper’s capability to accurately control D to under 4.1 mm and consistently increase force throughout the task whenever a DC signal was generated from the tactile sensor (Fig. 3f). The optical image displays the successful mitigation of the object’s movement due to the increase in grasp force by the gripper (Fig. 3g).

For the second set of experiments, rotational control experiments were conducted to further demonstrate the sensor’s capability to detect and mitigate rotational slip: step #1- initial position of the finger and the object, step #2- the finger is engaged so that the object does not rotate under its own weight due to the unequal center of mass, step #3- the weight (W) of 0.26 N made of a 3D printed part and a copper bar is added, due to which the object started to rotate. Initially, when the gripper grasped the object, no rotation or motion was detected by the sensor. As external weights were added, the object began to rotate (Fig. 3h, i). Without feedback, the gripper exhibited significant angular displacement (θ = 70°) (Fig. 3j). When the feedback is activated as soon as the Vout passes the 30-mV threshold, the servo is initiated and the ∆Fgrip increases (Fig. 3k, l) to ~1.2 N to stop the angular motion of the object. With this implementation of feedback from the BTS sensor, precise control was achieved by the gripper, reducing angular deviation to a minimal value (θ = 7°) (Fig. 3m). This result underscores the effectiveness of the sensor in enhancing the accuracy and reliability of robotic manipulation tasks.

Furthermore, experiments were performed to investigate the relationship between displacement D and vgripper at a constant pulling velocity (vpull = 18.33 mm/s) (Fig. 4a). In all experiments, the values of D were recorded when Fgrip reaches 3 N. It can be seen that D decreases as vgripper increases at constant vpull, which can be rationalized by a faster actuation of the gripper in response to the detected slip. Also, experiments were conducted to examine the relationship between D and vpull at a constant vgripper = 126.75 mm/s (Fig. 4b). Figure 4b shows that D also decreases as vpull increases within the tested vpull range. Such a trend may be rationalized by the fact that the input frictional power (Pfriction) is proportional to sliding velocity:

$${P}_{{{{\rm{friction}}}}}=f\cdot {v}_{{{{\rm{pull}}}}}$$
(1)

where f is the frictional force. The increasing Pfriction would result in a faster rising of the BTS sensor signal, leading to an earlier actuation of the gripper. However, we predict that a substantial further increase of vpull would eventually cause D to increase again, the gripper may no longer be able to react quickly enough to such rapid motion. We have also investigated the final rotation angle (θ) of the object as a function of vgripper in the angular displacement experiment (Fig. 4c). As the vgripper increases, θ was found to decrease, which is in line with the expectation as a faster gripper response would lead to a quicker stop of the rotational motion.

Fig. 4: Investigation of parametrized slip detection and mitigation.
figure 4

Moving distance of the object when the gripper grasp force (Fgrip) reaches 3 N (a) at different gripper actuation velocities (vgripper), while the pulling velocity of the mechanical tester is kept constant (vpull = 18.33 mm/s). b At different pulling velocity of the mechanical tester (vpull), while the gripper actuation velocity is kept constant (vgripper = 126.75 mm/s). c Final rotation angle (θ) of the object at different gripper actuation velocity (vgripper). The weight of the added object is the same for all the five experiments (F = mg = 0.26 N). d Graph showing the response time of BTS system with different velocities and the colored boundaries indicating the response time for different types of human MRs. The error bars represent the range within 1.5 times the interquartile range (IQR) of the sample data collected e Image of the BTS sensor integrated compliant gripper system on a robotic arm. f The detection time delay (Δtd) vs. Fgrip. It is evident that the detection of slip via BTS sensor is faster than GelSight. The error bars represent the range within 1.5 times the interquartile range (IQR) of the sample data collected. g The 95% confidence interval of the detection delay for BTS and GelSight are 28.7–39.8 ms and 89–103 ms, respectively. It is evident that the detection of slip via BTS sensor is faster than via GelSight (t-test statistic: −13.42 and p-value: 4.7e-32). h Schematic of the step-by-step procedure of the experiment conduction where, Step #1: No grasp; Step #2: Engaged (minimum grasp force Fgrip applied to prevent container dropping); Steps #3–9: dropping of the 1st, 2nd, 3rd, 4th, 5th, 6th, 7th bead. Stainless Steel beads with a mass of 17.0 g with 16 mm diameter are continuously dropped into a 3D printed container. i Video captures of the falling bead experiment with BTS control feedback at different steps, with their corresponding schematics depicted in j Force torque sensor signal, k BTS sensor signal, l GelSight score, and m Fgrip as a function of time throughout the experiment. The increasing Fgrip from the gripper at each bead-dropping event is triggered by the BTS sensor signal to mitigate the slip of the container.

Full size image

It is noted that the response time of human MRs depends on their types. The conduction speed of neurological signal for Meissner’s corpuscles (RA-I), Pacinian corpuscles (RA-II), Merkel cells (SA-I), and Ruffini endings (SA-II) has been reported to be ~26–91 m/s, ~30–90 m/s, ~16–96 m/s, and ~20–100 m/s, respectively14,74. Accordingly, the calculated response times for a 1 m traveling distance of human MRs fall into the range of 10–200 ms. It can be seen that the estimated response time of BTS approaches the limit of human MRs, showing great promise for enhancing the dexterity in future humanoid robots (Fig. 4d). (See Fig. S9 in Supplementary Information for more details).

In another experiment, we demonstrated a closed-loop control system by integrating the BTS with an adjustable stiffness gripper, which is capable of modifying grip force independent of grasp width75. To assess slip detection performance, we attached a BTS and a vision-based GelSight sensor to separate gripper fingers. GelSight, commonly used in robotic manipulation, estimates slip by tracking geometric contact features, making its performance highly dependent on the presence of such features. To ensure fairness in our comparison, we used a 3D-printed container with geometric patterns for the grasping experiments.

During the experiments, the robotic gripper was set to the minimum grip force necessary to prevent slip. To induce slip, we dropped 7 metal beads (~17 g each) from a height of 12 cm into the container (Fig. 4h, i). The impact caused the container to slide within the gripper. We recorded data from GelSight, BTS, and a 6-axis Torque/Force (T/F) sensor embedded in the robotic arm. The Lab Streaming Layer ensured precise synchronization. GelSight captured images at 20 frames per second, analyzed by computing the average pixel difference between consecutive frames, while BTS and force data were recorded at 1000 Hz. The T/F sensor identified the moment of impact, allowing us to estimate the latency of BTS and GelSight in detecting post-impact slip.

The results showed that impact-induced slip generated spikes in the T/F, GelSight, and BTS outputs, detected using a threshold on the local maxima of a moving window (Fig. 4j–l). BTS-detected slip triggered the gripper controller to incrementally increase grasp force76 and stop further slippage (Fig. 4m) (See Supplementary Movie 3). Without feedback loop activated, in contrast, the gripper remained at the same position and the object fell after the 5th consecutive bead was added (See Supplementary Movie 4). The largest displacement occurred after the first impact when the grip force was minimal. With each subsequent impact, the accumulated beads reduced the drop height and impact force, while the pre-impact grasp force increased, leading to less slippage.

To compare slip detection times, we conducted experiments without the controller, maintaining a constant grip force. We tested 10 initial grasp forces ranging from 0.69 to 5.48 N, with each trial involving a single bead drop and 15 repetitions under identical conditions. The spike in T/F sensor data identified the exact impact time, while slip detection time was defined as the time difference between impact and the corresponding sensor’s detection spike (Fig. 4f). The comparison results shown in Fig. 4g. ANOVA (Analysis of Variance) analysis indicated no significant effect (p-value 0.85) of initial grip force on detection delay (p = 0.801), allowing data from all trials to be combined. As shown in Fig. 4g, BTS achieved a significantly lower mean detection time (34 ms) compared to GelSight (96 ms), with an average difference of 62 ms. BTS demonstrates an improved detection time of slippage that would enable real-time slip detection and object retaining in robotic manipulation in the presence of external impact, while systems relying on vision-based tactile sensors such as GelSight would fail due to slower detection time and permitting larger post-impact displacement.

Contact mechanics analysis of the parameterized BTS output

The mathematical relationship between the BTS output and the mechanical input parameters is critical for facilitating advanced robotic manipulation including delicate manipulations and in-hand reorientation, where understanding the force and speed of contact is the key to avoiding damage to objects or changing the grasping strategy through object reorientation77. Here, a modeled contact of BTS is used to perform this analysis. The experimental setup consists of a linear actuator on which a Ti sheet was placed, and a PEDOT: PSS fabric on a PDMS finger of d = 15 mm attached to a force gauge. The experiments were performed for 30 reciprocal cycles at a moving distance of 8 mm. Figure 5a, b shows the performance of BTS under varying velocities and applied forces. The sensor generates short-circuit current (ISC) in response to an increase in both velocity of motion (v) (Fig. 5a) and the applied force (F) (Fig. 5b). The v-dependent current response spans from 0.75 to 116 mm/s, with higher velocities generating significantly larger currents up to 20 nA, whereas the lower velocities generating ~5 nA. Similarly, the F-dependent current response (Fig. 5b) ranges from 0.5 to 5.0 N, indicating the sensor’s capability to distinguish between different loads (see Figs. S10–S13 in Supplementary Information).

Fig. 5: Quantitative analysis of force- and velocity-dependent DC output.
figure 5

a Short-circuit current (ISC) generated by the PEDOT:PSS coated fabric on the modeled finger and Ti placed on the linear actuator driven at different velocities ranging from 0.75 to 116 mm/s. The inset shows the experimental setup with a force gauge and linear motor. b ISC generated under different applied forces (F) ranging from 1 to 5 N. c Schematic of the Hertz model with the contact area (A) under F. d Plot showing the ISC vs. F. The solid lines correspond to the data fitting based on Eq. 6. The error bars represent the standard deviation (SD) of the sample data collected for each velocity at their respective forces. e The plot shows the derived current density (JSC) increasing with v due to the enhanced frictional energy input and the intensified electron-hole pair excitation with increasing v.

Full size image

Figure 5d further elucidates the relationship between ISC and F at different velocities. As anticipated analytically, the ISC increases with increasing velocity for each corresponding F. Here, the Hertz contact mechanics model is used to analyze the relationship between ISC, F, and v (Fig. 5c). The contact radius (\({a}_{{{{\rm{Hertz}}}}}\)) and contact area (A) for Hertz model is given by78:

$${a}_{{{{\rm{Hertz}}}}}={\root 3 \of {\frac{{R}_{{{{\rm{tip}}}}}\cdot \,F}{{E}_{{{{\rm{tot}}}}}}}}$$
(2)

where, \({R}_{{{{\rm{tip}}}}}\) is the radius of the tip in contact, \(F\) is the force applied, and \({E}_{{{{\rm{tot}}}}}\) is the reduced young’s modulus. The \({R}_{{{{\rm{tip}}}}}\) is measured as 7.5 mm. \({E}_{{{{\rm{tot}}}}}\) can be expressed by:

$$\frac{1}{{E}_{{{{\rm{tot}}}}}}=\,\frac{3}{4}\left(\frac{1\,-\,{\nu }_{{{{\rm{sub}}}}}^{2}}{{E}_{{{{\rm{sub}}}}}}+\frac{1\,-\,{\nu }_{{{{\rm{tip}}}}}^{2}}{{E}_{{{{\rm{tip}}}}}}\right)$$
(3)

where,\({\nu }_{{{{\rm{sub}}}}}\),\({E}_{{{{\rm{sub}}}}}\) and \({\nu }_{{{{\rm{tip}}}}}\), \({E}_{{{{\rm{tip}}}}}\) are the Poisson’s ratio and Young’s modulus for the substrate and the tip respectively78. The contact area \(A\) can be further approximated as51,

$$A=\,\pi \cdot {a}_{{{{\rm{Hertz}}}}}^{2}$$
(4)

Considering the fact that the current output is proportional to contact area with a linear coefficient of current density:

$${I}_{{{{\rm{SC}}}}}={J}_{{{{\rm{SC}}}}}\cdot A$$
(5)

Assuming the intrinsic parameter JSC varies as a function of velocity, i.e., JSC(v), and combining Eqs. 2–5, one can obtain:

$${I}_{{{{\rm{SC}}}}}=\pi \cdot {J}_{{{{\rm{SC}}}}}\left(v\right){\left[\frac{3}{4}\left(\frac{1-{\nu }_{{{{\rm{sub}}}}}^{2}}{{E}_{{{{\rm{sub}}}}}}+\frac{1-{\nu }_{{{{\rm{tip}}}}}^{2}}{{E}_{{{{\rm{tip}}}}}}\right)\cdot {R}_{{{{\rm{tip}}}}}\cdot F\right]}^{\frac{2}{3}}$$
(6)

From Eq. 6, it can be predicted that the ISC is proportional to F2/3. The solid lines in Fig. 5d show the fitting results based on Eq. 6, where the Poisson’s ratio for Ti and PDMS of 0.34 (\({\nu }_{{{{\rm{sub}}}}}\)) and 0.495 (\({\nu }_{{{{\rm{tip}}}}}\)) and Young’s modulus of 116.0 GPa (\({E}_{{{{\rm{sub}}}}}\)) and 2.1 MPa (\({E}_{{{{\rm{tip}}}}}\)) are used. It can be seen that the theoretical prediction is in good accordance with the experimental data of ISC vs F at all v. From the data fitting in Fig. 5d, the values of JSC(v) can be extracted. In Fig. 5e, JSC vs v is plotted, which is fitted by a second-order polynomial approach for approximation. It can be seen that as the v increases from 0.75 to 116 mm/s, the JSC increases from 0.27 to 1.72 mA/m2. Such a trend may be explained by the increasing frictional energy input expressed by (Fig. 5e):

$${E}_{{{{\rm{input}}}}}=\,\int \left(f\cdot v\right){{{\rm{d}}}}t$$
(7)

where f is the frictional force, the product of fv is the frictional power, and t is the time. According to the tribovoltaic effect theory, the more energy is input, the more intensive electronic excitation of electron-hole pairs is expected at the sliding interface, resulting in higher DC output. In order to explicitly explain the JSC vs v relationship, a deeper understanding of the tribovoltaic physical mechanism is needed in future work.

Discussion

Inspired by the human MR, a self-powered bionic tactile sensing (BTS) system was designed and developed based on the tribovoltaic effect. A layered structure was tailored and integrated with a robotic gripper, acting as a RA MR-like friction sensing element. In conjunction with SA MR-like normal force sensing, BTS system has been proved to be effective in providing DC output as input data for robotic control. In our demonstration, we have successfully shown the sensing and mitigation object slip from the robotic gripper under external linear pulling force or intrinsic gravitational force. A Hertzian contact mechanics model has also been used to reveal the dependency of DC output on the force and velocity, paving the way for future reinforcement learning-based control systems. The BTS’s ability to generate distinguishable signals corresponding to different applied forces and velocities underscores its potential for real-world robotic applications. The flowchart in supplementary information (Fig. S14) outlines a futuristic perspective of the comprehensive robotic control system. The system could utilize the tactile signals in the reinforcement learning policy to enhance grip stability and dexterity. By incorporating slip detection as an additional degree of freedom in trajectory planning, the system can also adapt to various object manipulation tasks with higher precision and reduced errors.

Methods

Materials

1.1% in H2O, surfactant-free, high conductivity grade Poly(3,4-ethylenedioxythiophene) polystyrene sulfonate (PEDOT:PSS), ethylene glycol (EG), isopropanol (IPA), ethanol, 99.6% pure titanium (Ti) foil were procured from Sigma-Aldrich. The spandex fabric substrate was procured from Echoine Store through Amazon. Sylgard 184 (PDMS) was procured from Sigma-Aldrich. PET-ITO film was procured from Sigma-Aldrich. 3D printing filament was procured from Prusa. Ecoflex-0030 was procured from Smooth-On Store through Amazon.

Fabrication of the BTS sensor

For conducting polymer ink preparation, mixture A comprises 25 g of the PEDOT:PSS mixed with 12.5 g of ethanol. Mixture B was composed of 0.512 g of EG and 7.5 g of IPA. The weight ratio of PEDOT:PSS: ethanol: IPA: EG = 100: 50:30:2.05. The EG is added, as it has shown to increase the electrical conductivity due to the restructuring of the PEDOT chains and removal of PSS shells increasing the charge carrier mobility and density79. The electrical conductivity of PEDOT:PSS can also be enhanced by the addition of other chemicals such as dimethyl sulfoxide (DMSO) (See Fig. S15 in Supplementary Information). Heating the mixture to above 90 °C removes the water, replacing it with EG molecules. Alongside, adding solvents such as isopropyl alcohol (IPA) to PEDOT:PSS has shown to decrease the size of the insulating PSS agglomerates and to develop a more uniform film morphologically along with changing the viscosity of the prepared ink. The IPA has also shown to increase the VOC and short-circuit current density (JSC) in PEDOT:PSS based photovoltaic cells80. Ethanol helps promoting a homogeneous dispersion of PEDOT and PSS by reducing the phase separation between PEDOT and PSS molecules81. The two mixtures A and B were combined and subjected to magnetic stirring for 48 h to achieve a smooth, homogeneous solution for better ink penetration into the fabric and uniform coating. For coating treatment, a 6 × 6 in. cut of pristine spandex fabric was dipped in the prepared ink solution. The fabric was then placed under vacuum for 15 min in a vacuum desiccator and cured in a vacuum oven for 1 h at 120 °C. This process of dip and dry coating was repeated 3 times in total.

For the integration of the electrodes, the PEDOT:PSS coated fabric (Fig. 2b) was cut into strips. The metal electrode of the fabric and the Ti foil were cut to required dimensions. Here, the junction between the PEDOT:PSS fabric and the Ti foil acts as a DC generator node. Both the cut PEDOT:PSS fabric and the Ti foil were then bonded together with a thin layer of adhesive. This was then placed on top of the capacitive sensor and encased with waterproof vinyl layer. The prepared BTS sensor was then placed on the fabricated composite finger. Lead wires for the sensor were prepared by applying Ag/AgCl paste and attaching wires for the reception of signals generated from the prepared sensor. The composite finger fabricated was made of 3D printed polylactic acid (PLA).

Material characterization of PEDOT: PSS-coated fabric

To verify the integrity of the ink coating on the spandex substrate, SEM and Energy Dispersive X-ray Spectroscopy (EDS) were performed using Focused Ion Beam Scanning Electron Microscope (FIB-SEM) - Carl Zeiss AURIGA CrossBeam.

Mechanical characterization

The mechanical characterization was performed using an F-105 model mechanical tester with IntelliMESUR® software to record the data with the force sensors FS05-05 manufactured by MARK-10. The tensile test jig was manufactured in-house using a Prusa MK4 3D printer and the fabric was attached to the mechanical tester. The lead wires were attached using Ag/AgCl paste, and the resistance was measured using a Keithley DMM6500 61/2-digit digital multimeter. Data for load and strain was collected from the IntelliMESUR® software.

DC power characterization

DC power characterization was performed using a linear actuator from Fourien. Inc and force gauge (Torbal). The PEDOT:PSS coated spandex fabric was fixed on a 15 mm diameter sphere made of PDMS sphere and the Ti foil was placed on the platform of the actuator. For the cyclic testing, the load was fixed at 4 N and sliding speed of 53.63 mm/s, and the data was collected using a Keithley DMM6500 61/2-digit digital multimeter. The I-V curve characterization was performed at different loads of 0.5, 1.0, 1.5, 2.0, and 3.0 in static conditions without sliding and to collect the data with a Keithley 2450 SourceMeter.

Robotic demonstration

Mitigation of slip was achieved by utilizing a control law, which works on the principle of increasing the grip force by modulating the servo motor (DYNAMIXEL XC330-M288-T) angle to grasp the object. The closed-loop feedback, used for the demonstration uses reference signal of no slip (Vref = 0). The BTS sensor provides a DC signal (Vout) of the relative motion between the object and the gripper. The disturbance to the system such as pulling force (Mark-10 F105 with FS05-10 force sensor) and gravity (0.26 N offset weight), induces slip between gripper and the object. The continuous analog signal generated by the BTS is converted to digital signal by NI-DAQ (NI-DAQ USB-6003). The error computed between the sensor signal and the reference signal is used by the control law. The control law processes the error and modifies the servo angle to increase the grip force.

$${{{\rm{Error}}}}=\left|{V}_{{ref}}-\,{V}_{{out}}\right|$$
$${{{\rm{Servo}}}}\; {{{\rm{Angle}}}}\; {{{\rm{Change}}}}=\,\left\{\begin{array}{cc}0\hfill & {error} < 30\,{mV}\\ {{{\rm{servo}}}}\; {{{\rm{angle}}}}+0.8^{\circ } & {error}\ge 30\, {mV}\end{array}\right\}$$
(8)

Robotic manipulation with compliant gripper system

The compliant gripper system utilizes variable stiffness to adjust the grip force independent from the finger position. In other words, we can modulate the force without moving the fingers. This is achieved by adjusting airgaps between permanent magnets that act as nonlinear springs. The gripper is equipped with a linear potentiometer to measure the airgap. The grip force in Fig. 4m is determined using the airgap and the data-driven model for the variable stiffness system as described and validated in our previous work76.

The slip detection in the BTS data is based on applying a threshold on the moving average of the previous 10 data points with a rectangular weight. This is equivalent to applying a low-pass FIR filter with a cut-off frequency of ~44 Hz. For the GelSight the average of absolute difference between the previous two frames of the image is used as a slip score (See Fig. S16 in Supplementary Information for more details). This calculation utilizes OpenCV’s absdiff function, optimized with SIMD acceleration and GPU execution using CUDA streams for maximum efficiency. The computational time is approximately 50 µs, eliminating the need for additional filtering. The system configuration used for data processing consists of a 12th Generation Intel i7 CPU (14 cores), an Nvidia GeForce RTX 4070 GPU, and 32 GB DDR4 RAM, ensuring high-speed execution. Slip is detected through simple thresholding of the computed score. Slip is detected through simple thresholding of the computed score.

Upon slip detection, the controller incrementally reduces the air gap by 1.3 mm per detected slip, modulating the grip force according to the following equation:

$${f}_{m}\left(d\right)=\frac{{P}_{1}}{{d}^{3}+{P}_{2}d+{P}_{3}}$$
(9)

Where d is the airgap that is equal to the initial airgap \({d}_{0}\) needed for minimum grasp and the incremented displacement after the kth slip:

$$d={d}_{0}+0.0013\,k$$
(10)

\({P}_{1},\,{P}_{2},\,{P}_{3}\) are determined and validated based on a data-driven model described in our previous work76.Their values are equal to 5.5 × 10-6 N·m3, 6.85 × 10−5 m2, and 2.22 × 10−7 m3.