Viability of low solar efficiency materials for photoelectrochemical separations via thermodynamic modeling

Abstract

Photoelectrochemical systems harness onsite solar energy to drive chemical processes, enabling improvements in sustainability and decarbonization. Photoelectrochemical systems have been extensively studied for reactions such as hydrogen production; however, competitive costs are difficult to attain due to the limited solar efficiency of low-cost photoelectrochemically stable materials. Building on this premise, we propose that applications that do not require high solar-efficiency materials to deliver meaningful throughput are needed for photoelectrochemical systems. Using rigorous thermodynamic modeling grounded in experimental data, we demonstrate the existence of such applications in chemical separations, which comprise processes critical to tackling global challenges in water treatment and resource recovery. Operating domains and scales at which photoelectrochemical separations utilizing low solar efficiency materials can be practical and cost-competitive against modular photovoltaic-electrochemical systems are identified. This study demonstrates that photoelectrochemical separations have a design space broader than classical applications, and establishes thermodynamic limits and targets, paving the way for real-world impact with photoelectrochemical technology.

Introduction

The electrification of chemical processes, including reactions, separations, and other processing steps, is essential to improve sustainability and promote decarbonization by reducing energy consumption¹. Many approaches to process electrification are areas of active study, including the use of electrochemistry. In particular, the increased selectivity and control achieved through the use of electrochemistry to drive processes such as separations can also be important to address environmental challenges and aid in the recovery of critical resources to drive the energy transition^2,3. However, challenges in ensuring grid access and resilience, maintaining low transmission costs, and the continued sourcing of electricity from non-renewable sources make true sustainability difficult to achieve solely through process electrification^4,5,6,7.

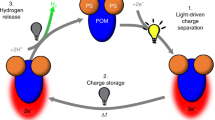
In this context, the development of electrochemical methods coupled to onsite renewable energy production, primarily solar, is one important approach². Two competing approaches are known: coupled photovoltaic-electrochemical (PV+EC) systems and integrated photoelectrochemical (PEC) systems (Fig. 1). In PV + EC, solar energy is converted to electricity via photovoltaic (PV) cells, which then power electrochemical (EC) operations (Fig. 1a, b). In PEC, photoactive electrodes directly convert solar energy to electrochemical energy within the same unit (Fig. 1c, d). PEC methods have been the subject of extensive research for hydrogen production and other reactions because of their perceived ability to have lower capital and resource requirements due to a reduction in the number of unit operations, ancillary systems, and process footprint compared to PV + EC⁸. However, technoeconomic analyses reveal that state-of-the-art PEC systems may counterintuitively be more expensive due to faster-than-expected decreases in PV costs and higher-than-expected PEC equipment costs^9,10. To a lesser extent, this difference in cost is a result of technology maturity and scale¹¹, which are themselves rooted in the inherently higher versatility and applicability of PV systems across electrified processes. More significantly, PEC equipment costs are rooted in fundamental materials and physics-based limitations.

Fig. 1: Comparison of photovoltaic-electrochemical (PV + EC) systems and photoelectrochemical (PEC) systems for separations.

a PV + EC systems consist of separate but connected PV and EC systems, where the PV system absorbs sunlight to produce the electric current that then drives the electrochemical separation in the EC system. b Internally, the EC system consists of a working electrode (WE) and counter electrode (CE), of which at least one electrode is functionalized with a redox interface. Current from the PV system charges the interface, which then selectively binds ions in the solution flowing between the electrodes. c On the other hand, solar-to-current conversion and the electrochemical process occur in a single unified unit operation that absorbs sunlight and also performs the separation. d Internally, a semiconductor layer between the conducting electrode surface and the redox interface absorbs light to produce charge carriers that separate within the electrode to charge the interface. The redox functionalization in (b, d) takes the form of a polymer coating², though other implementations are also possible²⁵. Batteries may be included in both PV+EC and PEC systems to store excess energy and modulate cell potentials.

PEC technology faces limitations in traditional chemical synthesis applications due to the balance between: (a) the overall efficiency (η_SC = η_S ⋅ η_EC), which is the product of the solar efficiency (η_S) and the electrochemical energy efficiency (η_EC); and (b) the amortized cost of equipment^9,10,12. The power density of sunlight is low relative to process needs in traditional PEC applications like water splitting, which are energy intensive (energy consumption of at least 237.2 kJ/mol)¹³, which combined with the cost of photoactive and catalytic materials, makes high solar efficiency critical. High-efficiency semiconductors like silicon can deliver high solar efficiencies but undergo photocorrosion in PEC cells, limiting lifespan and increasing costs^14,15. These same semiconductors do not face this restriction in PV solar cells, achieving higher efficiency at lower costs. Inexpensive photocorrosion-resistant semiconductors, mainly transition metal oxides, are the most promising for practical PEC applications, but exhibit much lower solar efficiencies, limiting throughput and increasing product costs¹⁶. Additionally, fundamental thermodynamic limitations due to fixed thermoneutral reaction potentials mean that PEC solar efficiencies in traditional applications are always lower than PV solar efficiencies, even with the same photoactive material^17,18.

These practical considerations result in a more adverse cost-efficiency trade-off for PEC systems compared to PV + EC systems. A significant amount of research aims to overcome this trade-off by increasing the solar efficiency of inexpensive and stable semiconductors through dye-sensitizers, multijunctions, doping, and structural modifications, or by reducing the cost of high solar efficiency semiconductors through improved manufacturing processes and increased resistance to photocorrosion, which can be challenging^8,13,15,19. Alternatively, focusing on low-energy applications of PEC technology, where efficiency is relatively unimportant, can overcome this trade-off more easily if such applications can be shown to exist. In such cases, the low solar efficiency of existing photocorrosion-stable semiconductors may not hinder PEC implementation, allowing practical value to be obtained from current materials. Moreover, since solar efficiency is relatively unimportant, it can be intentionally sacrificed by using inexpensive and lower quality materials in lower cost PEC hardware to reduce costs (such as by using amorphous metal oxides rather than crystalline silicon), enabling PEC technology to better compete with PV+EC processes. Here, we show that practical applications that satisfy these constraints can indeed be found in the field of electrochemical separations.

Separation and purification processes account for more than 5% of United States energy consumption—a result of both the energy intensity of each separation process, and the number of separation process deployed—with a strong push towards replacing energy-intensive methods like distillation with low-energy alternatives such as adsorption^20,21. Electrochemical adsorption/desorption (electrosorption) processes have been shown to be less energy intensive than classical adsorption, while also offering greater control over selectivity^2,22,23. Selective separations are important in environmental applications and resource recovery. A typical PEC separation process is shown in Fig. 1c, d, and involves a photoactive working electrode that converts absorbed light into excited charge carriers². These carriers are separated inside the electrode due to an electrochemical potential gradient, created by band bending, applied potentials, and other phenomena, and one group of carriers is injected into a redox-active interface, which becomes charged. The charged interface is designed to selectively bind ions from within a solution to be treated, which flows between the electrodes²³. The working electrode can be regenerated, and bound ions released either by stopping light exposure (free regeneration), or by also applying a reverse-bias to reverse interface charge (driven regeneration)². Simultaneous adsorption/desorption strategies are also known²⁴. PEC separations have shown promise in proof-of-concept desalination and wastewater treatment, but studies indicate that these applications are limited by efficiency like traditional PEC applications, resulting in low throughput^24,25.

However, the field of separations is broader than the applications currently attempted with PEC systems. As we show subsequently, many separations that theoretically satisfy the low-efficiency requirement for PEC to be more cost-competitive with PV+EC have been successfully demonstrated using electrochemical systems, but remain unexplored in the context of PEC technology. Separations may be categorized into treatment (removing undesirable solutes) and extraction (extracting useful solutes), though certain processes may combine the two. Applications also vary considerably based on the concentration of the solute, from high concentration processes like desalination to low concentration processes like removing trace per- and polyfluoroalkyl substances (PFAS) from water (Supplementary Table 1)^22,26. Here we present a thermodynamic model rooted in first principles and corrected for losses in real systems to provide greater fundamental understanding by connecting initial concentrations, process conditions, goals, and scales, with PEC energy and efficiency requirements. We show that PEC separations have distinct thermodynamic constraints and design rules in comparison with traditional reaction-based PEC applications, and can leverage a broader viable parameter space. The proposed model is then employed to identify systems and application areas in PEC separations that can satisfy process goals even at low solar efficiencies. Finally, the model is applicable to evaluating both high concentration and low concentration PEC separations.

We begin by modeling the energy consumption in general separation processes. We start with the minimum energy requirement predicted by thermodynamic free energy changes, and add corrections for various losses. Then, we turn to the amount of energy that can be extracted from sunlight in a given amount of time. Detailed-balance limits based on the Shockley-Queisser approach²⁷, used to guide research in PV and traditional PEC¹⁷, are derived for PEC separations and adjusted for losses. We show the solar design envelope for PEC separations is much broader than for traditional PEC applications and introduce a separator-semiconductor matching strategy that allows PEC separations to operate at the same solar efficiency as PV (which is known not to be possible in the context of water splitting or other reaction thermodynamics-based applications^17,18). Combining separation energy requirements with process throughput, we establish limits on solar and Faradaic efficiencies for practical applications, demonstrating that high solar efficiency is not critical for many real-world separations under practical conditions, and guiding the design of PEC separations systems at scale. Finally, we discuss how the absence of a need for high solar efficiency can help limit costs in PEC systems, enabling them to better compete with PV + EC.

Results

Energy consumption in separations

The minimum thermodynamic work required in any separation (W_sep) is given by the change in Gibbs free energy in the process (Eqs. (1)–(4))²⁸. Note that the dependence of the work requirement on concentration and other process parameters here is distinct from the reaction thermodynamics that governs applications like water splitting. Consider a typical water treatment process in which a stream containing a contaminant at concentration c_initial is to be treated to reduce this concentration to 0.1c_initial, while rejecting the excess contaminant in 10% of the incoming stream (Supplementary Note 1 and Supplementary Table 1). The minimum specific energy consumption, per volume of treated water obtained, is shown in Fig. 2a. The thermodynamic work requirement (W_min) at low contaminant concentrations is up to 15 orders of magnitude lower than that for water splitting. In this regime, when c_initial < 1 ppm, the contaminants are called micropollutants, and include species like lead and PFAS. It is important to eliminate these substances from water due to their impact on human and environmental health, and there is a major policy push towards the same^29,30,31,32. Energy requirements increase rapidly at higher c_initial, but remain lower than water splitting.

Fig. 2: Thermodynamic and corrected work requirements for water treatment and resource extraction.

a Thermodynamic minimum and adsorption/desorption swing and Nernstian corrected work requirement (Supplementary Notes 1–4, assuming typical parameter values shown therein) for water treatment, also indicating increase in work required as thermodynamic efficiency η_T decreases. Water treatment spans numerous applications with varying initial concentrations (which are similar in magnitude to final concentrations), shown here for the elimination of PFAS, lead, copper, nitrates, and salt from brines (Supplementary Table 1)^42,53,54,55, but energy requirements are always much lower than water splitting. (These curves use the molecular weight of sodium chloride to report molar quantities in mass units; see Supplementary Fig. 1 for the negligible effect of molecular weight on these curves) b, c Flow-corrected thermodynamic work requirements for water treatment at the household (b) and municipal (c) scales, and increases in those requirements with decreasing Faradaic efficiency, η_F, compared to water splitting. Note that the work requirement is normalized by the volume of the dilute product stream L_dilute in (a–c), which is the valuable stream of interest in treatment applications. d Thermodynamic, swing-corrected, and swing-and-flow-corrected work requirements in resource extraction applications, and corresponding increases due to Faradaic losses, also compared to water splitting. Resource extraction applications involve the enrichment of species across a wide range of concentrations spanning multiple unit operations (shown here for the extraction of rare earth elements (REEs) from brines and municipal waste, platinum group metals (PGMs) from mine tailings, lithium (Li) from brines and battery waste, and recovery of nitrogen/phosphorus from urine (nutrient recovery); see Supplementary Table 1)^{36,56,57,58,59,60,61,62}. Note that the work requirement is normalized by the volume of the concentrated product stream L_concentrate in (d), which is the valuable stream of interest in resource extraction applications.

The actual energy consumption in a real process is always higher than the thermodynamic prediction due to energy losses arising from system imperfections (avoidable losses) and inherent limitations in the process being implemented (unavoidable losses). It is important to account for these losses to assess real energy consumption, which is known to be significantly (>15%) higher than thermodynamic requirements in water splitting¹³. Unavoidable losses in electrosorptive separations include increases in energy consumption due to: (1) non-ideal mixing, (2) low solute concentrations (a Nernstian correction), (3) non-simultaneous production of concentrated and dilute streams (adsorption/desorption swing losses), including losses at the counter electrode, (4) performing the separation in a finite amount of time (flow losses), and (5) side reactions, like water splitting or binding competing ions, which may not be possible to eliminate. We consider losses due to side reactions and system imperfections in terms of empirical Faradaic efficiencies in subsequent sections. The non-ideal mixing correction is shown to be negligible in Supplementary Note 2. The Nernstian correction is small but important to consider relative to total work at low c_initial (Supplementary Note 3, Supplementary Fig. 2). The swing correction is also small (Supplementary Note 4), and the net effect of all these corrections maintains the total work requirement at a level greatly lower than that for water splitting (Fig. 2a). Data from lab-scale batch systems in which side reactions are appropriately suppressed and system imperfections are minimized should approach the thermodynamic prediction in 2a, and can be seen to do so to validate our approach (Supplementary Table 3 and Supplementary Fig. 3).

Corrections due to flow can, however, be large (Fig. 2b, c). These corrections depend on the scale of the process being considered, and we consider two typical scales for water treatment between which most operations would be expected to lie (Supplementary Note 5). Household treatment (flowrate Q = 0.05 L/s, contact time τ = 60 s) is representative of an under-the-sink filter³³, while municipal treatment (Q = 20 million gallons/day, τ = 30 min) is representative of a drinking water treatment plant in a U.S. city^34,35. The flow correction consists of a resistive correction due to finite current flow and a fluid flow-based correction due to the energy consumed in pumping the fluid between the electrodes (Eqs. (5)–(6)). At smaller inter-electrode spacing δ, the fluid flow-based correction dominates due to higher pressure drops, while the resistive correction dominates at larger δ due to longer current path-length. Therefore, there exists an optimal spacing, which is a function of Q, τ, and c_initial, and the values predicted by the model are similar to those obtained experimentally (Methods, equation (7), Supplementary Note 5, Supplementary Table 2, and Supplementary Fig. 4). The total flow-based correction, though significant, also does not increase separation work requirements beyond water splitting, and requirements at low c_initial remain more than 10 orders of magnitude lower.

Figure 2d shows the thermodynamic work requirement and corrected work requirements for resource extraction (Supplementary Notes 1–4). Our analysis considers resource extraction applications where the goal is the (selective) enrichment of a certain species. Those applications which involve selective separations without enrichment are always feasible, as apparent from subsequent sections and equation (4). The extraction objective is to extract 90% of the resource in the initial solution, producing a concentrated solution with solute mole fraction 0.01 (5.85 g/L in Fig. 2d), and is representative of real systems (Supplementary Table 1). In practice, resource extraction applications involve multiple unit operations, each of which upconcentrates the stream to a certain extent, so work requirements should be interpreted in terms of the position of the initial concentrations relative to the target concentration shown here. Note that the specific energy consumption here is normalized by the volume of the concentrated stream (the extraction objective), and not the dilute stream as in water treatment. Flow corrections are applied using Q = 20 million gallons/day and τ = 2 h, based on prior work³⁶ (Supplementary Note 5). The work requirement in resource extraction is also seen to be at least 3 orders of magnitude lower than water splitting.

Solar efficiency limits

It is desirable for the separation energy requirement to be supplied entirely by sunlight. As before, we first model the work that can be extracted from solar illumination as a thermodynamic limit, similar to the analysis of the Shockley-Queisser limit for PV²⁷, to which corrections are then applied to estimate real values for work and efficiency requirements. The analysis follows a similar approach as prior analyses, beginning with the PEC cell equation and illuminated diode equation, which link the semiconductor bandgap E_g, the potential across the semiconductor V_PV, and the resulting current density j (Methods, Eqs. (8)–(11), Supplementary Note 6 and Supplementary Fig. 5)^17,27. We assume complete absorption of photons above the bandgap and purely radiative recombination as is standard in such calculations^17,27. Our analysis is limited to single junctions in the absence of solar concentrators to compare our results with benchmarks^17,27 and limit costs for applications in water treatment, which are very cost-sensitive and do not produce a high value product³¹.

One of the principal limitations of PEC water splitting is the need to maintain a potential of at least 1.23 V (the thermoneutral potential of the oxygen evolution reaction relative to the standard hydrogen electrode) at the anode. In PEC separations, the potential required is that at which the redox-active interface becomes charged. Since redox-active interfaces can be constructed using diverse chemistries, each with a different redox potential, the potential required is no longer a fixed quantity but a parameter that can be tuned²³. Importantly, this choice of potential is agnostic to the application. Changing the redox potential in traditional PEC requires us to change the target reaction (i.e., the application area) or introduce intermediate reactions, but no such requirement exists for PEC separations. The interface will bind charged ions as long as it is itself charged, regardless of the potential at which the charging process occurs, though the rate and extent of binding may be affected. We call this potential the binding potential ϕ_b. As seen in Fig. 3a, b, reducing ϕ_b below 1.23 V allows greater current densities across all bandgaps, while peak solar energy conversion efficiencies increase and then decrease. The tunability of the redox interface therefore endows PEC separation systems with greater flexibility than traditional PEC applications. For instance, the lower energy requirements discussed in the previous section can potentially allow us to work at lower solar efficiencies by using small ϕ_b to obtain larger current densities and faster kinetics.

Fig. 3: Solar energy conversion in PEC separations systems using a single junction without the use of solar concentrators.

Theoretical current density (a) and corresponding efficiency (b) that can be obtained from the semiconductor in a PEC separations system (Eqs. (10)–(11)), as a function of bandgap, and shown for multiple values of the redox potential of the interface (Fig. 1d). c, d The redox potential which should be used for maximum solar energy conversion (left, (c)), the corresponding current density (right, (c)), and the corresponding conversion efficiency η_S (d), all as functions of the semiconductor bandgap E_g. Detailed balance limits are those calculated using the Shockley-Queisser approach^17,27. The entropy-limited efficiency is obtained by correcting the detailed balance limit for entropic overpotential losses required by the second law of thermodynamics as derived in prior work^38,39,40 and described in Supplementary Note 7. Subsequent corrections assuming practical limits on material properties for high-efficiency and earth-abundant materials (Supplementary Note 8) lead to a further reduction in maximum solar efficiency as in prior work¹⁷. The maximum solar efficiency values after each correction are shown in d. Note that the lack of smoothness in computed curves is an artifact of noise in the solar spectrum.

The optimal value of ϕ_b as a function of bandgap is obtained to determine the maximum solar efficiency (Eq. (10)). Figure 3c shows an approximately linear dependence between ϕ_b,opt, and E_g, allowing us to introduce the principle of separator-semiconductor matching: for every semiconductor, there exists an optimal redox potential, and the choices of interface chemistry and semiconducting material are therefore coupled to each other in optimum PEC separation system design. This principle is analogous to the existence of an optimum potential at which a PV solar cell should be operated to obtain maximum solar efficiency. In fact, ϕ_b plays an identical role as this PV potential in Eqs. (10)–(11), leading to the overall efficiency limit shown in Fig. 3d having a global peak exactly at the Shockley-Queisser limit. As such, PEC separations do not suffer from the additional thermodynamic penalty as water splitting PEC or photochemical systems derived in prior work^17,18, and can theoretically extract solar energy at the same efficiency as PV solar cells (compare the efficiency at ϕ_b = 1.23 V in Fig. 3b, which represents the optimal PEC water splitting solar efficiency derived in prior work¹⁷, with the peak efficiency in the detailed balance limit in Fig. 3d, which is the optimal PEC separations solar efficiency).

The additional thermodynamic penalty that applies to classical PEC and photochemical systems arises due to the inherent mismatch between the optimum potential that must be maintained across a semiconductor to maximize solar efficiency (a function of the solar spectrum), and the thermoneutral potential of the reaction which consumes or stores the absorbed solar energy³⁷. If one chooses to operate at a potential optimized for solar efficiency, one may potentially not exceed the thermoneutral potential of the reaction to be driven. Similarly, if one chooses to operate at or above the thermoneutral potential of the reaction to be driven, one may end up operating at a potential at which solar efficiency is low. Though strategies like the use of redox mediators can reduce the magnitude of this thermodynamic penalty relative to PV solar cells using the same light-absorbing materials, they cannot eliminate it entirely across all potentials³⁷. However, chemical separations have no well-defined thermoneutral potentials. The separation may be driven effectively regardless of the potential used to charge the electrode interface, and we may design an interface that can be charged at a potential that maximizes solar efficiency without restricting the performance of the separation step. The absence of a well-defined thermoneutral potential for the target process, combined with the tunability of the redox potential of the interface, lead to the lack of a thermodynamic penalty relative to PV solar cells that is described here.

As before, the theoretical efficiencies derived here must now be corrected for losses in real systems. We consider three such corrections here: (1) a theoretical entropy-based correction that arises out of additional solar energy conversion constraints imposed by the second law of thermodynamics, as derived in prior work (Supplementary Note 7)^38,39,40; and additional empirical corrections (beyond the baseline entropic correction) for (2) real high-efficiency systems, and (3) those built using earth-abundant materials. The latter corrections are constructed using estimates for potential and current losses in real systems based on the methodology introduced by Fountaine and others (Supplementary Note 8)¹⁷. These corrections do not reduce the solar efficiency by more than an order of magnitude, and the peak efficiency in each case (Fig. 3d) is higher than the corresponding limits for PEC water splitting^17,18. We compare the solar efficiencies predicted here to experimental values to validate the model (Supplementary Table 4 and Supplementary Fig. 6).

Overall efficiency requirements

In summary, the previous analyses show that PEC separations require less energy than traditional PEC applications like water splitting, while also being able to convert sunlight into electrochemical energy more effectively. Here, we combine solar efficiency and work requirements to obtain the operating regime for PEC separations in terms of overall efficiency. If the insolation (power flux of sunlight) ψ is received on an electrode of area A, for a PEC system with contact time τ, the total useful power obtained from sunlight is W_S = η_SCψA. W_S drives the separation process, which requires a power W_sepQ. When η_F = 1, ${W}_{S,min}={W}_{sep}^{({\eta }_{F}=1)}Q$ is the minimum power that must be obtained from sunlight. The overall efficiency must be at least ${\eta }_{SC,min}={W}_{sep}^{({\eta }_{F}=1)}Q/\psi A$ to obtain the minimum required power for separation due to the finite power density of sunlight, based on energy matching. On the other hand, the upper bound for η_SC is the thermodynamic solar efficiency limit (η_SC,max = η_S when η_F = 1). Figure 4a–c shows the upper and lower bounds derived here using flow-corrected thermodynamics, with the operating regime lying between them. In particular, the operating regime is significantly broader at lower c_initial for water treatment. Current matching or charge balancing can be satisfied at all points within this operating domain, since the total charge flux from the semiconductor exceeds the total ion flux under these conditions (see attached source code). Note that the operating regime restrictions shown here apply only to PEC and not to PV+EC, wherein the insolated area is decoupled from the area of the unit operation in which the separation is performed.

Fig. 4: Overall conversion efficiency operating envelope for PEC separations.

a–c The minimum overall efficiency for the separation to be feasible, η_SC,min (solid blue lines), and the maximum overall efficiency attainable, η_SC,max (solid orange lines), shown for water treatment at the household (a) and industrial (b) scales, and resource extraction (c). Increases in η_SC,min and reduction in η_SC,max as a function of decreasing Faradaic efficiency η_F are also indicated using dashed blue and orange lines, respectively. Note that these orange dashed lines follow the solid orange lines at lower c_initial before sharply curving downwards at higher c_initial in (a, b). d–f The corresponding limits on the semiconductor bandgap that may be used, as a result of finite current draw (i.e., current matching requirements, with the appropriate consideration of Faradaic efficiency) are shown for operation at the three scales of operation, along with decreases in these limits due to decreases in Faradaic efficiency.

A reduction in the Faradaic efficiency results in an increase in the total work required, raising the lower bound η_SC,min (Fig. 4a–c). Simultaneously, as required by current matching, the total current density that the semiconductor needs to provide also increases to compensate for Faradaic losses. However, the achievable current density is itself limited by the semiconductor bandgap because only those photons with energy greater than the bandgap energy are absorbed and converted into free charge carriers (Supplementary Fig. 5). As a result, there exists a maximum allowable bandgap beyond which a current density sufficient to drive the separation at a given throughput cannot be obtained for a given η_F and c_initial (Fig. 4d–f). An upper bound on the allowable bandgap and a lower bound on the required current density to satisfy current matching constrain the optimal ϕ_b for maximum solar efficiency discussed previously (Fig. 3c, d). This effect reduces the maximum solar efficiency and lowers the upper bound η_SC,max (orange dashed lines in Fig. 4a–c; also see provided source code). The net effect of Faradaic losses is the shrinking of the operating regime. In fact, as seen in Fig. 4a–c, curves for η_SC,min and η_SC,max intersect at particular values of c_initial, which shift as a function of η_F. Naturally, this η_F is the minimum Faradaic efficiency for which a PEC separation is viable at c_initial.

Faradaic efficiency and competing processes

The minimum Faradaic efficiency required for a separation to be viable, η_F,min, is shown in Fig. 5a, with higher Faradaic efficiencies essential to treating concentrated water streams or for resource extraction, but unimportant for low-concentration water treatment. Losses in Faradaic efficiency must occur through side reactions that divert a portion of the available charge carriers, and depend on the composition of the initial stream (Supplementary Note 9). The suitability of PEC separations does not solely depend on the value of the minimum Faradaic efficiency; one must consider the value of Faradaic efficiency that is achievable for a given c_initial, and whether that is higher than the minimum required. We therefore consider the Faradaic efficiencies that may be obtained in real systems (“Methods” and Supplementary Note 9) through a phenomenological model that assumes a single side-reaction in which a background species with concentration c_background participates, and K_s is the selectivity towards the binding of target ions (Eqs. (12)–(13)). Figure 5b shows Faradaic efficiency against c_initial/c_background, with higher selectivities (K_s ~ 10¹⁰) common when the competing reaction is water splitting, and lower selectivities (K_s ~ 10¹) common when competing with background ions (Supplementary Note 9). The x-axis of Fig. 5b ranges from the elimination of a ppt-level contaminant like PFAS in a background as concentrated as seawater (lowest c_initial/c_background), to desalination in the presence of a ppt-level competing contaminant (highest c_initial/c_background). Though one might expect from Fig. 5b that most Faradaic losses are due to competing ions when c_initial is low, numerous applications involve a c_background on the order of c_initial or lower. On the other hand, c_background = c_w, the constant molar concentration of water, when the competing reaction is water splitting, and c_initial/c_background decreases rapidly with decreasing c_initial. As such, water splitting can be a greater contributor to Faradaic losses at very low c_initial, despite the much lower selectivity for the water splitting reaction. Corresponding losses in η_EC are shown in Supplementary Fig. 7.

Fig. 5: Faradaic efficiency limits in PEC separations.

a The minimum Faradaic efficiency η_F,min for a separation to be viable at any given initial concentration. b Faradaic efficiency values η_F that may be expected assuming losses of Faradaic efficiency from competing reactions with background species with concentration c_background, shown for multiple selectivities (K_s). c, d The maximum background concentrations that are tolerated in obtaining the minimum Faradaic efficiency in a, shown for competition with water splitting (c) and background ions (d). Shaded regions indicate the domain of thermodynamic viability.

It is now meaningful to examine the maximum background concentration that may be tolerated in real systems by combining information about the necessary and achievable Faradaic efficiencies, requiring η_F > η_F,min. Figure 5c shows the maximum allowable background considering a water splitting side-reaction, and Fig. 5d considers a competing ion-binding side-reaction. The domain in which c_{background,max} > c_w in Fig. 5c is the domain of feasibility for a real system (full range of c_initial for treatment, and c_initial > 0.1 g/L for extraction). Further, the competing ion concentration limits in Fig. 5d are also quite high within the domain of feasibility, suggesting that most feedstocks may be used without pretreatment in the applications considered in this work, though side reactions still affect the operating regime. As such, the suitability of PEC systems is not limited by Faradaic efficiencies, provided they are suitably constructed, but by solar efficiency requirements and cost, as we now discuss.

Low solar efficiency PEC separations

The overall efficiency requirements shown in Fig. 4, at given values of Faradaic efficiency (which may be extracted from Fig. 5b for known values of the background concentration and selectivity), reduce to limits on solar efficiency for a given PEC separation to be viable or feasible (i.e., the minimum required efficiency is lower than the maximum attainable efficiency). The incorporation of electrochemical energy losses in the work requirement yields limits on solar efficiency rather than the overall efficiency in Fig. 4. In Fig. 6, we consider the range of solar efficiencies for thermodynamically viable systems for municipal-scale water treatment and resource extraction. The corresponding operating regime for household systems is shown in Supplementary Fig. 8. The minimum required solar efficiency is constructed using the fully corrected thermodynamic work requirement, accounting for non-ideal mixing, swings, Nernstian effects, flow corrections at a municipal/industrial extraction scale, and competing reactions with Faradaic efficiency varying across concentrations as predicted in Fig. 5b for a water-splitting side-reaction (K_s = 10¹⁰, as when the redox interface uses ferrocene, a common material in these applications)^2,23. We also consider the case of an imperfect system with avoidable energy losses that can increase work requirements to those seen in real experiments (minimum solar efficiency requirement shown using dashed lines in Fig. 6) (Supplementary Table 3 and Supplementary Fig. 3). Incidental losses to minor competitive binding are built into this value. The maximum solar efficiency limit of the operating regime is set at one-tenth of the entropy-corrected solar efficiency limit for earth-abundant materials (capping η_S at approximately 1%) to model inexpensive, well-studied, photocorrosion-resistant semiconductors like titanium dioxide. This restriction implies that the regime of viable PEC separations shown in Fig. 6a,b focuses on those applications which hold the greatest promise in lowering PEC cost relative to PV + EC, since a major limitation of current PEC methods has been the challenge in developing inexpensive photocorrosion-resistant high-efficiency semiconductors, as previously discussed.

Fig. 6: Solar efficiency limits and costs for feasible PEC separations using low-solar-efficiency single-junction semiconductors.

Viable solar efficiencies for water treatment at the municipal scale (a) and resource extraction involving enrichment (b), with minimum solar efficiency (solid blue/purple lines) and maximum solar efficiency (orange) limits fully corrected for losses. Dashed lines (avoidable losses) indicate the minimum solar efficiency requirements if the system is not appropriately designed and manufactured to eliminate avoidable losses through pathways such as contact resistances. Shaded regions, bounded by the minimum and maximum solar efficiency curves, indicate the regime of thermodynamically viable PEC separations, spanning those concentrations for which the minimum required efficiency (blue/purple) is lower than the maximum attainable efficiency (orange). Black vertical lines indicate the maximum concentration at which water treatment is viable (a) or minimum concentration at which resource extraction is viable (b). Water treatment spans numerous applications with varying initial concentrations, shown here as in Fig. 2 and Supplementary Table 1^42,53,54,55. Resource extraction applications involve the enrichment of species across a wide range of concentrations spanning multiple unit operations, shown here as in Fig. 2 and Supplementary Table 1)^{36,56,57,58,59,60,61}. Capital costs of PEC and PV+EC separations systems for municipal-scale water treatment to eliminate a contaminant with c_initial = 10 ppb (c) or c_initial = 1 g/L (d). Bars on the left show contributors to overall system cost, and those on the right show contributors solely to the photoactive components of the PEC and PV + EC systems (BoS Balance of system costs); see Supplementary Note 10 and Supplementary Tables 5–6. Source data for (c, d) are based on Supplementary Data 1 and also provided as a Source Data file.

The maximum attainable solar efficiency is independent of concentration, though the minimum solar efficiency required is a strong function of c_initial (Fig. 6a, b). As seen in Fig. 6a, minimum solar efficiency requirements for water treatment applications are very low at low c_initial (as low as η_S = 10⁻⁵ at c_initial = 1 ppb). Even when avoidable losses and system imperfections are considered, the η_S required is lower than 0.1% for ppt-ppm level water treatment, though seawater desalination applications are no longer feasible, with the minimum efficiency required exceeding the maximum attainable efficiency at high c_initial. The efficiency requirements at low c_initial may be further reduced by improving the suppression of water splitting (Supplementary Fig. 9). However, at high c_initial, water treatment is limited by solar efficiency due to the increased thermodynamic work requirements (Fig. 2 and Supplementary Fig. 9). These efficiency limitations at high c_initial have previously been observed experimentally in PEC desalination^24,25, and make it challenging to identify an appropriate semiconductor. On the other hand, Fig. 6b indicates a region of feasibility when c_initial > 1 g/L for resource extraction. This regime of interest includes the final step in enrichment processes, but also implies the feasibility of preconcentration steps involving small changes in concentration (since work requirements depend on c_initial only relative to the target concentration in equation (4)). These resource extraction applications involving enrichment up to one order of magnitude in concentration do not face solar efficiency limitations, but applications involving greater enrichment are limited by solar efficiency requirements due to increased thermodynamic work requirements.

We now turn to the capital costs of PEC systems used to drive separations that are not limited by a need for high solar efficiency, i.e., low initial concentration water treatment, or high initial concentration resource extraction. Figure 6c shows the cost breakdown of a PEC and PV+EC separations system determined as described in Supplementary Note 10 and Supplementary Tables 5–6 based on prior frameworks^9,41. Note, however, that certain design decisions in this work are distinct from those in prior work on hydrogen production^9,41, due to the inherent difference in the economics of hydrogen production (driven by sales) and water treatment (driven by regulations). PEC and PV + EC equipment are sized to treat water at the same throughput, which is representative of municipal-scale water treatment. Equipment sizes are limited by electrochemical ion transport limitations, with the size of the PEC system being identical to the size of the EC component of the PV + EC system. These components are sized using the previously introduced optimum electrode spacing, enabling us to compare the lowest energy (and hence, lowest cost) PEC system with the lowest cost PV + EC system for the given throughput. Furthermore, the inherent advantages of the PV + EC system, i.e., separate sizing of PV components and power conditioning to enable the PV and EC components to individually operate at their optimal power points, are considered in the model.

The cost of photoactive components (bars on the right) is seen to be small compared to the total cost of the system (bars on the left), due to the low solar energy requirement, allowing the use of thin-film low-efficiency semiconductors in the PEC system, and small commercial PV modules in the PV + EC system. Inexpensive photoactive components and the absence of membranes to separate hydrogen and oxygen make both systems less expensive than for water splitting^9,41. The total PEC cost is seen to be lower than the PV + EC cost due to differences in balance of system (BoS) costs associated with the photoactive components. PEC BoS costs are built into the overall module, while PV BoS costs in a PV + EC system add on to the BoS costs for the EC module. A similar difference in BoS costs was noted for water splitting systems in prior work⁴¹, though this difference may be offset by other costs, such as increased semiconductor costs in PEC systems, making them more expensive than PV + EC⁹. However, the low solar efficiency requirement in the separations applications proposed here enables the use of low-cost thin film semiconductors like titanium dioxide, that can be less expensive than commercial PV modules, even when the additional cost of fabrication in PEC systems is considered (Supplementary Note 10). As such, the low solar efficiency requirement can allow BoS cost reduction to more than offset additional PEC costs, enabling PEC separation systems to be less expensive than PV + EC systems. On the other hand, semiconductor costs in PEC increase greatly at high c_initial (Fig. 6d) due to the increase in the minimum solar efficiency required (Fig. 6a), resulting in an inability to use low-cost low-solar-efficiency semiconductors, and compounded by thermodynamic limitations on PEC solar efficiency (described above), bandgap limitations and a lack of economies of scale (Supplementary Note 10). As seen in Fig. 6d, the increase in PEC semiconductor cost for systems with a high solar efficiency requirement more than offsets in BoS savings that PEC may achieve over PV+EC. Uncertainty in the differences between PEC and PV+EC system costs is calculated as described in Supplementary Note 10 and shown in Supplementary Fig. 12, and does not affect these overall findings. Therefore, the low-solar-efficiency requirement is critical to making PEC more cost-competitive.

Discussion

In summary, PEC separations are distinct from traditional reaction-based PEC applications, exhibiting a theoretical potential for higher solar efficiencies coupled with a lower solar efficiency requirement. PEC water treatment at initial concentrations ranging from  <1 ppt to approximately 1 g/L and including applications like PFAS, lead, copper, and nitrate removal for PEC water treatment^{42,43,44,45,46} is practically feasible using currently known materials, as the solar efficiency requirements are very low. Similarly, PEC resource extraction is feasible with practical throughput at initial concentrations > 1 g/L (the final enrichment step), or in preconcentration steps involving enrichment within one order of magnitude, for applications like amino acid purification⁴⁷, nutrient recovery/urine revalorization⁴⁸, lithium recovery from battery waste or brines, and purification of rare earth elements and platinum group metals. Further broadening of the design space may be achieved by relaxing the requirements for separation throughput as appropriate in specific contexts, such as in the case of high-value resource extraction. The low solar efficiency requirement in the regimes of interest can limit costs and help PEC systems be more cost-competitive to deliver real-world impact. These applications can also support the commercialization of low-cost low-efficiency semiconductors which might not otherwise be considered suitable for traditional PEC applications. Indeed, the low solar efficiency requirements predicted in this work must also be considered when interpreting data—unlike traditional reaction-based applications, low solar efficiency is not a system limitation but a key system advantage in PEC separations.

However, if solar efficiency improvement and semiconductor stability are relatively unimportant in PEC separations, what then are the main research objectives? The model reveals several key areas to be prioritized in future PEC separations development. First, system design must be optimized to minimize the various avoidable contributors to the separation work requirement, including material imperfections and any background contaminants that can be eliminated by pretreatment, particularly for treating concentrated water streams and applications in resource extraction (Figs. 2, 6). Mass transfer and kinetics must also be considered. Though we have accounted for energy costs to drive the separation at a certain rate, actually obtaining equilibration on these time scales will require better system design at the mesoscopic and macroscopic scales⁴⁹. Further, to truly harness the promise of higher solar efficiency, additional redox active chemistries must be explored to allow complete control over ϕ_b and enable true separator-semiconductor matching (Fig. 3). Greater control over redox chemistries can enable us to tune the selectivity so as to minimize Faradaic losses (Fig. 5). Additionally, as with other emerging technologies, life cycle assessments and location and application-specific technoeconomic analyses will be needed before any particular PEC separations system is deployed. Care must be taken to appropriately suppress water splitting, which can greatly increase the energy consumption of the process (Fig. 5), or lead to bandgap limitations (Supplementary Fig. 10). Finally, it may be necessary to develop new photoactive materials with low bandgaps for separations involving high initial concentrations, to overcome bandgap constraints (Fig. 4) and solar efficiency requirements (Fig. 6). However, traditional low-cost metal oxide semiconductors with higher bandgaps can be directly applicable to low-concentration applications.

This work demonstrates that separations are a highly promising target application for photoelectrochemical research to deliver practical impact at scale. Although not every chemical process is necessarily amenable to electrification via solar energy due to fundamental, process, or practical considerations, we envision that research in PEC separations to overcome the challenges listed above will promote sustainability in numerous chemical processes and help support the energy transition.

Methods

Thermodynamic work requirement in separations

The Gibbs free energy of mixing sets the free energy of a solution relative to pure components (Supplementary Note 1).

$$\Delta {G}_{mix}=\Delta {H}_{mix}+nRT({x}_{1}{{\ln }}{x}_{1}+{x}_{2}{{\ln }}{x}_{2})$$

(1)

Here, ΔH_mix is the enthalpy of mixing, n is the total number of moles participating, R is the ideal gas constant, T is the temperature, and x₁ and x₂ are the mole fractions of the species being mixed (the solute and the solvent). Corrections to equation (1) are described in Supplementary Note 2. The work requirement to separate an initial stream into a concentrated and dilute stream is the difference between the free energies of those streams:

$$\frac{\Delta {G}_{sep}}{nRT}=(1-{R}_{w}){x}_{c}{{\ln }}\frac{{x}_{c}}{{x}_{i}}+{R}_{w}{x}_{d}{{\ln }}\frac{{x}_{d}}{{x}_{i}}$$

(2)

Here, R_w is the fraction of the initial stream rejected as the dilute stream, and x_c, x_d, and x_i are the mole fractions of the solute in the concentrated, dilute, and initial streams, respectively (see Supplementary Note 1 for the full derivation). We assume ΔH_mix ≈ 0 to obtain equation (2), since no net phase change occurs during the process. Then, per volume of useful stream (the dilute stream for treatment, and concentrated stream for extraction), the work requirements are given by:

$${W}_{treat}=\frac{\Delta {G}_{sep}{c}_{w}}{n{R}_{w}}={c}_{w}RT\left(\left(\frac{1}{{R}_{w}}-1\right){x}_{c}{{\ln }}\frac{{x}_{c}}{{x}_{i}}+{x}_{d}{{\ln }}\frac{{x}_{d}}{{x}_{i}}\right)$$

(3)

$${W}_{extract}=\frac{\Delta {G}_{sep}{c}_{w}}{n(1-{R}_{w})}={c}_{w}RT\left({x}_{c}{{\ln }}\frac{{x}_{c}}{{x}_{i}}+\frac{{R}_{w}}{1-{R}_{w}}{{\ln }}\frac{{x}_{d}}{{x}_{i}}\right)$$

(4)

Here, c_w is the molar concentration of the solvent (55.56M for water). Corrections to these work requirements are applied as described in Supplementary Notes 1–5.

Flow corrections and optimal electrode spacing

Of the corrections to the work requirement, the flow corrections that account for energy consumption when performing the separation on a finite timescale are the most significant. These consist of two components: a current-based correction (resistive losses from finite current flow), and a pumping correction (energy costs due to pumping) (see Supplementary Note 5 for full derivation). The current-based correction, per volume of useful stream, is given by:

$${W}_{I}=\frac{{I}^{2}{R}_{s}}{{Q}_{out}}=\frac{{(0.9F)}^{2}{c}_{initial}}{{\eta }_{F}^{2}\left({\Lambda }_{m}^{0}-K\sqrt{{c}_{initial}}\right)}\frac{{\delta }^{2}}{\tau }\frac{{Q}_{in}}{{Q}_{out}}$$

(5)

Here, I is the current supplied, R_s is the series resistance^22,50,51, Q_in and Q_out are the flow rates of the initial and useful streams respectively, F is the Faraday constant, η_F is the Faradaic efficiency, ${\Lambda }_{m}^{0}$ and K are Kohlrausch parameters, δ is the spacing between the electrodes, and τ is the setup contact time. The pumping correction, per volume of useful stream, is given by:

$${W}_{F}=\frac{{Q}_{in}\Delta P}{{Q}_{out}}=\frac{12\mu {Q}_{in}^{2}}{{\delta }^{3}{Q}_{out}}$$

(6)

Here, ΔP is the pressure drop and μ is the dynamic viscosity of the solution. Note that the two corrections scale in opposite directions as functions of δ. This competition leads to an optimum spacing at which the total flow correction is minimum:

$${\delta }_{opt}^{5}=\frac{18\mu {Q}_{in}\tau {\eta }_{F}^{2}\left({\Lambda }_{m}^{0}-K\sqrt{{c}_{initial}}\right)}{{(0.9F)}^{2}{c}_{initial}}$$

(7)

Note that δ_opt is directly proportional to process scale (Q_in and τ), and inversely proportional to c_initial. See Supplementary Table 2 and Supplementary Fig. 4 for typical values. δ_opt is used to obtain the total flow correction applied in Fig. 2.

Detailed-balance solar efficiency limit

We start with the cell equation:

$${V}_{binding}={E}_{cell}+{V}_{PV}-{V}_{inj}-{V}_{series}-{V}_{diffusion}$$

(8)

Here, V_binding is the potential of the redox interface, E_cell is the potential of the external cell or battery (if used to bias the semiconductor), V_PV is the photovoltage of the semiconductor, and V_inj, V_series, and V_diffusion are overpotential losses due to (1) injecting charge carriers into the redox material, across the semiconductor interface, (2) series resistances, and (3) mass transfer limitations, respectively. The potential and current density generated by the semiconductor are given by the illuminated diode equation⁵²:

$$j={j}_{L}-{j}_{0}\left(\exp \left(\frac{e{V}_{PV}}{{n}_{d}{k}_{B}T}\right)-1\right)$$

(9)

Here, j_L and j₀ are the illumination and recombination current densities (Supplementary Note 6 and Supplementary Fig. 5), e is the fundamental unit of charge, n_d is the diode ideality factor, and k_B is the Boltzmann constant. Eqs. (8) and (9) may be combined and solved to obtain the optimum redox potential ϕ_b,opt and the corresponding efficiency η_S (see Supplementary Note 6 for the full derivation):

$$\left(1+\frac{e{\phi }_{b,\! opt}}{{k}_{B}T}\right)\exp \frac{e{\phi }_{b,\! opt}}{{k}_{B}T}=\frac{{j}_{L}}{{j}_{0}}-1$$

(10)

$${\eta }_{S}=\frac{{\phi }_{b}}{\psi }\left({j}_{L}-{j}_{0}\left(\exp \frac{e{\phi }_{b}}{{k}_{B}T}-1\right)\right)$$

(11)

Equation (10) is solved numerically using the provided source code. Further corrections due to second law limitations and materials constraints are applied as described in Supplementary Notes 7–8.

Faradaic efficiency losses from competing reactions

If the selectivity ${K}_{s}=\frac{{k}_{b}}{{k}_{u}}$ is the ratio of the rate constant of target ion binding to the rate constant of the undesirable reaction, the Faradaic efficiency is given by (Supplementary Note 9):

$${\eta }_{F}=\frac{1}{1+\frac{1}{{K}_{s}}\frac{{c}_{background}}{{c}_{initial}}}$$

(12)

Here, c_background is the concentration of species participating in the competing reaction. Now, if the Faradaic efficiency has a minimum allowable value, the background concentration must have a maximum limit, given by:

$${c}_{background,max}={K}_{s}{c}_{initial}\left(\frac{1}{{\eta }_{F,\! min}}-1\right)$$

(13)