Abstract
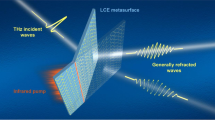
This paper presents a universal and versatile terahertz (THz) wavefront-phase manipulation by manipulating the two-dimensional phases of the near-infrared pulses. The near-infrared manipulation enables independent controls of two kinds of wavefront-phases with a two-dimensional phase modulator along two orthogonal directions. An implementation strategy of the near-infrared manipulation is further introduced by a dislocation scheme including two plates with conjugated-phase functions to output two collinear pulses with orthogonal polarizations and conjugated modulated phases. The manipulated phases can be converted to THz region by type-II phase-matched difference frequency conversion. A proof-of-principle experiment has confirmed the flexible and multiple near-infrared wavefront-phase manipulation and the conversion to THz region via dynamically generating and controlling THz vortex, Bessel, and vortex-Bessel fields with tunable topological charge and “diffraction-free” propagation distance. This work provides a powerful wavefront-phase manipulation, particularly in spectral regions where direct phase manipulation is technically challenging, e.g. in THz region.
Similar content being viewed by others
Introduction
Wavefront manipulation, a powerful method of light field manipulations, has enabled to generate various structured light fields, such as vortex beams1,2, Airy beams3 and Bessel beams4. In particular, through spatiotemporal coupling, many kinds of interesting light fields have been developed, including spatiotemporal vortex beams5, vortex rings6, light springs7, and photon conchs8, greatly enriching the light field family. In addition to the creation of novel structured light fields, many efforts have also made on dynamic light manipulation, e.g. by electrically controlling q-plate system to tune the topological charges of light fields9; by moving one of two diffractive optical elements to adjust optical properties of optical elements, e.g. lensing and vortex phase modulation10,11. Light manipulation can not only provide more degrees of freedom for various applications, but also paly important role in aberrational corrections12. Consequently, wavefront manipulation finds wide applications ranging from biomedical imaging13, information security and communication14,15, to micro/nano fabrication16 and particle manipulation17.
To date, most of the manipulations have been developed in visible or NIR regions. In the past decade, however, THz wavefront manipulation has attracted increasing attention due to the unique merits of THz fields: low photon energy, strong water absorption and high penetration18, predicting promising applications in particle acceleration, medical imaging, free-space communication, material inspection, security screening, and so on18,19,20,21,22.
As is well known, ultrafast THz field can be generated by optical rectification in nonlinear optical crystals, photoexcitation of photoconductive antennas and laser −plasma interactions23,24. Regretfully, none of these methods can directly transfer the structured phases of the pumps directly to the generated THz fields. Accordingly, most of the THz wavefront manipulations can only be realized by using special THz phase-modulators25,26,27,28, which are primarily static, such as zone plates25, diffractive optical elements26, and metasurfaces27. These devices inherently lack the flexibility, tunability, and versatility due to their fixed structural design. Recently, more attention has turned to develop the flexible THz phase modulators, e.g. graphene metasurface29, Moiré device30 and spatial light modulator31. Nevertheless, significant challenge is still there. Compared with their NIR counterparts, both THz materials and components are much more underdeveloped, which usually results in not only large inserted loss, low efficiency and narrow bandwidth, but also expensive, difficult fabrication hindering practical implementation28. Very recently, a THz spatial light modulator was reported to offer extensive control with quick response, opening possibilities for arbitrary THz phase shaping31. However, it suffers from limited modulation resolution, unwanted diffraction orders and considerable power loss. Anyway, to our knowledge, there is no report on the multiple-wavefront THz phase manipulation with a single scheme until now.
In this work, we propose an all-optical wavefront manipulation mechanism to realize THz wavefront manipulation by modulating the wavefronts of NIR pump beams using mature and readily available NIR components, instead of the THz counterparts. As such, the manipulation process can be performed entirely in the NIR domain, which also mitigates effectively the impact of THz diffraction during the manipulation. The NIR manipulation works on an innovative phase manipulation mechanism enabling independent controls of two kinds of wavefront-phases with a 2D phase modulator along two orthogonal directions. Its corresponding implementation strategy based on a dislocation scheme using two conjugated phase plates, which are two PB plates here. This scheme can generate two kinds of phase-manipulations plus their assemble by adjusting independently the 2D dislocations of the phase plates as long as the two wavefront functions have equal partial derivatives with respect to each other’s spatial coordinates. Furthermore, the modulated wavefront phases out of the scheme are then efficiently transferred into THz region via difference-frequency generation (DFG), thereby realize THz field manipulation.
A proof-of-principle experiment is presented to validate the all-optical manipulation mechanism and its implementation strategy, where two liquid crystal PB plates are used as the 2D phase modulator (2D-PM). By changing the relative dislocations of the PB plates along two orthogonal directions, the vortex, Bessel or vortex-Bessel NIR pump fields are generated. The modulated wavefront-phases are then converted into corresponding THz fields, including THz vortex, Bessel or vortex-Bessel fields. These THz structured fields hold promising applications in THz communication, imaging, sensing and others. The proposed mechanism and implementation strategy provides a flexible and effectual method for universal and versatile light field manipulation, particularly in the spectral regions like THz, where direct phase modulation is technically restricted.
Results
Modulation of vortex phase and logarithmic-axicon phase
Figure 1 illustrates the dislocation scheme of the THz wavefront modulation based 2D-PM and DFG. Here, 2D-PM includes a polarizer (P), two PB plates (PB1, 2) made of liquid crystal polymer, and a quarter wave-plate (QW). The PB1 and PB2 own the same modulation phase which is designed for the incidence with right-circular polarization. More details of PB1 and PB2 can be seen in the Supplementary Note 1. According to Fig. 1, one can move one of the PB plates (e.g. PB1) to get Bessel beam along x direction, vortex beam along y direction, or Bessel-vortex beam along both x and y directions.
The dislocation scheme outputs two pulses with orthogonal polarizations, which is exactly required for pumping type-II phase-matched DFG to generate THz pulse. The pumps propagate collinearly with conjugated phases, which ensures to have good phase stability and exact spatial mode-matching for high-efficient DFG28. Due to the pumps around 800 nm, a 1 mm <110> ZnTe crystal is used as THz generator32. Here, the pumps are chirped by a parallel grating pair to suppress the THz generation by optical rectification for high purity of the generated THz pulse by DFG.
To ensure the availability of liquid crystal 2D-PM, we check experimentally the introduced vortex phases (Fig. 2) and logarithmic-axicon phases (Fig. 3) by moving PB1 relative to PB2 along 2D orthogonal directions under the illumination of 800 nm laser with right-hand circularly polarization. According to Fig. 2a1−a10, as the vertical displacement ΔLy of PB1 increases from −218 μm to 211 μm, the topological charge of the generated vortex phase changes from 6 to −6. Here, no logarithmic-axicon phase is added to the vortex phase, indicating that 2D-PM can work for independently modulating the vortex phase along y direction.
Figure 2b describes the relationship between the topological charge of the vortex phase and the PB1 displacement ΔLy with the blue marks for the experimental results and a red line for the theoretical fitting, respectively. It shows that the topological charge decreases linearly with ΔLy. The change of topological charge by 1 corresponds to the change of ΔLy by −36 μm, which is consistent with the theoretical value (−35.4 μm). The results in Fig. 2 indicate that this design can be used to generate vortex phase with a tunable topological charge by simply moving one PB plate (PB1) along y direction.
Figure 3a1−a8 shows the measured spatial logarithmic−axicon phases within the region [−π, π] with the displacement ΔLx by moving PB1 along x (horizontal) direction. As ΔLx is adjusted from −340 μm to 120 μm, the color ring numbers or the logarithmic-axicon phases increase with |ΔLx|. Figure 3b1–b8 are the radial phases of Fig. 3a1−a8 after cascaded within a radial range from −4.2 mm to 4.2 mm, showing the logarithmic-axicon phases have positive peaks for ΔLx < 0 but negative peaks for ΔLx > 0. As ΔLx changes from −340 μm to 120 μm, the peak of the logarithmic-axicon phase gradually decreases from 23.6 rad to −8.6 rad. As predicted, the absolute values of the peaks increase with |ΔLx|. The logarithmic-axicon phases do not carry any vortex phase, indicating that 2D-PM changes independently the logarithmic-axicon phase by ΔLx.
Extracted the peak values of logarithmic-axicon phases in Fig. 3b1–b8, Fig. 4 shows the dependence of the peak values on PB1 displacement ΔLx. There, the blue marks stand for the experimental results and the red line for the theoretical fitting. Obviously, the logarithmic-axicon phase peak has a linear relation to ΔLx, with a phase increase of 2π with ΔLx by −85.2 μm. Summarily, Fig. 3 confirms that this design can manipulate independently logarithmic-axicon phase by simply moving PB1 along x direction.
Generation of THz vortex beam and THz Bessel beam
As described above, for an incidence with linear polarization, the outputs of the 2D-PM can be regarded as a pair of pulses collinearly propagating with orthogonally linear polarizations and conjugated phases. Accordingly, the phase difference between the pulse pair, or the modulated phase by moving PB1, can be transferred when the pulses are used as the pumps of type-II phase-matching DFG. Figure 5 is the setup to generate and manipulate vortex or/and Bessel THz fields by DFG when choosing vortex and logarithmic-axicon phases as the target modulated functions. In the setup, the used laser source is a Ti: sapphire laser system, which outputs 1 kHz/50 fs/800 nm linearly polarized pulse train. The output pulse train is chirped to 2.1 ps by a parallel grating pair, then divided into two parts by a beam splitter (BS): one as the probe (80 mW) and the other as the pump (780 mW). For the probe, a pulse stretcher (PS, a 180° folding right-angle ZF52 prism pair) is used for chirp compensation to compress the pulse duration back to 50 fs for high temporal resolution. The pump is firstly phase-manipulated by 2D-PM to evolve into a collinear pulse pair with vortex or/and logarithmic-axicon phases and orthogonal polarizations. Between the pulse pair, a time delay of 0.42 ps is induced by a 1-mm-thick α-BBO crystal. The pulse pair then go through lens L1 (f = 500 mm) and L2 (f = 150 mm) to pump a 1 mm 〈110〉 ZnTe crystal (ZT1) for the generation of THz fields by DGF. Here, the orthogonal polarizations and some chirps of the pulse pair are required to suppress the optical rectification effect33, while the time delay between two pulses can also be used to change the central frequency of the THz fields34. The THz fields are imaged onto another 1 mm 〈110〉 ZnTe crystal (ZT2) by THz lenses TL1 (f = 100 mm) and TL2 (f = 100 mm) for electro-optic sampling to characterize the spatiotemporal distribution of the THz fields. Here, dynamic subtraction35 is used to improve the measured signal-to-noise ratio. In the setup, 2D-PM, ZT1, ZT2 and the camera (CM, Andor, ZYLA-5.5-CL3SCMOS, 2560 × 2200) are situated with object-image conjugation. The temporal synchronization among the mechanical switch (MS), camera shutter, and delay line (TDL) is realized by a microcontroller for fast and effective measurements of the THz fields.
BS beam splitter, 2D-PM 2D phase modulator, P1-2 polarizer, QW quarter wave plate, α-BBO α-Ba(BO2)2 crystal, MS mechanical switch, L1-4 lenses, TL1-2 THz lenses, ZT1-2 〈110〉 ZnTe crystals, SW1-2 high resistance silicon wafers, TL1-2 THz lens, M1-3 mirrors, DSC dispersion compensator, TDL Delay line, CM sCMOS camera.
In this experiment, the generated THz pulses have typically a time duration of 6 ps and a central frequency of 2 THz (see the Supplementary Note 2). Figure 6 presents the THz field distributions measured by moving vertically PB1 at a distance of −31 μm. Here, Fig. 6a1–d1, a2–d2 and a3–d3 correspond to the electric field, the intensity, and the phase distributions of the THz field at different times, respectively. The recorded time interval is 133 fs. One can see the generated THz field exhibits a four-leaf petal-like amplitude distribution and a donut-shaped intensity profile. Its phase increases counterclockwise for an azimuthal angle from 0 to 4π, or the electric field and the phase distribution exhibit clockwise rotation with time. Figure 6a4–d4 are extracted from Fig. 6a3–d3 by the blue dots and the red lines for the experimental and the fitting results, respectively. Consequentially, the angular phase of the THz pulse increases linearly with azimuth at different times, which shows the generated THz vortex field has a topological charge of 2.
By moving PB1 vertically, the topological charge of the THz vortex pulse is modulated from −5 to 5. Figure 7a–c corresponds to the electric field, the intensity, and the phase of the measured THz pulses at the temporal points with peak intensities. In Fig. 7b, the diameter of the donut-shaped THz intensity gradually increases with the absolute value of topological charge. When the value is greater than 3, the THz ring tends to exceed the probe spot, resulting in a failed detection of the THz ring, thereby lower detected THz intensity and contrast. However, the THz vortex phase with different topological charges can still observed from the phase distribution, where the topological charge decreases linearly with the PB1 displacement. The topological charge changes 1 corresponds to a PB1 displacement of −16.9 μm, agreeing well with the theoretical value of −17.7 μm, as shown in Fig. 7d. It is worth noting that a PB1 displacement of 36 μm corresponds to change the topological charge by 1 in Fig. 2b, but by 2 in Fig. 7d, which is originated from the topological charge conservation during DFG for generating THz vortex pulse. So, the results in Fig. 7 confirms that this setup can generate THz vortex pulses with tunable topological charges.
By moving horizontally PB1, 2D-PM can impose a logarithmic-axicon phase into the pump pulse, thereby generate THz-Bessel pulse. Figure 8a1–d1 or a2–d2 are the results obtained by moving PB1 so that ΔLx = −6 μm or −56 μm. Figure 8a1 or a2 is the time-domain integration of the THz intensity, which has multiple ring structures with a central spot size of 415 μm or 463 μm, while Fig. 8b1 or b2 shows the 1D intensity distribution of the THz beam, extracted along the horizontal direction across the THz beam of Fig. 8a1 or a2. There, the blue dots represent the measured results, while the red lines are the theoretical fittings by the first-order Bessel function. The good agreements between the blue dots and the red lines imply that the generated THz fields are of THz Bessel beams. To check the diffraction of the generated THz Bessel beam, we move the THz crystal ZT2 along the propagation axis to detect the spot sizes of the THz Bessel beam at different propagation distances. Figure 8c1, c2 show the 1D intensity distributions of THz Bessel pulses measured at different axial positions, while Fig. 8d1, d2 are the corresponding the peak intensities of THz beams with the ZT2 displacement. From the figures, the THz Bessel beams generated at PB1 positions of −6 μm and −56 μm have different “diffraction-free” distances, ~9.5 mm and 15.3 mm, respectively, which are far longer than the Rayleigh length of the traditional Gaussian beams under the same conditions (1.43 mm for a Gaussian beam with a waist of 463 μm @ 2 THz). Based on the above measured results, this setup has successfully generated THz Bessel beams with adjustable diffraction-free distances by changing the PB1 horizontal position.
By adjusting simultaneously PB1 along both horizontal and vertical directions, both the vortex and logarithmic-axicon phases can be introduced simultaneously on the pump pulses. Figure 9 shows the generated THz pulse with the topological charges of −1 and −2, where Fig. 9a1-a2, b1-b2 and c1-c2 stand for the electric field, intensity and phase distributions of the THz fields, respectively. The generated THz pulses exhibit the electric field with multiple petal-shapes, the intensities with multiple ring-shapes, and spiral phase distributions, indicating the generated THz pulses are THz Bessel vortex pulses.
Discussion
This paper introduces a manipulation mechanism, enabling universal and versatile wavefront-phase control in THz regime. This manipulation operates with a flexible NIR wavefront-phase manipulation combined with type-II phase-matched DFG. The NIR manipulation works on a universal manipulation mechanism, which manipulates independently a pair of wavefront-phases by changing two-dimensionally the dislocations of a couple of phase-elements with conjugated phase functions. The independence is ensured as long as the partial derivatives of the target phase pair with respect to each other’s spatial coordinates are equal, which can be satisfied by many important phase pairs, such as logarithmic-axicon versus vortex phases (for Bessel and vortex beams) and 1D versus 2D cubic phases (for 1D and 2D Airy beams). Notably, when only a single target wavefront is required, the method can accommodate arbitrary phase profiles. In principle, any phase modulator, including the graphene-based metasurface, can be used to act as the two phase-elements if they can induce desired phases. Here, to realize the NIR manipulation, a dislocation scheme is designed, where two PB plates are used as the conjugated phase elements due to their high efficiency and easy fabrication. Besides the NIR manipulation, the scheme also outputs a pair of collinear pulses with conjugated phases and orthogonal polarizations.
By using the resulting pulse pair as the pumps, the manipulated wavefront-phases allow to be transferred from NIR to THz region by type-II DFG. As a result, all the work for THz manipulation is performed at NIR, thus eliminates the need for THz components and mitigates strong THz diffraction during manipulation. Furthermore, the dislocation-based design allows for flexible and scalable wavefront control.
A subsequent proof-of-principle experiment validates this universal and versatile THz manipulation by utilizing a dual-phase modulator with a pair of PB plates and a < 110> ZnTe crystal-based type-II DFG. By moving one of the PB plates along one or two of the spatial directions, we achieved logarithmic-axicon, vortex, or combinations of these phases. This method generates THz vortex beams with tunable topological charges from +5 to −5 and produces Bessel beams with diffraction-free distances of 7.86 mm and 15.95 mm through horizontal adjustment of the PB plate. Additionally, THz Bessel-vortex beams with topological charges of 1 and 2 have been created. These THz structured beams hold considerable potential for applications in THz imaging, sensing, communication, and THz-matter interaction. Summarily, this paper provides a flexible way for dynamic and multifaceted manipulation of light fields, particularly in the THz domain, where direct phase modulation is typically challenging.
Methods
Principle of Terahertz wavefront modulation
It is well known that THz pulse can be generated by nonlinear frequency conversion, including optical rectification36 and difference frequency33. The conversion can be described by three-wave nonlinear coupling equation as
Here, ETHz, Ep1 = Ap1·exp(iφp1) and Ep2 = Ap2·exp(iφp2) stands for THz field, as well as the two pump pulses with their amplitudes Ap1, Ap2 and phases φp1, φp2, while k is the coupling coefficient, respectively. From Eq. (1), it is obvious that the phase of the THz field is determined by the phase difference of the pumps. For optical rectification, THz field is originated from the difference frequency conversion between the spectral components of the same pulse, so some pump phases, e. g. vortex phase, fail to transform into the THz pulse during the conversion. However, for traditional difference frequency, it occurs between two separated pump pulses, so φp1 and φp2 can be manipulated separately. Consequentially, the generated THz phase can be manipulated by modulating the two pump phases separately. In other words, the manipulation in THz region can be replaced by the manipulation in near infrared (NIR) regime, which makes THz manipulation be much easier, simpler and more effective.
Obviously, the universality and versatility of the THz manipulation depends mainly on the NIR phase-manipulation which is described as following. Suppose that the modulation functions of the two phase-elements are ϕ (x, y) and −ϕ (x, y), they induce totally null phase if they are exactly aligned. When a dislocation between them occurs along x or y direction by Δx or Δy, the total phase variation, or the induced net-phase modulation of the phase-elements, shall be
or
Eq. (2a) and Eq. (2b) mean the net modulation phase Δϕx (x, y) or Δϕy (x, y) is ϕ (x, y) differential along the dislocation direction. Obviously, if
Δϕx (x, y) and Δϕy (x, y) can be changed independently. If Δϕx (x, y) and Δϕy (x, y) are nonzero simultaneously, the phase variation Δϕ (x, y) can be expressed
The discussion above shows, as long as the target phases φ1 (x, y) and φ2 (x, y) fulfill Eq. (3), the function ϕ (x, y) can be designed for the phase plates by solving Eqs. (2a) and (2b). Accordingly, this design can implement the independent light manipulations with φ1(x, y), φ2(x, y) or φ1(x, y)+φ2(x, y) by moving one of the plates along x, y directions or both of them.
There are lots of interesting function pair for the phase modulation meeting Eq. (3), e.g. logarithmic-axicon vs. vortex phases for Bessel beam vs. vortex beams, 1D vs. 2D cubic phase for 1D vs. 2D Airy beams, and so on. These mean that this mechanism can work for versatile manipulations with up to three target wavefront-phases by only one setup for flexible light phase manipulations. However, if only one target required, it is universally applicable to any wavefront function. This NIR phase-manipulation can output a pair of pulses with conjugated modulated phases and orthogonal polarizations. The orthogonal polarizations allow the pulse pair owning perfect polarization matching to pump type-II phase-matched DFG, which makes the modulated phases be transferred to the generated THz fields. All above mean this universal mechanism can work for flexible manipulations with multiple-wavefront phases owing wide applications.
Any phase modulators, e.g. graphene-based metasurface, can be used to carry out this work if they can induce desired phases. Here, two PB phase plates are chosen as the mutually conjugated phase modulators due to the high efficiency and easy fabrication. According to Eq. (1)~(4), we implement the concept of the MIR wavefront-phase manipulation by a dislocation scheme with a pair of PB phase plates. The detail design is subsequently described for the 2D-PM.
Realization of Terahertz wavefront modulation
To realize the proposed phase manipulation, a pair of NIR pulses are required as the pumps to generate THz wave by DFG according to Eq. (1). Here, type-II phase-matching is preferred to suppress optical rectification generally used for THz generation, which means it is better that the pump pulses have orthogonal polarizations besides the controllable phases described in Eqs. (2) and (3). In order to get this kind of pump pair, a dislocation scheme have been designed. It includes mainly a 2D phase modulator (2D-PM), a pair of identical PB optical elements (PB) made of liquid crystal polymers, situated after a polarizer (P) but before a quarter wave-plate (QWP). 2D-PM imposes phase-modulations and changes the output polarizations to the orthogonal directions for different circularly polarized inputs, which means that, if a circularly polarized beam passes through 2D-PM, it is equivalent to be phase-modulated by the two plates with conjugated phases37, thereby can achieve net-phase modulation as Eqs. (2a) and (2b). If the incident beam is a linearly polarized laser, it can be regarded as the superposition of its two orthogonal polarization components: one with right-circular polarization and the other with left-circular polarization. After 2D-PM, the outputs include two orthogonal circular-polarization beams with a conjugated net modulation phase. Finally, a quarter wave-plate (QW) with a fast axis orientation of 45° is used to convert the two circularly polarized beams into two with orthogonal linearly polarizations.
As an example, we choose the target phases φ1(x, y) and φ2(x, y) of 2D−PM to be logarithmic-axicon and vortex phases as followings
Here, a and b are size coefficients. It is easy to confirm that φ1 (x, y) of Eq. (5a) and φ2 (x, y) of Eq. (5b) meet Eq. (3). By substituting Eqs. (5a) and (5b) into Eqs. (2a) and (2b), the phase modulation ϕ (x, y) of the two PB-plates for right-circular polarized inputs shall be designed as
Data availability
The data that support the findings of this study are available from https://figshare.com/s/b975445bf3379bd83818.
Code availability
All code used in this study is available from the corresponding author upon request.
References
Shen, Y. et al. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 8, 90 (2019).
Forbes, A., Oliveira, M. de & Dennis, M. R. Structured light. Nat. Photon. 15, 253–262 (2021).
Efremidis, N. K., Chen, Z., Segev, M. & Christodoulides, D. N. Airy beams and accelerating waves: an overview of recent advances. Optica 6, 686–701 (2019).
Zhi, Z. et al. On-chip generation of Bessel–Gaussian beam via concentrically distributed grating arrays for long-range sensing. Light Sci. Appl. 12, 92 (2023).
Hancock, S. W., Zahedpour, S., Goffin, A. & Milchberg, H. M. Free-space propagation of spatiotemporal optical vortices. Optica 6, 1547–1553 (2019).
Wan, C., Cao, Q., Chen, J., Chong, A. & Zhan, Q. Toroidal vortices of light. Nat. Photon. 16, 519–522 (2022).
Lin, Q. et al. Direct space-time manipulation mechanism for spatio-temporal coupling of ultrafast light field. Nat. Commun. 15, 2416 (2024).
Chen, W. et al. Observation of chiral symmetry breaking in toroidal vortices of light. Phys. Rev. Lett. 132, 153801 (2024).
Zheng, S. et al. Liquid crystal-based order electrically controlled q-plate system. Opt. Express 27, 16103–16110 (2019).
Bernet, S. Combined diffractive optical elements with adjustable optical properties controlled by a relative rotation: tutorial. J. Opt. Soc. Am. A 38, 1521–1540 (2021).
Liu, X. et al. Spatiotemporal optical vortices with controllable radial and azimuthal quantum numbers. Nat. Commun. 15, 5435 (2024).
Katz, O., Small, E., Bromberg, Y. & Silberberg, Y. Focusing and compression of ultrashort pulses through scattering media. Nat. Photon. 5, 372–377 (2011).
Luo, J. et al. High-speed single-exposure time-reversed ultrasonically encoded optical focusing against dynamic scattering. Sci. Adv. 8, eadd9158 (2022).
Kim, I. et al. Pixelated bifunctional metasurface-driven dynamic vectorial holographic color prints for photonic security platform. Nat. Commun. 12, 3614 (2021).
Wang, J. et al. Orbital angular momentum and beyond in free-space optical communications. Nanophotonics 11, 645–680 (2022).
Zhang, L. et al. High-throughput two-photon 3D printing enabled by holographic multi-foci high-speed scanning. Nano Lett. 24, 2671–2679 (2024).
Yang, Y., Ren, Y.-X., Chen, M., Arita, Y. & Rosales-Guzmán, C. Optical trapping with structured light: a review. Adv. Photon. 3, 034001 (2021).
Yang, X. et al. Biomedical applications of terahertz spectroscopy and imaging. Trends Biotechnol. 34, 810–824 (2016).
Tang, H. et al. Stable and scalable multistage terahertz-driven particle accelerator. Phys. Rev. Lett. 127, 074801 (2021).
Yang, Y. et al. Terahertz topological photonics for on-chip communication. Nat. Photon. 14, 446–452 (2020).
Sirenko, A. A. et al. Total angular momentum dichroism of the terahertz vortex beams at the antiferromagnetic resonances. Phys. Rev. Lett. 126, 157401 (2021).
Afsah-Hejri, L., Hajeb, P., Ara, P. & Ehsani, R. J. A comprehensive review on food applications of terahertz spectroscopy and imaging. Compr. Rev. Food Sci. F. 18, 1563–1621 (2019).
Li, J. & Li, J. Terahertz (THz) generator and detection. Electr. Sci. Eng. 2, 11–25 (2020).
E, Y. et al. Progress, challenges, and opportunities of terahertz emission from liquids. J. Opt. Soc. Am. B 39, A43–A51 (2022).
Feng, X. et al. Direct emission of focused terahertz vortex beams using indium-tin-oxide-based fresnel zone plates. Adv. Opt. Mater. 11, 2201628 (2023).
Minkevičius, L. et al. Bessel terahertz imaging with enhanced contrast realized by silicon multi-phase diffractive optics. Opt. Express 27, 36358–36367 (2019).
Liu, W. et al. Multichannel terahertz quasi-perfect vortex beams generation enabled by multifunctional metasurfaces. Nanophotonics 11, 3631–3640 (2022).
Zeng, H. et al. A review of terahertz phase modulation from free space to guided wave integrated devices. Nanophotonics 11, 415–437 (2022).
Chen, D. et al. Tunable polarization-preserving vortex beam generator based on diagonal cross-shaped graphene structures at terahertz frequency. Adv. Opt. Mater. 11, 2300182 (2023).
Wang, G. et al. Moiré meta-device for flexibly controlled Bessel beam generation. Photonics Res. 11, 100–108 (2023).
Malevich, Y., Ergoktas, M. S., Bakan, G., Steiner, P. & Kocabas, C. Very-large-scale reconfigurable intelligent surfaces for dynamic control of terahertz and millimeter waves. Nat. Commun. 16, 2907 (2025).
Nahata, A., Weling, A. S. & Heinz, T. F. A wideband coherent terahertz spectroscopy system using optical rectification and electro-optic sampling. Appl. Phys. Lett. 69, 2321–2323 (1996).
Lin, Q. et al. Generation of terahertz vortex pulses without any need of manipulation in the terahertz region. Opt. Lett. 44, 887–890 (2019).
Danielson, J. R. et al. Intense narrow band terahertz generation via type-II difference-frequency generation in ZnTe using chirped optical pulses. J. Appl. Phys. 104, 033111 (2008).
Zhang, L., Karpowicz, N., Zhang, C., Zhao, Y. & Zhang, X. Real-time nondestructive imaging with THz waves. Opt. Commun. 281, 1473–1475 (2008).
Tóth, G., Polónyi, G. & Hebling, J. Tilted pulse front pumping techniques for efficient terahertz pulse generation. Light Sci. Appl. 12, 256 (2023).
Marrucci, L., Manzo, C. & Paparo, D. Pancharatnam-Berry phase optical elements for wavefront shaping in the visible domain: switchable helical modes generation. Appl. Phys. Lett. 88, 221102 (2006).
Acknowledgements
This work is partially supported by Guangdong Major Project of Basic Research (2020 B0301030009 (X.Y.)), National Key R&D Program of China (2023YFA1608504 (S.X.)), National Natural Science Foundation of China (92050203 (S.X.), 12404486 (Q.L.), 62275163 (X.Z.), 12174264 (Y.C.), and 62075138 (X.L.)); Natural Science Foundation of Guangdong Province (2021A1515011909 (X.L.), 2022A1515011457 (Y.C.)); Shenzhen Fundamental Research Program (JCYJ20210324095213037 (X.Z.)), Shenzhen Key Project for Technical Research (JSGG20211108092800001 (X.Z.)), Shenzhen Key Laboratory of Photonics and Biophotonics (ZDSYS20210623092 006020 (S.X.)) and the Scientific Instrument Developing Project of Shenzhen University (2023YQ006 (S. X.)).
Author information
Authors and Affiliations
Contributions
Q.L., F.F. and S.X. conceived the concept and design of the experiments. Q.L., F.F., X.Z., W.H., Y.C., C.W., and K.W. carried out the numerical analysis. Q.L., X.Z., Y.C., X.L. and H.Z. discussed the results. C.W. prepared the figures. S.X. and X.Y. supervised the entire work, and took part in the prepare of the manuscript together with J.L. All authors reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Bruno Piccirillo and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Lin, Q., Feng, F., Zeng, X. et al. A universal and versatile terahertz field manipulation mechanism by manipulating near-infrared phases with a dislocation scheme. Nat Commun 16, 6656 (2025). https://doi.org/10.1038/s41467-025-61935-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-61935-3