Introduction

Polariton chemistry has become a rapidly growing field, offering new possibilities for manipulating chemical properties by coupling molecular systems with the electromagnetic field of an optical cavity1,2,3,4,5,6. In particular, the vibrational strong coupling (VSC) between molecular vibrations and the infrared cavity has garnered significant interest in physics and chemistry4,5,6,7,8,9,10,11,12,13,14,15. It has been demonstrated that strong VSC effects, resulting in the formation of vibrational polaritons, can significantly modify chemical reactivity and selectivity3,7,8,9,10,11,16,17,18,19,20. Experimentally, it has also been reported that VSC alters intramolecular and intermolecular vibrational energy transfer (VET) processes in model molecular systems such as W(CO)6 and Fe(CO)512,13,21.

Despite seminal experimental breakthroughs, the theoretical understanding of energy transfer processes and their underlying mechanisms remains largely elusive20. In recent years, several theoretical studies have reported cavity-mediated VET at the single-molecule level, where only one molecule is strongly coupled to the cavity mode18,22,23,24,25. While these studies provide valuable microscopic insights into VSC-modified reactions, most practical VSC experiments involve polaritonic systems with macroscopic ensembles of molecules, typically on the order of 1010, that collectively couple to the photonic mode within the optical cavity, and the light-matter coupling strength for each molecule is relatively weak. Handling such large molecular ensembles poses significant challenges for theoretical derivations and simulations. Typically, the Tavis–Cummings model or other simplified Hamiltonians are employed to simulate VSC dynamics of many-molecule systems26,27,28. Although these models are useful, they lack the robustness needed to capture the complexity of realistic potential energy landscapes and the influence of structural disorder.

The collective VSC effect in large molecular ensembles has also been explored through classical cavity molecular dynamics (MD) simulations, offering key insights into cavity-modified energy transfer processes29,30. However, these simulations neglect quantum effects, which are essential because the formation of vibrational polaritons and their influence on chemical reactions are inherently quantum mechanical24,31,32,33. Another persistent challenge in polariton chemistry is understanding how the dynamics of individual molecules are altered by collective VSC20,34,35,36. Recent theoretical efforts have attempted to address this issue by simulating dilute, gas-phase molecular ensembles coupled to an optical cavity, while neglecting intermolecular interactions34,36. These approximations facilitate the efficient study of collective VSC effects, but they have not yet been extended to quantum dynamical simulations of realistic molecular systems coupled to cavities.

In this work, we advance beyond the single-molecule approximation by performing state-of-the-art ab initio quantum dynamical calculations of the vibrational population dynamics of OH stretches in the \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\)-cavity system, incorporating collective VSC effects. As the most common solvent and a frequent subject of VSC experiments37,38, water’s vibrational spectra and ionic conductivity under VSC have been investigated both experimentally and theoretically29,38,39,40,41. However, the impact of VSC on water’s vibrational dynamics remains unexplored. The study of VET rates and pathways in water has long been a topic of interest42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59, with vibrational relaxation involving a complex interplay between structural heterogeneity and the delocalized nature of OH stretches52,53,54,55,56,57,58,59. The \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) cluster shares a similar intermolecular H-bonding network pattern with liquid water. It has been shown to be of high stability and its magic number behavior stems from its optimized hydrogen-bond network, surface charge delocalization, and the ability to accommodate substitutions without structural compromise60,61,62,63. Thus, it serves a representative gas-phase model to understand proton hydration and aqueous water dynamics. This system also strikes a balance between computational feasibility, quantum mechanical accuracy, and the need to account for collective coupling effects in polariton chemistry. As such, \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) offers an ideal platform for investigating the quantum dynamical features of vibrational couplings and energy transfer in water under VSC.

We employ a combination of the cavity vibrational self-consistent field/configuration interaction (cav-VSCF/VCI) method23,64,65 and quantum wavepacket dynamics simulations. These are integrated with our recently developed full-dimensional potential energy surfaces (PES) at the CCSD(T) level and dipole moment surfaces (DMS) at the MP2 level for water66,67. The choice of the fully quantum VSCF/VCI approach is for the consideration of both accurate simulation of vibrational spectrum and explicit treatment of quantum features involving complicated overtones, combination bands, and Fermi resonances. This method enables a detailed characterization of vibrational dynamics, providing critical insights into energy transfer pathways. A similar theoretical framework was previously applied to analyze the subpicosecond relaxation dynamics of the OD and OH stretches in dilute HOD-ice systems68. In this study, we systematically investigate the population dynamics of the OH stretch and the associated energy transfer pathways both inside and outside the cavity, varying the light-matter coupling conditions. We further analyze and discuss the underlying mechanisms that give rise to the new landscape of vibrational dynamics under VSC.

Results

Vibrational spectra and population dynamics outside the cavity

Figure 1a depicts the \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) cluster outside the optical cavity. As detailed in Supplementary Fig. 2 and Supplementary Table 1 in Supplementary Information, the 3-dimensional cage structure of \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) encompasses various H-bond topologies. The distinctive structural information can be disentangled through the vibrational spectra, and we present the simulated spectra in Fig. 1b. The VSCF/VCI spectrum of \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) at the optimized minimum structure, predicts the water HOH bend at approximately 1650 cm−1 and OH stretches across a broad spectral band of 3000–3700 cm−1 centered around 3400 cm−1. Complete peak assignments of the simulated spectrum are included in Supplementary Table 2. Our theoretical predictions capture the general shape of the experimental linear IR spectrum of liquid water reasonably well69. To achieve better agreement and include inhomogeneous broadening by thermal effects, one needs to consider larger clusters or bulk liquid water system, along with extensive configuration sampling from MD simulations67. These are beyond the scope of the present study and are subjected to our future work.

Fig. 1: Vibrational spectra and OH population dynamics of \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) outside the optical cavity.
figure 1

a Schematic depiction of \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) placed outside the optical cavity. b Vibrational spectra of \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) outside the cavity from anharmonic vibrational self-consistent field/configuration interaction (VSCF/VCI) calculation and experimental infrared (IR) spectrum of liquid water69. The VSCF/VCI states energies and IR transition intensities are indicated in the stick spectrum, and are further broadened to generate the line spectrum with Gaussian functions of full width at half maximum (FWHM) of 70 cm−1. c–e Examples of time-dependent population of the OH stretch in monomer 1 (w1) and monomer 7 (w7) from 3 mode or 6 mode calculations. Three mode calculation involves the bend (νb) and two OH stretches (νOH1, νOH2) of one monomer. Six mode calculation includes three additional low-frequency intermolecular modes (ν1, ν2, ν3) and fully considers intermolecular mode couplings.

Full size image

The vibrational dynamics are characterized by the time-dependent change of the state population of excited OH stretch, where the corresponding OH stretch was initially excited to its fundamental state at t = 0 fs. Throughout the main text, we focus on two representative examples: monomer 1 (w1) and monomer 7 (w7), to illustrate the OH stretch vibrational dynamics. The complete labeling of all monomers, along with the full results for the OH stretch dynamics of all 21 monomers, is provided in the Supplementary Information. As will be shown, w1 and w7 exhibit distinct dynamic behaviors, highlighting two contrasting scenarios of vibrational relaxation. Here, we define successful relaxation as a significant population decrease–falling below 0.25–within a 1000 fs timescale. As will be shown below, the population dynamics of the OH stretch may exhibit oscillatory behavior. This feature partly arises from the finite size of the cluster system and the limited number of vibrational degrees of freedom included in the calculations. In more complex systems or larger-dimensional simulations, significantly stronger damping with virtually no oscillation is expected.

Figure 1c–e provide the vibrational population dynamics of OH stretches in w1 and w7, and the full dynamics results are presented in Supplementary Figs. 4 and 5. First, when only three intramolecular modes of each water are considered in the VSCF/VCI and wavepacket calculations, only few successful relaxations are observed. For example, in w1, the population change of the first OH stretch displays an oscillating feature. This can be easily explained by the mild intramolecular coupling between OH stretches and HOH bend overtone. To achieve full relaxation of the OH stretch in w1, we further included three additional low-frequency intermolecular vibrations and accounted for all intermolecular mode couplings in VSCF/VCI calculations. As shown in Fig. 1d, the OH stretch fundamental decays rapidly within a short time period. The population decrease of the OH stretch fundamental is strongly correlated with the rise of νOH1-w3 and 2ν3 + νb, where νOH1-w3 is the fundamental state of the first OH stretch in w3 and 2ν3 + νb is the combination band involving the third low-frequency intermolecular mode and the bending mode. This results from the mixing among OH stretches in different water molecules and also complicated combination bands involving intermolecular modes (“frustrated” rotations and translations). Additional examples of intermolecular mode-enabled relaxation of OH stretch are provided in Supplementary Fig. 6.

The population dynamics of the OH stretch in w7, shown in Fig. 1e, exemplify another category of VET pathway. This intramolecular relaxation process is characterized by a significant population decrease of the excited OH stretch, accompanied by a population increase in the HOH bend overtone. Notably, an oscillatory behavior is also observed throughout the dynamics. This process is the result of the well-known Fermi resonance with the bend overtone70 and occurs directly without the inclusion of additional intermolecular modes. This agrees with the previous work by Hynes53 and Skinner42,54 in investigating the relaxation of OH stretch fundamental in liquid water.

Our observations of the two main relaxation pathways align with the traditional localization picture. It should be noted that our 3-mode theoretical set-up does not consider the vibrational couplings among intramolecular modes from different water monomers. Unlike the 6-mode calculation with intermolecular modes and intermolecular coupling included, under the scheme of 3-mode calculations, delocalization behavior of OH stretch is disregarded and direct intermolecular energy transfer among OH groups of different monomers cannot be observed. However, as will be elucidated in the next section, the assumption of negligible vibrational couplings between monomers offers a clean and direct way to probe the VSC effect on the vibrational relaxations in water when optical cavity is involved.

VSC effects on spectra and vibrational dynamics

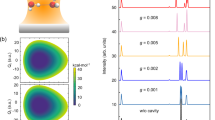
When \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) is placed inside the optical cavity with significant light-matter coupling, the direct observation of the VSC effect is the polaritonic vibrational spectra. Figure 2b illustrates the vibrational spectra of the \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\)-cavity system under various light-matter coupling strengths with cavity mode frequency of 3400 cm−1. Before discussing the spectral results, it should be noted that our new cav-VSCF/VCI spectra differ from those in the previous work65 due to the additional constraints now applied to the interaction terms involving cavity modes and molecular vibrations. As expected, an increase in the light-matter coupling factor g results in the rapid splitting of the intricate OH stretch band of 3000–3700 cm−1 into two distinct bands, signifying the formation of hybrid vibrational polaritons. The high-frequency spectral band is commonly referred to as the upper polariton (UP) state, while the lower-frequency spectral band represents the lower polariton (LP). The spectral separation between UP and LP, known as Rabi splitting, increases with larger light-matter coupling strength. Notably, almost no significant spectral features are observed between UP and LP states, especially when g is substantial. This lack of features does not imply the absence of vibrational states in this region. Instead, many states, known as dark states, exist with frequencies between UP and LP but do not carry infrared intensities65. Furthermore, it is observed that with strong VSC, the spectral peaks are relatively sharp, which is different from the inhomogeneous broadening feature of OH stretches in conventional liquid water. The absence of spectral broadening agrees with previous experimental measurements39.

Fig. 2: Vibrational strong coupling effects on the vibrational spectra and OH vibrational population dynamics.
figure 2

a Schematic depiction of \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) placed inside the optical cavity. b Polaritonic vibrational spectra of \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) with different light-matter coupling strength g (a.u.). The cavity frequency is indicated in the vertical dashed line. c Examples of time-dependent population of the OH stretch in monomer 1 (w1) and monomer 7 (w7) of \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\)-cavity system with different light-matter coupling factors g (a.u.). The cavity frequency is set as 3400 cm−1 for (b, c).

Full size image

In Supplementary Fig. 7, we further compare the calculated polaritonic spectrum of \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) with the experimental IR spectrum of liquid water under VSC41. As seen, reasonable Rabi splitting, asymmetry of polaritonic states, and corresponding lineshape are obtained from our cav-VSCF/VCI calculations. It should be noted that in VSC experiments, a large number of molecules, i.e., 1010, collectively couple to the cavity. In our current \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\)-cavity system, we capture only part of these collective coupling effects. Although our model goes beyond the single-molecule scenario and shows good agreement with the experimental spectrum (Supplementary Fig. 7), the coupling strength factors employed are still significantly larger than those achievable in experiments. Additionally, real cavity systems involve multiple cavity modes, and cavity loss effects must be accounted for. We plan to bridge the gap between current work and more realistic experimental conditions in our future work.

Before presenting the OH vibrational dynamics of the realistic \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) cluster within the cavity, it is important to explore how vibrational dynamics are altered within the cavity using the analytical Tavis–Cummings model. As shown in Supplementary Fig. 1 and discussed in Supplementary Section 1, we investigated how different vibrations characterized by varying dipole orientations, are influenced by VSC under resonance condition with the cavity mode ωc = 3400 cm−1. The TCM model successfully reproduces the expected spectral positions of UP, LP, and dark states. Further analysis of the population dynamics reveals that, under VSC, VET can be facilitated, particularly for vibrations with dipole moments closely aligned with the cavity polaritzation direction. However, the associated population changes remain relatively modest under resonance conditions. Actually, real molecules are not single-mode, two-level systems. Instead, a complex manifold of vibrational states (fundamentals, overtones, and combination bands) arising from different vibrational motions can actively participate in VET processes. It is therefore critical to assess whether cavity-enabled VET process persists in more complex and realistic molecular systems such as \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\).

Next, we present how the OH vibrational dynamics are modified by the VSC effect. Figure 2c showcases examples of vibrational population dynamics after exciting the OH stretch in monomer 1 and monomer 7 under different light-matter coupling strengths. The full results for all 21 monomers are presented in Supplementary Figs. 8 and 9. First, as shown in the upper panel of Fig. 2c, for certain OH stretches that do not successfully relax when outside the cavity, substantial population decrease is observed under VSC within optical cavity. This cavity-enabled relaxation is generally accelerated with stronger coupling factor g. These surprising observations offer direct evidence that VSC introduces new possibilities for VET in molecular systems, as confirmed in recent experiment12. For OH stretches undergoing intramolecular vibrational relaxations through Fermi resonance, the inclusion of VSC modifies the rate of population change as shown in the bottom panel of Fig. 2c. Again, the general trend is that with stronger light-matter coupling, the evolution of vibrational population gets apparently speed up.

Figure 3a, b provides detailed VET pathways when the cavity mode frequency is 3400 cm−1 with coupling factor g = 0.006 a.u. For the OH stretch in monomer 1, cavity-enabled VEP primarily occurs through direct intermolecular energy transfer among OH groups. The decrease in the population of the excited OH stretch in w1 is accompanied by the significant increase in the population of the OH stretch in monomer 2 (w2). Additionally, notable changes are observed in the populations of the bend overtone in w2 and the OH stretch fundamentals in monomers 3 (w3) and 11 (w11). As listed in Supplementary Table 1, w2, w3, and w11 belong to the first, second, and third hydration shells of w1, respectively. The strong mixing among these OH stretches indicates the cavity-induced delocalization of the OH stretch as well as efficient intermolecular VET. It is important to reiterate that our theoretical setup operates under the localization framework, where vibrational couplings between vibrational modes of different monomers are ignored, but this constraint is directly broken under VSC. Another surprising finding pertains to the conventionally intramolecular relaxation-dominated OH stretches. As seen in Fig. 3b, for the OH stretch in monomer 7, the dominant VET pathway remains the intramolecular one, where significant population change of the bend overtone is observed. However, the populations of the OH stretches in monomer 2 also increases. As indicated in Supplementary Table 1, monomer 2 is beyond the first hydration shell of monomer 7. Besides the cavity-enabled intermolecular VET between neighbouring molecules, the existence of cavity can provide new energy transfer pathways between remote molecules. The role of the cavity is primarily intermediate, as can be seen in the population change of cavity modes in Fig. 3a, b. More examples of cavity-induced intermolecular VET pathways involving different water monomers are provided in Supplementary Fig. 10. Combing with Supplementary Figs. 8 and 9, it can be observed that under collective VSC, the vibrational population dynamics of OH stretch, including rate and pathways, in different water monomers vary. This variation is primarily attributed to their specific molecular environments arising from the complex H-bond network. Overall, the increasing rate of energy transfer13 and the emergence of new intermolecular VET pathways align with recent experimental observations12.

Fig. 3: Vibrational strong coupling effects on OH vibrational energy transfer pathways.
figure 3

a, b Vibrational energy transfer pathways of OH stretch in monomer 1 (w1) and monomer 7 (w7) of \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\)-cavity system. c, d Dipole derivative correlation values and vibrational frequency shift (Δν) of OH stretches in \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) relative to the first OH stretch in monomer 1 and monomer 7, respectively. Red points correspond to primary population receivers observed in (a) and (b) respectively. The dipole derivative correlation value, Dipcorr is defined in main text. The cavity frequency is set as 3400 cm−1 with coupling strength g = 0.006 (a.u.) for (a–d).

Full size image

To delve into the mechanism how VSC modifies the intermolecular VET pathways, we analyzed two key characteristics of all OH stretches. For example, relative to the first OH stretch (3396.77 cm−1) in monomer 1, we calculated the spectral shift of other OH stretches across different molecules as Δν and the dipole derivative correlation defined as Dipcorr = max(∣dμx/dQ1∣∣dμx/dQi∣, ∣dμy/dQ1∣∣dμy/dQi∣). These two characteristics describe the similarity between two different OH stretches in terms of their excitation energies and sensitivity along the optical field polarization directions. The scatter plots corresponding to the OH stretches in w1 and w7 are shown in Fig. 3c, d, respectively. The primary population receivers during VET process are marked in red. Strikingly, for both w1 and w7, the new and prominent intermolecular VET pathways exhibit the same key features: small vibrational frequency deviations and large dipole derivative correlations. This provides direct evidence of cavity-induced vibrational resonances among OH groups across different water molecules. In addition to frequency similarity, these resonances occur when the dipole derivatives of the OH stretches are both relatively strong and aligned with the cavity’s polarization directions. Notably, such resonances can involve both nearby and distant water molecules. For instance, in Fig. 3c, the resonance participants w2 and w11 are located in the first and third hydration shells of w1, respectively. A similar observation is evident in Fig. 3d for monomer 7.

Mode-specific mechanism for cavity-modified vibrational dynamics

In addition to cavity-induced vibrational resonance, it is essential to explore the general mechanism by which collective VSC influences vibrational dynamics, particularly the common features of vibrations whose relaxation dynamics are altered. Detailed analyses are provided in Fig. 4 and Table 1. We begin by examining the number of significant relaxations among the 42 OH stretches, as illustrated in Fig. 4a, with detailed counts listed in Supplementary Table 3. Outside the cavity, only 9 OH stretches successfully relax via intramolecular vibrational couplings. However, when the \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) system is placed inside the cavity, even with a weak light-matter coupling strength of g = 0.001 a.u., the number of successful relaxations increases to 13. Under the VSC regime, with g = 0.006 a.u., this number nearly triples, indicating a dramatic enhancement of relaxation pathways.

Fig. 4: Mode-specific modification of OH relaxation under vibrational strong coupling.
figure 4

a Number of successful relaxations in \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\)-cavity system as a function of light-matter coupling factors g. A successful relaxation is defined that the population of OH stretch can be lower than 0.25 in the time interval of 0–1000 fs. b Scattering plot of the magnitude of dipole moment derivative (dμ/dQ) along x and y axis, f(dμ/dQ) = max(∣dμx/dQ∣, ∣dμy/dQ∣), of various OH stretches in different types of water molecules which cannot relax outside the cavity. Solid cycles indicate OH stretches can relax inside the cavity, while open cycles indicate OH stretches still cannot relax inside the cavity. c Stick distributions of vibrational configuration interaction (VCI) coefficients of OH stretch in monomer 1 under different light-matter coupling strengths. The cavity frequency is set as 3400 cm−1 for (a–c).

Full size image
Table 1 Number of OH stretches with different vibrational relaxation behaviors
Full size table

We further classify the 42 OH stretches based on their relaxation behaviors both outside and inside the cavity, as well as their corresponding hydrogen-bonding features. As summarized in Table 1, the 9 OH stretches that successfully relax outside the cavity correspond to H-bonded stretches in AADD and ADD water molecules. Under VSC, the primary effects on these stretches are modifications in their relaxation rates and the emergence of new intermolecular VET pathways, as demonstrated by the example of dynamics of monomer 7 in Figs. 2 and 3. Of the remaining 33 OH stretches that do not relax outside the cavity, 22 achieve relaxation under VSC conditions. These include monomers of various types, such as AADD, AAD, and ADD water molecules. However, 11 OH stretches remain unrelaxed even under VSC conditions, many of which correspond to OH stretches in AAD water molecules, particularly the free OH stretches.

An intuitive explanation for why some OH stretch dynamics are influenced by cavity coupling while others are not lies in the orientation of their transition dipole moments relative to the cavity field polarization. In Fig. 4b, we analyzed the anharmonic vibrational frequencies and dipole derivative information for the 33 OH stretches that do not relax outside the cavity. Similar to the definition above, the dipole derivative for each OH stretch is given by max(∣dμx/dQi∣, ∣dμy/dQi∣). As shown by the solid points in Fig. 4b, the OH stretches that exhibit significant changes in their relaxation dynamics under VSC tend to have relatively large dipole derivative magnitudes. These stretches span a broad spectral range of 3000–3600 cm−1 and are found in AAD, AADD, and ADD water molecules. In contrast, the 11 OH stretches that remain unrelaxed under VSC generally exhibit smaller dipole derivatives along the cavity’s polarization directions (x and y axes). Notably, these unrelaxed stretches also include H-bonded OH groups with relatively red-shifted frequencies, and nearly half of them correspond to free OH stretches in AAD water molecules. Additional analyses of the anisotropy of energy transfer within optical cavity are presented in Supplementary Section 6, where the population dynamics of all OH stretches with varying dipole moment orientations are shown. As observed, cavity-modified vibration energy transfer is significant for vibrations with dipole moment aligning along the cavity polarization direction. In contrast, when the transition dipole moment is oriented along z-axis, the corresponding vibrations do not couple to the cavity and virtually no VET process can be observed.

The cavity-modified VET rate and pathways can also be attributed to cavity-modified anharmonic vibrational coupling patterns, i.e., the collective couplings among the OH stretches enabled by the VSC. Figure 4c shows the stick distribution of VCI coefficients of OH stretch in monomer 1 under different light-matter coupling factors g. As shown in Eq. (6), the VSCF/VCI approach explicitly and quantitatively provides information on mode couplings among various vibrational states through the corresponding VCI expansion coefficients Ci. The magnitude of Ci reflects the extent to which a particular vibrational state contributes to the final VCI eigenstate. Thus, a larger number of VCI eigenstates with nonnegligible contribution from a specific vibration, such as the OH stretch in monomer 1, indicates stronger couplings between this OH stretch and other vibrational states during the formation of hybrid VCI eigenstates. Outside the cavity, the VCI coefficient of OH stretch predominately locates at around 3400 cm−1. Due to weak couplings with bend overtone and another high-frequency OH stretch, some components appear at 3240 cm−1 and 3507 cm−1. When \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) is inside the cavity, the molecular coupling patterns are greatly modified. With increasing coupling strength, the VCI coefficient of OH stretches spans an increasing spectral range of 2800–4000 cm−1. This is due to the formation of collective polaritonic states and the alignment of OH stretches’ transition dipole moment plays an important role in these processes. The cavity-induced direct coupling between OH stretches in different water monomers opens new routes for efficient vibrational relaxations. Even without participation of low-frequency intermolecular modes, the OH stretches show delocalization behavior among waters within and beyond the first hydration shell.

Effect of intermolecular modes and intermolecular couplings on cavity-modified vibrational energy transfer

Finally, it is necessary to investigate the role of low-frequency intermolecular modes (“frustrated” rotations and translations) and intermolecular couplings among all modes for \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\)-cavity system. Given it is computationally too expensive to include all intermolecular and intramolecular modes, we performed reduced cav-VSCF/VCI calculations incorporating all intramolecular vibrational modes, the cavity mode, and monomer’s three low-frequency intermolecular modes to study the population dynamics of corresponding water molecule. The resulting cav-VSCF/VCI simulations for w1 and w7 are presented in Fig. 5 and more examples are shown in Supplementary Fig. 11. As discussed in the previous section, the inclusion of three low-frequency modes and intermolecular couplings enables rapid and efficient relaxation of the OH stretch for \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) outside the cavity. When coupled to the cavity mode, as shown in Fig. 5a, c and Supplementary Fig. 11, the VSC further enhances intermolecular relaxation of OH stretches, reinforcing the general finding that efficient VET among molecules can be achieved through VSC12. While the inclusion of intermolecular couplings reduces the magnitude of the effect, there is still an appreciable difference between the vibrational relaxation in and out of the cavity. Actually, the enhancement of relaxation dynamics under VSC is more clearly demonstrated in Supplementary Fig. 21, where we present the short-time population dynamics over the 0–400 fs range. The relaxation rate, dP/dt, gets apparently faster under VSC even though the OH relaxation is already fast without the cavity. As in the cases of H2O and \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{2}\) shown in Supplementary Fig. 3, population oscillations are also observed in \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) at the long time. These oscillation features are related to the finite size of the clusters. It can be expected that significantly stronger damping with virtually no oscillations can be expected for larger system such as liquid water. In addition, the VSC primarily affect the short-time relaxation rate and also potentially significant in condensed phase system.

Fig. 5: Effect of intermolecular modes and intermolecular couplings on population dynamics under vibrational strong coupling.
figure 5

a, b Time-dependent populations of the OH stretch (νOH1-w1) and other intramolecular modes (νOH2-w1, 2νb-w1) in monomer 1 (w1) following excitation of νOH1-w1. c, d Time-dependent populations of the OH stretch (νOH1-w7) and other intramolecular modes (νOH2-w7, 2νb-w7) in monomer 7 (w7) after excitation of νOH1-w7. Black and purple curves correspond to simulations excluding low-frequency intermolecular modes and neglecting intermolecular couplings. Red and blue curves represent simulations that additionally include 3 low-frequency intermolecular modes and account for all intermolecular couplings. The cavity frequency is set as 3400 cm−1.

Full size image

The effect of VSC on the interplay between intramolecular and intermolecular energy transfer is also investigated. As shown in Fig. 5b and d, for both w1 and w7, without the inclusion of intermolecular modes and intermolecular mode couplings, after excitation of the OH stretch, the population increase of intramolecular modes is suppressed when cavity is involved. This suppression effect is further confirmed in the calculations with both intermolecular modes and couplings included, although it appears slightly weaker. Overall, under VSC, intramolecular energy transfer is generally suppressed, while intermolecular energy transfer is accelerated.

Additional studies are needed to fully assess the interplay between intramolecular and intermolecular energy transfer when all intermolecular modes are explicitly included. It is expected that the couplings among low-frequency intermolecular modes from different water monomers could be weak and may have limited incluence on the vibrational dynamics of high-frequency OH stretches68. Moreover, when significantly more molecules are considered, the overall coupling between the molecular ensemble and the cavity mode may become weaker. However, due to structural disorder, the local coupling strength for individual molecules may remain substantial, allowing VSC to continue playing an important role. These scenarios will be explored in future studies.

Discussion

In this study, we present compelling evidence detailing how the presence of optical cavity influences VET and dynamics of water. The accuracy of our quantum theoretical approaches is validated in the vibrational spectra and relaxation dynamics of pure water system, aligning well with previous experimental and theoretical calculations. Under the VSC, our cav-VSCF/VCI approach reasonably predicts the polaritonic vibrational spectra, capturing essential spectral features. The VSC effect significantly alters the vibrational population dynamics of OH stretch, impacting both pathways and rates. Notably, VSC breaks the localization framework and directly promotes the delocalization of OH stretch across different water molecules. In addition to the conventional intramolecular relaxation pathway, intermolecular VET pathways are easily realized even without the inclusion of extra intermolecular vibrational motions. This intermolecular energy transfer extends beyond the water’s first hydration shell, suggesting the potential for controlling remote molecules through VSC. As to the relaxation rate, the acceleration of vibration energy transfer with stronger light-matter coupling strength is a general trend. All these observations agree with the key findings in recent VSC experiments12,13. We also demonstrate that, although exhibiting similar general trends, the specific relaxation dynamics of individual water molecules respond differently to the collective VSC effect in terms of both rate and pathways.

The primary mechanism underlying cavity-induced VET is the correlation between the vibrational transition dipole moment vector and the cavity polarization directions. The extent of these dipole correlations plays a crucial role in determining the differences in individual molecules’ vibrational dynamics under VSC. This phenomenon has been explored theoretically in previous studies focusing on model systems20,71,72. However, our work provides systematic verification of this mechanism through fully quantum simulations of a realistic many-molecules molecular system, representing a significant step forward compared to single-molecule systems, which has been widely employed in both classical and quantum mechanical studies18,19,22. Another important mechanism for the emergence of new VET pathways is cavity-induced vibrational resonance, which involves vibrations in both nearby and remote molecules. The key factors enabling these resonances are the alignment of transition dipole moments with the cavity polarization and the vibrational frequency match between coupled molecules. Our quantum mechanical investigation of mode-specific mechanisms underlying cavity-modified VET pathways offers new insights into VSC-altered reaction dynamics. We hope that our findings as well as the realistic molecular system employed in this work can potentially guide the design of appropriate model Hamiltonian systems beyond simple two-level TCM model. Such appropriate models are crucial to analyze the collective VSC dynamics in macroscopic ensembles of molecules within optical cavity.

Our work achieves a fully quantum dynamical simulation of molecules-cavity system on realistic and CCSD(T)-level PES with collective coupling effect included. The \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) provides a balance between computational efficiency, structural similarity to liquid water, and the incorporation of necessary collective couplings. However, it should be noted again that the realistic cavity system involves significantly more molecules, multiple cavity modes, and the impact of cavity loss should be considered. In VSC experiments, a macroscopic number of molecules, Nmol ≈ 1010, collectively couple to the cavity mode, and the spectral Rabi splitting scales with \(\sqrt{{N}_{{{{\rm{mol}}}}}/\tilde{V}}\). To compensate for the lack of  ≈ 1010 molecules in our simulations, the coupling strength g in this work reflects a much smaller effective cavity volume \(\tilde{V}\) compared to experimental setups. For instance, with cavity frequency ω = 3400 cm−1 and coupling strength g = 0.006 a.u., the effective cavity volume \(\tilde{V}\) is 0.4 nm3, which falls within the picocavity regime.

Despite our work provide new quantum-mechanical-level understandings of how VSC affects the VET process in molecules under collective coupling, it remains challenging to quantum-mechanically investigate the cavity-modified VET processes as the number of molecules increase. In realistic VSC experiements, the coupling to the cavity for individual molecule can be relatively weak and more careful assessments are required. Future calculations will incorporate these effects by extending our approach to condensed-phase system, such as liquid water and dilute HOD in ice68. Employing semiclassical methods such as temperature-elevated path integral coarse-graining simulations (Te PIGs) and fast quasicentroid molecular dynamics ((f)-QCMD) can also be good choices as they provide a good balance of computational efficiency and adequate description of nuclear quantum effects73,74,75. Exploring the effects of vibrational dynamics after exciting polaritonic states and dark states will also be a focus of our future investigations. We hope that our theoretical findings in the current work provide new insights on how the VSC influences the energy transfer and chemical reactivities in molecular systems, as well as stimulating both experimental and theoretical investigations of cavity-induced properties in molecular systems.

Methods

Potential energy and dipole moment surfaces of water

We employed highly accurate, CCSD(T) level PES and MP2 level DMS of water for all the calculations in this work. The PES is taken from our recently developed machine learning potential, q-AQUA66. This potential represents the total energy of N-monomer water system (H2O)n through standard many body expansion at the 4-body level:

$${V}_{({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})_{{{\rm{n}}}}}={\sum}_{i=1}^{N}{V}_{{{{{\rm{w}}}}}_{i}}^{(1)}+{\sum}_{i > j}^{N}{V}_{{{{{\rm{w}}}}}_{i},{{{{\rm{w}}}}}_{j}}^{(2)}+{\sum}_{i > j > k}^{N}{V}_{{{{{\rm{w}}}}}_{i},{{{{\rm{w}}}}}_{j},{{{{\rm{w}}}}}_{k}}^{(3)}+{\sum}_{i > j > k > l}^{N}{V}_{{{{{\rm{w}}}}}_{i},{{{{\rm{w}}}}}_{j},{{{{\rm{w}}}}}_{k},{{{{\rm{w}}}}}_{l}}^{(4)}$$
(1)

where \({V}_{{{{{\rm{w}}}}}_{i}}^{(1)}\) is the spectroscopically accurate 1-body potential for the isolated monomer obtained from Partridge et al.76. \({V}_{{{{{\rm{w}}}}}_{i},{{{{\rm{w}}}}}_{j}}^{(2)},{V}_{{{{{\rm{w}}}}}_{i},{{{{\rm{w}}}}}_{j},{{{{\rm{w}}}}}_{k}}^{(3)}\), and \({V}_{{{{{\rm{w}}}}}_{i},{{{{\rm{w}}}}}_{j},{{{{\rm{w}}}}}_{k},{{{{\rm{w}}}}}_{l}}^{(4)}\) are the intrinsic 2-, 3-, 4-body interactions among water molecules. The 2-body potential is from a machine learning fit using 71,892 CCSD(T)/CBS 2-b energies. The 3-body and 4-body potentials were fitted based on 45,332 BSSE corrected CCSD(T)-F12a/aVTZ and 3692 CCSD(T)-F12a/haTZ data, respectively. The accuracy of q-AQUA has been systematically verified in structures, vibrational spectra, and dynamics tests across gas-phase water clusters and condensed phase liquid water66.

The dipole moment of water is taken from our previously developed WHBB DMS77, which also follows a many-body representation:

$${{{{\boldsymbol{\mu }}}}}_{({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})_{{{\rm{n}}}}}={\sum}_{i=1}^{N}{{{{\boldsymbol{\mu }}}}}_{{{{{\rm{w}}}}}_{i}}^{(1)}+{\sum}_{i > j}^{N}{{{{\boldsymbol{\mu }}}}}_{{{{{\rm{w}}}}}_{i},{{{{\rm{w}}}}}_{j}}^{(2)}$$
(2)

where the 1-body water dipole \({{{{\boldsymbol{\mu }}}}}_{{{{{\rm{w}}}}}_{i}}^{(1)}\), is taken from a highly accurate DMS for isolated monomer developed by Lodi et al.78. The 2-body dipole, \({{{{\boldsymbol{\mu }}}}}_{{{{{\rm{w}}}}}_{i},{{{{\rm{w}}}}}_{j}}^{(2)}\!\), is from a machine learning fit to roughly 30,000 MP2/aVTZ dipole moment data77. The final DMS for water has also been tested extensively in the IR spectral calculations of water clusters, liquid water, and ice.

cav-VSCF/VCI approach

We recently developed cavity vibrational self-consistent field/virtual state configuration interaction (cav-VSCF/VCI) approach to calculate polaritonic vibrational spectra of molecular system in an optical cavity64,65. This approach employs the Pauli-Fierz Hamiltonian20,79 to describe the system of N molecules with NQ mass-scaled rectilinear normal modes Q in an optical cavity of NC cavity modes:

$${\hat{H}}_{{{{\rm{QED}}}}}=-\frac{1}{2}{\sum}_{i}^{{N}_{{{{\rm{Q}}}}}}\frac{{\partial }^{2}}{\partial {Q}_{i}^{2}}+{\sum}_{k}^{{N}_{{{{\rm{C}}}}}}\frac{1}{2}{\hat{p}}_{k}^{2}+{V}_{{{{\rm{eff}}}}}({{{\bf{Q}}}},{{{\bf{q}}}})$$
(3)

where Veff(Q, q) is the effective potential energy of the molecule-cavity system, \({V}_{{{{\rm{eff}}}}}({{{\bf{Q}}}},{{{\bf{q}}}})=V({{{\bf{Q}}}})+{\sum}_{k}^{{N}_{{{{\rm{C}}}}}}\frac{1}{2}{\omega }_{k}^{2}{({\hat{q}}_{k}+\sqrt{\frac{2}{{\omega }_{k}^{3}}}g\hat{{{{\boldsymbol{\mu }}}}}\cdot {{{{\bf{e}}}}}_{k})}^{2}\). \({\hat{p}}_{k}\) and \({\hat{q}}_{k}\) are the momentum and position operators for cavity mode k. \(\hat{{{{\boldsymbol{\mu }}}}}\) is the dipole moment vector for the molecular system. ek is the polarization vector of the field for the cavity mode k. Each cavity mode k is assumed to have frequency ωk and polarization vector ek. g is the light-matter coupling strength factor, which is related to cavity mode frequency, permittivity ϵ0, and effective cavity volume \(\tilde{V}\), such that \(g=\sqrt{{\omega }_{k}/(2{\epsilon }_{0}\tilde{V})}\).

In analogous to the conventional VSCF/VCI approach, our cav-VSCF/VCI method expresses the hybrid nuclear-cavity vibrational wavefunction on the basis of corresponding VSCF states:

$$\Psi ({{{\bf{Q}}}},{{{\bf{q}}}}) =\mathop{\sum}_{m}{C}_{m}{\Phi }_{m}({{{\bf{Q}}}},{{{\bf{q}}}})\\ ={\sum}_{m}{C}_{m}{\prod }_{i=1}^{{N}_{{{{\rm{Q}}}}}}{\phi }_{i}^{m}({Q}_{i}){\prod }_{i=1}^{{N}_{{{{\rm{C}}}}}}{\chi }_{i}^{m}({q}_{i})$$
(4)

where Φm(Q, q) is the quantum VSCF state as direct product of NQ molecular modes, \({\phi }_{i}^{m}({Q}_{i})\), and NC cavity modes, \({\chi }_{i}^{m}({q}_{i})\). The VCI combination coefficients Cm are determined by diagonalizing the VCI Hamiltonian matrix. More details of the cav-VSCF/VCI method are referred to our previous work64,65.

A series of technical strategies have recently been implemented to enable large-scale cav-VSCF/VCI calculations on the large cavity-molecules system, i.e., \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\)65. However, due to non-zero interaction terms between modes from different molecules, these implementations cannot provide an absolutely localized scheme among molecules. Thus, it could not be directly employed to study how VSC modifies the localization scheme of the molecular system. In this work, we address this problem by imposing an additional constraint on the effective potential, Veff(Q, q). Under the n—mode representation framework, Veff(Q, q) is expressed as:

$${V}_{{{{\rm{eff}}}}}({{{\bf{Q}}}},{{{\bf{q}}}})= {\sum}_{i}{V}_{i}^{(1)}({Q}_{i})+{\sum}_{i}{V}_{i}^{(1)}({q}_{i})\\ +{\sum}_{i,j}{V}_{ij}^{(2)}({Q}_{i},{Q}_{j})+{\sum}_{i,j}{V}_{ij}^{(2)}({Q}_{i},{q}_{j})\\ +{\sum}_{i,j}{V}_{ij}^{(2)}({q}_{i},{q}_{j})+{\sum}_{i,j,k}{V}_{ijk}^{(3)}({Q}_{i},{Q}_{j},{Q}_{k})+\cdots$$
(5)

where \({V}_{i}^{(1)}({Q}_{i})\) and \({V}_{i}^{(1)}({q}_{i})\) are the one-mode potentials for the molecular normal mode and the cavity mode, respectively. \({V}_{ij}^{(2)}({Q}_{i},{Q}_{j})\), \({V}_{ij}^{(2)}({q}_{i},{q}_{j})\), \({V}_{ij}^{(2)}({Q}_{i},{q}_{j})\), etc. are the intrinsic 2-mode potentials for pairs of molecular normal modes, pairs of cavity modes, and pairs composed of a molecular normal mode and a cavity mode, etc.

To reduce the computational cost, we employ the local monomer approximation strategy80,81, Within this strategy, for each water molecule, standard local normal mode analysis generates 9 modes, where three of them are intramolecular modes (bend and stretches) and remaining six low-frequency modes are intermolecular one (“frustrated” rotations and translations). Our previous work ignores significant number of coupling terms between intramolecular vibrations from different molecules65. For example \({V}_{ij}^{(2)}({Q}_{i},{Q}_{j})\) and \({V}_{ijk}^{(3)}({Q}_{i},{Q}_{j},{Q}_{k})\) are set as 0 if one of the normal modes is from a different molecule. Additionally, in this work, to ensure absolutely zero couplings between intramolecular vibrations of different molecules, we impose a further constraint such that \({V}_{ijk}^{(3)}({q}_{i},{Q}_{j},{Q}_{k})\) is also set as 0 if Qj and Qk are from different molecules. This scheme significantly reduces the number of potential grid point calculations as the 3-mode potential requires \(\left(\left(\begin{array}{c}{N}_{{{{\rm{C}}}}}\\ 3\end{array}\right)+N\left(\begin{array}{c}{N}_{{{{\rm{C}}}}}\\ 2\end{array}\right)\left(\begin{array}{c}{N}_{{{{\rm{m}}}}}\\ 1\end{array}\right)+N\left(\begin{array}{c}{N}_{{{{\rm{C}}}}}\\ 1\end{array}\right)\left(\begin{array}{c}{N}_{{{{\rm{m}}}}}\\ 2\end{array}\right)+N\left(\begin{array}{c}{N}_{{{{\rm{m}}}}}\\ 3\end{array}\right)\right)\cdot {l}^{3}\) grid points, where l is the number of quadrature points per mode, N is the number of molecules, and Nm is the number of modes for each molecule. It should be noted that to fully describe the vibrational dynamics of OH stretches, the local monomer approximation employed in this work is not sufficient as the OH stretch excitations can delocalize over its hydration shells, ~15 water molecules58,82. However, together with previous implementations, this framework provides a platform to investigate how VSC affects molecular coupling patterns and localization behavior.

To demonstrate the effects of intermolecular modes and intermolecular mode couplings, we applied a different cav-VSCF/VCI scheme with non-approximated descriptions of the n-mode representation as given in Eq. (5). In this scheme, all the terms including \({V}_{ij}^{(2)}({Q}_{i},{Q}_{j})\), \({V}_{ijk}^{(3)}({Q}_{i},{Q}_{j},{Q}_{k})\), and \({V}_{ijk}^{(3)}({q}_{i},{Q}_{j},{Q}_{k})\) are explicitly calculated without arbitrary constraints. As can be expected, these sets of calculations are much more computationally expansive as the 3-mode potential requires \(\left(\begin{array}{c}{N}_{{{{\rm{C}}}}}+N{N}_{{{{\rm{m}}}}}\\ 3\end{array}\right)\cdot {l}^{3}\) grid points, which is several orders of magnitude larger than the grid size used in the localization scheme described above. To investigate the population dynamics of OH stretch of each monomer, such as w1, we included 3 low-frequency intermolecular modes of the corresponding monomer and all high-frequency intramolecular modes (66 molecular modes in total). Including more intermolecular modes will be more expensive in potential grid calculations and also VCI Hamiltonian construction. This subject to our further method implementation.

All the cav-VSCF/VCI frameworks has been implemented in our in-house version of MULTIMODE83,84 with an interface to the q-AQUA PES and WHBB DMS. Note, both PES and DMS are full dimensional which are used to obtain the effective potentials Veff at different nuclear configurations. Instead of frequently used Condon approximation, in our VSCF/VCI framework, the full dimensional DMS is further employed to calculate the transition dipole moment for IR intensity calculation using VCI wavefunctions85. In our new cav-VSCF/VCI calculations of \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\)-cavity system, the \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) is placed inside an optical cavity oriented along the x axis. A single cavity mode with two polarization directions (y and z) is considered. In most calculations, three intramolecular modes (2 OH stretches and 1 HOH bend) of each water monomer are included. Thus, at least 63 localized normal modes of \({({{{{\rm{H}}}}}_{2}{{{\rm{O}}}})}_{21}\) are considered. A 3-mode representation (3MR) of the effective potential, Veff, was applied where the potential is expanded up to 3-mode coupling terms, such as \({V}_{ijk}^{(3)}({Q}_{i},{Q}_{j},{Q}_{k})\). As to the dipole moment, a 2-mode representation (2MR) is applied where the dipole moment is expanded up to the 2-mode coupling terms, such as \({\mu }_{ij}^{(2)}({Q}_{i},{Q}_{j})\). Such strategy has been frequently applied to different molecular systems and proved to give results that are converged and comparable to experiments. The standard Gaussian broadening with full width at half maximum (FWHM) of 70 cm−1 was applied for generating the IR spectra based on VSCF/VCI and cav-VSCF/VCI eigenstates.

Quantum wavepacket dynamics simulation

The quantum wavepacket dynamics were conducted based on the cav-VSCF/VCI wavefunctions. Similar approach has been applied in vibrational relaxation dynamics calculations of dilute HOD in ice68. For simplicity, we rewrite the ith cav-VSCF/VCI wavefunction, Ψi as:

$${\Psi }_{i}={\sum}_{j}^{{N}_{{{{\rm{b}}}}}}{C}_{ij}{\Phi }_{j}$$
(6)

where Nb is the total number of VSCF basis functions Φj, Cij is the VCI expansion coefficient. Now, we use the non-stationary VSCF state to represent the initial wavepacket of OH stretch excitation, such that

$${\psi }_{k}(0)={\Phi }_{k}={\sum}_{j}^{{N}_{{{{\rm{b}}}}}}{C}_{kj}^{-1}{\Psi }_{j}\\ \,={\sum}_{j}^{{N}_{{{{\rm{b}}}}}}{C}_{kj}^{T}{\Psi }_{j}={\sum}_{j}^{{N}_{{{{\rm{b}}}}}}{C}_{jk}{\Psi }_{j}$$
(7)

where the orthogonal property of the eigenvector matrix C is applied. Thus, the time-dependent wavepacket is expressed by

$${\psi }_{k}(t)={\sum}_{j}^{{N}_{{{{\rm{b}}}}}}{C}_{jk}{\Psi }_{j}{e}^{-i{E}_{j}t/\hslash }$$
(8)

The auto-correlation function can be directly calculated as

$$Cor{r}_{k}(t)=\langle {\psi }_{k}(0)| {\psi }_{k}(t)\rangle={\sum}_{j}^{{N}_{{{{\rm{b}}}}}}{C}_{jk}^{2}{e}^{-i{E}_{j}t/\hslash }$$
(9)

As seen, Corrk(t)2 is the population change of the initial wavepacket ψk(0) and time-dependent population of another state Φl can be calculated as \(Cor{r}_{k}^{l}{(t)}^{2}\) where \(Cor{r}_{k}^{l}(t)\) is given by:

$$Cor{r}_{k}^{l}(t)=\langle {\Phi }_{l}(0)| {\psi }_{k}(t)\rangle={\sum}_{j}^{{N}_{{{{\rm{b}}}}}}{C}_{jl}{C}_{jk}{e}^{-i{E}_{j}t/\hslash }$$
(10)

We propagated the wavepacket dynamics for 1000 fs for each set of excited OH stretch. The population change for the initial excited OH stretch and the population of other states are recorded for further analyses. Note that our wavepacket dynamics is based on the VCI eigenstates and coefficients obtained at the stage of VSCF/VCI computations. Although this approach differs from conventional time-dependent quantum wavepacket dynamics, it is well suited for simulating time-dependent population dynamics and has been successfully employed to analyze the vibrational relaxation pathways of dilute HOD in Ice Ih68.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.