Muscle-inspired elasto-electromagnetic mechanism in autonomous insect robots

Xu, Changyu; Cao, Yajun; Zhao, Jingyang; Cao, Yujia; Huang, Yi; Lin, Yangyi; Wang, Dong; Zhang, Zhuang; Jiang, Hanqing

doi:10.1038/s41467-025-62182-2

Download PDF

Article
Open access
Published: 24 July 2025

Muscle-inspired elasto-electromagnetic mechanism in autonomous insect robots

Nature Communications volume 16, Article number: 6813 (2025) Cite this article

6212 Accesses
38 Altmetric
Metrics details

Subjects

Abstract

In nature, the dynamic contraction and relaxation of muscle in animals provide the essential force and deformation necessary for diverse locomotion, enabling them to navigate and overcome environmental challenges. However, most autonomous robotic systems still rely on conventional rigid motors, lacking the adaptability and resilience of muscle-like actuators. Existing artificial muscles, while promising for soft actuation, often require demanding operational conditions that hinder their use in onboard-powered small autonomous systems. In this work, we present the Elasto-Electromagnetic mechanism, an electromagnetic actuation strategy tailored for soft robotics. By structuring simple elastomeric materials, this mechanism mimics key features of biological muscle contraction and optimizes actuation properties. It achieves significant output force (~210 N/kg), large contraction ratio (up to 60%), rapid response (60 Hz), and low-voltage operation (<4 volts) within a robust, miniaturized framework. It also enhances energy efficiency by maintaining stable states without continuous power input, similar to catch muscles in mollusks. The resulting insect-scale soft robots, therefore, demonstrate adaptive crawling, swimming, and jumping, autonomously navigating open-field environments. This muscle-inspired electromagnetic mechanism, facilitated by elastic structural variations, expands the autonomy and functional capabilities of small-scale soft robots, with potential applications in rescue and critical signal detection.

Ultrafast small-scale soft electromagnetic robots

Article Open access 09 August 2022

2-dimensional impact-damping electrostatic actuators with elastomer-enhanced auxetic structure

Article Open access 26 August 2024

Multifunctional Magnetic Muscles for Soft Robotics

Article Open access 10 September 2024

Introduction

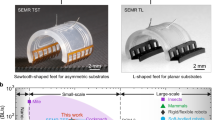
Muscles in animals function as powerful actuators, providing necessary output force and deformation through the simple contraction and relaxation of muscle fibers¹. Coupled with elegantly structured connection systems, these powerful muscles enable diverse and efficient locomotion patterns², which are particularly critical at smaller scales. At such scales, biological organisms must generate disproportionately large forces relative to their body mass to effectively overcome environmental resistances, a challenge clearly demonstrated by small insects that produce output forces exceeding 230 N/kg³, significantly higher than those produced by larger animals⁴ (Fig. 1a and Supplementary Table 1). This illustrates the critical need to develop robotic actuation methods in small scale capable of achieving similar force-to-mass ratios.

**Fig. 1: Muscle-inspired elasto-electromagnetic (EEM) mechanism for insect-scale soft robots.**

Current robotics technologies, while aimed at mimicking animal and human behaviors, fall short of fully incorporating bio-inspired contraction muscle actuation. Predominantly, these systems rely on the continuous rotational motion of electric motors, necessitating complex, rigid components such as bearings, reducers, and transmission gears to transform high-speed rotation into linear or articulated motions^5,6. Although electric motors have facilitated significant advancements in large-scale robotics^7,8,9,10,11, they encounter significant barriers when miniaturized due to increased friction, susceptibility to impact damage, and bulky motion structures, factors that become especially problematic in small-scale applications^12,13. Furthermore, the inherent rigidity of motor-based systems limits their adaptability to environmental uncertainties, thereby imposing stringent demands on force feedback and dynamic balance¹⁴. These challenges underscore their unsuitability for small-scale robotics, where softness and an efficient force-to-mass ratio are paramount.

Recognizing these limitations, researchers have explored actuation methods using smart materials^15,16, often referred to as artificial muscles. However, these efforts still fail to replicate the efficient and powerful muscle actuation seen in nature with full autonomy, as those smart material-based systems often require harsh conditions, such as strong external fields¹⁷, high voltages¹⁸, intense light¹⁹, or significant temperature changes²⁰ (see the subsection “Artificial muscles and comparative analysis” in the “Methods” section and Supplementary Table 2). Consequently, many small-scale robots remain tethered^{21,22,23,24,25} or reliant on external stimulations for actuation^{26,27,28,29,30,31}. Despite efforts to reduce these requirements for autonomous actuation under onboard power, the output forces of these centimeter-scale robots^{32,33,34,35,36,37,38} still fall short of biological force standards³⁹ ($0.5\times {{{{\rm{bodymass}}}}}^{-\tfrac{1}{3}}$ to $20\times {{{{\rm{bodymass}}}}}^{-\tfrac{1}{3}}$) (Fig. 1a), underscoring a significant gap. Moreover, these robotic systems often exhibit minimal contraction ratio/actuation stroke^{32,36,37,38,40,41}, severely limiting their locomotion capabilities and practical utility.

To address the need for powerful and autonomous actuation in soft robots, especially at insect scale, we introduce the elasto-electromagnetic (EEM) mechanism, an approach that extends conventional electromagnetic frameworks to soft actuation by leveraging the structural properties of elastomeric materials combined with magnetic attractive forces to emulate diverse biological muscle contractions (Fig. 1b). The EEM mechanism achieves significant output force, large contraction ratio, rapid response, and low-voltage operation within a streamlined, easily miniaturizable design. It offers a promising strategy for advancing autonomous soft robots and artificial muscles, with the capability to generate large output force and contraction ratios approaching those observed in biological systems (Fig. 1a), supporting autonomous locomotion under environmental resistance. Drawing inspiration from biological systems that convert muscle contractions into locomotion, we implement flexure-based linkage mechanisms in our insect-scale soft robots to efficiently perform locomotion modes such as inchworm-like crawling, legged crawling, swimming, and jumping, autonomously navigating varied and complex environments (Fig. 1c). Enhanced with sensing capabilities, these robots can perform critical tasks like hazardous signal detection and search-and-rescue missions, showcasing their potential for real-world applications (Fig. 1c).

Results

Components and mechanism

The muscle-inspired EEM system comprises three core components: a magnetized hard magnet, an elastomeric structure, and an electrical coil intertwined with soft magnetic spheres (Fig. 2a(i) and Supplementary Fig. 1c). Unlike traditional electric motors that rely on continuous rotation, the EEM system achieves muscle-like contraction by balancing magnetic and elastic forces. It also differs from linear or existing soft electromagnetic actuators, which primarily depend on Lorentz forces and typically require sustained currents or strong external fields^27,42,43,44. In our design, static magnetic interaction between hard and soft magnets plays a central role in deformation, while the Lorentz force helps modulate the balance between magnetic and elastic forces. The electric actuation current, which contributes to the net mechanical work, influences this modulation in two ways: first, by generating the Lorentz force between the electric coil and hard magnet, and second, by enhancing the magnetic moment in the soft magnets, thus amplifying the static magnetic interaction. This shift of the electromagnetic system enables enhanced output force (Supplementary Fig. 2a and b) as well as extended deformation and stroke under onboard-compatible power, which is critical for small-scale autonomous soft robots. (see the section “Distinction between EEM system and other electromagnetic systems” in the “Methods” section).

**Fig. 2: The muscle-inspired EEM actuation mechanism.**

On the other hand, the system’s elasticity, which is critical to its muscle-like functionality, is governed by the elastomeric structure’s ability to deform and recover, as illustrated in the force-displacement analysis (Fig. 2a(ii)). Unlike other artificial muscles that solely focus on the inherent properties of soft materials, this system leverages structural variations to diversify elastic responses and harnesses significant output force from magnetic interactions. This strategy eliminates the harsh actuation conditions often required by other artificial muscles, allowing efficient operation under onboard power. The material choices are flexible; here, we use NdFeB as the hard magnet, pure iron as the soft magnet, and polydimethylsiloxane (PDMS) as the elastomer (see the subsection “Materials properties” in the “Methods” section).

Modulation of forces

As the EEM system contracts, the hard magnet approaches the soft magnetic spheres and the coil, increasing the magnetic attractive force F_em (the combined effect of static magnetic and Lorentz force, defined as positive downward; black curve in Fig. 2a(ii)). Concurrently, deformation of the elastomer generates a counteracting elastic force F_e, defined as positive upward. F_em mimics muscular contraction and F_e drives muscle-like relaxation. Although reversed strong currents can occasionally induce magnetic repulsion, the magnetic interaction remains predominantly attractive—hence our use of the term magnetic attractive force—with repulsion primarily dominated by elastic restoring forces. This setup permits dual modulation of force balance: either by adjusting F_em via electrical currents or by altering F_e through structural design, as detailed below.

Adjusting the magnetic force via electrical currents

At a base state (I = 0), the system stabilizes at a relaxed equilibrium position x₀, where static magnetic and elastic forces are balanced. Applying a current (I = I₁) introduces a Lorentz force and elevates the magnetic attractive force (dashed blue curve), shifting the balance to a new equilibrium x₁ (Fig. 2b). This new stable position x₁ can be precisely controlled by varying the electrical signal I, thus enabling exact manipulations of the actuator’s contraction. As the current increases, contraction is eventually limited by the boundary position, ${x}_{{{{\rm{limit}}}}}$, where the hard magnet encounters the base (Fig. 2a(i)). This limit, set by the elastic structure, defines the EEM system’s contraction ratio. Further details are in Supplementary Information Note 1.

Modifying the elastic force response through the structural design

Through tailored structural design of the elastomer, the EEM system can be engineered to exhibit specific contraction/relaxation characteristics. In scenarios where no electrical current is applied, the design of the elastomeric structure determines the number of stable equilibrium points—whether one, two, or even three—each balanced with the magnetic attractive force F_em. A monostable system returns to its original state when unloaded, while multi-stable systems maintain distinct states even after external load removal (Fig. 2c(i)–(iii), Supplementary Video 1). This capability of realizing multiple stable states within a notably compact design is possible through a combined genetic algorithm (GA) with finite element analysis, which is very challenging to achieve using conventional structural design method⁴⁵ (see the subsection “Multi-stability in EEM systems” in the “Methods” section). This methodology, as detailed in Supplementary Information Note 2 and Supplementary Fig. 3, showcases the unique integration of elastic and magnetic forces.

Notably, state transitions can also be triggered through electrical current modulation (Supplementary Video 2). In monostable designs, current shifts the system to a new equilibrium, which reverts when power is off. In multi-stable configurations, the actuator maintains its newly acquired equilibrium states (labeled as state1, state2, and state3 in Fig. 2c(ii)–(iii)) without ongoing current (Supplementary Video 2), greatly enhancing energy efficiency. This functionality mimics catch muscles in mollusks that maintain a contracted state with minimal energy consumption⁴⁶, allowing actuators to hold functional positions autonomously with minimal power.

Transition process between states

Transitions between states can also be engineered by the strategic structural design (Fig. 2c(iv) and (v), Supplementary Video 3, and Supplementary Information Note 2). This structural design allows the system to either smoothly navigate between contraction states with minimal transition displacements or to undergo sudden step transitions that result in spontaneous energy release. Notably, the smooth contraction transitions are facilitated through multiple intersections between elastic and current-dependent magnetic attractive force curves (Fig. 2c(iv)), while sharp transitions enable rapid energy release (Fig. 2c(v)). The sharp transition yields high dynamic performance, including accelerated contraction speeds and enhanced momentum. For instance, the sub-centimeter-scale actuators with this characteristic can utilize the high momentum produced ($0.52\times {10}^{-3}{{{\rm{kg}}}}\cdot {{{\rm{m}}}}/{{{\rm{s}}}}$ in momentum and 0.67 m/s in takeoff velocity, which is comparable to that of a centimeter-scale jumping spider with 0.5–0.7 m/s⁴⁷) to execute jump motions (Fig. 2c(v) and Supplementary Video 3). Moreover, these actuators can be engineered to achieve a significant contraction ratio, reaching up to 60% of their height (Fig. 2c(vi) and Supplementary Video 3).

Theoretically, the presented structural optimization methodology can be utilized to achieve any designated contraction properties related to a specific force–displacement curve, similar to how natural muscles exhibit diverse actuation properties.

The EEM system’s high output force and large actuation stroke under onboard power-compatible conditions make it ideal for autonomous insect-scale soft robotics, where efficient motion transfer is critical. To achieve this, we engineered the elastic structure to also serve as a flexure linkage across different scales (sub-millimeter to decimeter) (Fig. 3a and Supplementary Video 4), converting linear contraction into end-effector movement while preserving a planar geometry. This integrated unit, termed the EEM motor, combines actuation and motion transfer, simplifying manufacturing while ensuring strong output force and extensive deformations.

The actuation characteristics of the EEM motor can be precisely tailored by modifying flexure linkage parameters (Supplementary Information Note 2), enabling monostable, bistable, or smooth actuation modes (Supplementary Fig. 3d and Supplementary Video 4). Notably, the bistable EEM motor is especially effective in minimizing power consumption during contraction/relaxation, a key consideration for untethered insect-scale robots where energy efficiency is essential. The centimeter-scale bistable EEM motor (0.8 g) demonstrates several key advantages. First, it generates a maximum output force of 0.38 N at 1.6 A (Supplementary Fig. 2e), equivalent to 48 times its own weight. The output force refers to the net force the actuator can exert externally during actuation, enabling it to overcome environmental resistance or carry loads. During the contraction phase, the EEM motor actuates downward, and the output force is defined as ${F}_{{{{\rm{em}}}}}-{F}_{{{{\rm{e}}}}}.\,$In the relaxation phase, as the motor actuates upward, the output force becomes ${F}_{{{{\rm{e}}}}}-{F}_{{{{\rm{e}}}}{{{\rm{m}}}}}$ (Fig. 3b(i)). The output force scales with applied current, and both maximum and average values for contraction and relaxation phases are presented in Fig. 3b(ii) (voltage <4 V). Additionally, it achieves a 30% actuation stroke, which is particularly important for efficient locomotive gaits in soft robotics. Both force and stroke are tunable via the proposed structural design methodology. For instance, modifying the elastomeric structure increases displacement to 5 mm (Supplementary fig. 4a), yielding a 49% stroke.

Benefiting from strong magnetic attraction force, the EEM motor operates efficiently at high frequencies, reaching up to 60 Hz (Supplementary Video 4) and completing a full contraction or relaxation stroke in under 4 ms (Supplementary Fig. 4b). Its bistable design requires energy only during brief state transitions, with no power needed to maintain position. Thus, we adopted a low-power actuation strategy (Fig. 3b(i)) using 6 ms current pulses applied only during transitions (see the subsection “Performance of the centimeter EEM motor” in the “Methods” section). This strategy significantly reduces energy use: the bistable motor consumes just 2.3%, 4.7%, 11.3%, 21.2%, and 38.4% of the power needed for full-stroke actuation compared to a monostable counterpart at 1, 2, 5, 10, and 20 Hz, respectively (Supplementary Fig. 4c). Notably, at 1 Hz, consumption is only 38 mW at 1.6 A. This bistable property mitigates the thermal accumulation issue common to most electromagnetic actuators in moderate actuation frequencies. In the bistable EEM motor, the Lorentz force, which is the primary contributor to heat, is only applied briefly during state transitions, and no current is needed to maintain the stable states, thereby reducing heat buildup during prolonged use. We have experimentally evaluated the EEM motor’s performance under continuous operation (>1 h) across different actuation frequencies and load conditions. Details of those experiments are provided in Supplementary Fig. 5 and see the subsection “Thermal effect and force characterization of the EEM motor” in the “Methods” section.

Furthermore, the motor’s deformation angle controlled via the flexure linkage mechanism is programmable and can reach up to 65° (Supplementary Fig. 3e), enabling versatile motions. Lastly, the motor demonstrates high durability, maintaining performance after a 30-m drop and over 4 million cycles (Supplementary Fig. 6). Compared to existing systems for autonomous insect-scale robots (<4 cm)^{32,33,34,35,36,37,38,40,41}, the EEM motor offers significantly greater force and stroke (Supplementary Fig. 4d, e and Supplementary Table 3), advancing the development of robots capable of overcoming environmental resistance and enabling efficient locomotion.

Leveraging 2D molding technology, the bistable EEM motor can be efficiently scaled to millimeter and decimeter sizes (Supplementary Video 5, and see the subsection “Millimeter and decimeter-scale EEM motors” in the “Methods” section). To support effective locomotion, the flexure linkage has been further extended to develop two robotic actuation joints: a translational joint for contraction and a rotational joint for flapping (Fig. 3c and Supplementary Video 6). Analogous to how biological muscles connect to the skeleton through various structural designs to achieve diverse motions, the EEM motor employs flexure linkages to translate simple contraction into complex locomotive capabilities. By leveraging these advanced actuation joints, we have created a range of autonomous soft robots at the insect scale, showcasing strong actuation efficiency and energy efficacy.

Inspired by terrestrial insect locomotion, we developed a compact soft crawler—just 16 mm × 10 mm × 10 mm, weighing 1.8 g—equipped with a bistable translational EEM joint, a 3.7 V lithium-ion battery (ZONCELL, 30 mAh), and an integrated control circuit (Fig. 4a and Supplementary Fig. 14a). This setup enables autonomous forward crawling through sequential contractions and relaxations (Supplementary Video 7). To enhance crawling efficiency, an additional leg was integrated to increase frictional asymmetry during actuation, with its geometry detailed in Supplementary Fig. 7a.

**Fig. 4: The autonomous insect-scale soft inchworm crawler.**

A standout feature of this autonomous crawler is its large output force of up to 0.41 N, benefiting from the muscle-inspired EEM (Supplementary Fig. 2e), significantly surpassing the typical 0.009–0.05 N force range of existing autonomous insect-scale soft crawlers^32,35,36,37, representing an 8–45× enhancement. This enhanced force allows it to potentially overcome large environmental resistance. As shown in Fig. 4b and Supplementary Video 7, the robot crawls effectively on surfaces: glass (5 μm), wood (15.2 μm), PVC (84.8 μm), and stone (650.4 μm) (Fig. 4c). The crawler’s versatility extends even to outdoor soil environments, underscoring its potential for practical applications like agricultural monitoring, search and rescue, or environmental surveillance. Thanks to the EEM motor’s large stroke, each stride covers 35% of its body length at 1 Hz (Fig. 4c(i))—far exceeding that of piezoelectric-based crawlers (0.17–0.6%)^32,36,37, and electroactive-based crawlers (25% at a much lower frequency of 0.05 Hz)³⁵. The stride length remains relatively stable across frequencies, with only a slight decrease observed at higher frequencies (Supplementary Fig. 7c). Speed measurements from 1 to 5 Hz (Fig. 4c(iii)) show a clear frequency-speed correlation. Notably, even on a rough stone surface, the crawler still maintains a competitive speed, demonstrating its robust movement capabilities. Crawling on inclined PVC surfaces at 5°, 10°, and 15° was also tested (Fig. 4c(iv)).

Despite these significant performance advancements, power consumption remains low—just 79 mW at 1 Hz—much lower than autonomous piezoelectric/dielectric actuators (397 mW)³⁷, electroactive actuators (550 mW)³⁵, and linear electric actuators (1.7 W)³⁸, which require continuous electrical power. The robot’s operational duration was experimentally tested by running it continuously on a 30 mAh battery until the supply voltage dropped below the circuit’s threshold. As shown in Fig. 4d(i), the runtime is inversely related to actuation frequency, exceeding one hour at 0.67 Hz. To evaluate thermal effects during continuous operation (setup shown in Supplementary Fig. 7b), we recorded the crawler’s temperature at actuation frequencies of 1, 2, 3, 4, and 5 Hz, with results presented in Fig. 4d(ii). Owing to the advantages of the EEM mechanism and bistable actuation property, heat buildup remains minimal at moderate frequencies, and the system reaches thermal equilibrium, allowing sustained operation without performance degradation until battery depletion. Notably, thermal effects are negligible at lower frequencies (1−3 Hz).

Similar to insects like ants, which can survive high falls due to a favorable mass-to-surface-area ratio (square-cube law), the soft crawler demonstrated significant impact resilience. After a 30-m drop, it exhibited no obvious damage and maintained full functionality (Fig. 5a and Supplementary Video 8), a result of both its lightweight and soft material construction. Further details of this experiment are provided in Supplementary Information Note 3A. To improve maneuverability, we modified the EEM actuator with two independently controlled coils (Supplementary Figs. 7d and 14b for control circuit), enabling directional crawling without increasing the robot’s size (Fig. 5b and Supplementary Video 7). Comprehensive performance metrics among existing autonomous clawers (<4 cm in scale), including size, output force, stride length, power consumption, speed, environmental adaptability, and softness, are detailed in Supplementary Table 4.

**Fig. 5: The autonomous insect-scale soft inchworm crawler and legged crawler.**

Inspired by terrestrial insects with articulated legs, we designed a legged crawler powered by rotational EEM actuation joints (Fig. 5c(i) and Supplementary Video 9). This design employs rotational motion to move the legs forwards and backwards and incorporate the geometry difference to adjust the friction to achieve effective actuation (Supplementary Fig. 8a). Measuring 14 mm × 20 mm × 19 mm and weighing just 1.9 g, the robot achieves a stride length of 42% (Supplementary Fig. 8b) and demonstrates adaptability across diverse surfaces, including navigating outdoor soil (Fig. 5c(ii), Supplementary Fig. 8c, and Supplementary Video 9). The actuation frequency is adjustable, enabling speed modulation to match terrain and task requirements (Supplementary Video 9).

We extended our muscle-inspired soft actuation system to aquatic environments by developing an autonomous insect-scale swimmer. Measuring 19 mm × 19 mm × 11 mm and weighing 2.2 g, the robot integrates a rotational EEM joint for paddling, a 3.7 V lithium-ion battery, a control circuit, and buoyancy elements for floatation (Fig. 6a(i) and Supplementary Fig. 9a). It operates untethered on the water surface and generates a maximum output force of 0.43 N (Supplementary Fig. 2e), significantly outperforming previous autonomous soft swimmers at similar scales (0.016–0.02 N)^34,35.

**Fig. 6: The autonomous insect-scale soft swimmer and jumper.**

By sequentially flapping between two stable states, the robot swims forward (Fig. 6a(ii) and Supplementary Video 10). Because fluid resistance differs between the upstroke and downstroke phases (Fig. 6a(iii)), we tested actuation strategies with phase time ratios of 1:9, 3:7, 5:5, 7:3, and 9:1 at 1 Hz. Results (Fig. 6a(iii)) show higher speeds when the upstroke occupies more of the cycle. We also evaluated performance across flapping frequencies with a 5:5 ratio, achieving speeds of 2.1 cm/s at 0.5 Hz, 2.4 cm/s at 0.67 Hz, 2.6 cm/s at 1 Hz, 3.6 cm/s at 2 Hz, and 6.2 cm/s at 5 Hz (Fig. 6a(iv)). These trends held across all phase ratios.

As evidenced in Fig. 6b and Supplementary Video 10, our swimmer performs effectively in real-world settings, including rivers, achieving 2.4 cm/s at 0.67 Hz with only 53 mW power consumption—enabling 1-h continuous operation on a 30 mAh battery. Its Cost of Transportation (COT = P/mgv) is 102—4–8× lower than comparable soft swimmers (COT = 432−878)^34,35(Supplementary Table 5). Directional swimming is enabled by integrating two independently controlled coils into the EEM joint, allowing complex planar trajectories without increasing size (Fig. 6c, Supplementary Fig. 9c), thereby enhancing maneuverability and application potential.

Jumping locomotion enables robots to overcome obstacles comparable to or larger than their body size, but requires high instantaneous energy output, especially challenging for actuators in autonomous insect-scale robots. As a result, most small-scale jumpers are either tethered^23,48, or rely on external power fields^49,50,51. Leveraging the EEM actuator’s large energy release capability (Fig. 2c(v)), we developed an autonomous insect-scale soft jumping robot measuring just 15 mm × 9 mm × 12 mm (Fig. 6d and Supplementary Video 11). Fully untethered and powered by an onboard battery, the robot can perform continuous jumps—a capability not previously demonstrated at this scale—reaching heights comparable to its own body height. Performance can be further improved by optimizing the EEM’s elastic design and impact dynamics.

As a prototyping demonstration, we equipped our autonomous insect-scale robots with sensors to enable advanced functionalities. Initially, a temperature and humidity sensor was integrated into the soft inchworm crawler (Fig. 7a, circuitry in Supplementary Fig. 14c). To showcase signal detection capabilities, we constructed a synthetic environment with two chambers: A, humidified by a heated water tank, and B, cooled with ice. The crawler navigated through narrow pathways into each chamber (Supplementary Video 12), successfully detecting and wirelessly transmitting temperature and humidity data via an infrared transmitter. This highlights the robot’s potential for environmental monitoring in confined and complex spaces.

**Fig. 7: The autonomous insect-scale robots with signal detection capability.**

We also integrated a chemical sensor—a miniature ethanol gas detector—into the autonomous soft swimmer (Fig. 7b, circuit in Supplementary Fig. 14d). In a test scenario, the swimmer entered a sealed chamber containing ethanol vapor and detected the elevated concentration, transmitting the data externally (Supplementary Video 13), demonstrating its capability for chemical sensing in constrained aquatic settings.

While this demonstration focuses on two sensor types, our integration approach is adaptable to various physical and chemical sensors. This versatility, combined with their proven autonomy in navigating challenging environments, positions these muscle-inspired EEM insect-scale soft robots as promising tools for scientific research and practical applications where access and maneuverability are paramount.

Discussion

In this study, we introduce the muscle-inspired elasto-electromagnetic (EEM) mechanism, a soft actuation approach that extends conventional electromagnetic systems through the integration of elastomeric structures and static magnetic interaction. This versatile and scalable mechanism delivers significant output force and contraction ratio under onboard power, addressing key limitations of existing artificial muscles that require harsh actuation conditions. These capabilities, along with the multi-stable designs, enable fully autonomous, untethered soft robots at insect-scale with minimal power consumption operating in open-field environments, and their integration with onboard sensing further highlights the potential for broad applications.

While the EEM actuator demonstrates large force output and contraction ratio, its thermal behavior and overall efficacy are inherently influenced by the quality of the coil circuit, due to the underlying characteristics of electromagnetic systems. Although the bistable configuration enables energy-efficient operation and helps reduce heat accumulation, thermal effects, particularly under high-frequency operation, still remain a concern, representing a key limitation compared to other soft actuation systems. Further optimization of the magnetic circuit and thermal management could enhance its efficacy and long-term durability. Additionally, integrating multiple EEM actuators into a compact design may result in potential magnetic interference, posing challenges to achieve fully decoupled actuation.

Currently, our autonomous soft robots are limited to centimeter-scale due to constraints in battery and circuit size. However, the EEM motor’s ability to operate at sub-millimeter scale with only 0.43 mW power (Supplementary Video 5) offers a promising path toward smaller robots. As miniaturization of batteries and circuits advances, millimeter-scale soft robots may become feasible, enabling applications in areas like minimally invasive biomedical tools. At sub-millimeter scales, however, challenges such as thermal expansion and electrostatic effects will require advanced mitigation strategies.

The locomotion and behaviors of our autonomous insect-scale soft robots are programmable, allowing sophisticated operational modes and environmental responsiveness. With integrated sensors and communication modules, they support mutual signaling and swarm control, enhancing detection, efficiency, and decision-making. Future work will focus on leveraging the EEM system to develop intelligent swarms, potentially revolutionizing their application in complex, variable environments.

While the current prototypes show strong potential, their locomotion remains unoptimized. The crawler’s leg could be improved for better terrain handling, and the jumper could be refined for greater height and control. Though this study focuses on terrestrial and surface swimming modes, the EEM system’s high-frequency, large-stroke actuation enables future applications in aerial and underwater robots. Despite room for refinement, the system’s high output force, large stroke, and bi-stability—requiring energy only during state transitions—underscore its potential to enable high-performance, autonomous insect-scale soft robots capable of performing complex and varied tasks.

Methods

Artificial muscles and comparative analysis

Aiming to emulate the high performance of animal muscles, numerous artificial muscles have been developed using smart materials to achieve contraction and expansion motions^52,53. These artificial muscles typically operate through intricate material modifications and require strong external stimuli—such as high electric or magnetic fields, intense light, high voltage, or extreme temperatures^15,52—leading to harsh actuation conditions that often restrict them to tethered or limited autonomy^{17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,54}. At small scales, this constraint is particularly critical (Supplementary Table 2). While some actuators made from piezoelectric/dielectric materials, or ionic polymers have demonstrated untethered motion at small scales^{32,33,34,35,36,37}, their output forces and contraction ratios remain significantly lower than natural muscles due to compromises made to accommodate harsh actuation conditions (Fig. 1a and Supplementary Table 3).

In this study, rather than focusing solely on material inherent properties, we harness structural variations in soft materials combined with strong magnetic attractive forces to create a muscle-inspired actuation system. This strategy circumvents the harsh conditions required to stimulate smart materials, facilitating easy actuation of artificial muscle. Consequently, insect-scale soft robots equipped with this system achieve full autonomy with significant output force and actuation stroke under onboard power. Our autonomous soft EEM robots—including the inchworm crawler, legged crawler, and swimmer—demonstrate maximum output forces of 0.41, 0.48, and 0.43 N, respectively, with an actuation stroke of 30%. For comparison, untethered piezoelectric/dielectric actuated robots of similar size generate a maximum force of only 0.05 N³⁶ and a maximum actuation stroke of 6%³⁷, representing an 8–10× improvement in output force and a 5× improvement in stroke. Similarly, the autonomous insect-scale robots constructed using electroactive actuators demonstrate a maximum output force of 0.02 N and stroke of 20%³⁴, meaning our system provides 20–24× greater force and 1.5× the actuation stroke. Even combustion-based SMA actuators⁴⁰, which achieve a large force of 0.3 N using combustion energy, are limited to an actuation stroke of just 0.8%, whereas our system achieves a 1.36–1.6× increase in force and a significant 37× improvement in stroke.

Furthermore, diverse actuation properties of the EEM actuators can also be tailored through a systematic structural design methodology. Particularly, the EEM system with multi-stable states, akin to the catch muscle in mollusks, demonstrates highly energy-efficient actuation, a feature not achievable by other autonomous artificial muscles. Inspired by the structural connection mechanisms found in animal muscles, we further integrated the flexure mechanism into the EEM system to enable diverse locomotive modes. This represents a significant advancement over existing artificial muscles, providing a powerful and robust actuation system for soft robots, especially at small scales.

Distinction between EEM system and other electromagnetic systems

While the EEM system shares some components with traditional linear electromagnetic (EM) actuators^38,44, its actuation mechanism differs in key aspects. In traditional EM actuators, Lorentz forces serve as the primary actuation driver, requiring continuous electrical input, and the actuation direction is typically perpendicular to the magnetic axis. In contrast, our EEM system primarily utilizes static magnetic attraction between hard and soft magnets along the magnetic axis to generate large deformation, with the Lorentz force modulating the balance between magnetic and elastic forces. This design approach enhances the net actuation force and extends the effective force range (Supplementary Fig. 2a and b).

Furthermore, the elastic components are not passive but play a central role in balancing the electromagnetic and elastic forces. Through our design methodology, we can systematically tailor the force-displacement behavior of the elastomeric structure, enabling precise control over actuation stroke, multi-stability, and energy efficiency. This tunability allows the EEM system to adapt to a wide range of robotic tasks. As a result, the actuator achieves a compact, scalable, and impact-resilient form factor, eliminating the need for rigid transmission elements such as bearings or sliders, which are typically incompatible with miniature soft robotic platforms.

Therefore, the EEM mechanism introduces an electromagnetic strategy for soft robots and is distinct from magnetic field optimization methods such as Halbach arrays. While Halbach arrays enhance local magnetic field strength, their effect rapidly decays with distance. In contrast, our soft-magnet-based static magnetic interaction along the magnetic axis sustains attraction across a longer range, enabling large-stroke soft actuation within compact volumes (Fig. 2c(vi)). Compared with a recent insect-scale EM actuator with a voice coil transducer-based design³⁸, our system achieves a 20× improvement in output force and a 4× increase in actuation stroke under similar onboard conditions, demonstrating enhanced performance for soft robotic autonomy at small scales.

While some soft electromagnetic systems incorporate soft components for deformation, they still rely primarily on Lorentz forces for actuation and typically require strong external fields to generate sufficient deformation^27,42,43. This reliance on external fields limits their applicability to controlled environments and restricts their potential for fully autonomous systems in open-field scenarios. The soft actuators reported by Shin et al.⁵⁵ and Song et al.⁵⁶, which incorporate ferromagnetic silicone elements, still use Lorentz force as the main deformation driver with the ferromagnetic components as secondary aids. Consequently, they do not fully leverage static magnetic force and still depend on external power and control, limiting their autonomy.

Materials properties

The elasto-electromagnetic (EEM) actuation mechanism comprises three key components: a hard magnet, an elastomeric structure, and an electrical coil integrated with soft magnetic spheres (Fig. 2a(i)). These components interact to generate muscle-like actuation through magnetic and elastic forces. The actuator is fabricated via a simple 2D molding process, avoiding complex 3D assembly and enabling easy miniaturization. The material selection of these components can be flexible to suit various application needs.

In this study, we use NdFeB (Grade N52) for the hard magnets due to its high strength. The measured magnetization is 9.82 × 10⁵ ± 0.11×10⁵A/m (Test machine: PPMS-16T VSM option; Five samples). The magnet dimensions vary by EEM motor scale: 4.7 mm × 4.7 mm × 1.6 mm for the centimeter-scale system, 1 mm × 0.9 mm × 0.3 mm for the millimeter-scale system, and 40 mm × 40 mm × 14 mm for the decimeter-scale system.

The soft magnetic spheres integrated in the electrical coil are made of high-purity iron (99.95%). Their magnetic response was measured using a vibrating-sample magnetometer (Quantum Design MPMS3). Five samples, each with a diameter of 2 mm, are prepared, and their average magnetic response under an external field is presented in Supplementary Fig. 1a. The result indicates that the magnetic response of the soft magnetic sphere can be approximated by a linear relationship with the applied field, ${{{{\bf{B}}}}}_{{{{\rm{applied}}}}}$ (unit: ${{{\rm{T}}}}$):

$${{{{\bf{m}}}}}_{{{{\rm{sphere}}}}}=K\cdot {{{{\bf{B}}}}}_{{{{\rm{applied}}}}},\,{{{\rm{with}}}}\, {K}=0.0123\,({{{\rm{A}}}}\cdot {{{{\rm{m}}}}}^{2}/{{{\rm{T}}}})$$

(1)

The variable ${{{{\bf{m}}}}}_{{{{\rm{sphere}}}}}$ represents the induced magnetic moment of the soft magnetic sphere (unit: ${{{\rm{A}}}}\cdot {{{{\rm{m}}}}}^{2}$).

The elastomer used is Polydimethylsiloxane (PDMS) (SYLGARD™ 184 by Dow Silicones Corporation), chosen for its compatibility with molding technology and excellent elastic property. It is prepared in a 10:1 base-to-curing agent mass ratio and cured at 80 °C for 2 h. The resulting Young’s modulus was measured as 1.017 ± 0.019 MPa (Discovery DMA 850, n = 5), shown in Supplementary Fig. 1b. Additionally, we have also tested the Young’s modulus of the PDMS with different baking times in the oven at 80 °C: 1, 3, and 4.5 h, yielding values of E₁ = 0.807 ± 0.025 MPa, E₃ = 1.083 ± 0.013 MPa, and E_4.5 = 1.185 ± 0.017 MPa, respectively. Five samples are prepared for each test.

Fabrication procedures

The electrical coil is first wound into a cuboid shape with specific dimensions using the NITTOKU winding machines (coils for centimeter-scale system: 4.1 mm × 4.1 mm inner size, 6.2 mm × 6.2 mm outer size, 2 mm length, and 0.15 mm diameter copper wire; Coils for millimeter-scale system: 0.65 mm × 0.65 mm inner size, 1.1 mm × 1.1 mm outer size, 0.45 mm length, and 0.06 mm diameter copper wire; Coils for decimeter-scale system: 34 mm × 34 mm inner size, 51 mm × 51 mm outer size, 18 mm length, and 0.8 mm diameter copper wire). The resistances of those electrical coils for centimeter, millimeter and decimeter-scale systems are 1.25, 1.62, and 1.17 Ω, respectively.

Soft magnetic spheres are then packed inside each coil and bonded using cured PDMS (Supplementary Fig. 1c(i)). In this study, we chose to use discrete soft magnetic spheres instead of a cuboid-shaped block to avoid magnetic anisotropy induced by geometry. Specifically, if the desired magnetizing direction does not align with the long axis of the cuboid-shaped soft magnet, the enhancement of the magnetic moment in the desired direction would be inefficient.

Thanks to the planner structure of the elastomeric component in the EEM actuation system, it can be easily fabricated using 2D molding technology. As the elastomeric structures in our experiments typically have a large value in thickness while having small features in width, we apply a two-step molding method (Supplementary Fig. 1c(ii)). First, a rigid pre-process mold with the same geometry as the elastomeric structure is created using standard 3D printing technology (for centimeter- and decimeter-scale EEM motors) or photolithography (for millimeter-scale EEM motors). By filling the pre-process mold with PDMS and curing it, we obtain a soft PDMS negative mold in the first molding process. Subsequently, the negative mold is coated with a silane layer (CAS number: 78560-45-9) to modify the mold surface, and PDMS is cast again to form the final elastomeric structure (Supplementary Fig. 1c(ii)). This approach allows for easy removal of the elastomer structure, even with a large thickness-to-width ratio, owing to the soft properties of the PDMS negative mold and the coating process. All elastomeric structures for the EEM motors in this study were fabricated using this two-step molding method.

Finally, the hard magnet and coil (with bonded soft magnetic spheres) are inserted into the molded elastomer to form the complete EEM motor and joints (Supplementary Fig. 1c(iii)). The specific geometries used in joints and robots are shown in Supplementary Fig. 1d.

Multi-stability in EEM systems

Unlike conventional multi-stable designs that rely solely on elastic potential energy, our EEM system incorporates both elastic and magnetic potential energies, enabling simpler, compact structures and providing significant design freedom. While the designs reported by Shin et al.⁵⁵ also incorporate magnetic potential to create a bistable structure, they focus on specific configurations and do not offer a generalized design framework. In contrast, our systematic design methodology facilitates the construction of bistable or even tri-stable actuators with simple structures across various scales. Furthermore, the contraction ratio and other actuation properties can be tailored to meet different requirements while maintaining multi-stable states.

Performance of the centimeter EEM motor

Fast response speed

High-speed camera recordings (MEMRECAM ACS-1 M40), as shown in Supplementary Video 4, demonstrate that the EEM actuator can complete a full contraction stroke in about just a few milliseconds (~4 ms contraction and ~2.5 ms relaxation) (Supplementary Fig. 4b). The stable switching performance of the bistable EEM motor at 60 Hz actuation frequency was recorded using a high-speed camera (MEMRECAM ACS-1 M40) and is shown in the second-to-last part of Supplementary Video 4, played at 40× slower speed to clearly illustrate the motion dynamics. While the EEM mechanism is capable of operating at such high frequencies—which can be advantageous in certain emergency scenarios—the associated power consumption increases proportionally, diminishing the energy-saving benefits provided by the bistable mechanism.

Power consumption

The bistable state EEM motor does not require energy input to maintain its position. Therefore, no current is needed when the EEM motor is in either of its stable states. Energy input is only necessary during the brief transition between these states. Due to the actuator’s fast response, the energy input during state transition is also minimized. To ensure reliable switching between the two states, we apply a slightly longer current pulse (6 ms) for the state transition. By utilizing this strategy, the power consumption of the bistable EEM motor in centimeter-scale is only about 38 mW at 1 Hz, with the current applied in one cycle shown in Fig. 3b(i). The resistance of the centimeter-scale electrical coil is 1.25 Ω.

Increasing the actuation frequency results in a proportional rise in power consumption. This behavior is similar to that observed in nature, in which higher actuation frequencies lead to significantly increased power consumption. Nonetheless, the bistable state design significantly reduces the power consumption of the EEM motor compared to a monostable state design (Supplementary Fig. 4c). The EEM actuation joints and the autonomous insect-scale robots presented in this work use similar current strategies. The applied current profiles and power consumption for each motion type are provided and detailed in Supplementary Fig. 12.

Output force

With the current applied during the actuation of the EEM motor (Fig. 3b), the magnetic attractive force can be calculated based on Supplementary Information Note 1. Combined with the FEM analysis of the elastic response, the maximum output force of the EEM motor is determined to be 0.38 N (Supplementary Fig. 2e). It should be noted that the output force can be further increased by applying more current, with the cost of higher power consumption (Fig. 3b(ii)). Notably, an output force of 0.38 N is already significantly higher than that of existing autonomous insect-scale robots of similar size and weight^{32,34,35,36,37,38}. While the autonomous insect-scale robot created by Yang et al.⁴⁰ achieves a similar level of force (0.3 N) using combustion energy, its practicality is limited by the small deformation stroke of only 0.8%, resulting in a locomotion speed of just 0.04 body lengths per second. The parameters and key performance of existing actuation systems for autonomous insect-scale robots are detailed in Supplementary Table 3. It is clear that the present muscle-inspired EEM system surpasses existing ones in almost every aspect (Supplementary Fig. 4d and e) and is comparable to those in nature^{3,4,39,57,58,59,60,61,62,63,64,65,66} (Fig. 1a). This high output force capability is critical for the actuators to overcome environmental resistance, carry payloads, or perform other useful mechanical tasks.

It is also worth noting that when environmental resistance is minimal and no external work is needed, excessive output force becomes unnecessary and may result in internal collisions, leading to energy dissipation. In such cases, the actuation current or pulse duration of the EEM system can be reduced to deliver only the energy required for effective deformation, thereby minimizing energy loss. Looking ahead, adaptive control strategies incorporating embedded sensors could be explored to dynamically adjust the output force based on varying environmental resistance or payloads, further improving energy efficiency.

Contraction ratio

The contraction ratio of our centimeter-scale EEM motor (30%) is calculated as the total contraction (2.2 mm) over the height of the actuator unit (7.4 mm). Similar to the EEM actuation system shown in Fig. 2c(vi), the contraction of the EEM motor can be further increased by adjusting the elastomeric structure. For instance, by designing the elastomeric structure as in Supplementary Fig. 4a, the contraction can even reach 5 mm, achieving a contraction ratio of 49%. With its superior contraction force and stroke, our muscle-inspired EEM system represents a significant enhancement over existing autonomous insect-scale actuators (Supplementary Fig. 4d and e), showing great potential for practical high-performance autonomous insect-scale robots.

Durability

The durability of the EEM motor has also been evaluated by continuously operating it for 55 days at an actuation frequency of 1 Hz. As shown in Supplementary Fig. 6a, the EEM motor successfully completes 4,769,000 cycles, maintaining its full contraction stroke capability due to hyper hyperelastic property of PDMS. Additionally, the soft nature of the EEM motor endows it with high impact resistance. Notably, after a 30-m drop, the EEM motor continues to function normally without any performance degradation (Supplementary Fig. 6b).

The performance of the EEM motor, therefore, significantly surpasses existing “artificial muscles” designed for autonomous insect-scale robots (<4 cm)^{32,33,34,35,36,37,38,40,41}, as evidenced in Supplementary Fig. 4d and e, and Supplementary Table 3. To ensure a fair comparison, we have evaluated the performance metrics of all artificial muscles, including our EEM system, for autonomous robots operating under onboard power conditions. Focusing on autonomous systems ensures a consistent basis for comparison, as with external fields or tethered power, achieving higher output force and deformation would be possible simply by increasing the power supply, which would not be an equitable basis for comparison. Furthermore, leveraging the framework in Supplementary Note 2, the elastic force–displacement curve of the elastomeric structure can be systematically optimized using genetic algorithms or other machine learning algorithms^67,68, enabling improved EEM performance and diverse actuation properties. These advancements in force and deformation play a key role in enabling practical insect-scale soft robots capable of overcoming environmental resistance and achieving efficient locomotion gaits.

Thermal effect and force characterization of the EEM motor

We first evaluated the thermal performance of the EEM motor under extended operation across a range of frequencies. Continuous operation tests were conducted for 1 h at frequencies of 1, 2, 3, 4, 5, 8, 10, and 15 Hz. As shown in Supplementary Fig. 5a(i)–(ii), the temperature rise remains moderate at these frequencies and eventually reaches thermal equilibrium, indicating that the actuator can operate reliably without performance degradation. This favorable thermal behavior is attributed to the energy-efficient bistable nature of the EEM motor, which requires current input only during brief transitions between stable states and none to maintain position. At higher frequencies (20, 30, 40, 50, and 60 Hz), increased switching frequency results in greater heat generation and faster thermal buildup, eventually limiting sustained operation. When the coil temperature exceeds ~120 °C, the magnetic response of the soft magnets begins to deteriorate (reduced magnetic permeability), compromising the actuator’s ability to switch reliably between stable states. This behavior is analogous to biological systems, where intense activity leads to heat buildup and the need for recovery. We quantified the continuous operation time until thermal failure at each frequency and presented these results in Supplementary Fig. 5a(iii). All temperature data were captured using a calibrated thermal camera (HIKMICRO HM-TPK20-3AQF/W).

In addition to evaluating heat buildup across different frequencies, we further characterized actuator performance under continuous operation in isotonic (constant load) and isometric (constant position) conditions. Before presenting these experiments, we emphasize a key distinction between the EEM system and conventional linear EM actuators: even without current input, the EEM motor can still exert net output force due to the static magnetic interaction and the elastic restoring force. This enables passive load resistance without continuous power—unlike existing EM actuators that require sustained current.

To evaluate isotonic performance, we conducted 1-h continuous operation tests while the EEM motor actuated between its two stable states under different constant loads ranging from 0.5 to 7.5 times its own body weight. Coil temperature was monitored throughout. The results confirmed that the actuator can sustain operation under load, with only moderate heat generation (Supplementary Fig. 5b). As the load increases, the EEM motor requires a longer current pulse during state switching, which increases energy consumption and leads to greater temperature rise (Supplementary Fig. 5b(ii)).

For isometric testing (constant position), we fixed a flexible resistive force sensor (PHLEXSENSE S6-100K) inside the EEM motor, as shown in Supplementary Fig. 5c(i). The motor was commanded to cyclically compress the sensor across a 1-h period at 1 Hz. A 2 A current pulse of 10 ms was used for state switching. Due to the brief duration and the sensor’s 100 Hz sampling rate, force peaks are only intermittently captured. To ensure accurate measurement at 2 A actuation, a 200 ms pulse was applied every 2 min (Supplementary Fig. 5c(iii)). The measured output force at a fixed displacement of 1.7 mm (Supplementary Fig. 5c(ii)) remains stable throughout the test, with minimal degradation. A portion of the raw force data by the sensor is also provided in Supplementary Fig. 5c(iii) to illustrate how the compression force changes during continuous operation.

Millimeter and decimeter-scale EEM motors

The millimeter-scale motor, measuring 2.4 mm × 2 mm × 1 mm involves a straightforward construction using a cuboid NdFeB magnet and a coil made from 0.06 mm diameter copper wire, wound using a NITTOKU winding machine. This motor operates efficiently between two stable states, consuming only 0.43 mW of power at 1 Hz (Supplementary Video 5). Similarly, the decimeter-scale motor, measuring 1.05 dm × 0.5 dm × 0.7 dm, is fabricated using standard 3D printing for its mold, demonstrating the EEM motor’s flexibility in scaling. It transitions smoothly between two states and showcases significant energy efficiency, with a power consumption of 1.8 W at 1 Hz and a maximum delivery force of 27 N (Supplementary Video 5). Unlike conventional rigid electric motors, which require costly planetary or harmonic reducers to synchronize rotational speeds between the motors and the robot’s end-effectors, the soft EEM motor is directly designed to drive end-effector motion. This attribute presents a cost-effective alternative for large-scale robotics, offering benefits in terms of both performance and scalability, making it a valuable addition to various robotic applications where size, flexibility, and power efficiency are critical.

Data availability

The data generated and analyzed during this study are provided in the main text and the Supplementary Information. Source data are provided with this paper. Relevant code, additional experimental data, and additional supplementary videos have been deposited in the open-access Figshare repository: https://figshare.com/projects/Elasto-Electromagnetic_Mechanism/243827. Source data are provided with this paper.

References

Dickinson, M. H. et al. How animals move: an integrative view. Science 288, 100–106 (2000).
Article ADS CAS PubMed Google Scholar
Schiaffino, S. & Reggiani, C. Fiber types in mammalian skeletal muscles. Physiol. Rev. 91, 1447–1531 (2011).
Article CAS PubMed Google Scholar
Full, R. J. & Ahn, A. N. Static forces and moments generated in the insect leg: comparison of a three-dimensional musculo-skeletal computer model with experimental measurements. J. Exp. Biol. 198, 1285–1298 (1995).
Article CAS PubMed Google Scholar
Genin, J., Willems, P., Cavagna, G., Lair, R. & Heglund, N. Biomechanics of locomotion in Asian elephants. J. Exp. Biol. 213, 694–706 (2010).
Article CAS PubMed Google Scholar
Miki, T. et al. Learning robust perceptive locomotion for quadrupedal robots in the wild. Sci. Robot. 7, eabk2822 (2022).
Article PubMed Google Scholar
Baines, R. et al. Multi-environment robotic transitions through adaptive morphogenesis. Nature 610, 283–289 (2022).
Article ADS CAS PubMed Google Scholar
Darvish, K. et al. Teleoperation of humanoid robots: aA survey. IEEE Trans. Robot. 39, 1706–1727 (2023).
Article Google Scholar
Seok, S. et al. Design principles for highly efficient quadrupeds and implementation on the MIT Cheetah robot. In 2013 IEEE International Conference on Robotics and Automation (IEEE) (ed. Parker, L. E.) 3307–3312 (IEEE, 2013).
Chong, B. et al. Multilegged matter transport: a framework for locomotion on noisy landscapes. Science 380, 509–515 (2023).
Article ADS MathSciNet CAS PubMed Google Scholar
De Croon, G. C. et al. Accommodating unobservability to control flight attitude with optic flow. Nature 610, 485–490 (2022).
Article ADS PubMed PubMed Central Google Scholar
Zhao, D., Luo, H., Tu, Y., Meng, C. & Lam, T. L. Snail-inspired robotic swarms: a hybrid connector drives collective adaptation in unstructured outdoor environments. Nat. Commun. 15, 3647 (2024).
Article ADS CAS PubMed PubMed Central Google Scholar
Chi, Y. et al. Bistable and multistable actuators for soft robots: structures, materials, and functionalities. Adv. Mater. 34, 2110384 (2022).
Article CAS Google Scholar
St. Pierre, R. & Bergbreiter, S. Toward autonomy in sub-gram terrestrial robots. Annu. Rev. Control Robot. Auton. Syst. 2, 231–252 (2019).
Article Google Scholar
Rus, D. & Tolley, M. T. Design, fabrication and control of soft robots. Nature 521, 467–475 (2015).
Article ADS CAS PubMed Google Scholar
Hines, L., Petersen, K., Lum, G. Z. & Sitti, M. Soft actuators for small-scale robotics. Adv. Mater. 29, 1603483 (2017).
Article Google Scholar
Ng, C. S. X. et al. Locomotion of miniature soft robots. Adv. Mater. 33, 2003558 (2021).
Article CAS Google Scholar
Hu, W., Lum, G. Z., Mastrangeli, M. & Sitti, M. Small-scale soft-bodied robot with multimodal locomotion. Nature 554, 81–85 (2018).
Article ADS CAS PubMed Google Scholar
Chen, Y. et al. Controlled flight of a microrobot powered by soft artificial muscles. Nature 575, 324–329 (2019).
Article ADS CAS PubMed Google Scholar
Shahsavan, H. et al. Bioinspired underwater locomotion of light-driven liquid crystal gels. Proc. Natl Acad. Sci. USA 117, 5125–5133 (2020).
Article ADS CAS PubMed PubMed Central Google Scholar
Wu, S., Hong, Y., Zhao, Y., Yin, J. & Zhu, Y. Caterpillar-inspired soft crawling robot with distributed programmable thermal actuation. Sci. Adv. 9, eadf8014 (2023).
Article CAS PubMed PubMed Central Google Scholar
Wu, Y. et al. Insect-scale fast moving and ultrarobust soft robot. Sci. Robot. 4, eaax1594 (2019).
Article PubMed Google Scholar
Tang, C. et al. A pipeline inspection robot for navigating tubular environments in the sub-centimeter scale. Sci. Robot. 7, eabm8597 (2022).
Article PubMed Google Scholar
Aubin, C. A. et al. Powerful, soft combustion actuators for insect-scale robots. Science 381, 1212–1217 (2023).
Article ADS CAS PubMed Google Scholar
De Rivaz, S. D. et al. Inverted and vertical climbing of a quadrupedal microrobot using electroadhesion. Sci. Robot. 3, eaau3038 (2018).
Article PubMed Google Scholar
Pang, W. et al. A soft microrobot with highly deformable 3D actuators for climbing and transitioning complex surfaces. Proc. Natl Acad. Sci. USA 119, e2215028119 (2022).
Article CAS PubMed PubMed Central Google Scholar
Xu, C., Yang, Z. & Lum, G. Z. Small-scale magnetic actuators with optimal six degrees-of-freedom. Adv. Mater. 33, 2100170 (2021).
Article CAS Google Scholar
Mao, G. et al. Ultrafast small-scale soft electromagnetic robots. Nat. Commun. 13, 4456 (2022).
Article ADS CAS PubMed PubMed Central Google Scholar
Han, M. et al. Submillimeter-scale multimaterial terrestrial robots. Sci. Robot. 7, eabn0602 (2022).
Article PubMed Google Scholar
Choi, M.-Y., Shin, Y., Lee, H. S., Kim, S. Y. & Na, J.-H. Multipolar spatial electric field modulation for freeform electroactive hydrogel actuation. Sci. Rep. 10, 2482 (2020).
Article ADS CAS PubMed PubMed Central Google Scholar
Zhao, Y. et al. Soft phototactic swimmer based on self-sustained hydrogel oscillator. Sci. Robot. 4, eaax7112 (2019).
Article PubMed Google Scholar
Ze, Q. et al. Soft robotic origami crawler. Sci. Adv. 8, eabm7834 (2022).
Article PubMed PubMed Central Google Scholar
Ji, X. et al. An autonomous untethered fast soft robotic insect driven by low-voltage dielectric elastomer actuators. Sci. Robot. 4, eaaz6451 (2019).
Article PubMed Google Scholar
Wehner, M. et al. An integrated design and fabrication strategy for entirely soft, autonomous robots. Nature 536, 451–455 (2016).
Article ADS CAS PubMed Google Scholar
Ko, J. et al. High-performance electrified hydrogel actuators based on wrinkled nanomembrane electrodes for untethered insect-scale soft aquabots. Sci. Robot. 7, eabo6463 (2022).
Article PubMed Google Scholar
Hu, N., Li, B., Bai, R., Xie, K. & Chen, G. A torsion-bending antagonistic bistable actuator enables untethered crawling and swimming of miniature robots. Research 6, 0116 (2023).
Article PubMed PubMed Central Google Scholar
Miao, Z. et al. Power autonomy and agility control of an untethered insect-scale soft robot. Soft Robot. 10, 749–759 (2023).
Article PubMed Google Scholar
Liang, J. et al. Electrostatic footpads enable agile insect-scale soft robots with trajectory control. Sci. Robot. 6, eabe7906 (2021).
Article PubMed Google Scholar
Liu, Z. et al. A wireless controlled robotic insect with ultrafast untethered running speeds. Nat. Commun. 15, 3815 (2024).
Article ADS CAS PubMed PubMed Central Google Scholar
Alexander, R. M. The maximum forces exerted by animals. J. Exp. Biol. 115, 231–238 (1985).
Article CAS PubMed Google Scholar
Yang, X., Chang, L. & Pérez-Arancibia, N. O. An 88-milligram insect-scale autonomous crawling robot driven by a catalytic artificial muscle. Sci. Robot. 5, eaba0015 (2020).
Article PubMed Google Scholar
Goldberg, B. et al. Power and control autonomy for high-speed locomotion with an insect-scale legged robot. IEEE Robot. Autom. Lett. 3, 987–993 (2018).
Article Google Scholar
Mao, G. et al. Soft electromagnetic actuators. Sci. Adv. 6, eabc0251 (2020).
Article ADS CAS PubMed PubMed Central Google Scholar
Li, W. et al. Self-vectoring electromagnetic soft robots with high operational dimensionality. Nat. Commun. 14, 182 (2023).
Article ADS CAS PubMed PubMed Central Google Scholar
Taberner, A., Hogan, N. C. & Hunter, I. W. Needle-free jet injection using real-time controlled linear Lorentz-force actuators. Med. Eng. Phys. 34, 1228–1235 (2012).
Article PubMed Google Scholar
Zhang, X. et al. Kirigami-based metastructures with programmable multistability. Proc. Natl Acad. Sci. 119, e2117649119 (2022).
Article MathSciNet CAS PubMed PubMed Central Google Scholar
Yamada, A., Yoshio, M., Kojima, H. & Oiwa, K. An in vitro assay reveals essential protein components for the “catch” state of invertebrate smooth muscle. Proc. Natl Acad. Sci. USA 98, 6635–6640 (2001).
Article ADS CAS PubMed PubMed Central Google Scholar
Chen, A., Kim, K. & Shamble, P. S. Rapid mid-jump production of high-performance silk by jumping spiders. Curr. Biol. 31, R1422–R1423 (2021).
Article CAS PubMed Google Scholar
Noh, M., Kim, S.-W., An, S., Koh, J.-S. & Cho, K.-J. Flea-inspired catapult mechanism for miniature jumping robots. IEEE Trans. Robot. 28, 1007–1018 (2012).
Article ADS Google Scholar
Arazoe, H. et al. An autonomous actuator driven by fluctuations in ambient humidity. Nat. Mater. 15, 1084–1089 (2016).
Article ADS CAS PubMed Google Scholar
Xu, C., Yang, Z., Tan, S. W. K., Li, J. & Lum, G. Z. Magnetic miniature actuators with six-degrees-of-freedom multimodal soft-bodied locomotion. Adv. Intell. Syst. 4, 2100259 (2022).
Article Google Scholar
Wang, Y. et al. Insect-scale jumping robots enabled by a dynamic buckling cascade. Proc. Natl Acad. Sci. USA 120, e2210651120 (2023).
Article CAS PubMed PubMed Central Google Scholar
Mirvakili, S. M. & Hunter, I. W. Artificial muscles: mechanisms, applications, and challenges. Adv. Mater. 30, 1704407 (2018).
Article Google Scholar
Li, X. et al. A jelly-like artificial muscle for an untethered underwater robot. Cell Rep. Phys. Sci. 5, 101957 (2024).
Zhao, Y. et al. Antagonistic-contracting high-power photo-oscillators for multifunctional actuations. Nat. Mater. 24, 116–124 (2025).
Shin, G. et al. Soft electromagnetic artificial muscles using high-density liquid-metal solenoid coils and bistable stretchable magnetic housings. Adv. Funct. Mater. 34, 2302895 (2024).
Article CAS Google Scholar
Song, K., Kim, S. & Cha, Y. Soft electromagnetic actuator for assembly robots. Smart Mater. Struct. 29, 067001 (2020).
Article ADS Google Scholar
Han, L., Wang, Z., Ji, A. & Dai, Z. The mechanics and trajectory control in locust jumping. J. Bionic Eng. 10, 194–200 (2013).
Article Google Scholar
Hustert, R. & Baldus, M. Ballistic movements of jumping legs implemented as variable components of cricket behaviour. J. Exp. Biol. 213, 4055–4064 (2010).
Article CAS PubMed Google Scholar
Nauwelaerts, S. & Aerts, P. Take-off and landing forces in jumping frogs. J. Exp. Biol. 209, 66–77 (2006).
Article PubMed Google Scholar
Biewener, A., Alexander, R. M. & Heglund, N. Elastic energy storage in the hopping of kangaroo rats (Dipodomys spectabilis). J. Zool. 195, 369–383 (1981).
Article Google Scholar
Aerts, P. Vertical jumping in Galago senegalensis: the quest for an obligate mechanical power amplifier. Philos. Trans. R. Soc. Lond. Ser. B: Biol. Sci. 353, 1607–1620 (1998).
Article Google Scholar
McGuigan, M. P., Yoo, E., Lee, D. V. & Biewener, A. A. Dynamics of goat distal hind limb muscle–tendon function in response to locomotor grade. J. Exp. Biol. 212, 2092–2104 (2009).
Article PubMed PubMed Central Google Scholar
Walter, R. M. & Carrier, D. R. Effects of fore–aft body mass distribution on acceleration in dogs. J. Exp. Biol. 214, 1763–1772 (2011).
Article PubMed Google Scholar
Bobbert, M. F. & Santamaría, S. Contribution of the forelimbs and hindlimbs of the horse to mechanical energy changes in jumping. J. Exp. Biol. 208, 249–260 (2005).
Article PubMed Google Scholar
Ching, T. et al. Crawling, climbing, perching, and flying by FiBa soft robots. Sci. Robot. 9, eadk4533 (2024).
Article PubMed Google Scholar
Tolley, M. T. et al. A resilient, untethered soft robot. Soft Robot. 1, 213–223 (2014).
Article Google Scholar
Jin, H., Zhang, E. & Espinosa, H. D. Recent advances and applications of machine learning in experimental solid mechanics: a review. Appl. Mech. Rev. 75, 061001 (2023).
Article ADS Google Scholar
Holland, J. H. Adaptation in Natural and Artificial Systems: an Introductory Analysis With Applications to Biology, Control, and Artificial Intelligence (MIT Press, 1992).

Download references

Acknowledgements

We thank the Westlake Center for Micro/Nano Fabrication for the facility support and technical assistance in the fabrication of the millimeter-scale EEM motor. We thank Z. Huang, D. Liu, X. Li, S. An, P. Wei, and Z. Zheng for helpful discussion. We thank the Research Center for Industries of the Future (RCIF) at Westlake University and Westlake Education Foundation for supporting this work. H.J. acknowledges support from the National Natural Science Foundation of China (Grant 12350003).

Author information

These authors contributed equally: Changyu Xu, Yajun Cao.

Authors and Affiliations

School of Engineering, Westlake University, Hangzhou, Zhejiang, China
Changyu Xu, Yajun Cao, Jingyang Zhao, Yujia Cao, Yangyi Lin, Zhuang Zhang & Hanqing Jiang
Westlake Institute for Advanced Study, Hangzhou, Zhejiang, China
Changyu Xu, Yajun Cao, Zhuang Zhang & Hanqing Jiang
Westlake Interactive Robot Technology (Hangzhou) Co. Ltd, Hangzhou, Zhejiang, China
Yi Huang
College of Electrical Engineering, Sichuan University, Chengdu, Sichuan, China
Dong Wang
Research Center for Industries of the Future, Westlake University, Hangzhou, Zhejiang, China
Hanqing Jiang

Authors

Changyu Xu
View author publications
Search author on:PubMed Google Scholar
Yajun Cao
View author publications
Search author on:PubMed Google Scholar
Jingyang Zhao
View author publications
Search author on:PubMed Google Scholar
Yujia Cao
View author publications
Search author on:PubMed Google Scholar
Yi Huang
View author publications
Search author on:PubMed Google Scholar
Yangyi Lin
View author publications
Search author on:PubMed Google Scholar
Dong Wang
View author publications
Search author on:PubMed Google Scholar
Zhuang Zhang
View author publications
Search author on:PubMed Google Scholar
Hanqing Jiang
View author publications
Search author on:PubMed Google Scholar

Contributions

C. Xu and H. Jiang designed and conceptualized the study. C. Xu and Yajun Cao derived the theoretical framework and planned the experiments. C. Xu, Yajun Cao, J. Zhao, Yujia Cao, and Y. Lin conducted the experiments. C. Xu and Y. Huang designed the control circuit. C. Xu, H. Jiang, and Yajun Cao contributed to manuscript writing and interpretation of the results. Z. Zhang and D. Wang provided constructive input during manuscript drafting and revision. All authors assisted in the preparation of the final manuscript.

Corresponding author

Correspondence to Hanqing Jiang.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Description of Additional Supplementary Files

Supplementary Video 1

Supplementary Video 2

Supplementary Video 3

Supplementary Video 4

Supplementary Video 5

Supplementary Video 6

Supplementary Video 7

Supplementary Video 8

Supplementary Video 9

Supplementary Video 10

Supplementary Video 11

Supplementary Video 12

Supplementary Video 13

Transparent Peer Review file

Source data

Source Data

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Xu, C., Cao, Y., Zhao, J. et al. Muscle-inspired elasto-electromagnetic mechanism in autonomous insect robots. Nat Commun 16, 6813 (2025). https://doi.org/10.1038/s41467-025-62182-2

Download citation

Received: 10 June 2025
Accepted: 14 July 2025
Published: 24 July 2025
DOI: https://doi.org/10.1038/s41467-025-62182-2