Introduction

In optics, the parallels between concepts in the spatial and temporal domains, often referred to as space-time duality1, have led to the development of many revolutionary photonic tools, impacting diverse fields of science and technology, including ultrafast physics, quantum optics, spectroscopy, microscopy, and signal processing. For example, the development time-stretch photonics2,3, analogous to dispersing elements in space, has enabled powerful tools, such as wideband analog-to-digital converters and ultrafast signal processors, uncovering phenomena like optical rogue waves, relativistic electron bunching, and quantum chaos, and unlocking new opportunities for applications such as cancer detection, blood testing, optical computing, and 3D light detection and ranging (lidar)4.

Inspired by this duality, we here devise a time-domain stereoscopic technique (TDS), enabling high-precision, large-dynamic-range, far-field 3D optical imaging. Initially, stereoscopic imaging is performed in the spatial domain, which mimics human eyes to perceive depth using two slightly offset cameras to capture two images of the same scene from different angles. The disparity between the two images yields a depth map, enabling 3D reconstruction5. While effective in fields like robotics and autonomous driving, stereo imaging is limited in axial resolution and accuracy due to insufficient spatially resolving capability, especially in low-contrast, reflective, or textureless environments.

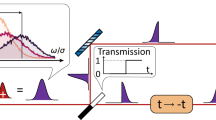
Analogous to its spatial-domain counterpart, TDS uses two temporally offset cameras to capture two images from the same laser pulse reflected by a target (Fig. 1a). The disparity between these images manifests in the time domain (Fig. 1b), and this temporal difference, decisive for depth retrieval, is determined precisely and rapidly by leveraging advanced time-domain techniques such as ultrafast optical sampling. Consequently, TDS addresses two key challenges for 3D imaging6,7,8: (1) integrating high axial resolution and precision with an extended imaging range or depth-of-field (DOF); and (2) performing 3D measurements in a high-speed, real-time fashion. Overcoming these challenges is crucial for surface metrology, remote sensing, mechanical dynamics, and tasks like object recognition, navigation, and scene reconstruction, which have widespread applications in areas like advanced manufacturing, security, and defense9,10.

Fig. 1: Concepts of TDS.
figure 1

a Simplified illustration of stereoscopy in space and in time. The light gray lines represent optical paths or time-of-flight. The symbols x and t correspond to space and time coordinates. b Optical sampling and time-domain disparities. In short, pulses arriving at different times produce different intensities on the two cameras. This intensity difference (ΔI), as a differential function of the pulses’ arrival time (Δt) relative to the time zero (the center of the gates), is used to determine distance.

Full size image

As a brief introduction, existing 3D optical imaging techniques can be crudely divided into two groups. The first covers large measurement distances (from a few meters to hundreds of meters) but with limited depth resolution and precision (at the millimeter or centimeter levels), including techniques such as stereoscopic imaging, time-of-flight (ToF) ranging cameras11, structured light projection12, and the 3D lidar family13,14,15. The second achieves nanometer precision but is limited to short ranges or DOF (typically to just a few millimeters), including techniques like serial time-encoded amplified microscopic imaging16, optical sampling imaging based on electro-optical or nonlinear effects17,18,19,20, and interferometric imaging and tomography21,22,23,24, primarily utilizing an interferometer with a moving arm. Meanwhile, the emergence of optical combs, a coherent light source precisely controlled in both time and frequency domains, opens up new opportunities for lidar25,26,27,28 and high-dimensional imaging29,30. Particularly, dual-comb interferometry, without the limitation of moving parts, enables rapid, long-range absolute distance measurements via heterodyne detection of two mutually coherent combs25. This dual-comb concept has been successfully adopted for hyperspectral digital holography29. However, the requirement for two tightly locked coherent combs, along with the high computational load and low refresh rate, limits its applicability due to complexity, cost, and real-time constraints. Therefore, despite its importance, high-precision, large-range 3D imaging with real-time measurement capability has remained a missing element in the field. The TDS method we propose offers a promising solution to bridge this gap.

In this paper, we present the concept and setup of time-domain stereoscopic imaging, demonstrate its capabilities in remote 3D imaging, precision, and high-speed measurements, and conclude with performance comparisons and future prospects.

Results

Basic concept and principle

Figure 1a conceptually compares TDS with conventional stereo imaging (see details in Supplementary Fig. 1 and Supplementary Table 1). In both cases, achieving high depth precision and accuracy hinges on precisely measuring minute disparities. This task proves challenging in the space domain (fundamentally due to the diffraction limit); conversely, exploiting the time domain benefits from advancements in optical comb and precise timing technologies. Specifically, in TDS, a laser pulse reflected by a target is captured by two cameras gated with a slight temporal offset, yielding distinct electrical signals (Fig. 1b). This imbalance (ΔI) is governed by the temporal difference (Δt) between the pulse flight time (TD) and the paired time gates, where Δt = TD-m/fr and m/fr represents a multiple of the repetition period of the gates (provided the two gates are synchronized). The pulse and the paired gates overlap optimally at a zero-crossing point (the middle case in Fig. 1b), where Δt = 0 and TD = m/fr. The integer m = fr1/Δfr, where Δfr = fr2-fr1, is obtained in a stroboscopic fashion, as m/fr1 = (m + 1)/fr2, given two adjacent zero-crossing points at fr1 and fr2, with fr1<fr2. Consequently, a target distance (D) is determined as D = c·TD/2nr = c/(2nr·Δfr), where nr is the reflective index of the air and c is the speed of light in a vacuum. Note that there are two prerequisites: (1) timing the gates precisely, which is available using optical combs; (2) the gates shorter than or comparable to the laser pulse, achievable via optical gating.

A key advantage of TDS over a conventional ToF camera is its superior noise immunity. A similar analogy can be drawn when comparing single-detector cross-correlation with balanced cross-correlation (BCC) in laser synchronization experiments31,32,33. The balanced one significantly improves timing precision to the attosecond level, surpassing the former by orders of magnitude, through the elimination of common-mode optical and electrical noise. This advantage also applies to TDS, rendering it inherently sensitive to minute changes in time as well as in distance—a core feature of this approach. Note that the BCC scheme has been adopted for high-precision single-point rangefinding34. Here, we explore its potential for TDS imaging that exploits time-domain parallax.

In our proof-of-concept demonstration, TDS is carried out by a balanced imaging system (Fig. 2a) comprising a type-II periodically poled KTiOPO4 (PPKTP) crystal and two identical cameras. The linearly polarized reference pulse serves as an optical gate for sampling the detection pulse with orthogonal polarization. Optical sampling occurs twice within the same PPKTP crystal via a bidirectional sum-frequency generation process. This type-II crystal induces temporal walk-off between the detection pulse and the reference gate pulse, causing the detection pulse to be sampled twice with a small temporal offset before being captured by the respective cameras.

Fig. 2: Schematics of TDS based on a balanced cross-correlator.
figure 2

a Balanced imaging with two optical sampling cameras. PBS, polarization beamsplitter; QWP, quarter wave plate; DM, dichroic mirror; PPKTP, periodically poled KTiOPO4; I1, I2, electrical signal intensity for a pixel of camera 1 (camera 2). b Balanced signals as a function of repetition frequency (fr) tuning of an electro-optical (EO) comb. In (a), an EO comb emits ultrashort optical pulses that travel to the target, reflect off surfaces, and return to a balanced cross-correlator. Inside this correlator, the orthogonally polarized detection and reference pulses pass through the PPKTP crystal twice, generating bidirectional sum-frequency signals as they temporally overlap inside the crystal. The sum-frequency beams then project two correlated images of a target onto the respective cameras, which are synchronized to the fr tuning. By subtracting the intensities of two correlated pixels (each from a camera), one can derive the balanced signal (ΔI) at any spatial point. In (b), a target distance is calculated as D = c/(2nr·Δfr), where nr, c, and Δfr represent the reflective index of the air, the speed of light in a vacuum, and the frequency difference between two consecutive zero-crossing points (at fr1 and fr2).

Full size image

Two points in this scheme should be noted. First, an ultrashort pulsed laser with a well-defined, rapidly tunable repetition frequency across a broad range is essential. To achieve this, we utilize a frequency-swept electro-optical (EO) comb. In practice, to measure distance, we record the balanced signal (ΔI) while linearly sweeping the comb’s fr, and then identify the zero-crossing points during data post-processing, as illustrated in Fig. 2b. Second, the central region of the balanced curve establishes a direct correspondence between intensity and time (or intensity and displacement), enabling 3D measurements from single frames.

Experimental setup

Our setup begins with an EO comb seeded by a narrow-linewidth CW laser at 1550 nm (Fig. 3a). This comb shares a configuration similar to previously reported sources35,36, as detailed in the Methods section and Supplementary Fig. 2. Briefly, the EO comb translates a radio-frequency (RF) sinusoidal wave, generated by a hydrogen-maser-disciplined RF synthesizer, into a sequence of sub-500 fs optical pulses, using a single intensity modulator and dispersion managed nonlinear fibers. Notably, the EO comb’s fr is directly set by the RF synthesizer, offering several benefits, including the elimination of frequency locking and counting, as well as wide-range frequency tuning with high linearity (Fig. 3b). The comb’s response to the RF driving signal is instantaneous, with negligible deviation within the resolution bandwidth of observation (Fig. 3b inset). Also, the comb maintains its pulse shape and temporal width when increasing the tuning speed or the modulation frequency (fm), as shown in Fig. 3c, showing the potential for fast measurement (discussed later). Importantly, the comb inherits the excellent frequency stability of the RF synthesizer (reaching 4 × 10-13 in 300 s, as shown in Fig. 3d), ensuring precise distance assessment.

Fig. 3: Experimental setup and characterization of the EO comb.
figure 3

a Experimental setup. Col., collimator; EDFA, erbium-doped fiber amplifier; HWP, Half-wave plate; M1-6, mirrors; 50/50, fiber coupler. The focus length for lenses L1 and L3 is 100 mm, and for L2 and L4 is 75 mm. The dashed box shows a 90 MHz sine wave being converted into a train of ultrashort pulses by an EO comb. b Linearly sweeping the comb’s repetition frequency (fr) from 90 to 300 MHz within 210 ms. Inset: RF spectra obtained by short-time Fourier transform, showing instantaneous frequencies of the RF synthesizer and the EO comb. c Autocorrelation traces of the EO comb versus modulation frequencies (fm). The data is measured after the detection collimator, and the frequency deviation is fixed at 250 kHz. d Fractional stability of the EO comb and the RF synthesizer. The comb stability deteriorates after 200 s due to the use of fibers. e, f High-resolution and large field-of-view images of the resolution target (1951-USAF) recorded by one of the cameras. The central patterns in (e, f) correspond to groups 6 and 0, respectively.

Full size image

For remote sensing, the comb output is amplified to 200 mW average power via an erbium-doped fiber amplifier (EDFA) and equally split between the detection and reference arms. In the detection light path, the comb pulses pass through a beam expander, subsequently illuminating a 3D scene with staggered mirrors and a resolution test target (1951 USAF) in front. A quarter-wave plate (QWP) and a polarization beamsplitter (PBS) serve as a free-space circulator, guiding the reflected detection pulses to another beam expander for optical scaling, and then to the balanced imager through a second PBS, which combines the detection and orthogonally polarized reference pulses.

The balanced imaging unit comprises twin 4 f imaging systems—one with lenses L1 and L2, and the other with lenses L3 and L4—in the opposing light paths (indicated by pink arrows in Fig. 3a). The two imaging subsystems share a single type-II PPKTP crystal, where object images from both directions converge at its center in the Fourier plane. Inside, the reference pulses convert the detection pulses into sum-frequency signals at 775 nm, which are captured by two synchronized CMOS (complementary metal-oxide-semiconductor) cameras. Note that, to serve as a pump light for sum-frequency generation, the 2.2 mm diameter (full width at 1/e2) reference beam bounces through the crystal without focusing, minimizing spatial filtering effects on lateral resolution. As such, we achieve an optimal lateral resolution of 6 μm (limited by the crystal’s transverse section) with a field-of-view (FOV) of 560 × 420 μm² (Fig. 3e). Currently, the 4 mm crystal (operating at room temperature) limits the acceptance angle to 3.5° (Supplementary Fig. 3) due to phase-matching restrictions commonly encountered by nonlinear optical imagers. This problem can be solved by changing the operating temperature or the poling structure of a nonlinear crystal19,20. Nevertheless, adjusting the magnifications of the two beam expanders in our setup allows for a broader view, such as a FOV of 3.5 × 2.6 cm² in Fig. 3f, at the cost of a degraded lateral resolution (315 μm) due to the cameras’ fixed pixel density (1440 × 1080 pixels). To maintain high lateral resolution over a large FOV, high-resolution images obtained by beam steering can be stitched together, such as a full image of the 1951-USAF target (7.62 × 7.62 cm²) made from 46 sub-images (Supplementary Fig. 4).

Remote 3D imaging and depth measurement

First, we demonstrate TDS for 3D imaging by detecting four staggered mirror targets at a standoff distance of > 1.3 m (from a reference point). Figure 4a exemplifies 2D images recorded by the two cameras at a frame rate of 165 fps (frames per second), with the comb fr linearly changing from 165.33 to 165.60 MHz. For these images, we identify spatially correlated pixel pairs, such as points A1 and A2 or B1 and B2 (Fig. 4a), by matching corresponding features with a widely-used scale-invariant feature transform (SIFT) algorithm37. We then obtain the balanced signals from the paired pixels A1A2 and B1B2, as plotted in Fig. 4b. By linear fitting the central portions of the signals, we determine the zero-crossing points at 165.372 MHz and 165.510 MHz for A1A2 and B1B2, respectively. We continue tuning fr, searching for the second zero-crossing points and calculating Δfr as 16.54 MHz for A1A2 and 16.55 MHz for B1B2, which determine their absolute distances to be d0 + 1.308 m and d0 + 1.3 m, respectively. The effective optical path difference (d0) between the detection and reference arms at the reference point in Fig. 3a is pre-calibrated to be 15.5 m.

Fig. 4: Demonstration of TDS for 3D imaging.
figure 4

a 2D image recorded by the cameras. b Balanced signals measured for pixel pairs A1A2 and B1B2. c 3D point cloud. Here, x, y, and z stand for spatial coordinates. The color bar represents the values in the z-axis (i.e., the depths). d Picture of a glass plate with a thin metallic foil attached to it. e Topographic imaging of the glass plate. The optical path (Δd ·nr) between the foil and back surface is measured to be 4.694 mm, resulting in a plate thickness of Δd = 3.128 mm for the glass refractive index nr = 1.5008.

Full size image

In this measurement, we simultaneously obtain range information for dense spatial points (up to 4.67 × 107 pixel pairs), visualized as a false-color 3D point cloud in Fig. 4c. For display, the axial (z) coordinates are referenced to the point B1B2. Also, points lacking illumination or without a sufficient signal-to-noise ratio (SNR) are not displayed. Note that the fr tuning step size is 606 Hz/frame, resulting in an axial resolution of 33 µm (Methods). This resolution can be improved to 54 nm with a step size of 1 Hz/frame at the cost of longer tuning time.

In another example, we perform 3D imaging on a 30%-reflective unpolished metallic foil attached to a 1-inch glass plate (Fig. 4d). This target is positioned 1.3 m away. Figure 4e presents a topographic image showing reflections from both the foil and the glass back surface. This showcases our method’s ability to remotely profile metal component surfaces and complex patterns, which is applicable for industrial inspection.

Axial precision and imaging depth

Next, we assess measurement precision and accuracy by measuring the displacements of a mirror mounted on a translation stage. We compare the TDS results with the truth data obtained by a CW interferometer. Statistical analysis over 50 individual measurements (without averaging) at each displacement yields a 2-σ standard deviation (SD) within ± 10 μm, where the mean values deviate from the truth data by less than 2 μm (Fig. 5a). With 500-fold averaging, the ranging precision improves to ± 400 nm with an accuracy reaching sub-100 nm (Fig. 5b). Note that, as shown in Fig. 5c, the measured SD linearly depends on signal-to-noise ratio (SNR), which can be improved by using a high-power comb and low-noise cameras.

Fig. 5: Evaluation of measurement precision and imaging depth.
figure 5

a Comparison measurement between our TDS imager (without averaging) and a CW laser interferometer. The offset distance is 1.3 m. b Measurements with 500-fold averaging. c Standard deviation (SD) evolving with signal-to-noise ratio (SNR). d Allan deviation of measurement versus averaging time (averaging number). The standoff distance is ~ 2 m. Note that the data in (a, b, and d) are calculated for imaging points with SNR > 300. e Balanced signal and EO comb pulse full width at half maximum (FWHM) recorded with tuning fr from 90 to 300 MHz. f Imaging of reflections from parts of a positive (front) and a negative 1951-USAF target (behind). They separate at 1.85 m, limited by our optical platform.

Full size image

For further evaluation, we perform Allan deviation measurements. Experimentally, we fix the comb’s fr at a zero-crossing point, converting intensity variations of the balanced signal to deviations in distance by a conversion factor of 3.03 μm. The same factor is also used for evaluating the background noise of a camera (by blocking the comb light). Figure 5d shows the results with data acquired at a frame rate of 165 fps. Our method (data in light blue) results in a precision of ~ 80 nm in 25 s, which is close to the camera’s noise background (in purple) and is nearly 50 times better than the unbalanced results (~ 4 μm, shown in pink and green) obtained by single cameras (“Methods”), demonstrating the key advantage of our method over direct ToF cameras. The off-the-shelf cameras we currently use limit the axial precision due to their moderate sensitivity and uncontrolled electronic noise. Replacing the cameras with two low-noise single-point photodetectors achieves 30 nm ranging precision in 2 s at a distance of >30 m (see Supplementary Fig. 5).

Essentially, TDS is a ranging technique, subject to dead zones dictated by the tunable range of fr. Luckily, the EO comb, without an optical cavity, exhibits a broad tuning range of over 200 MHz, with fr tunable from 90 to 300 MHz (Fig. 5e), limited by the bandwidth of electronics for EO comb generation. Nevertheless, this tuning range results in a dead zone of 0–0.5 m, which has been offset by the extra optical path in the detection arm and can therefore be neglected. Note that sweeping fr across a broad range changes the comb pulse width (Fig. 5e) due to unbalanced nonlinearity and dispersion, impacting the SNR and the widths of balanced signals (Supplementary Fig. 6). However, thanks to the balanced architecture, the zero-crossing points remain unaffected, maintaining their frequencies (fr) and separations (Δfr). Consequently, our method permits large measurable ranges and imaging depths. An example for range imaging at a folded distance of 9.6 m is shown in Supplementary Fig. 7. With this enhanced ranging capability, our system can image objects at largely different depths. For instance, the images of two staggered objects are displayed in Fig. 5f, and their spatial separation (1.85 m) is measured. Note that, for the displayed lateral resolution of 890 μm, the theoretical DOF allowed by our imaging system is 2.4 m (Supplementary Note 1). A larger DOF can be achieved, but at the cost of reduced lateral resolution.

High-speed 3D measurement

Finally, we demonstrate the real-time measuring capability of our method, which is based on the intensity-to-displacement relationship established by fixing the fr at a zero-crossing point. As exemplified in Fig. 6a, the highly linear region of a balanced curve (shadowed in gray) links its intensity to a target displacement (Δd), which is pre-calibrated by scanning the reference arm. Alternatively, calibration can be done without motion by sweeping the fr (“Methods”). As such, our method enables parallel displacement and velocity measurements of moving targets within a single frame, a task that is difficult for interferometric imagers due to the complexity of signal processing.

Fig. 6: Results of rapid displacement and velocity measurements.
figure 6

a Balanced signal versus target displacements (Δd). b Rapid imaging of two targets moving towards each other. c Trajectories at two selected imaging points. d Results of velocity measurements. e Balanced signals recorded at modulation frequencies of fm = 100 kHz and 1 MHz. For these measurements, the slow cameras are replaced by two fast photodetectors at 1 GHz bandwidth. In this case, the refresh rate of balanced signals is set by the fm. For the frequency modulation mode, the center fr of the EO comb is set at 165 MHz with a frequency deviation fixed at 250 kHz. Note that such a small fr tuning range negligibly impacts the comb pulse width.

Full size image

In an experiment, we capture reflections of two mirrors (behind the 1951-USAF target) moving oppositely at similar speeds of ~ 5 mm/s. Using pre-calibrated intensity-to-displacement relationships (similar to the one in Fig. 6a), we simultaneously measure displacements at over a million spatial points with 132 Hz data refresh rate, corresponding to a temporal resolution of 7.576 ms and a pixel rate of 205.3 megapixels/s. Figure 6b exemplifies the 3D images in motion. The trajectories of two counter-propagating imaging points (each on a mirror) are plotted in Fig. 6c, the derivatives of which reveal the instantaneous velocities of the two mirrors (Fig. 6d). Our setup currently allows a maximum measurable velocity of 330 mm/s, limited by the linear region (~ 2 mm) and the cameras’ maximum frame rate (165 fps, corresponding to a pixel rate of 256.6 MHz). Employing high-speed CMOS cameras (e.g., Photron, Mini AX200, with a frame rate up to 900k fps) can increase the measurable velocity to, e.g., 520 m/s. Also, the real-time measurable displacements (< 2 mm) can be extended by rapidly tuning the fr, which allows fast adjustment of the zero-crossing point and calibration of Δd, e.g., within 0.5 μs using high-speed photodetectors (Fig. 6e). Therefore, our method shows great potential for capturing dynamic 3D scenes, enabling studies of mechanical vibrations and deformations38.

Discussion

Benefiting from optical sampling and femtosecond EO comb synthesis, our system achieves sub-100 nm precision at a meter-level distance for 3D imaging. As shown in Fig. 7, the dynamic range of our setup, defined as 10·log(measurable range/precision), reaches 74 dB, underscoring its advantage over the aforementioned systems and other 3D imagers39,40,41,42,43,44. Besides, compared to mode-locked laser combs in some advanced lidar or imaging systems28,30,45,46, the cavity-free EO comb in our setup offers additional merits in terms of reduced complexity, ease of operation, lower cost, and greater environmental immunity—all crucial for practical use. Also, recent advances in lithium niobate photonics have enabled on-chip fs EO comb generation47, paving the way for a more compact and minimized system design.

Fig. 7: Axial precision versus measurable range for different 3D imaging systems.
figure 7

These systems can be classified into two groups: one characterized by high precision (marked with a green shadow) and the other by large measurement ranges (orange shadow). A trend in 3D imaging technology is the integration of these two features to broaden the scope of applications.

Full size image

Like other nonlinear optical sampling imagers19,20, our system encounters challenges in lateral resolution, angular FOV, and, most critically, light detection efficiency. Fortunately, advancements in nonlinear optical materials and semiconductor sensors present potential solutions. For instance, larger PPKTP crystals theoretically permit higher lateral resolution, and linearly chirped ones might expand the angular FOV to, e.g., 36.7°, with minimal conversion efficiency loss (Supplementary Fig. 3). Moreover, the development of electron-multiplying CCDs has enabled nonlinear upconversion imaging at the single-photon level20, albeit with longer integration times. This level of sensitivity enables our method to perform scanner-less range imaging, even over long distances, or in low-light conditions, as well as high-precision 3D profiling of rough, low-reflective surfaces.

With ongoing advances in semiconductor sensors and digital camera technology—particularly in pixel density, sensitivity, and speed—our method is promising for various applications6,7,8,9,10, such as identifying defects on semiconductor wafers, examining crucial automotive and aerospace components for micro-level deformations, ensuring precise positioning during laser machining processes, and characterizing dynamic behaviors in micromechanical devices, among others. In addition, shifting the comb wavelength to the mid-infrared region would enable broader applications in biomedical imaging and materials science19,20.

In conclusion, we present a time-domain stereoscopic approach that offers high precision over large imaging ranges and facilitates rapid, parallel displacement and velocity measurements, thereby introducing a powerful tool for diverse 3D imaging applications.

Methods

EO comb generation

To generate the EO comb, a CW laser at 1550 nm (Adjustik E15, NKT Photonics; linewidth < 0.1 kHz; 40 mW) is fed into an intensity modulator (IM, 40 GHz bandwidth; KY-MU-15-DQ-A, Keyang Photonics), which is driven by an electrical pulse generator that converts the output of an RF synthesizer (N5173B, Keysight) into 30-ps electrical pulses. The IM output is amplified to 150 mW using a custom-built fiber amplifier, followed by a 180 m-long dispersion-managed highly nonlinear fiber for spectral broadening. This fiber has a zero-dispersion wavelength at 1550 nm, a linear dispersion slope of 0.03 ps/(nm²·km), a loss coefficient of less than 1.5 dB/km, and a nonlinear coefficient greater than 10 W⁻¹km⁻¹. The comb pulses (-10 dB spectral width > 10 nm) are then compressed by fiber Bragg gratings, producing sub-500 fs optical pulses.

Balanced TDS imaging system

As shown in Fig. 3a, the imaging system employs two identical CMOS cameras (MV-CA016-10UM) to capture the correlated sum-frequency signals. An electrical circuit triggers the cameras in sync with the frequency tuning of the RF synthesizer. In the BCC unit, a type-II PPKTP crystal (CASTECH, 1 × 2 × 4 mm3 for height, width, and length) is used for two key reasons. First, it creates a temporal walk-off between two orthogonally polarized pulses, necessary for balanced signal generation. To make this walk-off adjustable, an additional polarized beamsplitter (PBS) and two mirrors (M5 and M6 in Fig. 3a) are incorporated, with their relative positions adjustable. Note that the walk-off effect inevitably limits the sum-frequency generation efficiency (~ 0.053 mW/W2). Further discussion is provided in Supplementary Note 1. Second, the crystal prevents second harmonic generation of each pulse, ensuring a zero background.

Calculation of SNR and axial resolution

The SNR of a balanced trace is defined as its peak value divided by the SD of a background region where the detection and reference pulses are fully separated. The axial resolution (Rz) of TDS is determined by δf, the tuning step of fr, as Rz = c/2nr ·Δfr/(fr + δf )·δf, where the speed of light c = 299,792,458 m/s and the refractive index in air nr = 1.0003. Therefore, we have an axial resolution of 33 µm for δf = 606 Hz/frame and 54 nm for δf = 1 Hz/frame, when fr = 166.3 MHz and Δfr = 16.6 MHz. Also, based on the above relationship, we can calibrate the curve in Fig. 6a by sweeping the fr.

Intensity-to-displacement conversion factors

For calculating the intensity-to-displacement conversion factor, we measure a balanced trace similar to that in Fig. 6a and then linearly fit the central region, resulting in a slope of 3 μm, i.e., the conversion factor. For Allan deviation measurement with a single camera, we use a conversion factor of 6.1 μm, obtained by linear fitting the central part of the rising edge of a cross-correlation trace. We then measure the intensity fluctuations at the center point of the rising edge with a fixed fr.