Abstract
Gate-tunable transmon qubits are based on quantum conductors used as weak links within hybrid Josephson junctions. These gatemons have been implemented in just a handful of systems, all relying on extended conductors, namely epitaxial semiconductors or exfoliated graphene. Here we present the coherent control of a gatemon based on a single molecule, a one-dimensional carbon nanotube, which is integrated into a circuit quantum electrodynamics architecture. The measured qubit spectrum can be tuned with a gate voltage and reflects the quantum dot behavior of the nanotube. Our ultraclean integration, using a hexagonal boron nitride substrate, results in record coherence times of 200 ns for carbon nanotube-based qubits. Furthermore, we investigate its decoherence mechanisms, thus revealing a strong gate dependence and identifying charge noise as a limiting factor. On top of positioning carbon nanotubes as contenders for future quantum technologies, our work paves the way for studying microscopic fermionic processes in low-dimensional quantum conductors.
Similar content being viewed by others
Introduction
Superconducting qubits, which have emerged as a leading approach in quantum information science, are based on Josephson tunnel junctions that act as quintessential nonlinear, non-dissipative elements1. It is possible to replace the tunnel junction with a hybrid Josephson junction utilizing a quantum conductor as a weak link2,3. This approach, backed by recent advances in low-dimensional materials, paved the way for innovative qubit designs like transmon, fluxonium, and Andreev qubits4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20. Among these emerging architectures, gatemon qubits stand out4,5,6,7,8,9,10,11,12, offering remarkable functionalities such as qubit frequency tunability through applied gate voltage—providing a practical alternative to magnetic flux control—and enhanced resilience to magnetic fields21,22, making them well-suited for applications in electron and nuclear spin resonance. Implementing such hybrid circuit quantum electrodynamics (cQED) architectures23,24, which combine low-dimensional materials with superconducting circuits, unlocks exciting possibilities at the intersection of quantum information science and condensed matter physics. The unique electronic properties of these quantum materials indeed shape the qubit’s operational behavior, exemplified by the physics of Dirac fermions that is observed in graphene gatemons10. This synergy also establishes a sensitive platform for probing the microscopic behavior of fermions in quantum materials, relying on minimally invasive microwave signals rather than traditional transport measurements.
To date, the quantum control of gatemon qubits has been demonstrated in devices based on extended conductors, such as semiconducting nanowires, two-dimensional electron/hole gases, and graphene4,5,6,7,8,9,10,11,12. Here we propose a gatemon based on a single molecule: a carbon nanotube. This intrinsically one-dimensional object has a uniquely limited number of internal electronic degrees of freedom, which could play a key role in designing protected qubits25,26 and supressing decoherence mechanisms, including quasiparticle poisoning—widely regarded as a major barrier to realizing high-coherence gatemons27,28. More importantly, implementing a gatemon with such an elementary junction of only one conduction channel, makes the underlying fermionic physics of the molecule accessible in a controlled environment. The electron-electron interactions play a crucial role in carbon nanotubes, which opens up great prospects in the context of many-body physics29,30,31,32,33,34. Carbon nanotubes constitute a compelling platform for charge or spin qubit implementation35,36,37,38,39,40,41,42,43. These non-superconducting architectures suffer from short coherence times, \({T}_{2}^{*}\) being typically of the order of 10 ns, and consequently difficulties in achieving coherent control. Implementing a superconducting qubit based on a carbon nanotube is thus a promising direction to explore. This requires to integrate a carbon nanotube-based Josephson junction within a cQED architecture, which was realized in a single experimental study so far44. In this work, we report the first coherent control of a nanotube-based gatemon, achieving a record coherence time \({T}_{2}^{*}\) of 200 ns with significant potential for improvement, as we observe that \({T}_{2}^{*}\) increases exponentially with qubit frequency. This landmark achievement is attributed to the ultraclean integration of the nanotube within our superconducting circuits, effectively minimizing disorder in the surroundings of the nanotube. To do so, we utilize hexagonal boron nitride (hBN) as a substrate, drawing from advancements in graphene physics10,45,46. This crystalline hBN-nanotube stack is free of atomic-scale defects, which are known to undermine the performance of superconducting qubits47. These advancements position carbon nanotube-based gatemons as a compelling platform for exploring and overcoming coherence challenges in next-generation quantum devices.
Results
Architecture of the circuit
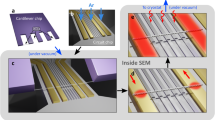
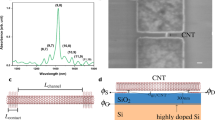
Our circuit, which is schematized in Fig. 1a, is primarily composed of two key elements: the nanotube gatemon that functions as a qubit, and a superconducting microwave resonator to readout the qubit state. The core component of this hybrid cQED architecture is the nanotube Josephson junction. It is fabricated using a novel technique48 that integrates an ultraclean single-walled carbon nanotube into prefabricated superconducting circuits on an insulating silicon substrate. To achieve this, the nanotube, adhered to a thin hBN layer, is mechanically transferred onto two superconducting Nb (35 nm)–Au (10 nm) bilayer electrodes, such that it is encapsulated between the hBN and the silicon substrate. This configuration not only shields the device from degradation due to air exposure, but also suspends the nanotube between the superconducting electrodes, ensuring that the section carrying the supercurrent avoids direct contact with the substrate. This arrangement significantly enhances the cleanliness of the device and reduces potential sources of disorder compared to previous works44. The carbon nanotube is capacitively coupled to an aluminum top electrode through the hBN layer, just tens of nanometers thick. The voltage Vg of this top gate controls the chemical potential and, consequently, the electronic density of states in the nanotube. By performing independent transport measurements we have shown that Josephson junctions fabricated using this technique exhibit gate-tunable critical currents Ic, with supercurrents as high as 8 nA48, comparable to that of conventional transmon qubits. Nanotube Josephson junctions thus behave as supercurrent field-effect transistors49. In the microwave domain, this translates into a gate-dependent non-linear inductance LJ or, equivalently, into a Josephson energy \({E}_{J}={\varphi }_{0}^{2}/{L}_{J}\), where φ0 is the reduced flux quantum7.
a Schematic of the hybrid cQED architecture containing a carbon nanotube Josephson junction. The nanotube is transferred onto two Nb–Au electrodes (gold) to form a Josephson junction of energy EJ that can be tuned with gate voltage Vg. Together with the shunt capacitor of energy EC it implements a gatemon qubit (orange box), which is capacitively coupled to the readout resonator (light blue). b False-colored micrograph of the nanotube gatemon. The central charge island (purple), which implements the shunt capacitor, is coupled to a λ/2 resonator and connected to the ground plane through the carbon nanotube Josephson junction. The carbon nanotube (not visible) is covered by hBN (green) and a top gate (dark blue). c Layout of the full chip with two independent hybrid cQED architectures. Device A corresponds to the bottom one, its resonator being highlighted in blue. Bonding pad on the bottom of the chip is used for top gate control.
The nanotube Josephson junction is embedded into a superconducting circuit, thus forming a hybrid cQED architecture. In practice, the junction connects between a metallic island and the ground plane of the circuit, as shown in the optical micrograph of Fig. 1b. This island implements a shunting capacitor of energy EC and forms, together with the nanotube Josephson junction, an anharmonic oscillator. Its ground and first excited states, \(| g\left.\right\rangle\) and \(| e\left.\right\rangle\), serve as the qubit states at the frequency \({f}_{q}\approx \sqrt{8{E}_{J}{E}_{C}}/h\)50. For state readout, the qubit is capacitively coupled to a coplanar λ/2 cavity (highlighted light blue in Fig. 1d). Due to hybridization of the cavity and qubit modes, the cavity’s resonance frequency depends on the qubit state and frequency50, which in turn is tunable by the gate voltage via LJ. In the following, measurements from two different devices A and B are presented. Device B is similar to device A (shown in Fig. 1b, c), with a slightly higher cavity resonance, larger qubit-cavity coupling, and an on-chip band-pass filter on the gate line as detailed in Supplementary Section II.
Spectroscopy of nanotube gatemon devices
We first focus on device A and measure the transmission of the λ/2 cavity in order to extract its resonance frequency fr. Varying the gate voltage Vg modulates the nanotube Josephson junction’s inductance LJ, which causes a frequency shift δfr of the resonator. Figure 2a shows this frequency shift δfr = fr − fr0 over a large range of gate voltage, where fr0 = 5.056 GHz is the bare-resonator frequency. Around Vg = 0 V, we observe a broad region where fr remains largely independent of Vg, which results from the semiconducting gap of the nanotube where the supercurrent is zero and LJ diverges. Beyond this gap, the resonator exhibits positive frequency shifts up to 1 MHz that varies strongly with Vg, as can be seen in the close-up view of Fig. 2b. This gate-dependent shift indicates a hybridization between the resonator and the nanotube qubit. Figure 2c shows the same measurement for device B, with a gate-dependent frequency shift of the resonator that exceeds 10 MHz.
a One-tone spectroscopy of device A measuring the shift δfr of the cavity at 5.056 GHz. Outside a band gap of about 9 V, dense forests of positive shifts indicate the presence of the qubit mode at lower frequency. Larger δfr is caused by smaller qubit-cavity detuning due to higher qubit frequency, which stems from larger supercurrent in the carbon nanotube Josephson junction. b, c One-tone spectroscopy for device A (close up of (a)) and device B. d, e Two-tone spectroscopy of the gate-dependent qubit mode for the same gate voltage ranges. Shown is δfr compared to the vertical average (device A) or change in cavity transmission S21 compared to no second tone drive \({S}_{21}^{{{{{\rm{off}}}}}}\) (device B). Spectra of device A exhibit regularly spaced peaks owing to quantum phase transitions changing the charge parity (letters e/o for even/odd in (b)) of the quantum dot. Contrarily, the gate dependence for device B is smoother, the nanotube junction being in a regime of a superconducting quantum dot strongly coupled to the electrodes. Both devices show spurious modes, visible as horizontal lines. The qubit linewidth for frequencies below 2 GHz is up to ~1 GHz due to charge dispersion.
The cQED architecture provides a powerful platform for probing the nanotube qubit as the readout resonator experiences a frequency shift that depends on the qubit’s state. We thus apply an additional drive signal at frequency fd in order to excite qubit transitions from state \(\left\vert g\right\rangle\) to \(\left\vert e\right\rangle\), while monitoring the resonator close to its resonance frequency. Such a two-tone spectroscopy measurement allows for a precise determination of the qubit frequency fq. Figure 2d, e shows the qubit spectra for devices A and B as a function of gate voltage. They both exhibit a gate-dependence fq(Vg) that is directly reminiscent from the one observed in cavity spectroscopy (Fig. 2b, c), which further demonstrates the qubit-resonator hybridization. These spectra allow us to extract for device A (respectively B) a charging energy EC = 260 MHz (resp. 330 MHz) and a qubit-cavity coupling strength g ≈ 50 MHz (resp. 120 MHz)50. The stronger coupling and higher qubit frequency of device B explain the greater δfr measured in Fig. 2c. Crucially, both spectra display a large tunability of the qubit frequency fq over 4 GHz, demonstrating that the qubit behaves as a gatemon. This tunability arises from the fact that the nanotube Josephson energy EJ depends on the gate voltage, and can be varied between a few hundred of MHz and up to 8 GHz. Using the simple relation EJ = φ0Ic (valid for a tunnel junction), the critical current of the nanotube junctions is estimated to be ~0.6–16 nA. These values are consistent with results reported in transport measurements48, taking into account the known discrepancy between switching current and critical current in small junctions.
More fundamentally, the voltage-tunability of EJ originates from the electrostatic control of the Andreev bound states, which are localized in the nanotube and are responsible for the Josephson effect51. This fermionic origin is revealed by analyzing the gate-dependent spectra in Fig. 2, which are very different for the two devices. For device A, the spectra exhibit sharp peaks when varying Vg, especially visible in Fig. 2b. These are a hallmark of quantum dot behavior, where the nanotube exhibits characteristics akin to Coulomb blockade effect commonly seen in transport measurements. Each peak indeed corresponds to the addition of a single charge to the nanotube, when an electronic level within the quantum dot is brought into resonance with the Fermi energy of the electrodes. The abrupt frequency jumps at the peaks are reminiscent of 0–π quantum phase transitions observed in supercurrent measurements of nanotube junctions52,53,54,55. Such a phenomenon is predicted to occur in interacting quantum dot-based Josephson junctions when the coupling Γ of the dot to the superconducting electrodes is moderate compared to the Coulomb repulsion U56,57,58. The competition between pairing and repulsion interaction results in sudden changes of the fermionic ground state with different parities. Even parity Andreev bound states carry more supercurrent than odd parity ones, which translates into jumps of fq. This allows us to assign to each gate voltage region a parity for the charge state of the carbon nanotube, as shown in Fig. 2b. For device B (Fig. 2c, e), the spectra exhibit a smoother gate-dependence. In that case, almost no parity-changes are observed and the nanotube behaves as a weakly-interacting quantum dot, whose electronic levels are tuned by Vg causing smooth oscillations in fq. This suggests that the ratio Γ/U is here larger compared to device A, which we interpret as a stronger coupling Γ to the electrodes. The latter translates into an increased Josephson energy EJ, thus explaining the higher observed qubit frequency which reaches up to 4.3 GHz. Finally, the smaller linewidth observed at higher qubit frequency promises better coherence properties.
Quantum control and coherence measurements
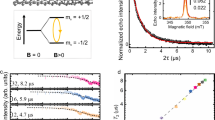
To demonstrate that a system functions as a two-level system or qubit, it is essential to establish its coherent control in the time domain. We focus in the following on device B that has shown the best coherence, and first investigate it at a constant gate voltage. Similar measurements for device A are available in Supplementary Section VI. We drive the qubit with an initial pulse at frequency fd~fq for a duration τRabi, followed by a second pulse at the resonator frequency fr for qubit readout. Figure 3a, which shows the qubit state as a function of both τRabi and fd, exhibits the characteristic chevron pattern associated with Rabi oscillations. At resonance fd = fq (white arrow at 4.32 GHz), the qubit state undergoes coherent oscillations in the Bloch sphere from \(\left\vert g\right\rangle\) to \(\left\vert e\right\rangle\) with the Rabi frequency ΩR = 107 MHz. Driving with a detuning δ = fd − fq induces oscillations at higher frequency \(\Omega=\sqrt{{\Omega }_{R}^{2}+{\delta }^{2}}\) with a reduced contrast. The measurement reveals a second chevron pattern centered at fgf/2 ≈ 4.25 GHz corresponding to a two-photon transition of energy hfgf between the ground state \(\left\vert g\right\rangle\) and the second excited state \(\left\vert \; f\right\rangle\). The two-photon nature of the transition is evident in the enhanced δ dependence of the Rabi frequency, \(\Omega=\sqrt{{\Omega }_{g\,f}^{2}+4{\delta }_{g\,f}^{2}}\), where Ωgf ≈ 55 MHz denotes the two-photon Rabi frequency at resonance and δgf = fd − fgf/259. From this measurement, we can extract a qubit anharmonicity α = fgf − 2fq of −142 MHz. We have measured values of α between −62 and −201 MHz for various gate voltages (see Supplementary Section IX). This metric, which was too small to be extracted in the case of the graphene gatemon10, is critical to evaluate a qubit quality as it determines a lower bound for a pulse duration. Contrary to the case of the tunnel junction-based transmon, the anharmonicity α is not simply given by −EC but varies with Vg as it depends on microscopic parameters of the nanotube gatemon7. Interestingly, we observe a large deviation of ∣α∣ with respect to EC, with values that can go below the standard boundary EC/47. This uncommon observation could be related to the quantum dot nature of our carbon nanotube Josephson junction, as recently predicted in ref. 60.
a Rabi oscillations as a function of drive frequency fd and pulse duration τRabi. The two observed chevron patterns correspond to the qubit transition at 4.32 GHz (white arrow) and a two-photon transition to the second excited state 71 MHz below (black arrow). The signal is the change of cavity transmission S21 compared to the ground state transmission \({S}_{21}^{| g\left.\right\rangle }\). b Relaxation measurement (blue points) following a π-pulse. The exponential fit (black line) leads to T1 = 191 ± 2 ns. c Ramsey oscillations as a function of drive frequency fd and time delay τRamsey between two π/2 Gaussian pulses. The oscillation frequency is given by the detuning of the drive from the qubit frequency. d Ramsey oscillations measured at +20 MHz detuning (blue points), which is a line cut in (c) indicated as dashed line. The fit of an exponentially decaying cosine (black line) results in a coherence time of \({T}_{2}^{*}=228\pm 12\,{{{{\rm{ns}}}}}\). All measurements were performed on device B at Vg = −4.2376 V.
Going further, we investigate the coherence properties of the nanotube gatemon. The Rabi oscillations are used to calibrate the π and π/2-pulses, which allow us to prepare the qubit in the states \(| e\left.\right\rangle\) and \(\left(| g\left.\right\rangle+| e\left.\right\rangle \right)/\sqrt{2}\) respectively. We first apply a π-pulse followed by a readout pulse delayed by the time τRelax, which results in an exponential decay of the qubit state as shown in Fig. 3b. The extracted T1 = 191 ns indicates the characteristic duration for the qubit to lose energy and relax to its ground state. Next, we measure the qubit dephasing using Ramsey interferometry, where we apply two π/2-pulses at frequency fd separated by a waiting time τRamsey. Figure 3c, d display Ramsey oscillations at the detuning frequency δ = fd − fq, which correspond to precession of the qubit state in the Bloch sphere at the equator. From their decay envelopes we extract a coherence time \({T}_{2}^{*}=228\,\,{\mbox{ns}}\). The similar timescale of T1 and \({T}_{2}^{*}\) indicates that decoherence originates from both energy relaxation and pure dephasing.
To gain deeper insight into the mechanisms limiting coherence, we extensively measured our nanotube gatemon at many values of gate voltage Vg. Figure 4 shows the relaxation time T1 and the coherence time \({T}_{2}^{*}\) acquired for a large set of Vg and plotted as a function of the qubit frequency fq. The relaxation time measurement exhibits a global trend, with T1 increasing at low qubit frequency and reaching up to 942 ns. The origin of this dependence is not known. More importantly, Fig. 4a shows a large spread of T1 values, with no strong correlation in fq. Energy relaxation is here likely limited by microscopic mechanisms that are gate-dependent. On the contrary, the coherence time measurements exhibit a strong correlation, as \({T}_{2}^{*}\) increases with fq and reaches up to 233 ns. We can explain this dependence using the transmon model50 that predicts a dephasing time scaling as \({e}^{\sqrt{8{E}_{J}/{E}_{C}}}\). The range of fq spanned in Fig. 4b corresponds to a ratio EJ/EC varied between 11 and 25. We thus model our data by \({T}_{2}^{*}\propto {e}^{h{f}_{q}/{E}_{C}}\) (black curve in Fig. 4b), using the fact that the coherence time is here much lower than 2T1 and thus dephasing-limited. Note how at lower fq the smaller EJ/EC ratio also manifests itself in a broad qubit linewidth due to offset charge noise, as evident in Fig. 2d, e. We thus demonstrate that our qubit can be gradually tuned from a Cooper pair box to the transmon regime50. Further analysis reveals that \({T}_{2}^{*}\) is not limited by gate noise on EJ (see Supplementary Section VIII). This detailed understanding provides a clear path for improving the nanotube gatemon coherence.
a Relaxation time T1 for three different gate regions, shown by different markers (see associated qubit spectroscopy in Supplementary Section VII). b Coherence time \({T}_{2}^{ * }\) corresponding to the same gate points. Both times T1 and \({T}_{2}^{ * }\) are plotted as a function of qubit frequency fq (bottom x-axis) and corresponding EJ/EC (top x-axis), using \(h{f}_{q}=\sqrt{8{E}_{J}{E}_{C}}-{E}_{C}\). The exponential behavior (black line) of \({T}_{2}^{ * }\propto {e}^{h{f}_{q}/{E}_{C}}\) is due to charge dispersion. All measurements were performed on device B.
In summary, we have demonstrated quantum control of a superconducting qubit made with an ultraclean carbon nanotube-based Josephson junction. The nanotube-based gatemon qubit exhibits a voltage tunability of its frequency over more than 4 GHz and an anharmonicity up to 200 MHz. Time-domain measurements establish quantum coherence of the nanotube gatemon, resulting in a coherence (relaxation) time as high as 233 ns (942 ns), an improvement by a factor of 4 (27) compared to its graphene counterpart10. This suggests that reducing the number of conduction channels effectively suppresses certain decoherence mechanisms, for example, the coupling to spurious two-level systems or poisoning of Andreev bound states in the weak link by non-equilibrium quasiparticles27,61 Moreover, these coherence times approach the first-generation gatemons that were based on semiconducting nanowires4. Increasing coherence would require more systematic studies8,62, a trend that is likely to be followed by nanotube gatemons. More generally, these results make our device the most coherent carbon-based qubit ever implemented63 and the first one to be integrated within a cQED architecture, which opens the way towards long-range coupling mediated by microwave photons. This marks a pivotal step towards harnessing single molecules for quantum computing applications.
Going further, our investigations reveal the critical role of charge noise in limiting coherence, suggesting that optimizing the ratio EJ/EC could enhance qubit performance. We anticipate substantial improvements in coherence by optimizing microwave engineering of the gatemon environment and by refining nanotube integration in order to minimize disorder. The latter could be achieved by employing higher-quality substrates or implementing bottom gates to shield against defects and stray charges. These efforts will strengthen the nanotube’s potential as a promising candidate for innovative quantum technologies. Future progress should be achieved by exploring diverse architectures relying on nanotube Josephson junctions, such as fluxonium or Andreev qubits.
More fundamentally, designing hybrid superconducting circuits that integrate low-dimensional quantum materials represents a promising approach to explore the underlying microscopic fermionic processes at play. We could here reveal the quantum dot behavior of the nanotube in the qubit spectrum. Interestingly, no coherence of the gatemon qubit could be measured when the parity of the fermionic ground state is odd. On top of the role played by offset charge noise at low EJ/EC, this could originate from the degeneracy of the odd fermionic Andreev ground state. We plan in the future to probe in a highly sensitive and non-invasive way the Andreev bound states that form in the nanotube14,18,51,64,65, as well as nonlocal states in Andreev molecules66,67 and more generally the spin and valley degrees of freedom of nanotubes37,42,68. Going further, such platforms should make it possible to study many-body physics that arise from Coulomb repulsion or intriguing topological phases that are predicted to form in one-dimensional materials69,70,71.
Data availability
The data that support the finding of this work and the analysis code to reproduce the figures are available from the Zenodo repository at https://doi.org/10.5281/zenodo.1558422572.
References
Kjaergaard, M. et al. Superconducting qubits: current state of play. Annu. Rev. Condens. Matter Phys. 11, 369 (2020).
Likharev, K. K. Superconducting weak links. Rev. Mod. Phys. 51, 101 (1979).
Tinkham, M. International Series in Pure and Applied Physics. In Introduction to Superconductivity (McGraw Hill, 1996)
Larsen, T. W. et al. Semiconductor-nanowire-based superconducting qubit. Phys. Rev. Lett. 115, 127001 (2015).
de Lange, G. et al. Realization of microwave quantum circuits using hybrid superconducting-semiconducting nanowire Josephson elements. Phys. Rev. Lett. 115, 127002 (2015).
Casparis, L. et al. Gatemon benchmarking and two-qubit operation. Phys. Rev. Lett. 116, 150505 (2016).
Kringhøj, A. et al. Anharmonicity of a superconducting qubit with a few-mode Josephson junction. Phys. Rev. B 97, 1 (2018).
Luthi, F. et al. Evolution of nanowire transmon qubits and their coherence in a magnetic field. Phys. Rev. Lett. 120, 100502 (2018).
Casparis, L. et al. Superconducting gatemon qubit based on a proximitized two-dimensional electron gas. Nat. Nanotechnol. 13, 915 (2018).
Wang, J. I.-J. et al. Coherent control of a hybrid superconducting circuit made with graphene-based van der Waals heterostructures. Nat. Nanotechnol. 14, 120 (2019).
Sagi, O. et al. A gate tunable transmon qubit in planar Ge. Nat. Commun. 15, 6400 (2024).
Kiyooka, E. et al. Gatemon qubit on a germanium quantum-well heterostructure. Nano Lett. 25, 562 (2025).
Hays, M. et al. Direct microwave measurement of Andreev-bound-state dynamics in a semiconductor-nanowire Josephson junction. Phys. Rev. Lett. 121, 47001 (2018).
Tosi, L. et al. Spin-orbit splitting of Andreev states revealed by microwave spectroscopy. Phys. Rev. X 9, 011010 (2019).
Larsen, T. W. et al. Parity-protected superconductor-semiconductor qubit. Phys. Rev. Lett. 125, 56801 (2020).
Pita-Vidal, M. et al. Gate-tunable field-compatible fluxonium. Phys. Rev. Appl. 14, 064038 (2020).
Bargerbos, A. et al. Singlet-doublet transitions of a quantum dot Josephson junction detected in a transmon circuit. PRX Quantum 3, 030311 (2022).
Pita-Vidal, M.et al. Direct manipulation of a superconducting spin qubit strongly coupled to a transmon qubit. Nat. Phys. 1 https://doi.org/10.1038/s41567-023-02071-x (2023).
Bargerbos, A. et al. Spectroscopy of spin-split Andreev levels in a quantum dot with superconducting leads. Phys. Rev. Lett. 131, 097001 (2023).
Strickland, W. M. et al. Gatemonium: a voltage-tunable fluxonium. PRX Quantum 6, 010326 (2025).
Kroll, J. G. et al. Magnetic field compatible circuit quantum electrodynamics with graphene Josephson junctions. Nat. Commun. 9, 4615 (2018).
Kringhøj, A. et al. Magnetic-field-compatible superconducting transmon qubit. Phys. Rev. Appl. 15, 054001 (2021).
Kurizki, G. et al. Quantum technologies with hybrid systems. Proc. Natl. Acad. Sci. USA 112, 3866 (2015).
Clerk, A. A., Lehnert, K. W., Bertet, P., Petta, J. R. & Nakamura, Y. Hybrid quantum systems with circuit quantum electrodynamics. Nat. Phys. 16, 257 (2020).
Vakhtel, T. & van Heck, B. Quantum phase slips in a resonant Josephson junction. Phys. Rev. B 107, 195405 (2023).
Vakhtel, T. et al. Tunneling of fluxons via a Josephson resonant level. Phys. Rev. B 110, 045404 (2024).
Aumentado, J., Catelani, G. & Serniak, K. Quasiparticle poisoning in superconducting quantum computers. Phys. Today 76, 34 (2023).
Zheng, H. et al. Coherent control of a few-channel hole type Gatemon qubit. Nano Lett. 24, 7173 (2024).
Deshpande, V. V. & Bockrath, M. The one-dimensional Wigner crystal in carbon nanotubes. Nat. Phys. 4, 314 (2008).
Pecker, S. et al. Observation and spectroscopy of a two-electron Wigner molecule in an ultraclean carbon nanotube. Nat. Phys. 9, 576 (2013).
Sárkány, L., Szirmai, E., Moca, C. P., Glazman, L. & Zaránd, G. Wigner crystal phases in confined carbon nanotubes. Phys. Rev. B 95, 115433 (2017).
Shapir, I. et al. Imaging the electronic Wigner crystal in one dimension. Science 364, 870 (2019).
Arroyo-Gascón, O., Fernández-Perea, R., Suárez Morell, E., Cabrillo, C. & Chico, L. One-dimensional moiré superlattices and flat bands in collapsed chiral carbon nanotubes. Nano Lett. 20, 7588 (2020).
Zhou, X. et al. Pressure-induced flat bands in one-dimensional moiré superlattices of collapsed chiral carbon nanotubes. Phys. Rev. B 109, 045105 (2024).
Churchill, H. O. H. et al. Relaxation and dephasing in a two-electron 13C nanotube double quantum dot. Phys. Rev. Lett. 102, 166802 (2009).
Delbecq, M. R. et al. Coupling a quantum dot, fermionic leads, and a microwave cavity on a chip. Phys. Rev. Lett. 107, 256804 (2011).
Laird, E. A., Pei, F. & Kouwenhoven, L. P. A valley-spin qubit in a carbon nanotube. Nat. Nanotechnol. 8, 565 (2013).
Delbecq, M. R. et al. Photon-mediated interaction between distant quantum dot circuits. Nat. Commun. 4, 1400 (2013).
Viennot, J. J., Delbecq, M. R., Dartiailh, M. C., Cottet, A. & Kontos, T. Out-of-equilibrium charge dynamics in a hybrid circuit quantum electrodynamics architecture. Phys. Rev. B 89, 165404 (2014).
Viennot, J. J., Dartiailh, M. C., Cottet, A. & Kontos, T. Coherent coupling of a single spin to microwave cavity photons. Science 349, 408 (2015).
Pei, T. et al. Hyperfine and spin-orbit coupling effects on decay of spin-valley states in a carbon nanotube. Phys. Rev. Lett. 118, 1 (2017).
Penfold-Fitch, Z. V., Sfigakis, F. & Buitelaar, M. R. Microwave spectroscopy of a carbon nanotube charge qubit. Phys. Rev. Appl. 7, 1 (2017).
Khivrich, I. & Ilani, S. Atomic-like charge qubit in a carbon nanotube enabling electric and magnetic field nano-sensing. Nat. Commun. 11, 1 (2020).
Mergenthaler, M. et al. Circuit quantum electrodynamics with carbon-nanotube-based superconducting quantum circuits. Phys. Rev. Appl. 15, 1 (2021).
Dean, C. R. et al. Boron nitride substrates for high-quality graphene electronics. Nat. Nanotechnol. 5, 722 (2010).
Wang, J. I.-J. et al. Hexagonal boron nitride as a low-loss dielectric for superconducting quantum circuits and qubits. Nat. Mater. 21, 398 (2022).
Lisenfeld, J. et al. Electric field spectroscopy of material defects in transmon qubits. npj Quantum Inf. 5, 1 (2019).
Annabi, S. et al. Josephson junctions based on ultraclean carbon nanotubes. Phys. Rev. Appl. 22, 064035 (2024).
Jarillo-Herrero, P., van Dam, J. A. & Kouwenhoven, L. P. Quantum supercurrent transistors in carbon nanotubes. Nature 439, 953 (2006).
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007).
Pillet, J.-D. et al. Andreev bound states in supercurrent-carrying carbon nanotubes revealed. Nat. Phys. 6, 965 (2010).
van Dam, J. A., Nazarov, Y. V., Bakkers, E. P. A. M., De Franceschi, S. & Kouwenhoven, L. P. Supercurrent reversal in quantum dots. Nature 442, 667–670 (2006).
Jørgensen, H. I., Novotný, T., Grove-Rasmussen, K., Flensberg, K. & Lindelof, P. E. Critical current 0-π transition in designed Josephson quantum dot junctions. Nano Lett. 7, 2441–2445 (2007).
Maurand, R. et al. First-order 0-π quantum phase transition in the Kondo regime of a superconducting carbon-nanotube quantum dot. Phys. Rev. X 2, https://doi.org/10.1103/physrevx.2.011009 (2012).
Delagrange, R.et al. 0-π quantum transition in a carbon nanotube Josephson junction: universal phase dependence and orbital degeneracy. Phys. Rev. B 93, https://doi.org/10.1103/physrevb.93.195437 (2016).
Vecino, E., Martín-Rodero, A. & Yeyati, A. L. Josephson current through a correlated quantum level: Andreev states and π junction behavior. Phys. Rev. B 68, https://doi.org/10.1103/physrevb.68.035105 (2003).
Meng, T., Florens, S. & Simon, P. Self-consistent description of Andreev bound states in Josephson quantum dot devices. Phys. Rev. B 79, 224521 (2009).
Zazunov, A., Yeyati, A. L. & Egger, R. Josephson effect for SU(4) carbon-nanotube quantum dots, Phys. Rev. B 81, https://doi.org/10.1103/physrevb.81.012502 (2010).
Linskens, A. F., Holleman, I., Dam, N. & Reuss, J. Two-photon Rabi oscillations. Phys. Rev. A 54, 4854–4862 (1996).
Fatemi, V., Kurilovich, P. D., Akhmerov, A. R. & Heck, B. V. Nonlinearity of transparent SNS weak links decreases sharply with length. SciPost Physics 18, 091 (2025).
Zgirski, M. et al. Evidence for long-lived quasiparticles trapped in superconducting point contacts. Phys. Rev. Lett. 106, 257003 (2011).
Feldstein-Bofill, D. et al. Gatemon qubit revisited for improved reliability and stability. Preprint at https://doi.org/10.48550/arXiv.2412.11611 (2024).
Baydin, A. et al. Carbon nanotube devices for quantum technology. Materials 15, 1535 (2022).
Janvier, C. et al. Coherent manipulation of Andreev states in superconducting atomic contacts. Science 349, 1199 (2015).
Hays, M. et al. Continuous monitoring of a trapped superconducting spin. Nat. Phys. 16, 1103 (2020).
Pillet, J.-D., Benzoni, V., Griesmar, J., Smirr, J.-L. & Girit, Ç. Ö. Nonlocal Josephson effect in Andreev molecules. Nano Lett. 19, 7138 (2019).
Haxell, D. Z. et al. Demonstration of the Nonlocal Josephson Effect in Andreev Molecules. Nano Lett. 23, 7532 (2023).
Neukelmance, B. et al. Microsecond-lived quantum states in a carbon-based circuit driven by cavity photons. Nat Commun 16, 5636 (2025).
Klinovaja, J., Schmidt, M. J., Braunecker, B. & Loss, D. Helical modes in carbon nanotubes generated by strong electric fields. Phys. Rev. Lett. 106, 156809 (2011).
Klinovaja, J., Gangadharaiah, S. & Loss, D. Electric-field-induced Majorana fermions in armchair carbon nanotubes. Phys. Rev. Lett. 108, 196804 (2012).
Marganska, M., Milz, L., Izumida, W., Strunk, C. & Grifoni, M. Majorana quasiparticles in semiconducting carbon nanotubes. Phys. Rev. B 97, 075141 (2018).
Riechert, H., Data and code for “The carbon nanotube gatemon qubit”. Zenodo https://doi.org/10.5281/zenodo.15584225 (2025).
Acknowledgements
We thank J. I. J. Wang and W. D. Oliver from the EQuS group at MIT with their invaluable help on the microwave design. Gratitude is extended to S. Cances for participation to the project in its early stages. We thank D. Marković, R. Ribeiro-Palau, and the SPEC of CEA-Saclay, in particular the Quantronics group, for their help on nanofabrication and microwave expertise, and to D. Roux and R. Mohammedi from LPMC for their technical support. L.B. acknowledges support of the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No. 947707). J.-D.P. acknowledges support of Agence Nationale de la Recherche through grant ANR-20-CE47-0003. This work has been supported by the French ANR-22-PETQ-0003 Grant under the France 2030 plan. K.W. and T.T. acknowledge support from the JSPS KAKENHI (Grant Numbers 21H05233 and 23H02052), the CREST (JPMJCR24A5), JST, and World Premier International Research Center Initiative (WPI), MEXT, Japan.
Author information
Authors and Affiliations
Contributions
J.-D.P. and L.B. designed and supervised the experiment. H.R. fabricated the samples and carried out the measurements. H.R., S.A., A.P., H.D., M.H., E.A., J.G., J.-D.P. and L.B. contributed to nanofabrication and microwave measurements at cryogenic temperatures. K.W. and T.T. provided the hexagonal boron nitride flakes. H.R., J.-D.P. and L.B. analyzed the data. H.R., J.-D.P. and L.B. wrote the manuscript with feedback from all co-authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Riechert, H., Annabi, S., Peugeot, A. et al. The carbon nanotube gatemon qubit. Nat Commun 16, 7197 (2025). https://doi.org/10.1038/s41467-025-62283-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-62283-y