Route-centric ant-inspired memories enable panoramic route-following in a car-like robot

Abstract

Solitary foraging ants excel at route following using minimal neural resources, Robots don’t. Recent biological studies proposed lateralized, nest-centric memories to explain ants’ direct visual homing but did not address how ants follow curved visual routes away from their nest. We present a biologically inspired neuromorphic model for one-shot panoramic route learning and continuous route following, implemented on a compact car-like robot, Antcar. We demonstrate that route-centric lateralized memories, inspired by the insect mushroom body, enable Antcar to achieve bi-directional route-following, with motivation-driven recognition of route extremities and familiarity-based velocity control. With rigorous Lyapunov-based stability analysis and an empirical memory scalability evaluation, the model was tested over 1.6 km across 113 challenging real-world trials. The system achieves less than 25 cm median lateral error using minimal resources (800-pixel input, 300 MB RAM, 500 mW power, and 18.75 kB memory per 50 m route), offering insights into insect cognition and advancing autonomous robotics under strict resource constraints.

Introduction

Insect navigation has long intrigued researchers across various fields, from biology to robotics, driving the development of cutting-edge technologies for autonomous mobile robots^1,2,3. Autonomous navigation remains a demanding and interdisciplinary challenge with applications ranging from space exploration to last miles delivery^4,5, especially in scenarios where robots cannot rely on satellite systems⁶. Simultaneously, robots serve as valuable tools for studying insects navigation and brain structure, advancing neuromorphic engineering^7,8,9,10,11.

In Robotics, visual teach-and-repeat methods combined with dead-reckoning techniques have gained in popularity^12,13,14,15. However, experienced solitary foraging ants navigate along familiar routes using only visual memories, without relying on dead reckoning (called path integration in insect literature)^16,17,18. This behavior has inspired various robotic models, although current implementations are generally limited to short-range experiments of about ten meters, with modest computational efficiency, precision, and accuracy^{19,20,21,22,23,24}. While ant-inspired models achieve results comparable to conventional computer vision approaches^13,25, they struggle in dynamic environments where computational efficiency must be balanced with resource use.

These challenges are partly due to early navigation models that emphasized hymenopteran behavior rather than underlying brain processes. Early models, referred to as perfect memory models, stored periodic snapshots at specific waypoints^26,27. Then, during autonomous route following (or exploitation), forced scanning movements compared acquired views to an image bank, using rotational image differences to establish the most familiar image and desired heading, a process known as the insect-based visual compass^{28,29,30,31,32,33}. However, these approaches has revealed two main limitations when applied in robotics.

The first limitation involves the cumulative storage of snapshots, which significantly increases memory and computational demands as the route lengthens, making it unsuitable for long-distance navigation. This issue was partially addressed by the Infomax neural network³⁴, which enables efficient encoding of increasing numbers of images without a corresponding rise in memory load^20,32,35. However, Infomax requires substantial adjustments to synaptic weights for each input through a non-local learning mechanism, limiting its biological plausibility.

In parallel, research on the Mushroom Body (MB), a key part of the insect brain, has highlighted its essential role in olfactory and visual learning^36,37. In the MB, learning occurs through synaptic depression between thousands of Kenyon Cells (KCs) – intrinsic neurons that sparsely encode sensory input – and a few Mushroom Body Output Neurons (MBONs), which modulate behavioral responses based on learned associations. These processed signals are then transmitted to downstream neural circuits, influencing decision-making³⁸. The first MB model simulating visual route following used a Spiking Neural Network with 20,000 KCs and one MBON to compute familiarity³⁹. Despite this advancement, a second limitation remains: navigation requires forced, systematic scanning, which slows robotic movement due to non-continuous command updates²¹. Also, this limitation does not reflect natural ant behavior, where scanning occurs only occasionally^40,41,42.

To address the second limitation, an early robotic implementation combined a klinokinesis model with perfect memory, enhancing short-distance route-following by replacing cumbersome scanning with alternating, ballistic left and right turns where familiarity adjusted turn amplitude¹⁹ (later also observed in ants⁴³).

To move beyond random, undirected kinesis, an early visual homing strategy was proposed that simulates directed movement toward a goal (e.g., a nest). In this model, tested in a particle-based simulation, the firing activity of KCs—which encode visual input—is categorized based on the path integration vector into two pairs of lateralized MBONs. Specifically, views acquired when the nest lies to the left are assigned to the left MBON, and vice versa^44,45. This approach mirrors how insects, through continuous lateral body oscillations, sample multiple directions around their nest position^43,46.

In this paper, we focus on route following, which is considered distinct from visual homing in the ant navigation framework, and aligns with Visual Teach & Repeat paradigms in robotics⁴⁷. While visual homing is goal-directed and attractor-based, route following relies on on-route visual memories⁴⁸. Some recent robotic models have attempted to extend lateralization to route following by splitting the field of view into left and right memories. However, these methods have shown limited success in real-world conditions^23,49, and they diverge from biological evidence: in ants, the entire panoramic field is processed binocularly by the MB⁵⁰. Our approach, therefore, uses the full panoramic view and categorizes visual input with right and left MBON in a route-centric manner, i.e., with respect to a local route orientation, without splitting the field-of-view.

Building on our earlier one-MBON model for route learning in an indoor robot^21,22, and the lateralization principle for nest-centric homing in simulation⁴⁵, we present a fully-embodied, biologically realistic, and route-centric lateralized MB architecture implemented and tested on a real-world robot. This work introduces several contributions that significantly advance the field:

(i) Route-centric lateralized learning: We replace the nest-centered categorization with a local, route-aligned reference frame, enabling two lateralized MBONs (right and left) to memorize panoramas as seen on the right or left of the route. This supports curved and goal-directed navigation without requiring a global home vector. (ii) Bi-directional navigation with start/end recognition: Two additional MBONs allow the robot to recognize route extremities, enabling stop and back-and-forth route following, a behavior observed in ants^51,52,53,54. (iii) Familiarity-based velocity control: The robot adapts its speed based on visual familiarity, accelerating on known routes and decelerating in novel environments, mirroring ant behavior⁴⁰. (iv) Analytical stability via oscillatory learning: We show that oscillatory heading movements during learning lead to stable route following, supported by a Lyapunov-based proof of convergence in the local route frame. (v) Empirical memory scalability analysis: We propose a metric to quantify memory capacity in relation to network hyperparameters, providing insights into the scalability of Mushroom Body-based architectures for longer and more complex routes. (vi) Extensive real-world validation: Embedded in the compact Antcar robot (Fig. 1, 2a), our model was tested across 113 autonomous trajectories covering 1.6 km in both indoor and outdoor settings with different environmental conditions and challenges. The system achieved median lateral and angular errors of 24 cm and 4°, with processing rates of 16 Hz during exploitation and 38 Hz during learning — all using a single 32 × 32-pixel panoramic camera and minimal computational resources: 300 megabytes of RAM, 500 mW power consumption, and just 18.75 kilobytes of memory. Overall, this paper delivers a biologically grounded and resource-efficient implementation of the proposed panoramic, route-centric and lateralized visual route-following on a physical robot. It integrates neural plausibility, theoretical robustness, and practical feasibility, bridging the gap between insect-inspired models and real-world autonomous robotics.

Fig. 1: Biological inspiration for robotic navigation.

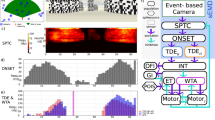
An ant in the foreground symbolizes nature’s efficient navigational strategies, while the Antcar robot in the background integrates these principles into a neuromorphic system. The blurred image captures only the large masses of the environment, similar to the low-pass spatial filter in the ant’s visual system, which retains these large features even when objects obstruct the view between the robot and the building. ^ⓒTifenn Ripoll - VOST Collectif / Institut Carnot STAR.

Results

Our proposed MB model emulates ant visual processing by encoding panoramic images as low resolution neural representations (800-pixel input), enabling efficient learning and route recognition with minimal computational demands (see Methods for details, Fig. 2b). The model operates in two main phases: learning (Fig. 2c) and exploitation (Fig. 2d). During the learning phase, our self-supervised model encodes the route using two route-centric MBONs, with a in silico scanning, and stores place-specific memories for the nest and feeder as route extremities (see “Methods”, Fig. 2c). In the exploitation phase, the robot processes each view through all memory pathways, yielding four familiarity values (left, right, nest and feeder MBON activities). The lateralized difference of route familiarities (λ_diff) directs steering, while the maximum familiarity value modulates forward speed. In addition, a motivational control modulates motor gain, allowing the robot to stop or reverse based on a familiarity threshold set by place-specific MBONs (see “Methods”, Fig. 2d).

Fig. 2: Overview of the route-centric lateralized memories model implemented in the Antcar robot.

This figure illustrates the processing pipeline from image encoding to navigation control, spanning both the learning and exploitation phases. a The Antcar robot: a compact car-like platform equipped with a panoramic camera and a GPS-RTK (Global Positioning System - Real-Time Kinematic) system for ground truth data. b Image encoding: this process mimics the ant’s visual system. Panoramic images (I) are captured, blurred, sub-sampled, and edge-filtered to produce a low-resolution 32 × 32 pixel panorama (IS). The resulting image is then transformed into Projection Neurons (PN), expanded into Excitatory Post-Synaptic Projections (EP), and reduced into Action Potentials (AP) via a κ-WTA function, forming the sparse Kenyon Cell (KC) representation. c Learning phase: the robot follows a route (C) from a start point (N). An in silico scan (simulated image rotation) generates images with a defined angular error ($\hat{{\theta }_{{{\rm{e}}}}}$), used to continuously categorize views at 38 Hz in a route-centric manner---i.e., as facing to the right or left of the local route orientation. These continuous categorizations drive the update of synaptic weights in the corresponding Mushroom Body Output Neurons (MBONs), allowing visual inputs to be associated with specific route memories in a self-supervised fashion. Joystick inputs are used to define learning boundaries at the start and end of the route, modulating plasticity. d Exploitation phase: the robot seeks to minimize lateral (d) and angular (θ_e) errors with respect to the learned route. The encoded image continuously activates MBONs at 16Hz based on previously learned synaptic weights, enabling the robot to infer route orientation and adjust its steering and speed accordingly. MBON familiarity indices (λ) operate in an opponent process: differences in familiarity between left and right MBONs guide steering, while the overall familiarity magnitude modulates speed. Special MBONs associated with route extremities affect motivational states, enabling route polarity correction or halting movement.

This study begins with an offline analysis of the proposed self-supervised, route-centric MB model using two route MBONs to assess stability (Fig. 3), followed by experimental route-following tasks in challenging indoor and outdoor environments (Figs. 4, 5 and 6). Next, a homing task is described, in which the robot follows a long outdoor route in reverse toward the starting area, designated as the nest (N), and stops nearby, utilizing three MBONs (Fig. 7). Finally, a shuttling task is introduced, where the robot, after a single learning trial with two route MBONs and two extremities MBONs for the nest and feeder, autonomously shuttles to and fro between these two locations, driving both forward and backward (Fig. 7).

Fig. 3: Offline familiarity mapping for learning of indoor and outdoor routes.

This figure illustrates the familiarities differentiation and maximum value of route Mushroom Body Output Neurons (MBONs) during offline analysis of panoramic images and positional data from indoor (Mediterranean Flight Arena) and outdoor (Luminy Campus, Marseille, France) environments. The mapping was performed using an oscillation amplitude (A) of 45°. a, b Raw familiarities from the left and right MBONs. c, f Familiarity difference index (λ_diff) mapped in the route’s frame of reference, showing variations with both lateral (d) and angular (θ_e) errors. The defined operating area is highlighted in pink. d, g familiarity maximum index (${\lambda }_{\max }$) mapped similarly. e Overview of the indoor environment with the learned route highlighted in red. h Overview of the outdoor environment i, j Cross-sectional view of λ_diff and ${\lambda }_{\max }$, respectively, plotted against θ_e when d is zero. Indoor conditions are represented by a solid line, and outdoor conditions by a dotted line. k Pearson correlation coefficient illustrating the linear relationship between λ_diff and θ_e as a function of oscillation amplitude A. This plot also indicates the learning time required for a single oscillation cycle per image captured by the robot.

Fig. 4: Indoor route following experiments.

Effects of steering direction and lighting variation with artificial visual cues. Detailed environmental configurations and familiarity data are shown in Supplementary Fig. S4 and the accompanying video. a Autonomous route following experiments for two distinct learned routes (route 1: solid black line, route 2: dashed black line), each approximately 8 m long and represented independently by separate pairs of route MBONs. Learned trajectories are indicated in red. b Kidnapped robot tests performed independently for each learned route, assessing robustness to positional uncertainty. c, d Route following tests performed under bright (c) and dim (d) lighting conditions, while routes were learned under standard office lighting. e–g Overview images of the indoor experimental environment.

Fig. 5: Robust visual route following in dynamic environments.

Antcar robot navigating indoor and outdoor routes under challenging conditions after a single learning phase. a, b Indoor experiments along an 8 m route marked with artificial visual cues, featuring walking pedestrians (a) and large dynamical occlusions (b). c, d Outdoor experiments along a narrow (1.5 m) forest-like footpath of 21 m length, without (c) and with (d) static occlusions. e, g Third-person views of indoor and outdoor experimental environments. f, h Robot’s first-person views illustrating dynamic and static occlusions in the frontal field of view.

Fig. 6: Real-world experiments of outdoor route-following with shared memories in a semi-urban environment.

a First-day experiments: learning and autonomous route following with several cars along the 55 m road. b, f Overviews of the outdoor environment on the first and second days, respectively. c, d, g, h Familiarities difference (λ_diff) and maximum (${\lambda }_{\max }$) values plotted against distance traveled on the first and second days, respectively. e Second-day experiments conducted at the same hour demonstrate autonomous route following using day-one memories in an altered, car-free environment.

Fig. 7: Real-world experiments of outdoor homing and indoor shuttling.

a Outdoor homing experiments along a 50 m L-shaped route in a cloudy environment. Two route MBONs and one motivation MBON guided an autonomous return route in the opposite direction. b Indoor shuttling experiments with artificial visual cues, using two route MBONs and two place MBONs. Autonomous routes swing back (blue) and forth (black). In both figures, the inset shows the robot’s point of view. c Familiarity nest index (λ_N) plotted against distance traveled under a fixed stopping condition (p = 0.2). d Familiarity nest (λ_N) and feeder (λ_F) indices plotted against the traveled distance, with an inset zooming in on the values to highlight the backward and forward movements.

Self-supervised route-centric lateralized memories model

The continuous in-silico rotation of the panoramic image, along with the route-centric hypothesis and the robot’s assumption that each captured image corresponds to the route direction, drives a self-supervised route-learning mechanism. We first evaluated the self-supervised model for route learning (using only two MBONs) with a dataset of indoor and outdoor parallel routes (Fig. 3e, h). Results demonstrated that, with a controlled oscillation amplitude during learning, the model accurately estimated its heading error based on the differential familiarity λ_diff, handling angular deviations up to 135° indoors and 90° outdoors (Fig. 3c, f, i). Furthermore, the maximum familiarity index ${\lambda }_{\max }$, used as feedback for speed control, increased proportionally with heading error, enabling the robot to slow down when misaligned with the route. This behavior was consistent even when the robot was moved laterally off-route. Outdoors, these gradients were steeper (Fig. 3c, d, f and g), indicating a higher visual contrast with larger landmarks.

The model’s ability to identify heading error accurately across training oscillation amplitudes up to 135° (Fig. 3k, see also Supplementary Note 1 and Supplementary Fig. S1) suggests that this parameter may not require further tuning below this threshold. However, larger oscillation amplitudes increased computation time, especially on the Raspberry Pi platform (0.4s for  ± 45°, Fig. 3k). Notably, the familiarity difference index (Fig. 3i) closely matched the spatial derivative of the maximum familiarity index, corresponding to the catchment area and turn rate amplitude observed in ants (Fig. 3j, Supplementary Note 1, 2, Supplementary Figs. S1 and S2⁴⁴).

This analysis helped establish the operational limits of our MB model, maintaining stable behavior within a lateral error (d) of 2 meters and an angular error (θ_e) within the learning oscillation amplitude, set here at 45°. For asymptotic stability (i.e., the system’s ability to return to equilibrium), we assumed a proportional relationship between λ_diff and θ_e, supported by the Pearson correlation coefficient being close to 1 (Fig. 3k) and expressed as K_diff ⋅ λdiff = − θ_e, where K_diff is a tuned negative gain. Integrating this relationship into the robot’s motion equations, we applied a Lyapunov function for stability analysis. Results confirmed that the system converged to equilibrium points at de = 0 and ${\theta }_{{{\rm{e}}}}^{e}=0$, effectively correcting small deviations and enabling the robot to remain aligned with the learned route. The full derivation of these equations and Lyapunov stability proof are provided in the Methods (section 6) and Supplementary Note 3, 4 and Supplementary Fig. S3.

Route-following: robustness to visual changes

The proposed self-supervised approach for route learning was validated through a series of indoor and outdoor route-following tasks in fully autonomous mode, with only two MBONs. After a first outbound route with online learning, where images were captured continuously to update synaptic weights in real-time, the robot demonstrated robust route-following in various configurations (Figs. 4, 5 and 6). First, the Antcar robot successfully navigated two routes in a cluttered indoor environment of approximately 8 meters (median lateral error  ± median absolute deviation (MAD) = 0.21 ± 0.09 m, angular error  ± MAD = 3.4 ± 6.2°, Fig. 4a, e and Fig. 8a). Moreover, the robot showed resilience in a kidnapped robot scenario, realigning with the learned route after being displaced from 1 to 2 m away and oriented from 0 to 50 degree, (lateral error  ± MAD = 0.26  ± 0.14 m, angular error ± MAD = 6.45 ± 4.19°, Fig. 4b, and Fig. 8a). Only one predictable crash occurred when the robot exceeded theoretical angular limits (see Supplementary Fig. S5).

Fig. 8: Performance during route following overview.

a Detailed error analysis for each experiment. b Weighted bi-variate distribution for lateral (d) and angular errors (θ_e) across 13 experimental configurations.

Further tests assessed the robot’s adaptability to bright and dim light conditions (Fig. 4c, f, d, g). Despite a single learning trial under standard lighting (815 Lux), the robot accurately followed its route in bright (1340 Lux) and dim (81 Lux) lighting, with similar lateral and angular errors across tests (Fig. 8). This indicates that the route-centric MB-based control system is robust to significant changes in illumination.

In indoor dynamic conditions with pedestrians and camera occlusions (Figs. 5a, b), the robot maintained reliable route-following performance. When encountering pedestrians, the lateral error was  ± MAD = 0.27  ± 0.15 m and the angular error was  ± MAD = 4 ± 2.8° (Figs. 5a, e and  8a). Similarly, in the presence of dynamic occlusions, the robot achieved a lateral error of  ± MAD = 0.22 ± 0.13 m and an angular error of  ± MAD = 4.7 ± 3.3° (Figs. 5b, f and 8a). The presence of pedestrians and occlusions resulted in a reduction of maximum familiarity, leading to slower speeds and increased oscillatory motion—approximately 15% slower than in experiments without these disturbances (Fig. 5a, b, Supplementary Figs. S5 and Supplementary Movie 1). Across all seven autonomous routes with dynamic occlusions, occlusions occupied on average 11% of the image area, with peaks up to 56% (see Methods and Supplementary Fig. S4 for occlusion detection using YOLOv11⁵⁵).

Outdoor experiments demonstrated the model’s robustness in diverse settings—from a narrow 1.5 m pathway in a tree-like environment to a wider 5 m semi-urban route—while maintaining stable performance under static occlusions and altered conditions. On a semi-cloudy day, a 20 m route was learned and accurately recapitulated with low errors (lateral error  ± MAD = 0.3  ± 0.12 m; angular error  ± MAD = 4 ± 2.3°; Figs. 5c and 8a). Then, a static occlusion was introduced, consisting in a fixed black spot in the frontal field of view, covering 4 to 15% of the entire visual field (and 8 to 30% of the front view), the performance remained robust (lateral error  ± MAD = 0.38 ± 0.10 m; angular error ± MAD = 5.6  ± 3°; Figs. 5d and 8a).

Over a 55 m route under altered conditions, the robot first navigated a sunny day with low errors (lateral error  ± MAD = 0.39  ± 0.13 m; angular error  ± MAD = 5.8  ± 2.8°; Figs. 6a and 8a). The following day, at the same hour, with parked cars removed and a higher speed gain (cruising at 1.5 m/s versus 1 m/s), errors increased slightly (lateral error  ± MAD = 1.3 ± 0.5 m; angular error  ± MAD = 6.  ± 3.2°; Figs. 6e and 8a) yet remained within acceptable limits. During exploitation, the difference and maximum index values were marginally higher on the second day (Fig. 6g, h) than during the first day (Fig. 6c, d), likely due to the increased lateral error. These results underscore the system’s resilience and adaptability under challenging conditions (See environment’s picture taken at similar place from day one Fig.6b to day two Fig. 6f).

Homing: homeward route and stop

Building on the validated route-following strategy, further tests refined the robot’s behavior, focusing on ant-like homing. Homing, by definition, include graphicsis the ability to return to a specific location after displacement. To test this, we evaluated the robot’s ability to follow a 50 m outdoor route in reverse, stopping at a designated nest area (point N in Fig. 7a). During learning, a 180° shift in the visual oscillation pattern simulated the “turn back and look” behavior observed in ants and led to homeward route following.

The robot successfully followed the 50 m route in reverse under cloudy outdoor conditions (lateral error  ± MAD = 0.9  ± 0.5 m, angular error  ± MAD = 6.3 ± 4.2°, Figs, 6a, 8a). Although maximum familiarity was higher than in previous outdoor experiments (see Supplementary Note 6, Supplementary Fig. S5 and Supplementary Table S1), overall accuracy remained stable and emerging oscillatory movements was demonstrated (see Supplementary Movie 1).

To enable autonomous stopping at the nest, a place-specific MBON was used to learn ‘nest-views’ at the starting point of the route. Subsequent ‘recognition’ in this MBON, based on a familiarity threshold, acted as a motivational cue to halt route-following behavior and reduce the robot’s linear velocity. This mechanism was sufficient for the robot to successfully reach and stop at the nest area in 4 out of 5 trials, with a median stopping distance of 1.4 m (Fig. 7c, see also Supplementary Fig. S7b for detailed familiarities values over distance).

Shuttling: foodward and homeward routes

Reverse route-following is also commonly observed in ants and was successfully replicated on board Antcar. Homing ants can pull food items backward when it is too large to carry forward, maintaining body alignment with the outbound route learned forward, and using outbound memories with an opposite valance⁵³. Shuttling tests show the robot’s ability to switch movement direction and drive backward while maintaining alignment with the outbound route (Fig. 6b).

This foraging behavior was made possible by incorporating two additional place MBONs, which learned a series of panoramic views defining each endpoint of the route (feeder and nest). During shuttling, the model triggered a switch in motor gain polarity upon recognizing these panoramic views corresponding to the feeder or nest areas. In a cluttered indoor environment along a 6-meter learned route, the robot autonomously shuttled to and fro between the feeder and the nest, covering a total distance of 160 meters without interruption. Using a similar familiarity threshold on the two route-extremity MBONs, the robot detected the endpoints 22 times, achieving a median stopping distance of 0.31 m (Fig. 7d) (See Supplementary Fig. S7a for detailed familiarities values over distance).

This continuous shuttling revealed distinct differences in error profiles between forward and backward movement (Fig. 7b). During forward motion, the robot maintained stable control with minimal deviations (lateral error ± MAD = 0.1 ± 0.03 m, angular error ± MAD = 1.26 ± 0.83°, Fig. 7b). However, during backward motion, the traction-driven setup amplified steering effects, resulting in slightly larger deviations from both accuracy and precision, though overall performance remained acceptable (lateral error ± MAD = 0.19  ± 0.08 m, angular error ± MAD = 2.7 ± 2.1°, Figs. 7b and 8a). The increased ‘motor’ variability led to a lower visual recognition signal and thus usefully affected speed, which decreased by 14% compared to forward motion (see Supplementary Note 6, Supplementary Fig. S5 and Supplementary Table S1). Nonetheless, the robot consistently realigned with the correct path after such minor deviations. These results highlight the model’s versatility across different driving dynamics, capability to implement inverted steering, and adaptability to variations in motor kinematics and propulsion.

Performance summary

Across all experiments, including both indoor and outdoor route-following, homing and shuttling tasks, the model demonstrated robust and stable navigation performance, completing 113 autonomous trajectories with a total of 1.6 km traveled. The theoretical limits of the system were validated, with convergence toward equilibrium points consistently achieved under various environmental conditions, even in the presence of noise (lateral error ± MAD = 0.24 ± 0.13 m, angular error ± MAD = 4 ± 2.7°, Fig. 8b). Lateral errors were within acceptable margins for both indoor and outdoor contexts, aligning within the standard widths of roads in France (5 m) and typical indoor corridor (1.5 m).

In addition, statistical analysis showed no significant differences in the lateral or angular errors across the eleven test scenarios (Kruskal-Wallis test, H = 2.10 for lateral error, p = 0.99; H = 8 for angular error, p = 0.76), underscoring the system’s reliability across diverse conditions (see Statistical Information). These results highlight the robustness and adaptability of the route-centric MB model in dynamic environments, confirming its potential applicability in a variety of navigation contexts.

Steering memory capacity

In classical single-MBON familiarity models, memory capacity (m) is defined by an error probability (P_error), the chance of confusing an unfamiliar visual pattern with a learned one³⁹. With our chosen parameters (N = 15, 000, κ = 0.01), theoretical estimates predict a memory capacity of m = 346 KC activity patterns stored for a 1% error probability equivalent to roughly 38m of route in a cluttered environment³⁹. However, such binary classification metrics fail to capture the complexity of our route-centric lateralized MBON steering mechanism.

To better quantify our model’s steering-specific memory performance, we propose an empirical metric (Pl_error), defined as the proportion of visual patterns incorrectly activating the opposite MBON (e.g., images associated with a leftward orientation producing lower familiarity on the left MBON than on the right MBON, and vice versa). Therefore, we define a steering-specific memory capacity (see Fig. 9, Methods section and Supplementary Fig. S8).

Fig. 9: Memory capacity analysis.

a Error proportion Pl_error (defined as cases where the current visual pattern activates the incorrect lateralized MBON) as a function of route length and visual patterns learned, from outdoor experiments conducted on day one. b Route length that our MB architecture can store, maintaining an error proportion below 1%, plotted against the number of neurons and k-WTA parameter. The dataset is from a 250 m outdoor route (real), and extrapolation is made on two couples of parameter (because it did not reach the 1% before 250 m, see Supplementary Fig. S8). Under our current network parameters (N = 15, 000, κ = 0.01), our route memory capacity with a 1% error probability corresponds to approximately 65 m.

Under our metric, during extended route-following experiments in a semi-urban setting (55 m, 430 unique KC activity patterns, Fig. 6), our network achieved 0.7% of error, below the critical threshold of 1% confusion probability (Fig. 9a). Further analysis of memory scalability using a larger dataset (up to 250 m; Supplementary Fig. S8) indicated that under our current network parameters (N = 15, 000, κ = 0.01), a 1% error probability yields an estimated 500 patterns, corresponding to about 65 m of stored route in this conditions. A basic linear extrapolation indicated that with a larger network (N = 100, 000, κ = 0.005), routes as long as 600 m could be reliably encoded at the error threshold of 1% (Fig. 9b).

Discussion

We introduced a fully embodied, biologically grounded route-following system that unifies route-centric lateralized visual memory, panoramic input encoding, and neuromorphic control within a real-world robotic platform. Unlike prior ant-inspired models, which remained limited to short-range tasks or simulations, our model delivers continuous, one-shot learning and stable bi-directional navigation of visual routes — using only a single 800-pixel sensor, four MBONs, and light computational resources. These results mark a significant step forward in insect-inspired embodied cognition for real-world robotic autonomy.

The angular error between the agent’s head direction and the dynamic local route orientation (i.e., route-centric, defined in the Methods as the Frenet frame⁵⁶) emerged as both a challenge during exploitation—where the system tends to minimize this error—and a cue during learning, where the categorization process depends on its polarity. Our model demonstrated homing behavior using either a 180° shift in visual oscillation or by inverting motor gains, thus enabling forward and backward movements with only a single foodward learning route. In addition, visual place memories stored in supplementary MBONs, paired with a motivational control system, allowed the robot to recognize route endpoints and modulate motor gains, halting movement or reversing foraging motivation. With a single learning pass in one direction, the agent could follow the route forward, backward, and in reverse, controlled by oscillation parameters and motivational cues. Only motivational rules required adjustment to switch between route following, homing, and shuttling, underscoring the model’s flexibility.

Compared to earlier ant-inspired familiarity-based models, generally limited to short, indoor routes or stop-and-scan strategies, our system demonstrates practical advantages in scalability, efficiency, and real-world adaptability^{19,20,21,22,23,24}. Our memory footprint and command computation time are significantly lower than those reported in panoramic visual route-following methods¹³, which require 3 megabytes per kilometer and 400 ms per control update. In contrast, our model operates at 0.3 megabytes per kilometer and produces commands within 75 ms on a lightweight embedded board—enabling real-time operation in constrained platforms. In addition, it achieves competitive performance compared to snapshot-based visual route-following methods that use odometry¹⁵.

This route-centric lateralized MB model distinguishes itself through reduced time and space complexity for route direction processing compared to perfect memory, snapshot, and insect-based visual compass approaches. Whereas time and space complexity increase with the number of images in perfect memory or snapshot models, our MB model maintains constant space complexity, relying only on the synaptic matrix size KCtoMBON. In addition, in contrast to visual compass approaches, where computational complexity scales with in-silico scan range and resolution during exploitation (${{\mathcal{O}}}(n)$), our MB model maintains a constant factor (${{\mathcal{O}}}(1)$) since in-silico scanning is only required during learning. For instance, while an insect-based visual compass scanning a  ± 45° range at 1° resolution requires 90 comparisons per image, our model requires only two comparisons, eliminating the need for angular scanning in exploitation. Notably, our model produced commands five times faster than the insect-based visual compass approach on the same robot platform^21,22.

Our contribution also aligns well with current biological observations, particularly highlighting the effectiveness of latent learning, where continuous learning bypass the need to control “when to learn”^32,45. The opposed event-triggered and snapshot-based learning models producing place learning^15,27 where used here only to recognize the place of interests, such as the nest and the feeder, to switch motivation, but were not engaged for route guidance. Also, our MB model prioritized body orientation within the route frame rather than splitting the visual field^23,49, aligning with biological observations in ants with unilateral visual impairment, showing that these insects store and recognize fundamentally binocular views⁵⁰. Interestingly, the linear relationship observed between familiarity measures and route-centric angular error during exploitation closely mirrors experimental findings in ants with nest-centric models⁴⁴. This relationship enabled us to demonstrate the asymptotic stability of the system within a defined domain, ensuring the consistent and predictable behavior essential for a robotic navigation model⁵⁷.

Furthermore, oscillatory learning behavior mirrors ant behavior, where initial routes involve slow, rotational movements, transitioning to direct paths on subsequent journeys⁴⁰. These oscillations typically fall within  ± 100°, with peaks around  ± 45° in unfamiliar terrain^41,43. The robot’s ability to slow down and produce emerging mechanical oscillation upon entering unfamiliar areas (see Fig. 5a, b and Supplementary Movie 1) are consistent with such naturalistic behaviors. Finally, Antcar’s homing capability was maintained even when navigating backward, closely mirroring ant behavior while dragging food^51,52,53,58. Overall, our attempt to integrate multiple MBONs, oscillations, “turn back and look” behavior, and motivational control mechanisms echoes insect mechanisms^2,38, and the resulting expression when implemented in the robot echoes insect behaviors.

This study addresses several core needs identified in research on embodied neuromorphic intelligence^6,8, such as robustness to visual changes, adaptability to real-world environments, and support for extended route learning. Our algorithm’s efficiency allows computational power for additional tasks, making it valuable in GPS-compromised or SLAM-disrupted scenarios (Simultaneous Localization And Mapping). The robot’s low-resolution, wide-angle vision proves resilient against moving objects that often disrupt SLAM. Our model is particularly effective in dynamic environments or scenarios where traditional odometry—whether visual, inertial, step-counting, or wheel-rotation—is unreliable. It can serve as a low-resource backup system (running on a 4-core CPU) alongside other processes, or be integrated with additional sensors to enhance state estimation robustness^59,60.

Interestingly, the semi-random encoding process, specifically the PNtoKC synaptic projections, introduces a “fail-secure” memory-sharing mechanism. If synaptic weights for encoding differ, memory sharing becomes inaccessible, an advantageous feature for swarm robotics or cross-robot memory sharing. Future research could enhance this approach but also transitioning this model to a spiking neural network on neuromorphic hardware could further enhance computational efficiency and biological fidelity¹¹. In addition, incorporating obstacle avoidance^61,62, would improve performance in dynamic environments.

Our upward-facing fisheye camera provides a 360° view at minimal cost, and in silico rotation keeps the learning route straight. However, if the ground is not planar, in silico rotation may not accurately represent physical rotation, thus learn an image that the robot will never encounter. Moreover, bypassing image unwrapping and calibration speeds computation but reduces the influence of distal cues, especially in large open fields where the horizon is severely deformed and can appear uniform. Interestingly, salt lake ants in such environments have developed enhanced horizontal resolution and accuracy, and build artificial visual cues near the nest entrance⁶³.

A reduced visual field, as seen in more general cases, may preclude in silico scanning, necessitating an estimation of the angular error between the road frame and the agent. Collett et al.⁶⁴ proposed that ants use route segment odometry for navigation, suggesting a potential alternative. In insects, dopaminergic neurons (DAN) modulate MBON synapses from Kenyon cell inputs in response to motor stimuli, effectively acting as a “supervisor” for sensory cue categorization⁶⁵. There are plenty of feedback from motor areas towards the MB (both DANs and MBON)⁶⁶ that could enable to orchestrate visual memory formation, for instance, based on whether the current body orientation is left or right from a goal compass direction⁴⁵. Similarly, our model’s left-right classification functionally mimics the effect of dopaminergic feedbacks (onto MB), which activity would be based on whether the current body orientation is left or right from the local route heading.

Our approach does not cover beeline homing post-foraging, or search behaviors near points of interest, although these could be added by adding path integration mechanisms⁶⁷ or using the current visual mechanism but adding “learning walk” behaviors around places of interest⁴⁵. Although anti-Hebbian learning effectively improves familiarity discriminability by sparsifying KCtoMBON synapses, there is a theoretical limit to this benefit. Excessive sparsification would lead to memory saturation (dramatic forgetting), where the MBON output no longer discriminates between familiar and unfamiliar inputs. Therefore, it suggests an opportunity for further exploration by adjusting KCs numbers or connectivity by testing different MB learning mechanisms with feedback or prediction error⁶⁸.

Finally, our system’s memory capacity metric (500 patterns) is higher than the theoretical estimation from Ardin et al. (346 patterns)³⁹. This discrepancy may arises because the theoretical model assumes random, independent KC activations, whereas in continuous route learning, KC activations are correlated and structured. In addition, our empirical error calculation depends on our visual preprocessing, hardware and the semi-urban environment. Also, the memory capacity error computed here can be linked to the sparsity of the KCtoMBON synaptic weight, avoiding a possible dramatic forgetting when all the KCs are used (i.e., the KCtoMBON vector is 0). To extend route length while reducing error, we could increase the number of KCs (see Fig. 9); however, this may slow processing due to larger matrices—though the impact may be minimal on a GPU. Alternatively, incorporating additional pairs of MBONs for different route segments could enable longer and multiple route memories without affecting processing time and, therefore, considering an extrapolated memory footprint of only 0.3 megabytes per kilometer. Also, expanding the number of MBONs, akin to the 100 in honey bees⁶⁹, along with a mechanism (such as a context-based selection) to dynamically activate the appropriate MBON pair would enable more complex motivational states, multi-route memory storage, and broader navigational abilities⁷⁰.

Inspired by the neuroethology of ants, our route-centric, lateralized MB model provides an effective bridge between theoretical insights and practical application in insect-inspired robotic navigation. This egocentric architecture demonstrates how biologically plausible neural circuits can support robust, scalable, and adaptive behavior in real-world robots—using accessible hardware, panoramic input, and minimal computing resources. These results reinforce the promise of neuromorphic approaches for embodied autonomy and broaden opportunities for both robotic systems and experimental studies in comparative cognition.

Methods

This section describes the methodology used in the present study, focusing on the Encoding, Learning, and Exploitation processes of the proposed MB model (Figs. 2b–d and 10). We also provide details on the hardware setup, control architecture, and stability analysis.

Fig. 10: Simplified mushroom body neural network.

The network includes four MBONs fitted during the exploration phase. For visualization, the EP, AP, and KCtoMBON connections are reshaped into matrix-like formats. KCtoMBON synapses are initially fully connected prior to learning.

Image encoding

Inspired by the visual system of ants⁷¹, the model encoded real-world images into sparse, binary neural representations to efficiently handle visual input.

The encoding function (Figs. 2b, 10 and Supplementary Note 5) processed panoramic images from a camera with a 220° vertical and 360° horizontal field of view. This wide field of view enabled the camera to capture from slightly below the horizon to nearly directly below itself. To enhance natural contrast, the green channel of each image was selected⁷¹, followed by Gaussian smoothing (σ = 3 pixels) to reduce noise. The chosen σ corresponds to an acceptance angle of about 4. 4° (σ + FOV/r), slightly larger than the estimated visual acceptance angle of the Melophorus species⁷². The image was then downsampled to a low-resolution 32 × 32 pixel thumbnail (0.145 pixel per degree), approximating the visual resolution of ants at 7.1° between adjacent photoreceptors⁶³. Next, a Sobel filter extracted edges, mimicking lateral inhibition as seen in insect optical lobes⁷³. These processed images were flattened into n = 800 Visual Projection Neurons (${{\bf{PN}}}\,\in \,{{\mathbb{R}}}^{n}$), comparable to the number of ommatidia in Cataglyphis ants. These processing steps, with the aim of mimicking the output of the optic lobes, are described in detail in Supplementary Note 5 and in Fig. 10.

The PNs were further expanded into Kenyon Cells (KCs) using a fixed, sparse pseudo-random binary synaptic matrix (PNtoKC, equation (1)). Each KC received input from four PNs, enhancing the visual encoding’s discriminative power within the MB, forming an Excitatory Post Synaptic Projection (EP) vector (see equation (2) and Fig. 10).

$${{\bf{PNtoKC}}}=\left[\begin{array}{ccccc}0&1&0&\ldots \,&1\\ 1&0&1&\ldots \,&0\\ \vdots &\vdots &\vdots &\ddots &\vdots \\ 0&1&0&\ldots \,&1\end{array}\right]\ \in \ {{\mathbb{R}}}^{N\times n}$$

(1)

So, the product

$${{\bf{EP}}}\,=\, {{\bf{PNtoKC}}} \cdot {{\bf{PN}}}$$

(2)

will be an N-dimensional vector, i.e., ${{\bf{EP}}}\in {{\mathbb{R}}}^{N}$. The EP vector size was set to N = 15, 000 for the route MBONs (MBON_R and MBON_L), while for place-specific MBONs (MBON_N and MBON_F), which required fewer images, N was set to 5000.

A κ-Winner-Take-All (WTA) mechanism was applied to capture the highest contrasts, creating a high-dimensional, sparsified binary vector (see Fig. 10). This vector, referred to as the Action Potential (AP, equation (3)), consequently activated only 1% of KCs (κ = 0.01), giving N_u = N*κ active neurons, such that:

$${{\bf{AP}}}_{i}=\left\{\begin{array}{ll}{{\bf{EP}}}_{i},& {{\bf{EP}}}_{i} \, \in \,\, \{k\,\,{{\mbox{largest element of}}\,{{\bf{EP}}}}\} \\ 0 & \,{\mbox{otherwise}}\end{array}\right.$$

(3)

Where i is the neurons number, and AP ∈ {0, 1}^N. This final binary representation served as the encoded visual input to be learned. All parameters were predefined by literature and experimental tests, but not further optimized.

Routes and places learning

The learning process is governed by synaptic depression through anti-Hebbian learning. For each MBONs, their synaptic weight vector (KCtoMBON) dynamically adjusted their binary weight based on input from the AP layer.

$${{{\bf{KCtoMBON}}}}_{i}=\left\{\begin{array}{ll}0,\hfill & \,{\mbox{if}}\,{{{\bf{AP}}}}_{i}=1 \\ {{{\bf{KCtoMBON}}}}_{i},& \,{{\mbox{otherwise}}}\,\end{array}\right.$$

(4)

Where KCtoMBON ∈ {0, 1}^N. At the beginning, for each MBONs, their KCtoMBON vector are fully connected (i.e., all AP neuron are connected to the MBONs). During learning, each time the KCtoMBON have the same weight as the current AP (1), the respective synaptic connection is depressed (weight from 1 to 0) in the designed KCtoMBON (equation (4)). For the route, the KCtoMBON vector is designed (therefore depressed) according to the route-centric left or right looking direction (equation (4)). The model assumed the robot perfectly aligned to the route being learned. The body rotation was estimated as ${\hat{\theta }}_{e}={\theta }_{{{\rm{e}}}}+{\theta }_{c}$, where therefore θ_e = 0 during learning, and θ_c is the image rotation angle. The encoded binary image (AP) was learn in one MBONs based on the polarity of ${\hat{\theta }}_{e}$, such that:

$$\left\{\begin{array}{ll}{{\rm{Learn}}}({{\bf{AP}}},{{{\bf{KCtoMBON}}}}_{R}),& \,{\mbox{if}}\,{\hat{\theta }}_{e}\le 0\\ {{\rm{Learn}}}({{\bf{AP}}},{{{\bf{KCtoMBON}}}}_{L}),& \,{\mbox{if}}\,{\hat{\theta }}_{e}\ge 0\end{array}\right.$$

(5)

Where Learn() is the function in equation (4). The simulated oscillatory movements during learning were obtained by rotating each captured image in steps, creating a sweep of rotations (θ_c) described by the following function:

$${\theta }_{c}(n)=A\cdot \sin \left(n\cdot {{\Delta }}\theta+\phi \right)\quad \,{{\mbox{for}}}\,n=0,1,2,\ldots,\frac{2A}{{{\Delta }}\theta }$$

(6)

where A represents the oscillation amplitude, Δθ the step size, and ϕ the phase shift. The step size was fixed at Δθ = 5°, with A = 45° for route MBONs and A = 30° for place MBONs. The phase shift was ϕ = 180° only for the homing task (Fig. 7). The place MBONs learning was triggered by an external stimulus, specified by the robot operator.

Synaptic weights (KCtoMBON) were stored in CSR format (Compressed Sparsed Row), achieving significant data compression to 148 kilobits independently of the route length (from 6 m to 55 m), reducing memory requirements by 99.97% from cumulative image storage. This self-supervised model continuously learned visual input at high throughput without memory overload, as only novel views (i.e., newly recruited KCs) modulated synapses. Several panoramic views were learned to define the start and finish areas in their respective MBONs, serving as motivational cues.

Exploitation process and control architecture

During exploitation, the model calculated familiarity scores (λ) by comparing the current input (AP) with each MBON’s synaptic weight matrix (KCtoMBON):

$$\lambda=\frac{1}{{N}_{u}}{\sum }_{i=1}^{N}{{{\bf{AP}}}}_{i}\cdot {{{\bf{KCtoMBON}}}}_{i}$$

(7)

This familiarity score, ranging from 0 (unfamiliar) to 1 (familiar), was used to assess route alignment. The lateralized difference in familiarities between the left and right MBONs (λ_diff, equation (8) and Fig. 10), which indicates whether the current view is more oriented to the left or right of the route, guided the robot’s steering angle (φ). Meanwhile, the maximum familiarity (${\lambda }_{\max }$), representing how familiar the current view is, modulated its speed (v).

$${\lambda }_{{{\rm{diff}}}}={\lambda }_{L}-{\lambda }_{R}\quad and\quad {\lambda }_{\max }=\max ({\lambda }_{L},{\lambda }_{R})$$

(8)

Thus, the control input U was defined as:

$$\begin{array}{r}{{\bf{U}}}=\left[\begin{array}{c}v\\ \varphi \end{array}\right]=\left[\begin{array}{c}M\cdot {K}_{v}\cdot {\mathrm{sat}}\,(1-{\lambda }_{\max })\\ M\cdot {K}_{\varphi }\cdot {\lambda }_{{{\rm{diff}}}}\end{array}\right]\end{array}$$

(9)

Here, K_v and K_φ are proportional gains that control linear and angular velocities, while the saturation function (sat()) establishes a minimum throttle level, ensuring minimum speed even at low familiarity levels to allow the robot to turn (due to his mechanical constraint). The motivational state (M) regulated transitions between behaviors, based on familiarity thresholds within place-specific MBONs. During route following, M was consistently set to 1. In homing experiments, where the objective was to stop at the nest, M initially started at 1 and switched to 0 once the familiarity of the nest-specific MBON (λ_N) fell below a fixed threshold (p = 0.2), signaling arrival at the nest. For shuttling tasks, M alternated between values of 1 and  − 1 as the robot reached each route extremity, driven by a familiarity threshold of the two place-specific MBONs (λ_N and λ_F).

Theoretical analysis of the robot stability

Stability in mobile agents, biological or robotic, is essential for reliable, predictable behavior. In non-linear control theory, an agent’s motion is generally modeled as $\dot{x}=f({{\bf{x}}},{{\bf{U}}})$, where x is the state vector (e.g., position or velocity), U is the control input, and f describes system dynamics. A desired equilibrium point x_e is achieved by defining a control input U_e such that f(x_e, U_e) = 0, allowing the system to maintain stability and return to equilibrium after disturbances. Stability is typically assessed using a Lyapunov function⁵⁷, which ensures the system converges to a stable state over time.

In contrast to conventional control approaches, we applied a neuroethologically inspired control input derived from ant behavior and assessed its stability via an a posteriori Lyapunov analysis. The robot’s motion was modeled in a Frenet frame, a moving reference frame coincident with the nearest point on the route, to minimize lateral and angular errors, defined by x = [d, θ_e]. Empirical data for stability assessment was collected in indoor and outdoor environments (paths of approximately 6 meters with 855 learned images each), providing distinct visual contexts (Figs. 2, 3). The robot’s equations of motion from a global to the Frenet frame are ref. ⁷⁴:

$$\left[\begin{array}{c}\dot{s}\\ \dot{d}\\ {\dot{\theta }}_{e}\\ \end{array}\right]=\left[\begin{array}{c}v\left(\cos {\theta }_{{{\rm{e}}}}-\tan \varphi \sin {\theta }_{{{\rm{e}}}}\right)\\ v\left(\sin {\theta }_{{{\rm{e}}}}+\tan \varphi \cos {\theta }_{{{\rm{e}}}}\right)\\ v\frac{\tan \varphi }{L}\\ \end{array}\right],$$

(10)

where s is the arc length along the route, d is the lateral error, and θ_e is the angular error.

This kinematic model, along with by empirical observations (Fig. 3), enabled us to establish an asymptotically stable domain for lateral and angular errors (d and θ_e), ensuring reliable route-following performance even with minor disturbances. The full theoretical stability proof and derivations of the model in the Frenet frame are provided in the Supplementary Note 3 and 4.

Antcar robot and ground truth system

The experiments were conducted using Antcar (Figs. 1 and 2a), a PiRacer AI-branded car-like robot. Antcar features four wheels, with two rear drive wheels powered by 37-520 DC motors (12V, 1:10 reduction rate) and a front steering mechanism controlled by an MG996R servomotor (9kg/cm torque, 4.8V). The robot’s chassis measures 13 × 24 × 19.6 cm and is powered by three rechargeable 18650 batteries (2600 mAh, 12.6 V output). Antcar’s primary sensor is a 220° Entaniya™ fisheye camera, mounted upward to capture panoramic images at 160 × 160px × 3 resolution, processed using OpenCV on a Raspberry Pi 4 Model B (Quad-core Cortex-A72, 1.8 GHz, 4GB RAM), running Ubuntu 20.04. Note that there was no closed-loop control on the wheel rotation speed. Raspberry Pi manages real-time performance and controls the motors through a custom ROS architecture.

Real-time communication is facilitated by ROS Noetic, either via Wi-Fi (indoor) or a 4G dongle (outdoor). The robot can be controlled manually using a keyboard, joystick or with a GPS waypoint, but in autonomous visual-only mode, it follows its own internal control law. Control inputs—steering angle (φ) and throttle (v) are processed using the PyGame library. Real-time data visualization and post-experiment monitoring are achieved via Foxglove.

Antcar has a maximum velocity of 1.5 m/s and a maximum steering angle of 1 rad, with a wheelbase of 0.15 m. The robot’s configuration states q = (x, y, θ) were tracked using different systems. Indoor experiments utilized eighteen Vicon™ motion capture cameras, with infrared markers on Antcar providing precise tracking at 50 Hz with 1 mm accuracy. Outdoor experiments employed a GPS-RTK system with a SparkFun GPS-RTK Surveyor, providing 14 mm accuracy at 2 Hz (GPS-RTK stands for Global Positioning System - Real-Time Kinematic). Ground speed and angular speed were calculated through position differentiation. The base station used for GPS corrections was a Centipede LLENX station located at 24 km (Marseille Provence Airport) from the experiment site in Marseille. Note that the ground truth acquisition system was run on the Raspberry Pi along with the MB model.

Lateral error was calculated by finding the nearest point on the learning route using the Euclidean distance, with the shortest distance representing the absolute lateral error. Angular error was defined as the absolute difference in heading between the nearest learning route point and the current position. The euclidean distance between the agent and the nest or feeder areas was calculated to estimate the distance when the robot switched behavior (i.e familiarity dropped below the threshold).

Memory capacity computation

To compute our memory capacity and Pl_error, we used a 250 m dataset (Supplementary Fig. S8). The metric was computed over the operating area defined by the learning oscillation. The computation was performed incrementally: for each new learned image (rotated from  − 45° to 45° in 5° steps), all previously encountered images were tested (rotated from  − 45° to 45° in 1° steps), we didn’t take into account the value between − 1° and 1°. For each tested image i, the familiarity difference λ_diff [i] was calculated. An error indicator e_i was then defined by comparing the sign of λ_diff [i] with that of the heading error θ_e[i]:

$${e}_{i}=\left\{\begin{array}{ll}1\quad &\,{\mbox{if}}\,{\mathrm{sign}}\,({\lambda }_{{{\rm{diff}}}} \, [i]) \, \ne \, {\mathrm{sign}}\,(\,{\theta }_{{{\rm{e}}}}[i])\\ 0\quad &\,{\mbox{otherwise}}\,\end{array}\right.$$

(11)

Finally, the cumulative mean error up to test image i is given by:

$${{{\rm{Pl}}}}_{{{\rm{error}}}}(i)=\frac{1}{i+1}\mathop{\sum }_{j=0}^{i}{e}_{j}$$

(12)

Statistical informations

The errors used for statistics were recorded at each command decision timing. Due to non-normality in error values (with outliers retained), Box-Cox transformations were applied to stabilize variance across experiments, reducing the impact of outliers caused by indoor obstacles that hid the robot from the motion capture system or by GPS-RTK inaccuracies outdoors. The groups was compared using the Kruskal-Wallis test⁷⁵, and median values are reported with median absolute deviation (MAD), as median  ± MAD. The package Python SciPy⁷⁶ was used for the statistics. The overall medians and bivariate distribution plots were weighted by the number of measurements per experiment for the Fig. 8.